B2 - Analytische Geometrie

Ein Bildschirmschoner zeigt einen sich drehenden Würfel, der sich in einem (auf dem Monitor nicht sichtbaren) dreidimensionalen Koordinatensystem bewegt. Für die Animation des Würfels und die Darstellung der Beleuchtungsverhältnisse sind verschiedene Berechnungen nötig.

Einige dieser Berechnungen sollen im Folgenden an einem einfachen Beispiel durchgeführt werden. Zum Anfangszeitpunkt besitzen die Punkte $A$ , $B$ , und $D$ der Grundfläche die folgenden Koordinaten:

$A(-4\mid1\mid1)$ , $B(1\mid1\mid1)$ und $D(-4\mid6\mid1)$

1.1

Zeichne die Punkte $A,$ $B$ und $D$ in ein selbst erstelltes Koordinatensystem ein, wie es in Abbildung 1 dargestellt ist.

Gib die Koordinaten der übrigen Eckpunkte des Würfels an und zeichne das Bild des Würfels.

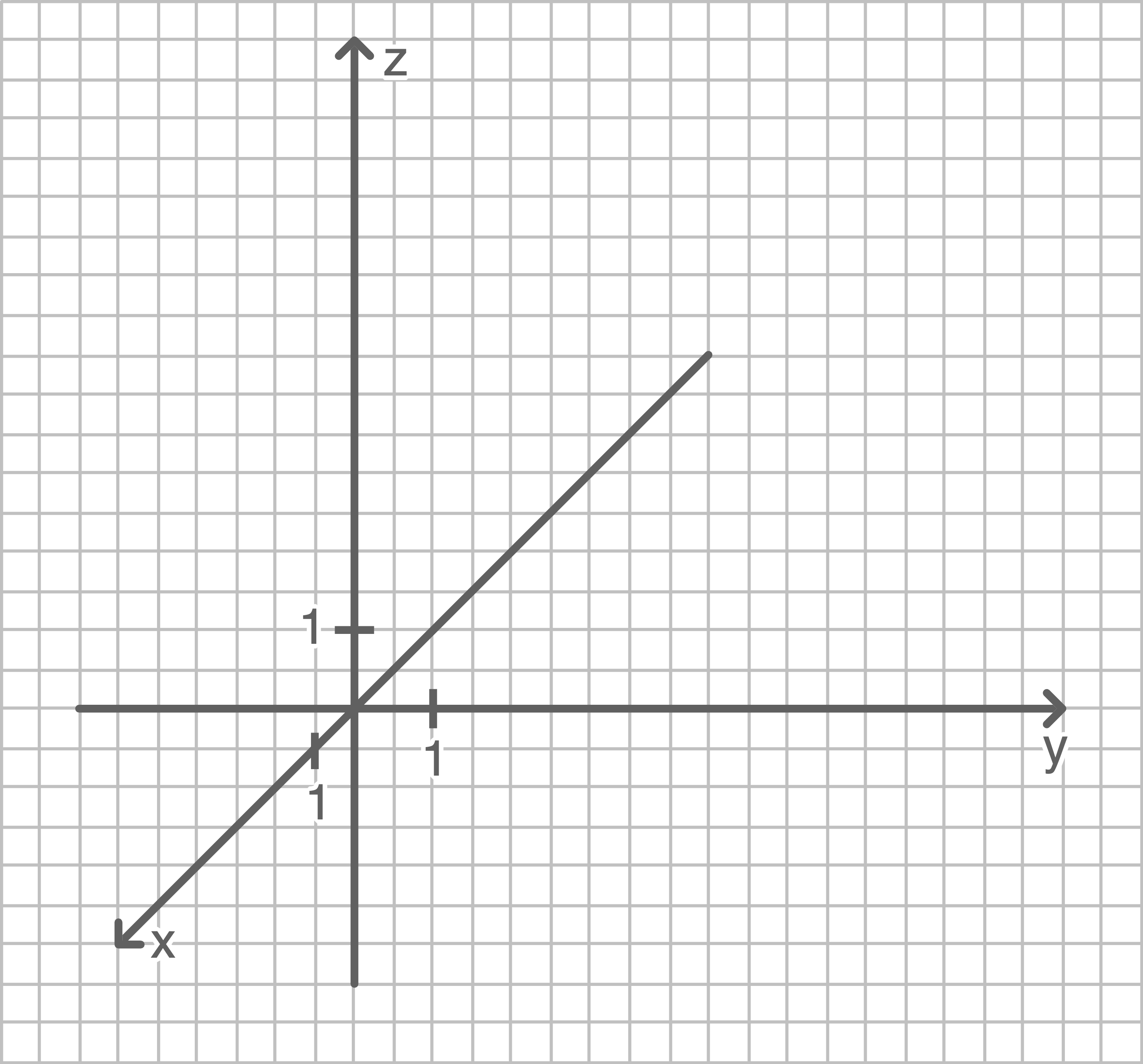
Abbildung 1

(4 BE)

1.2

Im Punkt $L(-40\mid23\mid26)$ befindet sich eine punktförmige Lichtquelle, durch die ein Schatten des Würfels auf der $xy$ -Ebene entsteht. Dabei wird unter anderem der Eckpunkt $(-4\mid1\mid6)$ in die $xy$ -Ebene projiziert.

Berechne die Koordinaten des Bildpunktes.

(5 BE)

1.3

Ein Beobachter im Punkt $P(20\mid-7\mid16)$ sieht die Reflexion der punktförmigen Lichtquelle $L$ aus Aufgabe 1.2 im Punkt $R(0\mid3\mid6)$ auf der Würfeloberseite.

Um die Position des Punktes $R$ auf der Oberseite des Würfels zu bestimmen, benötigt man eine Ebene $E_1$ durch $P$ und $L$ , die senkrecht zur Oberseite des Würfels steht. Der Punkt $R$ erfüllt dann die beiden folgenden Bedingungen:

$\text{I.}$

$R$ liegt auf der Schnittgeraden $g$ der Ebene $E_1$ mit der Würfeloberseite.

$\text{II.}$

Der Einfallswinkel zwischen dem einfallenden Lichtbündel und dem Normalenvektor der Würfeloberseite im Punkt $R$ ist gleich dem Ausfallswinkel zwischen dem reflektierten Lichtbündel und diesem Normalenvektor.

1.3.1

Zeige, dass $R$ Bedingung $\text{I}$ erfüllt.

(7 BE)

1.3.2

Zeige, dass $R$ Bedingung $\text{II}$ erfüllt.

(6 BE)

Da bei der Berechnung der folgenden Animation des Würfels die entstehenden Koordinaten schwer einzuzeichnen sind, wird das 3-D-Koordinatensystem wie im Folgenden beschrieben in ein "deckungsgleiches" 2-D-Koordinatensystem abgebildet und die dann berechneten zweidimensionalen Koordinaten eingezeichnet.

Die Abbildungsmatrix $T$ überführt die Koordinaten aus dem dreidimensionalen in den zweidimensionalen Raum.

Über das 3-D-Koordinatensystem wird ein 2-D-Koordinatensystem so gelegt, dass die Koordinatenursprünge übereinstimmen und die $x$ -Achse des 2-D-Koordinatensystems sich mit der $y$ -Achse des 3-D-Koordinatensystems deckt. Die $y$ -Achse des 2-D-Koordinatensystems deckt sich mit der $z$ -Achse des 3-D-Koordinatensystems. Aus den dreidimensionalen Einheitsvektoren ergeben sich neue zweidimensionale Vektoren.

Beispiel: Der Einheitsvektor $\begin{pmatrix}0\\1\\0\end{pmatrix}$ geht in den Vektor $\begin{pmatrix}1\\0\end{pmatrix}$ über.

Punkte können jetzt mit den Koordinaten des 2-D-Koordinatensystems angegeben werden.

Beispiel: Aus dem Punkt $D(-4\mid6\mid1)$ wird der Punkt $\(D$ .

2.1

Bestimme die Abbildungsmatrix $T.$

(4 BE)

2.2

Gegeben sei die Matrix $F=\pmatrix{\cos\alpha& -\sin\alpha& 0\\\sin\alpha&\cos\alpha& 0 \\0& 0& 1 } .$

Erläutere die geometrische Wirkung der Abbildung, die durch die Matrix $M=T\cdot F$ beschrieben wird.

(4 BE)

1.1

Punkte einzeichnen

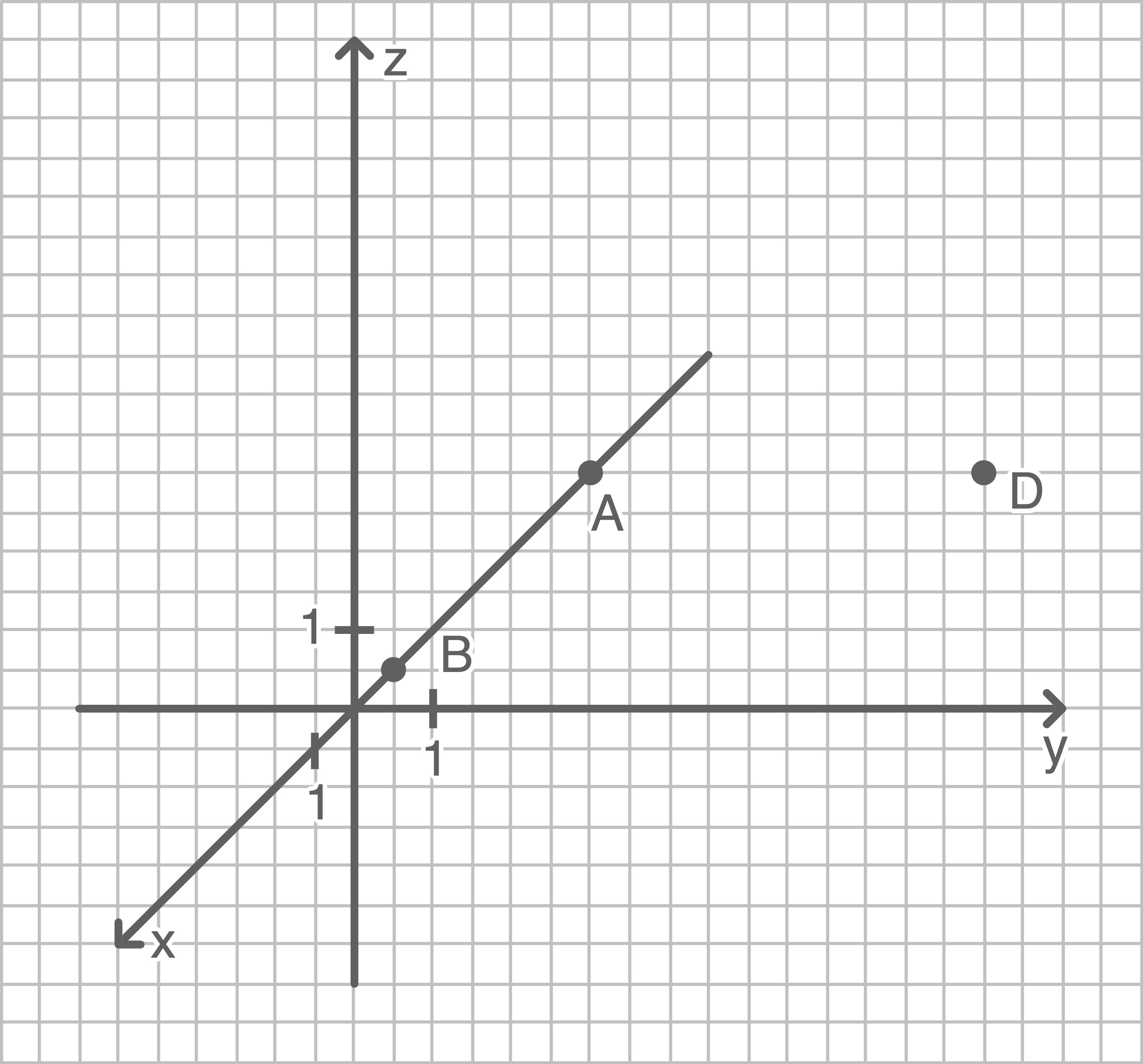Koordinaten angeben

$\overline{AD}$ stellt eine der Seiten der Würfelgrundfläche dar. Die Punkte $A$ und $D$ stimmen in den $x$ - und $z$ -Koordinaten überein und weichen in der $y$ -Koordinate um $5 \;\text{LE}$ voneinander ab. Folglich betragen die Seitenlänge und die Höhe des Würfels jeweils $5\; \text{LE}.$

Die Koordinaten der übrigen Eckpunkte ergeben sich also zu:

$C(1\mid6\mid1)$

$E(-4\mid1\mid6)$

$F(1\mid1\mid6)$

$G(1\mid6\mid6)$

$H(-4\mid6\mid6)$

Würfel einzeichnen

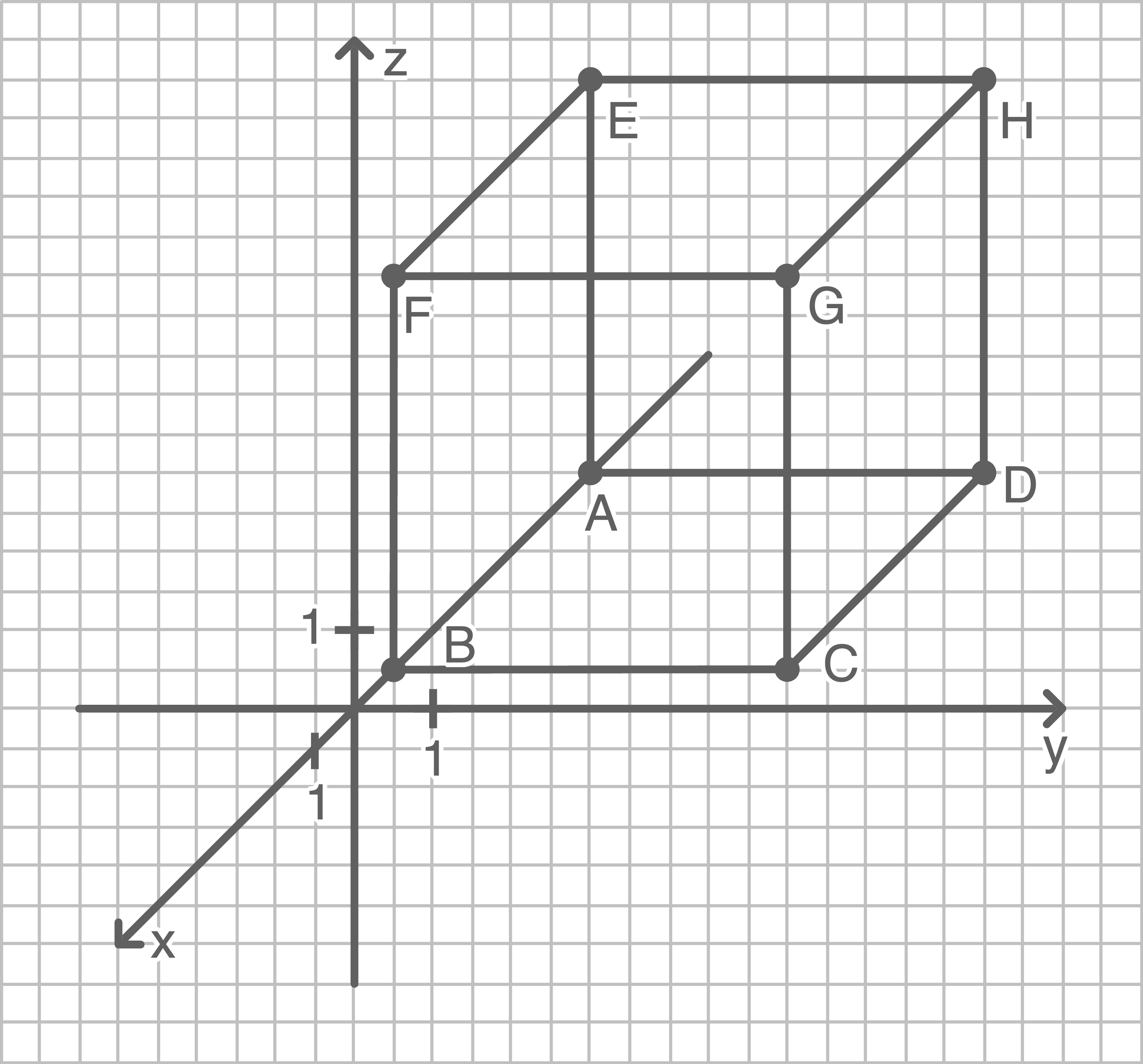
1.2

1. Schritt: Geradengleichung aufstellen

Mit dem Ortsvektor $\overrightarrow{OE}$ von $E$ als Stützvektor und dem Verbindungsvektor $\overrightarrow{LE}$ als Richungsvektor ergibt sich:

$\begin{array}[t]{rll} g:\; \vec{x}&=& \overrightarrow{OE}+r\cdot\overrightarrow{LE}&\\[5pt] &=& \begin{pmatrix}-4\\1\\6\end{pmatrix}+r\cdot\begin{pmatrix}36\\-22\\-20\end{pmatrix} \end{array}$

2. Schritt: Schnittpunkt mit der $\boldsymbol{xy}$ -Ebene bestimmen

Eine Ebenengleichung der $xy$ -Ebene ist beispielsweise:

$E_{xy}: \; z=0$

Einsetzen der $z$ -Koordinate der Geraden in $E_{xy}$ liefert nun:

$\begin{array}[t]{rll} z&=&0 &\quad \scriptsize \\[5pt] 6-20r&=&0 &\quad \scriptsize \mid +20r \\[5pt] 6&=& 20r &\quad \scriptsize \mid :20 \\[5pt] \dfrac{3}{10}&=& r \end{array}$

Einsetzen von $r=\dfrac{3}{10}$ in die Geradengleichung ergibt:

$\(\begin{array}[t]{rll} \overrightarrow{OE$

Der Bildpunkt besitzt somit die Koordinaten $\(E$

1.3.1

1. Schritt: Ebene $\boldsymbol{E_1}$ durch $\boldsymbol{P}$ und $\boldsymbol{L}$ aufstellen

Ein Stützvektor von $E_1$ ist gegeben durch $\overrightarrow{OP}$ . Da $E_1$ senkrecht zur Würfeloberseite und somit senkrecht zu $E_2$ steht, ergeben sich die Richtungsvektoren zu $\overrightarrow{PL}$ und $\vec{n_2},$ wobei $\vec{n_2}$ ein Normalenvektor der Ebene $E_2$ ist.

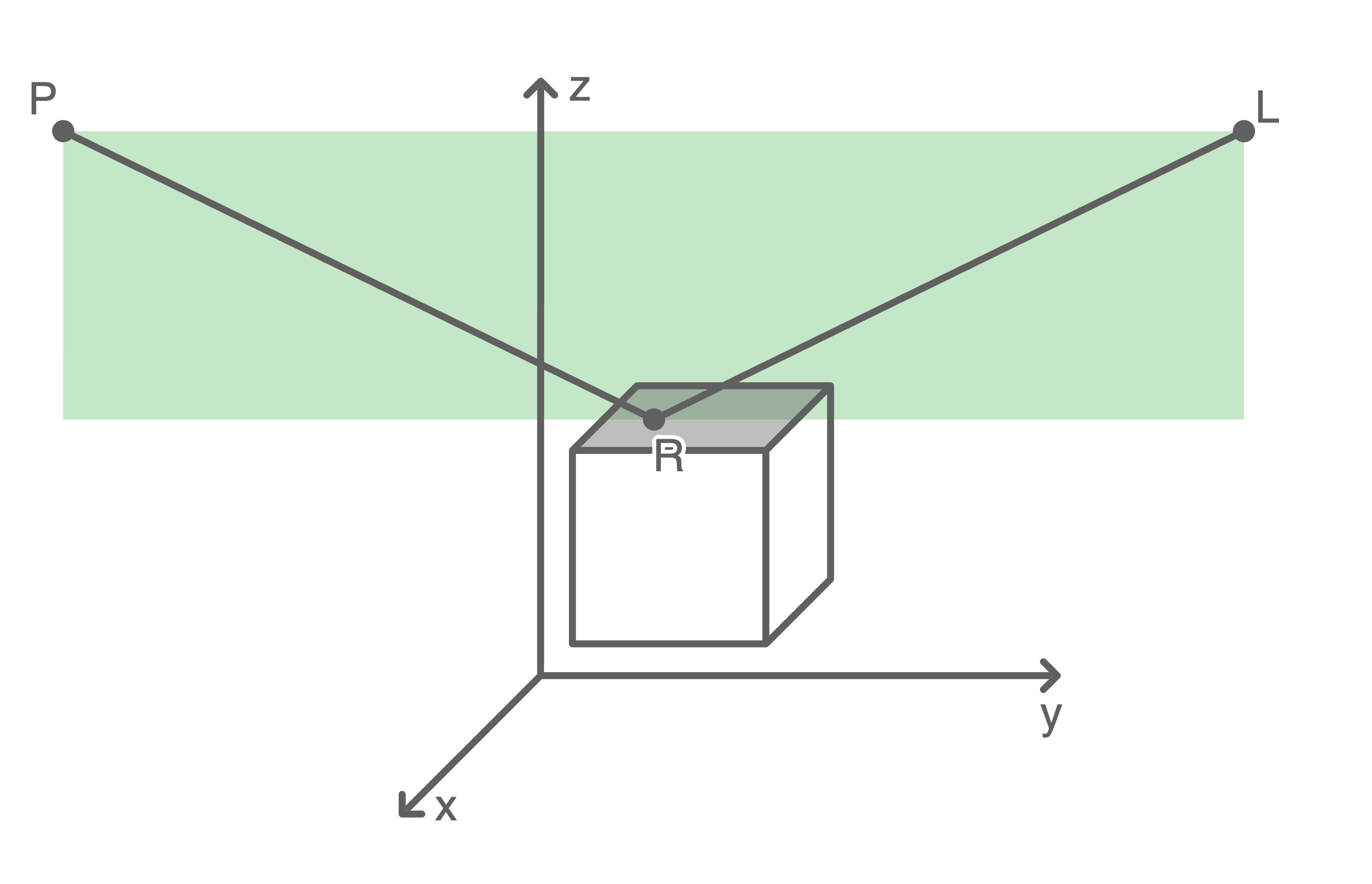
Raumskizze

Es gilt also:

$E_1: \overrightarrow{x} = \overrightarrow{OP}+r\cdot \overrightarrow{PL}+s\cdot\vec{n_2}$

Vollständigen Rechenweg anzeigen

2. Schritt: Ebene $\boldsymbol{E_2}$ aufstellen

$E_2$ liegt um $z=6$ verschoben parallel zur $xy$ -Ebene, eine Ebenengleichung folgt also mit $E_2: z=6$

3. Schritt: Gleichung der Schnittgeraden $\boldsymbol{g}$ bestimmen

Einsetzen der $z$ -Koordinate von $E_1$ in $E_2$ liefert:

Rechenweg anzeigen

$r= -1-\dfrac{1}{10}s$

Einsetzen von $r$ in die Gleichung der Ebene $E_1$ ergibt nun:

Rechenweg anzeigen

$g: \vec{x} = \begin{pmatrix}80\\-37\\6\end{pmatrix}+s\cdot\begin{pmatrix}6\\-3\\0\end{pmatrix}$

4. Schritt: Punktprobe durchführen

Damit $R$ auf der Schnittgeraden $g$ liegt, muss gelten:

$\overrightarrow{OR}&=&\begin{pmatrix}80\\-37\\6\end{pmatrix}+s\cdot\begin{pmatrix}6\\-3\\0\end{pmatrix}$

Rechenweg anzeigen

Für $s=-\dfrac{40}{3}$ ist diese Gleichung gelöst.

$R$ liegt somit auf der Schnittgeraden $g$ der Ebene $E_1$ mit der Würfeloberseite.

1.3.2

1. Schritt: Verbindungsvektoren bestimmen

$\begin{array}[t]{rll} \overrightarrow{LR}&=&\overrightarrow{OR}-\overrightarrow{OL} & \\[5pt] &=& \begin{pmatrix}0\\3\\6\end{pmatrix}-\begin{pmatrix}-40\\23\\26\end{pmatrix}& \\[5pt] &=& \begin{pmatrix}40\\-20\\-20\end{pmatrix}& \\[5pt] \end{array}$

$\begin{array}[t]{rll} \overrightarrow{PR}&=& \overrightarrow{OR}-\overrightarrow{OP}& \\[5pt] &=& \begin{pmatrix}0\\3\\6\end{pmatrix}-\begin{pmatrix}20\\-7\\16\end{pmatrix}& \\[5pt] &=& \begin{pmatrix}-20\\10\\-10\end{pmatrix} \end{array}$

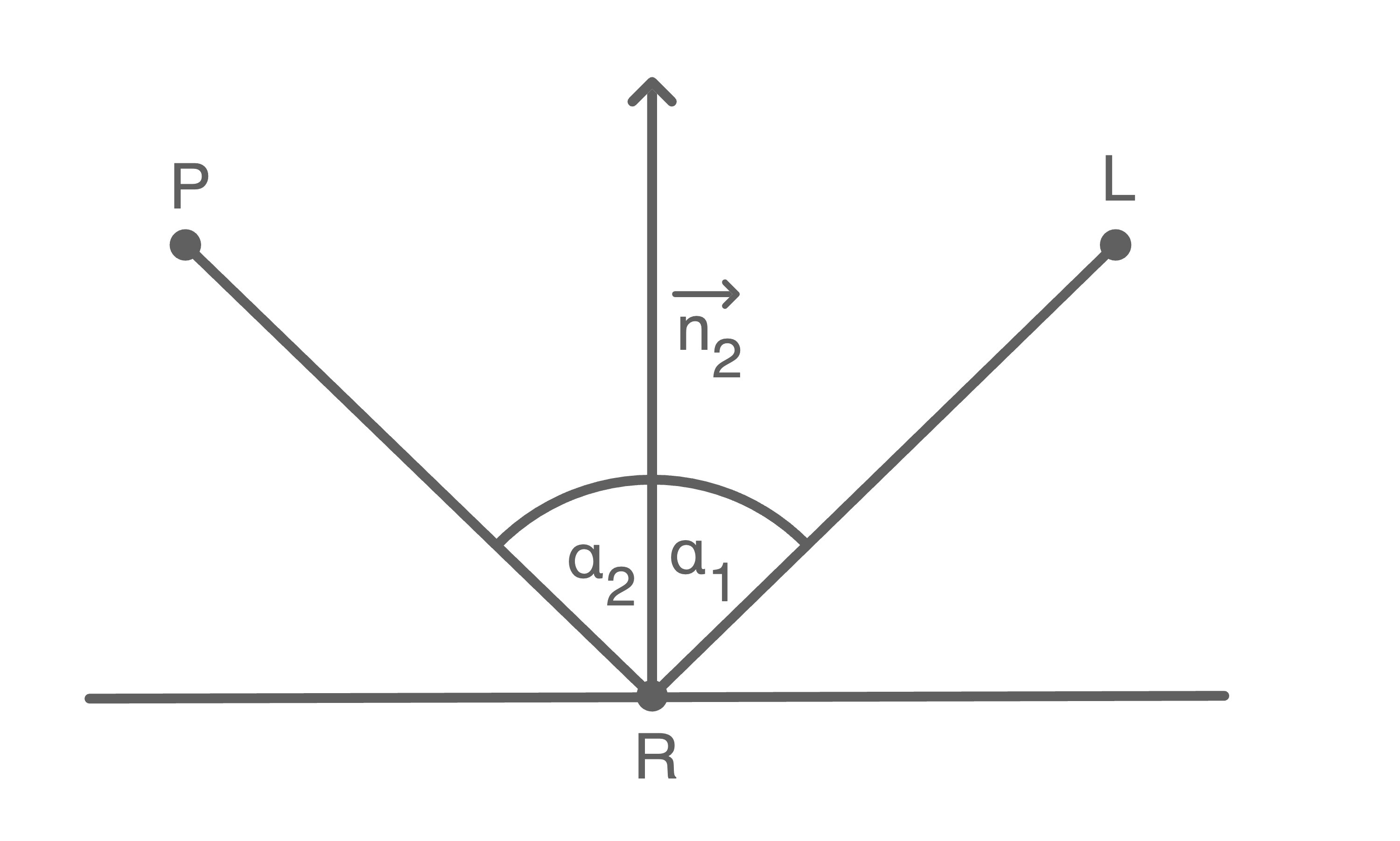
Hilfsskizze (nicht maßstäblich)

2. Schritt: Winkel $\boldsymbol{\alpha_1}$ berechnen

Es gilt:

$\alpha_1 \approx 65,9^\circ$

Rechenweg anzeigen

3. Schritt: Winkel $\boldsymbol{\alpha_2}$ berechnen

$\alpha_2 \approx 65,9^\circ$

Rechenweg anzeigen

Wegen $\cos(\alpha_1)=-\dfrac{1}{\sqrt{6}}=\cos(\alpha_2)$ gilt $\alpha_1=\alpha_2$ .

Damit ist der Winkel zwischen $\overrightarrow{LR}$ und $\vec{n_2}$ identisch mit dem Winkel zwischen $\overrightarrow{PR}$ und $\vec{n_2}.$

2.1

$T$ soll den Vektor $\begin{pmatrix}x\\y\\z\end{pmatrix}$ mit drei Koordinaten in einen Vektor $\begin{pmatrix}a\\b\end{pmatrix}$ mit zwei Koordinaten überführen. Also hat $T$ drei Spalten und zwei Zeilen:

$\begin{pmatrix}c&d&e\\f&g&h\end{pmatrix}\cdot\begin{pmatrix}x\\y\\z\end{pmatrix}=\begin{pmatrix}a\\b\end{pmatrix}$

Es sind drei Bedingungen gegeben:

Bedingung 1:

Der Einheitsvektor $\pmatrix{0\\1\\0}$ geht in den Vektor $\pmatrix{1\\0}$ über:

$\begin{pmatrix}c&d&e\\f&g&h\end{pmatrix}\cdot\begin{pmatrix}0\\1\\0\end{pmatrix}=\begin{pmatrix}1\\0\end{pmatrix}$

Daraus folgt:

Rechnungen anzeigen

$d=1, g=0$

Bedingung 2:

Die $y$ -Achse des 2-D-Koordinatensystems deckt sich mit der $z$ -Achse des 3-D-Koordinatensystems.
Es muss also gelten:

$\begin{pmatrix}c&1&e\\f&0&h\end{pmatrix}\cdot\begin{pmatrix}0\\0\\1\end{pmatrix}=\begin{pmatrix}0\\1\end{pmatrix}$

Daraus folgt:

$\begin{array}[t]{rll} c\cdot0+1\cdot0+e\cdot1&=&0 &\Rightarrow e=0 &\quad \scriptsize \\[5pt] f\cdot0+0\cdot0+h\cdot1&=&1 &\Rightarrow h=1 \end{array}$

Bedingung 3:

Aus dem Punkt $D(-4\mid 6 \mid 1)$ wird der Punkt $\( D$

$\begin{pmatrix}c&1&0\\f&0&1\end{pmatrix}\cdot\begin{pmatrix}-4\\6\\1\end{pmatrix}=\begin{pmatrix}8\\3\end{pmatrix}$

Daraus folgt:

$\begin{array}[t]{rll} c\cdot(-4)+1\cdot6+0\cdot1&=& 8 &\Rightarrow c=-\dfrac{1}{2} &\quad \scriptsize \\[5pt] f\cdot(-4)+0\cdot6+1\cdot1&=& 3 &\Rightarrow f=-\dfrac{1}{2} \end{array}$

Insgesamt die Abbildungsmatrix $T$ also mit:

$T=\begin{pmatrix}-\dfrac{1}{2}&1&0\\-\dfrac{1}{2}&0&1\end{pmatrix}$

2.2

Hier werden durch die Matrix $M$ zwei geometrische Abbildungen, die nacheinander ablaufen, in einem Schritt durchgeführt:

Die Matrix $F$ führt eine Drehung im dreidimensionalen Raum um die z-Achse durch.

Die Matrix $T$ bildet die resultierenden Koordinaten nach der Drehung vom dreidimensionalen in den zweidimensionalen Raum ab.

Die Matrix $M$ beschreibt somit eine Drehung im dreidimensionalen Raum um die $z$ -Achse, gefolgt von einer Abbildung in den zweidimensionalen Raum. Die genaue Drehung hängt von den Werten von $\alpha$ ab.

1.1

Punkte einzeichnen

Koordinaten angeben

Die Koordinaten der übrigen Eckpunkte ergeben sich also zu:

$C(1\mid6\mid1)$

$E(-4\mid1\mid6)$

$F(1\mid1\mid6)$

$G(1\mid6\mid6)$

$H(-4\mid6\mid6)$

Würfel einzeichnen

1.2

1. Schritt: Geradengleichung aufstellen

Mit dem Ortsvektor $\overrightarrow{OE}$ von $E$ als Stützvektor und dem Verbindungsvektor $\overrightarrow{LE}$ als Richungsvektor ergibt sich:

$\begin{array}[t]{rll} g:\; \vec{x}&=& \overrightarrow{OE}+r\cdot\overrightarrow{LE}&\\[5pt] &=& \begin{pmatrix}-4\\1\\6\end{pmatrix}+r\cdot\begin{pmatrix}36\\-22\\-20\end{pmatrix} \end{array}$

2. Schritt: Schnittpunkt mit der $\boldsymbol{xy}$ -Ebene bestimmen

Eine Ebenengleichung der $xy$ -Ebene ist beispielsweise:

$E_{xy}: \; z=0$

Einsetzen der $z$ -Koordinate der Geraden in $E_{xy}$ liefert nun:

$\begin{array}[t]{rll} z&=&0 &\quad \scriptsize \\[5pt] 6-20r&=&0 &\quad \scriptsize \mid +20r \\[5pt] 6&=& 20r &\quad \scriptsize \mid :20 \\[5pt] \dfrac{3}{10}&=& r \end{array}$

Einsetzen von $r=\dfrac{3}{10}$ in die Geradengleichung ergibt:

$\(\begin{array}[t]{rll} \overrightarrow{OE$

Der Bildpunkt besitzt somit die Koordinaten $\(E$

1.3.1

1. Schritt: Ebene $\boldsymbol{E_1}$ durch $\boldsymbol{P}$ und $\boldsymbol{L}$ aufstellen

Raumskizze

Es gilt also:

$E_1: \overrightarrow{x} = \overrightarrow{OP}+r\cdot \overrightarrow{PL}+s\cdot\vec{n_2}$

Vollständigen Rechenweg anzeigen

2. Schritt: Ebene $\boldsymbol{E_2}$ aufstellen

$E_2$ liegt um $z=6$ verschoben parallel zur $xy$ -Ebene, eine Ebenengleichung folgt also mit $E_2: z=6$

3. Schritt: Gleichung der Schnittgeraden $\boldsymbol{g}$ bestimmen

Einsetzen der $z$ -Koordinate von $E_1$ in $E_2$ liefert:

Rechenweg anzeigen

$r= -1-\dfrac{1}{10}s$

Einsetzen von $r$ in die Gleichung der Ebene $E_1$ ergibt nun:

Rechenweg anzeigen

$g: \vec{x} = \begin{pmatrix}80\\-37\\6\end{pmatrix}+s\cdot\begin{pmatrix}6\\-3\\0\end{pmatrix}$

4. Schritt: Punktprobe durchführen

Damit $R$ auf der Schnittgeraden $g$ liegt, muss gelten:

$\overrightarrow{OR}&=&\begin{pmatrix}80\\-37\\6\end{pmatrix}+s\cdot\begin{pmatrix}6\\-3\\0\end{pmatrix}$

Rechenweg anzeigen

Für $s=-\dfrac{40}{3}$ ist diese Gleichung gelöst.

$R$ liegt somit auf der Schnittgeraden $g$ der Ebene $E_1$ mit der Würfeloberseite.

1.3.2

1. Schritt: Verbindungsvektoren bestimmen

Hilfsskizze (nicht maßstäblich)

2. Schritt: Winkel $\boldsymbol{\alpha_1}$ berechnen

Es gilt:

$\alpha_1 \approx 65,9^\circ$

Rechenweg anzeigen

3. Schritt: Winkel $\boldsymbol{\alpha_2}$ berechnen

$\alpha_2 \approx 65,9^\circ$

Rechenweg anzeigen

Wegen $\cos(\alpha_1)=-\dfrac{1}{\sqrt{6}}=\cos(\alpha_2)$ gilt $\alpha_1=\alpha_2$ .

Damit ist der Winkel zwischen $\overrightarrow{LR}$ und $\vec{n_2}$ identisch mit dem Winkel zwischen $\overrightarrow{PR}$ und $\vec{n_2}.$

2.1

$\begin{pmatrix}c&d&e\\f&g&h\end{pmatrix}\cdot\begin{pmatrix}x\\y\\z\end{pmatrix}=\begin{pmatrix}a\\b\end{pmatrix}$

Es sind drei Bedingungen gegeben:

Bedingung 1:

Der Einheitsvektor $\pmatrix{0\\1\\0}$ geht in den Vektor $\pmatrix{1\\0}$ über:

$\begin{pmatrix}c&d&e\\f&g&h\end{pmatrix}\cdot\begin{pmatrix}0\\1\\0\end{pmatrix}=\begin{pmatrix}1\\0\end{pmatrix}$

Daraus folgt:

Rechnungen anzeigen

$d=1, g=0$

Bedingung 2:

Die $y$ -Achse des 2-D-Koordinatensystems deckt sich mit der $z$ -Achse des 3-D-Koordinatensystems.
Es muss also gelten:

$\begin{pmatrix}c&1&e\\f&0&h\end{pmatrix}\cdot\begin{pmatrix}0\\0\\1\end{pmatrix}=\begin{pmatrix}0\\1\end{pmatrix}$

Daraus folgt:

$\begin{array}[t]{rll} c\cdot0+1\cdot0+e\cdot1&=&0 &\Rightarrow e=0 &\quad \scriptsize \\[5pt] f\cdot0+0\cdot0+h\cdot1&=&1 &\Rightarrow h=1 \end{array}$

Bedingung 3:

Aus dem Punkt $D(-4\mid 6 \mid 1)$ wird der Punkt $\( D$

$\begin{pmatrix}c&1&0\\f&0&1\end{pmatrix}\cdot\begin{pmatrix}-4\\6\\1\end{pmatrix}=\begin{pmatrix}8\\3\end{pmatrix}$

Daraus folgt:

$\begin{array}[t]{rll} c\cdot(-4)+1\cdot6+0\cdot1&=& 8 &\Rightarrow c=-\dfrac{1}{2} &\quad \scriptsize \\[5pt] f\cdot(-4)+0\cdot6+1\cdot1&=& 3 &\Rightarrow f=-\dfrac{1}{2} \end{array}$

Insgesamt die Abbildungsmatrix $T$ also mit:

$T=\begin{pmatrix}-\dfrac{1}{2}&1&0\\-\dfrac{1}{2}&0&1\end{pmatrix}$

2.2

Hier werden durch die Matrix $M$ zwei geometrische Abbildungen, die nacheinander ablaufen, in einem Schritt durchgeführt:

Die Matrix $F$ führt eine Drehung im dreidimensionalen Raum um die z-Achse durch.

Die Matrix $T$ bildet die resultierenden Koordinaten nach der Drehung vom dreidimensionalen in den zweidimensionalen Raum ab.