B2 - Analytische Geometrie

In einem deutschen Mittelgebirge wurde vor einiger Zeit im Rahmen eines Artenschutzprojekts eine Wisentherde in einem begrenzten Gebiet $A$ ausgewildert. Wisente, die auch europäische Bisons genannt werden, sind die letzte Art frei lebender Rinder in Europa. Im Laufe der Zeit konnte man im Rahmen des Artenschutzprojekts beobachten, dass die zugehörigen Tiere sich nicht nur in dem für sie vorgesehenen Gebiet $A$ aufhalten, sondern es auch zu Wanderbewegungen in die benachbarten Gebiete $B$ und $C,$ in denen vor der Auswilderung keine Wisente lebten, kommt. Die Wanderbewegungen werden mit Hilfe von GPS-Trackern verfolgt.
In einem Modell werden Verteilungen der Population auf die drei Gebiete durch Vektoren der Form $\pmatrix{a\\b\\c}$ dargestellt, wobei $a, b, c$ die prozentualen Anteile der Wisente in den Gebieten $A, B, C$ angeben.
Die Wanderbewegungen der Wisente zwischen dem Gebiet $A$ und den benachbarten Gebieten $B$ und $C$ von einem Jahr $n$ zum nächsten können durch die Übergangsmatrix $M =\pmatrix{0,95&0,2&0,1\\0,04&0,8&0 \\ 0,01 & 0 & 0,9}$ und die Gleichung $M \cdot \overrightarrow{x_n} = \overrightarrow{x_n+1}$ dargestellt werden.

1.1

Beschrifte das Übergangsdiagramm (Material) mit den passenden Werten und erläutere exemplarisch die Bedeutung der Werte in der ersten Spalte der Übergangsmatrix $M.$

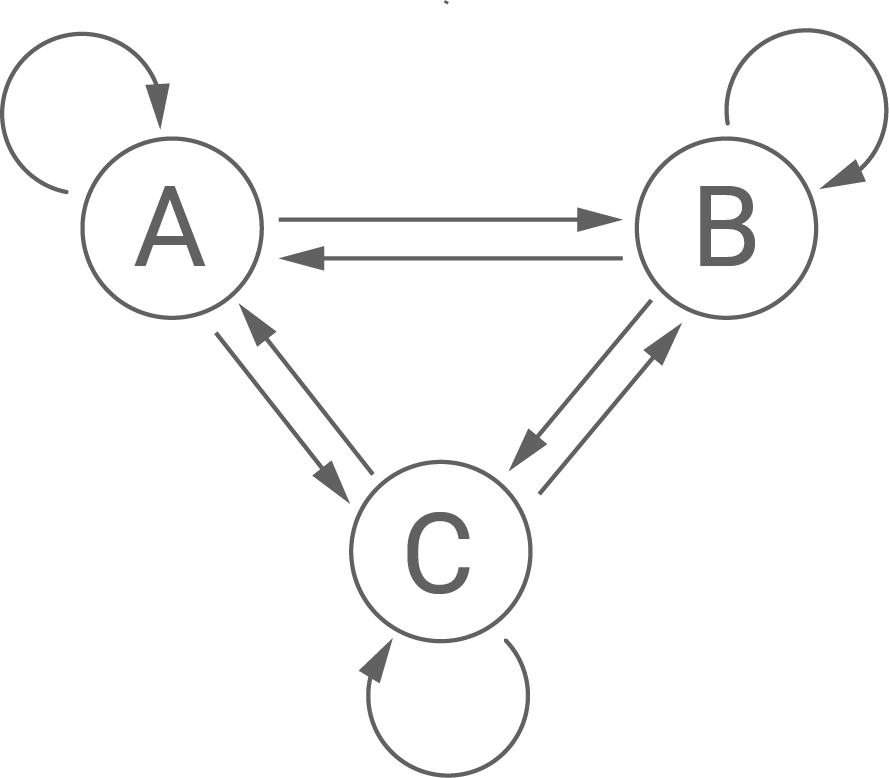
Uebergangsmatrix Wisentherde Hessen Abi 2018

Material

(5 BE)

1.2

Die prozentuale Verteilung der Wisente zu Beginn der Auswilderung kann durch den Anfangsvektor $\overrightarrow{x_0}$ dargestellt werden. Erkläre, warum im Sachzusammenhang $\overrightarrow{x_0} = \pmatrix{1\\0\\0}$ gelten muss. Bestimme anschließend die Verteilungen $\overrightarrow{x_1}$ und $\overrightarrow{x_2}$ der beiden folgenden Jahre.

(3 BE)

1.3

Erkläre, wieso man die Verteilung nach $n$ Jahren mit Hilfe der Matrix-Vektor-Gleichung $\overrightarrow{x_n} = M^n\cdot \overrightarrow{x_0}$ bestimmen kann.

(2 BE)

1.4

Bestimme die gemäß der Modellierung zu erwartende Anzahl der Wisente in den Gebieten $A, B$ und $C$ nach 10 Jahren, wenn insgesamt $75$ Wisente in den drei Gebieten leben.

(4 BE)

Die Besitzer des Gebiets $B$ protestierten nach einiger Zeit energisch gegen das Projekt, da die Wisente in ihren Augen die Bäume zerstören. Ihr Versuch, das Projekt zu stoppen, scheiterte jedoch und sie forderten vom Trägerverein des Artenschutzprojekts, zumindest den Anteil der in Gebiet $B$ lebenden Wisente auf einen stabilen Anteil von ca. $5\,\%$ zu senken.
Der Vektor $\overrightarrow{x_F}$ gebe die Verteilung der Population auf die drei Gebiete zu einem bestimmten Zeitpunkt an.

2.1

Für den Vektor $\overrightarrow{x_F}$ gilt: $\overrightarrow{x_F} = M\cdot \overrightarrow{x_F}.$
Erkläre, welche Bedeutung der Vektor $\overrightarrow{x_F}$ im Sachzusammenhang besitzt.

(2 BE)

2.2

Das zur Matrix-Vektor-Gleichung $\overrightarrow{x_F} = M\cdot \overrightarrow{x_F}$ zugehörige lineare Gleichungssystem besitzt unendlich viele Lösungen.
Bestimme diese Lösungen. Erkläre, warum im Sachzusammenhang eine eindeutige Lösung existiert, und ermittle diese.
$\bigg[$ Zur Kontrolle: $\overrightarrow{x_F} \approx \pmatrix{0,769\\0,154\\0,077}$ $\bigg]$

(7 BE)

2.3

Deute das Ergebnis aus Aufgabe 2.2 im Hinblick auf die Forderung der Besitzer.

(2 BE)

2.4

Um die geforderte $5\,\%$ -Quote einzuhalten, soll das Wechselverhalten der Wisente beeinflusst werden. Dies soll ausschließlich durch Beeinflussung der Wanderbewegungen vom Gebiet $B$ in die Gebiete $A, B$ und $C$ geschehen. Das Ziel ist es, eine gleich bleibende Verteilung von $85 \,\%$ der Tiere in Gebiet $A, 5\,\%$ der Tiere in Gebiet $B$ und $10\,\%$ der Tiere in Gebiet $C$ zu erhalten.
Leite die zugehörige Übergangsmatrix $N$ her.

(5 BE)

1.1

Übergangsdiagramm beschriften

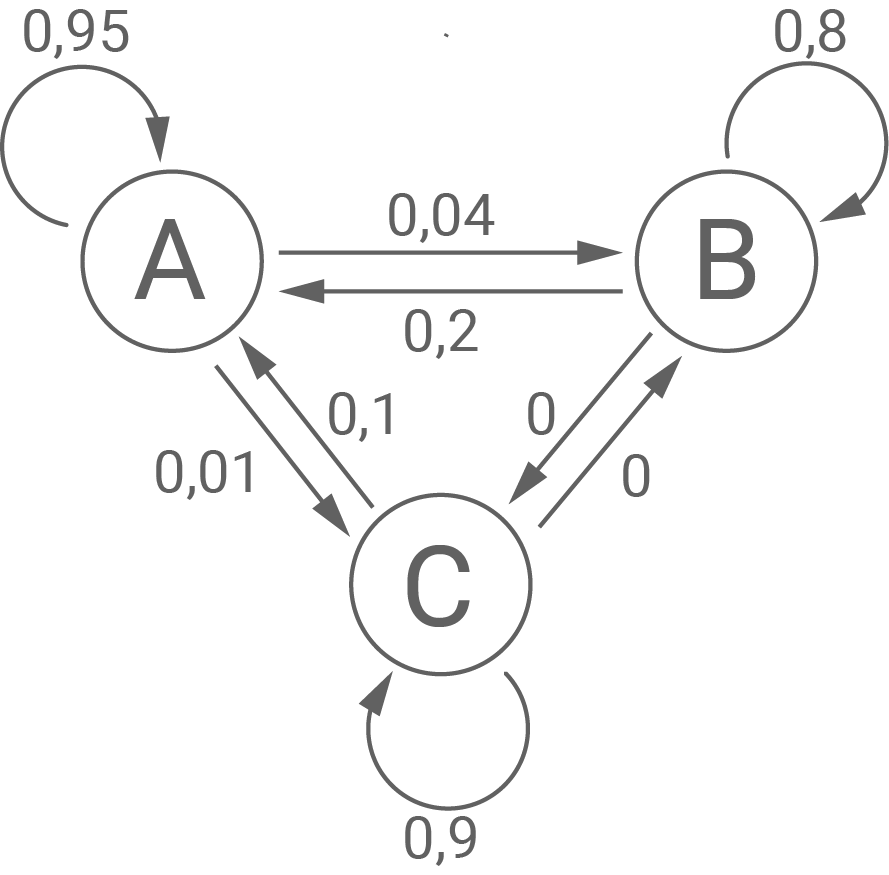Uebergangsdiagramm Beschriftung Hessen Abi 2018

Abb.1: Beschriftetes Übergangsdiagramm

Werte erläutern

In der ersten Spalte sind die Übergangswahrscheinlichkeiten für die Wisente in Gebiet $A$ angegeben. Innerhalb eines Jahres wandern also $4\,\%$ der Wisente aus Gebiet $A$ nach Gebiet $B$ und $1\,\%$ nach Gebiet $C.$ $95\,\%$ der Wisente bleiben in Gebiet $A.$

1.2

Anfangsvektor erklären

Zu Beginn der Auswilderung wird die komplette Wisentherde in Gebiet $A$ ausgewildert. Alle Wisente befinden sich daher zu Beginn in Gebiet $A$ während sich in Gebiet $B$ und $C$ keine befinden. Somit befinden sich zu diesem Zeitpunkt $100\,\%$ der Wisente in Gebiet $A.$ Der Anfangsvektor $\overrightarrow{x_0}$ muss also $\pmatrix{1\\0\\0}$ sein.

Verteilungen der Folgejahre bestimmen

Mit der Gleichung aus dem Einführungstext folgt:

$x_1= \pmatrix{0,95 \\ 0,04 \\ 0,01 }$

Rechenweg anzeigen

$x_2= \pmatrix{0,9115\\ 0,07 \\ 0,0185}$

Rechenweg anzeigen

1.3

Gleichung erklären

Aus dem Einführungstext ist folgende Gleichung bekannt:

$\overrightarrow{x_{n+1}} = M\cdot \overrightarrow{x_n}$

Es gelten also beispielsweise folgende Beziehungen:

$\begin{array}[t]{rll} \text{I} & \overrightarrow{x_{1}} &=& M\cdot \overrightarrow{x_0} \\[5pt] \text{II} & \overrightarrow{x_{2}} &=& M\cdot \overrightarrow{x_1 } \\[5pt] \end{array}$

Wegen $\text{I}$ gilt dann:

$\overrightarrow{x_2} = M\cdot M \cdot \overrightarrow{x_0} = M^2 \cdot \overrightarrow{x_0}$

Für $\overrightarrow{x_n}$ lässt sich dies also zurückführen zu:

$\overrightarrow{x_n}= M^i \cdot \overrightarrow{x_{n-i}} \text{ für }0\leq i\leq n$

Rechenweg anzeigen

Dies kann nun so oft weitergeführt werden, bis $i$ den Wert $n$ erreicht hat. Dann ergibt sich:

$\overrightarrow{x}_n =M^n \cdot \overrightarrow{x}_{n-n} = M^n \cdot \overrightarrow{x}_{0}$

1.4

Die prozentuale Verteilung der Wisente nach zehn Jahren ergibt sich mithilfe der Übergangsmatrix $M:$

$\overrightarrow{x}_{10} \approx \pmatrix{0,795 \\ 0,149 \\ 0,056}$

Rechenweg anzeigen

Laut Aufgabenstellung gibt es insgesamt $75$ Wisente:

$75\cdot\pmatrix{0,795 \\ 0,149 \\ 0,056} \approx \pmatrix{59,625 \\ 11,175\\ 4,2}$

Da nur ganzzahlige Werte im Sachzusammenhang sinnvoll sind, muss sinnvoll auf ganze Zahlen gerundet werden. Nach zehn Jahren befinden sich also etwa $60$ Wisente in Gebiet $A,$ $11$ Wisente in Gebiet $B$ und $4$ Wisente in Gebiet $C.$

2.1

Bedeutung erklären

Hat die Population einmal die Verteilung $\overrightarrow{x_F}$ erreicht, bleibt sie so. Ab diesem Zeitpunkt bleiben also immer gleich viele Wisente in Gebiet $A,$ in Gebiet $B$ und in Gebiet $C.$

2.2

Lösungen bestimmen

Mit $\overrightarrow{x_F} =\pmatrix{a\\b\\c}$ folgt:

$\begin{array}[t]{rll} \overrightarrow{x_F}&=& M\cdot \overrightarrow{x_F} \\[5pt] \pmatrix{a\\b\\c}&=& \pmatrix{0,95&0,2&0,1\\0,04&0,8&0 \\ 0,01 & 0 & 0,9}\cdot \pmatrix{a\\b\\c} \\[5pt] \end{array}$

Mit dem solve-Befehl des CAS ergibt sich:

$a = 10 \cdot t,$ $b= 2\cdot t,$ $c = t$

Mit $t \in \mathbb{R}$ ist eine Konstante bezeichnet.

Die Lösungen des Gleichungssystems sind folglich gegeben durch $\overrightarrow{x_{F_{t}}} = t\cdot\pmatrix{10 \\ 2 \\1}.$

Eindeutige Lösung ermitteln

Da es sich bei $\overrightarrow{x_F}$ im Sachzsuammenhang um eine prozentuale Verteilung der Wisente handelt, muss die Summe der Vektoreinträge $1$ ergeben und jeder Vektoreintrag positiv sein.

$\begin{array}[t]{rll} 1&=& 10t + 2t +t \\[5pt] 1&=& 13t &\quad \scriptsize \mid\; :13 \\[5pt] \frac{1}{13}&=& t\\[5pt] 0,0769 &\approx& t \end{array}$

Die im Sachzusammenhang eindeutige Lösung lautet folglich:

$\overrightarrow{x_F} = \frac{1}{13} \cdot \pmatrix{10 \\ 2 \\ 1} \approx \pmatrix{0,769 \\ 0,154 \\ 0,077}$

2.3

Ergebnis deuten

Wenn die Population der Wisente einmal die prozentuale Verteilung $\overrightarrow{x_F}$ annimmt, bleibt diese auch langfristig gesehen so. In Gebiet $B$ leben dann etwa $15,4\,\%$ der ausgewilderten Wisente. Damit die Forderung der Besitzer erfüllt wird, müssen dann also Maßnahmen ergriffen werden, um die Wisente in Gebiet $B$ dauerhaft umzuverteilen.

2.4

Übergangsmatrix herleiten

Da lediglich das Wechselverhalten der Tiere von Gebiet $B$ in die drei Gebiete verändert werden soll, verändern sich im Vergleich zur Übergangsmatrix $M$ nur die Einträge der zweiten Spalte.

Diese können beispielsweise mit $a,$ $b$ und $c$ bezeichnet werden.

Die gewünschte Verteilung soll dann wie folgt lauten: $\overrightarrow{x} = \pmatrix{0,85\\0,05\\0,1}$

Es ergibt sich also folgende Gleichung:

Rechenweg anzeigen

$\pmatrix{0,85\\0,05\\0,1} =\pmatrix{0,8175 + a\cdot 0,05 \\0,034 + b\cdot 0,05 \\ 0,0985 + c\cdot 0,05 }$

Es lässt sich nun folgendes Gleichungssystem aufstellen:

$\begin{array}{lrll} \text{I}\quad&0,85&=& 0,8175 + a\cdot 0,05 \\ \text{II}\quad&0,05&=& 0,034 + b\cdot 0,05 \\ \text{III}\quad& 0,1&=& 0,0985 + c\cdot 0,05 \\ \end{array}$

Mit dem CAS kann das Gleichungssystem gelöst werden. Es ergibt sich:

$a=0,65$

$b=0,32$

$c=0,03$

Die zugehörige Übergangsmatrix lautet also $N =\pmatrix{0,95 & 0,65 & 0,1\\0,04 & 0,32 & 0 \\ 0,01 & 0,03 & 0,9}.$

Bildnachweise [nach oben]

[1]