A1 - Analysis
Der Bitterfelder Bogen ist eine  hohe begehbare architektonische Stahlskulptur, die als das neue Wahrzeichen im ehemaligen Bitterfeld-Wolfener Chemie- und Braunkohlerevier bezeichnet werden kann. Er besteht aus drei Bögen, die leicht zueinander geneigt sind (Abbildung 1).
Zur Vereinfachung kann angenommen werden, dass diese drei Bögen in Ebenen liegen, die zum Boden senkrecht und somit parallel zueinander sind. Weitere Maße können Abbildung 2 entnommen werden.
hohe begehbare architektonische Stahlskulptur, die als das neue Wahrzeichen im ehemaligen Bitterfeld-Wolfener Chemie- und Braunkohlerevier bezeichnet werden kann. Er besteht aus drei Bögen, die leicht zueinander geneigt sind (Abbildung 1).
Zur Vereinfachung kann angenommen werden, dass diese drei Bögen in Ebenen liegen, die zum Boden senkrecht und somit parallel zueinander sind. Weitere Maße können Abbildung 2 entnommen werden.

 (1) (1) (1) (1) (1) (1) (1).png)

Abbildung 1
Quelle: http://www.bitterfelder-bogen.de
 (1) (1) (1) (1) (1) (1) (1).png)
Abbildung 2
Quelle: http://www.bitterfelder-bogen.de
1.1
Im Prospekt wird beschrieben, dass in die beiden Zwischenräume eine  Steigung aufweisende Rampenanlage eingehängt ist.
Fußwege führen in langgestrecktem Zick-Zack-Kurs in die Höhe. Alle Wege sind stufenlos und von metallenen Geländern gesichert. Jede Biegung des insgesamt ca.
Steigung aufweisende Rampenanlage eingehängt ist.
Fußwege führen in langgestrecktem Zick-Zack-Kurs in die Höhe. Alle Wege sind stufenlos und von metallenen Geländern gesichert. Jede Biegung des insgesamt ca.  langen Wanderweges hat eine kleine Plattform.
Bestimme den Höhenunterschied, den ein
langen Wanderweges hat eine kleine Plattform.
Bestimme den Höhenunterschied, den ein  langer geradliniger Wanderweg bei einem Steigungungswinkel von
langer geradliniger Wanderweg bei einem Steigungungswinkel von  überwindet.
Beurteile anhand des Ergebnisses und des einleitenden Textes die Angaben im Prospekt.
überwindet.
Beurteile anhand des Ergebnisses und des einleitenden Textes die Angaben im Prospekt.
(4 BE)
1.2
Für Rollstuhlfahrer darf die Steigung höchstens  betragen.
Berechne die Steigung in
betragen.
Berechne die Steigung in  bei einem Steigungswinkel von
bei einem Steigungswinkel von  und entscheide, ob ein solcher Wanderweg für Rollstuhlfahrer geeignet ist.
und entscheide, ob ein solcher Wanderweg für Rollstuhlfahrer geeignet ist.
Im Folgenden soll der äußere Rand eines Bogens modelliert werden.
(3 BE)
2
In einem ersten Versuch werden quadratische Funktionen für diese Modellierung verwendet.
2.1
Bestimme den Funktionsterm einer quadratischen Funktion, die den äußeren Rand eines Bogens beschreibt, mit Hilfe der Informationen aus dem einleitenden Text und aus Abbildung 2.
(6 BE)
2.2
In Abbildung 1 ist zu erkennen, dass der Bogen an der höchsten Stelle einen Knick hat.
Erkläre, welche Konsequenzen dies für die Modellierung des Bogenrandes mit Hilfe von quadratischen Funktionen hat.
(3 BE)
3
In einem zweiten Versuch soll der äußere Rand des Bogens durch folgende Funktionen beschrieben werden:
![\(\begin{array}{rl}
K_{1}(x)=&\sqrt{1296-\left(x-\dfrac{1}{10}\right)^{2}}-8,
\\
x\in[-35;\;0] \text{ und}
\\
\\
K_{2}(x)=&\sqrt{1296-\left(x+\dfrac{1}{10}\right)^{2}}-8,
\\
x\in[0;\;35]
\end{array}\)](https://www.schullv.de/resources/formulas/115b17069a3e953cb921963c4b94d4b147e963c14569de5f61f93a77fd8bda38_light.svg)
3.1
Zeige, dass der so definierte äußere Rand des Bogens achsensymmetrisch zur  -Achse ist.
-Achse ist.
(4 BE)
3.2
Bestimme den maximalen Höhenunterschied zwischen  und dem Graphen der quadratischen Funktion aus Aufgabe 2.1.
und dem Graphen der quadratischen Funktion aus Aufgabe 2.1.
 Wenn Aufgabe 2.1 nicht gelöst wurde, kann die quadratische Funktion
Wenn Aufgabe 2.1 nicht gelöst wurde, kann die quadratische Funktion  mit
mit  verwendet werden.
verwendet werden.![\(\big]\)](https://www.schullv.de/resources/formulas/0c6dff9ed6a80b0cc013679b53aff551dd11abb4691ba32076d10b15d6195a5d_light.svg)
(4 BE)
3.3
Ermittle den Schnittwinkel der Graphen von  und
und  an der höchsten Stelle des Bogens.
an der höchsten Stelle des Bogens.
(6 BE)
3.4
Das komplette Bauwerk soll eine Stoffhülle erhalten.
Bestimme die benötigte Stofffläche und erläutere dein Vorgehen.
Information: Länge eines Graphen
Die Länge des Graphen einer differenzierbaren Funktion  zwischen den Punkten
zwischen den Punkten  und
und  wird durch folgende Formel berechnet:
wird durch folgende Formel berechnet:
 ,
,

(7 BE)
3.5
Ermittle das umbaute Volumen dieses Bauwerks.
(3 BE)
1.1
Höhenunterschied bestimmen
![\(\begin{array}[t]{rll}
\sin (\alpha)&=& \dfrac{\text{Gegenkathete}}{\text{Hypotenuse}}& \\[5pt]
\sin (6 ^\circ) &=& \dfrac{h}{540\,\text{m}}&\quad \scriptsize \,\bigg \vert \, \cdot 540\,\text{m} \\[5pt]
\sin (6^\circ) \cdot 540\,\text{m}&=& h& \\[5pt]
56,45\,\text{m} &\approx& h
\end{array}\)](https://www.schullv.de/resources/formulas/f44821513c16301b5499ac3bb2940e24db706a635f736a533500dc0acb27b27f_light.svg)
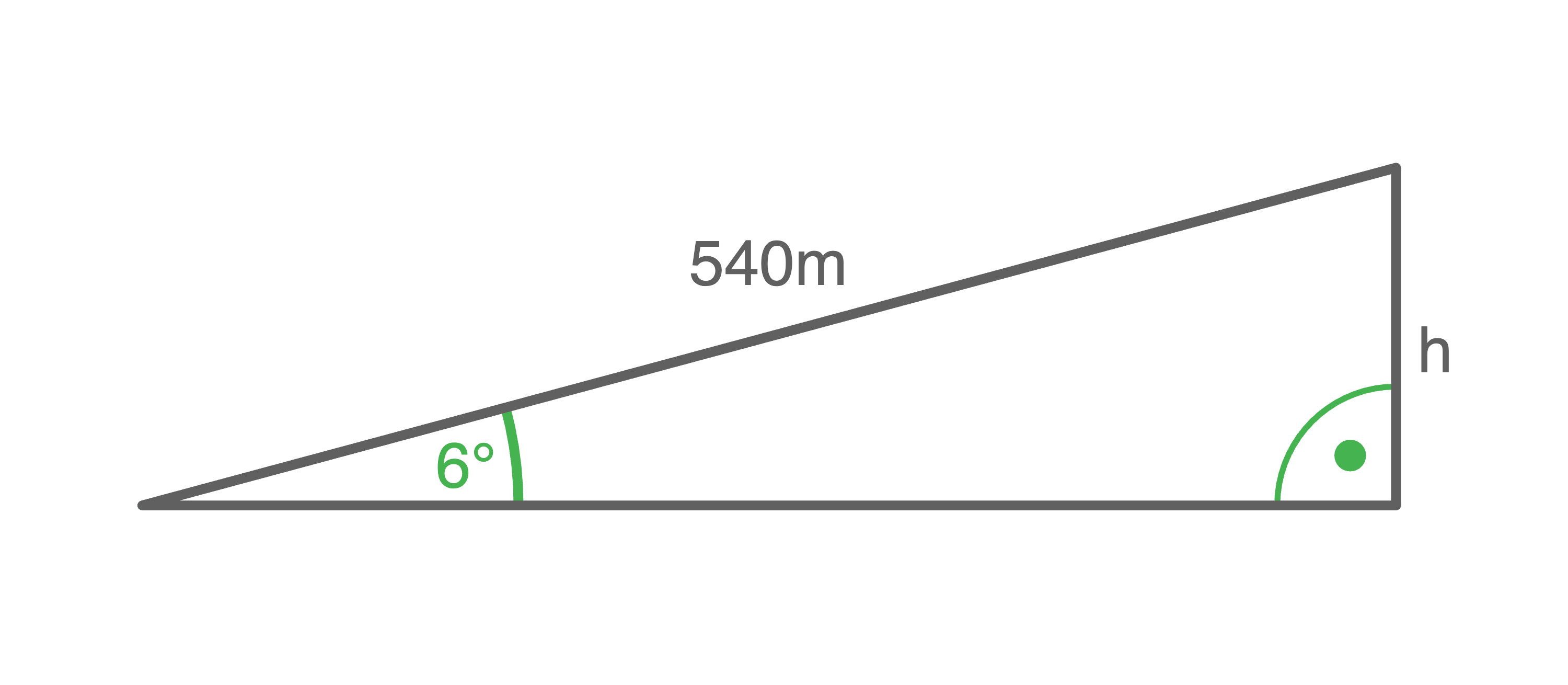 Ein
Ein  langer geradliniger und um
langer geradliniger und um  geneigter Wanderweg überwindet also einen Höhenunterschied von ungefähr
geneigter Wanderweg überwindet also einen Höhenunterschied von ungefähr  Angaben beurteilen
Im Vergleich des Höhenunterschied zu der Größe bzw. dem überwundenen Höhenunterschieds des Bogens fällt auf, dass dieser nur
Angaben beurteilen
Im Vergleich des Höhenunterschied zu der Größe bzw. dem überwundenen Höhenunterschieds des Bogens fällt auf, dass dieser nur  hoch ist und lediglich einen Höhenunterschied von
hoch ist und lediglich einen Höhenunterschied von  überwindet.
Ein Grund dafür könnte sein, dass die Skulptur jeweils an den äußeren Enden eine waagerechte Plattform besitzt, die ebenfalls in die Länge des
überwindet.
Ein Grund dafür könnte sein, dass die Skulptur jeweils an den äußeren Enden eine waagerechte Plattform besitzt, die ebenfalls in die Länge des  langen Aufstiegs zählt.
Ein weiterer Grund könnte sein, dass der Anstiegswinkel im Prospekt nicht richtig angegeben wurde und dieser in Wahrheit kleiner ist.
langen Aufstiegs zählt.
Ein weiterer Grund könnte sein, dass der Anstiegswinkel im Prospekt nicht richtig angegeben wurde und dieser in Wahrheit kleiner ist.

Hilfsskizze (nicht maßstäblich)
1.2
Steigung berechnen
Eine Steigung von  entspricht einer Zunahme der Höhe um 6 Meter pro 100 Meter in waagerechter Richtung.
entspricht einer Zunahme der Höhe um 6 Meter pro 100 Meter in waagerechter Richtung.
![\(\begin{array}[t]{rll}
\tan (\alpha)&=&\dfrac{\text{Gegenkathete}}{\text{Ankathete}} & \\[5pt]
\tan (6^\circ)&=& \dfrac{h_s}{100\,\text{m}}&\quad \scriptsize \mid\; \cdot 100\,\text{m} \\[5pt]
\tan (6^\circ) \cdot 100\,\text{m}&=& h_s& \\[5pt]
10,51\,\text{m}&\approx& h_s
\end{array}\)](https://www.schullv.de/resources/formulas/aa14ae281b5eae257ba8adb4b5a48ab40190f0b244b5a0fb6c21b0c8113e7b15_light.svg)
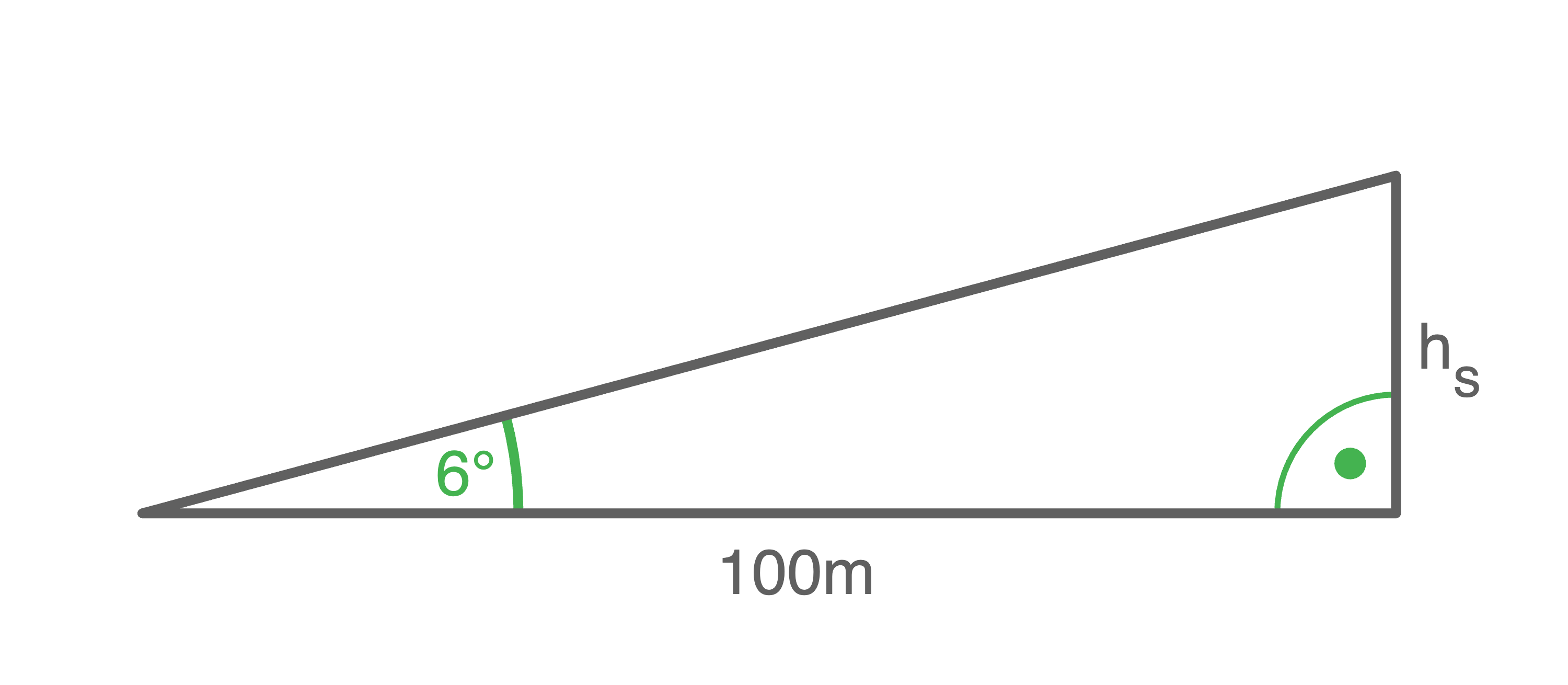 Ein um
Ein um  geneigter Wanderweg besitzt also einen Anstieg von
geneigter Wanderweg besitzt also einen Anstieg von  Entscheidung
Ein solcher Wanderweg ist folglich nicht für Rollstuhlfahrer geeignet.
Entscheidung
Ein solcher Wanderweg ist folglich nicht für Rollstuhlfahrer geeignet.

Hilfsskizze (nicht maßstäblich)
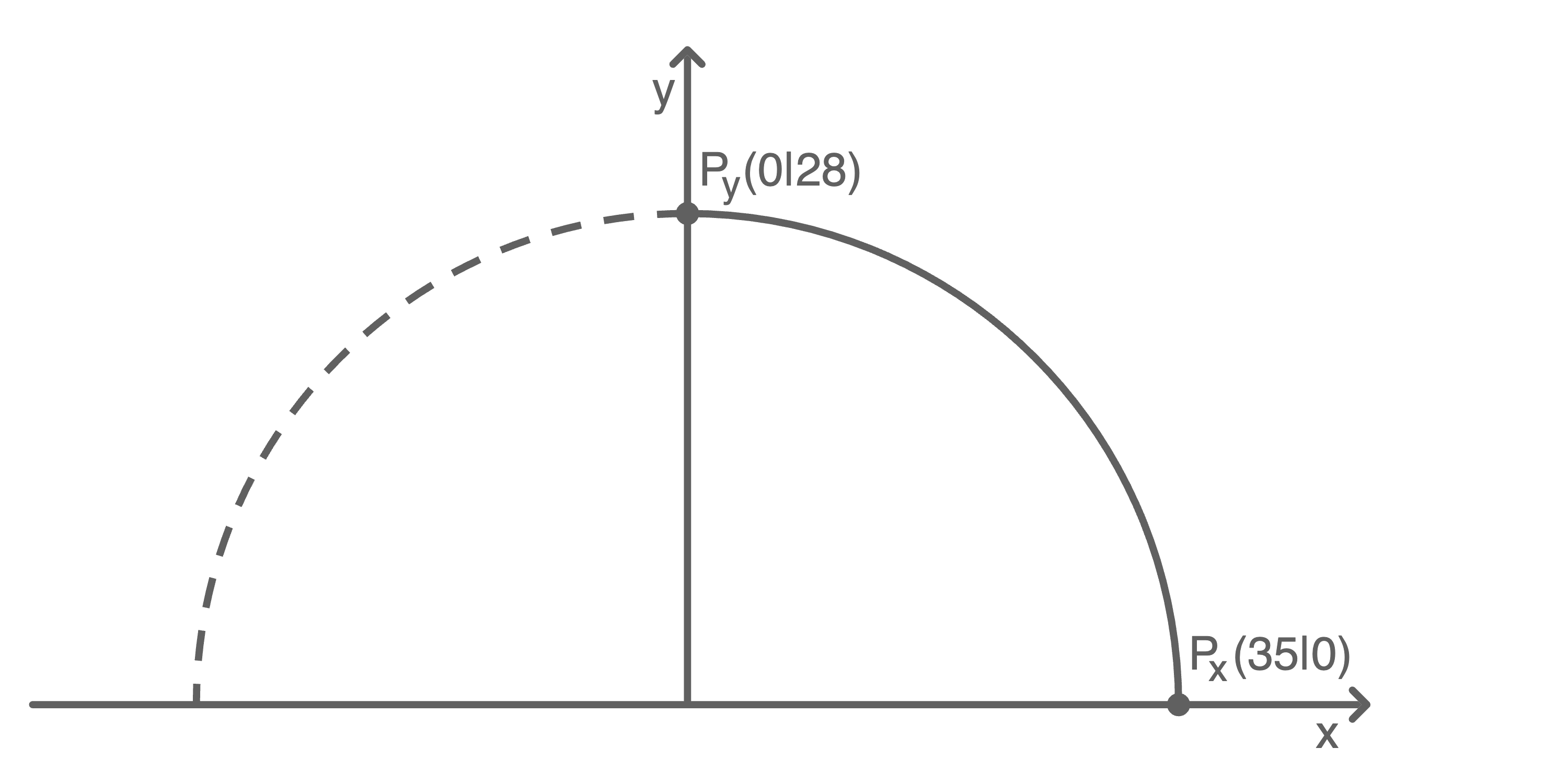
2.1
Allgemeine quadratische Funktionsgleichung:
 Es kann davon ausgegangen werden, dass der Bogen symmetrisch zur
Es kann davon ausgegangen werden, dass der Bogen symmetrisch zur  -Achse ist. Die
-Achse ist. Die  -Achse liegt folglich genau in der Mitte des Bogens und verläuft durch dessen höchsten Punkt. Die
-Achse liegt folglich genau in der Mitte des Bogens und verläuft durch dessen höchsten Punkt. Die  -Achse beschreibt den Boden, auf dem der Bogen steht.
-Achse beschreibt den Boden, auf dem der Bogen steht.
 Im CAS kann die Funktion
Im CAS kann die Funktion  gespeichert und das lineare Gleichungssystem aufgestellt werden:
gespeichert und das lineare Gleichungssystem aufgestellt werden:


 Das CAS liefert
Das CAS liefert  und
und  Die quadratische Funktion ergibt sich also zu:
Die quadratische Funktion ergibt sich also zu:

Aufgrund der Symmetrie lässt sich die quadratische Funktion vereinfachen zu:
 Zur Bestimmung der beiden Parameter ist ein Gleichungssystem mit 2 Bedingungen erforderlich.
Zur Bestimmung der beiden Parameter ist ein Gleichungssystem mit 2 Bedingungen erforderlich.
- Da der Bogen eine Höhe von
hat, ergibt sich
- Aus der Gesamtänge von
folgt

2.2
Da der Bogen an der höchsten Stelle einen Knick hat, bedeutet dies, dass die Krümmung des Bogens an dieser Stelle nicht stetig ist. Quadratische Funktionen können jedoch nur eine einfache Parabel erzeugen.
Die Verwendung von quadratischen Funktionen kann also möglicherweise zu einer ungenauen Modellierung führen, insbesondere im Bereich des Knickpunktes.
Zur genaueren Modellierung des Knicks könnten Funktionen höheren Grades verwendet werden oder eine abschnittsweise definierte Funktion mit zwei quadratischen Gleichungen für den linken und den rechten Teil des Bogens aufgestellt werden.
3.1
Ein Graph ist genau dann achsensymmetrisch zur  -Achse, wenn gilt:
-Achse, wenn gilt:
 Mit den Definitionsbereichen folgt also, dass gelten soll:
Mit den Definitionsbereichen folgt also, dass gelten soll:
![\(\begin{array}[t]{rll}
K_2(-x)&=& K_1(x)& \\[5pt]
\sqrt{1296 - \left(-x + \dfrac{1}{10}\right)^2} - 8&=& \sqrt{1296 - \left(x - \dfrac{1}{10}\right)^2} - 8&\\[5pt]
\sqrt{1296 - \left(-\left(x - \dfrac{1}{10}\right)\right)^2} - 8&=& \sqrt{1296 - \left(x - \dfrac{1}{10}\right)^2} - 8& \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/58773c29dd919924ce792fe080fe3aacc334ef4711b26e6977a21ec56e60f3e1_light.svg) Da sich die beiden Funktionen nur im Vorzeichen von
Da sich die beiden Funktionen nur im Vorzeichen von  unterscheiden und dieser Term in beiden Gleichungen anschließend quadriert wird, gilt
unterscheiden und dieser Term in beiden Gleichungen anschließend quadriert wird, gilt  Der äußere Rand des Bogens ist folglich achsensymmetrisch zur
Der äußere Rand des Bogens ist folglich achsensymmetrisch zur  -Achse.
-Achse.
3.2
1. Schritt: Differenzfunktion  aufstellen
aufstellen
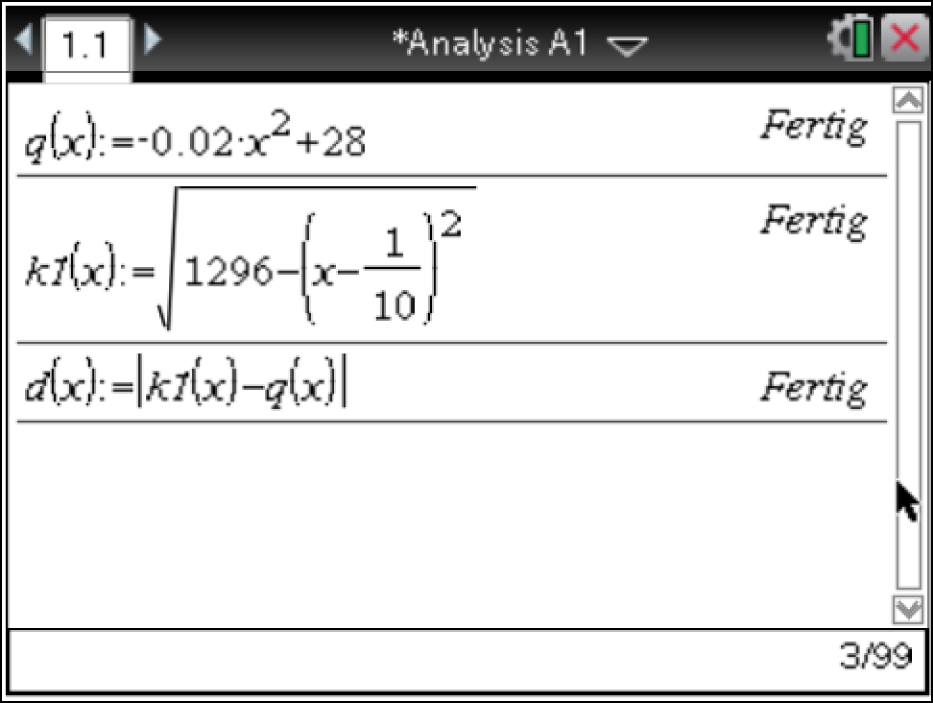 2. Schritt: Maximum bestimmen
2. Schritt: Maximum bestimmen
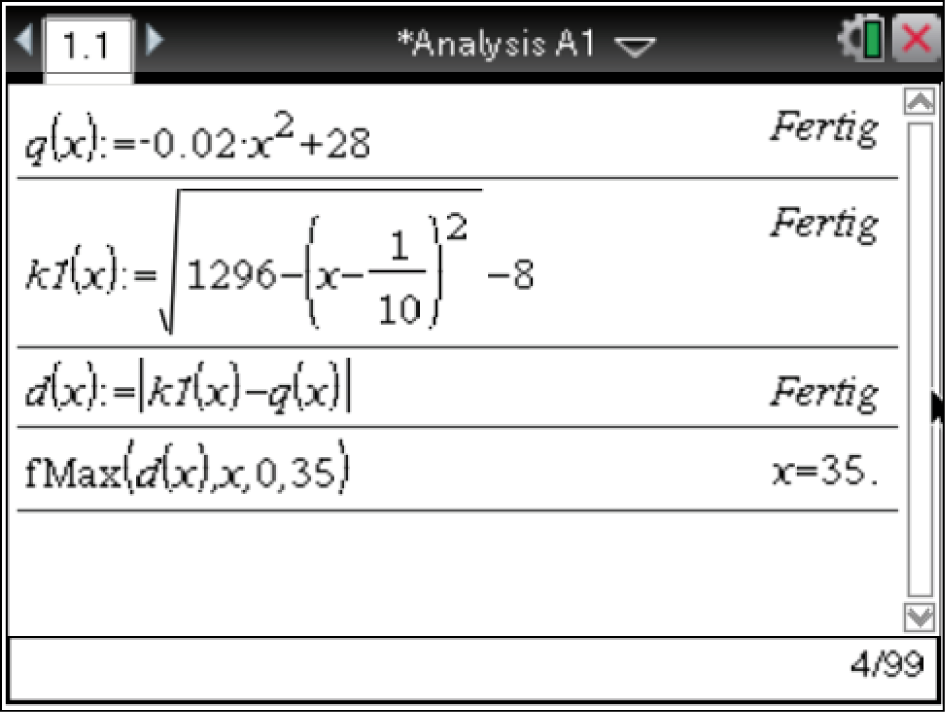 Das CAS liefert, dass sich die Maximalstelle am Rand des Intervalls an der Stelle
Das CAS liefert, dass sich die Maximalstelle am Rand des Intervalls an der Stelle  befindet.
3. Schritt:
befindet.
3. Schritt:  -Koordinate berechnen
Mit dem CAS ergibt sich:
-Koordinate berechnen
Mit dem CAS ergibt sich:
![\(d(35) \approx 2,67 \; [\text{m}]\)](https://www.schullv.de/resources/formulas/7874fe4b02896a1a69f1b902177ff26590d4a0d2fa4466d25f953d16897c1233_light.svg) Der maximale Höhenunterschied zwischen dem Graphen von
Der maximale Höhenunterschied zwischen dem Graphen von  und
und  beträgt also etwa
beträgt also etwa 
Die beiden Funktionen  und
und  können im CAS definiert werden.
Die Differenzfunktion
können im CAS definiert werden.
Die Differenzfunktion  ergibt sich nun aus dem Betrag der Differenz von
ergibt sich nun aus dem Betrag der Differenz von  und
und 


Der maximale Höhenunterschied entspricht der  -Koordinate des Maximums der Differenzfunktion.
Mit dem Befehl
-Koordinate des Maximums der Differenzfunktion.
Mit dem Befehl  des CAS kann das globale Maximum von
des CAS kann das globale Maximum von  bestimmt werden:
bestimmt werden:
 Als Funktion wird
Als Funktion wird  , als Variable wird
, als Variable wird  und als Intervall wird
und als Intervall wird ![\([0;35]\)](https://www.schullv.de/resources/formulas/788c38377e301c1dfbe94c12b026d44168202c2f152874d0198195624b82c30a_light.svg) gewählt.
gewählt.

3.3
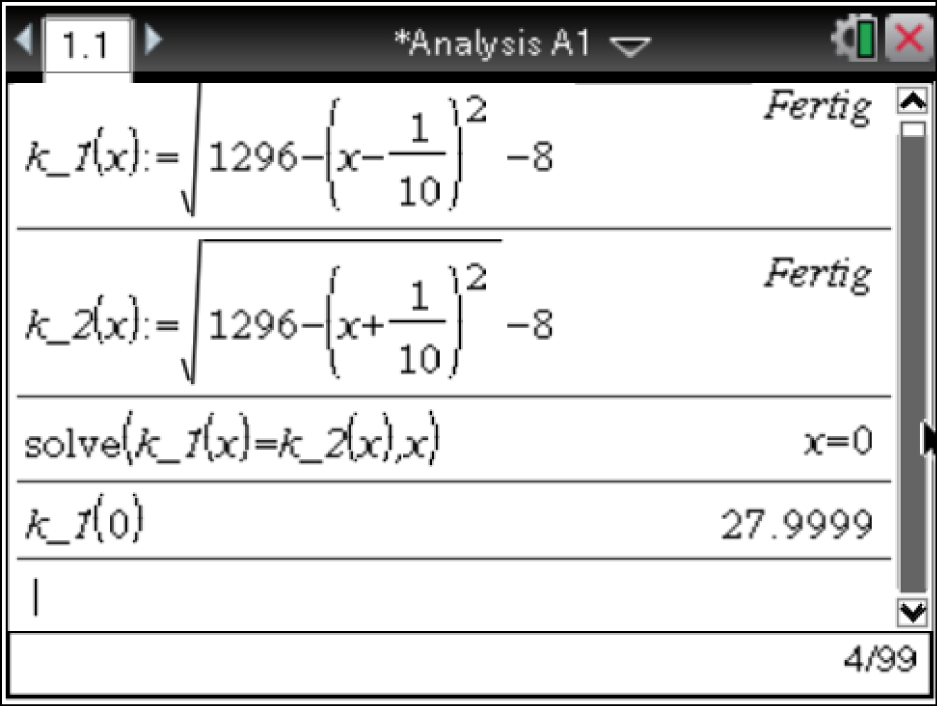
1. Schritt: Schnittpunkt  bestimmen
bestimmen
 2. Schritt: Winkel zur Horizontalen ermitteln
2. Schritt: Winkel zur Horizontalen ermitteln
 Die Winkel zur Horizontalen folgen also mit:
Die Winkel zur Horizontalen folgen also mit:
![\(\begin{array}[t]{rll}
\tan(\alpha_1)&=& 0,0028& \quad \scriptsize \mid \tan^{-1}\\[5pt]
\alpha_1&\approx& 0,16& \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/6c5ae4157cab3f67e901d4552f697d1cdcf9bb5b78aa1ee6eedb1208fa6f7f6c_light.svg)
![\(\begin{array}[t]{rll}
\tan(\alpha_2)&=& -0,0028^\circ & \quad \scriptsize \mid \tan^{-1}\\[5pt]
\alpha_2&\approx& -0,16^\circ& \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/724fdb4d360c9c90db223f25e3eb8198c9ffda4b2789034bfc627d7821940037_light.svg) 3. Schritt: Schnittwinkel
3. Schritt: Schnittwinkel  berechnen
Für den Schnittwinkel gilt:
berechnen
Für den Schnittwinkel gilt:
![\(\begin{array}[t]{rll}
\alpha_S&=& 180\text{°} - |\alpha_1| - |\alpha_2| & \\[5pt]
&\approx& 180\text{°} - 0,16\text{°}- 0,16\text{°}& \\[5pt]
&=& 179,68\,\text{°}& \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/cfef80203049eac01c35afd6c2de7c5eff31f6f8efe8198c31cf90a872a36672_light.svg) Die Graphen von
Die Graphen von  und
und  schneiden sich an der höchsten Stelle des Bogens unter einem Winkel von
schneiden sich an der höchsten Stelle des Bogens unter einem Winkel von 
Im CAS können die beiden Funktionsterme  und
und  definiert werden und mit Hilfe des
definiert werden und mit Hilfe des  -Befehls die Schnittstellen der Graphen ermittelt werden.
Das CAS liefert die Schnittstelle
-Befehls die Schnittstellen der Graphen ermittelt werden.
Das CAS liefert die Schnittstelle  Die
Die  -Koordinate folgt mit:
-Koordinate folgt mit:
 Die Graphen von
Die Graphen von  und
und  schneiden sich somit im Punkt
schneiden sich somit im Punkt 

Für den Winkel  bzw.
bzw.  der Graphen
der Graphen  bzw.
bzw.  zur Horizontalen im betrachteten Punkt
zur Horizontalen im betrachteten Punkt  gilt:
gilt:
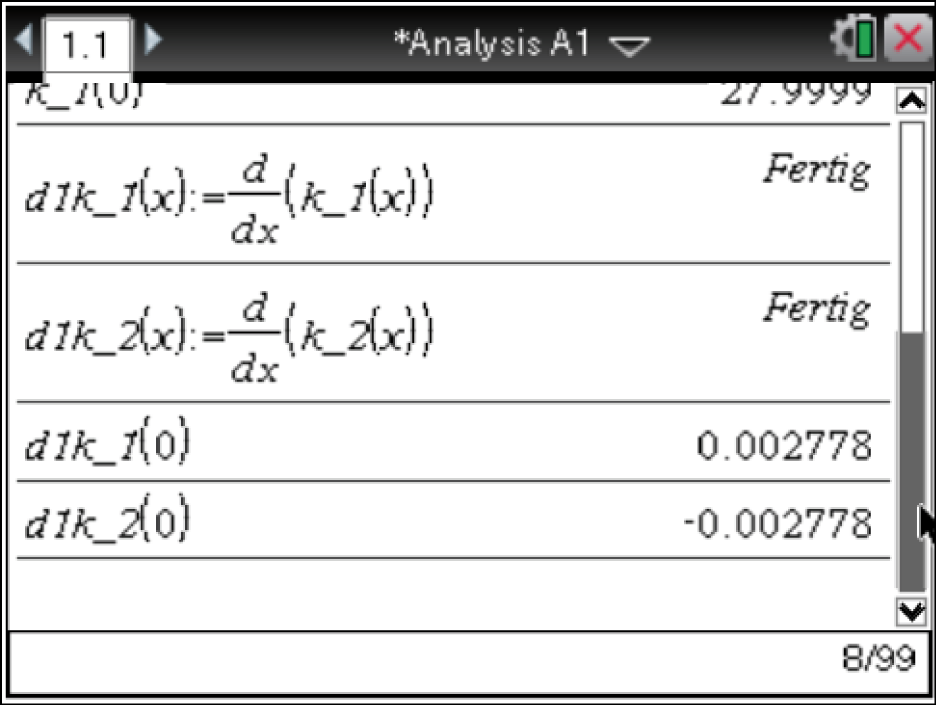
 Hierbei beschreibt
Hierbei beschreibt  die Steigung der Funktion im betrachteten Punkt
die Steigung der Funktion im betrachteten Punkt  Diese entspricht jeweils der Ableitung an der Stelle
Diese entspricht jeweils der Ableitung an der Stelle 
 Der CAS liefert:
Der CAS liefert:
 und
und 

3.4
Die Oberfläche des Bauwerks, welche die Stoffhülle abdecken soll, kann in drei Bereiche unterteilt werden:
 1. Schritt:
1. Schritt:  berechnen
berechnen
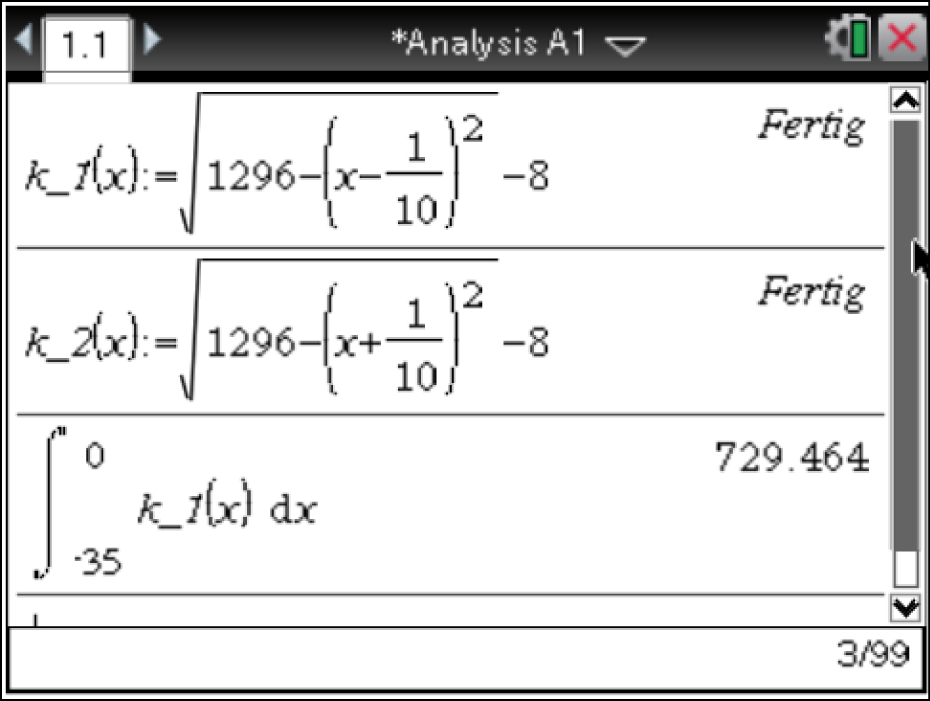 Es gilt also:
Es gilt also:
![\(\begin{array}[t]{rll}
A_{v/h}&=& 2 \cdot 729,46\,\text{m}^2 & \\[5pt]
&=& 1458,92\,\text{m}^2
\end{array}\)](https://www.schullv.de/resources/formulas/a84bffa20eddde8fc096de62aaefb088dc3836f08a57752be18c88be0c08e2e2_light.svg) 2. Schritt: Bogenlänge
2. Schritt: Bogenlänge  ermitteln
ermitteln
 3. Schritt:
3. Schritt:  bestimmen
Aus Abbildung 2 folgt die Breite des Bauwerks mit
bestimmen
Aus Abbildung 2 folgt die Breite des Bauwerks mit  Der Flächeninhalt des Zwischenstreifens ergibt sich also zu:
Der Flächeninhalt des Zwischenstreifens ergibt sich also zu:
![\(\begin{array}[t]{rll}
A&=& L\cdot b & \\[5pt]
&=& 96,76\,\text{m} \cdot 14\,\text{m}& \\[5pt]
&=& 1354,64\,\text{m}^2
\end{array}\)](https://www.schullv.de/resources/formulas/82523fcd54dadb3788f1acb9942ccd71b03b89286304896646f7422f46a9b64b_light.svg) 4. Schritt: Gesamtflächeninhalt berechnen
Die Menge des benötigten Stoffes ergibt sich nun durch die Summe der einzelnen Flächeninhalte:
4. Schritt: Gesamtflächeninhalt berechnen
Die Menge des benötigten Stoffes ergibt sich nun durch die Summe der einzelnen Flächeninhalte:
![\(\begin{array}[t]{rll}
A_{ges}&=& A_v + A_h + A_S& \\[5pt]
&=& 1458,92\,\text{m}^2 + 1458,92\,\text{m}^2+ 1354,64\,\text{m}^2& \\[5pt]
&=& 4271,92
\end{array}\)](https://www.schullv.de/resources/formulas/dee33d228e2f2b398f88fd5b39e8aa12661c635bfe2e11cc105ec32fa074a0d3_light.svg) Es werden also insgesamt etwa
Es werden also insgesamt etwa  Stoff benötigt, um das Bauwerk einzuhüllen.
Stoff benötigt, um das Bauwerk einzuhüllen.
- Fläche vorne mit dem Flächeninhalt
- Fläche hinten mit dem Flächeninhalt
- Zwischenstreifen mit dem Flächeninhalt
Aufgrund der Achsensymmetrie des Bogens ist es ausreichend,  über dem Intervall
über dem Intervall ![\([-35;0]\)](https://www.schullv.de/resources/formulas/e0f86dd90ddfbb3ae0aeeb1628b0c7d70ef8f811198cadafc3e6ce56fc1e0cb3_light.svg) zu integrieren. Das Doppelte des resultierenden Flächeninhalts entspricht dann
zu integrieren. Das Doppelte des resultierenden Flächeninhalts entspricht dann  bzw.
bzw. 
 Angeben der Integrationsgrenzen
Angeben der Integrationsgrenzen  und
und  der Funktion
der Funktion  und der Variablen
und der Variablen  nach der integriert werden soll, liefert:
nach der integriert werden soll, liefert:
![\(\displaystyle\int_{-35}^{0}K_1(x)\;\mathrm dx\approx 729,46 \; [\text{m}^2]\)](https://www.schullv.de/resources/formulas/96e358c29f4a3a9ea199422c5316af0cde3eff4490422888ffdd44c720b76d4e_light.svg)

Aufgrund der Symmetrie genügt es auch hier, nur den Graphen von  zu betrachten. Die Länge des Bogens ergibt sich dann aus dem Doppelten der Länge des Bogens über
zu betrachten. Die Länge des Bogens ergibt sich dann aus dem Doppelten der Länge des Bogens über ![\([-35;0].\)](https://www.schullv.de/resources/formulas/a04a7cb0fd5e34a20cbcccdcb0caf98309ea12db847048d89dc532706e873822_light.svg) Mit dem CAS kann die Funktion
Mit dem CAS kann die Funktion  abgeleitet werden:
abgeleitet werden:
 Einsetzen der Integralgrenzen
Einsetzen der Integralgrenzen  und
und  sowie der Funktion
sowie der Funktion  in die Formel zur Berechnung der Länge eines Graphen liefert:
in die Formel zur Berechnung der Länge eines Graphen liefert:
![\(\begin{array}[t]{rll}
L&=& \displaystyle\int_{-35}^{0}\sqrt{1+\left(K_1](https://www.schullv.de/resources/formulas/6b17bb772ba53c16758f6eee09634a15fafada40f7ab7c50fe8eb1146114524a_light.svg)
Die Länge des Bogens beträgt also etwa
3.5
Für das Volumen eines Prismas gilt:
 Die Grundfläche
Die Grundfläche  entspricht hierbei der Fläche der vorderen bzw. hinteren Fläche des Bogens mit dem Flächeninhalt
entspricht hierbei der Fläche der vorderen bzw. hinteren Fläche des Bogens mit dem Flächeninhalt  bzw.
bzw.  Die Höhe des Prismas ist gegeben durch die Breite des Bogens.
Das Volumen
Die Höhe des Prismas ist gegeben durch die Breite des Bogens.
Das Volumen  des Bogens ergibt sich also zu:
des Bogens ergibt sich also zu:
![\(\begin{array}[t]{rll}
V&=& G \cdot h & \\[5pt]
&=& 1458,92\,\text{m}^2 \cdot 14\,\text{m}& \\[5pt]
&=& 20424,88\,\text{m}^3
\end{array}\)](https://www.schullv.de/resources/formulas/7bda9c7dafd80fb0ae3f1790cee6bb2bcd0647496fe9b3081c273797eefd02fb_light.svg) Das Volumen des Bauwerks beträgt folglich etwa
Das Volumen des Bauwerks beträgt folglich etwa 
1.1
Höhenunterschied bestimmen
![\(\begin{array}[t]{rll}
\sin (\alpha)&=& \dfrac{\text{Gegenkathete}}{\text{Hypotenuse}}& \\[5pt]
\sin (6 ^\circ) &=& \dfrac{h}{540\,\text{m}}&\quad \scriptsize \,\bigg \vert \, \cdot 540\,\text{m} \\[5pt]
\sin (6^\circ) \cdot 540\,\text{m}&=& h& \\[5pt]
56,45\,\text{m} &\approx& h
\end{array}\)](https://www.schullv.de/resources/formulas/f44821513c16301b5499ac3bb2940e24db706a635f736a533500dc0acb27b27f_light.svg)
 Ein
Ein  langer geradliniger und um
langer geradliniger und um  geneigter Wanderweg überwindet also einen Höhenunterschied von ungefähr
geneigter Wanderweg überwindet also einen Höhenunterschied von ungefähr  Angaben beurteilen
Im Vergleich des Höhenunterschied zu der Größe bzw. dem überwundenen Höhenunterschieds des Bogens fällt auf, dass dieser nur
Angaben beurteilen
Im Vergleich des Höhenunterschied zu der Größe bzw. dem überwundenen Höhenunterschieds des Bogens fällt auf, dass dieser nur  hoch ist und lediglich einen Höhenunterschied von
hoch ist und lediglich einen Höhenunterschied von  überwindet.
Ein Grund dafür könnte sein, dass die Skulptur jeweils an den äußeren Enden eine waagerechte Plattform besitzt, die ebenfalls in die Länge des
überwindet.
Ein Grund dafür könnte sein, dass die Skulptur jeweils an den äußeren Enden eine waagerechte Plattform besitzt, die ebenfalls in die Länge des  langen Aufstiegs zählt.
Ein weiterer Grund könnte sein, dass der Anstiegswinkel im Prospekt nicht richtig angegeben wurde und dieser in Wahrheit kleiner ist.
langen Aufstiegs zählt.
Ein weiterer Grund könnte sein, dass der Anstiegswinkel im Prospekt nicht richtig angegeben wurde und dieser in Wahrheit kleiner ist.

Hilfsskizze (nicht maßstäblich)
1.2
Steigung berechnen
Eine Steigung von  entspricht einer Zunahme der Höhe um 6 Meter pro 100 Meter in waagerechter Richtung.
entspricht einer Zunahme der Höhe um 6 Meter pro 100 Meter in waagerechter Richtung.
![\(\begin{array}[t]{rll}
\tan (\alpha)&=&\dfrac{\text{Gegenkathete}}{\text{Ankathete}} & \\[5pt]
\tan (6^\circ)&=& \dfrac{h_s}{100\,\text{m}}&\quad \scriptsize \mid\; \cdot 100\,\text{m} \\[5pt]
\tan (6^\circ) \cdot 100\,\text{m}&=& h_s& \\[5pt]
10,51\,\text{m}&\approx& h_s
\end{array}\)](https://www.schullv.de/resources/formulas/aa14ae281b5eae257ba8adb4b5a48ab40190f0b244b5a0fb6c21b0c8113e7b15_light.svg)
 Ein um
Ein um  geneigter Wanderweg besitzt also einen Anstieg von
geneigter Wanderweg besitzt also einen Anstieg von  Entscheidung
Ein solcher Wanderweg ist folglich nicht für Rollstuhlfahrer geeignet.
Entscheidung
Ein solcher Wanderweg ist folglich nicht für Rollstuhlfahrer geeignet.

Hilfsskizze (nicht maßstäblich)
2.1
Allgemeine quadratische Funktionsgleichung:
 Es kann davon ausgegangen werden, dass der Bogen symmetrisch zur
Es kann davon ausgegangen werden, dass der Bogen symmetrisch zur  -Achse ist. Die
-Achse ist. Die  -Achse liegt folglich genau in der Mitte des Bogens und verläuft durch dessen höchsten Punkt. Die
-Achse liegt folglich genau in der Mitte des Bogens und verläuft durch dessen höchsten Punkt. Die  -Achse beschreibt den Boden, auf dem der Bogen steht.
-Achse beschreibt den Boden, auf dem der Bogen steht.
 Im CAS kann die Funktion
Im CAS kann die Funktion  gespeichert und das lineare Gleichungssystem aufgestellt werden:
gespeichert und das lineare Gleichungssystem aufgestellt werden:



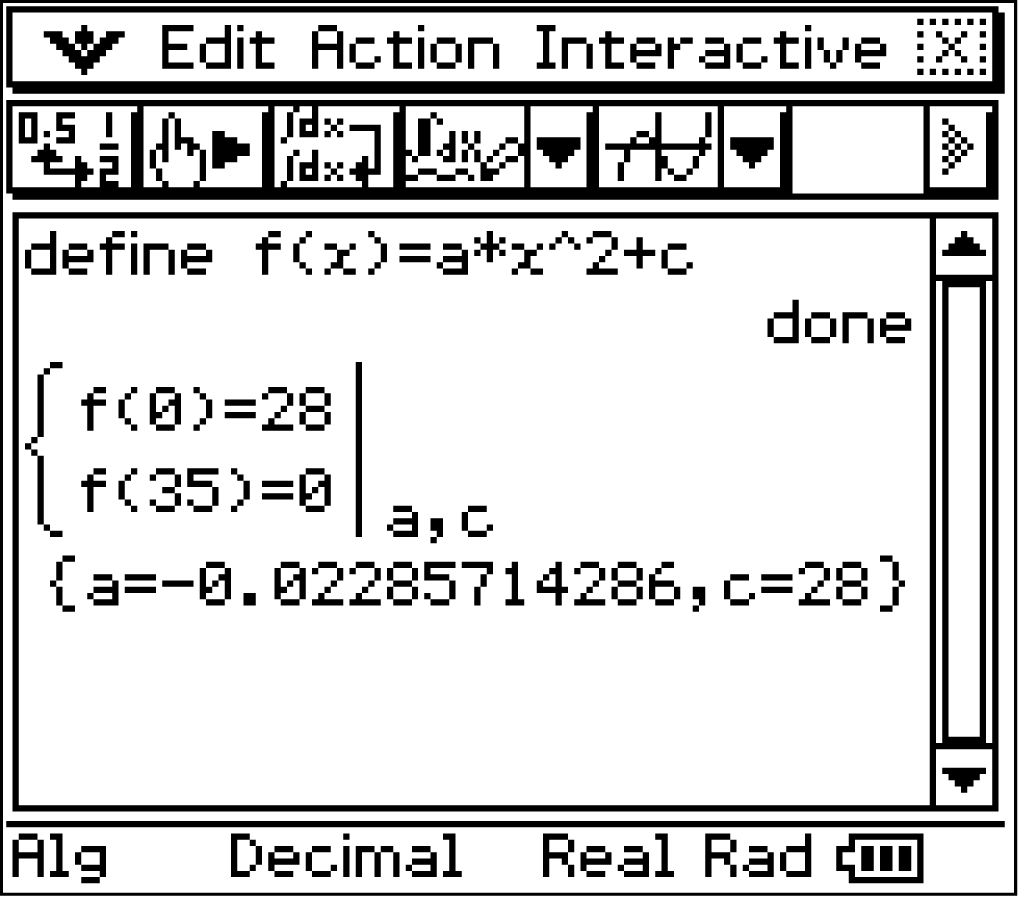 Das CAS liefert
Das CAS liefert  und
und  Die quadratische Funktion ergibt sich also zu:
Die quadratische Funktion ergibt sich also zu:

Aufgrund der Symmetrie lässt sich die quadratische Funktion vereinfachen zu:
 Zur Bestimmung der beiden Parameter ist ein Gleichungssystem mit 2 Bedingungen erforderlich.
Zur Bestimmung der beiden Parameter ist ein Gleichungssystem mit 2 Bedingungen erforderlich.
- Da der Bogen eine Höhe von
hat, ergibt sich
- Aus der Gesamtänge von
folgt


2.2
Da der Bogen an der höchsten Stelle einen Knick hat, bedeutet dies, dass die Krümmung des Bogens an dieser Stelle nicht stetig ist. Quadratische Funktionen können jedoch nur eine einfache Parabel erzeugen.
Die Verwendung von quadratischen Funktionen kann also möglicherweise zu einer ungenauen Modellierung führen, insbesondere im Bereich des Knickpunktes.
Zur genaueren Modellierung des Knicks könnten Funktionen höheren Grades verwendet werden oder eine abschnittsweise definierte Funktion mit zwei quadratischen Gleichungen für den linken und den rechten Teil des Bogens aufgestellt werden.
3.1
Ein Graph ist genau dann achsensymmetrisch zur  -Achse, wenn gilt:
-Achse, wenn gilt:
 Mit den Definitionsbereichen folgt also, dass gelten soll:
Mit den Definitionsbereichen folgt also, dass gelten soll:
![\(\begin{array}[t]{rll}
K_2(-x)&=& K_1(x)& \\[5pt]
\sqrt{1296 - \left(-x + \dfrac{1}{10}\right)^2} - 8&=& \sqrt{1296 - \left(x - \dfrac{1}{10}\right)^2} - 8&\\[5pt]
\sqrt{1296 - \left(-\left(x - \dfrac{1}{10}\right)\right)^2} - 8&=& \sqrt{1296 - \left(x - \dfrac{1}{10}\right)^2} - 8& \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/58773c29dd919924ce792fe080fe3aacc334ef4711b26e6977a21ec56e60f3e1_light.svg) Da sich die beiden Funktionen nur im Vorzeichen von
Da sich die beiden Funktionen nur im Vorzeichen von  unterscheiden und dieser Term in beiden Gleichungen anschließend quadriert wird, gilt
unterscheiden und dieser Term in beiden Gleichungen anschließend quadriert wird, gilt  Der äußere Rand des Bogens ist folglich achsensymmetrisch zur
Der äußere Rand des Bogens ist folglich achsensymmetrisch zur  -Achse.
-Achse.
3.2
1. Schritt: Differenzfunktion  aufstellen
aufstellen
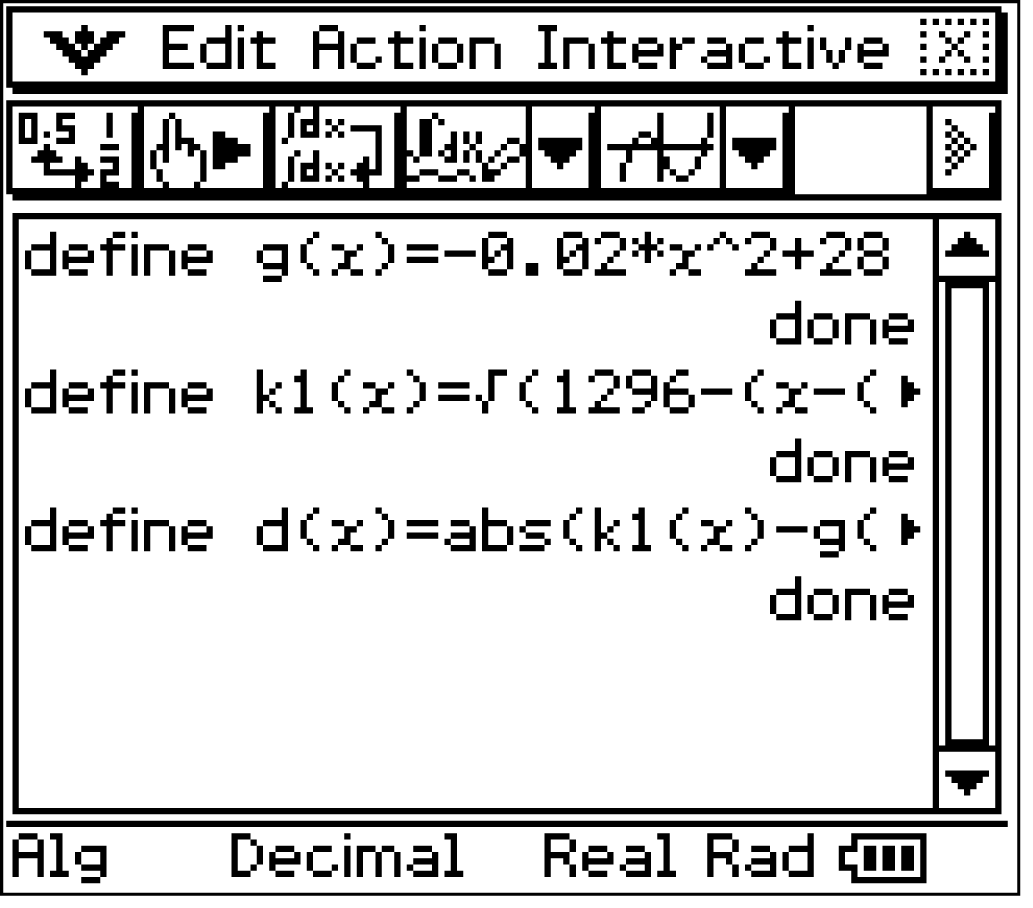 2. Schritt: Maximum bestimmen
2. Schritt: Maximum bestimmen
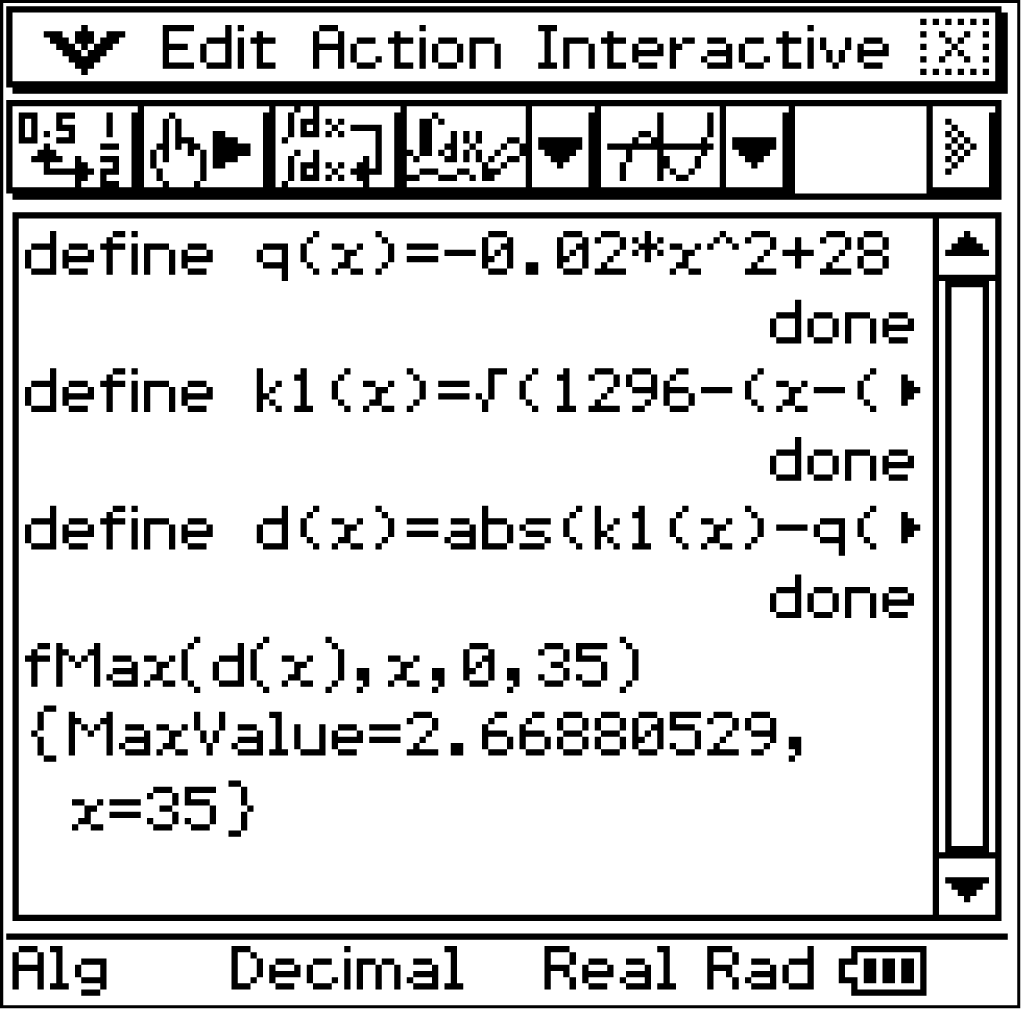 Das CAS liefert, dass sich die Maximalstelle am Rand des Intervalls an der Stelle
Das CAS liefert, dass sich die Maximalstelle am Rand des Intervalls an der Stelle  befindet.
3. Schritt:
befindet.
3. Schritt:  -Koordinate berechnen
Mit dem CAS ergibt sich:
-Koordinate berechnen
Mit dem CAS ergibt sich:
![\(d(35) \approx 2,67 \; [\text{m}]\)](https://www.schullv.de/resources/formulas/7874fe4b02896a1a69f1b902177ff26590d4a0d2fa4466d25f953d16897c1233_light.svg) Der maximale Höhenunterschied zwischen dem Graphen von
Der maximale Höhenunterschied zwischen dem Graphen von  und
und  beträgt also etwa
beträgt also etwa 
Die beiden Funktionen  und
und  können im CAS definiert werden.
Die Differenzfunktion
können im CAS definiert werden.
Die Differenzfunktion  ergibt sich nun aus dem Betrag der Differenz von
ergibt sich nun aus dem Betrag der Differenz von  und
und 


Der maximale Höhenunterschied entspricht der  -Koordinate des Maximums der Differenzfunktion.
Mit dem Befehl
-Koordinate des Maximums der Differenzfunktion.
Mit dem Befehl  des CAS kann das globale Maximum von
des CAS kann das globale Maximum von  bestimmt werden:
bestimmt werden:
 Als Funktion wird
Als Funktion wird  , als Variable wird
, als Variable wird  und als Intervall wird
und als Intervall wird ![\([0;35]\)](https://www.schullv.de/resources/formulas/788c38377e301c1dfbe94c12b026d44168202c2f152874d0198195624b82c30a_light.svg) gewählt.
gewählt.

3.3
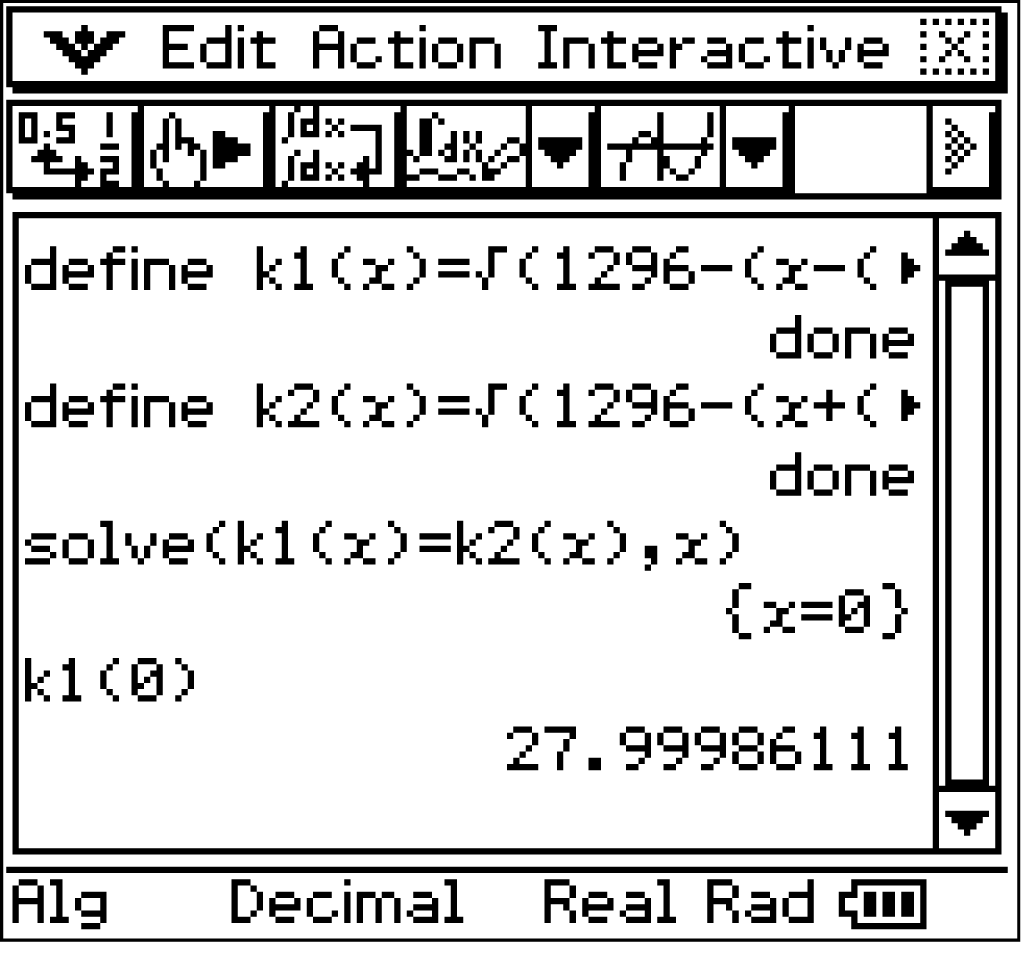
1. Schritt: Schnittpunkt  bestimmen
bestimmen
 2. Schritt: Winkel zur Horizontalen ermitteln
2. Schritt: Winkel zur Horizontalen ermitteln
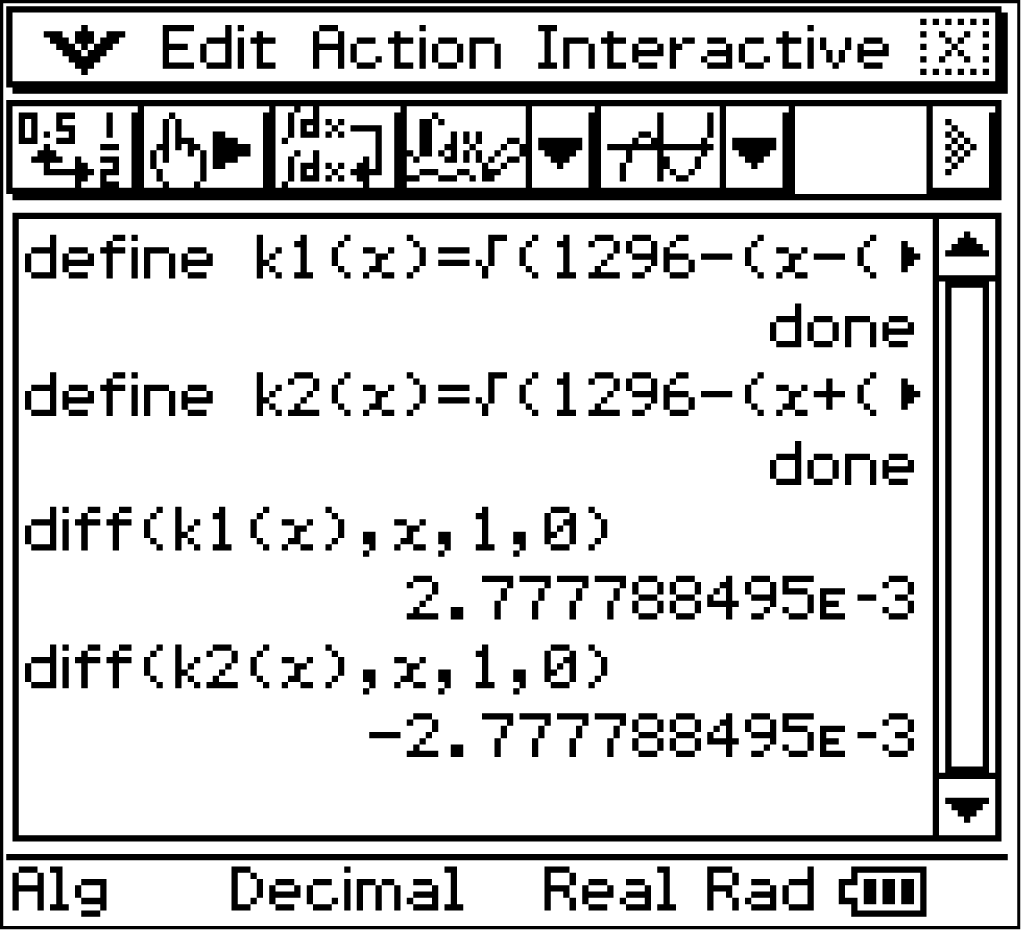 Die Winkel zur Horizontalen folgen also mit:
Die Winkel zur Horizontalen folgen also mit:
![\(\begin{array}[t]{rll}
\tan(\alpha_1)&=& 0,0028& \quad \scriptsize \mid \tan^{-1}\\[5pt]
\alpha_1&\approx& 0,16& \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/6c5ae4157cab3f67e901d4552f697d1cdcf9bb5b78aa1ee6eedb1208fa6f7f6c_light.svg)
![\(\begin{array}[t]{rll}
\tan(\alpha_2)&=& -0,0028^\circ & \quad \scriptsize \mid \tan^{-1}\\[5pt]
\alpha_2&\approx& -0,16^\circ& \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/724fdb4d360c9c90db223f25e3eb8198c9ffda4b2789034bfc627d7821940037_light.svg) 3. Schritt: Schnittwinkel
3. Schritt: Schnittwinkel  berechnen
Für den Schnittwinkel gilt:
berechnen
Für den Schnittwinkel gilt:
![\(\begin{array}[t]{rll}
\alpha_S&=& 180\text{°} - |\alpha_1| - |\alpha_2| & \\[5pt]
&\approx& 180\text{°} - 0,16\text{°}- 0,16\text{°}& \\[5pt]
&=& 179,68\,\text{°}& \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/cfef80203049eac01c35afd6c2de7c5eff31f6f8efe8198c31cf90a872a36672_light.svg) Die Graphen von
Die Graphen von  und
und  schneiden sich an der höchsten Stelle des Bogens unter einem Winkel von
schneiden sich an der höchsten Stelle des Bogens unter einem Winkel von 
Im CAS können die beiden Funktionsterme  und
und  definiert werden und mit Hilfe des
definiert werden und mit Hilfe des  -Befehls die Schnittstellen der Graphen ermittelt werden.
Das CAS liefert die Schnittstelle
-Befehls die Schnittstellen der Graphen ermittelt werden.
Das CAS liefert die Schnittstelle  Die
Die  -Koordinate folgt mit:
-Koordinate folgt mit:
 Die Graphen von
Die Graphen von  und
und  schneiden sich somit im Punkt
schneiden sich somit im Punkt 

Für den Winkel  bzw.
bzw.  der Graphen
der Graphen  bzw.
bzw.  zur Horizontalen im betrachteten Punkt
zur Horizontalen im betrachteten Punkt  gilt:
gilt:
 Hierbei beschreibt
Hierbei beschreibt  die Steigung der Funktion im betrachteten Punkt
die Steigung der Funktion im betrachteten Punkt  Diese entspricht jeweils der Ableitung an der Stelle
Diese entspricht jeweils der Ableitung an der Stelle 
 Der CAS liefert:
Der CAS liefert:
 und
und 

3.4
Die Oberfläche des Bauwerks, welche die Stoffhülle abdecken soll, kann in drei Bereiche unterteilt werden:
 1. Schritt:
1. Schritt:  berechnen
berechnen
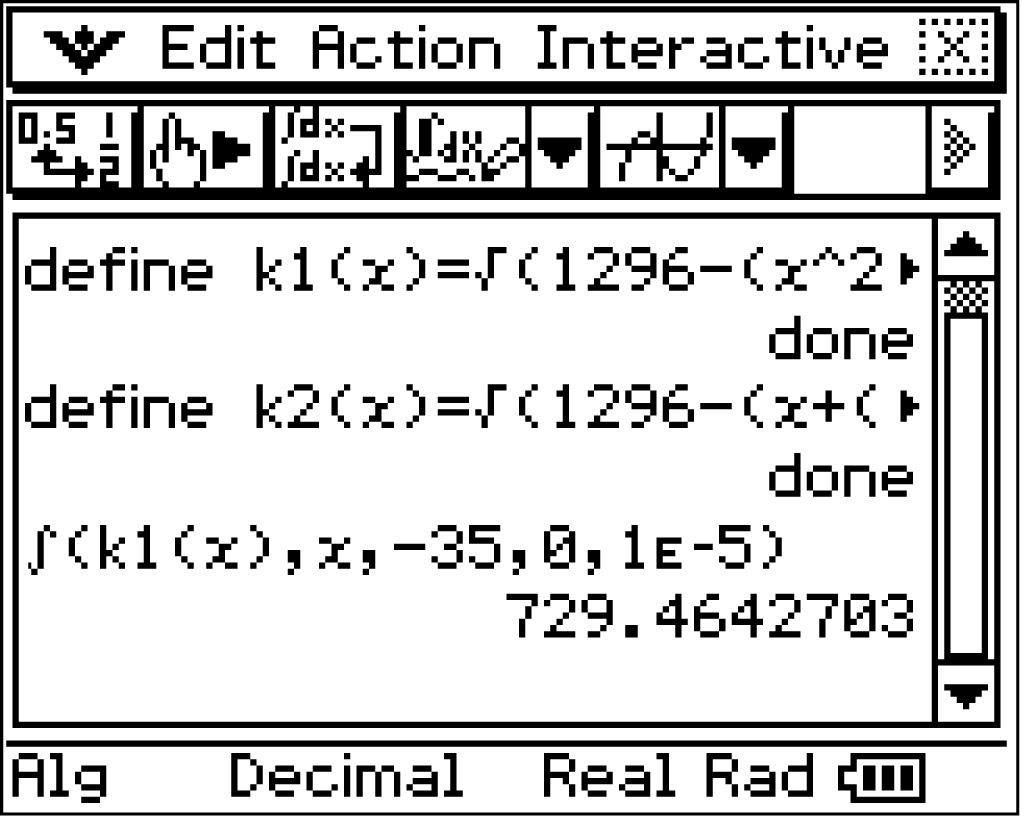 Es gilt also:
Es gilt also:
![\(\begin{array}[t]{rll}
A_{v/h}&=& 2 \cdot 729,46\,\text{m}^2 & \\[5pt]
&=& 1458,92\,\text{m}^2
\end{array}\)](https://www.schullv.de/resources/formulas/a84bffa20eddde8fc096de62aaefb088dc3836f08a57752be18c88be0c08e2e2_light.svg) 2. Schritt: Bogenlänge
2. Schritt: Bogenlänge  ermitteln
ermitteln
 Die Länge des Bogens beträgt also etwa
Die Länge des Bogens beträgt also etwa  3. Schritt:
3. Schritt:  bestimmen
Aus Abbildung 2 folgt die Breite des Bauwerks mit
bestimmen
Aus Abbildung 2 folgt die Breite des Bauwerks mit  Der Flächeninhalt des Zwischenstreifens ergibt sich also zu:
Der Flächeninhalt des Zwischenstreifens ergibt sich also zu:
![\(\begin{array}[t]{rll}
A&=& L\cdot b & \\[5pt]
&=& 96,76\,\text{m} \cdot 14\,\text{m}& \\[5pt]
&=& 1354,64\,\text{m}^2
\end{array}\)](https://www.schullv.de/resources/formulas/82523fcd54dadb3788f1acb9942ccd71b03b89286304896646f7422f46a9b64b_light.svg) 4. Schritt: Gesamtflächeninhalt berechnen
Die Menge des benötigten Stoffes ergibt sich nun durch die Summe der einzelnen Flächeninhalte:
4. Schritt: Gesamtflächeninhalt berechnen
Die Menge des benötigten Stoffes ergibt sich nun durch die Summe der einzelnen Flächeninhalte:
![\(\begin{array}[t]{rll}
A_{ges}&=& A_v + A_h + A_S& \\[5pt]
&=& 1458,92\,\text{m}^2 + 1458,92\,\text{m}^2+ 1354,64\,\text{m}^2& \\[5pt]
&=& 4271,92
\end{array}\)](https://www.schullv.de/resources/formulas/dee33d228e2f2b398f88fd5b39e8aa12661c635bfe2e11cc105ec32fa074a0d3_light.svg) Es werden also insgesamt etwa
Es werden also insgesamt etwa  Stoff benötigt, um das Bauwerk einzuhüllen.
Stoff benötigt, um das Bauwerk einzuhüllen.
- Fläche vorne mit dem Flächeninhalt
- Fläche hinten mit dem Flächeninhalt
- Zwischenstreifen mit dem Flächeninhalt
Aufgrund der Achsensymmetrie des Bogens ist es ausreichend,  über dem Intervall
über dem Intervall ![\([-35;0]\)](https://www.schullv.de/resources/formulas/e0f86dd90ddfbb3ae0aeeb1628b0c7d70ef8f811198cadafc3e6ce56fc1e0cb3_light.svg) zu integrieren. Das Doppelte des resultierenden Flächeninhalts entspricht dann
zu integrieren. Das Doppelte des resultierenden Flächeninhalts entspricht dann  bzw.
bzw. 
 Angeben der Integrationsgrenzen
Angeben der Integrationsgrenzen  und
und  der Funktion
der Funktion  und der Variablen
und der Variablen  nach der integriert werden soll, liefert:
nach der integriert werden soll, liefert:
![\(\displaystyle\int_{-35}^{0}K_1(x)\;\mathrm dx\approx 729,46 \; [\text{m}^2]\)](https://www.schullv.de/resources/formulas/96e358c29f4a3a9ea199422c5316af0cde3eff4490422888ffdd44c720b76d4e_light.svg)

Aufgrund der Symmetrie genügt es auch hier, nur den Graphen von  zu betrachten. Die Länge des Bogens ergibt sich dann aus dem Doppelten der Länge des Bogens über
zu betrachten. Die Länge des Bogens ergibt sich dann aus dem Doppelten der Länge des Bogens über ![\([-35;0].\)](https://www.schullv.de/resources/formulas/a04a7cb0fd5e34a20cbcccdcb0caf98309ea12db847048d89dc532706e873822_light.svg) Mit dem CAS kann die Funktion
Mit dem CAS kann die Funktion  abgeleitet werden:
abgeleitet werden:
 Einsetzen der Integralgrenzen
Einsetzen der Integralgrenzen  und
und  sowie der Funktion
sowie der Funktion  in die Formel zur Berechnung der Länge eines Graphen liefert:
in die Formel zur Berechnung der Länge eines Graphen liefert:
![\(\begin{array}[t]{rll}
L&=& \displaystyle\int_{-35}^{0}\sqrt{1+\left(K_1](https://www.schullv.de/resources/formulas/6b17bb772ba53c16758f6eee09634a15fafada40f7ab7c50fe8eb1146114524a_light.svg)

3.5
Für das Volumen eines Prismas gilt:
 Die Grundfläche
Die Grundfläche  entspricht hierbei der Fläche der vorderen bzw. hinteren Fläche des Bogens mit dem Flächeninhalt
entspricht hierbei der Fläche der vorderen bzw. hinteren Fläche des Bogens mit dem Flächeninhalt  bzw.
bzw.  Die Höhe des Prismas ist gegeben durch die Breite des Bogens.
Das Volumen
Die Höhe des Prismas ist gegeben durch die Breite des Bogens.
Das Volumen  des Bogens ergibt sich also zu:
des Bogens ergibt sich also zu:
![\(\begin{array}[t]{rll}
V&=& G \cdot h & \\[5pt]
&=& 1458,92\,\text{m}^2 \cdot 14\,\text{m}& \\[5pt]
&=& 20424,88\,\text{m}^3
\end{array}\)](https://www.schullv.de/resources/formulas/7bda9c7dafd80fb0ae3f1790cee6bb2bcd0647496fe9b3081c273797eefd02fb_light.svg) Das Volumen des Bauwerks beträgt folglich etwa
Das Volumen des Bauwerks beträgt folglich etwa 
