B1 – Analysis

Wenn ein Patient eine Tablette einnimmt, wird das Medikament im Laufe der Zeit im Blut aufgenommen. Parallel zur Aufnahme im Blut beginnt der Körper, das Medikament wieder abzubauen. Im Gebiet der Pharmakokinetik werden diese Zusammenhänge untersucht und Modelle entwickelt, um Aussagen über die Wirkung von Medikamenten treffen zu können. Eine Tablette wird zum Zeitpunkt $\mathrm{t}=0$ eingenommen. In Abhängigkeit von der Zeit t wird die Medikamentenkonzentration im Blut betrachtet. Dabei kann der zeitliche Verlauf der Zunahmerate der Medikamentenkonzentration im Blut durch eine (monoton fallende) Exponentialfunktion beschrieben werden.

Die Graphen der drei Funktionen $m,$ $z$ und $a$ sind in Material 1 dargestellt. Dabei gibt $m$ die Medikamentenkonzentration, $z$ die Zunahmerate und $a$ die Abnahmerate der Medikamentenkonzentration im Blut eines bestimmten Patienten an.
Skizziere den Graphen der Funktion $\(m$ mit $\(m$ in Abbildung 1.

Abbildung 1

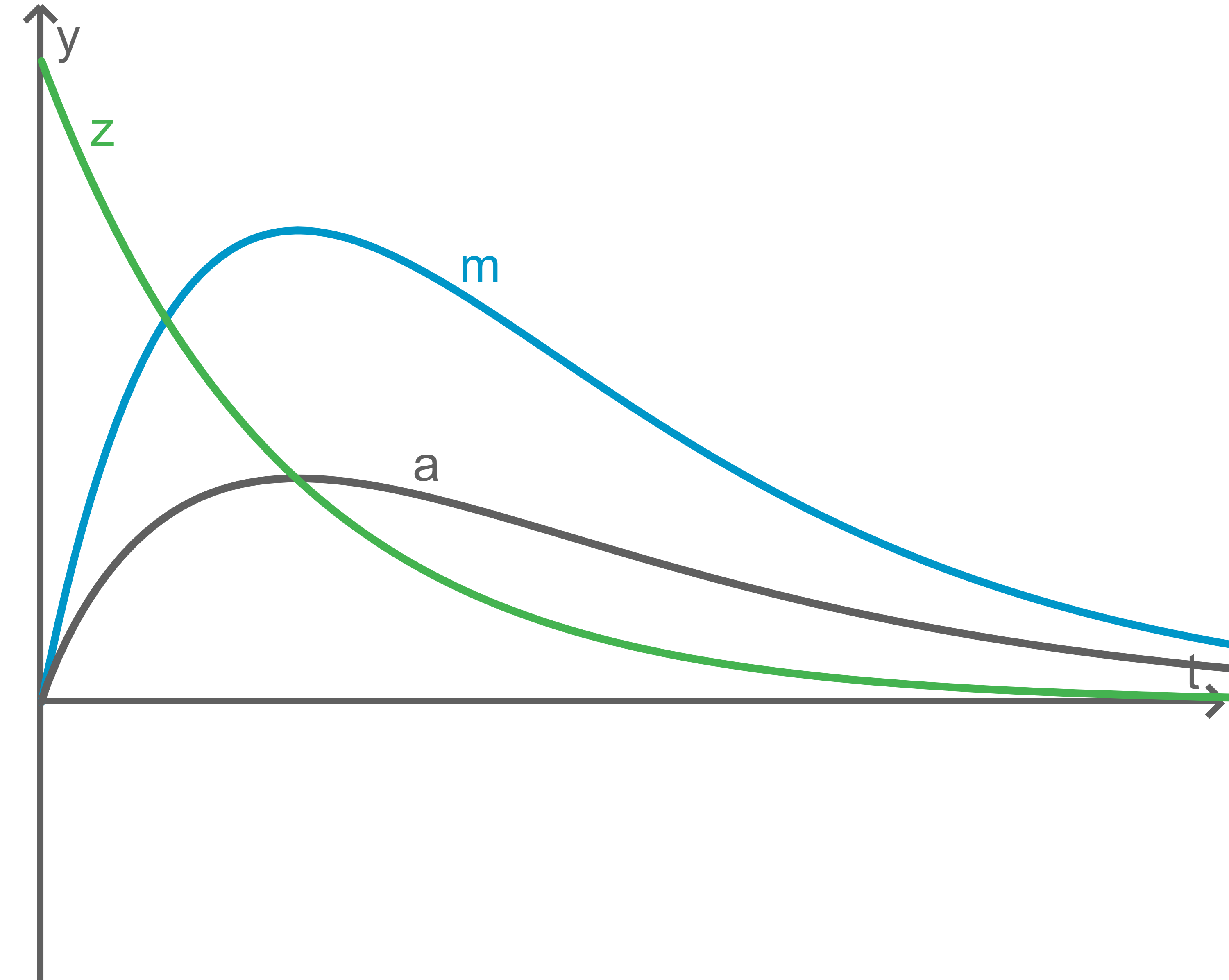
Beschreibe die Bedeutung der Nullstelle von $\(m$ und die Bedeutung der Stelle, an der der Graph von $\(m$ einen Tiefpunkt hat, im Hinblick auf die Medikamentenkonzentration im Blut des Patienten.

(5 BE)

Für bestimmte Patienten lässt sich die Medikamentenkonzentration im Blut durch eine Funktion der Schar $f_{c ; k}$ mit $f_{c ; k}(t)=c \cdot t \cdot \mathrm e^{-k \cdot t}$ beschreiben, wobei $c$ und $k$ positive Konstanten sind.

2.1

Zeige rechnerisch, dass für den Zusammenhang zwischen den Funktionen der Schar $f_{c ; k}$ und den Ableitungsfunktionen $\(f_{c ; k}$ die Gleichung $\(f_{c ; k}$ gilt.

(3 BE)

2.2

Zeige, dass für die Ableitungsfunktionen $\(f_{c ; k}$ die Gleichung $\(f_{c ; k}$ gilt.
Berechne die Wendestelle der Schar $f_{c ; k}.$
Hinweis: Die Untersuchung der notwendigen Bedingung ist ausreichend.

(5 BE)

2.3

Der Inhalt der Fläche zwischen den Graphen der Funktionen der Schar $f_{c ; k}$ und der $t$ -Achse ist ein Maß für die Bioverfügbarkeit des Medikaments. Die Funktionenschar $F_{c ; k}$ mit $F_{c ; k}(t)=\left(-\frac{c}{k} \cdot t-\frac{c}{k^2}\right) \cdot \mathrm e^{-k \cdot t}$ ist eine Stammfunktionenschar von $f_{c ; k}.$
Zeige unter Angabe einer geeigneten Grenzwertargumentation, dass $\lim\limits_{x\to\infty}\displaystyle\int_{0}^{x}f_{c ; k}(t)\;\mathrm dt=\frac{c}{k^2}$ gilt.

(3 BE)

Der Verlauf der Medikamentenkonzentration im Blut eines anderen Patienten, der um 19:00 Uhr $(t=0)$ eine Tablette einnimmt, lässt sich durch eine sogenannte Bateman-Funktion $b$ mit $b(t)=10 \cdot\left(\mathrm e^{-0,25 \cdot t}-\mathrm e^{-0,5 \cdot t}\right)$ beschreiben, wobei $t$ die Zeit in Stunden nach Einnahme der Tablette und $b(t)$ die Medikamentenkonzentration im Blut in Milligramm pro Liter beschreibt. Der Graph von $b$ ist in Abbildung 2 dargestellt.

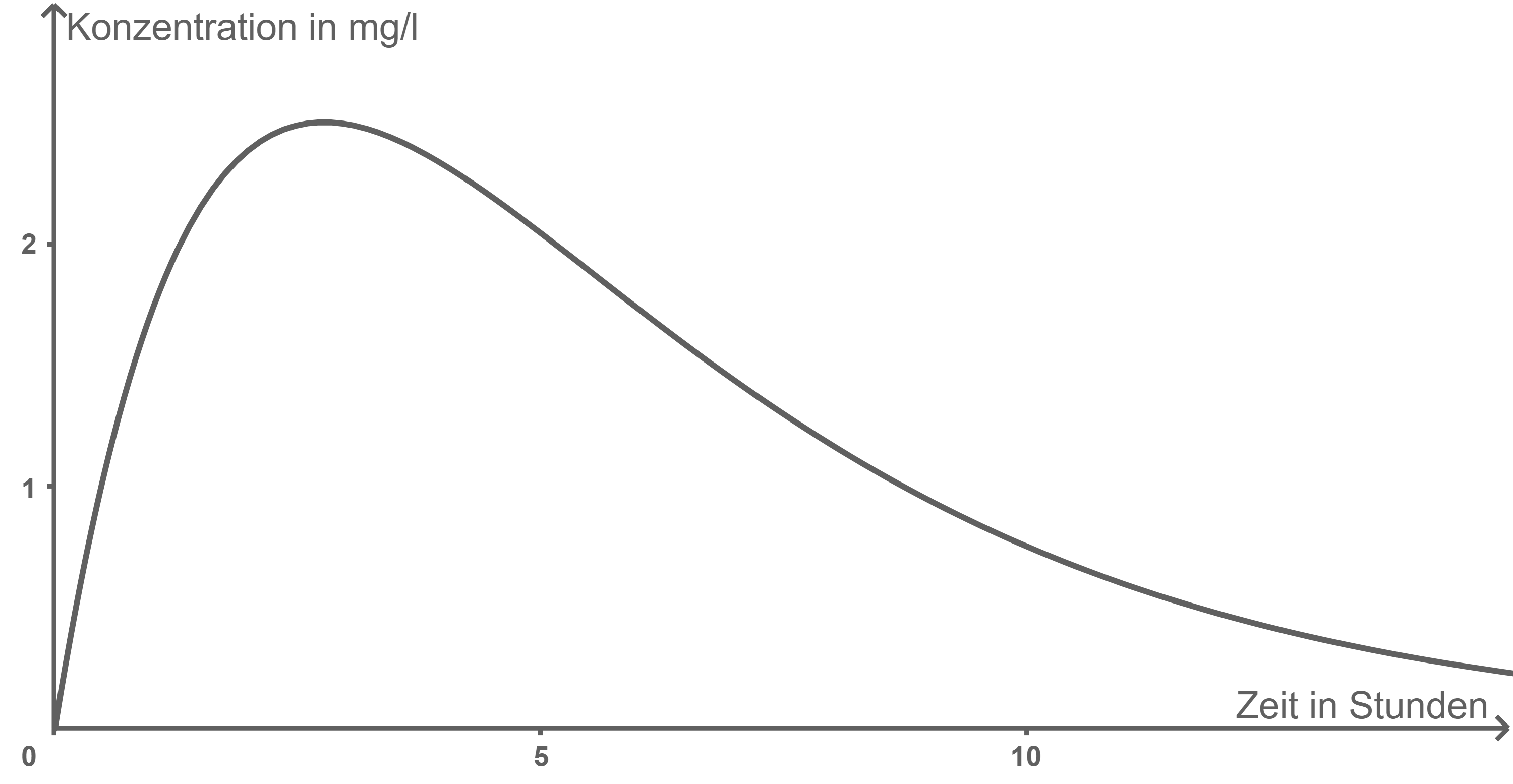
Abbildung 2

3.1

Berechne den Wert des Terms $\frac{1}{12} \cdot \displaystyle\int_{0}^{12}b(t)\;\mathrm dt$ und deute das Ergebnis im Sachzusammenhang.

(5 BE)

3.2

Berechne den Zeitpunkt, zu dem die Medikamentenkonzentration im Blut maximal ist.

Hinweis: Die Untersuchung der notwendigen Bedingung ist ausreichend.

(4 BE)

3.3

Das Medikament wirkt, wenn die Medikamentenkonzentration im Blut mindestens 1 Milligramm pro Liter beträgt. Ein Schaden für den Körper kann entstehen, wenn die Medikamentenkonzentration auf über 4 Milligramm pro Liter steigt. Durch die gleichzeitige Einnahme von zwei Tabletten verdoppelt sich die Medikamentenkonzentration zu jedem Zeitpunkt.
Ermittle, um wie viel Prozent sich die Wirkungsdauer des Medikaments durch die gleichzeitige Einnahme von zwei Tabletten gegenüber der Einnahme von einer Tablette verlängert.
Beurteile, ob durch die gleichzeitige Einnahme von zwei Tabletten ein Schaden für den Körper entstehen kann.

(5 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Graphen skizzieren

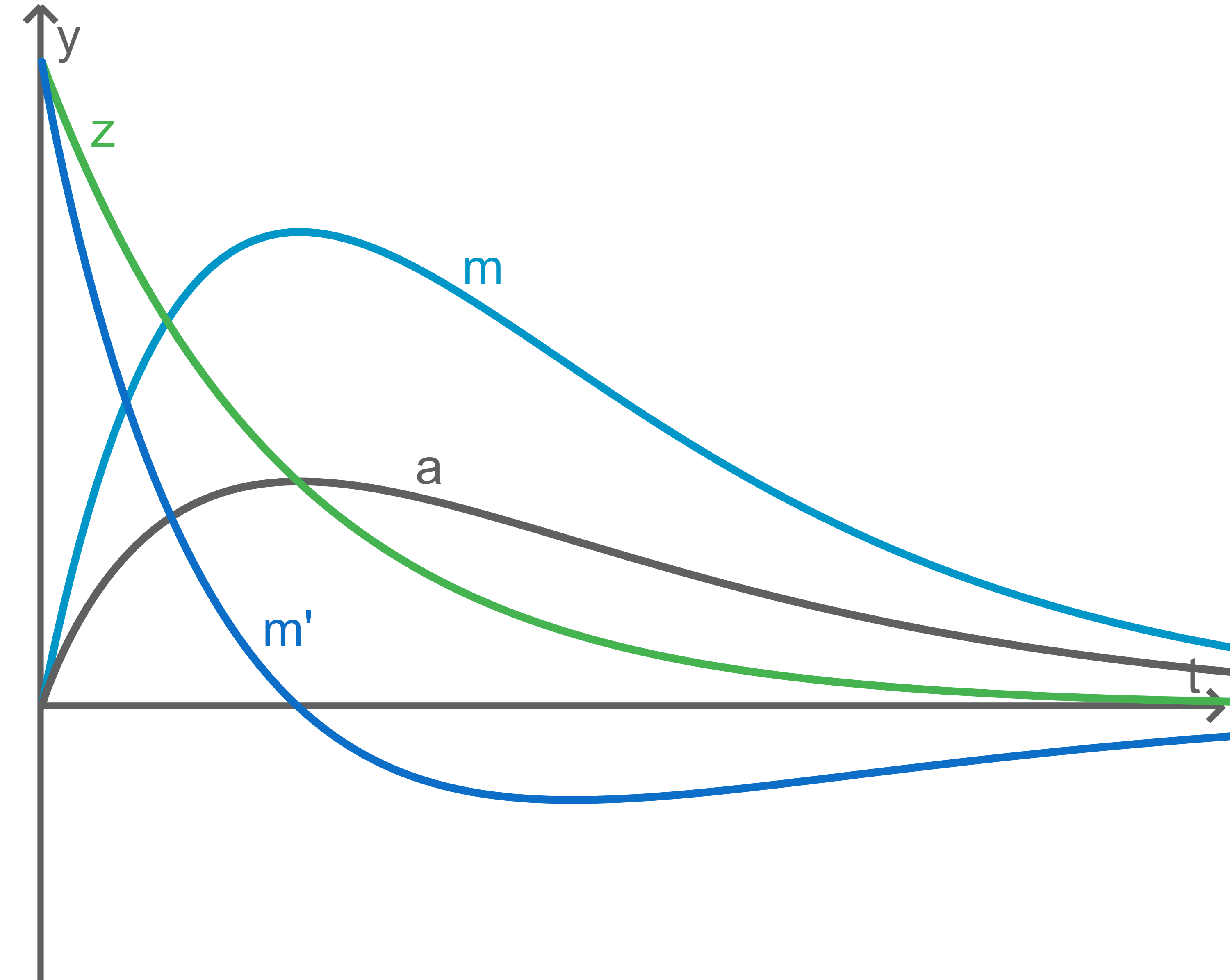
Bedeutung der beiden Stellen angeben

Die Funktion $\(m$ beschreibt die Änderungsrate der Medikamentenkonzentration. Die Nullstelle des Graphen von $\(m$ gibt somit den Zeitpunkt an, zu dem $m$ einen Hochpunkt besitzt, d.h. zu dem die Medikamentenkonzentration maximal ist.
An der Stelle des Tiefpunkts des Graphen von $\(m$ nimmt die Medikamentenkonzentration damit am stärksten ab.

2.1

Für die Ableitung von $f_{c;k}$ liefert der CAS:

$\(f_{c;k}$

2.2

Für die zweite Ableitung von $f_{c;k}$ liefert der CAS:

$\(f_{c;k}$

Anwenden der notwendigen Bedingung $\(f_{c;k}$ für Wendestellen liefert mit dem solve-Befehl des CAS:

$t=\dfrac{2}{k}$

Da laut Aufgabenstellung die Untersuchung der notwendigen Bedingung ausreichend ist, folgt damit, dass die Schar $f_{c;k}$ an der Stelle $t=\frac{2}{k}$ eine Wendestelle besitzt.

2.3

Rechenweg anzeigen

$\lim\limits_{x\to\infty}\displaystyle\int_{0}^{x}f_{c;k}(t)\;\mathrm dt$ $= \lim\limits_{x\to\infty}\left(\left(-\frac{c}{k} \cdot x-\frac{c}{k^2}\right) \cdot \mathrm{e}^{-k \cdot x}-\left(-\frac{c}{k^2}\right)\right)$

Es gilt $\lim\limits_{x\to\infty}\left(-\frac{c}{k} \cdot x-\frac{c}{k^2}\right)=-\infty$ und $\lim\limits_{x\to\infty}\mathrm{e}^{-k \cdot x}=0.$ Da die $\mathrm e$ -Funktion allerdings deutlich schneller gegen Null geht als die lineare Funktion gegen ihren Grenzwert, besitzt das Produkt der beiden Terme den Grenzwert Null. Damit folgt:

Rechenweg anzeigen

$\lim\limits_{x\to\infty}\left(\left(-\frac{c}{k} \cdot x-\frac{c}{k^2}\right) \cdot \mathrm{e}^{-k \cdot x}-\left(-\frac{c}{k^2}\right)\right)$ $= \frac{c}{k^2}$

Damit ist die gewünschte Gleichung $\lim\limits_{x\to\infty}\displaystyle\int_{0}^{x}f_{c;k}(t)\;\mathrm dt=\frac{c}{k^2}$ gezeigt.

3.1

Wert berechnen

Rechenweg anzeigen

$\dfrac{1}{12}\cdot\displaystyle\int_{0}^{12}b(t)\;\mathrm dt \approx 1,5$

Ergebnis im Sachzusammenhang deuten

In den ersten $12$ Stunden nach Einnahme der Tablette beträgt die durchschnittliche Medikamentenkonzentration im Blut des Patienten ca. $1,5$ Milligramm pro Liter.

3.2

Für die Ableitung von $b$ liefert der CAS:

$\(b$

Anwenden der notwendigen Bedingung $\(b$ für Extremstellen liefert mit dem solve-Befehl des CAS:

$t\approx2,77$

Da die Untersuchung der notwendigen Bedingung ausreichend ist, folgt somit, dass die Medikamentenkonzentration im Blut ca. $2,77$ Stunden nach Einnahme der Tablette maximal ist.

3.3

Prozentuale Verlängerung ermitteln

$\begin{array}[t]{rlll} b(t)&=&1 \\[5pt] 10 \cdot\left(\mathrm e^{-0,25 \cdot t}-\mathrm e^{-0,5 \cdot t}\right)&=&1 \end{array}$

Mit dem solve-Befehl des CAS folgt:

$\begin{array}[t]{rlll} t_1&\approx&0,478 \\[5pt] t_2&\approx&8,732 \end{array}$

Bei der doppelten Medikamentenkonzentration gilt:

$\begin{array}[t]{rlll} 2\cdot b(t)&=&1 \\[5pt] 20 \cdot\left(\mathrm e^{-0,25 \cdot t}-\mathrm e^{-0,5 \cdot t}\right)&=&1 \end{array}$

Mit dem solve-Befehl des CAS folgt:

$\begin{array}[t]{rlll} t_3&\approx&0,217 \\[5pt] t_4&\approx&11,766 \end{array}$

Insgesamt ergibt sich:

$\dfrac{t_4-t_3}{t_2-t_1}\approx1,4$

Die Wirkungsdauer des Medikaments verlängert sich somit um ca. $0,4=40\,\%.$

Möglichen Schaden beurteilen

Die Abbildung liefert, dass die $y$ -Koordinate des Hochpunktes des Graphen von $b$ größer als $2$ ist. Nach Verdopplung der Medikamentenkonzentration ist diese somit größer als $4,$ sodass durch die gleichzeitige Einnahme von zwei Tabletten ein Schaden für den Körper entstehen kann.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?