A2 - Analysis
1
In der nachfolgenden Tabelle ist die Entwicklung der Schulden der Länder und Gemeinden in Deutschland zwischen  und
und  dargestellt.
dargestellt. 
1.1
Zeichne die Werte in das folgende Koordinatensystem.
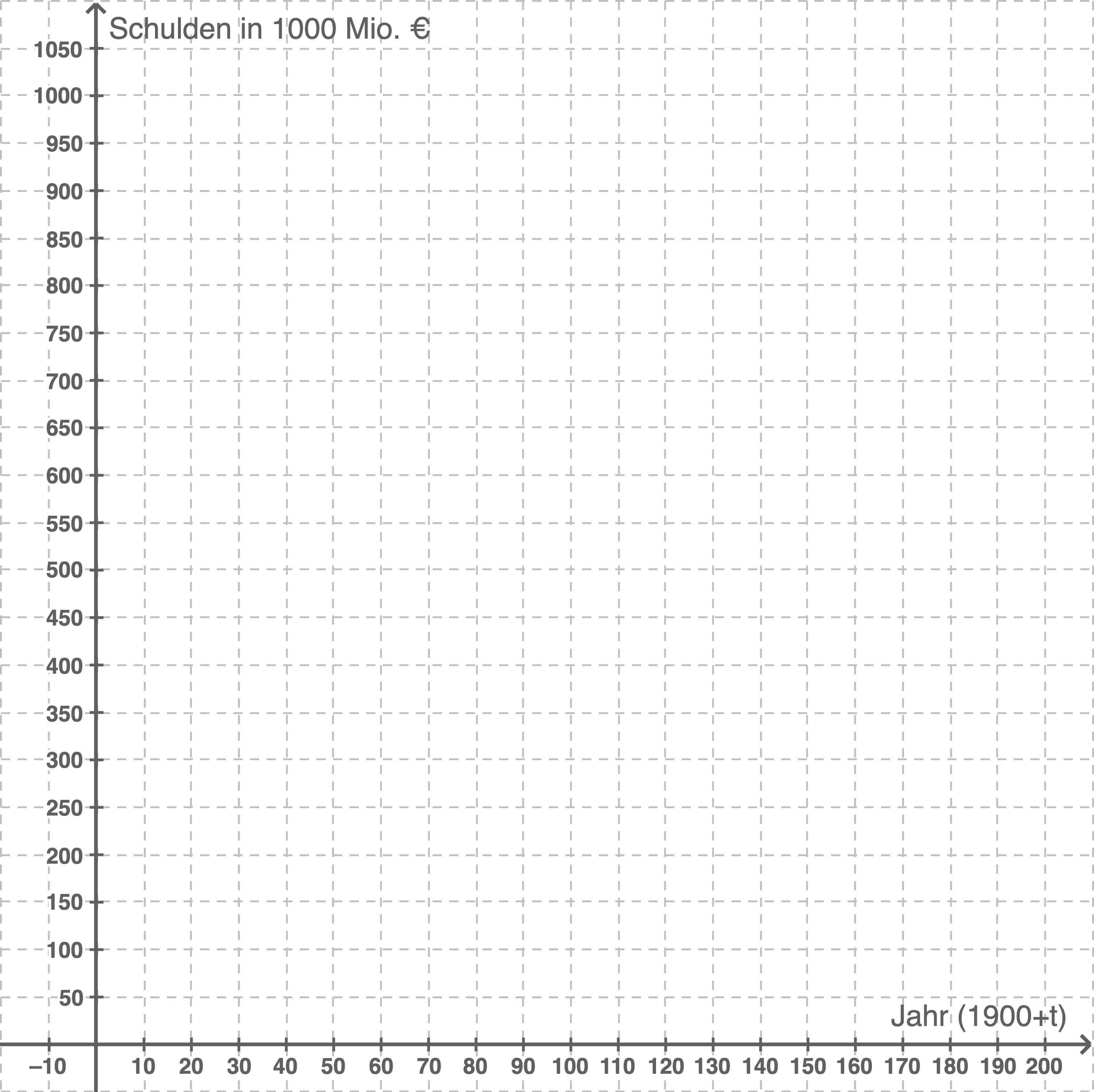

(4 BE)
1.2
Bestimme eine quadratische Funktion und eine Exponentialfunktion, die zu den gegebenen Wertepaaren möglichst gut passen.
Beurteile diese in Bezug auf ihre Eignung für die Modellierung der Entwicklung der Schulden für den angegebenen Zeitraum.
Beurteile diese in Bezug auf ihre Eignung für die Modellierung der Entwicklung der Schulden für den angegebenen Zeitraum.
(6 BE)
2
Eine andere Möglichkeit, die Entwicklung der Schulden zu modellieren, ist die Verwendung der Funktion  mit
mit
 (
( wie oben,
wie oben,  in Mio. € ).
in Mio. € ).
2.1
Skizziere den Graphen von  im Material für
im Material für  .
.
Erläutere anhand des Graphen, um welchen Funktionstyp es sich hier handeln könnte.
Begründe anhand der typischen Eigenschaften dieses Funktionstyps, warum er in diesem Sachzusammenhang angemessen sein kann.
Erläutere anhand des Graphen, um welchen Funktionstyp es sich hier handeln könnte.
Begründe anhand der typischen Eigenschaften dieses Funktionstyps, warum er in diesem Sachzusammenhang angemessen sein kann.
(5 BE)
2.2
Beschreibe den Aufbau des folgenden Terms und erläutere, was damit berechnet wird.

(5 BE)
3
Wenn du mit dem Rechner die Ableitung von  bildest, erhältst du im Allgemeinen das Ergebnis:
bildest, erhältst du im Allgemeinen das Ergebnis: 
3.1
Berechne die Ableitung der Funktion  mit einer geeigneten Ableitungsregel und zeige die Äquivalenz mit dem oben angeführten Rechnerergebnis.
mit einer geeigneten Ableitungsregel und zeige die Äquivalenz mit dem oben angeführten Rechnerergebnis.
(9 BE)
3.2
Es sei  die obere Grenze der Funktion
die obere Grenze der Funktion  .
.
Bestimme und erläutere die Bedeutung von
und erläutere die Bedeutung von  sowie der einzelnen Faktoren auf der rechten Seite der Gleichung
sowie der einzelnen Faktoren auf der rechten Seite der Gleichung  im Sachzusammenhang.
im Sachzusammenhang.
Bestimme
(6 BE)
4
Die Summe aller Zinsen, die für diese Schulden im Zeitraum vom Beginn des Jahres  bis zum Ende des Jahres
bis zum Ende des Jahres  angefallen sind, soll ermittelt werden. Gehe dazu vereinfachend davon aus, dass sich der Schuldenstand im Laufe eines Jahres nicht ändert und jeweils am Jahresende Zinsen in Höhe von
angefallen sind, soll ermittelt werden. Gehe dazu vereinfachend davon aus, dass sich der Schuldenstand im Laufe eines Jahres nicht ändert und jeweils am Jahresende Zinsen in Höhe von  anfallen. Ermittle mit Hilfe der Funktion
anfallen. Ermittle mit Hilfe der Funktion  eine geeignete Näherung für den gesuchten Wert.
eine geeignete Näherung für den gesuchten Wert.
(5 BE)
1 Quelle: Statistisches Bundesamt.
1
1.1
Zu beachten ist, dass auf der  -Achse des Koordinatensystems die Schulden in
-Achse des Koordinatensystems die Schulden in  Mio
Mio  aufgetragen sind und in der Wertetabelle nur in Mio €.
aufgetragen sind und in der Wertetabelle nur in Mio €.
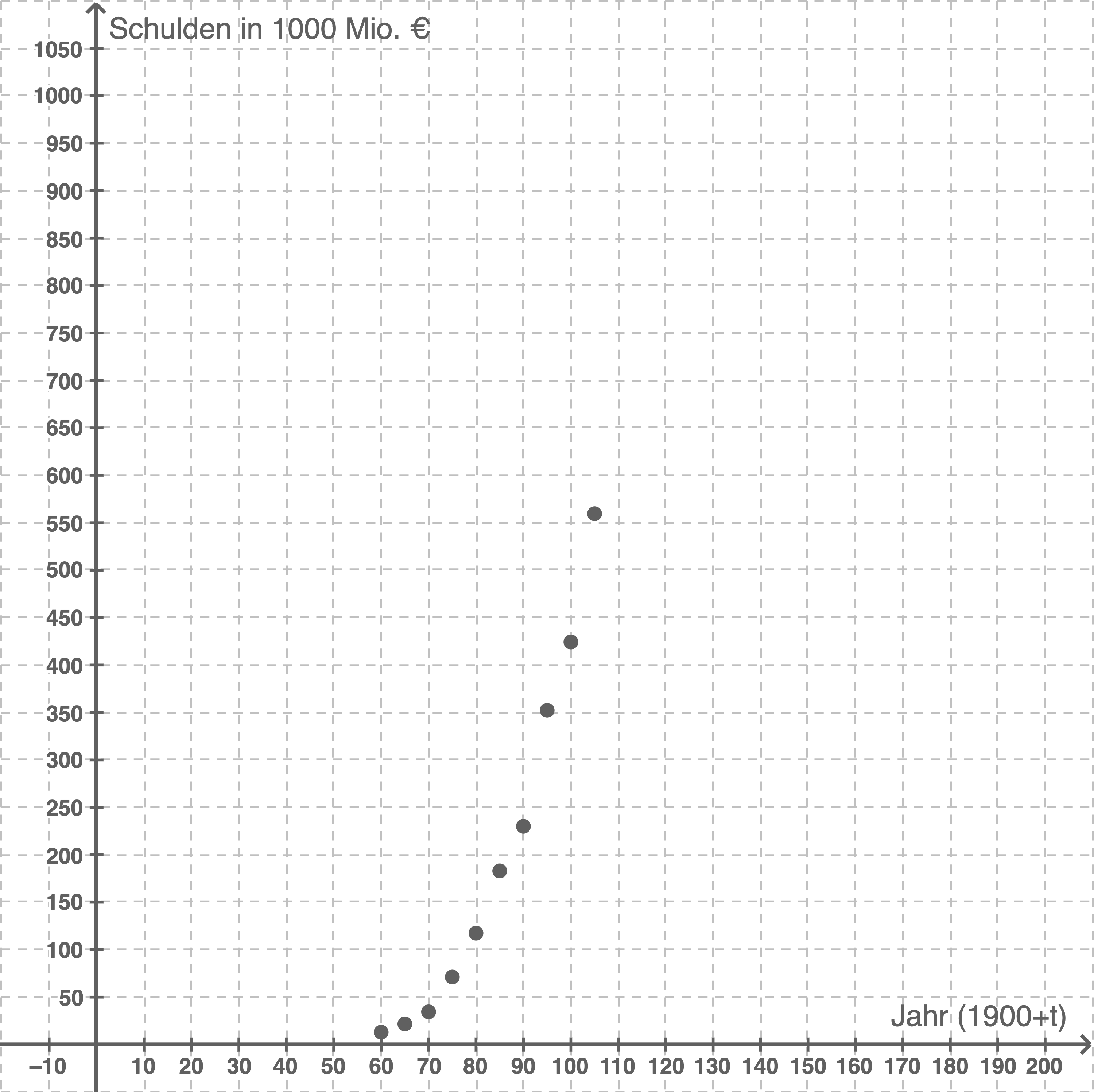

1.2
Die gesuchten Funktionen können mit dem CAS bestimmt werden.
Dazu muss die Wertetabelle im Lists \& Spreadsheets-Modus gespeichert werden:
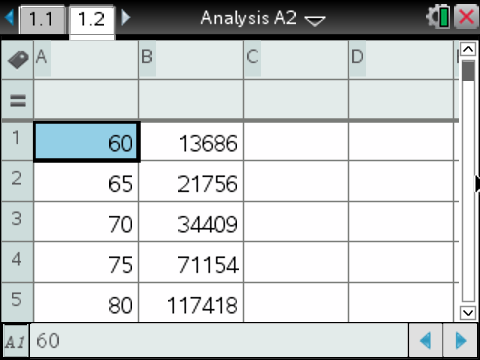 Quadratische Funktion bestimmen
Die quadratische Funktion
Quadratische Funktion bestimmen
Die quadratische Funktion  hat die Form
hat die Form  Die Koeffizienten
Die Koeffizienten  ,
,  und
und  können nun mit folgendem Befehl berechnet werden:
können nun mit folgendem Befehl berechnet werden:
 - und
- und  -Werte können nun die entsprechenden Spalten in der Wertetabelle angegeben werden:
-Werte können nun die entsprechenden Spalten in der Wertetabelle angegeben werden:
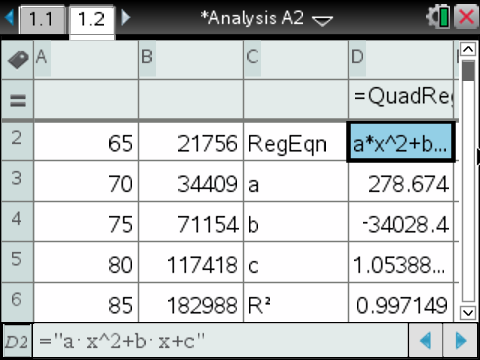 Die Koeffizienten folgen mit
Die Koeffizienten folgen mit  ,
,  und
und  .
Damit lautet der Funktionsterm von
.
Damit lautet der Funktionsterm von  :
Exponentialfunktion bestimmen
Die Exponentialfunktion
:
Exponentialfunktion bestimmen
Die Exponentialfunktion  hat die Form
hat die Form  Die Koeffizienten
Die Koeffizienten  und
und  können mit folgendem Befehl bestimmt werden:
können mit folgendem Befehl bestimmt werden:
 - und
- und  -Werte können nun die entsprechenden Spalten der Wertetabelle angegeben werden:
-Werte können nun die entsprechenden Spalten der Wertetabelle angegeben werden:
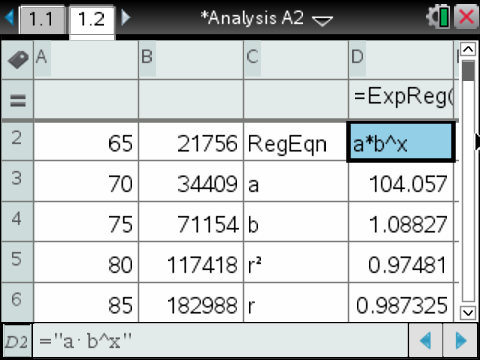 Die Koeffizienten folgen nun mit
Die Koeffizienten folgen nun mit  und
und  .
Damit lautet der Funktionsterm von
.
Damit lautet der Funktionsterm von  :
:
 Funktionen beurteilen
Mit dem CAS können die zugehörigen Graphen zu den beiden Funktionstypen erstellt werden und mit den eingezeichneten Werten aus dem vorherigen Aufgabenteil verglichen werden.
Nach dem Wechseln in das Graph-Menü können die beiden Funktionsterme von
Funktionen beurteilen
Mit dem CAS können die zugehörigen Graphen zu den beiden Funktionstypen erstellt werden und mit den eingezeichneten Werten aus dem vorherigen Aufgabenteil verglichen werden.
Nach dem Wechseln in das Graph-Menü können die beiden Funktionsterme von  und
und  gespeichert werden:
gespeichert werden:
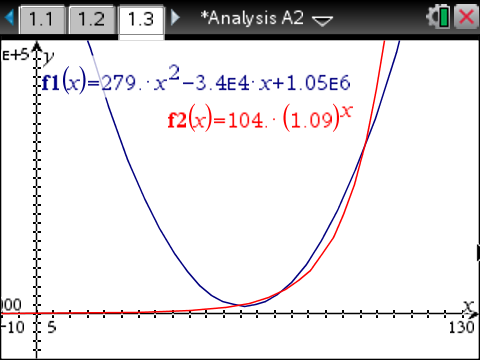 Die quadratische Funktion verläuft parabelförmig. Für die ersten Jahrzehnte nach 1900 sinken die Schulden folglich stark und nähern sich null an, bis sie etwa 60 Jahre später ähnlich wie die Werte aus der Tabelle steigen.
Die Exponentialfunktion hingegen nähert sich asymptotisch der negativen
Die quadratische Funktion verläuft parabelförmig. Für die ersten Jahrzehnte nach 1900 sinken die Schulden folglich stark und nähern sich null an, bis sie etwa 60 Jahre später ähnlich wie die Werte aus der Tabelle steigen.
Die Exponentialfunktion hingegen nähert sich asymptotisch der negativen  -Achse an und steigt ab etwa 1940 exponentiell an. Die Werte streben stark gegen Unendlich.
Beide Funktionen nehmen im abgebildeten Bereich ähnliche Werte wie die Werte der Tabelle an. Anhand der Wertetabellen beider Funktionen können diese nun genauer überprüft werden:
-Achse an und steigt ab etwa 1940 exponentiell an. Die Werte streben stark gegen Unendlich.
Beide Funktionen nehmen im abgebildeten Bereich ähnliche Werte wie die Werte der Tabelle an. Anhand der Wertetabellen beider Funktionen können diese nun genauer überprüft werden:
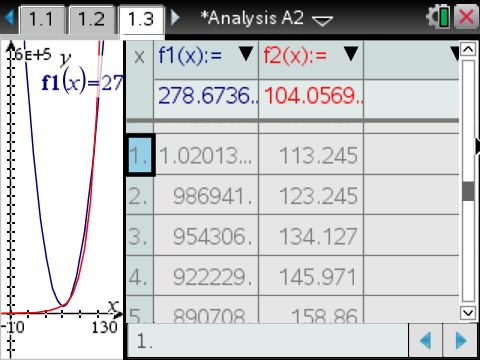 Durch Vergleichen der Werte der beiden Funktionen mit der Wertetabelle fällt auf, dass sich die quadratische Funktion in fast jedem angegeben Jahr besser anpasst als die Exponentialfunktion. Besonders für das letzte Jahr
Durch Vergleichen der Werte der beiden Funktionen mit der Wertetabelle fällt auf, dass sich die quadratische Funktion in fast jedem angegeben Jahr besser anpasst als die Exponentialfunktion. Besonders für das letzte Jahr  ist der Unterschied extrem:
Die quadratische Funktion eignet sich somit sehr gut zur Modellierung im geeigneten Zeitraum, die Exponentialfunktion hingegen weniger gut.
ist der Unterschied extrem:
Die quadratische Funktion eignet sich somit sehr gut zur Modellierung im geeigneten Zeitraum, die Exponentialfunktion hingegen weniger gut.

4: Statistik  1:
1:  6: Quadratische Regression
6: Quadratische Regression
Für die 
4: Statistik  1:
1:  A: Exponentielle Regression
A: Exponentielle Regression
Für die 

7: Tabelle  1:
1:
Durch Anpassen der Tabellenwerte erhält man folgende Wertetabellen:

2
2.1
Graph skizzieren
Mit dem CAS kann der Graph angezeigt werden, dabei muss das Koordinatensystem des CAS dem Material angepasst werden. Dies kann im WINDOW-Menü bearbeitet werden:
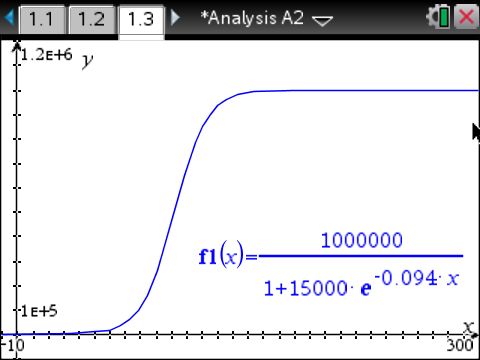 Der abgebildete Graph kann nun in das Material übernommen werden:
Der abgebildete Graph kann nun in das Material übernommen werden:
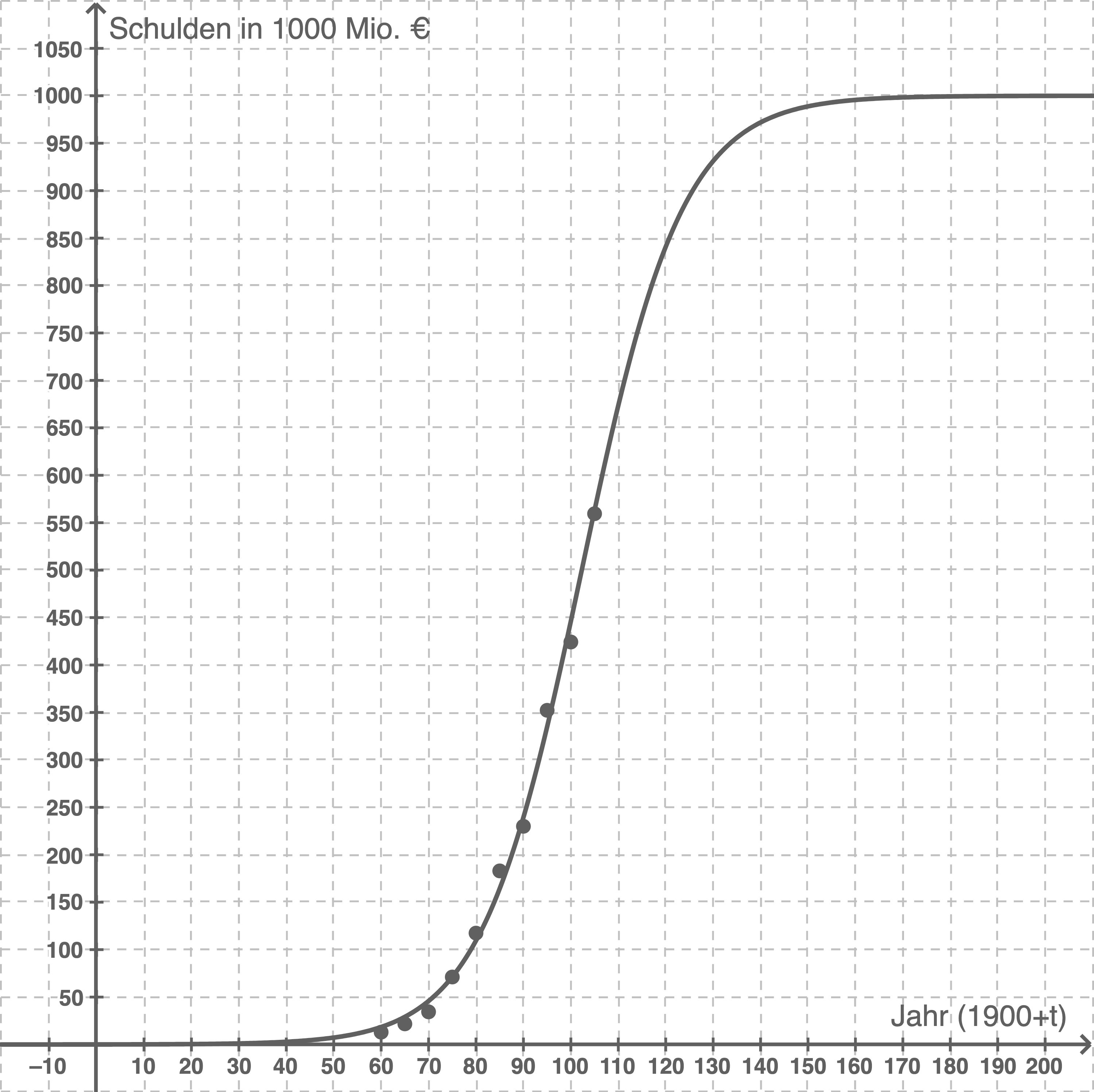 Funktionstyp erläutern
Es kann abgelesen werden, dass die Funktion sowohl für
Funktionstyp erläutern
Es kann abgelesen werden, dass die Funktion sowohl für  als auch für
als auch für  einen Grenzwert besitzt. Für
einen Grenzwert besitzt. Für  ist die
ist die  -Achse eine waagerechte Asymptote der Funktion, für
-Achse eine waagerechte Asymptote der Funktion, für  besitzt
besitzt  auch eine waagrechte Asymptote gegen einen Wert von etwa
auch eine waagrechte Asymptote gegen einen Wert von etwa  .
Hierbei handelt es sich folglich um eine gebrochene Exponentialfunkton. Die
.
Hierbei handelt es sich folglich um eine gebrochene Exponentialfunkton. Die  -Funktion besitzt die Grenzwerte
-Funktion besitzt die Grenzwerte  und
und  , die je nach Vorzeichen des Exponenten angepasst werden können. Durch weitere Parameter kann die Funktion auf die hier zu sehende Form gebracht werden.
Eignung erläutern
Gebrochene Exponentialfunktionen weisen jeweils einen Grenzwert für kleine und große
, die je nach Vorzeichen des Exponenten angepasst werden können. Durch weitere Parameter kann die Funktion auf die hier zu sehende Form gebracht werden.
Eignung erläutern
Gebrochene Exponentialfunktionen weisen jeweils einen Grenzwert für kleine und große  auf. Dies eignet sich zur Modellierung der Schulden eines Staates, da die Schulden zuerst immer weiter steigen, danach jedoch gegen einen bestimmten Maximalwert laufen und diesen nicht weiter überschreiten.
auf. Dies eignet sich zur Modellierung der Schulden eines Staates, da die Schulden zuerst immer weiter steigen, danach jedoch gegen einen bestimmten Maximalwert laufen und diesen nicht weiter überschreiten.


2.2
1. Schritt: Funktionswerte beschreiben
 . Dieser Wert ist somit die Abweichung der Funktion
. Dieser Wert ist somit die Abweichung der Funktion  von den tatsächlichen Schulden im Jahr
von den tatsächlichen Schulden im Jahr  .
3. Schritt: Quadrat
Hier wird das Quadrat der obigen Differenz berechnet. Dies hat zur Folge, dass alle Werte nun positiv sind. Dieser Wert ist somit die quadratische Abweichung der Funktion
.
3. Schritt: Quadrat
Hier wird das Quadrat der obigen Differenz berechnet. Dies hat zur Folge, dass alle Werte nun positiv sind. Dieser Wert ist somit die quadratische Abweichung der Funktion  von den tatsächlichen Schulden im Jahr
von den tatsächlichen Schulden im Jahr  .
4. Schritt: Summe
Nun wird eine Summe über die Quadrate gebildet. Die Summe läuft von
.
4. Schritt: Summe
Nun wird eine Summe über die Quadrate gebildet. Die Summe läuft von  bis
bis  . Somit werden die Differenzen über alle Jahre von
. Somit werden die Differenzen über alle Jahre von  bis
bis  in
in  -er Schritten berechnet. Dies sind gerade alle in der Wertetabelle angegeben Werte. Die Summe beschreibt also die quadratische Abweichung der Funktion
-er Schritten berechnet. Dies sind gerade alle in der Wertetabelle angegeben Werte. Die Summe beschreibt also die quadratische Abweichung der Funktion  von allen in der Wertetabelle angegebenen Werten.
von allen in der Wertetabelle angegebenen Werten.
: Die durch die Funktion
angenäherten Schulden zum Zeitpunkt
.
: Die tatsächlichen Schulden zum Zeitpunkt
.
3
3.1
Ableitung berechnen
Da es sich bei der Funktion  um eine gebrochene Funktion handelt, wird an dieser Stelle die Quotientenregel benötigt.
Mit
um eine gebrochene Funktion handelt, wird an dieser Stelle die Quotientenregel benötigt.
Mit  und
und  folgt:
Äquivalenz zeigen
Durch Erweitern mit
folgt:
Äquivalenz zeigen
Durch Erweitern mit  folgt:
Damit ist die Äquivalenz der beiden Ausdrücke gezeigt.
folgt:
Damit ist die Äquivalenz der beiden Ausdrücke gezeigt.
3.2
Obere Grenze  bestimmen
Da die Funktion
bestimmen
Da die Funktion  monoton wachsend ist, entspricht der Grenzwert von
monoton wachsend ist, entspricht der Grenzwert von  der gesuchten oberen Grenze
der gesuchten oberen Grenze  .
Berechnen des Grenzwerts von
.
Berechnen des Grenzwerts von  :
Die obere Grenze
:
Die obere Grenze  der Funktion
der Funktion  ist folglich
ist folglich  .
Bedeutung der Ableitung erläutern
Die Ableitung
.
Bedeutung der Ableitung erläutern
Die Ableitung  gibt die Änderungsrate der Funktion
gibt die Änderungsrate der Funktion  an. Der Funktionswert
an. Der Funktionswert  beschreibt im Sachzusammenhang den Schuldenstand in Mio.€ im Jahr
beschreibt im Sachzusammenhang den Schuldenstand in Mio.€ im Jahr  Die Ableitung
Die Ableitung  beschreibt somit die Änderungsrate der Schulden bzw. den Zuwachs an Schulden in Mio. € im Jahr
beschreibt somit die Änderungsrate der Schulden bzw. den Zuwachs an Schulden in Mio. € im Jahr  .
Bedeutung der Faktoren erläutern
.
Bedeutung der Faktoren erläutern
- Faktor
Der Faktor
beschreibt eine Konstante, welche nicht von
abhängig ist und dafür sorgt, dass die Gleichheit erfüllt ist.
- Faktor
Der Faktor
beschreibt den Schuldenstand zum Zeitpunkt
. Ist der Schuldenstand
sehr niedrig, also
, so gilt für den Faktor
Für das Produkt der Faktoren gilt somit:
Somit gilt
für kleine
. Der Zuwachs der Schulden zum Zeitpunkt
ist somit sehr niedrig, falls die Schulden zum Zeitpunkt
sehr niedrig sind.
- Faktor
Der Faktor
beschreibt die Differenz zwischen dem Schuldenstand zum Zeitpunkt
und der oberen Grenze
. Ist der Schuldenstand
sehr hoch, also
, so gilt für den Faktor
Für das Produkt der Faktoren gilt somit:
Somit gilt
für große
. Der Zuwachs der Schulden zum Zeitpunkt
ist somit sehr niedrig, falls die Schulden zum Zeitpunkt
sehr hoch sind.
4
Die im Jahr  anfallenden Zinsen können mit dem durchschnittlichen Schuldenstand
anfallenden Zinsen können mit dem durchschnittlichen Schuldenstand  des Jahres
des Jahres  und dem Zinssatz von
und dem Zinssatz von  bestimmt werden. Die Summe der Zinsen der Jahre von
bestimmt werden. Die Summe der Zinsen der Jahre von  bis
bis  ergeben dann die gesuchte Näherung.
Der durchschnittlichen Funktionswert
ergeben dann die gesuchte Näherung.
Der durchschnittlichen Funktionswert  einer Funktion
einer Funktion  im Intervall
im Intervall ![\(\left[a;b\right]\)](https://www.schullv.de/resources/formulas/17818209ab83b5875fd5fb4cb16a774cda3e6470ce6bae88138263a93b57c7d6_light.svg) wird wie folgt berechnet:
wird wie folgt berechnet:
 Für das Intervall
Für das Intervall ![\(\left[t;t+1\right]\)](https://www.schullv.de/resources/formulas/b1702dcfcd8cdb3741358d281169adfc74da8c914f1e2d46616c7142cf372dab_light.svg) ergibt sich also:
ergibt sich also:
![\(\begin{array}[t]{rll}
d_t&=&\dfrac{1}{\left(t+1\right)-\left(t\right)} \displaystyle\int_{t}^{t+1} f_3(x)\;\mathrm dx\\[5pt]
&=&\dfrac{1}{1} \displaystyle\int_{t}^{t+1} f_3(x)\;\mathrm dx\\[5pt]
&=& \displaystyle\int_{t}^{t+1} f_3(x)\;\mathrm dx
\end{array}\)](https://www.schullv.de/resources/formulas/bee5a85bf34611380e3359f880efb90e2cfa6dbf7a73917ed2e72af5655dfb1b_light.svg) Die Zinsen
Die Zinsen  im Jahr
im Jahr  folgen nun mit
folgen nun mit  Für die Summe aller Zinsen von Beginn des Jahres
Für die Summe aller Zinsen von Beginn des Jahres  bis zum Ende des Jahres
bis zum Ende des Jahres  ergibt sich:
Das Integral kann mit dem CAS berechnet werden. Dazu muss in das Calculator-Menü gewechselt und dort der Funktionsterm von
ergibt sich:
Das Integral kann mit dem CAS berechnet werden. Dazu muss in das Calculator-Menü gewechselt und dort der Funktionsterm von  gespeichert werden.
gespeichert werden.
 und der oberen Grenze
und der oberen Grenze  folgt:
folgt:
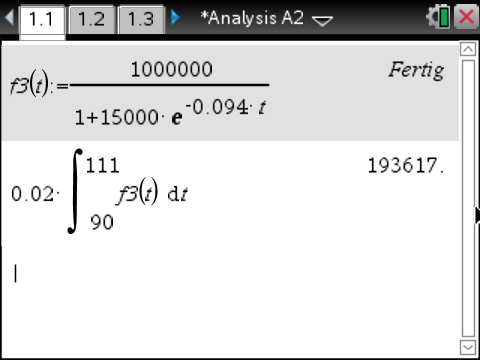 Somit ergibt sich:
Somit ergibt sich:
 Die Zinsen der Schulden betragen folglich näherungsweise
Die Zinsen der Schulden betragen folglich näherungsweise  Mio. €.
Mio. €.
4: Analysis  3: Integral
3: Integral
Durch Wählen der unteren Grenze 
1
1.1
Zu beachten ist, dass auf der  -Achse des Koordinatensystems die Schulden in
-Achse des Koordinatensystems die Schulden in  Mio
Mio  aufgetragen sind und in der Wertetabelle nur in Mio €.
aufgetragen sind und in der Wertetabelle nur in Mio €.


1.2
Die gesuchten Funktionen können mit dem CAS bestimmt werden.
Dazu muss die Wertetabelle im Tabellenkalkulat-Modus gespeichert werden:
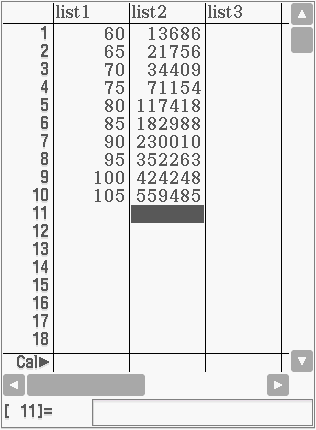 Quadratische Funktion bestimmen
Die quadratische Funktion
Quadratische Funktion bestimmen
Die quadratische Funktion  hat die Form
hat die Form  Die Koeffizienten
Die Koeffizienten  ,
,  und
und  können nun mit folgendem Befehl berechnet werden:
können nun mit folgendem Befehl berechnet werden:
 - und
- und  -Werte können nun die entsprechenden Spalten in der Wertetabelle angegeben werden:
-Werte können nun die entsprechenden Spalten in der Wertetabelle angegeben werden:
 Die Koeffizienten folgen mit
Die Koeffizienten folgen mit  ,
,  und
und  .
Damit lautet der Funktionsterm von
.
Damit lautet der Funktionsterm von  :
Exponentialfunktion bestimmen
Die Exponentialfunktion
:
Exponentialfunktion bestimmen
Die Exponentialfunktion  hat die Form
hat die Form  Die Koeffizienten
Die Koeffizienten  und
und  können mit folgendem Befehl bestimmt werden:
können mit folgendem Befehl bestimmt werden:
 - und
- und  -Werte können nun die entsprechenden Spalten der Wertetabelle angegeben werden:
-Werte können nun die entsprechenden Spalten der Wertetabelle angegeben werden:
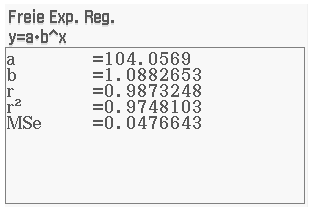 Die Koeffizienten folgen nun mit
Die Koeffizienten folgen nun mit  und
und  .
Damit lautet der Funktionsterm von
.
Damit lautet der Funktionsterm von  :
:
 Funktionen beurteilen
Mit dem CAS können die zugehörigen Graphen zu den beiden Funktionstypen erstellt werden und mit den eingezeichneten Werten aus dem vorherigen Aufgabenteil verglichen werden.
Nach dem Wechseln in das Grafik-Menü können die beiden Funktionsterme von
Funktionen beurteilen
Mit dem CAS können die zugehörigen Graphen zu den beiden Funktionstypen erstellt werden und mit den eingezeichneten Werten aus dem vorherigen Aufgabenteil verglichen werden.
Nach dem Wechseln in das Grafik-Menü können die beiden Funktionsterme von  und
und  gespeichert werden:
gespeichert werden:
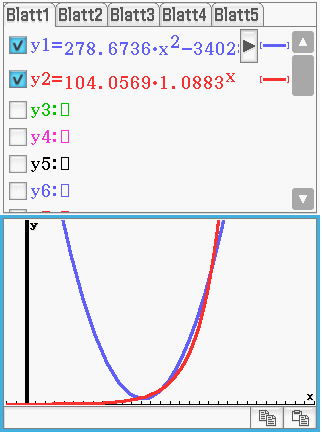 Die quadratische Funktion verläuft parabelförmig. Für die ersten Jahrzehnte nach 1900 sinken die Schulden folglich stark und nähern sich null an, bis sie etwa 60 Jahre später ähnlich wie die Werte aus der Tabelle steigen.
Die Exponentialfunktion hingegen nähert sich asymptotisch der negativen
Die quadratische Funktion verläuft parabelförmig. Für die ersten Jahrzehnte nach 1900 sinken die Schulden folglich stark und nähern sich null an, bis sie etwa 60 Jahre später ähnlich wie die Werte aus der Tabelle steigen.
Die Exponentialfunktion hingegen nähert sich asymptotisch der negativen  -Achse an und steigt ab etwa 1940 exponentiell an. Die Werte streben stark gegen Unendlich.
Beide Funktionen nehmen im abgebildeten Bereich ähnliche Werte wie die Werte der Tabelle an. Mit dem CAS können nun die Wertetabellen der beiden Funktionen angezeigt und näher untersucht werden:
-Achse an und steigt ab etwa 1940 exponentiell an. Die Werte streben stark gegen Unendlich.
Beide Funktionen nehmen im abgebildeten Bereich ähnliche Werte wie die Werte der Tabelle an. Mit dem CAS können nun die Wertetabellen der beiden Funktionen angezeigt und näher untersucht werden:
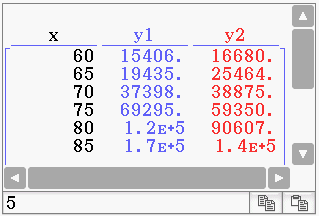 Durch Vergleichen der Werte der beiden Funktionen mit der Wertetabelle fällt auf, dass sich die quadratische Funktion in fast jedem angegeben Jahr besser anpasst als die Exponentialfunktion. Besonders für das letzte Jahr
Durch Vergleichen der Werte der beiden Funktionen mit der Wertetabelle fällt auf, dass sich die quadratische Funktion in fast jedem angegeben Jahr besser anpasst als die Exponentialfunktion. Besonders für das letzte Jahr  ist der Unterschied extrem:
Die quadratische Funktion eignet sich somit sehr gut zur Modellierung im geeigneten Zeitraum, die Exponentialfunktion hingegen weniger gut.
ist der Unterschied extrem:
Die quadratische Funktion eignet sich somit sehr gut zur Modellierung im geeigneten Zeitraum, die Exponentialfunktion hingegen weniger gut.

Calc  Regressionen
Regressionen  Quadratische Regression
Quadratische Regression
Für die 
Calc  Regressionen
Regressionen  Exp. Regression
Exp. Regression
Für die 


2
2.1
Graph skizzieren
Mit dem CAS kann der zugehörige Graph zur Funktion  angezeigt und das Koordinatensystem entsprechend angepasst werden:
angezeigt und das Koordinatensystem entsprechend angepasst werden:
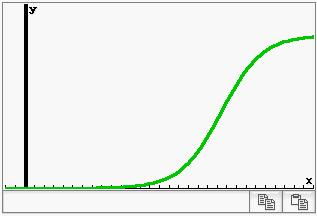 Der abgebildete Graph kann nun in das Material übernommen werden:
Der abgebildete Graph kann nun in das Material übernommen werden:
 Funktionstyp erläutern
Es kann abgelesen werden, dass die Funktion sowohl für
Funktionstyp erläutern
Es kann abgelesen werden, dass die Funktion sowohl für  als auch für
als auch für  einen Grenzwert besitzt. Für
einen Grenzwert besitzt. Für  ist die
ist die  -Achse eine waagerechte Asymptote der Funktion, für
-Achse eine waagerechte Asymptote der Funktion, für  besitzt
besitzt  auch eine waagrechte Asymptote gegen einen Wert von etwa
auch eine waagrechte Asymptote gegen einen Wert von etwa  .
Hierbei handelt es sich folglich um eine gebrochene Exponentialfunkton. Die
.
Hierbei handelt es sich folglich um eine gebrochene Exponentialfunkton. Die  -Funktion besitzt die Grenzwerte
-Funktion besitzt die Grenzwerte  und
und  , die je nach Vorzeichen des Exponenten angepasst werden können. Durch weitere Parameter kann die Funktion auf die hier zu sehende Form gebracht werden.
Eignung erläutern
Gebrochene Exponentialfunktionen weisen jeweils einen Grenzwert für kleine und große
, die je nach Vorzeichen des Exponenten angepasst werden können. Durch weitere Parameter kann die Funktion auf die hier zu sehende Form gebracht werden.
Eignung erläutern
Gebrochene Exponentialfunktionen weisen jeweils einen Grenzwert für kleine und große  auf. Dies eignet sich zur Modellierung der Schulden eines Staates, da die Schulden zuerst immer weiter steigen, danach jedoch gegen einen bestimmten Maximalwert laufen und diesen nicht weiter überschreiten.
auf. Dies eignet sich zur Modellierung der Schulden eines Staates, da die Schulden zuerst immer weiter steigen, danach jedoch gegen einen bestimmten Maximalwert laufen und diesen nicht weiter überschreiten.


2.2
1. Schritt: Funktionswerte beschreiben
 . Dieser Wert ist somit die Abweichung der Funktion
. Dieser Wert ist somit die Abweichung der Funktion  von den tatsächlichen Schulden im Jahr
von den tatsächlichen Schulden im Jahr  .
3. Schritt: Quadrat
Hier wird das Quadrat der obigen Differenz berechnet. Dies hat zur Folge, dass alle Werte nun positiv sind. Dieser Wert ist somit die quadratische Abweichung der Funktion
.
3. Schritt: Quadrat
Hier wird das Quadrat der obigen Differenz berechnet. Dies hat zur Folge, dass alle Werte nun positiv sind. Dieser Wert ist somit die quadratische Abweichung der Funktion  von den tatsächlichen Schulden im Jahr
von den tatsächlichen Schulden im Jahr  .
4. Schritt: Summe
Nun wird eine Summe über die Quadrate gebildet. Die Summe läuft von
.
4. Schritt: Summe
Nun wird eine Summe über die Quadrate gebildet. Die Summe läuft von  bis
bis  . Somit werden die Differenzen über alle Jahre von
. Somit werden die Differenzen über alle Jahre von  bis
bis  in
in  -er Schritten berechnet. Dies sind gerade alle in der Wertetabelle angegeben Werte. Die Summe beschreibt also die quadratische Abweichung der Funktion
-er Schritten berechnet. Dies sind gerade alle in der Wertetabelle angegeben Werte. Die Summe beschreibt also die quadratische Abweichung der Funktion  von allen in der Wertetabelle angegebenen Werten.
von allen in der Wertetabelle angegebenen Werten.
: Die durch die Funktion
angenäherten Schulden zum Zeitpunkt
.
: Die tatsächlichen Schulden zum Zeitpunkt
.
3
3.1
Ableitung berechnen
Da es sich bei der Funktion  um eine gebrochene Funktion handelt, wird an dieser Stelle die Quotientenregel benötigt.
Mit
um eine gebrochene Funktion handelt, wird an dieser Stelle die Quotientenregel benötigt.
Mit  und
und  folgt:
Äquivalenz zeigen
Durch Erweitern mit
folgt:
Äquivalenz zeigen
Durch Erweitern mit  folgt:
Damit ist die Äquivalenz der beiden Ausdrücke gezeigt.
folgt:
Damit ist die Äquivalenz der beiden Ausdrücke gezeigt.
3.2
Obere Grenze  bestimmen
Da die Funktion
bestimmen
Da die Funktion  monoton wachsend ist, entspricht der Grenzwert von
monoton wachsend ist, entspricht der Grenzwert von  der gesuchten oberen Grenze
der gesuchten oberen Grenze  .
Berechnen des Grenzwerts von
.
Berechnen des Grenzwerts von  :
Die obere Grenze
:
Die obere Grenze  der Funktion
der Funktion  ist folglich
ist folglich  .
Bedeutung der Ableitung erläutern
Die Ableitung
.
Bedeutung der Ableitung erläutern
Die Ableitung  gibt die Änderungsrate der Funktion
gibt die Änderungsrate der Funktion  an. Der Funktionswert
an. Der Funktionswert  beschreibt im Sachzusammenhang den Schuldenstand in Mio.€ im Jahr
beschreibt im Sachzusammenhang den Schuldenstand in Mio.€ im Jahr  Die Ableitung
Die Ableitung  beschreibt somit die Änderungsrate der Schulden bzw. den Zuwachs an Schulden in Mio. € im Jahr
beschreibt somit die Änderungsrate der Schulden bzw. den Zuwachs an Schulden in Mio. € im Jahr  .
Bedeutung der Faktoren erläutern
.
Bedeutung der Faktoren erläutern
- Faktor
Der Faktor
beschreibt eine Konstante, welche nicht von
abhängig ist und dafür sorgt, dass die Gleichheit erfüllt ist.
- Faktor
Der Faktor
beschreibt den Schuldenstand zum Zeitpunkt
. Ist der Schuldenstand
sehr niedrig, also
, so gilt für den Faktor
Für das Produkt der Faktoren gilt somit:
Somit gilt
für kleine
. Der Zuwachs der Schulden zum Zeitpunkt
ist somit sehr niedrig, falls die Schulden zum Zeitpunkt
sehr niedrig sind.
- Faktor
Der Faktor
beschreibt die Differenz zwischen dem Schuldenstand zum Zeitpunkt
und der oberen Grenze
. Ist der Schuldenstand
sehr hoch, also
, so gilt für den Faktor
Für das Produkt der Faktoren gilt somit:
Somit gilt
für große
. Der Zuwachs der Schulden zum Zeitpunkt
ist somit sehr niedrig, falls die Schulden zum Zeitpunkt
sehr hoch sind.
4
Die im Jahr  anfallenden Zinsen können mit dem durchschnittlichen Schuldenstand
anfallenden Zinsen können mit dem durchschnittlichen Schuldenstand  des Jahres
des Jahres  und dem Zinssatz von
und dem Zinssatz von  bestimmt werden. Die Summe der Zinsen der Jahre von
bestimmt werden. Die Summe der Zinsen der Jahre von  bis
bis  ergeben dann die gesuchte Näherung.
Der durchschnittlichen Funktionswert
ergeben dann die gesuchte Näherung.
Der durchschnittlichen Funktionswert  einer Funktion
einer Funktion  im Intervall
im Intervall ![\(\left[a;b\right]\)](https://www.schullv.de/resources/formulas/17818209ab83b5875fd5fb4cb16a774cda3e6470ce6bae88138263a93b57c7d6_light.svg) wird wie folgt berechnet:
wird wie folgt berechnet:
 Für das Intervall
Für das Intervall ![\(\left[t;t+1\right]\)](https://www.schullv.de/resources/formulas/b1702dcfcd8cdb3741358d281169adfc74da8c914f1e2d46616c7142cf372dab_light.svg) ergibt sich also:
ergibt sich also:
![\(\begin{array}[t]{rll}
d_t&=&\dfrac{1}{\left(t+1\right)-\left(t\right)} \displaystyle\int_{t}^{t+1} f_3(x)\;\mathrm dx\\[5pt]
&=&\dfrac{1}{1} \displaystyle\int_{t}^{t+1} f_3(x)\;\mathrm dx\\[5pt]
&=& \displaystyle\int_{t}^{t+1} f_3(x)\;\mathrm dx
\end{array}\)](https://www.schullv.de/resources/formulas/bee5a85bf34611380e3359f880efb90e2cfa6dbf7a73917ed2e72af5655dfb1b_light.svg) Die Zinsen
Die Zinsen  im Jahr
im Jahr  folgen nun mit
folgen nun mit  Für die Summe aller Zinsen von Beginn des Jahres
Für die Summe aller Zinsen von Beginn des Jahres  bis zum Ende des Jahres
bis zum Ende des Jahres  ergibt sich:
Das Integral kann mit dem CAS berechnet werden. Dazu muss in das Haupt-Menü gewechselt und dort der Funktionsterm von
ergibt sich:
Das Integral kann mit dem CAS berechnet werden. Dazu muss in das Haupt-Menü gewechselt und dort der Funktionsterm von  gespeichert werden.
gespeichert werden.
 und der oberen Grenze
und der oberen Grenze  folgt:
folgt:
 Somit ergibt sich:
Somit ergibt sich:
 Die Zinsen der Schulden betragen folglich näherungsweise
Die Zinsen der Schulden betragen folglich näherungsweise  Mio. €.
Mio. €.
Interaktiv  Berechnungen
Berechnungen 

Durch Wählen der unteren Grenze 