A2 - Analysis
Das Moses Mabhida Stadion in Durban, Südafrika (Abbildung 1) ist eines der Stadien, in denen die Fußballweltmeisterschaft 2010 ausgetragen wurde. Das charakteristische Element ist der Stahlbogen, der das Stadion überspannt. Die äußere Bogenspannweite am Boden beträgt  und die Höhe im Scheitelpunkt
und die Höhe im Scheitelpunkt  Wähle für die folgenden Berechnungen das Koordinatensystem so, dass die Bodenlinie auf der
Wähle für die folgenden Berechnungen das Koordinatensystem so, dass die Bodenlinie auf der  -Achse und der höchste Punkt des Bogens auf der
-Achse und der höchste Punkt des Bogens auf der  -Achse liegt.
-Achse liegt.
1
Der äußere Rand des Bogens soll zum einen durch die Polynomfunktion  mit
mit  , zum anderen durch die Kosinusfunktion
, zum anderen durch die Kosinusfunktion  mit
mit  beschrieben werden.
Bestimme die Parameter
beschrieben werden.
Bestimme die Parameter  und
und  sowie
sowie  und
und  so, dass die Graphen der Funktionen jeweils die im Text genannten Eigenschaften haben.
so, dass die Graphen der Funktionen jeweils die im Text genannten Eigenschaften haben.
(1 BE)
2
Im Folgenden soll die Bogenform durch eine Funktion aus der Schar  beschrieben werden.
beschrieben werden.
2.1
Untersuche die Bedeutung der Parameter  und
und  für die Graphen von
für die Graphen von 
(6 BE)
2.2
Gib zwei Gleichungen an, um die Parameter  und
und  so zu bestimmen, dass die Informationen aus dem einleitenden Text eingehalten werden.
so zu bestimmen, dass die Informationen aus dem einleitenden Text eingehalten werden.
(2 BE)
2.3
Es gelte  und
und  .
Bestimme nun, für welche Werte von
.
Bestimme nun, für welche Werte von  sich die Funktionswerte von
sich die Funktionswerte von  und
und  bzw. diejenigen von
bzw. diejenigen von  und
und  am stärksten unterscheiden, und gib die Unterschiede an diesen Stellen an.
Konnten
am stärksten unterscheiden, und gib die Unterschiede an diesen Stellen an.
Konnten  und
und  in Aufgabe 1 nicht bestimmt werden, können die folgenden Funktionen verwendet werden:
in Aufgabe 1 nicht bestimmt werden, können die folgenden Funktionen verwendet werden:
 und
und  .
.
(6 BE)
3
Für die Länge  des Bogens des Graphen einer Funktion
des Bogens des Graphen einer Funktion  von der Stelle
von der Stelle  bis zur Stelle
bis zur Stelle  wird im Folgenden die Formel
wird im Folgenden die Formel  hergeleitet:
hergeleitet:
3.1
Erkläre die Herleitungsschritte aus der Aufgabenstellung bis einschließlich Zeile  Beachte dazu die Zeichnung in Abbildung 2.
Beachte dazu die Zeichnung in Abbildung 2.
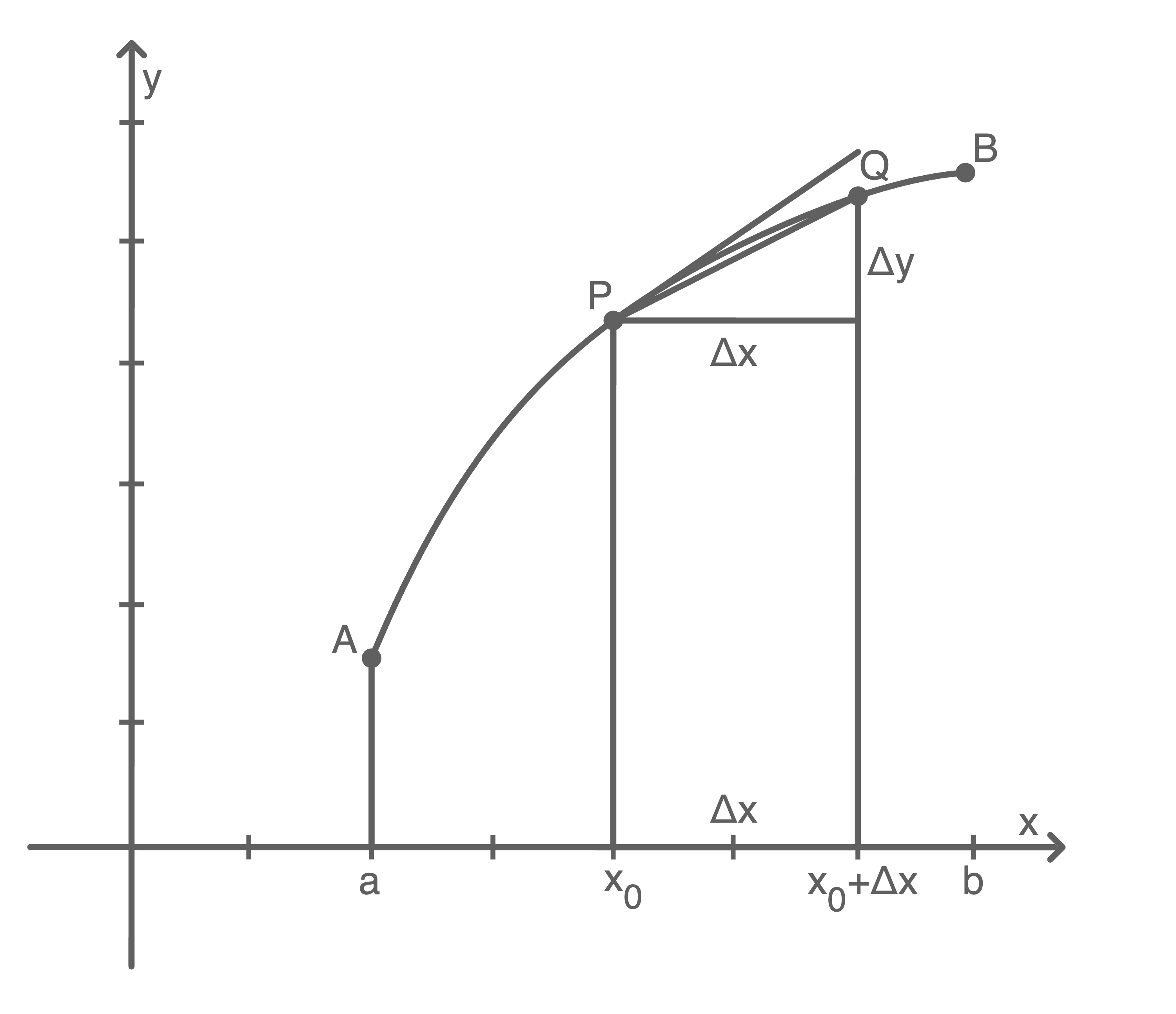
Abbildung 2
(7 BE)
3.2
Zeige, dass 
 gilt.
Hinweis: Bilde zunächst auf beiden Seiten der Gleichung die Ableitung.
gilt.
Hinweis: Bilde zunächst auf beiden Seiten der Gleichung die Ableitung.
(8 BE)
3.3
Entlang des Stahlbogens verläuft auf einer Seite eine Bahn, mit der man vom Boden bis zur Aussichtsplattform im Scheitelpunkt des Bogens fahren kann.
Bestimme mit Hilfe der oben genannten Formel für  und der Beziehung aus Aufgabe 3.2 die Länge der dabei zurückgelegten Strecke für
und der Beziehung aus Aufgabe 3.2 die Länge der dabei zurückgelegten Strecke für 
(5 BE)
1
Parameter der Polynomfunktion bestimmen
Der Parameter  beschreibt den betrag des
beschreibt den betrag des  -Werts der Nullstellen des Graphen von
-Werts der Nullstellen des Graphen von  Da die äußere Bogenspannweite und somit der Abstand der Nullstellen
Da die äußere Bogenspannweite und somit der Abstand der Nullstellen  beträgt und der Bogen symmetrisch zur
beträgt und der Bogen symmetrisch zur  -Achse ist, folgen die Nullstellen mit
-Achse ist, folgen die Nullstellen mit  Der Parameter
Der Parameter  ist somit gegeben durch
ist somit gegeben durch  Einsetzen der Koordinaten des Scheitelpunkts in
Einsetzen der Koordinaten des Scheitelpunkts in  liefert nun:
Der Graph, der die Kurve mit den gegebenen Eigenschaften beschreibt, kann also durch die folgende Polynomfunktion
liefert nun:
Der Graph, der die Kurve mit den gegebenen Eigenschaften beschreibt, kann also durch die folgende Polynomfunktion  beschrieben werden:
Parameter der Kosinusfunktion bestimmen
Da die Amplitude
beschrieben werden:
Parameter der Kosinusfunktion bestimmen
Da die Amplitude  den größten Abstand der Funktion von der
den größten Abstand der Funktion von der  -Achse darstellt, entpricht der Wert von
-Achse darstellt, entpricht der Wert von  dem
dem  -Wert des Scheitelpunkts. Es folgt also
-Wert des Scheitelpunkts. Es folgt also  Die Bogenspannweite von
Die Bogenspannweite von  entspricht einer halben Periodenlänge, es gilt also
entspricht einer halben Periodenlänge, es gilt also  Der Graph, der die Kurve mit den gegebenen Eigenschaften beschreibt, kann also durch die folgende Kosinusfunktion
Der Graph, der die Kurve mit den gegebenen Eigenschaften beschreibt, kann also durch die folgende Kosinusfunktion  dargestellt werden:
dargestellt werden:
![\(\begin{array}[t]{rll}
c(x)&=& 103\cdot \cos\left(\dfrac{2\pi}{680}\cdot x\right)&\\[5pt]
&=& 103\cdot \cos(0,009\cdot x)
\end{array}\)](https://www.schullv.de/resources/formulas/7da16835bd891d1e4230592764ee2ad506e7780b140bb3f0808c0dba546f47fa_light.svg)
2.1
Bedeutung des Parameters 
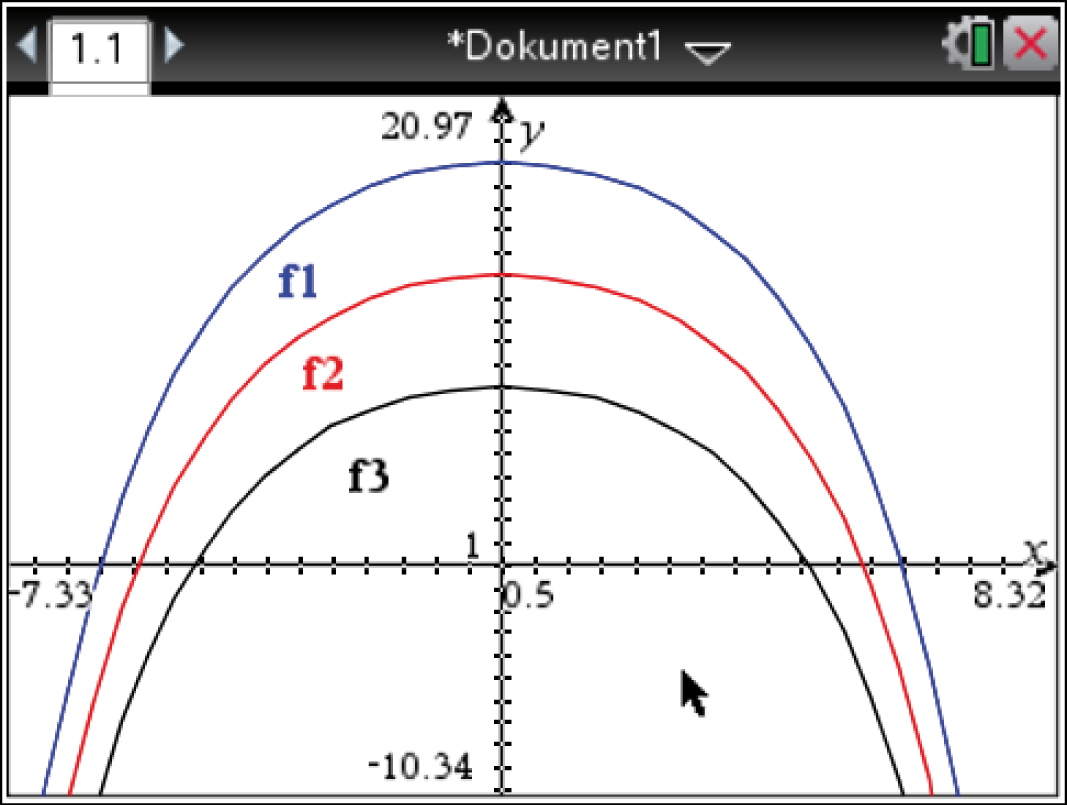 Bedeutung des Parameters
Bedeutung des Parameters 
Um den Einfluss des Parameters  zu untersuchen, können verschiedene Werte für
zu untersuchen, können verschiedene Werte für  eingesetzt werden und die entsprechenden Graphen mit festgelegtem
eingesetzt werden und die entsprechenden Graphen mit festgelegtem  mit Hilfe des CAS im
mit Hilfe des CAS im  -Modus gezeichnet werden.
Der Abbildung kann entnommen werden, dass der Parameter
-Modus gezeichnet werden.
Der Abbildung kann entnommen werden, dass der Parameter  die Graphen der Scharfunktion entlang der
die Graphen der Scharfunktion entlang der  -Achse verschiebt und somit Einfluss auf den
-Achse verschiebt und somit Einfluss auf den  -Achsenabschnitt hat, der dem Maximum der entsprechenden Funktion entspricht.
Der Parameter
-Achsenabschnitt hat, der dem Maximum der entsprechenden Funktion entspricht.
Der Parameter  hat dabei keinen Einfluss auf die Streckung bzw. Stauchung der Graphen von
hat dabei keinen Einfluss auf die Streckung bzw. Stauchung der Graphen von 

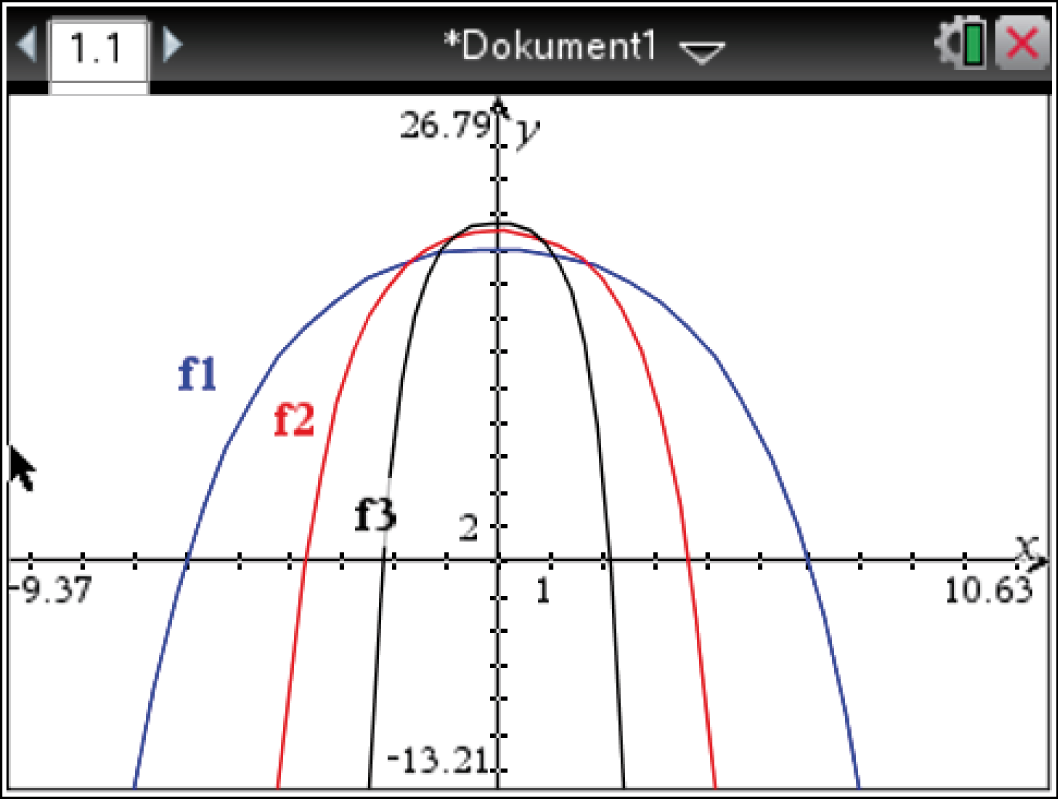
Durch Zeichnen verschiedener Graphen der Scharfunktion mit fixem Wert von  und verschiedenen Werten von
und verschiedenen Werten von  mit Hilfe des CAS lässt sich schließen:
Umso größer der Wert von
mit Hilfe des CAS lässt sich schließen:
Umso größer der Wert von  ist, desto stärker sind die Graphen von
ist, desto stärker sind die Graphen von  gestaucht.
Der Parameter
gestaucht.
Der Parameter  streckt bzw. staucht somit die Graphen der Schar.
Zudem nimmt der
streckt bzw. staucht somit die Graphen der Schar.
Zudem nimmt der  -Achsenabschnitt mit zunehmendem Wert von
-Achsenabschnitt mit zunehmendem Wert von  ab.
ab.  beeinflusst somit auch den Maximalwert der Funktionen der Schar.
beeinflusst somit auch den Maximalwert der Funktionen der Schar.

2.2
Der einleitende Text liefert die folgenden Informationen über den Graphen:
 -Achse liegen soll und somit durch den Punkt
-Achse liegen soll und somit durch den Punkt  beschrieben werden kann, muss gelten:
beschrieben werden kann, muss gelten:
![\(\begin{array}[t]{rll}
k(0)&=& 103 & \\[5pt]
C - \dfrac{1}{2 \lambda} \cdot \left( \mathrm e^{\lambda \cdot 0} + \mathrm e^{-\lambda \cdot 0}\right)&=& 103& \\[5pt]
C - \dfrac{1}{2 \lambda} \cdot \left( 1 + 1\right)&=& 103 & \\[5pt]
C - \dfrac{1}{\lambda}&=& 103
\end{array}\)](https://www.schullv.de/resources/formulas/a3409cd9f5551ca977241e74586f1bc353fb078445127d9a76d8a3d1e9f163c5_light.svg) Aufgrund der Symmetrie und der Bogenspannweite von
Aufgrund der Symmetrie und der Bogenspannweite von  folgen die Schnittstellen des Graphen mit der
folgen die Schnittstellen des Graphen mit der  -Achse mit
-Achse mit  und
und  Es gilt also:
Es gilt also:
![\(\begin{array}[t]{rll}
k(170)&=& 0 & \\[5pt]
C - \dfrac{1}{2 \lambda} \cdot \left( \mathrm e^{\lambda \cdot 170} + \mathrm e^{-\lambda \cdot 170}\right)&=& 0 & \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/a2098496554f0da8145bc10bfaa4278461f78486d500a87f03d044e5e1fdb6fe_light.svg) Zwei Gleichungen, um die Parameter
Zwei Gleichungen, um die Parameter  und
und  zu bestimmen, sind somit gegeben durch:
zu bestimmen, sind somit gegeben durch:
- Die
-Achse soll so gewählt werden, dass der höchste Punkt des Bogens auf der
-Achse liegt.
- Die
-Achse soll so gewählt werden, dass die Bodenlinie auf der
-Achse liegt.
- Der höchste Punkt liegt
über dem Boden.
- Die Bogenspannweite beträgt
2.3
1. Schritt: Differenzfunktionen aufstellen
Im CAS können die drei Funktionen  und
und  mit den gegebenen Werten aus der Aufgabenstellung definiert werden:
Die Differenzfunktionen ergeben sich nun zu:
mit den gegebenen Werten aus der Aufgabenstellung definiert werden:
Die Differenzfunktionen ergeben sich nun zu:
![\(\begin{array}[t]{rll}
d_1(x) &=& \left|p(x) - k(x)\right|& \\[5pt]
d_2(x) &=& \left|c(x) - k(x)\right|
\end{array}\)](https://www.schullv.de/resources/formulas/62592837595513de921af9dced32adb4d5177c127341ffd8f362857f8dc544c5_light.svg)

 2. Schritt: Extremstellen bestimmen
Mit dem CAS können nun die Extremstellen der beiden Differenzfunktionen berechnet werden oder alternativ graphisch bestimmt werden:
2. Schritt: Extremstellen bestimmen
Mit dem CAS können nun die Extremstellen der beiden Differenzfunktionen berechnet werden oder alternativ graphisch bestimmt werden:
 -Werte in
-Werte in  bzw.
bzw.  liefert:
liefert:
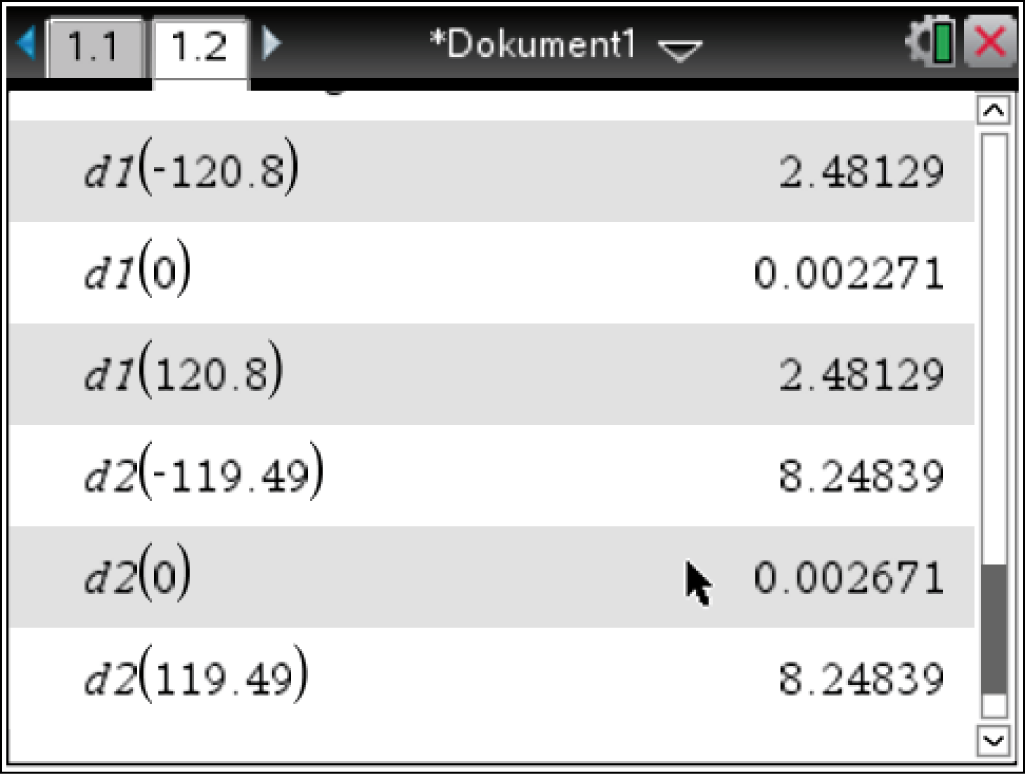 Somit gilt:
Der Abstand zwischen den Graphen von
Somit gilt:
Der Abstand zwischen den Graphen von  und
und  ist an den Stellen
ist an den Stellen  und
und  mit
mit  maximal.
Der Abstand zwischen den Graphen von
maximal.
Der Abstand zwischen den Graphen von  und
und  ist hingegen an den Stellen
ist hingegen an den Stellen
 und
und  mit
mit  maximal.
maximal.


Für  ergeben sich:
ergeben sich:
![\(\begin{array}[t]{rll}
x_1&=& -120,8 & \\[5pt]
x_2&=& 0 & \\[5pt]
x_3&=& 120,8
\end{array}\)](https://www.schullv.de/resources/formulas/cd5f4d5ed4fbb7d30d48793c3428dc204299937a82dfb1147287b90adb64078f_light.svg)
Für  ergeben sich:
ergeben sich:
![\(\begin{array}[t]{rll}
x_4&=& -119,49 & \\[5pt]
x_5&=& 0 & \\[5pt]
x_6&=& 119,49
\end{array}\)](https://www.schullv.de/resources/formulas/1a77bde310b6dc4b3d1dc270ae6396eb91044aa89fefd0d853e7ca7af094342f_light.svg)
3. Schritt: Funktionswerte berechnen
Einsetzen der 
3.1
1. Schritt:
 ist die
ist die  -Koordinate von
-Koordinate von  und
und  beschreibt die Differenz der
beschreibt die Differenz der  -Werte von
-Werte von  und
und 
Der Wert stellt somit die
stellt somit die  -Koordinate von
-Koordinate von  dar.
Die Länge des Kurvenbogens
dar.
Die Länge des Kurvenbogens  ist folglich die Differenz von
ist folglich die Differenz von  und
und  .
Es gilt also:
.
Es gilt also:
![\(\begin{array}[t]{rll}
\overset{\displaystyle\frown}{PQ}&=&\overset{\displaystyle\frown}{AQ} -\overset{\displaystyle\frown}{AP}& \\[5pt]
&=& L_a(x_0+\Delta x)-L_a(x_0)
\end{array}\)](https://www.schullv.de/resources/formulas/733bf2f4e3794374bdf831ce9e3d98cc603982dc61d2c32241556d572c937e08_light.svg) 2. Schritt:
In diesem Schritt wird die Länge der Strecke von
2. Schritt:
In diesem Schritt wird die Länge der Strecke von  zu
zu  berechnet und mit
berechnet und mit  verglichen.
Es gilt:
verglichen.
Es gilt:
 .
Diese Strecke stellt eine Sekante dar und kann maximal so groß wie der Bogen
.
Diese Strecke stellt eine Sekante dar und kann maximal so groß wie der Bogen  sein.
Somit gilt:
sein.
Somit gilt:
 3. Schritt:
Die Gleichung wir auf beiden Seiten mit
3. Schritt:
Die Gleichung wir auf beiden Seiten mit  dividiert:
Auf der rechten Seite ergibt sich dadurch der Differenzenquotient der Funktion
dividiert:
Auf der rechten Seite ergibt sich dadurch der Differenzenquotient der Funktion 
Der Wert
3.2
Einsetzen von  in den linken Term liefert:
Auf beiden Seiten kann nun die Ableitung gebildet werden. Hierbei entspricht die Ableitung eines Integrals der Funktion selbst.
Auflösen der Gleichung liefert nun:
Da nun auf beiden Seiten derselbe Ausdruck steht, folgt, dass die Gleichung gilt.
in den linken Term liefert:
Auf beiden Seiten kann nun die Ableitung gebildet werden. Hierbei entspricht die Ableitung eines Integrals der Funktion selbst.
Auflösen der Gleichung liefert nun:
Da nun auf beiden Seiten derselbe Ausdruck steht, folgt, dass die Gleichung gilt.
3.3
Die Länge  des Stahlbogens kann mit folgender Formel berechnet werden:
Der Scheitelpunkt liegt bei
des Stahlbogens kann mit folgender Formel berechnet werden:
Der Scheitelpunkt liegt bei  Einsetzen von
Einsetzen von  und den Intervallgrenzen
und den Intervallgrenzen  und
und  ergibt:
Die Länge der von der Bahn zurückgelegten Strecke beträgt somit etwa
ergibt:
Die Länge der von der Bahn zurückgelegten Strecke beträgt somit etwa 
1
Parameter der Polynomfunktion bestimmen
Der Parameter  beschreibt den betrag des
beschreibt den betrag des  -Werts der Nullstellen des Graphen von
-Werts der Nullstellen des Graphen von  Da die äußere Bogenspannweite und somit der Abstand der Nullstellen
Da die äußere Bogenspannweite und somit der Abstand der Nullstellen  beträgt und der Bogen symmetrisch zur
beträgt und der Bogen symmetrisch zur  -Achse ist, folgen die Nullstellen mit
-Achse ist, folgen die Nullstellen mit  Der Parameter
Der Parameter  ist somit gegeben durch
ist somit gegeben durch  Einsetzen der Koordinaten des Scheitelpunkts in
Einsetzen der Koordinaten des Scheitelpunkts in  liefert nun:
Der Graph, der die Kurve mit den gegebenen Eigenschaften beschreibt, kann also durch die folgende Polynomfunktion
liefert nun:
Der Graph, der die Kurve mit den gegebenen Eigenschaften beschreibt, kann also durch die folgende Polynomfunktion  beschrieben werden:
Parameter der Kosinusfunktion bestimmen
Da die Amplitude
beschrieben werden:
Parameter der Kosinusfunktion bestimmen
Da die Amplitude  den größten Abstand der Funktion von der
den größten Abstand der Funktion von der  -Achse darstellt, entpricht der Wert von
-Achse darstellt, entpricht der Wert von  dem
dem  -Wert des Scheitelpunkts. Es folgt also
-Wert des Scheitelpunkts. Es folgt also  Die Bogenspannweite von
Die Bogenspannweite von  entspricht einer halben Periodenlänge, es gilt also
entspricht einer halben Periodenlänge, es gilt also  Der Graph, der die Kurve mit den gegebenen Eigenschaften beschreibt, kann also durch die folgende Kosinusfunktion
Der Graph, der die Kurve mit den gegebenen Eigenschaften beschreibt, kann also durch die folgende Kosinusfunktion  dargestellt werden:
dargestellt werden:
![\(\begin{array}[t]{rll}
c(x)&=& 103\cdot \cos\left(\dfrac{2\pi}{680}\cdot x\right)&\\[5pt]
&=& 103\cdot \cos(0,009\cdot x)
\end{array}\)](https://www.schullv.de/resources/formulas/7da16835bd891d1e4230592764ee2ad506e7780b140bb3f0808c0dba546f47fa_light.svg)
2.1
Bedeutung des Parameters 
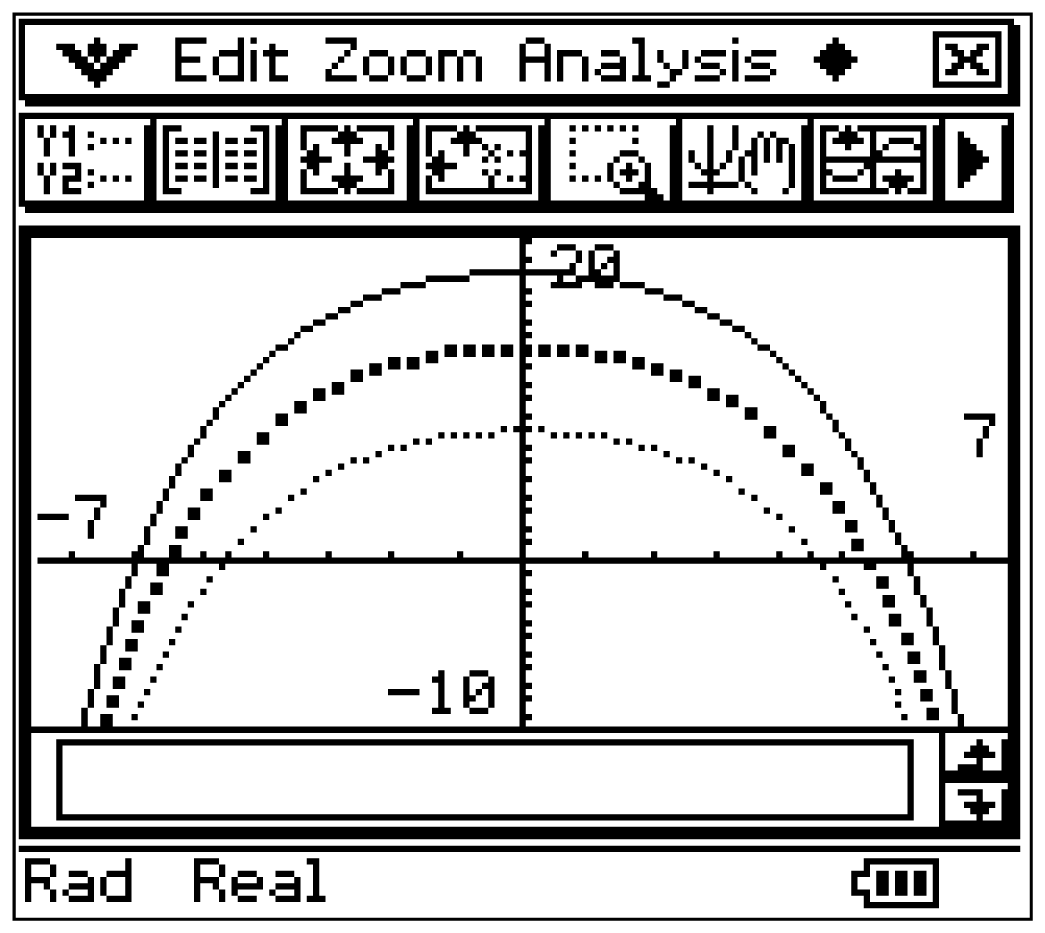 Bedeutung des Parameters
Bedeutung des Parameters 
Um den Einfluss des Parameters  zu untersuchen, können verschiedene Werte für
zu untersuchen, können verschiedene Werte für  eingesetzt werden und die entsprechenden Graphen mit festgelegtem
eingesetzt werden und die entsprechenden Graphen mit festgelegtem  mit Hilfe des CAS im
mit Hilfe des CAS im  -Modus gezeichnet werden.
Der Abbildung kann entnommen werden, dass der Parameter
-Modus gezeichnet werden.
Der Abbildung kann entnommen werden, dass der Parameter  die Graphen der Scharfunktion entlang der
die Graphen der Scharfunktion entlang der  -Achse verschiebt und somit Einfluss auf den
-Achse verschiebt und somit Einfluss auf den  -Achsenabschnitt hat, der dem Maximum der entsprechenden Funktion entspricht.
Der Parameter
-Achsenabschnitt hat, der dem Maximum der entsprechenden Funktion entspricht.
Der Parameter  hat dabei keinen Einfluss auf die Streckung bzw. Stauchung der Graphen von
hat dabei keinen Einfluss auf die Streckung bzw. Stauchung der Graphen von 

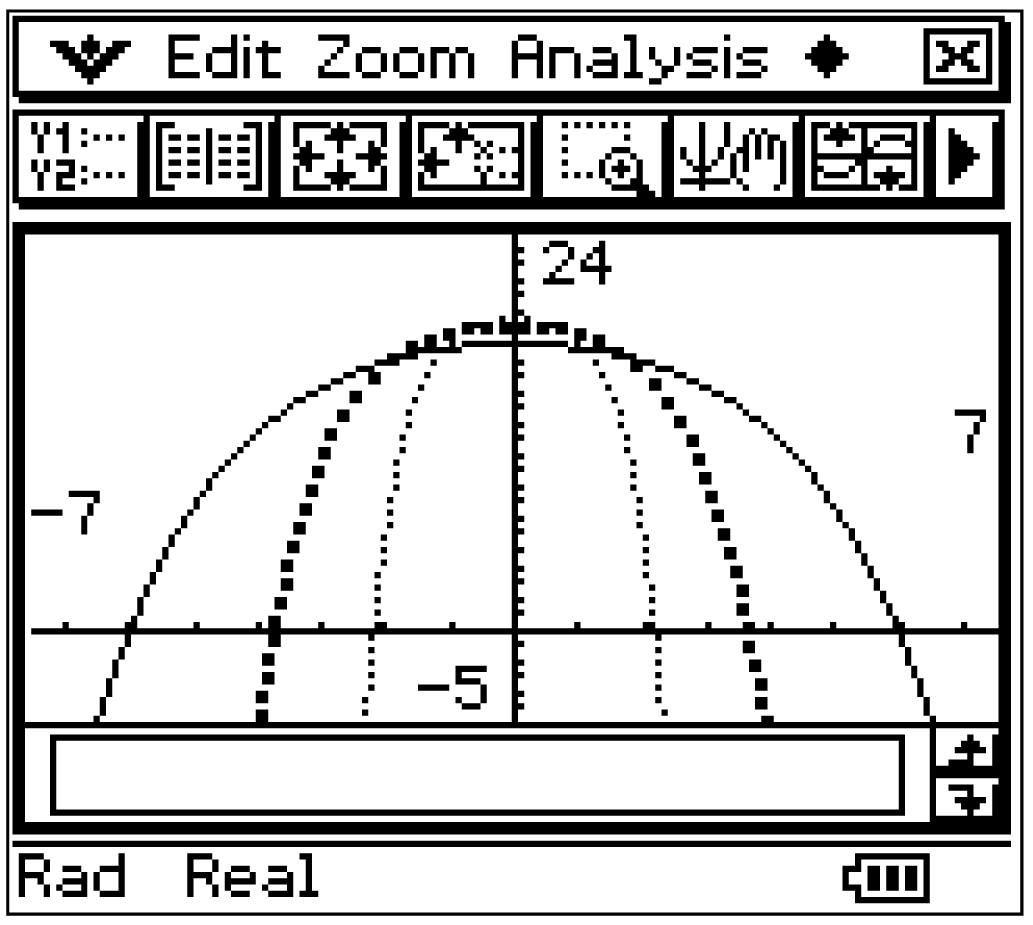
Durch Zeichnen verschiedener Graphen der Scharfunktion mit fixem Wert von  und verschiedenen Werten von
und verschiedenen Werten von  mit Hilfe des CAS lässt sich schließen:
Umso größer der Wert von
mit Hilfe des CAS lässt sich schließen:
Umso größer der Wert von  ist, desto stärker sind die Graphen von
ist, desto stärker sind die Graphen von  gestaucht.
Der Parameter
gestaucht.
Der Parameter  streckt bzw. staucht somit die Graphen der Schar.
Zudem nimmt der
streckt bzw. staucht somit die Graphen der Schar.
Zudem nimmt der  -Achsenabschnitt mit zunehmendem Wert von
-Achsenabschnitt mit zunehmendem Wert von  ab.
ab.  beeinflusst somit auch den Maximalwert der Funktionen der Schar.
beeinflusst somit auch den Maximalwert der Funktionen der Schar.

2.2
Der einleitende Text liefert die folgenden Informationen über den Graphen:
 -Achse liegen soll und somit durch den Punkt
-Achse liegen soll und somit durch den Punkt  beschrieben werden kann, muss gelten:
beschrieben werden kann, muss gelten:
![\(\begin{array}[t]{rll}
k(0)&=& 103 & \\[5pt]
C - \dfrac{1}{2 \lambda} \cdot \left( \mathrm e^{\lambda \cdot 0} + \mathrm e^{-\lambda \cdot 0}\right)&=& 103& \\[5pt]
C - \dfrac{1}{2 \lambda} \cdot \left( 1 + 1\right)&=& 103 & \\[5pt]
C - \dfrac{1}{\lambda}&=& 103
\end{array}\)](https://www.schullv.de/resources/formulas/a3409cd9f5551ca977241e74586f1bc353fb078445127d9a76d8a3d1e9f163c5_light.svg) Aufgrund der Symmetrie und der Bogenspannweite von
Aufgrund der Symmetrie und der Bogenspannweite von  folgen die Schnittstellen des Graphen mit der
folgen die Schnittstellen des Graphen mit der  -Achse mit
-Achse mit  und
und  Es gilt also:
Es gilt also:
![\(\begin{array}[t]{rll}
k(170)&=& 0 & \\[5pt]
C - \dfrac{1}{2 \lambda} \cdot \left( \mathrm e^{\lambda \cdot 170} + \mathrm e^{-\lambda \cdot 170}\right)&=& 0 & \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/a2098496554f0da8145bc10bfaa4278461f78486d500a87f03d044e5e1fdb6fe_light.svg) Zwei Gleichungen, um die Parameter
Zwei Gleichungen, um die Parameter  und
und  zu bestimmen, sind somit gegeben durch:
zu bestimmen, sind somit gegeben durch:
- Die
-Achse soll so gewählt werden, dass der höchste Punkt des Bogens auf der
-Achse liegt.
- Die
-Achse soll so gewählt werden, dass die Bodenlinie auf der
-Achse liegt.
- Der höchste Punkt liegt
über dem Boden.
- Die Bogenspannweite beträgt
2.3
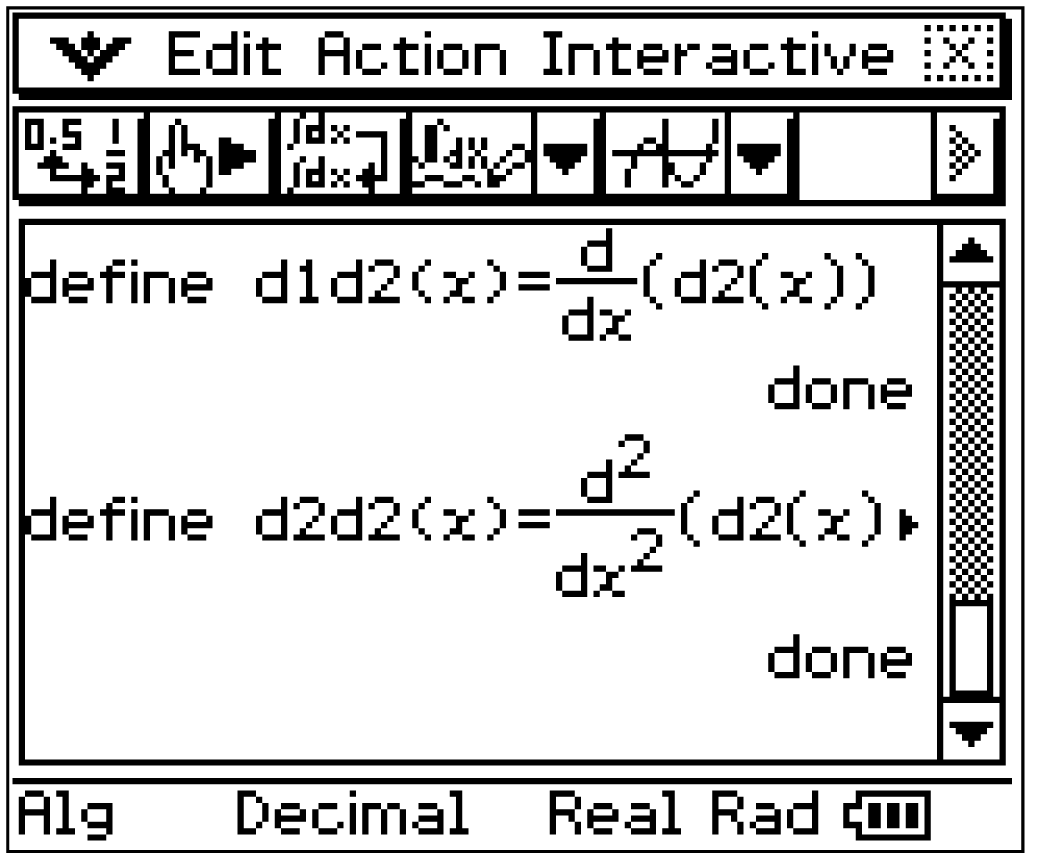
1. Schritt: Differenzfunktionen aufstellen
Im CAS können die drei Funktionen  und
und  mit den gegebenen Werten aus der Aufgabenstellung definiert werden:
mit den gegebenen Werten aus der Aufgabenstellung definiert werden:
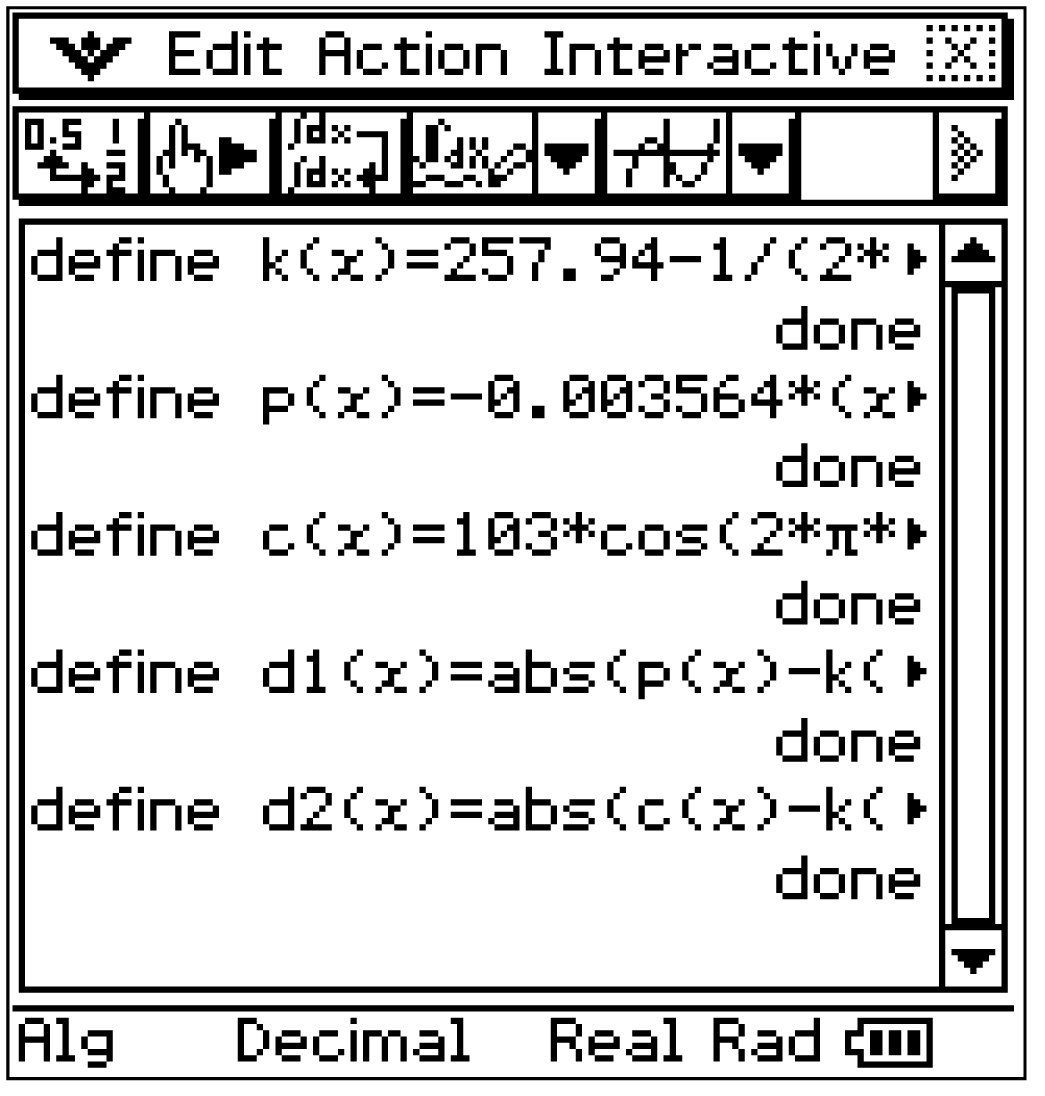 Die Differenzfunktionen ergeben sich nun zu:
Die Differenzfunktionen ergeben sich nun zu:
![\(\begin{array}[t]{rll}
d_1(x) &=& \left|p(x) - k(x)\right|& \\[5pt]
d_2(x) &=& \left|c(x) - k(x)\right|
\end{array}\)](https://www.schullv.de/resources/formulas/62592837595513de921af9dced32adb4d5177c127341ffd8f362857f8dc544c5_light.svg)

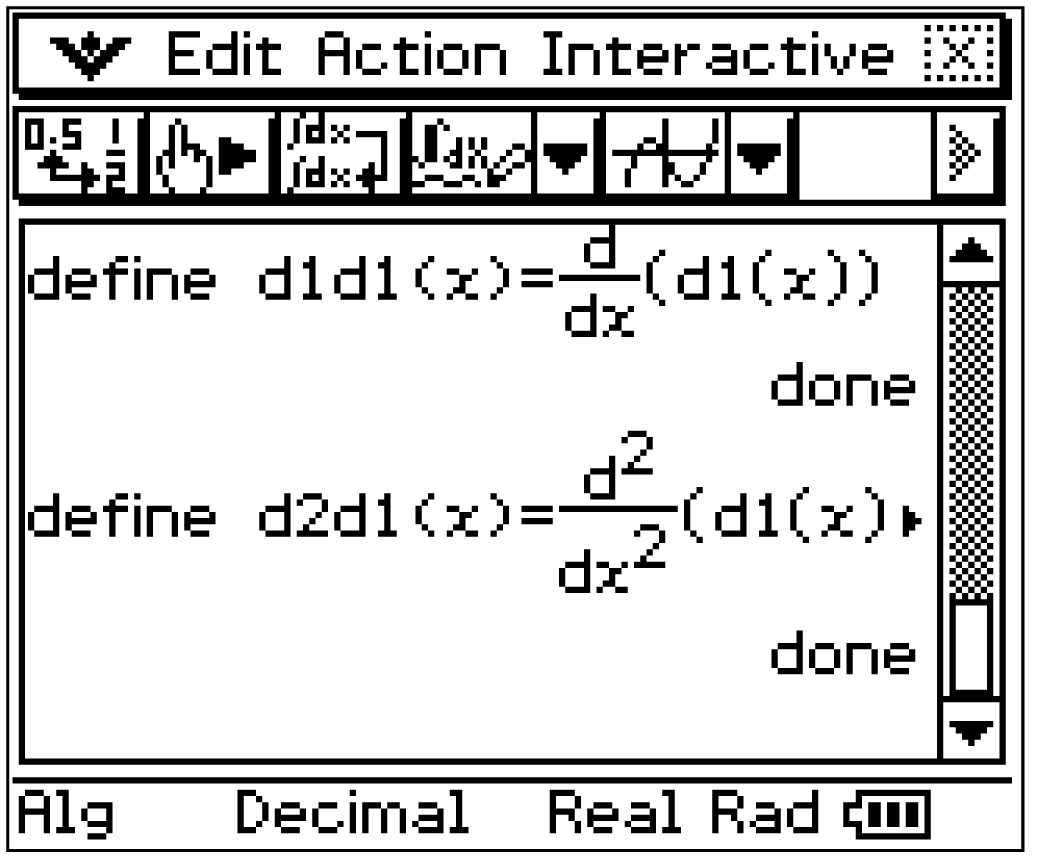
 2. Schritt: Extremstellen bestimmen
Mit dem CAS können nun die Extremstellen der beiden Differenzfunktionen berechnet werden oder alternativ graphisch bestimmt werden:
2. Schritt: Extremstellen bestimmen
Mit dem CAS können nun die Extremstellen der beiden Differenzfunktionen berechnet werden oder alternativ graphisch bestimmt werden:
 -Werte in
-Werte in  bzw.
bzw.  liefert:
liefert:
 Somit gilt:
Der Abstand zwischen den Graphen von
Somit gilt:
Der Abstand zwischen den Graphen von  und
und  ist an den Stellen
ist an den Stellen  und
und  mit
mit  maximal.
Der Abstand zwischen den Graphen von
maximal.
Der Abstand zwischen den Graphen von  und
und  ist hingegen an den Stellen
ist hingegen an den Stellen
 und
und  mit
mit  maximal.
maximal.



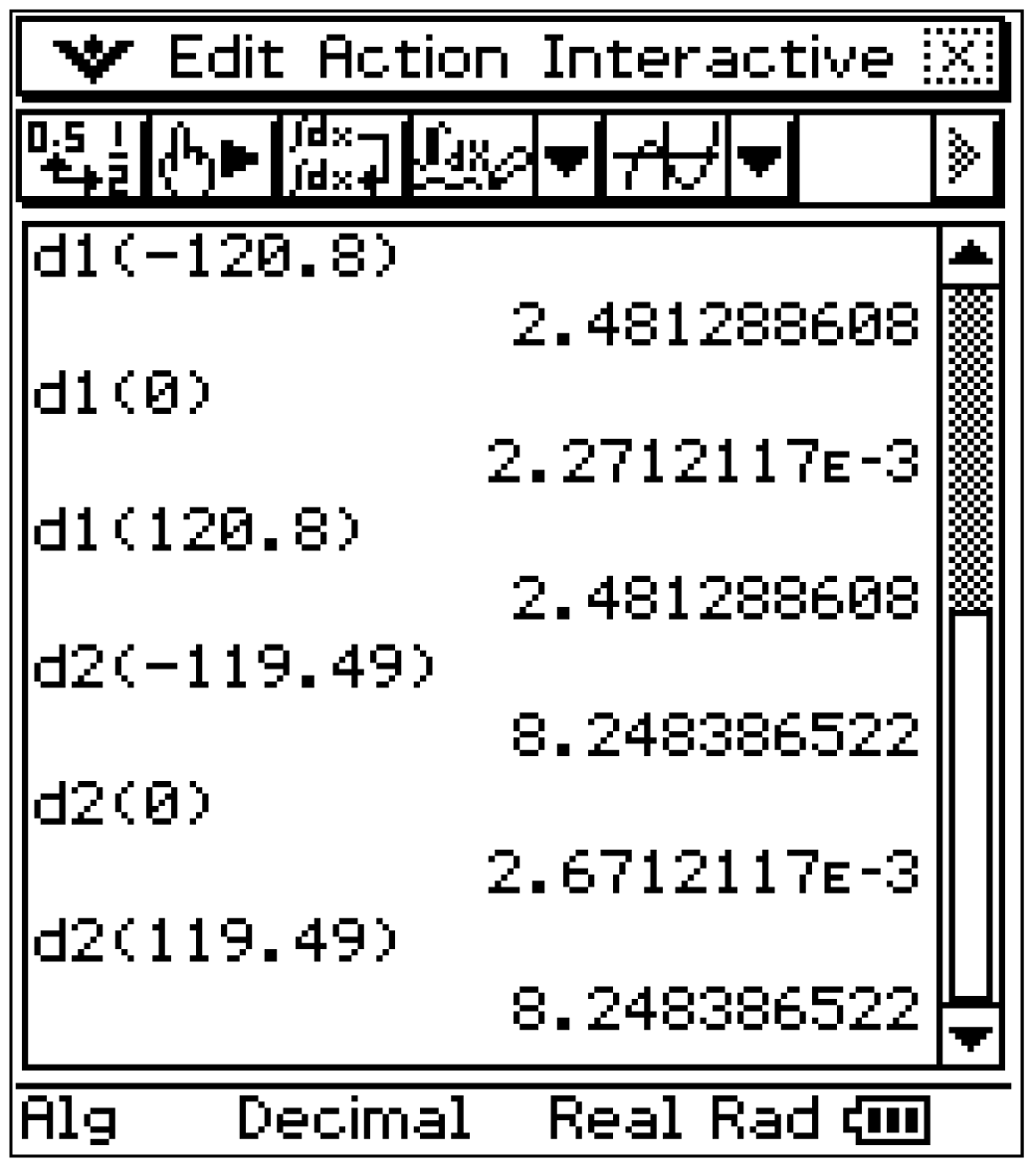
Für  ergeben sich:
ergeben sich:
![\(\begin{array}[t]{rll}
x_1&=& -120,8 & \\[5pt]
x_2&=& 0 & \\[5pt]
x_3&=& 120,8
\end{array}\)](https://www.schullv.de/resources/formulas/cd5f4d5ed4fbb7d30d48793c3428dc204299937a82dfb1147287b90adb64078f_light.svg)
Für  ergeben sich:
ergeben sich:
![\(\begin{array}[t]{rll}
x_4&=& -119,49 & \\[5pt]
x_5&=& 0 & \\[5pt]
x_6&=& 119,49
\end{array}\)](https://www.schullv.de/resources/formulas/1a77bde310b6dc4b3d1dc270ae6396eb91044aa89fefd0d853e7ca7af094342f_light.svg)
3. Schritt: Funktionswerte berechnen
Einsetzen der 
3.1
1. Schritt:
 ist die
ist die  -Koordinate von
-Koordinate von  und
und  beschreibt die Differenz der
beschreibt die Differenz der  -Werte von
-Werte von  und
und 
Der Wert stellt somit die
stellt somit die  -Koordinate von
-Koordinate von  dar.
Die Länge des Kurvenbogens
dar.
Die Länge des Kurvenbogens  ist folglich die Differenz von
ist folglich die Differenz von  und
und  .
Es gilt also:
.
Es gilt also:
![\(\begin{array}[t]{rll}
\overset{\displaystyle\frown}{PQ}&=&\overset{\displaystyle\frown}{AQ} -\overset{\displaystyle\frown}{AP}& \\[5pt]
&=& L_a(x_0+\Delta x)-L_a(x_0)
\end{array}\)](https://www.schullv.de/resources/formulas/733bf2f4e3794374bdf831ce9e3d98cc603982dc61d2c32241556d572c937e08_light.svg) 2. Schritt:
In diesem Schritt wird die Länge der Strecke von
2. Schritt:
In diesem Schritt wird die Länge der Strecke von  zu
zu  berechnet und mit
berechnet und mit  verglichen.
Es gilt:
verglichen.
Es gilt:
 .
Diese Strecke stellt eine Sekante dar und kann maximal so groß wie der Bogen
.
Diese Strecke stellt eine Sekante dar und kann maximal so groß wie der Bogen  sein.
Somit gilt:
sein.
Somit gilt:
 3. Schritt:
Die Gleichung wir auf beiden Seiten mit
3. Schritt:
Die Gleichung wir auf beiden Seiten mit  dividiert:
Auf der rechten Seite ergibt sich dadurch der Differenzenquotient der Funktion
dividiert:
Auf der rechten Seite ergibt sich dadurch der Differenzenquotient der Funktion 
Der Wert
3.2
Einsetzen von  in den linken Term liefert:
Auf beiden Seiten kann nun die Ableitung gebildet werden. Hierbei entspricht die Ableitung eines Integrals der Funktion selbst.
Auflösen der Gleichung liefert nun:
Da nun auf beiden Seiten derselbe Ausdruck steht, folgt, dass die Gleichung gilt.
in den linken Term liefert:
Auf beiden Seiten kann nun die Ableitung gebildet werden. Hierbei entspricht die Ableitung eines Integrals der Funktion selbst.
Auflösen der Gleichung liefert nun:
Da nun auf beiden Seiten derselbe Ausdruck steht, folgt, dass die Gleichung gilt.
3.3
Die Länge  des Stahlbogens kann mit folgender Formel berechnet werden:
Der Scheitelpunkt liegt bei
des Stahlbogens kann mit folgender Formel berechnet werden:
Der Scheitelpunkt liegt bei  Einsetzen von
Einsetzen von  und den Intervallgrenzen
und den Intervallgrenzen  und
und  ergibt:
Die Länge der von der Bahn zurückgelegten Strecke beträgt somit etwa
ergibt:
Die Länge der von der Bahn zurückgelegten Strecke beträgt somit etwa 