Analysis 2.1

Stadtwappen

Gegeben sind die Funktionenschar $f_a$ mit $f_a(x)=x^4-2ax^2+a^2$ ; $a \in \mathbb{R},a \neq 0$ und die Funktion $g$ mit $g(x)=2x^2-2$ . Die Graphen der Schar $f_a$ sind $G_a$ und der Graph von $g$ ist $K$ .

Weise nach, dass alle Graphen $G_a$ achsensymmetrisch zur $y$ -Achse verlaufen. Ermittle die Koordinaten der Schnittpunkte von $G_a$ mit den beiden Koordinatenachsen.

(9P)

Bestimme die Koordinaten und die Art der lokalen Extrempunkte von $G_a$ in Abhängigkeit von $a$ .
Für jeden Parameter $a$ mit $a\gt 0$ sind die drei lokalen Extrempunkte Eckpunkte eines Dreiecks. Wenn der Parameterwert $a$ verdoppelt wird, vervielfacht sich der Flächeninhalt des ursprünglichen Dreiecks $A_\Delta$ .
Das neue Dreieck hat den Flächeninhalt $A_{neu}=v \cdot A_\Delta$ .
Ermittle den Faktor $v$ .

(12P)

Die Graphen $G_1$ und $K$ schließen im Intervall $[-1;1]$ eine Fläche ein, die als Schablone für das Wappen einer Stadt genutzt werden soll.

Berechne den zugehörigen Flächeninhalt.

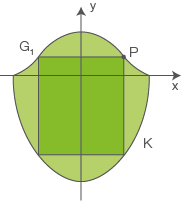Diagramm einer geometrischen Figur mit einem Rechteck und einer kurvenförmigen Linie. Achsen x und y sind eingezeichnet.

Abb. 1 Skizze

(5P)

Der Punkt $P$ liegt im I. Quadranten $G_1$ (siehe Abbildung). $P$ ist Eckpunkt eines Rechtecks, dessen Seiten achsenparallel verlaufen und dessen weitere Eckpunkte auf den Begrenzungslinien des Wappens liegen. Innerhalb dieses Rechtecks soll das Wappentier abgebildet werden.

Zeige, dass der Flächeninhalt eines solchen Rechtecks mit der Gleichung $A(x)=2x^5-8x^3+6x$ berechnet werden kann und ermittle den maximalen Flächeninhalt des Rechtecks. Auf den Nachweis des Maximums wird verzichtet.

(9P)

Die untere Begrenzung des Stadtwappens soll statt durch die quadratische Parabel $K$ mithilfe einer anderen quadratischen Parabel modelliert werden. Dabei sollen die Symmetrie des Wappens sowie die Schnittpunkte $S_1(-1\mid0)$ und $S_2(1\mid0)$ mit $G_1$ zwar erhalten bleiben, sich aber die Fläche des Wappens um 2 FE vergrößern.

Ermittle eine Funktionsgleichung der neuen Parabel.

(5P)

(40P)

Bildnachweise [nach oben]

[1]

$\blacktriangleright$ Achsensymmetrie zur $\boldsymbol{y}$ -Achse zeigen

Bei dieser Aufgabe sollst du zeigen, dass die Graphen $G_a$ achsensymmetrisch zur $y$ -Achse sind. Dafür muss gelten: $f(x)=f(-x)$ . Dies formst du solange um, bis du eine allgemein gültige Aussage erhältst.

Tipp:

Ist ein Graph achsensymmetrisch zur y-Achse, so gilt $f(x)=f(-x)$ .

$\begin{array}[t]{rll} f_a(x)&=& f_a(-x)\\[5pt] x^4-2ax^2+a^2&=& x^4-2ax^2+a^2 \end{array}$

Vollständige Lösung anzeigen

Damit ist die Äquivalenz gezeigt und die Graphen der Funktionenschar sind somit achsensymmetrisch zur $y$ -Achse.

$\blacktriangleright$ Schnittpunkte mit Koordinatenachsen berechnen

Um die Koordinaten des Schnittpunkts mit der $y$ -Achse zu berechnen, berechnest du den Funktionswert an der Stelle $x=0$ . Damit du den Schnittpunkt mit der $x$ -Achse berechnen kannst, setzt du den Funktionsterm der Funktionenschar gleich Null.

$\begin{array}[t]{rll} f_a(0)&=& 0^4-2a\cdot 0^2+a^2 \\[5pt] &=& a^2 \end{array}$

Für die Schnittpunkte mit der $x$ -Achse folgt mithilfe der Substitution:

$\begin{array}[t]{rll} 0 &=& f_a(x) \\[5pt] 0 &=& x^4-2ax^2+a^2 &\quad \scriptsize \text{Substitution } z=x^2 \\[5pt] 0 &=& z^2-2az+a^2 &\quad \scriptsize \mid\; pq\text{-Formel} \\[5pt] z_{1/2} &=& -\frac{-2a}{2}\pm \sqrt{\left(\frac{-2a}{2} \right)^2-a^2} \\[5pt] &=& a\pm \sqrt{a^2-a^2}\\[5pt] &=&a\pm 0 \\[5pt] &=& a &\quad \scriptsize \text{Resubstitution } \\[5pt] x_{1/2}&=& \pm \sqrt{a} \end{array}$

Diese Gleichung hat nur für $a\gt 0$ eine Lösung. Das bedeutet $G_a$ schneidet die $y$ -Achse im Punkt $S(0\mid a^2).$ Die $x$ -Achse schneidet $G_a$ für $a\lt 0$ nicht, für $a\gt 0$ in den Punkten $S_{x_1}(-\sqrt{a}\mid 0)$ und $S_{x_2}(\sqrt{a}\mid 0).$

$\blacktriangleright$ Lokale Extrempunkte bestimmen

Du hast die Funktionenschar $f_a$ gegeben und sollst deren Graph auf Extrempunkte untersuchen. Für eine Extremstelle $x_E$ benötigst du die beiden folgenden Kriterien:

Notwendiges Kriterium: $\, f‘(x_E)=0$
Hinreichendes Kriterium:
- Ist $f‘‘(x_E)\gt 0$ , handelt es sich um eine Minimalstelle.
- Ist $f‘‘(x_E)\lt 0$ , handelt es sich um eine Maximalstelle.

Du kannst also wie folgt vorgehen:

Bestimme die ersten beiden Ableitungsfunktionen $f‘$ und $f‘‘$ .
Wende das notwendige Kriterium an, indem du $f‘(x)=0$ setzt und nach $x$ löst.
Überprüfe das hinreichende Kriterium, indem du die Lösung aus 2. in $f‘‘(x)$ einsetzt. So bestimmst du gleichzeitig die Art der Extrema.
Berechne die Funktionswerte von $f$ an den Extremstellen.

1. Schritt: Ableitungsfunktionen bestimmen

$\begin{array}[t]{rll} f(x)&=& x^4-2ax^2+a^2\\[10pt] f‘(x)&=& 4x^3-4ax\\[10pt] f‘‘(x)&=& 12x^2-4a \end{array}$

2. Schritt: Notwendiges Kriterium anwenden

Durch Gleichsetzen von $f‘(x)$ mit Null, erhältst du mögliche Extremstellen:

$\begin{array}[t]{rll} f‘(x)&=&0 \\[5pt] 4x^3-4ax&=& 0 &\quad \scriptsize \mid\; :4\\[5pt] x^3-ax&=& 0 \\[5pt] x\cdot \left(x^2-a\right) &=& 0 \end{array}$

Damit das Produkt Null ist, muss einer der Faktoren Null sein. So erhältst du als eine erste Lösung $x_1=0$ .

$\begin{array}[t]{rll} x^2-a&=& 0 &\quad \scriptsize \mid\; +a\\[5pt] x^2 &=& a &\quad \scriptsize \mid\; \sqrt{}\\[5pt] x &=& \pm\sqrt{a} \end{array}$

Mögliche Extremstellen sind also:

Für alle $a:\quad$ $x_1=0$
Für $a\gt 0:\quad$ $x_2=-\sqrt{a}$ und $x_3=\sqrt{a}$

3. Schritt: Hinreichendes Kriterium überprüfen

Es reicht lediglich $\sqrt{a}$ oder $-\sqrt{a}$ einzusetzen, da die Graphen von $f_a‘‘$ achsensymmetrisch zur $y$ -Achse sind.

$\begin{array}[t]{rll} f‘‘\left(\sqrt{a}\right)&=& 12\cdot \left(\sqrt{a}\right)^2-4a \\[5pt] &=& 12a-4a \\[5pt] &=& 8a \gt 0 \text{ für } a\gt 0\\[5pt] \end{array}$

$\begin{array}[t]{rll} f‘‘(0)&=& 12\cdot 0^2-4a \\[5pt] &=& -4a \; \lt 0 \text{ für } a\gt 0 \quad \text{ bzw.} \gt 0 \text{ für } a\lt 0\\[5pt] \end{array}$

4. Schritt: Funktionswerte berechnen

$\begin{array}[t]{rll} f\left(\sqrt{a}\right)&=& \left(\sqrt{a}\right)^4-2a\left(\sqrt{a}\right)^2+a^2 \\[5pt] &=& a^2-2a^2+a^2 \\[5pt] &=& 0 \end{array}$

$\begin{array}[t]{rll} f(0)&=& 0^4-2a\cdot0^2+a^2 \\[5pt] &=& a^2 \end{array}$

Insgesamt ergibt sich also:

Für $a\gt 0$ besitzt der Graph von $f_a$ drei lokale Extrempunkte: Zwei lokale Tiefpunkte mit den Koordinaten $P_2\left(\sqrt{a} \mid 0\right)$ und $P_3\left(-\sqrt{a} \mid 0\right)$ und einen lokalen Hochpunkt mit den Koordinaten $P_1\left(0\mid a^2\right).$
Für $a\lt 0$ besitzt der Graph von $f_a$ einen lokalen Extrempunkt: Einen lokalen Tiefpunkt mit den Koordinaten $P_1\left(0\mid a^2\right).$

$a=0$ ist laut Aufgabenstellung ausgeschlossen.

$\blacktriangleright$ Flächeninhaltsverhältnis berechnen

Da der Graph achsensymmetrisch ist, kann der Flächeninhalt des Dreiecks, welches durch die drei Extrempunkte begrenzt ist, berechnet werden, indem du als Breite den $x$ -Wert einer der äußeren Extrempunkte verdoppelst und als Höhe nimmst du den Funktionswert des Extrempunktes an der Stelle $x_1$ . Danach verdoppelst du $a$ , berechnest den neuen Flächeninhalt und bildest das Verhältnis, um $v$ zu berechnen.

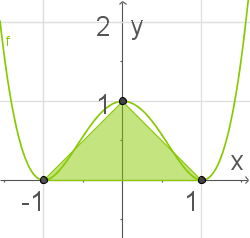Graf einer Funktion mit einer parabelförmigen Kurve und einem grünen Bereich zwischen den x-Werten -1 und 1.

Abb. 1: Dreieck

$\begin{array}[t]{rll} A_\Delta&=& \dfrac{2\sqrt{a}\cdot a^2}{2} \\[5pt] &=&\sqrt{a}\cdot a^2 \end{array}$

$\begin{array}[t]{rll} A_{neu}&=& \dfrac{2\sqrt{2a}\cdot (2a)^2}{2} \\[5pt] &=&\sqrt{2a} \cdot 4a^2 \\[5pt] &=& 4\cdot\sqrt{2}\cdot\sqrt{a}\cdot a^2 \end{array}$

$\begin{array}[t]{rll} v&=& \dfrac{A_{neu}} {A_\Delta} \\[5pt] &=& \dfrac{4\cdot\sqrt{2}\cdot\sqrt{a}\cdot a^2}{\sqrt{a}\cdot a^2} \\[5pt] &=& 4\sqrt{2} \end{array}$

Das bedeutet, dass der Flächeninhalt von $A$ sich bei einer Verdopplung von $a$ um den Faktor $v=4\sqrt{2}$ vervielfacht.

$\blacktriangleright$ Flächeninhalt des Wappens berechnen

Um den Flächeninhalt des Wappens zu berechnen, musst du das Integral zwischen den Funktionen $G_1$ und $K$ im Intervall $[-1;1]$ berechnen. Dafür berechnest du das Integral von $G_1-K$ im angegebenen Intervall.

$\begin{array}[t]{rll} \displaystyle\int_{-1}^{1}\left(\left(x^4-2x^2+1\right)-\left(2x^2-2\right)\right)\;\mathrm dx \end{array}$

Vollständige Lösung anzeigen

Der Flächeninhalt des Wappens beträgt damit $A=\frac{56}{15}\text{[FE]}$ .

$\blacktriangleright$ Flächeninhalt des Rechtecks berechnen

Um den Flächeninhalt des Rechtecks bestimmen zu können, brauchst du dessen Breite und Höhe. Die Breite ergibt sich aus der $x$ -Koordinaten von $P$ . Da $G_1$ achsensymmetrisch zur $y$ -Achse ist, ist die Breite des Rechtecks das Doppelte der $x$ -Koordinate von $P$ . Die Höhe berechnest du als Differenz der Funktionswerte von $G_1$ und $K$ . Da $P$ auf $G_1$ liegt, lauten die Koordinaten von $P(x\mid x^4-2x^2+1)$ .

Abb. 2

$\begin{array}[t]{rll} b(x) &=& 2\cdot x \\[5pt] &=& 2x \end{array}$

$\begin{array}[t]{rll} h(x) &=& f_1(x)-g(x) \\[5pt] &=& x^4-2x^2+1 - \left(2x^2-2\right) \\[5pt] &=& x^4-2x^2+1 - 2x^2+2 \\[5pt] &=& x^4-4x^2 +3 \end{array}$

$\begin{array}[t]{rll} A(x)&=& h(x) \cdot b(x)\\[5pt] &=& \left(x^4-4x^2 +3\right)\cdot\left(2x\right) \\[5pt] &=& 2x^5-8x^3+6x \end{array}$

Damit hast du gezeigt, dass der Flächeninhalt des Rechtecks mit der Gleichung $A(x)=2x^5-8x^3+6x$ berechnet werden kann. Nun sollst du noch dessen Maximum berechnen. Dafür leitest du $A$ ab und berechnest den Extremwert.

Du hast die Funktion $A(x)$ gegeben und sollst deren Graph auf Extrempunkte untersuchen. Für eine Extremstelle $x_E$ benötigst du die beiden folgenden Kriterien:

Notwendiges Kriterium: $\, A‘(x_E)=0$
Hinreichendes Kriterium:
- Ist $A‘‘(x_E)\gt 0$ , handelt es sich um eine Minimalstelle.
- Ist $A‘‘(x_E)\lt 0$ , handelt es sich um eine Maximalstelle.

Du kannst also wie folgt vorgehen:

Bestimme die ersten beiden Ableitungsfunktionen $A‘$ und $A‘‘$ .
Wende das notwendige Kriterium an, indem du $A‘(x)=0$ setzt und nach $x$ löst.
Das hinreichende Kriterium brauchst du laut Aufgabenstellung nicht überprüfen.
Berechne die Funktionswerte von $A(x)$ an den Extremstellen.

1. Schritt: Ableitungsfunktionen bestimmen

$\begin{array}[t]{rll} A(x)&=& 2x^5-8x^3+6x \\[10pt] A‘(x)&=& 10x^4-24x^2+6 \\[10pt] A‘‘(x)&=& 40x^3-48x \end{array}$

2. Schritt: Notwendiges Kriterium anwenden

Durch Gleichsetzen von $A‘(x)$ mit Null, erhältst du mögliche Extremstellen. Um das in diesem Fall lösen zu können, substituierst du $x^2=u$ , berechnest mithilfe der PQ-Formel die Nullstellen und resubstituierst dann wieder.

$\begin{array}[t]{rll} A‘(x)&=&0 \\[5pt] 10x^4-24x^2+6&=&0 &\quad \scriptsize \mid\; x^2=u \\[5pt] 10u^2-24u+6&=& 0 &\quad \scriptsize \mid\;:10 \\[5pt] u^2-\frac{12}{5}u+\frac{3}{5}&=&0 \end{array}$

$\begin{array}[t]{rll} u&=& -\left(\frac{-\frac{12}{5}}{2}\right)\pm\sqrt{\left(\frac{\frac{12}{5}}{2}\right)^2-\frac{3}{5}} \\[5pt] &=&\frac{6}{5}\pm\sqrt{\frac{36}{25}-\frac{3}{5}} \\[5pt] &=&\frac{6}{5} \pm \sqrt{\frac{36}{25}-\frac{15}{25}} \\[5pt] &=&\frac{6}{5}\pm\sqrt{\frac{21}{25}} \\[5pt] \end{array}$

Resubstitution ergibt:

$\begin{array}[t]{rll} x&=& \sqrt{u} \\[5pt] x_{1/2}&=& \pm \sqrt{\frac{6}{5}+\sqrt{\frac{21}{25}}}\\[5pt] &\approx& \pm 1,45 \\[5pt] x_{3/4}&=& \pm \sqrt{\frac{6}{5}-\sqrt{\frac{21}{25}}}\\[5pt] &\approx& \pm 0,53 \end{array}$

Da $x$ nur im Intervall [-1;1] liegen kann, sind nur $x_3$ und $x_4$ wichtig. Da es sich um ein Polynom 5. Grades handelt, dessen Graph nicht gespiegelt wurde, muss sich an der Stelle $x_3=0,53$ das Maximum befinden.

3. Schritt: Hinreichendes Kriterium überprüfen

Dies musst du laut Aufgabenstellung nicht überprüfen.

4. Schritt: Funktionswerte berechnen

$\begin{array}[t]{rll} A(0,53)&=& 2,07 \end{array}$

Vollständige Lösung anzeigen

Der maximale Flächeninhalt des Rechtecks beträgt $A=2,07\text{[FE]}$ .

$\blacktriangleright$ Parabelgleichung aufstellen

Du sollst nun die Parabelgleichung für die neue Parabel aufstellen. Hierfür hast du zwei Punkte $S_1$ und $S_2$ der Parabel gegeben und weißt, dass sie symmetrisch zur $y$ -Achse sein soll. Weiterhin ist gegeben, dass der Inhalt des Wappens um 2 FE größer werden soll. Da die obere Grenze weiterhin $G_1$ ist, muss gelten, dass das Integral im Intervall [-1;1] der neuen Parabel um 2 größer sein muss als das Integral von $K$ . Die allgemeine Parabelgleichung lautet: $y=ax^2+bx+c$ . Mithilfe dieser Gleichung und den Bedingungen kann ein Gleichungssystem aufgestellt werden, welches du nach $a$ , $b$ und $c$ löst.

$\begin{array}[t]{rll} \,\bigg \vert \, \displaystyle\int_{-1}^{1}\left(ax^2+bx+c\right)\;\mathrm dx\,\bigg \vert \,&=&\frac{14}{3} \\[5pt] \,\bigg \vert \, \left[\frac{a}{3}x^3+\frac{b}{2}x^2+cx\right]_{-1}^1\,\bigg \vert \,&=&\frac{14}{3}\\[5pt] \,\bigg \vert \, \frac{a}{3}-\frac{b}{2}+c-\left(-\frac{a}{3}+\frac{b}{2}-c\right)\,\bigg \vert \,&=&\frac{14}{3}\\[5pt] \,\bigg \vert \, \frac{2}{3}a-b+2c\,\bigg \vert \, &=& \frac{14}{3}\\[5pt] \end{array}$

Setzt du die Koordinaten der zwei Punkte $S_1$ und $S_2$ in die Parabelgleichung ein, erhältst du folgende zwei Gleichungen:

$\begin{array}[t]{rll} a\cdot(-1)^2+b\cdot(-1)+c&=& 0\\[5pt] a-b+c&=& 0\\[5pt] \end{array}$

$\begin{array}[t]{rll} a\cdot1^2+b\cdot1+c&=& 0\\[5pt] a+b+c&=& 0\\[5pt] \end{array}$

Aus diesen beiden Gleichungen kannst du herauslesen, dass $b=0$ gelten muss, denn egal ob du $b$ addierst oder subtrahierst, ändert sich der Wert nicht. Addierst du dann die beiden Gleichung, erhältst du:

$\begin{array}[t]{rll} 2a+2c&=& 0 &\quad \scriptsize \mid\; :2\\[5pt] a+c&=& 0 &\quad \scriptsize \mid\;-c \\[5pt] a&=& -c \end{array}$

Nun setzt du deine Ergebnisse in die Bedingung, welche sich aus dem Flächeninhalt ergeben hat, ein und erhältst so die Werte für die Parameter der Parabelgleichung.

$\begin{array}[t]{rll} \frac{2}{3}a-0+2\cdot(-a)&=& \frac{14}{3} \\[5pt] a&=& 3,5 \end{array}$

Vollständige Lösung anzeigen

Damit ergibt sich für die neue Parabel die Gleichung $y=3,5x^2-3,5$ .

Bildnachweise [nach oben]

[1]

[2]