Analysis Aufgabe 1
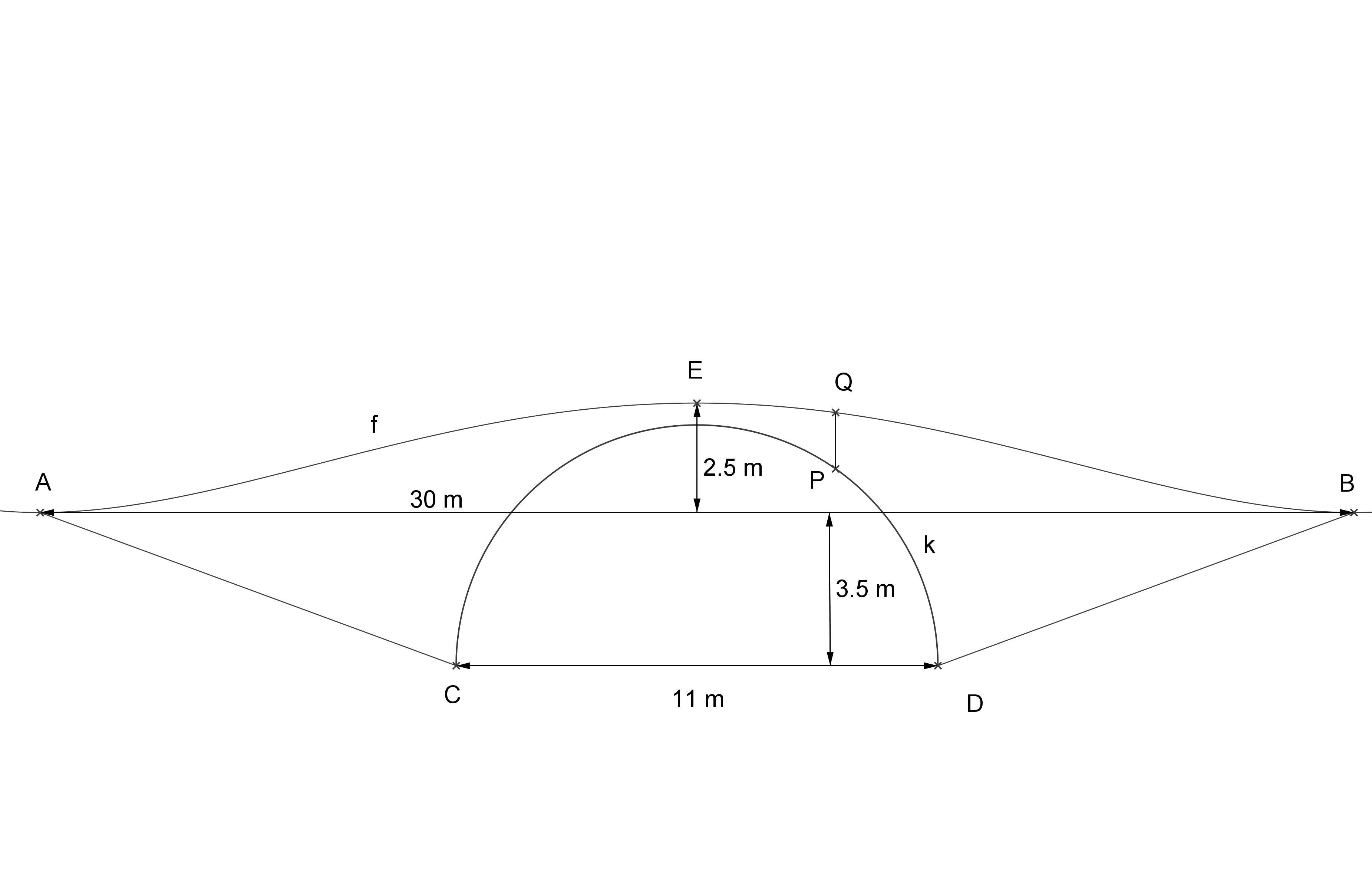
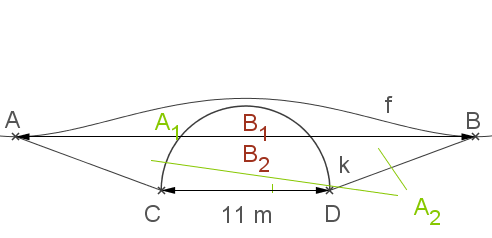
In einem Park überspannt eine Steinbrücke einen Kanal. Die folgende Abbildung zeigt die achsensymmetrische Seitenansicht, also den Längsschnitt der Brücke.
Die Bodenlinie  liegt
liegt  unter dem höchsten Punkt
unter dem höchsten Punkt  der Brücke und
der Brücke und  über dem Wasserspiegel
über dem Wasserspiegel  . Die Länge der Strecke
. Die Länge der Strecke  beträgt
beträgt  . Die horizontalen Zufahrtswege schließen in den Punkten
. Die horizontalen Zufahrtswege schließen in den Punkten  und
und  knickfrei an den Brückenbogen an.
knickfrei an den Brückenbogen an.
Das zur Beschreibung verwendete Koordinatensystem hat seinen Ursprung im Mittelpunkt der Strecke . Eine Längeneinheit entspricht einem Meter in der Wirklichkeit.
. Eine Längeneinheit entspricht einem Meter in der Wirklichkeit.
Das zur Beschreibung verwendete Koordinatensystem hat seinen Ursprung im Mittelpunkt der Strecke
a)
Der obere Rand des Brückenbogens verläuft von  über
über  nach
nach  . Er kann zwischen
. Er kann zwischen  und
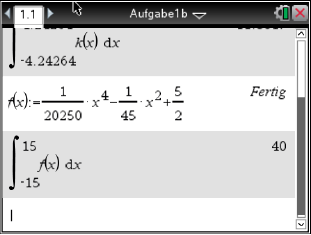
und  durch eine ganzrationale Funktion
durch eine ganzrationale Funktion  vierten Grades beschrieben werden.
vierten Grades beschrieben werden.
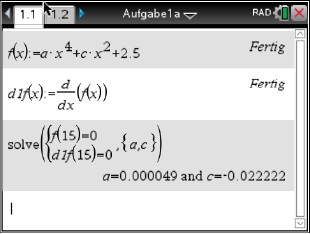
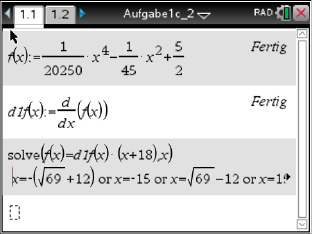
- Bestimme einen Funktionsterm von
.
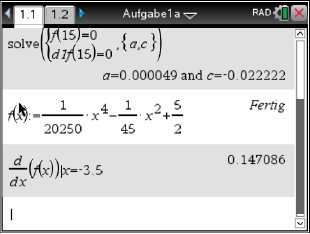
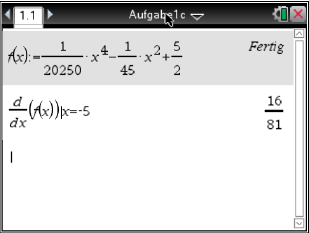
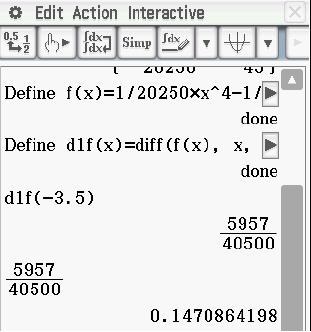
[Kontrolle: - Berechne die Steigung des Graphen
an der Stelle
.
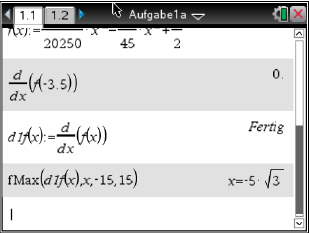
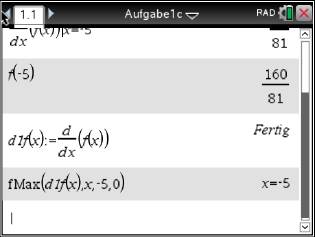
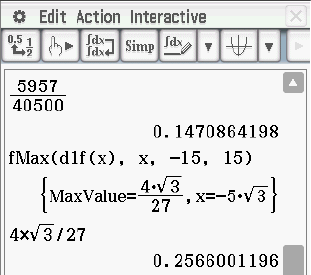
- Berechne die größte Steigung des Graphen von
im Intervall [-15;15].
(10P)
b)
In der Seitenansicht der Brücke verläuft die Böschung des Kanals geradlinig von  nach
nach  sowie von
sowie von  nach
nach  . Die Öffnung der Brücke ist ein Halbkreis mit dem Durchmesser
. Die Öffnung der Brücke ist ein Halbkreis mit dem Durchmesser  und wird durch den Graphen der Funktion
und wird durch den Graphen der Funktion  mit
mit

beschrieben.
Die Bodenlinie teilt die oben abgebildeten Seitenfläche der Brücke in zwei Teilflächen.
Berechne die Inhalte dieser Teilflächen.
beschrieben.
Die Bodenlinie teilt die oben abgebildeten Seitenfläche der Brücke in zwei Teilflächen.
Berechne die Inhalte dieser Teilflächen.
(10P)
c)
Für Besichtigungstouren stehen den Besuchern Elektrofahrzeuge zur Verfügung. Diese Fahrzeuge können eine maximale Steigung von  überwinden.
überwinden.
Die vorgegebene Route überquert die Brücke von nach
nach  . Um eine Überfahrt zu ermöglichen, soll auf der linken Brückenseite eine geradlinige Rampe verlegt werden, die auf Höhe der Bodenlinie im Punkt
. Um eine Überfahrt zu ermöglichen, soll auf der linken Brückenseite eine geradlinige Rampe verlegt werden, die auf Höhe der Bodenlinie im Punkt  genau
genau  vor der Mitte der Brücke beginnt und in einem Punkt
vor der Mitte der Brücke beginnt und in einem Punkt  tangential an den Brückenbogen anschließt.
tangential an den Brückenbogen anschließt.
Die vorgegebene Route überquert die Brücke von
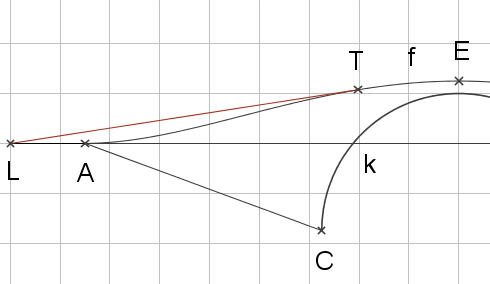
- Zeichne den Verlauf der Rampe in die folgende maßstabsgetreue Abbildung ein und ermittle mit Hilfe dieser Zeichnung die ungefähre Steigung der Rampe.
- Berechne die Koordinaten des Punktes
, ohne die zeichnerisch ermittelten Werte zu verwenden.
- Eine ältere Planung sah eine steilere Rampe vor, die im Punkt
an den Brückenbogen tangential anschließen sollte.
Zeige, dass diese Rampe zum Punktgeführt hätte und dass die Forderung nach einer maximalen Steigung von weniger als
auf dem gesamten Weg von
nach
erfüllt worden wäre.
(12P)
d)
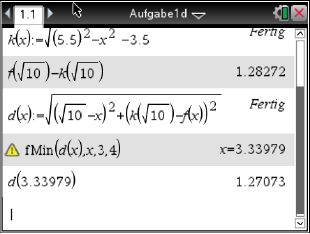
Ein Kabel soll vom Punkt  am unteren Rand der Brücke zu einem Punkt
am unteren Rand der Brücke zu einem Punkt  am oberen Rand der Brücke verlegt werden (siehe Abbildung 1).
am oberen Rand der Brücke verlegt werden (siehe Abbildung 1).
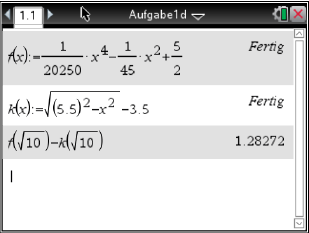
- Berechne die Länge der Strecke
bei vertikalem Verlauf des Borlochs.
- Bestimme bei unveränderter Lage des Punktes
die Stelle im Intervall
, an der der Punkt
liegen muss, damit das Bohrloch möglichst kurz wird. Gib dessen Länge an.
(8P)
Bildnachweise [nach oben]
© 2016 - SchulLV.
© 2016 - SchulLV.
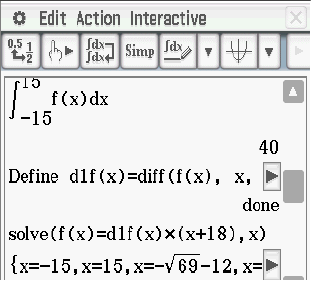
a)
menu  4: Analysis
4: Analysis  1: Ableitung.
1: Ableitung.
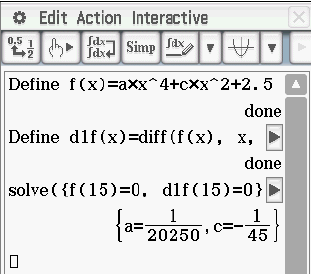
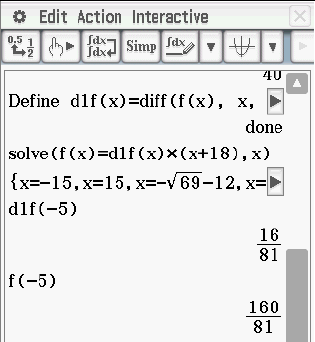
Jetzt überlegst du dir welche Informationen du noch nicht verwendet hast, um den Funktionsterm zu bestimmen. Zum einen geht die Funktion durch den Punkt
menu  4: Analysis
4: Analysis  1: Ableitung.
1: Ableitung.
bestimmen.
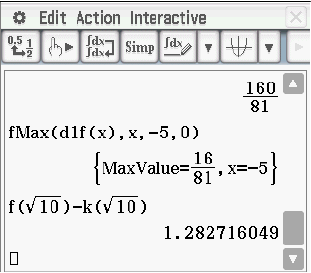
menu  4: Analysis
4: Analysis  8: Funktionsmaximum.
8: Funktionsmaximum.
Gebe dabei als untere
b)
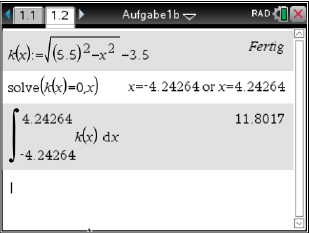
menu  4: Analysis
4: Analysis  3: Integral.
3: Integral.
c)
d)
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
a)
b)
c)
d)
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.