Analytische Geometrie

Ein Sportler trainiert in einer Kletterhalle. Die Situation wird in einem geeigneten Koordinatensystem modelliert, wobei eine Längeneinheit einem Meter in der Realität entspricht.
Die $x_1x_2$ -Ebene stellt den Hallenboden dar. Der Kletterer steht zunächst auf dem Startpunkt $(0\mid0\mid0)$ . Er klettert an der Wand $PQRS$ hoch, greift von dort auf die Wand $RSTU$ über und hangelt sich an ihr nach vorne bis zur Kante $\overline{TU}.$

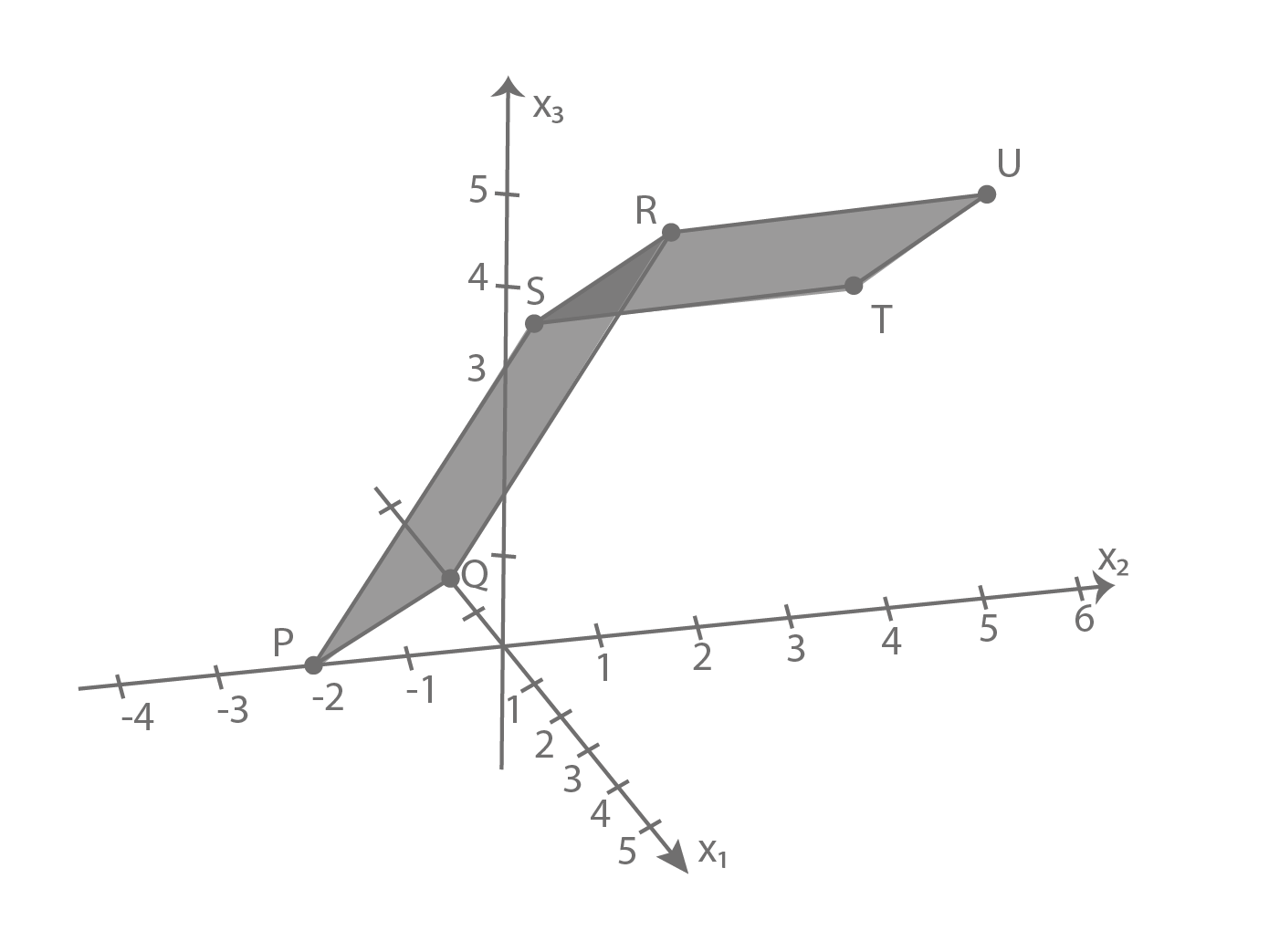Grafik eines dreidimensionalen Koordinatensystems mit Punkten P, Q, R, S, T und U.

Die ebenen Vierecke $PQRS$ und $RSTU$ haben die Eckpunkte

$P(0\mid-2\mid0)$ , $Q(-2\mid0\mid0)$ , $R(-1\mid2\mid4)$ , $S(1\mid0\mid4)$ , $T(2\mid3\mid4,5)$ und $U(0\mid5\mid4,5)$ .

Das Viereck $PQRS$ liegt in der Ebene $E$ .

a1)

Berechne die Länge der Kante $\overline{PQ}$ .

(2 P)

a2)

Zeige, dass das Viereck $PQRS$ ein Parallelogramm, aber kein Rechteck ist.

(5 P)

a3)

Bestimme eine Gleichung der Ebene $E$ in Koordinatenform.

[Kontrolle: $E: 4x_1+4x_2-3x_3=-8$ ]

(4 P)

a4)

Berechne den Schnittpunkt der Ebene $E$ mit der $x_3$ -Achse und gib die Höhe der Wand senkrecht über dem Startpunkt an.

(4 P)

a5)

Untersuche, ob es in der Ebene $E$ einen Punkt $(x_1\mid x_2\mid2)$ mit ganzzahligen Koordinaten $x_1$ und $x_2$ gibt.

(3 P)

In der Nähe der Kante $\overline{TU}$ hängt bei $G(3\mid 3,5\mid 4,5)$ eine Glocke, die mit einer Leine am Hallendach befestigt ist. Zum Abschluss seiner Trainingseinheit läutet der Kletterer diese Glocke mit der einene Hand, während er sich mit der anderen Hand an demjenigen Punkt $K$ auf der Kante $\overline{TU}$ festhält, der den geringsten Abstand zu $G$ hat.

Durch $T$ und $U$ verläuft die Gerade

Geradengleichung anzeigen

b1)

Bestimme den Fußpunkt $F$ des Lotes von $G$ auf $g$ .

(5 P)

b2)

Begründe, dass $K$ und $F$ nicht identisch sind.

(2 P)

b3)

Künftig soll die Glocke an einem anderen Punkt $G^*$ platziert werden. Der Punkt $G^*$ befindet sich in einer Höhe von 4,5 m und ist gleich weit von $T$ und $U$ entfernt; sein Abstand vom Mittelpunkt $M$ der Kante $\overline{TU}$ beträgt 35 cm.

Ermittle die Koordinaten des Punktes $M$ und die Koordinaten eines Punktes $G^*$ mit den beschrieben Eigenschaften.

(5 P)

Im Rahmen einer Renovierung wird darüber nachgedacht, den Winkel zwischen den beiden Wänden zu verändern. Für jedes $a \in\mathbb{R}$ ist durch $E_a: x_1+x_2-ax_3=1-4a$ eine Ebene $E_a$ gegeben. Jede dieser Ebenen enthält die Gerade durch $R$ und $S$ .

c1)

Es gibt genau eine Zahl $a$ mit $E_a=E$ . Bestimme diese Zahl.

(3 P)

c2)

$E_8$ ist diejenige Ebene, in der das Viereck $RSTU$ liegt. Berechne den Schnittwinkel der Ebenen $E$ und $E_8$ .

(3 P)

c3)

Bestimme alle Zahlen $a$ , so dass sich $E$ und $E_a$ unter einem 60°-Winkel schneiden.

(4 P)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

a1)

$\mid\overrightarrow{PQ}\mid=\left|\pmatrix{-2-0\\0-(-2)\\0-0}\right|=\left|\pmatrix{-2\\2\\0}\right|$ $=\sqrt{(-2)^2+2^2+0^2}$ $=\sqrt{8}\approx 2,83$

Die Kante hat eine Länge von ungefähr $2,83\;\text{m}.$

a2)

Ein Viereck ist ein Parallelogramm, wenn zwei gegenüberliegende Seiten parallel und gleich lang sind.

$\overrightarrow{SR}=\pmatrix{-1-1\\2-0\\4-4}=\pmatrix{-2\\2\\0}=\overrightarrow{PQ}$

Die Seiten $\overline{SR}$ und $\overline{PQ}$ sind somit parallel.

$\mid\overrightarrow{SR}\mid=\sqrt{8}=\mid\overrightarrow{PQ}\mid$

Die beiden Seiten sind auch gleich lang. Damit handelt es sich bei $PQRS$ um ein Parallelogramm.

In einem Rechteck betragen alle Innenwinkel $90°.$

$\overrightarrow{PQ}\circ\overrightarrow{PS}=\pmatrix{-2\\2\\0}\circ\pmatrix{1\\2\\4}$ $=-2+4+0=2$

Das Skalarprodukt der beiden Vektoren erigbt nicht null. Somit stehen die Seiten $\overline{PQ}$ und $\overline{PS}$ nicht senkrecht aufeinander. Es kann sich also nicht um ein Rechteck handeln.

a3)

Berechnen eines Normalenvektors $\overrightarrow{n}$ von $E:$

Vollständigen Rechenweg anzeigen

$\overrightarrow{n}=\pmatrix{8\\8\\-6}$

Mit $\dfrac{1}{2}\cdot\overrightarrow{n}=\pmatrix{4\\4\\-3}$ gilt für die Koordinatengleichung :

$4 \cdot x_1+4 \cdot x_2 -3 \cdot x_3=d$

Einsetzten von $P:$

$4\cdot0+4\cdot(-2)+(-3)\cdot0=-8$

Die Ebenengleichung lautet $E: 4x_1+4x_2-3x_3=-8.$

a4)

Da die Punkte auf der $x_3$ -Achse liegen, gilt: $x_1=x_2=0.$ Für den gesuchten Schnittpunkt muss also gelten:

Vollständigen Rechenweg anzeigen

$x_3= \dfrac{8}{3}$

Somit liegen die Koordinaten des Schnittpunkts $S$ bei $\left(0\,\bigg \vert \, 0\,\bigg \vert \, \dfrac{8}{3}\right).$

$\mid\overrightarrow{S}\mid=\sqrt{\left(\dfrac{8}{3}\right)^2}=2,\overline{6}$

Die Höhe der Wand senkrecht über dem Schnittpunkt beträgt ca. $2,67\;\text{m}.$

a5)

$x_3=2$ wird in die Ebene $E$ eingesetzt:

$\begin{array}[t]{rll} 4x_1+4x_2-3\cdot2&=& -8 &\quad \scriptsize \mid\; +6 \\[5pt] 4x_1+4x_2&=& -2 &\quad \scriptsize \mid\; :4 \\[5pt] x_1 + x_2 &=& -\dfrac{1}{2} \end{array}$

Es gibt keine ganzzahligen Werte für $x$ und $y$ , für die die Gleichung gilt. Somit gibt es keinen Punkt mit den beschriebenen Eigenschaften in $E.$

b1)

Zunächst wird die Hilfsebene $H$ erstellt, die senkrecht zu $g$ verläuft und $G$ enthält. Als Normalenvektor kann der Richtungsvektor von $g$ verwendet werden.

$H: -2x_1+2x_2=d$

Einsetzen des Punktes $G$ liefert:

$(-2)\cdot3+2\cdot3,5=1$

DIe Ebenengleichung von $H$ ist somit gegeben durch $H:-2x_1+2x_2=1.$

Nun werden die Koordinaten der Punkte auf $g$ in $H$ eingesetzt:

Vollständigen Rechenweg anzeigen

$r=-\dfrac{1}{8}$

Der Schnittpunkt von $g$ mit $H$ lässt damit wie folgt berechnen:

$\overrightarrow{OF}=\pmatrix{2\\3\\4,5}-\dfrac{1}{8}\cdot\pmatrix{-2\\2\\0}$ $=\pmatrix{2,25\\2,25\\4,5}$

Die Koordinaten von $F$ sind $(2,25\mid2,25\mid4,5).$

b2)

Für $0 \leq r \leq 1$ liegen die Punkte der Geraden $g$ auf der Kante $\overline{TU}.$

Es gilt: $\overrightarrow{OF}=\overrightarrow{OT}+r\cdot\overrightarrow{TU}$ mit $r=-\dfrac{1}{8}$

Da $r$ nicht zwischen $0$ und $1$ liegt, liegt $F$ nicht auf der Kante $\overline{TU}.$

$K$ dagegen liegt auf der Kante $\overline{TU}.$ Somit können $F$ und $K$ nicht identisch sein.

b3)

Koordinaten von $M$ berechnen

Zunächst werden die Koordinaten des Punktes $M$ bestimmt:

$\overrightarrow{OM}=\pmatrix{2\\3\\4,5}+\dfrac{1}{2}\cdot\pmatrix{-2\\2\\0}$ $=\pmatrix{1\\4\\4,5}$

Somit gilt $M(1\mid4\mid4,5).$

Koordinaten von $G^*$ berechnen

Zunächst wird ein Vektor $\overrightarrow{v}$ bestimmt, der senkrecht zu $\overrightarrow{TU}=\pmatrix{-2\\2\\0}$ steht. Für $\overrightarrow{v}$ muss also $\overrightarrow{v}\circ \overrightarrow{TU}=0$ gelten. Außerdem muss die $x_3-$ Koordinate gleich $0$ sein, da die Glocke auf einer Höhe von $4,5\,\text{m}$ hängen soll und der Punkt $M$ sich auf dieser Höhe befindet.

Die Bedingungen sind beispielsweise für $\overrightarrow{v}=\pmatrix{1\\1\\0}$ erfüllt.
Nun kann $G^*$ bestimmt werden:

$\overrightarrow{OG^*}=\overrightarrow{OM}+\dfrac{0,35}{\mid\overrightarrow{v}\mid}\cdot\overrightarrow{v}$

$\overrightarrow{OG^*}=\pmatrix{1\\4\\4,5}+\dfrac{0,35}{\sqrt{2}}\cdot\pmatrix{1\\1\\0}$ $\approx\pmatrix{1,25\\4,25\\4,5}$

Somit hat $G^*$ die Koordinaten $(1,25\mid4,25\mid4,5).$

c1)

Da jede Ebene $E_a$ die Gerade durch $R$ und $S$ enthält reicht es ein $a$ zu bestimmen, für das die Normalenvektoren von $E$ und $E_a$ Vielfache voneinander sind:

$\pmatrix{4\\4\\-3}=s\cdot\pmatrix{1\\1\\-a}$

Für $s=4$ sind die Vektoren Vielfache voneinander und es gilt:

$\pmatrix{4\\4\\-3}=4\cdot\pmatrix{1\\1\\-a}$

Aus der $y$ -Komponente lässt sich nun $a$ berechnen:

$\begin{array}[t]{rll} -3 &=& -4a &\quad \scriptsize \mid\; :(-4) \\[5pt] \dfrac{3}{4}&=&a \end{array}$

c2)

$\overrightarrow{n_{E}}=\pmatrix{4\\4\\-3}\quad\overrightarrow{n_{E_{8}}}=\pmatrix{1\\1\\-8}$

Für den Schnittwinkel $\alpha$ gilt:

Vollständigen Rechenweg anzeigen

$\cos(\alpha)\approx 0,615$

Anwenden von $\cos^{-1}$ auf beide Seiten der Gleichung liefert $\alpha\approx 52,05°.$

c3)

Damit sich $E$ und $E_a$ unter einem Winkel von $60^{\circ}$ schneiden muss folgendes gelten:

Vollständigen Rechenweg anzeigen

$\cos(60°)= \dfrac{8+3a}{\sqrt{41}\cdot \sqrt{2+a^2}}$

Mit $\cos(60°)=\dfrac{1}{2}$ muss gelten:

Vollständigen Rechenweg anzeigen

$a_{1/2} = \dfrac{96}{5} \pm \sqrt{\left(\dfrac{96}{5}\right)^2+\dfrac{174}{5}}$

Für $a_1\approx -0,89$ und $a_2\approx39,29$ schneiden sich $E$ und $E_a$ unter einem $60^{\circ}-$ Winkel.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?