Hilfsmittelfreier Teil

HMF 1 - Analysis (Pool 1)

Die Graphen der Funktionen $f$ mit $f(x)=12x-3x^2$ und $g$ mit $g(x)=6x$ schneiden sich an genau zwei Stellen.

1.1

Zeige, dass sich die Graphen von $f$ und $g$ an den Stellen $0$ und $2$ schneiden.

(2 BE)

1.2

Die Funktion $d$ mit $d(x)=f(x)-g(x)$ hat genau eine Maximalstelle. Berechne diese.

(3 BE)

HMF 2 - Analysis (Pool 1)

Gegeben ist die Schar der in $\mathbb{R}$ definierten Funktionen $f_a$ mit $f_a(x)=ax^3 + ax^2$ und $a>0.$

2.1

Gib den Wert von $a$ an, so dass der Punkt $(1 \mid 6)$ auf dem Graphen von $f_a$ liegt.

(1 BE)

2.2

Berechne in Abhängigkeit von $a$ den Inhalt der Fläche, die der Graph von $f_a$ mit der $x$ -Achse vollständig einschließt.

(4 BE)

HMF 3 - Analytische Geometrie (Pool 1)

Gegeben ist ein Parallelogramm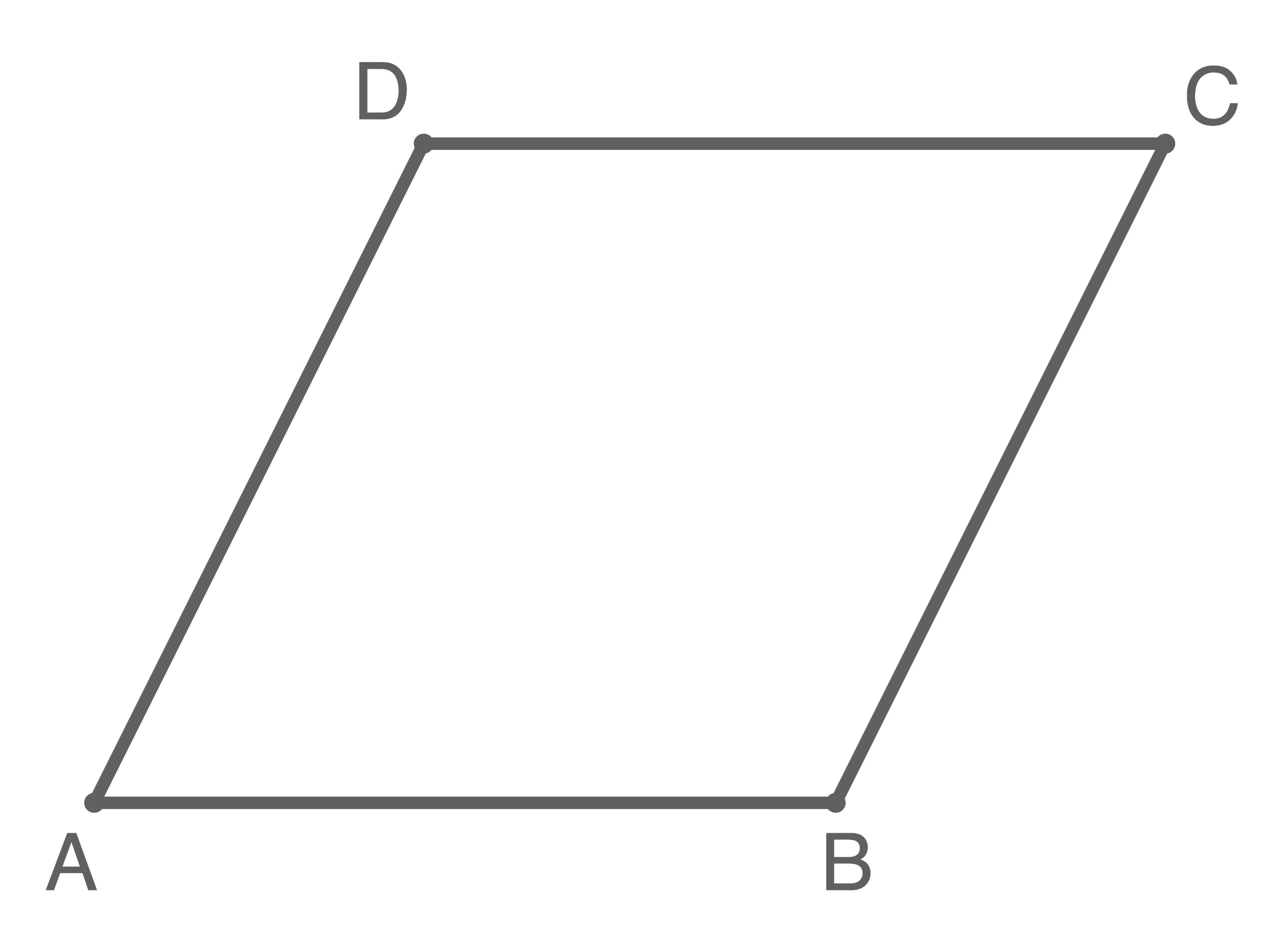 $ABCD$ mit den Punkten $A(-1 \mid 2 \mid 4), B(1 \mid 3 \mid 2)$ und $C(2 \mid 1 \mid 0).$

Skizze:

3.1

Bestimme die Koordinaten von Punkt $D.$

(2 BE)

3.2

Weise rechnerisch nach, dass das Parallelogramm $ABCD$ eine Raute, aber kein Quadrat ist.

(3 BE)

HMF 4 - Stochastik (Pool 1)

In einer Schulklasse mit 24 Kindern bildet ein Drittel der Kinder das Volleyball-Team für ein anstehendes Sportfest. Am Tag des Sportfests sind zwei der Team-Mitglieder und vier der übrigen Kinder der Klasse nicht anwesend.

Von der Klassenliste mit allen 24 Kindern wird ein Kind zufällig ausgewählt. Betrachtet werden die folgenden Ereignisse:

$M:$ „Das Kind ist Team-Mitglied.“
$A:$ „Das Kind ist anwesend.“

4.1

Ergänze die fehlenden Wahrscheinlichkeiten in der abgebildeten Vierfeldertafel.

	$M$	$\overline{M}$	$\Sigma$
$A$
$\overline{A}$	$\dfrac{2}{24}$	$\dfrac{4}{24}$
$\Sigma$			$1$

(3 BE)

4.2

Untersuche, ob die Ereignisse $M$ und $A$ stochastisch unabhängig sind.

(2 BE)

HMF 5 - Analysis (Pool 2)

Die Abbildung zeigt den Graphen der Ableitungsfunktion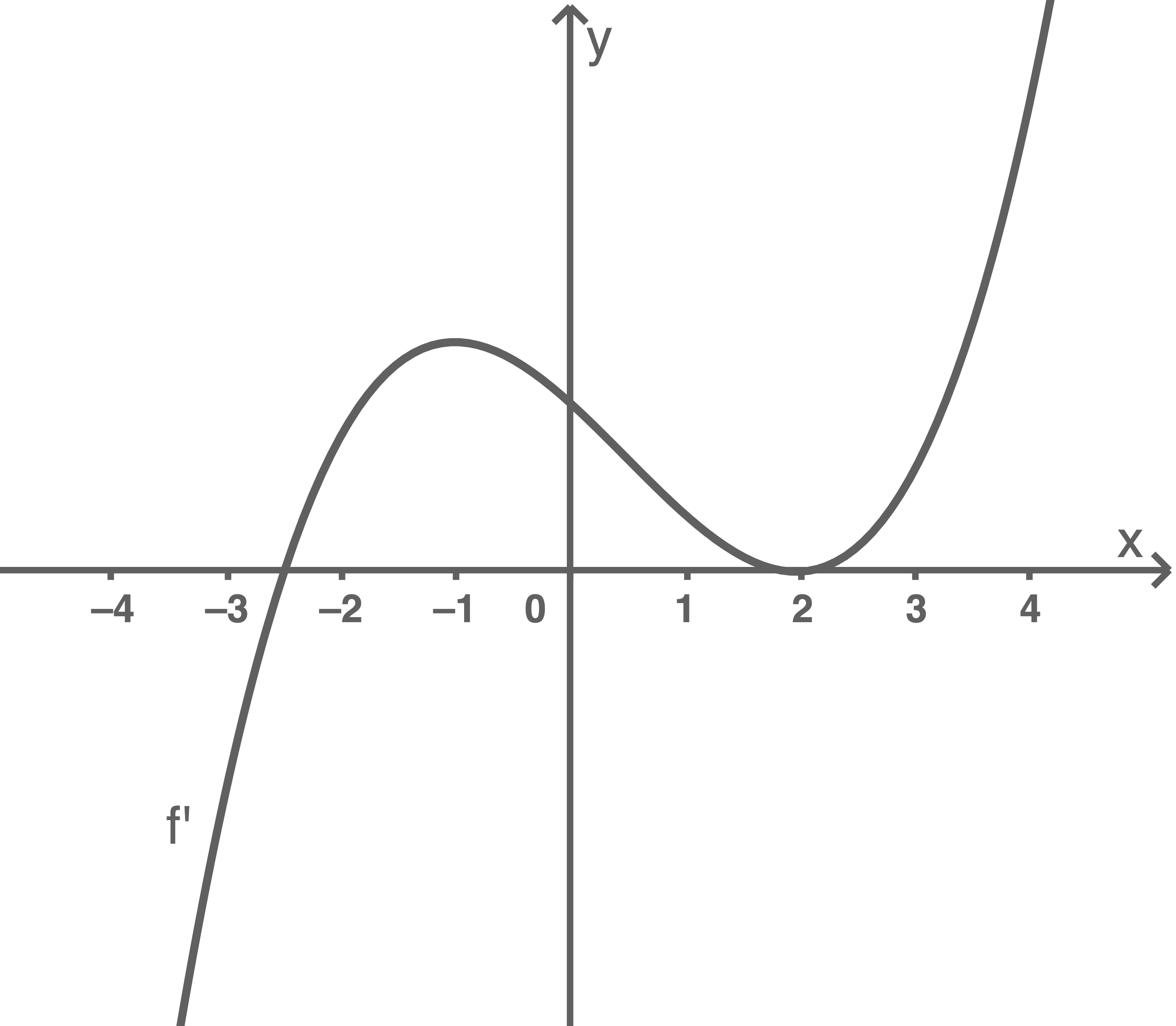 $\(f$ einer ganzrationalen Funktion $f$ vierten Grades. An der Stelle $x=2$ berührt der Graph von $\(f$ die $x$ -Achse.

5.1

Begründe, dass der Graph der Funktion $f$ einen Tiefpunkt hat.

(2 BE)

5.2

Erläutere, gegebenenfalls mithilfe einer Skizze, dass die Funktion $f$ höchstens zwei Nullstellen hat.

(3 BE)

HMF 6 - Analysis (Pool 2)

Gegeben ist für jede positive reelle Zahl $a$ die in $\mathbb{R}$ definierte Funktion $f_a$ mit $f_a(x) = a \cdot x^2.$ Die Abbildung zeigt den Graphen von $f_{\frac{1}{2}}$ sowie die Tangente $t$ an den Graphen von $f_{\frac{1}{2}}$ im Punkt $\left(4 \mid f_{\frac{1}{2}}(4)\right).$

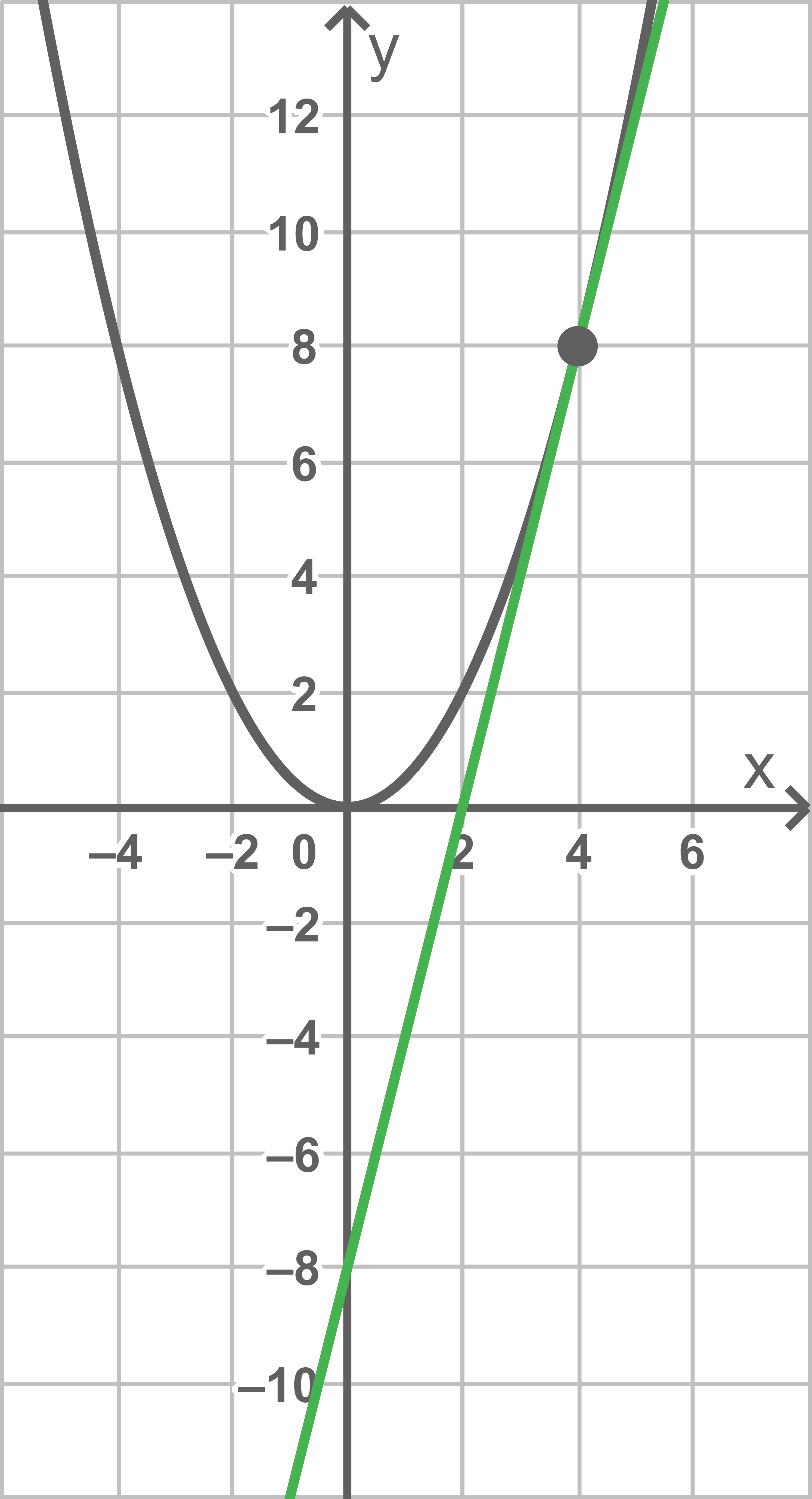
6.1

Gib anhand der Abbildung eine Gleichung der Tangente $t$ an.

(1 BE)

6.2

Weise nach, dass für jeden Wert $u \in \mathbb{R}$ die Tangente an den Graphen von $f_a$ im Punkt $(u \mid f_a(u))$ die $y$ -Achse im Punkt $(0 \mid -f_a(u))$ schneidet.

(4 BE)

HMF 7 - Analytische Geometrie (Pool 2)

Die Mittelpunkte der Seitenflächen eines Würfels sind die Eckpunkte eines Oktaeders (vgl. Abbildung). Die Eckpunkte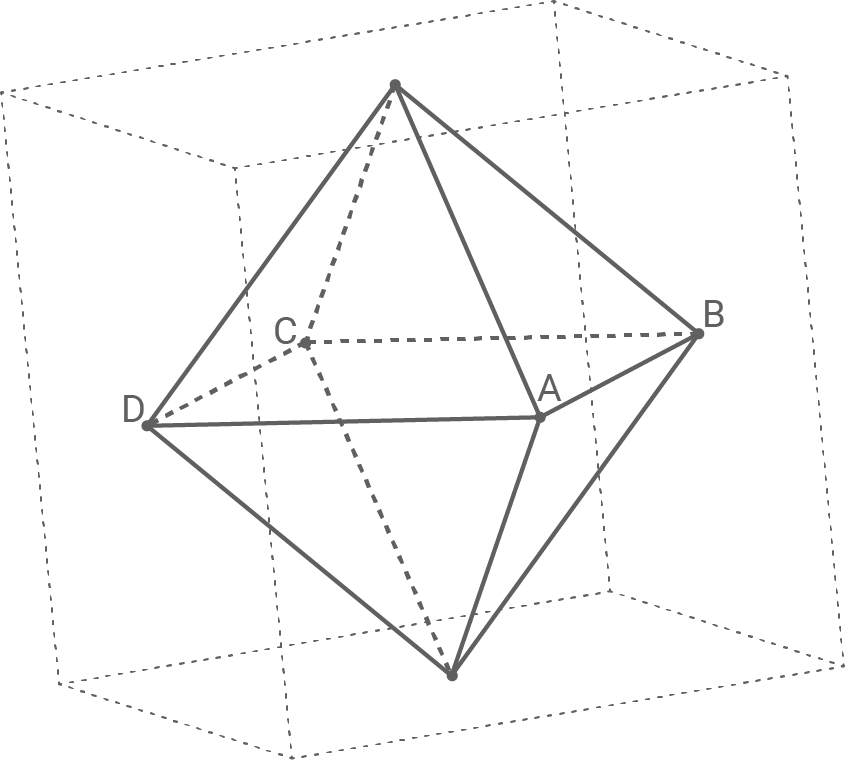 $A(1 \mid 2 \mid 1), B,$ $C(-3 \mid -6 \mid 9)$ und $D$ des Oktaeders liegen in der Ebene $H$ mit der Gleichung $2x_1+x_2+2x_3=6.$

7.1

Weise nach, dass die Kantenlänge des Würfels 12 beträgt.

(2 BE)

7.2

Bestimme die Koordinaten eines der beiden Eckpunkte des Oktaeders, die nicht in $H$ liegen.

(3 BE)

HMF 8 - Analytische Geometrie (Pool 2)

Gegeben ist die Schar der Geraden $g_k: \overrightarrow{x} = \pmatrix{k\\-4k\\k} + t \cdot \pmatrix{4\\8\\1}$ mit $t \in \mathbb{R}$ und $k \in \mathbb{R}.$

8.1

Begründe, dass alle Geraden der Schar parallel zueinander sind.

(1 BE)

8.2

Betrachtet wird das Quadrat mit folgenden Eigenschaften:

Die Punkte $O(0 \mid 0 \mid 0)$ und $P(11 \mid 4 \mid 5)$ sind Eckpunkte des Quadrats.
Zwei Seiten des Quadrats liegen auf Geraden der Schar.

Weise nach, dass $O$ und $P$ keine benachbarten Eckpunkte dieses Quadrats sind.

(4 BE)

HMF 9 - Stochastik (Pool 2)

Die Zufallsgröße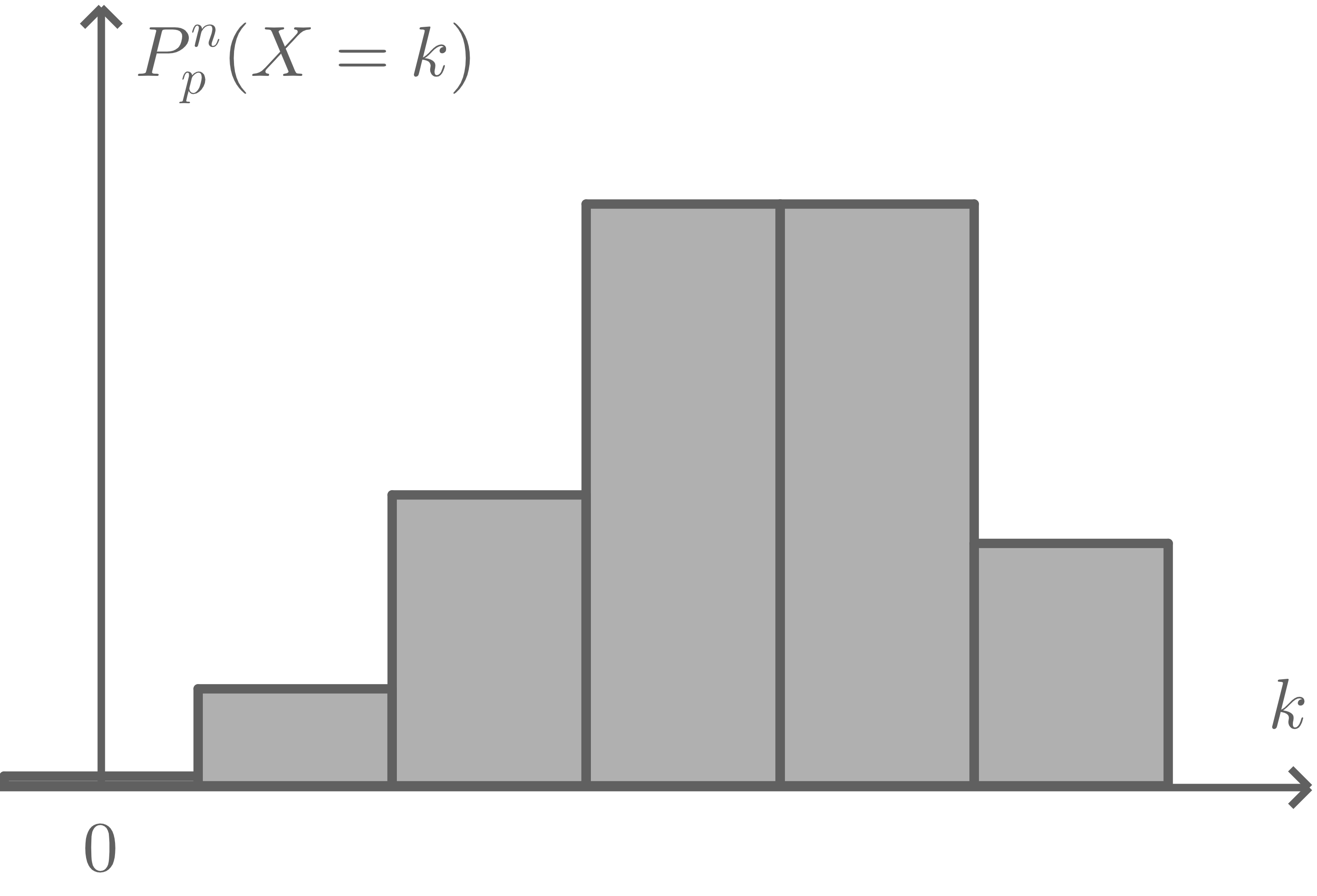 $X$ ist binomialverteilt mit den Parametern $n$ und $p$ mit $0 \lt p \lt 1.$ Das Histogramm zeigt die Wahrscheinlichkeitsverteilung von $X.$ Zwei der insgesamt sechs Säulen sind gleich hoch.

Gib $n$ an und ermittle $p.$

(5 BE)

HMF 10 - Stochastik (Pool 2)

Betrachtet werden drei Behälter $A, B$ und $C$ mit weißen und schwarzen Kugeln. Die Behälter sind von außen nicht unterscheidbar. Es gilt:

Im Behälter $A$ befinden sich dreimal so viele weiße wie schwarze Kugeln.
Im Behälter $B$ befinden sich 12 weiße und 4 schwarze Kugeln.
Im Behälter $C$ befinden sich 3 schwarze Kugeln und weiße Kugeln, deren Anzahl mit $w$ bezeichnet wird.

Bei einem Spiel wird einer der drei Behälter zufällig ausgewählt und anschließend daraus eine Kugel zufällig gezogen.

Ist bei diesem Spiel die gezogene Kugel schwarz, kann die Wahrscheinlichkeit dafür, dass der Behälter $C$ ausgewählt wurde, mit dem Term $\dfrac{\frac{1}{3} \cdot \frac{3}{w+3}}{ \frac{1}{3} \cdot \frac{3}{w+3} + \frac{2}{3} \cdot \frac{1}{4}}$ berechnet werden.

Weise dies nach und berechne $w,$ wenn die beschriebene Wahrscheinlichkeit den Wert $\frac{1}{5}$ hat.

(5 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Lösung HMF 1 - Analysis (Pool 1)

1.1

Die beiden Graphen schneiden sich an einer Stelle, wenn ihre Funktionswerte dort übereinstimmen:

$f(0)=0=g(0)$

$f(2)=12=g(2)$

Daher schneiden sich die beiden Graphen an den Stellen $0$ und $2.$

1.2

$\begin{array}[t]{rll} d(x)&=& f(x)-g(x) \\[5pt] &=& 12x-3x^2-6x \\[5pt] &=& 6x-3x^2 \end{array}$

$\(d$

Notwendige Bedingung für Extremstellen anwenden:

$\(\begin{array}[t]{rll} f$

Da laut Aufgabenstellung genau eine Maximalstelle existiert, muss die hinreichende Bedindung nicht überprüft werden und sie ist durch $x=1$ gegeben.

Lösung HMF 2 - Analysis (Pool 1)

2.1

Der Punkt $(1 \mid 6)$ liegt auf dem Graphen von $f_a,$ wenn $f_a(1) = 6$ gilt.

$f_a(1) = a \cdot 1^3 + a \cdot 1^2 = 2a$

Gleichsetzen liefert:

$\begin{array}[t]{rll} 2a &=& 6 &\quad \scriptsize \mid\; :2 \\[5pt] a &=& 3 \end{array}$

Der Wert von $a$ ist somit $3.$

2.2

Nullstellen von $f_a(x)$ berechnen:

$\begin{array}[t]{rll} f_a(x)&=& 0 \\[5pt] a\cdot x^3+a\cdot x^2&=& 0 \\[5pt] a \cdot x^2 \cdot (x + 1)&=& 0 \end{array}$

Mit dem Satz vom Nullprodukt folgen die Nullstellen $x = 0$ und $x = -1.$

Die gesuchte Fläche berechnet sich damit wie folgt:

$\begin{array}[t]{rll} \displaystyle\int_{-1}^{0} f_a(x) \, \mathrm{d}x&=& \displaystyle\int_{-1}^{0} a \cdot (x^3 + x^2) \, \mathrm{d}x \\[5pt] &=& a\cdot\displaystyle\int_{-1}^{0} x^3 + x^2 \, \mathrm{d}x \\[5pt] &=& a \cdot \left[\dfrac{x^4}{4} + \dfrac{x^3}{3}\right]_{-1}^{0} \\[5pt] &=& a \cdot \left(0 - \left(\dfrac{1}{4} - \dfrac{1}{3}\right)\right) \\[5pt] &=& a \cdot \dfrac{1}{12} \end{array}$

Der Flächeninhalt beträgt somit $\dfrac{a}{12}$ Flächeneinheiten.

Lösung HMF 3 - Analytische Geometrie (Pool 1)

3.1

Um die Koordinaten von Punkt $D$ zu bestimmen, wird der Vektor $\overrightarrow{OD}$ berechnet:

Rechenweg anzeigen

$\overrightarrow{OD} = \pmatrix{0 \\ 0 \\ 2}$

Die Koordinaten von Punkt $D$ sind daher $D(0 \mid 0 \mid 2).$

3.2

$\begin{array}[t]{rll} \left|\overrightarrow{AB}\right| &=& \left|\pmatrix{2 \\ 1 \\ -2}\right| \\[5pt] &=& \sqrt{2^2 + 1^2 + (-2)^2} \\[5pt] &=& \sqrt{4 + 1 + 4} \\[5pt] &=& \sqrt{9} = 3 \end{array}$

$\begin{array}[t]{rll} \left|\overrightarrow{BC}\right| &=& \left|\pmatrix{1 \\ -2 \\ -2}\right| \\[5pt] &=& \sqrt{1^2 + (-2)^2 + (-2)^2} \\[5pt] &=& \sqrt{1 + 4 + 4} \\[5pt] &=& \sqrt{9} = 3 \end{array}$

Da es sich um ein Parallelogramm handelt, sind somit alle vier Seiten gleich lang und handelt es sich um eine Raute. Es bleibt noch zu zeigen, dass diese Raute kein Quadrat ist.

Dazu wird das Skalarprodukt der Vektoren $\overrightarrow{AB}$ und $\overrightarrow{BC}$ berechnet:

Rechenweg anzeigen

$\overrightarrow{AB} \circ \overrightarrow{BC} \neq 0$

Da das Skalarprodukt ungleich null ist, schließen die Vektoren keinen rechten Winkel ein, und die Raute $ABCD$ ist kein Quadrat.

Lösung HMF 4 - Stochastik (Pool 1)

4.1

Zunächst wird die Anzahl der Kinder im Team ermittelt:

$\dfrac{1}{3} \cdot 24 = 8$

Da zwei Team-Mitglieder und vier der übrigen Kinder nicht anwesend sind, ergibt sich folgende Verteilung:

	$M$	$\overline{M}$	$\Sigma$
$A$	$\dfrac{6}{24}$	$\dfrac{12}{24}$	$\dfrac{18}{24}$
$\overline{A}$	$\dfrac{2}{24}$	$\dfrac{4}{24}$	$\dfrac{6}{24}$
$\Sigma$	$\dfrac{8}{24}$	$\dfrac{16}{24}$	$1$

4.2

Um zu überprüfen, ob die Ereignisse $M$ und $A$ stochastisch unabhängig sind, wird die Bedingung $P_A(M) = P(M)$ geprüft.

$P(M) = \dfrac{8}{24} = \dfrac{1}{3}$

$P_A(M) =\dfrac{P(A\cap M)}{P(A)}= \dfrac{\frac{6}{24}}{\frac{18}{24}} = \dfrac{6}{18} = \dfrac{1}{3}$

Wegen $P_A(M) = P(M)$ sind die Ereignisse stochastisch unabhängig.

Lösung HMF 5 - Analysis (Pool 2)

5.1

Die Funktion $\(f$ hat eine Nullstelle mit einem Vorzeichenwechsel von negativen zu positiven Werten bei $x\approx -2,5.$

5.2

Der Graph von $f$ lässt sich durch eine Verschiebung des skizzierten Graphen in Richtung der $y$ -Achse erzeugen. Daher hat der Graph von $f$ einen Tiefpunkt, aber keinen Hochpunkt. Dies führt dazu, dass $f$ höchstens zwei Nullstellen besitzt.

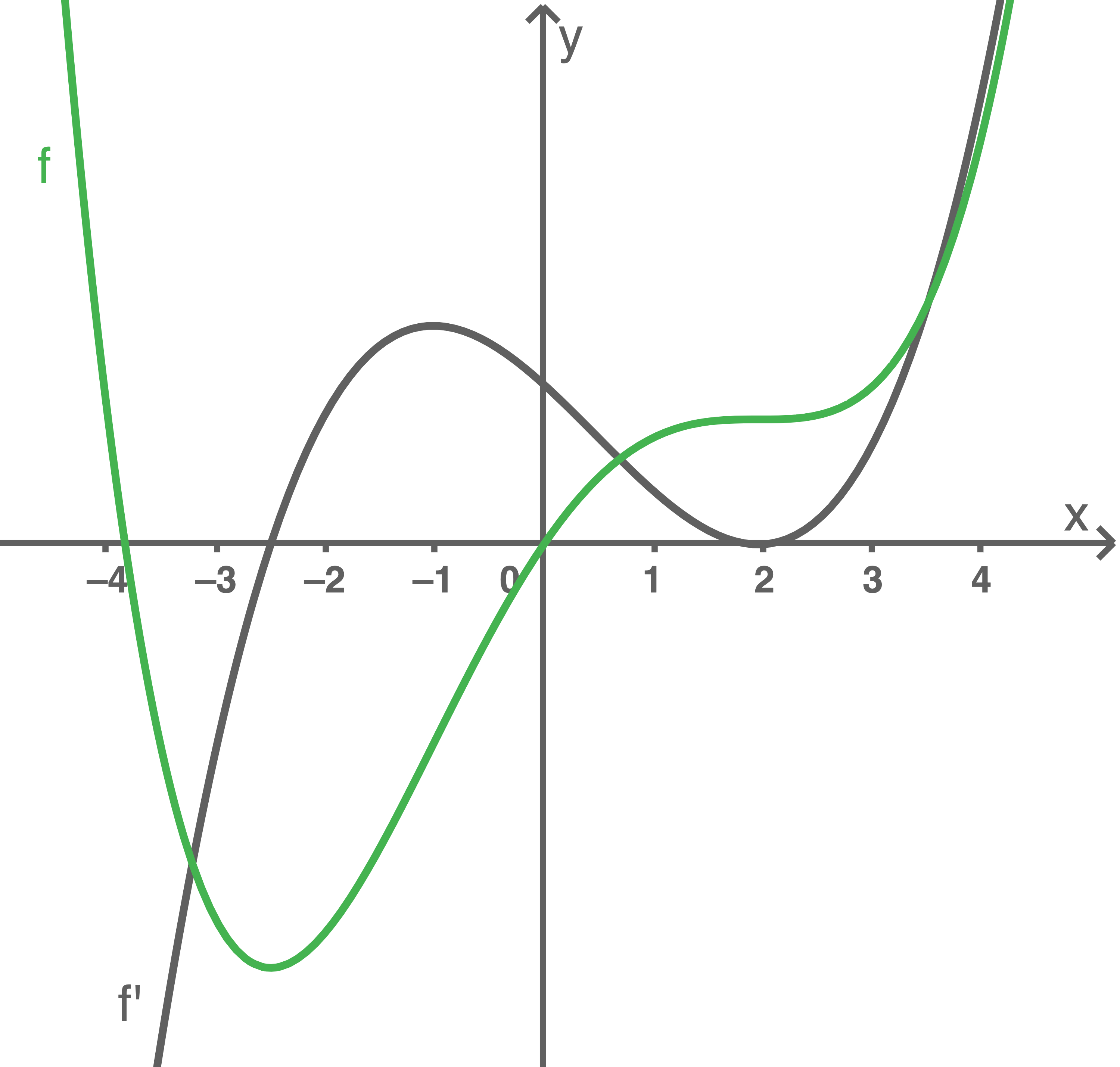
Skizze

Lösung HMF 6 - Analysis (Pool 2)

6.1

Aus der Abbildung kann die Steigung $m=4$ sowie der $y$ -Achsenabschnitt bei $y=-8$ der Tangente abgelesen werden.

Eine Gleichung der Tangente ist somit $y=4x-8.$

6.2

$y$ -Koordinate angeben:

$f_a(u)=au^2$

Ableitung von $f_a$ bestimmen:

$\(f_a$

Die Steigung $m$ der Tangente an der Stelle $u$ ergibt sich also mit:

$\(m=f_a$

Einsetzen der Steigung sowie der Koordinaten des Punktes $(u\mid au^2)$ in die allgemeine Tangentengleichung liefert:

$\begin{array}[t]{rll} t: \quad y&=& m\cdot x+c& \\[5pt] au^2&=&2au\cdot u + c &\quad \scriptsize \mid\;-2au^2 \\[5pt] -au^2&=& c \end{array}$

Somit schneidet die Tangente die $y$ -Achse an der Stelle $c=-au^2=-f_a(u)$ und folglich im Punkt $(0\mid-f_a(u)).$

Lösung HMF 7 - Analytische Geometrie (Pool 2)

7.1

Die Kantenlänge des Würfels entspricht der Strecke $\overline{AC}.$ Für diese gilt:

$\begin{array}[t]{rll} \left\vert\overrightarrow{AC}\right\vert&=&\left\vert\pmatrix{-3\\-6\\9}-\pmatrix{1\\2\\1}\right\vert \\[5pt] &=&\left\vert\pmatrix{-4\\-8\\8}\right\vert \\[5pt] &=&\sqrt{(-4)^2+(-8)^2+8^2} \\[5pt] &=&\sqrt{144} \\[5pt] &=& 12 \;[\,\text{LE}] \end{array}$

7.2

Punkte, die nicht in $H$ liegen, sind die obere bzw. die untere Spitze des Oktaeders und liegen senkrecht über dem Mittelpunkt von $ABCD.$

Für den Mittelpunkt $M$ der Strecke $\overline{AC}$ gilt:

$\begin{array}[t]{rll} \overrightarrow{OM}&=&\overrightarrow{OA}+\dfrac{1}{2}\cdot\overrightarrow{AC} \\[5pt] &=&\pmatrix{1\\2\\1}+\dfrac{1}{2}\cdot\pmatrix{-4\\-8\\8} \\[5pt] &=&\pmatrix{-1\\-2\\5} \end{array}$

Aus der Ebenengleichung von $H$ kann der Normalenvektor $\overrightarrow{n}=\pmatrix{2\\1\\2}$ abgelesen werden. Dieser steht senkrecht zur Ebene $H$ und besitzt die Länge:

$\begin{array}[t]{rll} \vert\overrightarrow{n}\vert&=& \sqrt{2^2+1^2+2^2} & \\[5pt] &=& \sqrt{9} & \\[5pt] &=& 3 \end{array}$

Da die Kantenlänge des Würfels $12$ beträgt, ist der Abstand des gesuchten Eckpunktes des Oktaeders zu $M$ durch 6 Längeneinheiten, also der doppelten Länge des Normalenvektors, gegeben.

Ein möglicher Ortsvektor der oberen Spitze $S$ folgt also mit:

$\begin{array}[t]{rll} \overrightarrow{OS}&=& \overrightarrow{OM}+2\cdot\overrightarrow{n}& \\[5pt] &=& \pmatrix{-1\\-2\\5}+2\cdot\pmatrix{2\\1\\2}& \\[5pt] &=& \pmatrix{3\\0\\9} \end{array}$

Mögliche Koordinaten für den gesuchten Punkt sind somit gegeben durch $(3\mid0\mid9).$

Lösung HMF 8 - Analytische Geometrie (Pool 2)

Der Richtungsvektor der Geradenschar hängt nicht von $k$ ab, somit sind alle Geraden der Schar parallel zueinander.

Falls die Punkte $O$ und $P$ benachbarte Eckpunkte wären, könnten sie entweder auf der gleichen Geraden der Geradenschar liegen, oder auf zwei unterschiedlichen. In ersten Fall muss $\overrightarrow{OP}$ ein Vielfaches von dem Richtungsvektor der Geradenschar sein. Das liefert folgendes Gleichungssystem:

$\begin{array}{lrll} \text{I}\quad&11&=&4s \\ \text{II}\quad&4&=&8s \\ \text{III}\quad&5&=&s \\ \end{array}$

Einsetzen der Lösung $s=5$ aus Gleichung $\text{III}$ in Gleichung $\text{I}$ ergibt $11=4\cdot5=20,$ was einen Widerspruch liefert. Somit besitzt das Gleichungssystem keine Lösung, das heißt $O$ und $P$ sind keine benachbarten Eckpunkte, die auf derselben Gerade der Schar liegen.

Im zweiten Fall muss $\overrightarrow{OP}$ orthogonal zum Richtungsvektor der Geradenschar liegen. Überprüfen ergibt:

$\begin{array}[t]{rll} \pmatrix{11\\4\\5}\circ\pmatrix{4\\8\\1}&=& 11\cdot4+4\cdot8+5\cdot1 \\[5pt] &=& 44+32+5 \\[5pt] &=& 81\neq 0 \end{array}$

Somit sind $O$ und $P$ auch keine benachbarten Eckpunkte, die auf verschiedenen Geraden der Schar liegen. Damit können $O$ und $P$ insgesamt keine benachbarten Eckpunkte des Quadrats sein.

Lösung HMF 9 - Stochastik (Pool 2)

Aus dem Histogramm lässt sich ablesen, dass es sich um eine binomialverteilte Zufallsgröße $X$ mit $n=5$ handelt. Zwei der sechs Säulen sind gleich hoch, nämlich für $k=3$ und $k=4$ .