Analysis 2

Surfbretter können am Computer konstruiert und dann automatisch aus einem Styroporblock gefräst werden. Die folgende Abbildung zeigt die Draufsicht eines Surfbretts, das bezüglich der eingezeichneten $x$ -Achse achsensymmetrisch ist.

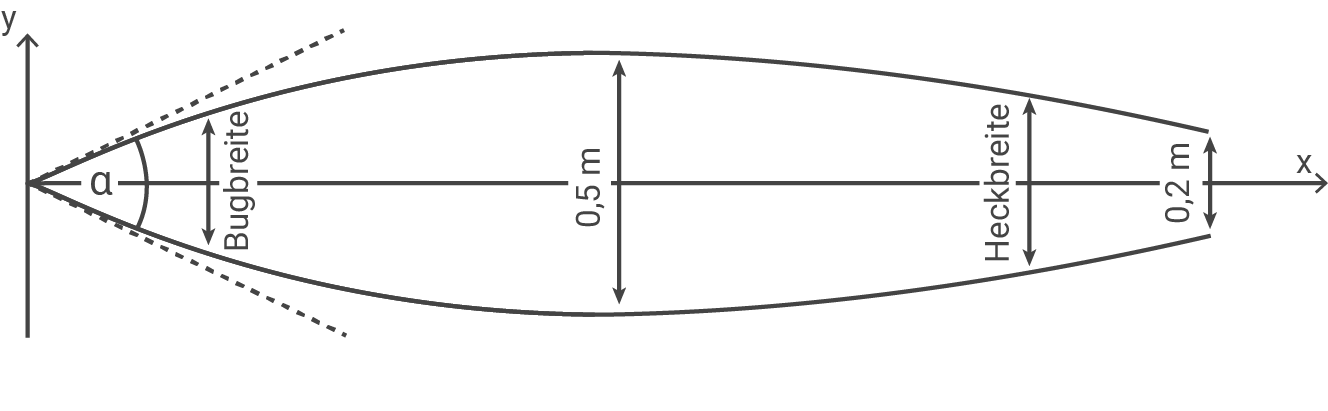Diagramm eines Bootes mit Abmessungen für Bugbreite und Heckbreite.

Abbildung 1

Eine Längeneinheit entspricht einem Meter in der Wirklichkeit.

Eine Surferin wünscht sich ein wie in der Zeichnung dargestelltes Shortboard der Länge $2 \; \text{m}$ . Die größte Breite von $0,5 \; \text{m}$ wird genau in der Mitte zwischen Bugspitze und dem Ende des Hecks erreicht. Am Ende des Hecks hat das Surfbrett eine Breite von $0,2 \; \text{m}$ m. Der in Fahrtrichtung gesehen rechte Rand des Surfbretts (in der Abbildung der obere Teil) soll durch den Graphen einer ganzrationalen Funktion $f$ dritten Grades modelliert werden.

a1)

Bestimme einen Funktionsterm von $f$ .

[Kontrolle: $f(x)=0,05\cdot x^3-0,35\cdot x^2+0,55\cdot x$ ]

(4 P)

a2)

Zum Vergleich verschiedener Surfbrett-Designs wird oft neben der größten Breite des Surfbretts die Breite des Bretts jeweils $1 \; \text{Fuß}$ $(30,48 \; \text{cm})$ von der Spitze des Bugs und vom Ende des Hecks entfernt gemessen (siehe obige Abbildung).

Berechne die Bugbreite und die Heckbreite für das vorgegebene Modell.

(3 P)

a3)

Es gibt zwei Stellen, an denen das Surfbrett eine Breite von $40 \; \text{cm}$ aufweist.

Ermittle den Abstand dieser beiden Stellen voneinander.

(3 P)

a4)

Berechne den Öffnungswinkel $\alpha$ an der Spitze des Surfbrettes.

(3 P)

a5)

Nimm vereinfachend an, dass das Surfbrett eben ist und eine einheitliche Dicke von $5 \; \text{cm}$ hat.

Berechne das Volumen des Surfbretts und gib dieses Volumen in Litern an.

(4 P)

Neben dem im Aufgabenteil a) untersuchten Shortboard gibt es noch viele andere Bauformen von Surfbrettern. Der in Fahrtrichtung gesehen rechte Rand (in der folgenden Abbildung der obere Teil) eines Funboards wird vollständig durch den Graphen der Funktion $g$ mit

$g(x)=0,3\cdot\sqrt{1-(x-1)^2}$

zwischen den beiden Nullstellen von $g$ beschrieben.

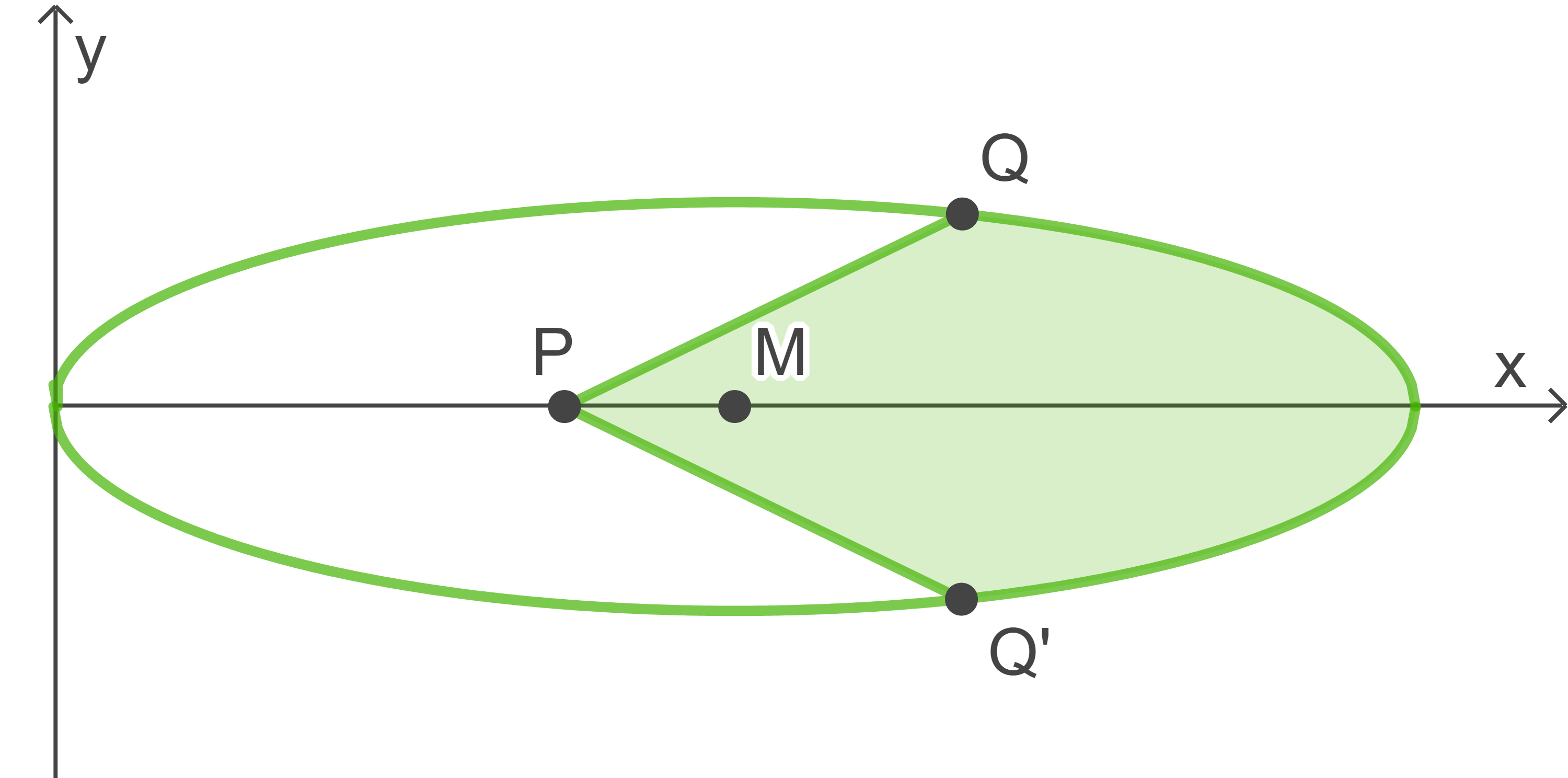
Grafik eines Ellipsen mit Punkten P, M, Q und Q' sowie den Achsen x und y.

Abbildung 2

b1)

Zeige, dass das Funboard eine Länge von $2,0 \; \text{m}$ hat.

(2 P)

b2)

Gib das Verhalten von $\(g$ für $x \rightarrow 2$ an und interpretiere dieses Verhalten im Sachzusammenhang.

(3 P)

b3)

Ein Funboard gleicher Bauart soll - wie in der Abbildung dargestellt - teilweise farbig lackiert werden. Dabei soll der Punkt $P (0,75 \mid 0)$ geradlinig mit den beiden zur $x$ -Achse symmetrisch angeordneten Punkten $Q (b \mid g(b))$ bzw. $\(Q$ verbunden sein. $Q$ ist so zu platzieren, dass der Flächeninhalt des gefärbten Teils der Hälfte der Gesamtfläche entspricht. Stelle eine Gleichung auf, die die Situation in Abhängigkeit von $b$ beschreibt und bestimme die Koordinaten von $Q$ .

(5 P)

Für jedes $k\gt 0$ wird durch $g_k(x)=0,15\cdot k\cdot\sqrt{1-\left(\dfrac{2}{k}\cdot x-1\right)^2}$ mit $x\in[0;k]$ eine Funktion $g_k$ gegeben. Für geeignete $k$ beschreibt der Graph von $g_k$ erneut den in Fahrtrichtung gesehen rechten Rand eines Funboards.

c1)

Es gibt ein $k\gt0$ , für das $g_k=g$ gilt (mit $g$ aus Teilaufgabe b)). Gib den entsprechenden Wert für $k$ an.

(1 P)

c2)

Der Graph von $g_k$ ist an jeder Stelle $x$ mit $0\gt x\gt k$ rechtsgekrümmt.

Zeige, dass die größte Breite für das durch $g_k$ modellierte Funboard an der Stelle $x=\dfrac{k}{2}$ angenommen wird.

(3 P)

c3)

Ein Surfer wünscht sich ein durch $g_k$ modelliertes Funboard, das eine Länge von $2,5 \; \text{m}$ aufweist. Bestimme den zugehörigen Wert von $k$ und ermittle die größte Breite dieses Funboards.

(4 P)

c4)

Je größer das Verhältnis von größter Breite zur Länge ist, desto stabiler verhält sich ein Surfbrett im Wasser. Weise nach, dass sich alle durch $g_k$ modellierten Funboards stabiler im Wasser verhalten als das Shortboard aus Aufgabenteil a).

(5 P)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

a1)

Es muss gelten:

$f(0)=0$
$f(1)=0,25$
$f(2)=0,1$
$\(f$

Mit dem Ansatz $f(x)=ax^3+bx^2+cx+d$ gilt auch $\(f$

Einsetzten der Koordinaten des Ursprungs in $f$ liefert:

$\begin{array}[t]{rll} 0a+0b+0c+d&=&0 \\[5pt] d&=&0 \end{array}$

Damit ergeben sich für die Funktion $f$ folgende Gleichungen:

$\text{I}: a+b+c=0,25$
$\text{II}: 3a+2b+c=0$
$\text{III}: 8a+4b+2c=0,1$

Das Gleichungssystem kann mithilfe des CAS gelöst werden.

$\blacktriangleright$ TI nspire CAS

menu $\to$ 3: Algebra $\to$ 7

$\blacktriangleright$ Casio Classpad II

keyboard $\to$ Math1 $\to$ $\{^{\Box}_{\Box}$

$a=0,05\quad b=-0,35\quad c=0,55$

Insgesamt gilt also $f(x)=0,05x^3-0,35x^2+0,55x.$

a2)

Bugbreite: $2\cdot f(0,3048)\approx 0,2731\;\text{[LE]}$ $\mathrel{\widehat{=}}27,31\;\text{cm}$
Heckbreite: $2\cdot f(2-0,3048)\approx 0,3401\;\text{[LE]}$ $\mathrel{\widehat{=}}34,01\;\text{cm}$

a3)

Gesucht sind die Lösungen der Gleichung $f(x)=0,2.$

Der CAS liefert $x_1=0,5272,$ $x_2=1,5374,$ $x_3=4,9354.$

$x_3$ entfällt, da $4,9354\gt2.$

$x_2-x_1=1,5374-0,5272$ $=1,0102$

Die beiden Stellen sind ca. $1,01\;\text{m}$ voneinander entfernt.

a4)

$\(f$

Vollständigen Rechenweg anzeigen

$\alpha \approx 57,62^{\circ}$

a5)

Der Flächeninhalt der Grundfläche des Surfbretts kann als doppelter Inhalt der Fläche unter der Funktion $f(x)$ bestimmt werden:

$A=2\cdot \displaystyle\int_{0}^{2}f(x)\;\mathrm dx=\dfrac{11}{15}\;\text[{m}^2]$

Nun kann das Volumen bestimmt werden:

$V=A\cdot h=\dfrac{11}{15}\;\text{m}^2\cdot 0,05\;\text{m}$ $\approx 0,03667\;\text{m}^3$

Das Volumen des Surfbretts beträgt ungefähr $36,67$ Liter.

b1)

Der CAS liefert für die Gleichung $g(x)=0$ die Lösungen $x_1=0$ und $x_2=2.$

Die Länge des Funboards beträgt somit $2\,\text{m}-0\,\text{m}=2\,\text{m}.$

b2)

$\blacktriangleright$ TI nspire CAS

menu $\to$ 4: Analysis $\to$ 1: Ableitung

$\blacktriangleright$ Casio Classpad II

keyboard $\to$ Math2 $\to$ $\frac{d}{d \Box}\Box$

$\(g$

Vollständigen Rechenweg anzeigen

$\( \lim\limits_{x\to2} g$

Der Zähler näher sich für $x\rightarrow 2$ dem konstanten Wert $-3$ an, während der Nenner gegen $0$ geht. Damit geht der gesamte Ausdruck gegen $-\infty.$

Das bedeutet, dass das Heck das Board abgerundet abschließt und dort keine Spitze hat.

b3)

Der Flächeninhalt der gefärbten Fläche der rechten Boardhälfte setzt sich zusammen aus dem Flächeninhalt des rechtwinkligen Dreiecks $PP(b)Q$ und dem Flächeninhalt der Fläche unter der Funktion $g$ im Intervall $[b;2].$

Gesucht ist also die Lösung der folgenden Gleichung:

$0,5 \cdot (b-0,75)\cdot g(b)+\displaystyle\int_{b}^{2}g(x)\;\mathrm dx$ $=0,5\cdot \displaystyle\int_{0}^{2}g(x)\;\mathrm dx$

$0,5\cdot (b-0,75)\cdot g(b)+\displaystyle\int_{b}^{2}g(x)\;\mathrm dx$ $=0,4712$

Mit dem CAS lässt sich $b\approx 1,2403$ berechnen.

Daraus ergeben sich die Koordinaten von $Q(1,2403\mid0,2912)$

c1)

Gesucht ist eine Lösung der Gleichung $g_k(x)=g(x)$

$0,15\cdot k \cdot \sqrt{1-\left(\dfrac{2}{k}\cdot x-1\right)^2}$ $=0,3\cdot k\cdot\sqrt{1-(x-1)^2}$

Der CAS liefert $k=2$

c2)

Für $x=\dfrac{k}{2}$ gilt $\(g$ also ist die notwendige Bedingung für ein lokales Maximum erfüllt.

Da der Graph an jeder Stelle $x$ mit $0\lt x\lt k$ rechtsgekrümmt ist, liegt das lokale Maximum an der Stelle $x=\dfrac{k}{2}.$

c3)

Die Länge des Surfbretts kann folgendermaßen bestimmt werden:

$g_k(x)=0$

Der CAS liefert die Lösungen $x_1=0$ und $x_2=k.$

Die Länge jedes Surfbretts beträgt also $k-0=k.$

Somit gilt für ein $2,5$ Meter langes Surfbrett: $k=2,5$

Die größte Breite des Surfbretts lässt sich wie folgt berechnen:

$g_{2,5}(1,25)=0,375$

Die größte Breite des Surfbretts beträgt also $2\cdot 37,5\,\text{cm}=75\,\text{cm}$

c4)

Das Shortboard aus der Teilaufgabe a) hat folgendes Verhältnis:

$\dfrac{0,5}{2}=0,25$

Für das Verhältnis aller Funboards gilt allgemein:

$\dfrac{2\cdot g_k\left(\dfrac{k}{2}\right)}{k}=\dfrac{2\cdot 0,15\cdot k}{k}=0,3$

Alle durch $g_k$ modellierte Funboards liegen somit stabiler im Wasser als das Shortboard aus Teilaufgabe a).

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?