Analysis 2

Die Abbildung 1 zeigt eine Holzfigur. Diese wird auf der Seite liegend als Rotationskörper modelliert, der durch Rotation des Graphen einer Funktion $f$ um die $x$ -Achse in einem Koordinatensystem entsteht (siehe Abbildung 2).

Dabei gilt $f(x)=-0,01 x^4+0,14 x^3-0,67 x^2$ $+1,2 x+3,02$ mit $0 \leq x \leq 8.$

Eine Längeneinheit im Modell entspricht einem Zentimeter in der Wirklichkeit.

Grüne, abgerundete Figur mit Punkten als Augen und V-förmigem Mund, Pfeile und Beschriftungen

Abbildung 1

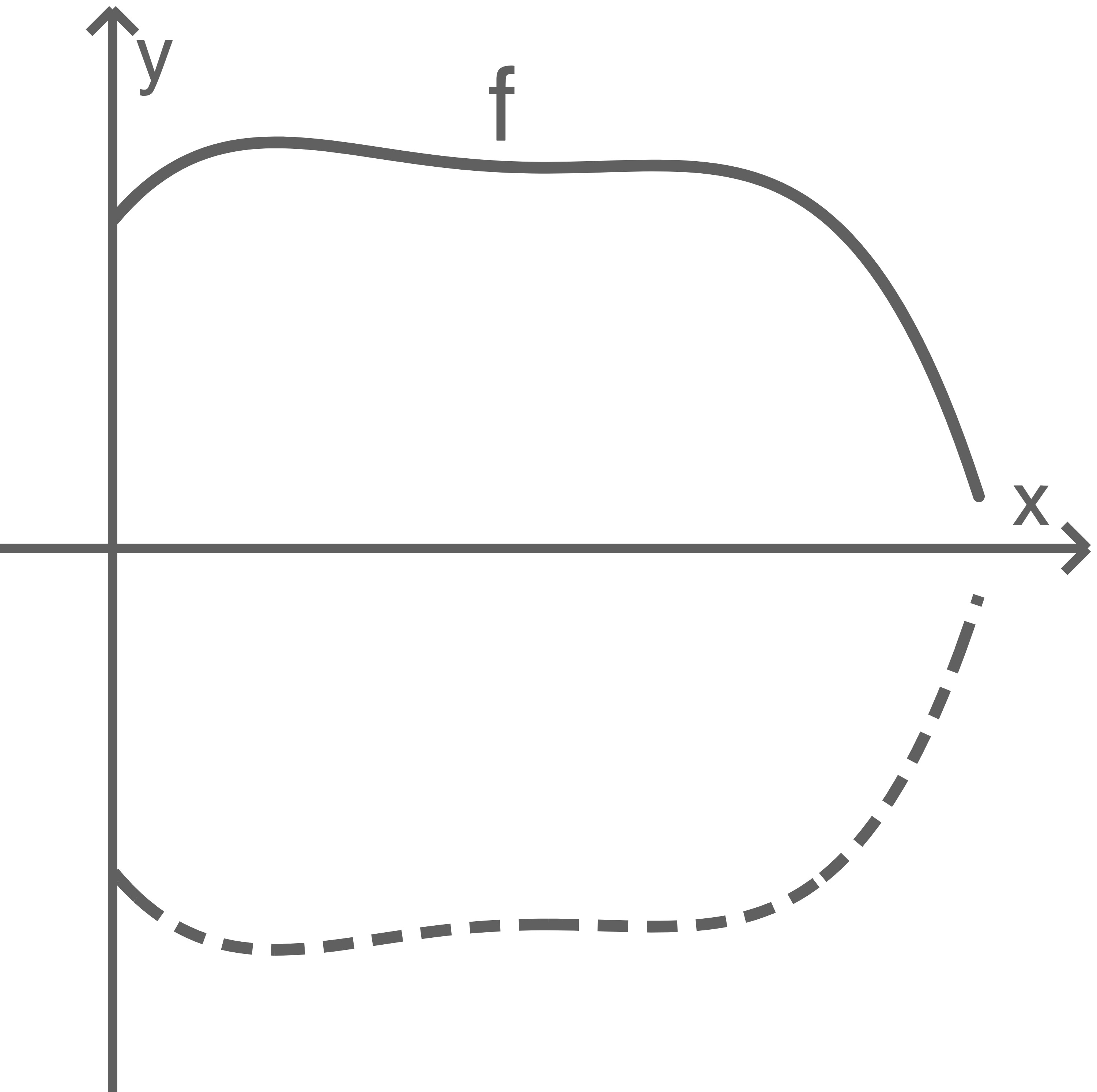
Koordinatensystem mit x- und y-Achse, obere durchgezogene Kurve f und untere gestrichelte Kurve

Abbildung 2

Die Holzfigur steht aufrecht auf einer ebenen Tischplatte.

a1)

Gib die Höhe der Figur an.

(1 BE)

a2)

Berechne den Umfang und den Inhalt der kreisförmigen Grundfläche der Figur.

(4 BE)

a3)

Bestimme rechnerisch die Breite der Figur.

(4 BE)

a4)

Berechne die Größe des Schnittwinkels des Graphen von $f$ und der $y$ -Achse.

(3 BE)

a5)

Aus der Holzfigur sollen durch Schnitte parallel zur Tischplatte Scheiben herausgeschnitten werden, so dass jede dieser herausgeschnittenen Scheiben die folgenden Anforderungen erfüllt:

Die Scheibe ist $1\;\text{cm}$ hoch.
Die Grundfläche der Scheibe hat denselben Durchmesser wie ihre Deckfläche.

Ermittle, wie viele solcher Scheiben höchstens aus dieser einen Holzfigur herausgeschnitten werden können.

(4 BE)

Nun wird der obere Teil der Holzfigur neu modelliert. Diese Modellierung erfolgt für $5 \leq x \leq 8$ durch Rotation des Graphen einer Funktion $g$ um die $x$ -Achse. Für $0 \leq x \leq 5$ wird die Holzfigur weiterhin mithilfe von $f$ modelliert.

b1)

Für geeignet gewählte reelle Zahlen $a$ und $b$ ist $g(x)=a \cdot(x+1) \cdot \sqrt{b-x}.$
Bestimme $a$ und $b$ so, dass der Graph von $f$ an der Stelle $x=5$ sprung- und knickfrei in den Graphen von $g$ übergeht.

(4 BE)

Verwende für die weiteren Berechnungen nun $g(x)=\frac{44 \cdot \sqrt{3}}{225} \cdot(x+1) \cdot \sqrt{8-x}.$

b2)

Zeichne den Graphen der Funktion $g$ für $5 \leq x \leq 8$ in die Abbildung 3.

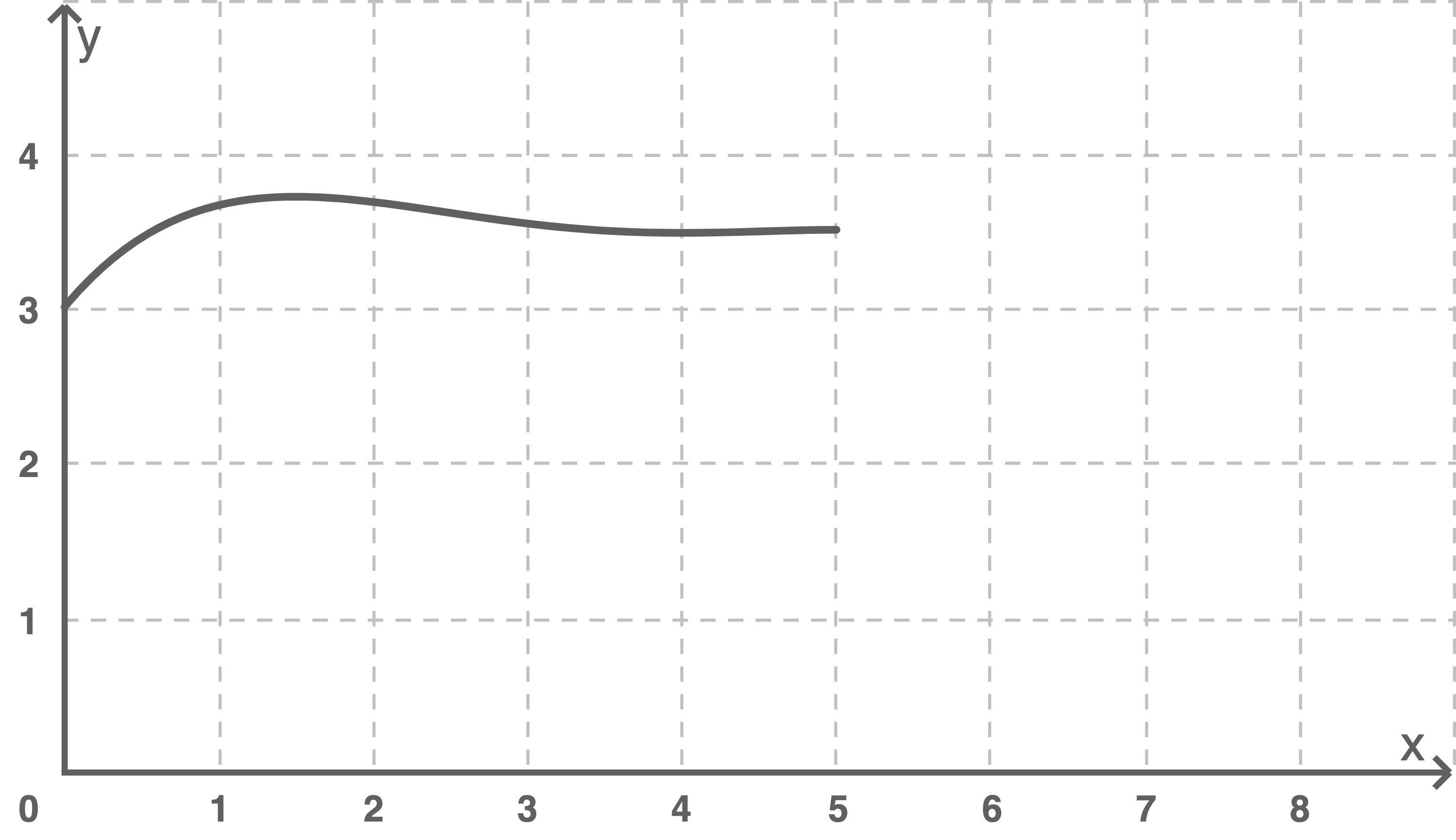
Koordinatensystem mit Raster und einer glatten Kurve, die bei y≈3 startet, leicht bis ca. 3,7 ansteigt und dann sanft abfällt.

Abbildung 3

(2 BE)

b3)

Berechne das Volumen der Holzfigur entsprechend der neuen Modellierung durch die Funktionen $f$ und $g.$

(4 BE)

Für den Inhalt $A_M$ der Mantelfläche eines Kegelstumpfes gilt $A_M=\left(r_1+r_2\right) \cdot \pi \cdot s,$ wobei $r_1$ und $r_2$ die Radien der beiden Kreisflächen darstellen und $s$ die Länge einer Mantellinie des Kegelstumpfes angibt (siehe Abbildung 4).

Kegelstumpf mit oberem Radius r2, unterem Radius r1, gestrichelter Achse und geneigter Mantellinie s

Abbildung 4

Der Term

Term anzeigen

wird verwendet, um einen Näherungswert für den Inhalt der Mantelfläche des durch $f$ über dem Intervall $[0 ; 8]$ erzeugten Rotationskörpers zu berechnen.

Erläutere die geometrischen Überlegungen, die diesem Term zugrunde liegen.

(4 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

a1)

$8 \;\text{cm}$

a2)

Der Radius der Grundfläche entspricht $f(0).$ Einsetzen von $x=0$ in $f(x)$ liefert mit dem CAS:

$f(0)= 3,02$

Somit folgt für den Umfang $U:$

$\begin{array}[t]{rlll} U &=& 2\pi\cdot3,02 \\[5pt] &\approx& 19 \;[\text{cm}] \end{array}$

Für den Flächeninhalt $A$ folgt:

$\begin{array}[t]{rlll} A &=& \pi\cdot3,02^2 \\[5pt] &=& 28,7 \;[\text{cm}^2] \end{array}$

a3)

Die Figur ist an der Stelle am breitesten, an der $f$ sein globales Maximum besitzt.

Erste Ableitung aufstellen

$\(f$

Notwendige Bedingung für Extremstellen anwenden

$\(\begin{array}[t]{rlll} f$

Mit dem solve-Befehl des CAS folgt:

$\begin{array}[t]{rlll} x_1 &=& 1,5 \\[5pt] x_2 &=& 4 \\[5pt] x_3 &=& 5 \end{array}$

Anhand des Krümmungsvehaltens des Graphen von $f$ lässt sich aus Abbildung 2 ablesen, dass bei $x_1=1,5$ das globale Maximum von $f$ im Intervall $[0;8]$ liegt.

Somit folgt für die Breite $B$ der Figur:

Rechenweg anzeigen

$B \approx 7,5 \;\text{cm}$

a4)

Steigung an der $\boldsymbol{y}$ -Achse bestimmen

Rechenweg anzeigen

$\( f$

Da es nur um die Stelle $x=0$ geht, wird ab jetzt nur noch die Tangente an den Graphen von $f$ in diesem Punkt betrachtet. Sie hat die Steigung $1,2.$

Winkel $\boldsymbol{\varphi}$ zwischen Tangente und $\boldsymbol{x}$ -Achse bestimmen

$\begin{array}[t]{rlll} \tan(\varphi) &=& 1,2 &\mid\; \tan^{-1} \\[5pt] \varphi &=& \tan^{-1}(1,2) \\[5pt] \varphi &\approx& 50,2^{\circ} \end{array}$

Winkel $\boldsymbol{\alpha}$ zwischen Tangente und $\boldsymbol{y}$ -Achse bestimmen

Da die $y$ -Achse senkrecht zur $x$ -Achse steht, muss man den Winkel zur $x$ -Achse von $90^{\circ}$ abziehen, um den Winkel zur $y$ -Achse zu erhalten:

$\begin{array}[t]{rlll} \alpha &\approx& 90^{\circ}-50,2^{\circ} \\[5pt] &=& 39,8^{\circ} \end{array}$

a5)

Damit die obere und die untere Fläche einer Scheibe gleich groß sind, muss der Funktionswert von $f$ an beiden Schnittstellen gleich sein. Da die Scheibe $1\;\text{cm}$ hoch ist, liefert das die Gleichung $f(x)=f(x+1).$ Auflösen nach $x$ mit dem solve-Befehl des CAS liefert:

$\begin{array}[t]{rlll} x_1 &\approx& 1,06 \\[5pt] x_2 &\approx& 3,56 \\[5pt] x_3 &\approx& 4,38 \end{array}$

Überprüfung der Abstände

Da jede Scheibe $1\;\text{cm}$ hoch ist, dürfen sich die Intervalle der Schnittpunkte nicht überlappen. Für die mögliche zweite Scheibe gilt jedoch:

$\begin{array}[t]{rlll} x_2+1 &=& 3,56+1\\[5pt] &=& 4,56 \end{array}$

Somit gilt $x_2+1\gt x_3,$ d.h. der dritte Schnittpunkt liegt zu nah am zweiten und es können somit höchstens zwei Scheiben aus der Holzfigur herausgeschnitten werden.

b1)

Damit der Übergang zwischen $f$ und $g$ an der Stelle $x=5$ sprungfrei und knickfrei erfolgt, müssen die Funktionswerte und die Steigungen an dieser Stelle übereinstimmen. Die Bedingungen sind:

$\(\begin{array}{lrll} \text{I}\quad&f(5)&=& g(5)&\quad \scriptsize\\ \text{II}\quad&f$

Aus $\text{I}$ folgt:

Rechenweg anzeigen

$3,52 = a \cdot 6 \cdot \sqrt{b-5}$

Ableitung $\(\boldsymbol{g$ bilden

$\(g$

Aus $\text{II}$ folgt:

Rechenweg anzeigen

$0 = a\left(\sqrt{b-5}-\dfrac{6}{2 \sqrt{b-5}}\right)$

Ausgeschrieben ergibt sich das LGS somit wie folgt:

$\begin{array}{lrll} \text{I}\quad&3,52&=& a \cdot 6 \cdot \sqrt{b-5} &\quad \\ \text{II}\quad&0&=& a\left(\sqrt{b-5}-\dfrac{6}{2 \sqrt{b-5}}\right) &\quad \\ \end{array}$

Mit dem solve-Befehl des CAS folgt für $a$ und $b:$

$\begin{array}[t]{rlll} a &=& \dfrac{44 \sqrt{3}}{225} \\[5pt] b &=& 8 \end{array}$

b2)

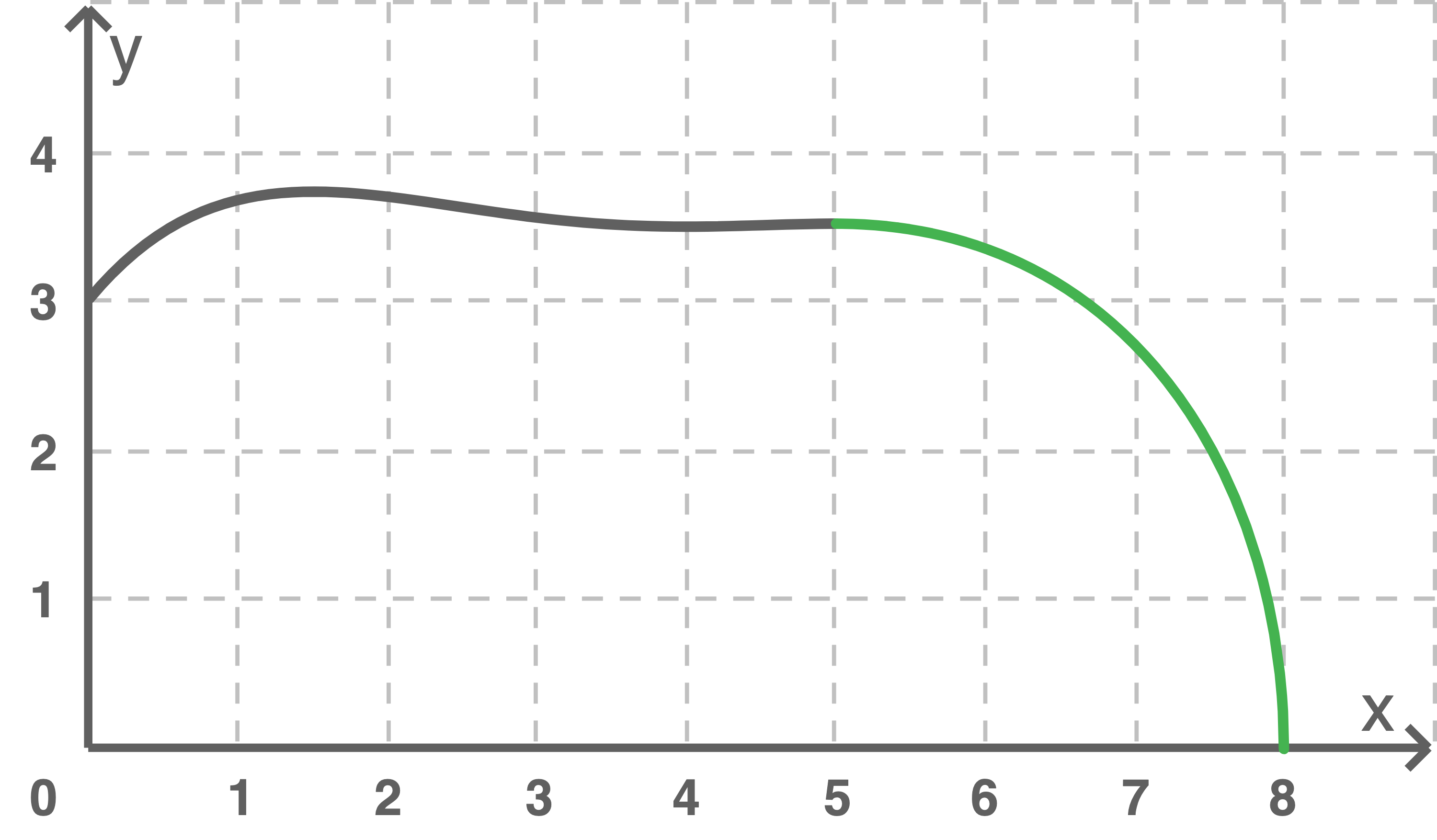
Koordinatensystem mit Achsen x,y und einer grauen Kurve; rechter Abschnitt grün hervorgehoben und abfallend bis x≈8

b3)

Die Figur besteht aus zwei Teilen: für $0 \leq x \leq 5$ wird sie durch $f(x)$ beschrieben und für $5 \leq x \leq 8$ durch $g(x).$ Somit folgt für das Volumen der Holzfigur:

$V = \pi \cdot\displaystyle\int_0^5(f(x))^2 \;\text{d} x+\pi \cdot\displaystyle\int_5^8(g(x))^2 \;\text{d}x$

Mit dem CAS ergibt sich für das Volumen $V$ damit:

$V\approx 279,8 \;\text{cm}^3$

Der Rotationskörper wird in acht gleich Teilstücke mit gleicher Höhe unterteilt. Jedes dieser Teilstücke wird näherungsweise als ein Kegelstumpf betrachtet, der eine Höhe von $1 \;\text{cm}$ besitzt.
Für jeden dieser Kegelstümpfe $K_i$ werden die Radien der beiden Kreisflächen durch die Funktionswerte $f(i)$ und $f(i+1)$ beschrieben.

Die Mantellinie $s$ eines solchen Kegelstumpfs entspricht der schrägen Verbindungslinie zwischen den beiden Kreisrändern. Nach dem Satz des Pythagoras ergibt sich ihre Länge $s$ wie folgt:

$s=\sqrt{1^2+(f(i+1)-f(i))^2}$

Da der gesamte Rotationskörper aus diesen acht Kegelstümpfen zusammengesetzt ist, ergibt sich der gesamte Mantelflächeninhalt, indem die Mantelflächen aller acht Teilstücke addiert werden.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?