HMF 1 - Analysis

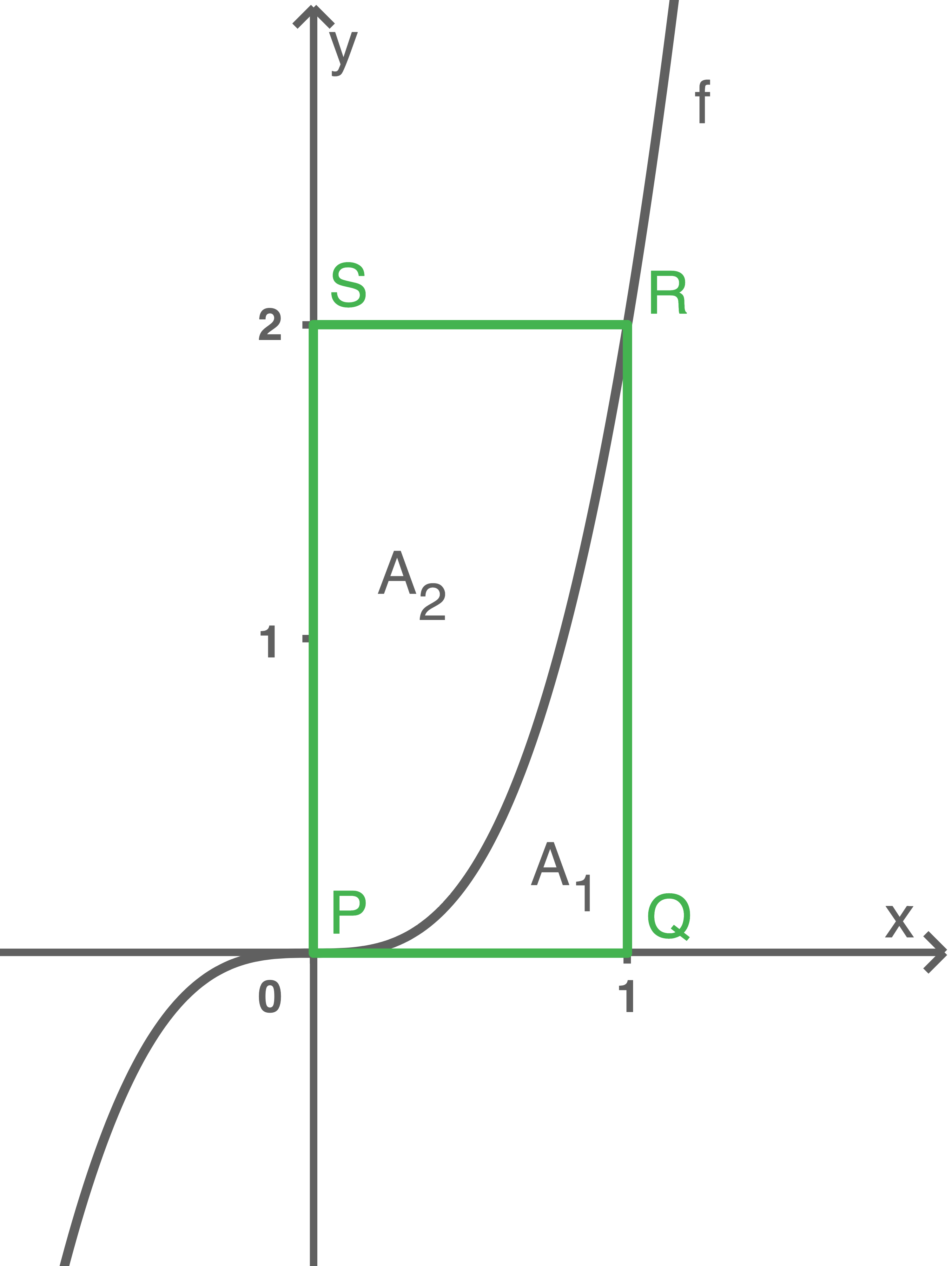
Die Abbildung zeigt den Graphen der Funktion $f$ mit $f(x)=2 x^3$ und das Rechteck $P Q R S$ mit $P(0 \mid 0), Q(1 \mid 0), R(1 \mid 2), S(0 \mid 2).$
Der Graph teilt das Rechteck in zwei Flächen, deren Flächeninhalte mit $A_1$ und $A_2$ bezeichnet sind.

1.1

Zeige, dass der Punkt $R$ auf dem Graphen von $f$ liegt.

(1 BE)

1.2

Berechne $A_1$ und $A_2.$

(4 BE)

Koordinatensystem mit Kurve und grünem Rechteck (x=0..1, y=0..2), Ecken P,Q,R,S und markierten Bereichen A1 und A2

HMF 2 - Analysis

Gegeben ist die in $\mathbb{R}$ definierte Funktion $f$ mit $f(x)=\frac{1}{4} x^3-3 x.$

2.1

Es gilt $\(f$
Zeige, dass $2$ eine Extremstelle von $f$ ist.

(2 BE)

2.2

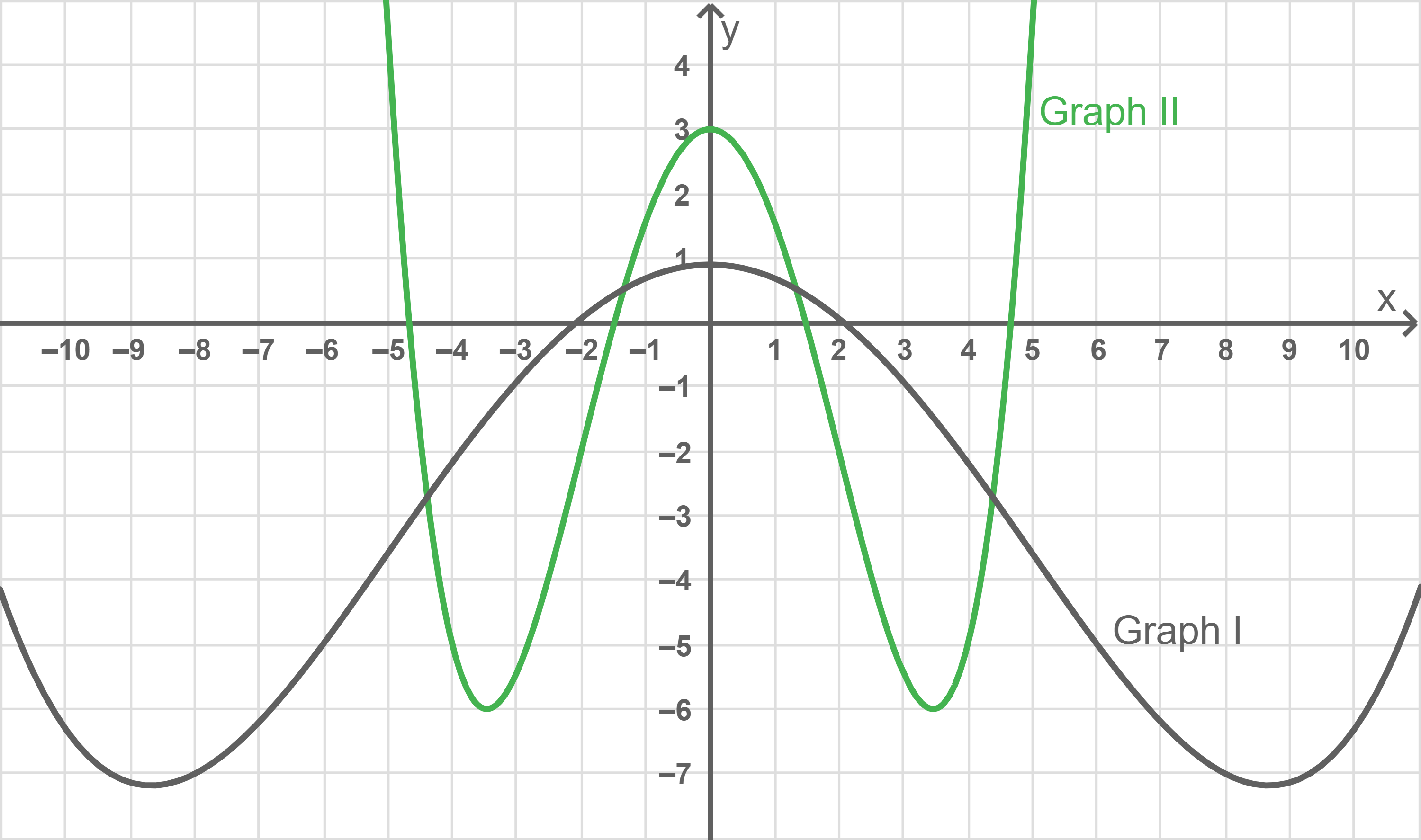
Einer der abgebildeten Graphen I und II ist der Graph einer Stammfunktion von $f.$ Gib diesen Graphen an und begründe deine Angabe.

(3 BE)

HMF 3 - Analytische Geometrie

In der Ebene $E: x_2+2 x_3=6$ liegt der Punkt $A(10\mid y\mid 0,5).$

3.1

Berechne den Wert von $y.$

(1 BE)

3.2

Betrachtet wird die Lotgerade vom Punkt $P(8\mid12\mid 2)$ auf die Ebene $E.$
Bestimme die Koordinaten des zugehörigen Lotfußpunktes $F.$

(4 BE)

HMF 4 - Stochastik

Für ein Zufallsexperiment mit den beiden Ereignissen $A$ und $B$ sind die folgenden Wahrscheinlichkeiten gegeben:

	$\color{#ffff}{B}$	$\color{#ffff}{\overline{B}}$	$\color{#ffff}{\displaystyle\sum}$
$\color{#ffff}{A}$	$0,32$		$0,4$
$\color{#ffff}{\overline{A}}$		$0,12$
$\color{#ffff}{\displaystyle\sum}$	$0,8$		$1$

4.1

Ergänze die fehlenden Wahrscheinlichkeiten in der Vierfeldertafel.

(2 BE)

4.2

Prüfe, ob $P_A(B)=P(B)$ gilt.

(3 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

HMF 1 - Analysis

1.1

Punkt $\boldsymbol{R}$ in $\boldsymbol{f(x)}$ einsetzen

$\begin{array}[t]{rlll} f(1) &=& 2\cdot1^3 \\[5pt] &=& 2 \end{array}$

Somit liegt der Punkt $R$ auf dem Graphen von $f.$

1.2

Flächeninhalt des Rechtecks berechnen

$\begin{array}[t]{rlll} A_R &=& 2\cdot1 \\[5pt] &=& 2 \end{array}$

Flächeninhalt $\boldsymbol{A_1}$ berechnen

$\begin{array}[t]{rlll} A_1 &=& \displaystyle\int_{0}^{1}f(x)\;\mathrm{d}x \\[5pt] &=& \displaystyle\int_{0}^{1}2x^3\;\mathrm{d}x \\[5pt] &=& \left[\dfrac{1}{2}x^4\right]_0^1 \\[5pt] &=& \dfrac{1}{2}\cdot1^4-\dfrac{1}{2}\cdot0^4 \\[5pt] &=& \dfrac{1}{2} \end{array}$

Flächeninhalt $\boldsymbol{A_2}$ berechnen

$\begin{array}[t]{rlll} A_2 &=& A_R-A_1 \\[5pt] &=& 2-\dfrac{1}{2} \\[5pt] &=& \dfrac{3}{2} \end{array}$

HMF 2 - Analysis

2.1

Für die erste Ableitung von $f$ gilt:

$\(\begin{array}[t]{rlll} f$

Einsetzen von $x=2$ liefert:

$\(\begin{array}[t]{rlll} f$

Somit ist die notwendige Bedingung für Extremstellen in $x=2$ erfüllt. Da die hinreichende Bedingung für Extremstellen bereits in der Aufgabenstellung gegeben ist, folgt somit, dass $2$ eine Extremstelle von $f$ ist.

2.2

Da $f$ bei $x=2$ eine Extremstelle besitzt, hat jede Stammfunktion von $f$ bei $x=2$ eine Wendestelle. Aus der Abbildung folgt somit, dass Graph II der Graph einer Stammfunktion von $f$ ist.

HMF 3 - Analytische Geometrie

3.1

$\begin{array}[t]{rlll} y+2\cdot0,5 &=& 6 &\mid\; -1 \\[5pt] y &=& 5 \end{array}$

3.2

Lotgerade $\boldsymbol{g}$ aufstellen

Ein möglicher Richtungsvektor der Lotgeraden ist der Normalenvektor der Ebene $E.$

$g:\overrightarrow{x}=\pmatrix{8\\12\\2}+r\cdot\pmatrix{0\\1\\2}$

Gerade $\boldsymbol{g}$ in $\boldsymbol{E}$ einsetzen

$\begin{array}[t]{rlll} (12+r)+2\cdot(2+2r) &=& 6 \\[5pt] 12+r+4+4r &=& 6 &\mid\; -16 \\[5pt] 5r &=& -10 &\mid\; :5 \\[5pt] r &=& -2 \end{array}$

$\boldsymbol{\overrightarrow{OF}}$ berechnen

$\begin{array}[t]{rlll} \overrightarrow{OF} &=& \pmatrix{8\\12\\2}-2\cdot\pmatrix{0\\1\\2}\\[5pt] &=& \pmatrix{8\\10\\-2} \end{array}$

Für die Koordinaten von $F$ folgt somit: $F=(8 \mid 10 \mid -2).$

HMF 4 - Stochastik

4.1

	$\color{#ffff}{B}$	$\color{#ffff}{\overline{B}}$	$\color{#ffff}{\displaystyle\sum}$
$\color{#ffff}{A}$	$0,32$	$0,08$	$0,4$
$\color{#ffff}{\overline{A}}$	$0,48$	$0,12$	$0,6$
$\color{#ffff}{\displaystyle\sum}$	$0,8$	$0,2$	$1$

4.2

$\begin{array}[t]{rlll} P_A(B) &=& \dfrac{P(B \cap A)}{P(A)} \\[5pt] &=& \dfrac{0,32}{0,4} \\[5pt] &=& 0,8 \\[5pt] &=& P(B) \end{array}$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?