Pool 2

HMF 5 - Analysis

Gegeben ist die Funktion $g$ mit $g(x)=\mathrm{e}^{\frac{1}{2} x}-5 x.$

5.1

Gib einen Funktionsterm einer Stammfunktion von $g$ an.

(2 BE)

5.2

Es gibt genau eine reelle Zahl $a,$ so dass der Graph der Funktion $g$ an der Stelle $x=a \cdot \ln (10)$ eine waagerechte Tangente besitzt.

Bestimme $a.$

(3 BE)

HMF 6 - Analysis

Gegeben ist die Funktion $f$ mit $f(x)= \sqrt{x-2}$ und $x \in[2 ;+\infty[.$
Die Abbildung zeigt den Graphen $G$ von $f$ sowie den Punkt $P(3\mid1).$
Die Gerade mit der Gleichung $y=\dfrac{1}{2}x-\dfrac{1}{2}$ ist die Tangente an $G$ im Punkt $P$ und hat mit $G$ nur den Punkt $P$ gemeinsam.

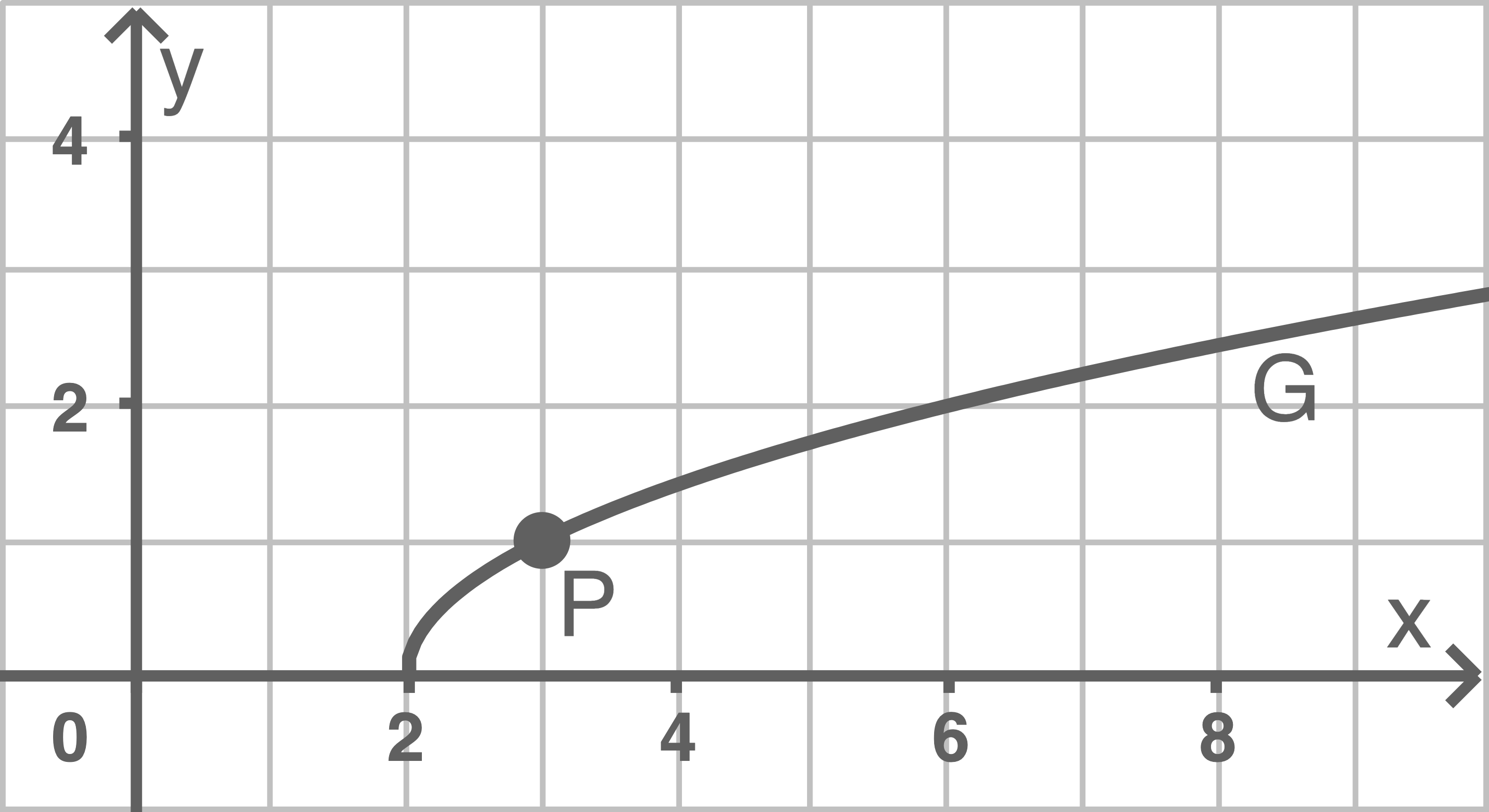
Graf mit einer Kurve und den Punkten P und G im Koordinatensystem. Achsen beschriftet mit x und y.

6.1

Zeichne die Tangente in Abbildung 2 ein.

(1 BE)

6.2

Betrachtet werden alle Geraden, die mit $G$ sowohl den Punkt $P$ als auch einen weiteren Punkt gemeinsam haben.

Gib die Steigungen dieser Geraden an.

(4 BE)

HMF 7 - Analytische Geometrie

Gegeben ist die Schar der Ebenen $E_a: 3 x_1+a x_2+6 x_3=12$ mit $a\gt0.$

7.1

Zeige, dass jede Ebene $E_a$ die $x_1$ -Achse an der Stelle $x_1=4$ und die $x_3$ -Achse an der Stelle $x_3=2$ schneidet.

(2 BE)

7.2

Der Ursprung des Koordinatensystems und die Schnittpunkte der Ebene $E_a$ mit den Koordinatenachsen bilden die Eckpunkte einer Pyramide mit dreieckiger Grundfläche.

Bestimme den Wert für $a,$ so dass das Volumen der Pyramide $16$ beträgt.

(3 BE)

HMF 8 - Analytische Geometrie

Für jede reelle Zahl $k$ wird die Gerade $g_k: \overrightarrow{x}=\pmatrix{5-6k\\3k\\4-9k}+r \cdot\pmatrix{2\\-1\\3}$ mit $r \in \mathbb{R}$ betrachtet.

8.1

Zeige, dass für keinen Wert von $k$ der Punkt $(0\mid0\mid 0)$ auf $g_k$ liegt.

(2 BE)

8.2

Beurteile die folgende Aussage: „Alle Geraden $g_k$ sind identisch.“

(3 BE)

HMF 9 - Stochastik

Die Zufallsgröße $X$ ist binomialverteilt mit den Parametern $n$ und $p$ mit $p\lt1.$
Es ist bekannt, dass $P(X=1)$ vierzehnmal so groß ist wie $P(X=0)$ und dass der Erwartungswert von $X$ gleich $10$ ist.

Berechne die Werte von $p$ und $n.$

(5 BE)

HMF 10 - Stochastik

Betrachtet wird ein Würfel, dessen Seiten mit den Zahlen von $1$ bis $6$ durchnummeriert sind.

10.1

Der Würfel wird zweimal geworfen. Die Zufallsgröße $X$ gibt das Produkt der dabei erzielten Zahlen an.

Begründe, dass $P(X=10)=P(X=15)$ ist.

(2 BE)

10.2

Nun wird der Würfel $n$ -mal geworfen, wobei $n$ größer als $2$ ist.

Ermittle einen Term, mit dem man die Wahrscheinlichkeit für das folgende Ereignis berechnen kann: „Das Produkt der $n$ erzielten Zahlen ist $2, 3$ oder $5.$ “

(3 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

HMF 5 - Analysis

5.1

$G(x)=2\text{e}^{\frac{1}{2}x}-\dfrac{5}{2}x^2$

5.2

Damit der Graph der Funktion $g$ an der Stelle eine waagerechte Tangente besitzt, muss der Graph an dieser Stelle eine Steigung von $0$ haben.

Ableitung $\(\boldsymbol{g$ aufstellen

$\(g$

$\(\boldsymbol{g$ setzen und nach $\boldsymbol{x}$ auflösen

$\(\begin{array}[t]{rlll} g$

Somit gilt $a=2.$

HMF 6 - Analysis

6.1

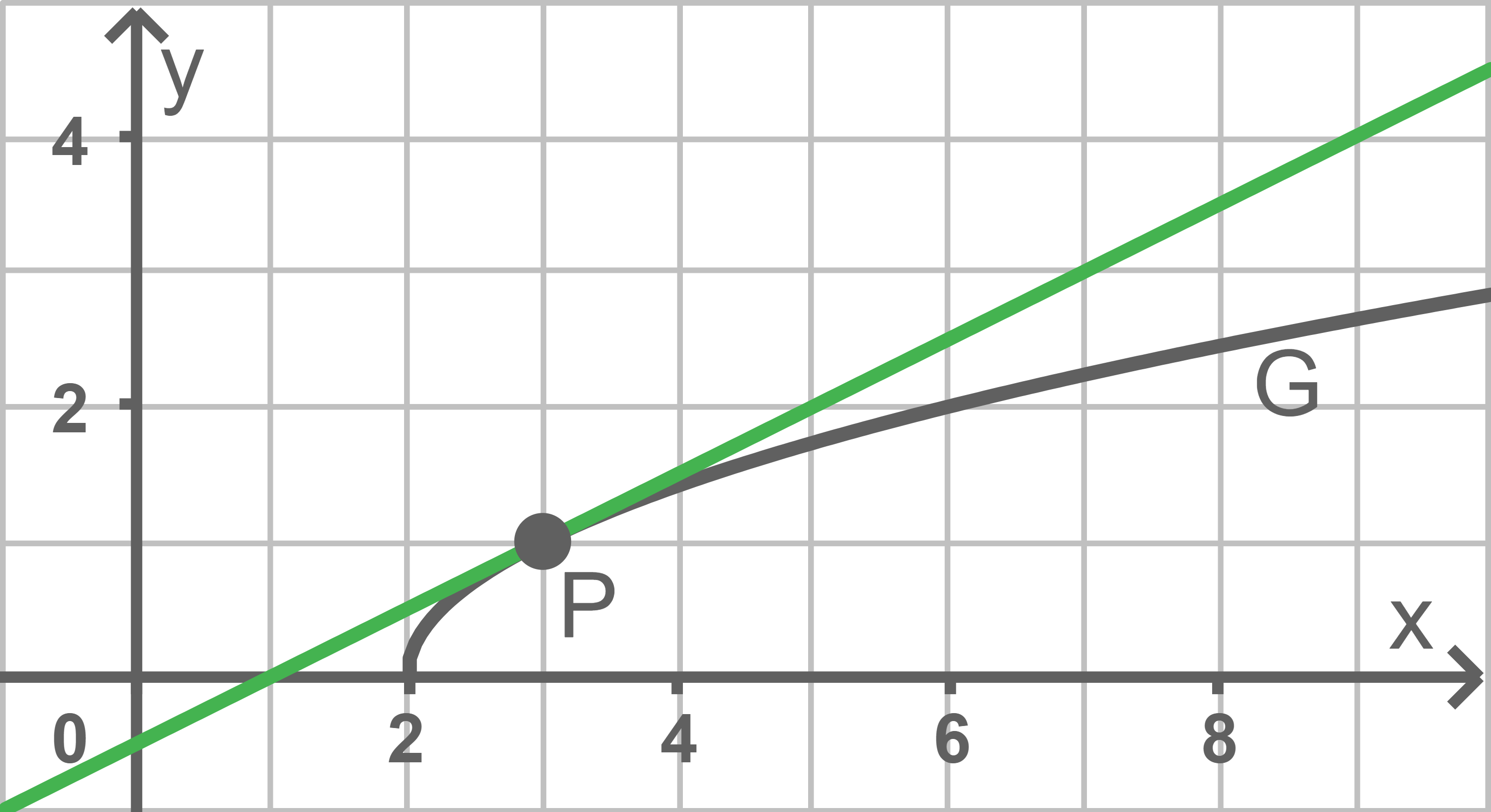
Diagramm mit zwei Kurven, einer grünen und einer grauen, im Koordinatensystem dargestellt. Punkt P ist markiert.

6.2

Für die Steigungen $m$ der Geraden mit der Eigenschaft aus der Aufgabenstellung gilt $\frac{1}{2}\lt m \leq 1$ oder $0\lt m\lt\frac{1}{2}.$

HMF 7 - Analytische Geometrie

7.1

Schnittpunkt mit der $\boldsymbol{x_1}$ -Achse berechnen

Dafür müssen $x_2=x_3=0$ gesetzt werden.

$\begin{array}[t]{rlll} 3x_1+a\cdot0+6\cdot0 &=& 12 &\mid\; :3 \\[5pt] x_1 &=& 4 \end{array}$

Schnittpunkt mit der $\boldsymbol{x_3}$ -Achse berechnen

Dafür müssen $x_1=x_2=0$ gesetzt werden.

$\begin{array}[t]{rlll} 3\cdot0+a\cdot0+6x_3 &=& 12 &\mid\; :6 \\[5pt] x_3 &=& 2 \end{array}$

Somit wird die $x_1$ -Achse immer an der Stelle $x_1=4$ und die $x_3$ -Achse an der Stelle $x_3=2$ geschnitten.

7.2

Schnittpunkt mit der $\boldsymbol{x_2}$ -Achse berechnen

Dafür müssen $x_1=x_3=0$ gesetzt werden.

$\begin{array}[t]{rlll} 3\cdot0+a x_2+6\cdot0 &=& 12 &\mid\; :a \\[5pt] x_2 &=& \dfrac{12}{a} \end{array}$

Die Formel für das Volumen einer Pyramide lautet $V = \frac{1}{3}\cdot G \cdot h.$

Die Formel für die Grundfläche einer Pyramide lautet $G=\frac{1}{2}\cdot a \cdot b.$

Da die Pyramide durch die Schnittpunkte der Ebene $E_a$ mit den Koordinatenachsen gebildet wird, gilt:

$a=x_1=4$

$b=x_3=2$

$h=x_2=\frac{12}{a}$

Somit folgt:

$\begin{array}[t]{rlll} V &=& 16 \\[5pt] \dfrac{1}{3}\cdot \dfrac{1}{2} \cdot 4 \cdot 2 \cdot \dfrac{12}{a} &=& 16 &\mid\; \cdot a \\[5pt] 16 &=& 16a &\mid\; :16 \\[5pt] 1 &=& a \end{array}$

Somit muss $a=1$ sein, damit das Volumen der Pyramide $16$ beträgt.

HMF 8 - Analytische Geometrie

8.1

Nullsetzen der Geradengleichung liefert folgendes lineares Gleichungssystem:

$\begin{array}{lrll} \text{I}\quad&5-6k+2r&=&0 \\ \text{II}\quad&3k-r&=&0 \\ \text{II}\quad&4-9k+3r&=&0 \end{array}$

Aus Gleichung $\text{II}$ folgt direkt $r=3k.$ Einsetzen in z.B. Gleichung $\text{I}$ liefert:

$\begin{array}[t]{rlll} 5-6k+2\cdot3k&=&0 \\[5pt] 5&=&0 \end{array}$

Da das unabhängig von $k$ falsch ist, gibt es keinen Wert von $k$ sodass $(0\mid0\mid0)$ auf $g_k$ liegt.

8.2

Aufteilen des Stützvektors von $g_k$ in Werte unabhängig von $k$ und abhängig von $k$ liefert:

$\pmatrix{5\\0\\4}+k\cdot\pmatrix{-6\\3\\-9}$

Da der zweite Vektor das $(-3)$ -fache des Richtungsvektors von $g_k$ ist, wird jede Gerade $g_k$ mit $s=r-3k$ durch folgende Geradengleichung beschrieben:

$g:\overrightarrow{x}=\pmatrix{5\\0\\4}+s\cdot\pmatrix{2\\-1\\3}$

Damit sind alle Geraden $g_k$ identisch.

HMF 9 - Stochastik

Mit $E(X)=10$ folgt:

$\begin{array}[t]{rlll} E(X) &=& 10 \\[5pt] n\cdot p &=& 10 \end{array}$

Für Binomialverteilungen gilt:

$P(X=k)=\displaystyle\binom{n}{k} p^k(1-p)^{n-k}$

Aus dem Aufgabentext geht hervor, dass $P(X=1)=14\cdot P(x=0)$ ist. Damit gilt:

$\begin{array}[t]{rlll} P(X=1) &=& 14\cdot P(X=0) \\[5pt] \displaystyle\binom{n}{1}\cdot p^1\cdot (1-p)^{n-1} &=& 14\cdot\displaystyle\binom{n}{0}\cdot p^0\cdot (1-p)^{n-0} \\[5pt] n\cdot p \cdot (1-p)^{n-1} &=& 14\cdot(1-p)^n \\[5pt] 10 \cdot (1-p)^{n-1} &=& 14\cdot(1-p)^n &\mid\; : (1-p)^{n-1} \\[5pt] 10 &=& 14\cdot(1-p) &\mid\; -14 \\[5pt] -4 &=& -14p &\mid\; :(-14)\\[5pt] \dfrac{2}{7} &=& p \end{array}$

Somit gilt für $n:$

$\begin{array}[t]{rlll} n \cdot p &=& 10 \\[5pt] n \cdot \dfrac{2}{7} &=& 10 &\mid\; :\dfrac{2}{7}\\[5pt] n &=& 35 \end{array}$

Somit ist $p=\frac{2}{7}$ und $n=35.$

HMF 10 - Stochastik

8.1

Sowohl $10$ als auch $15$ können jeweils nur durch genau ein Produkt von zwei Zahlen erhalten werden, nämlich das Produkt von $2$ und $5$ bzw. das Produkt von $3$ und $5.$ Hierbei ist egal, in welcher Reihenfolge die beiden Zahlen gewürfelt werden, d.h. es gibt jeweils zwei Ergebnisse, die $X=10$ bzw. $X=15$ liefern. Da jede zahl auf dem Würfel mit gleicher Wahrscheinlichkeit erzielt wird, gilt damit $P(X=10)=P(X=15).$

8.2

Die Zahlen $2,3$ und $5$ sind Primzahlen. Somit ist die einzige Möglichkeit, dass das Produkt der $n$ erzielten Zahlen $2,3$ oder $5$ ist, dass $(n-1)$ -mal die Zahl $1$ gewürfelt wird, und einmal $2,3$ bzw. $5.$ Da es $n$ mögliche Würfe gibt, in denen die Zahl ungleich $1$ gewürfelt werden kann, folgt für die gesuchte Wahrscheinlichkeit $p$ somit:

$p=3\cdot n\cdot\dfrac{1}{6}\cdot\left(\dfrac{1}{6}\right)^{n-1}$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?