Analytische Geometrie 1

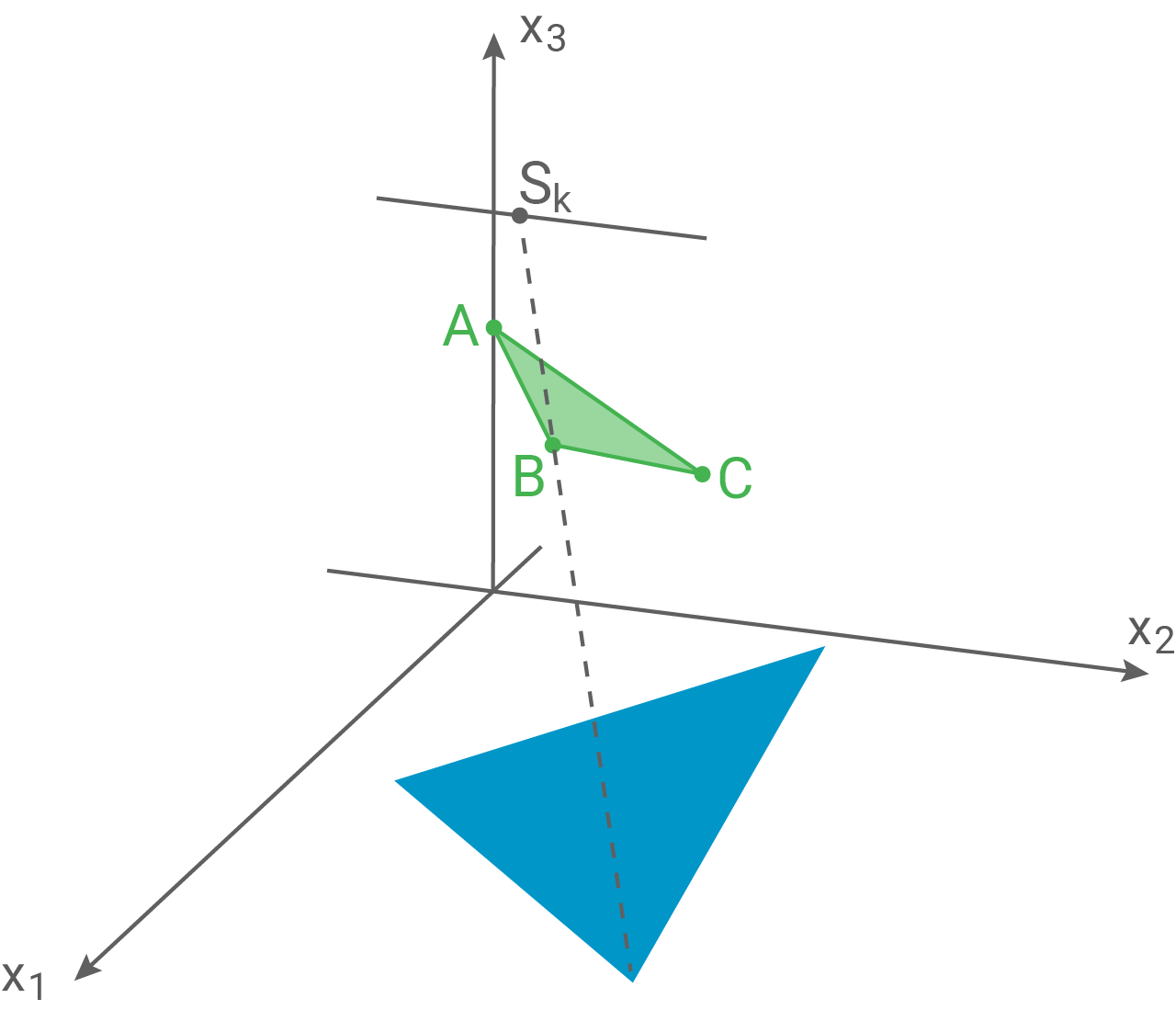
Über einer Bühne wird ein Segeltuch angebracht. In einem Koordinatensystem wird das Segeltuch durch das Dreieck $A B C$ mit den Eckpunkten $A(0\mid0\mid 8), B(6\mid4\mid 7)$ und $C(-1\mid6\mid 4)$ modelliert. Die $x_1 x_2$ -Ebene stellt die Lage der Bühne dar.
Eine Längeneinheit entspricht einem Meter in der Wirklichkeit.

a1)

Zeige, dass das Dreieck $A B C$ gleichschenklig, aber nicht gleichseitig ist.

(4 BE)

a2)

Das Dreieck $A B C$ liegt in einer Ebene $E.$
Bestimme eine Gleichung von $E$ in Koordinatenform.

$\left[\text{zur Kontrolle: } -2 x_1+5 x_2+8 x_3=64 \right]$

(3 BE)

a3)

Der Neigungswinkel des Segeltuchs entspricht dem Schnittwinkel zwischen der Ebene $E$ und der $x_1 x_2$ -Ebene.
Berechne die Größe dieses Schnittwinkels.

(3 BE)

Ein Scheinwerfer kann auf einer Schiene hin- und herbewegt werden. Der Scheinwerfer wird als punktförmig angenommen. Seine möglichen Positionen werden durch die Menge der Punkte $S_k(-4\mid k\mid 10)$ mit $k \in[-5 ; 5]$ beschrieben.
Im Scheinwerferlicht erzeugt das Segeltuch einen Schatten auf der Bühne.

3D-Koordinatensystem mit grünem Dreieck (A, B, C) oben, blauem Dreieck unten und gestrichelter Projektionslinie zum Punkt S_k

b1)

Ermittle alle möglichen Abstände, die zwischen der Position des Scheinwerfers und der durch $A$ beschriebenen Ecke des Segeltuchs vorliegen können.

(4 BE)

b2)

Die durch $B$ beschriebene Ecke des Segeltuchs erzeugt einen Schattenpunkt auf der Bühne.
Untersuche, ob es eine Position des Scheinwerfers gibt, so dass dieser Schattenpunkt durch einen Punkt auf einer der Koordinatenachsen in der $x_1x_2$ -Ebene beschrieben wird.

(6 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

a1)

Vektor $\boldsymbol{\overrightarrow{AB}}$ aufstellen

$\begin{array}[t]{rlll} \overrightarrow{AB} &=& \overrightarrow{OB}-\overrightarrow{OA} \\[5pt] &=& \pmatrix{6\\4\\7}-\pmatrix{0\\0\\8} \\[5pt] &=& \pmatrix{6\\4\\-1} \end{array}$

Länge $\boldsymbol{\left| \overrightarrow{AB} \right|}$ berechnen

$\begin{array}[t]{rlll} \left| \overrightarrow{AB} \right| &=& \sqrt{6^2+4^2+(-1)^2} \\[5pt] &=& \sqrt{53} \end{array}$

Vektor $\boldsymbol{\overrightarrow{AC}}$ aufstellen

$\begin{array}[t]{rlll} \overrightarrow{AC} &=& \overrightarrow{OC}-\overrightarrow{OA} \\[5pt] &=& \pmatrix{-1\\6\\4}-\pmatrix{0\\0\\8} \\[5pt] &=& \pmatrix{-1\\6\\-4} \end{array}$

Länge $\boldsymbol{\left| \overrightarrow{AC} \right|}$ berechnen

$\begin{array}[t]{rlll} \left| \overrightarrow{AC} \right| &=& \sqrt{(-1)^2+6^2+(-4)^2} \\[5pt] &=& \sqrt{53} \end{array}$

Vektor $\boldsymbol{\overrightarrow{BC}}$ aufstellen

$\begin{array}[t]{rlll} \overrightarrow{BC} &=& \overrightarrow{OC}-\overrightarrow{OB} \\[5pt] &=& \pmatrix{-1\\6\\4}-\pmatrix{6\\4\\7} \\[5pt] &=& \pmatrix{-7\\2\\-3} \end{array}$

Länge $\boldsymbol{\left| \overrightarrow{BC} \right|}$ berechnen

$\begin{array}[t]{rlll} \left| \overrightarrow{BC} \right| &=& \sqrt{(-7)^2+2^2+(-3)^2} \\[5pt] &=& \sqrt{62} \end{array}$

Somit sind genau zwei Seiten des Dreiecks $ABC$ gleich lang. Das Dreieck ist also gleichschnenklig.

a2)

Normalenvektor $\boldsymbol{\overrightarrow{n}}$ der Ebene $\boldsymbol{E}$ bestimmen

$\begin{array}[t]{rlll} \overrightarrow{n} &=& \overrightarrow{AB} \times \overrightarrow{AC} \\[5pt] &=& \pmatrix{6\\4\\-1}\times\pmatrix{-1\\6\\-4} \\[5pt] &=& \pmatrix{4\cdot(-4)-(-1)\cdot6\\-1\cdot(-1)-6\cdot(-4)\\6\cdot6-4\cdot(-1)}\\[5pt] &=& \pmatrix{-10\\25\\40} \end{array}$

Mit $\frac{1}{5}\cdot\overrightarrow{n}$ als Normalenvektor von $E$ folgt:

$E: -2x_1+5x_2+8x_3=d$

Punkt $\boldsymbol{A}$ in $\boldsymbol{E}$ einsetzen

$\begin{array}[t]{rlll} -2\cdot0+5\cdot0+8\cdot8 &=& d \\[5pt] 64 &=& d \end{array}$

Somit folgt für eine mögliche Ebenengleichung von $E:$

$E: -2x_1+5x_2+8x_3=64$

a3)

Ein möglicher Normalenvektor $n_{x_1x_2}$ der $x_1x_2$ -Ebene ist:

$\overrightarrow{n}_{x_1x_2}=\pmatrix{0\\0\\1}$

Somit folgt für den Winkel $\varphi:$

$\begin{array}[t]{rlll} \cos(\varphi)&=& \dfrac{\left| n_E \circ n_{x_1x_2}\right|}{\left| n_E \right|\cdot\left| n_{x_1x_2} \right|} \\[5pt] \cos(\varphi) &=& \dfrac{\left| \pmatrix{-2\\5\\8} \circ \pmatrix{0\\0\\1} \right|}{\left| \pmatrix{-2\\5\\8} \right|\cdot\left| \pmatrix{0\\0\\1} \right|} &\mid\; \cos^{-1} \\[5pt] \varphi &=& \cos^{-1}\left(\dfrac{\left| (-2)\cdot0+5\cdot0+8\cdot1 \right|}{\sqrt{(-2)^2+5^2+8^2}\cdot\sqrt{0^2+0^2+1^2}}\right) \\[5pt] \varphi &\approx& 33,9^\circ \end{array}$

Somit beträgt der Neigungswinkel des Segeltuchs $\varphi=33,9^\circ.$

b1)

Vektor $\boldsymbol{\overrightarrow{AS_k}}$ aufstellen

$\begin{array}[t]{rlll} \overrightarrow{AS_k} &=& \overrightarrow{OS_k}-\overrightarrow{OA} \\[5pt] &=& \pmatrix{-4\\k\\10}-\pmatrix{0\\0\\8} \\[5pt] &=& \pmatrix{-4\\k\\2} \end{array}$

Länge $\boldsymbol{\left| \overrightarrow{AS_k} \right|}$ berechnen

$\begin{array}[t]{rlll} \left| \overrightarrow{AS_k} \right| &=& \sqrt{(-4)^2+k^2+2^2} \\[5pt] &=& \sqrt{20+k^2} \end{array}$

$k$ kann Werte von $[-5 ; 5]$ annehmen. Durch das quadrieren von $k$ reicht es, die positiven Werte zu betrachten. Damit folgt für die extremsten Werte von $k:$ $k=0$ und $k=5.$ Für den Abstand $\left| \overrightarrow{AS_0} \right|$ folgt:

$\begin{array}[t]{rlll} \left| \overrightarrow{AS_0} \right| &=& \sqrt{20+0^2} \\[5pt] &\approx& 4,47 \end{array}$

Für den Abstand $\left| \overrightarrow{AS_5} \right|$ folgt:

$\begin{array}[t]{rlll} \left| \overrightarrow{AS_5} \right| &=& \sqrt{20+5^2} \\[5pt] &\approx& 6,71 \end{array}$

Somit sind alle Abstände zwischen ca. $4,47\;\text{m}$ und $6,71\;\text{m}$ möglich.

b2)

Gerade $\boldsymbol{g}$ durch $\boldsymbol{B}$ und $\boldsymbol{S_k}$ aufstellen

$\begin{array}[t]{rlll} g:\overrightarrow{x} &=& \overrightarrow{OB}+t\cdot\overrightarrow{BS_k} \\[5pt] &=& \pmatrix{6\\4\\7}+t\cdot\left(\pmatrix{-4\\k\\10}-\pmatrix{6\\4\\7}\right) \\[5pt] &=& \pmatrix{6\\4\\7}+t\cdot\pmatrix{-10\\k-4\\3} \end{array}$

Weil die Koordinatenachse in der $x_1x_2$ -Ebene liegen soll, muss die $x_3$ -Koordinate der Gerade Null sein. Somit folgt für $t:$

$\begin{array}[t]{rlll} 0 &=& 7+3t &\mid\; -3t \\[5pt] -3t &=& 7 &\mid\; :(-3) \\[5pt] t &=& -\dfrac{7}{3} \end{array}$

Schnittpunkt mit der $\boldsymbol{x_2}$ -Achse berechnen

$\begin{array}[t]{rlll} x_1 &=& 0 \\[5pt] 6+\left(-\dfrac{7}{3}\right)\cdot(-10) &=& 0 \\[5pt] \dfrac{88}{3} &\neq& 0 \end{array}$

Da $x_1$ niemals null wird, gibt es keine Position, sodass der Schatten auf die $x_2$ -Achse fällt.

Schnittpunkt mit der $\boldsymbol{x_1}$ -Achse berechnen

$\begin{array}[t]{rlll} x_2 &=& 0 \\[5pt] 4+\left(-\dfrac{7}{3}\right)\cdot(k-4) \dfrac{7}{3}k &=& 0 &\mid\; +\dfrac{7}{3}k \\[5pt] \dfrac{40}{3} &=& \dfrac{7}{3}k &\mid\; :\dfrac{7}{3} \\[5pt] 5,71 &\approx& k \end{array}$

Da $k$ nur im Intervall $[-5;5]$ definiert ist, gibt es auch keinen Punkt auf der $x_1$ -Achse, auf den der Schatten fällt.
Somit gibt es keine Position des Scheinwerfers, so dass der Schatten des Punktes $B$ auf einer der Koordinatenachsen in der $x_1x_2$ -Ebene fällt.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?