Stochastik

Alle in deinen Lösungen verwendeten Zufallsgrößen müssen explizit eingeführt werden. Mache auch Angaben über die Verteilung der jeweiligen Zufallsgrößen.

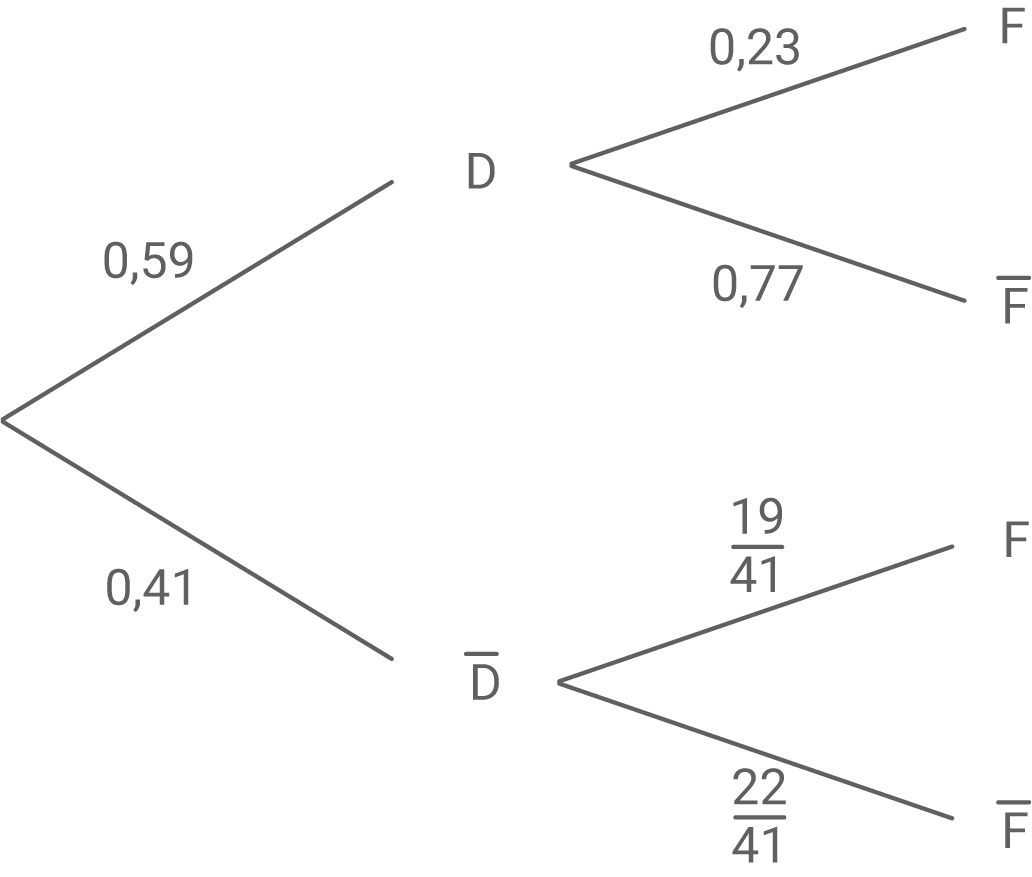
Unter den Versicherten eines Krankenversicherungsunternehmens haben $59\,\%$ Datenschutzbedenken $(D).$ Einige der Versicherten nutzen ein Fitnessarmband $(F).$ Von den Versicherten mit Datenschutzbedenken nutzen $23\,\%$ ein Fitnessarmband. $19\,\%$ aller Versicherten haben keine Datenschutzbedenken und nutzen ein Fitnessarmband.

a1)

Stelle den Sachverhalt in einem beschrifteten Baumdiagramm dar.

(3 P)

a2)

Unter allen Versicherten wird eine Person zufällig ausgewählt.
Bestimme die Wahrscheinlichkeit dafür, dass sie kein Fitnessarmband nutzt und Datenschutzbedenken hat.

(2 P)

a3)

Eine unter allen Versicherten zufällig ausgewählte Person nutzt ein Fitnessarmband. Bestimme die Wahrscheinlichkeit dafür, dass sie Datenschutzbedenken hat.

(3 P)

a4)

Die Zahl $0,23$ und der Term $0,59 \cdot 0,23+0,19$ geben Wahrscheinlichkeiten im Sachzusammenhang an. Es gilt $0,23 \neq 0,59 \cdot 0,23+0,19.$

Begründe damit, dass die Ereignisse „Eine unter allen Versicherten zufällig ausgewählte Person hat Datenschutzbedenken." und „Eine unter allen Versicherten zufällig ausgewählte Person nutzt ein Fitnessarmband." stochastisch abhängig sind.

(3 P)

$100$ Versicherte des Unternehmens werden zufällig ausgewählt.

a5)

Berechne die Wahrscheinlichkeit dafür, dass

höchstens 70 der ausgewählten Versicherten Datenschutzbedenken haben;
mehr als $50 \%$ der ausgewählten Versicherten Datenschutzbedenken haben;
mindestens 54 und höchstens 64 der ausgewählten Versicherten Datenschutzbedenken haben.

(6 P)

a6)

Ersetzt man die Platzhalter $a$ und $b$ in geeigneter Weise, so kann mit dem Term

$1-\displaystyle\sum_{k=51}^{100}\pmatrix{100 \\ k}\cdot 0,59^{k} \cdot a^{b}$

die Wahrscheinlichkeit eines Ereignisses im Sachzusammenhang berechnet werden. Gib an, wodurch die Platzhalter zu ersetzen sind, und beschreibe das zugehörige Ereignis.

(3 P)

Eine Händlerin bezieht Fitnessarmbänder von einer Firma. Die Armbänder werden in Kartons geliefert. Ein Karton enthält 36 Schachteln mit jeweils einem Armband. Insgesamt sind 12 weiße, 12 rote und 12 blaue Armbänder in einem Karton.

b1)

Aus einem vollständig gefüllten Karton werden zufällig und ohne Zurücklegen drei Schachteln entnommen.

Gib ein Ereignis mit der Wahrscheinlichkeit $\frac{12}{36} \cdot \frac{11}{35} \cdot \frac{10}{34}$ an.
Berechne die Wahrscheinlichkeit dafür, dass mindestens zwei der drei Schachteln ein weißes Armband enthalten.

(5 P)

b2)

Die Händlerin besitzt zwei Kartons der Firma. Einer dieser Kartons ist noch vollständig gefüllt, der andere Karton enthält nur noch 30 Schachteln, denn aus diesem sind 6 Schachteln mit weißen Armbändern verkauft worden.
Die Händlerin wählt einen der zwei Kartons zufällig aus, dann entnimmt sie aus diesem Karton zufällig eine Schachtel.
Bestimme die Wahrscheinlichkeit dafür, dass die Händlerin

kein weißes Armband erhält;
zufällig den vollständigen Karton ausgewählt hat, wenn sie ein weißes Armband erhält.

(7 P)

Ein Händler ist im Internet auf die Information gestoßen, dass $7\,\%$ der produzierten Fitnessarmbänder fehlerhaft seien. Der Händler vermutet, dass weniger Armbänder fehlerhaft sind. Um dies zu überprüfen, führt er einen Signifikanztest mit der Nullhypothese "Der Anteil der fehlerhaften Armbänder beträgt mindestens $7\,\%.$ " durch.

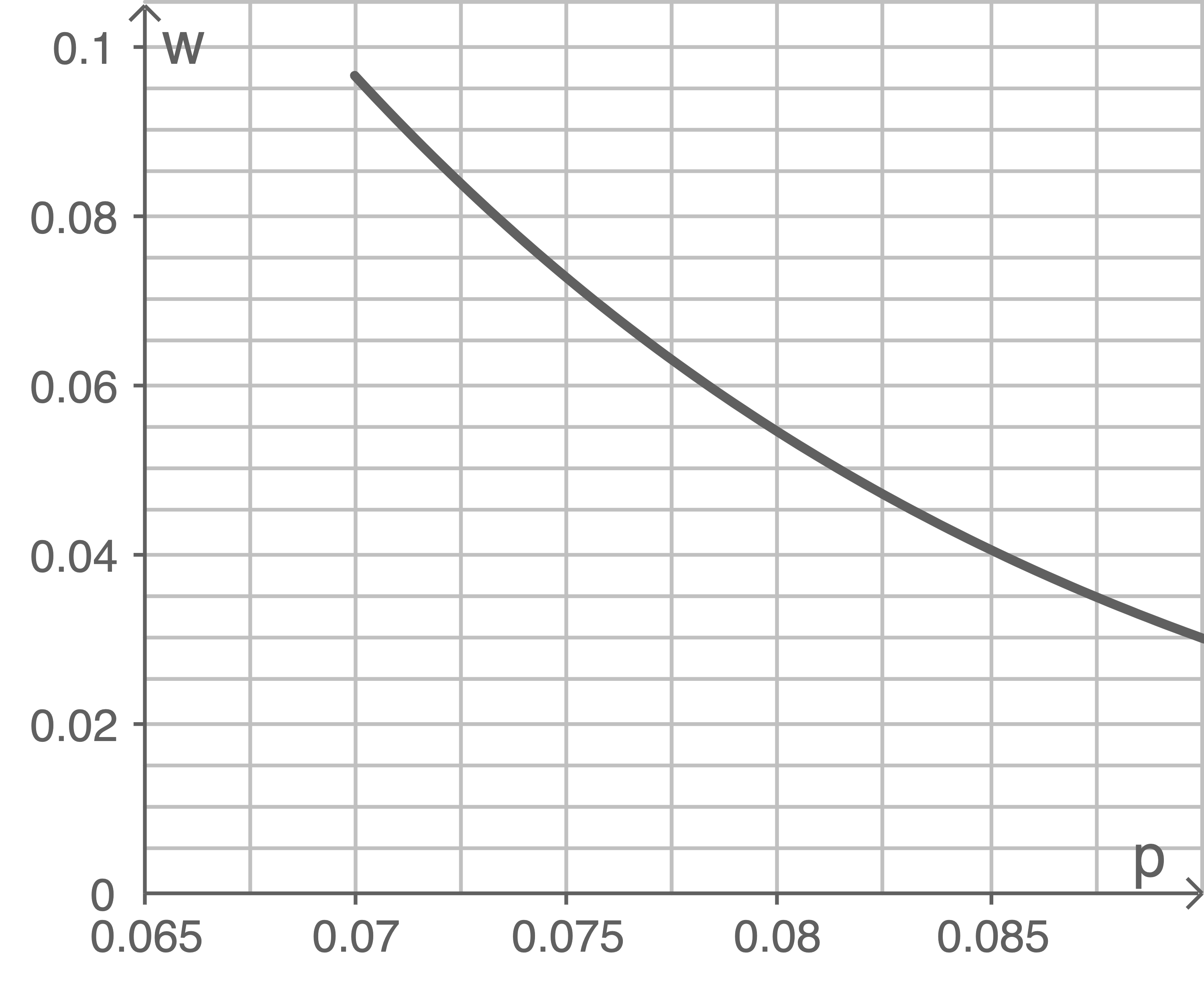
c1)

Beschreibe den Fehler erster Art im Sachzusammenhang.

(2 P)

Für diesen Test gilt:

(1)

Die Nullhypothese wird abgelehnt, wenn höchstens vier Armbänder fehlerhaft sind.

(2)

Der Abbildung kann die Wahrscheinlichkeit $w$ für den Fehler erster Art in Abhängigkeit vom Anteil $p$ fehlerhafter Armbänder entnommen werden.

Wahrscheinlichkeit - Schleswig-Holstein Abi 2022 (Stochastik)

c2)

Begründe anhand der Abbildung, dass das Signifikanzniveau nicht $9\,\%$ ist.

(2 P)

c3)

Ermittle den Umfang der für den Test verwendeten Stichprobe.

(4 P)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

a1)

$D:$ Eine Person hat Datenschutzbedenken.

$F:$ Eine Person nutzt ein Fitnessarmband.

Aus der Aufgabenstellung sind bekannt:

$P(D) = 0,59$

$P(\overline{D}) = 1-0,59 = 0,41$

$P_D(F) = 0,23$

$P_D(\overline{F}) = 1-0,23 = 0,77$

$P(\overline{D}\cap F) = 0,19$

Die Wahrscheinlichkeit $P_{\overline{D}}(F)$ lässt sich mit Hilfe der Formel für bedingte Wahrscheinlichkeiten berechnen:

$P_{\overline{D}}(F) = \dfrac{P(\overline{D}\cap F) }{P(\overline{D})} = \dfrac{0,19}{0,41} = \dfrac{19}{41}$

$P_{\overline{D}}(\overline{F}) =1- \dfrac{19}{41} = \dfrac{22}{41}$

Baumdiagramm - Schleswig-Holstein Abi 2022 (Stochastik)

a2)

$P(D \cap \overline{F})=0,59 \cdot 0,77$ $=0,4543 \approx 45\,\%$

a3)

$P_{F}(D)=\dfrac{P(D \cap F)}{P(F)}=\dfrac{0,59 \cdot 0,23}{0,59 \cdot 0,23+0,19}$ $=0,4166 \approx 42\,\%$

a4)

Da unter den Versicherten mit Datenschutzbedenken $23\, \%$ ein Fitnessarmband nutzen, folgt $P_{D}(F)=0,23.$
Der Term $0,59\cdot 0,23+0,19$ beschreibt den Anteil der Versicherten, die ein Fitnessarmband nutzen, unter allen Versicherten; also folgt $P(F)=0,59 \cdot 0,23+0,19.$
Daher ist $P_{D}(F) \neq P(F).$ Somit sind die Ereignisse $D$ und $F$ stochastisch abhängig.

a5)

$X:$ Anzahl der Versicherten mit Datenschutzbedenken.
$X$ ist binomialverteilt mit den Parametern $n=100$ und $p=0,59.$

Mit den Funktionen des Taschenrechners für die Binomialverteilung können die Wahrscheinlichkeiten berechnet werden:

$P(X\leq 70) \approx 0,9913 \approx 99\,\%$

$P(X \gt 50)=1-P(X \leq 50)$ $\approx 1-0,0428 = 0,9572 \approx 96\, \%$

$P(54 \leq X \leq 64)$ $= P(X \leq 64)-P(X \leq 53)$ $\approx 0,8687-0,1320=0,7367 \approx 74\, \%$

a6)

Ein Vergleich mit der Formel für die Wahrscheinlichkeiten der Binomialverteilung ergibt:

Für $a=1-0,59=0,41$ und $b=100-k$ ist das zugehörige Ereignis „Höchstens die Hälfte der ausgewählten Versicherten hat Datenschutzbedenken.".

b1)

Ereignis angeben

„Es werden drei weiße Armbänder gezogen.“

Wahrscheinlichkeit für mindestens zwei weiße Armbänder berechnen

$Y:$ Anzahl der gezogenen Schachteln mit weißen Armbändern. $Y$ ist hypergeometrisch verteilt.

$P(Y=2)+P(Y=3)$ $=\dfrac{\pmatrix{ 12 \\ 2} \cdot\pmatrix{ 24 \\ 1}}{\pmatrix{ 36 \\ 3}}+\dfrac{\pmatrix{ 12 \\ 3}\cdot\pmatrix{ 24 \\ 0}}{\pmatrix{ 36 \\ 3}}$ $=\dfrac{451}{1785} \approx 0,2527 \approx 25\,\%$

b2)

Wahrscheinlichkeit für kein weißes Armband bestimmen

Die Wahrscheinlichkeit für das Ereignis „Es wurde der vollst?ndige Karton ausgewählt und dann eine Schachtel, die kein weißes Armband enthält, entnommen." ist $\frac{1}{2} \cdot \frac{24}{36}=\frac{1}{3}$ .

Die Wahrscheinlichkeit für das Ereignis „Es wurde der unvollst?ndige Karton ausgewählt und dann eine Schachtel, die kein weißes Armband enthält, entnommen." beträgt $\frac{1}{2}, \frac{24}{30}=\frac{2}{5}$ .

Die Wahrscheinlichkeit dafür, keine Schachtel mit weißem Armband zu ziehen, beträgt daher $\frac{1}{3}+\frac{2}{5}=\frac{11}{15} \approx 73\,\%.$

Wahrscheinlichkeit für den vollständigen Karton bestimmen

$V$ : „Es wurde der vollstàndige Karton ausgewählt."

$W:$ „Es wird eine Schachtel mit einem weißen Armband entnommen."

$P_{W}(V)=\dfrac{P(V \cap W)}{P(W)}$ $=\dfrac{P(V \cap W)}{P(V \cap W)+P(\bar{V} \cap W)}$ $=\dfrac{\frac{1}{2} \cdot \frac{12}{36}}{\frac{1}{2} \cdot \frac{12}{36}+\frac{1}{2} \cdot \frac{6}{30}}=\dfrac{5}{8} \approx 63\,\%$

c1)

Der Fehler 1. Art liegt vor, wenn die Nullhypothese verworfen wird, also von einem Anteil fehlerhafter Armbänder von unter $7\,\%$ ausgegangen wird, obwohl die Nullhypothese wahr ist, d.h. die Wahrscheinlichkeit für fehlerhafte Armbänder größer oder gleich $7\,\%$ ist.

c2)

Aus der Abbildung kann für den Fehler 1 . Art für $p=0,07$ eine Wahrscheinlichkeit von etwa $9,7\,\%$ entnommen werden.

Da die Wahrscheinlichkeit des Fehlers 1 . Art immer kleiner oder gleich dem Signifikanzniveau ist, ist $9\,\%$ als Signifikanzniveau nicht möglich.

c3)

Die Zufallsgröße $X_{n}$ beschreibt die Anzahl der fehlerhaften Armbänder und ist binomialverteilt mit den Parametern $n$ und $p=0,07.$

Aus der Abbildung ergibt sich $P\left(X_{n} \leq 4\right)= w(0,07) \approx 0,097.$

Systematisches Probieren führt auf:

$n$	$P(X_n\leq 4)$
$112$	$0,1007$
$113$	$0,0966$

Daher beträgt der Stichprobenumfang $n=113.$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?