Analysis 1
Die Funktion  mit
mit
 ;
; ![\(x\in [0;7]\)](https://www.schullv.de/resources/formulas/7cc7589950b09fa98889c9c16689797ba69b6392788ab5ae783da07fab663f61_light.svg)
beschreibt näherungsweise das Höhenprofil eines Straßenradrennens. Dabei gibt die in horizontaler Richtung zurückgelegte Strecke in Kilometern und
die in horizontaler Richtung zurückgelegte Strecke in Kilometern und  die Höhe in Metern an.
die Höhe in Metern an.
 werde die Querschnittsfläche
werde die Querschnittsfläche  eines Fahrradreifens
eines Fahrradreifens  durch die Funktionen
durch die Funktionen  und
und  beschrieben. Dabei beschreibt
beschrieben. Dabei beschreibt  die Metallfelge und
die Metallfelge und  den Gummimantel. Eine Längeneinheit entspricht einem Zentimeter.
den Gummimantel. Eine Längeneinheit entspricht einem Zentimeter.
Die folgenden Abbildungen zeigen die Graphen von und
und  sowie von
sowie von  und
und  zwischen ihren jeweiligen Schnittstellen.
zwischen ihren jeweiligen Schnittstellen.

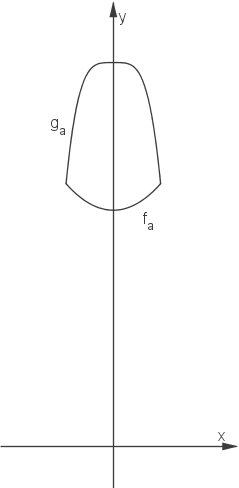
beschreibt näherungsweise das Höhenprofil eines Straßenradrennens. Dabei gibt
a)
- Ermittle diejenigen Stellen des Profils, an denen dieselbe Höhe wie zu Beginn des Rennens erreicht wird.
- Berechne den maximalen Höhenunterschied des Profils.
- Bestimme die größte Steigung der Straße und gib diese in Prozent an.
- Skizziere den Graphen von
in einem geeigneten Koordinatensystem.
(18P)
Für jedes |
|
|
|
|
Die folgenden Abbildungen zeigen die Graphen von


b)
- Berechne die maximale Breite des Reifens
.
- Bestimme den Winkel, unter dem Metallfelge und Gummimantel beim Reifen
aufeinander treffen.
- Bestimme den Flächeninhalt von
. Begründe, warum der Flächeninhalt von
unabhängig von
ist.
(13P)
c) Ein Modell des Reifens  entsteht durch Rotation von
entsteht durch Rotation von  um die
um die  -Achse.
-Achse.
- Berechne das Volumen des Reifens
.
- Der Inhalt der Querschnittsfläche
ist unabhängig von
. Erkläre, warum das Volumen des Reifens
dennoch von
abhängig ist.
(5P)
d) Gegeben ist der Punkt  auf dem Graphen von
auf dem Graphen von  . Es soll derjenige Punkt
. Es soll derjenige Punkt  auf dem Graphen von
auf dem Graphen von  im Intervall
im Intervall ![\([-0,8; 0,8]\)](https://www.schullv.de/resources/formulas/924d2435d03551c69e4c40506705f183c01bdc3d8fdb43548752d2b781427f2e_light.svg) bestimmt werden, für den die Länge der Strecke
bestimmt werden, für den die Länge der Strecke  maximal ist.
maximal ist.
Gib einen Ansatz an und beschreibe das weitere Vorgehen.
Gib einen Ansatz an und beschreibe das weitere Vorgehen.
(4P)
Hier ist die Funktion  durch eine Funktionsgleichung gegeben.
durch eine Funktionsgleichung gegeben.
![\(\begin{array}[t]{rll}
h(x) &=& 2x^3-18x^2+30x &;& x \in [0;7]\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/e210b2c939dba6592d4b34c50e44315ed9c5555b8645248af1a49ac809bd5a46_light.svg) Der Graph der Funktion soll das Höhenprofil eines Radrennens zeigen.
Der Graph der Funktion soll das Höhenprofil eines Radrennens zeigen.  ist die Entfernung vom Startpunkt. Der Funktionswert
ist die Entfernung vom Startpunkt. Der Funktionswert  gibt die Höhe dieser Stelle an.
gibt die Höhe dieser Stelle an.
a)  Bestimme Stellen mit gleicher Höhe wie der Startpunkt
Hier sollst du diejenigen Stellen im Profil finden, die die selbe Höhe haben wie der Startpunkt. Die Höhe ist der Funktionswert
Bestimme Stellen mit gleicher Höhe wie der Startpunkt
Hier sollst du diejenigen Stellen im Profil finden, die die selbe Höhe haben wie der Startpunkt. Die Höhe ist der Funktionswert  . Du bestimmst zunächst den Funktionswert am Startpunkt
. Du bestimmst zunächst den Funktionswert am Startpunkt  und setzt dann den Funktionsterm mit diesem Wert gleich. Löse anschließend die Gleichung nach
und setzt dann den Funktionsterm mit diesem Wert gleich. Löse anschließend die Gleichung nach  auf.
auf.
![\(\begin{array}[t]{rll}
h(x=0)&=&2\cdot 0 -18\cdot 0 +30 \cdot 0 \\[5pt]
&=&0\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/20c677d7ccbab18a4bcbc3bc9df7f5ff5c15c23e3da00ada24ad19aef5d16d1e_light.svg) Die Höhe zu Beginn des Rennens liegt bei
Die Höhe zu Beginn des Rennens liegt bei  m.
m.
![\(\begin{array}[t]{rll}
h(x=0)&=&h(x)\\[5pt]
0&=&2x^3-18x^2+30x \\[5pt]
0&=&x\cdot(2\cdot x^2-18\cdot x +30) \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/91f9a2482066c3dd58dcbec848c7261bb5874519e611d31d1329641335f0e8be_light.svg) Der Satz vom Nullprodukt besagt, dass ein Produkt Null wird, wenn ein Faktor Null wird. Daher betrachtest du im folgenden nur den Teil in den Klammern:
Der Satz vom Nullprodukt besagt, dass ein Produkt Null wird, wenn ein Faktor Null wird. Daher betrachtest du im folgenden nur den Teil in den Klammern:
![\(\begin{array}[t]{rll}
0&=&2x^2-18x+30 &\quad&\scriptsize\mid\; :2\\[5pt]
0&=&x^2-9x+15\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/4a652ac6b77e9e8d2210f5062ad5c599af53129cba4cca7bd8fd429856929315_light.svg) Mit der
Mit der  -Formel oder Mitternachtsformel erhältst du zwei Lösungen für die Gleichung:
-Formel oder Mitternachtsformel erhältst du zwei Lösungen für die Gleichung:
 Lösungsweg A:
Lösungsweg A:  -Formel
Für Gleichungen der Form:
-Formel
Für Gleichungen der Form:
![\(\begin{array}[t]{rll}
0&=& x^2+px+q\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/fd0b1fcf99b12a44ac4d485d808ce46a954fb77bf81dc508c7cb10f517426878_light.svg) liefert die
liefert die  -Formel zwei Lösungen:
-Formel zwei Lösungen:

![\(\begin{array}[t]{rll}
x_{1/2}&=&-\dfrac{-9}{2}\pm\sqrt{\left(\dfrac{-9}{2}\right)^2-15} \\[5pt]
&=&\dfrac{9}{2}\pm\sqrt{\dfrac{81-60}{4}}\\[5pt]
&=&\dfrac{9}{2}\pm\dfrac{\sqrt{21}}{2}\\[5pt]
x_1&=&\dfrac{9}{2}+\dfrac{\sqrt{21}}{2}\approx 6,8\\[5pt]
x_2&=&\dfrac{9}{2}-\dfrac{\sqrt{21}}{2}\approx 2,2\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/27686a985dcf503dc162aa8aa4fa6a1fc3d065c7f42bb5a5366de8d0029fbe11_light.svg)
 Lösungsweg B: Mitternachtsformel
Für Gleichungen der Form:
Lösungsweg B: Mitternachtsformel
Für Gleichungen der Form:
![\(\begin{array}[t]{rll}
0&=&a x^2+bx+c\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/f627066c2de85e096d5d77ceb67aa9d286583fdbb329c875c94b2c9356890d27_light.svg) liefert die Mitternachtsformel zwei Lösungen:
liefert die Mitternachtsformel zwei Lösungen:

![\(\begin{array}[t]{rll}
x_{1/2}&=&\dfrac{+9\pm\sqrt{9^2-4\cdot15}}{2} \\[5pt]
&=&\dfrac{9\pm\sqrt{81-60}}{2}\\[5pt]
&=&\dfrac{9\pm\sqrt{21}}{2}\\[5pt]
x_1&=&\dfrac{9}{2}+\dfrac{\sqrt{21}}{2}\approx 6,8\\[5pt]
x_2&=&\dfrac{9}{2}-\dfrac{\sqrt{21}}{2}\approx 2,2\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/c5f8bbbf2cf4e9dd372034ce59f8b859dacf0e921298abf2300f51dc3795f4a8_light.svg) Nach ungefähr
Nach ungefähr  km und nach ungefähr
km und nach ungefähr  km ist das Rennen an Stellen gleicher Höhe wie zu Beginn des Rennens.
km ist das Rennen an Stellen gleicher Höhe wie zu Beginn des Rennens.
 Berechne den maximalen Höhenunterschied des Profils
Um den maximalen Höhenunterschied des Profils zu berechnen, musst du die Differenz des höchsten und des niedrigsten Funktionswertes bestimmen. Die Punkte höchster und niedrigster Höhe sind die Hoch- und Tiefpunkte des Graphen der Funktion.
Eine Funktion
Berechne den maximalen Höhenunterschied des Profils
Um den maximalen Höhenunterschied des Profils zu berechnen, musst du die Differenz des höchsten und des niedrigsten Funktionswertes bestimmen. Die Punkte höchster und niedrigster Höhe sind die Hoch- und Tiefpunkte des Graphen der Funktion.
Eine Funktion  hat an der Stelle
hat an der Stelle  eine Extremstelle, sofern die folgenden Bedingungen erfüllt sind:
eine Extremstelle, sofern die folgenden Bedingungen erfüllt sind:
 liegt eine Maximalstelle, für
liegt eine Maximalstelle, für  eine Minimalstelle vor.
1. Schritt: Ableitungen bilden
Die Ableitung der Funktion bildest du mit der Potenzregel.
eine Minimalstelle vor.
1. Schritt: Ableitungen bilden
Die Ableitung der Funktion bildest du mit der Potenzregel.
![\(\begin{array}[t]{rll}
h(x)&=&2x^3-18x^2+30x\\[5pt]
h‘(x)&=&6x^2-36x+30\\[5pt]
h‘‘(x)&=&12x-36\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/2bbd076ffa161b54d31334ccba4d85528d913ae33f93883f5120c5a222232cb3_light.svg) 2. Schritt: Notwendige Bedingung überprüfen
2. Schritt: Notwendige Bedingung überprüfen
![\(\begin{array}[t]{rll}
h‘(x)&=&0\\[5pt]
6x^2 - 36x +30 &=& 0 &\quad&\scriptsize\mid\; :6\\[5pt]
x^2-6x+5&=&0\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/16a300904cd110379bd8ca36d18a1b7b266131eb022f679cfb3f34718d2f8cee_light.svg) Mit der
Mit der  -Formel oder der Mitternachtsformel erhältst du zwei Lösungen für die Gleichung:
-Formel oder der Mitternachtsformel erhältst du zwei Lösungen für die Gleichung:
 Lösungsweg A:
Lösungsweg A:  -Formel
-Formel
![\(\begin{array}[t]{rll}
x_{1/2}&=&-\dfrac{p}{2}\pm\sqrt{\left(\dfrac{p}{2}\right)^2-q} \\[5pt]
&=&3\pm\sqrt{9-5}\\[5pt]
&=&3\pm2\\[5pt]
x_1&=&1\\[5pt]
x_2&=&5\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/00a2075ca64a77a01f8d40417a6c03c20e3e99d310a3820c2927bbb1ecf2a549_light.svg)
 Lösungsweg B: Mitternachtsformel
Lösungsweg B: Mitternachtsformel
![\(\begin{array}[t]{rll}
x_{1/2}&=&\dfrac{-b\pm\sqrt{b^2-4ac}}{2a} \\[5pt]
&=&\dfrac{6\pm\sqrt{36-20}}{2}\\[5pt]
&=&\dfrac{6\pm4}{2}\\[5pt]
x_1&=&1\\[5pt]
x_2&=&5\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/28cfa8bf738c642d33bc8301ae870c6cb25b3c5df6946ab0d4088713f23df7bd_light.svg) Die Stellen der Hoch- und Tiefpunkte sind
Die Stellen der Hoch- und Tiefpunkte sind  und
und  .
3. Schritt: Hinreichende Bedingung überprüfen
Überprüfe, ob es sich um Hoch- oder Tiefpunkte handelt.
.
3. Schritt: Hinreichende Bedingung überprüfen
Überprüfe, ob es sich um Hoch- oder Tiefpunkte handelt.
![\(\begin{array}[t]{rll}
h‘‘(1)&=&12\cdot 1 -36\\[5pt]
&=&-24<0\\[5pt]
h‘‘(5)&=&12\cdot 5 - 36 \\[5pt]
&=&24>0\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/057735d34c5d8ff8a9e6827f11d54f65a8b9bedef7376059481d18872d19147c_light.svg) An der Stelle
An der Stelle  liegt ein Hochpunkt, an der Stelle
liegt ein Hochpunkt, an der Stelle  liegt ein Tiefpunkt.
4. Schritt: Differenz zwischen Hoch- und Tiefpunkt bestimmen
Um den Höhenunterschied
liegt ein Tiefpunkt.
4. Schritt: Differenz zwischen Hoch- und Tiefpunkt bestimmen
Um den Höhenunterschied  zu erhalten, setzt du die Extremstellen in den Funktionsterm ein und bildest die Differenz.
zu erhalten, setzt du die Extremstellen in den Funktionsterm ein und bildest die Differenz.
![\(\begin{array}[t]{rll}
h(x=1)&=&2\cdot1^3-18\cdot 1^2 +30\cdot 1\\[5pt]
&=&2-18+30\\[5pt]
&=&14\\[5pt]
h(x=5)&=&2\cdot5^3-18\cdot 5^2 +30\cdot 5\\[5pt]
&=&2\cdot 125 -18\cdot 25 +150\\[5pt]
&=&250-450+150\\[5pt]
&=&-50\\[5pt]
\Delta H &=& 14- (-50)\\[5pt]
&=&64\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/458db8dbb49a797864b1b0cd383128593144d3972bb9bb4e8b5770335ac33dd7_light.svg) Der maximale Höhenunterschied beträgt
Der maximale Höhenunterschied beträgt  m.
m.
 Bestimme die größte Steigung
Die Steigung wird immer durch den Funktionswert der ersten Ableitung
Bestimme die größte Steigung
Die Steigung wird immer durch den Funktionswert der ersten Ableitung  angegeben. Um die größte Steigung zu bestimmen, musst du das Maximum der ersten Ableitung
angegeben. Um die größte Steigung zu bestimmen, musst du das Maximum der ersten Ableitung  finden. Ein Maximum erhältst du, wenn zwei Bedingungen erfüllt sind:
finden. Ein Maximum erhältst du, wenn zwei Bedingungen erfüllt sind:
![\(\begin{array}[t]{rll}
h(x)&=&2x^3-18x^2+30x\\[5pt]
h‘(x)&=&6x^2-36x+30\\[5pt]
h‘‘(x)&=&12x-36\\[5pt]
h‘‘‘(x)&=&12\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/555a961078e71de2af51e95d7be53a7fda94164d07fb588f8ea622d73c086a4f_light.svg) Du siehst, dass die hinreichende Bedingung nie erfüllt wird. Das heißt, es gibt keinen Hochpunkt der Steigung. Die Steigung muss deshalb am Rand des Definitionsbereichs maximal sein.
2. Schritt: Steigung am Rand des Definitionsbereichs bestimmen
Die Funktion ist für
Du siehst, dass die hinreichende Bedingung nie erfüllt wird. Das heißt, es gibt keinen Hochpunkt der Steigung. Die Steigung muss deshalb am Rand des Definitionsbereichs maximal sein.
2. Schritt: Steigung am Rand des Definitionsbereichs bestimmen
Die Funktion ist für ![\(x\in[0;7]\)](https://www.schullv.de/resources/formulas/3a55bf8ad68fcd6ab815bc94e2529f11f0f9f1f76206aa0acb810f7b98776a8d_light.svg) definiert. Du wertest die Steigung, also die erste Ableitung, an den Stellen
definiert. Du wertest die Steigung, also die erste Ableitung, an den Stellen  und
und  aus.
aus.
![\(\begin{array}[t]{rll}
h‘(x=0)&=&6\cdot 0^2 - 36\cdot 0 +30\\[5pt]
&=&30\\[5pt]
h‘(x=7)&=&6\cdot 7^2 -36\cdot 7 +30 \\[5pt]
&=&294-252+30\\[5pt]
&=&72\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/9fd75a730428fdf9d8a672a63d30d1167878096765628d8b7ac082e3dfc7b7d2_light.svg) Die Steigung ist somit an der Stelle
Die Steigung ist somit an der Stelle  im Rennen maximal. Sie beträgt
im Rennen maximal. Sie beträgt  3. Schritt: Steigung in Prozent angeben
Abschließend sollst du die Steigung in Prozent angeben. Die mittlere Änderungsrate einer Funktion ist definiert als:
3. Schritt: Steigung in Prozent angeben
Abschließend sollst du die Steigung in Prozent angeben. Die mittlere Änderungsrate einer Funktion ist definiert als:
![\(\begin{array}[t]{rll}
h‘(x)=\dfrac{\Delta h(x)}{\Delta x}
\end{array}\)](https://www.schullv.de/resources/formulas/b58ebe24d1f264d5e9a0cc370941cae7ba10f9c4a0a4bf584013d936757bc823_light.svg) Das heißt, der Funktionswert der Ableitung ist die Strecke, die man in Richtung der positiven
Das heißt, der Funktionswert der Ableitung ist die Strecke, die man in Richtung der positiven  -Achse gehen muss, wenn man um eine Einheit in Richtung der positiven
-Achse gehen muss, wenn man um eine Einheit in Richtung der positiven  -Achse geht. Um die Steigung in Prozent zu erhalten, musst du die Steigung mit 100% multiplizieren. Beachte jetzt, dass die Strecke
-Achse geht. Um die Steigung in Prozent zu erhalten, musst du die Steigung mit 100% multiplizieren. Beachte jetzt, dass die Strecke  in km und die Höhe
in km und die Höhe  in Metern gegeben ist. Die Steigung ist deshalb:
in Metern gegeben ist. Die Steigung ist deshalb:
![\(\begin{array}[t]{rll}
S_{\%}&=&100\%\cdot 72\cdot\dfrac{1\,\text{m}}{1000\,\text{m}}\\[5pt]
&=&7,2\%
\end{array}\)](https://www.schullv.de/resources/formulas/f42ecc38897ea75bd2a70922606566ab4dcc59aaf4336531447662f9478ad432_light.svg) Die maximale Steigung ist am Zieleinlauf
Die maximale Steigung ist am Zieleinlauf  . Sie beträgt
. Sie beträgt  %.
%.
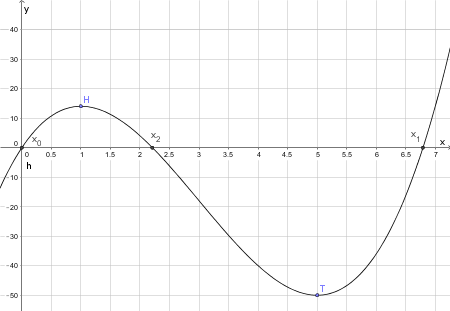
 Skizziere den Graphen von
Skizziere den Graphen von  Jetzt sollst du den Graphen von
Jetzt sollst du den Graphen von  skizzieren. Nutze aus, dass du bereits Hochpunkt
skizzieren. Nutze aus, dass du bereits Hochpunkt  und Tiefpunkt
und Tiefpunkt  des Graphen berechnet hast. Zudem hast du Nullstellen bei
des Graphen berechnet hast. Zudem hast du Nullstellen bei  ,
,  und
und  .
.
- notwendige Bedingung:
- hinreichende Bedingung:
- Notwendige Bedingung:
- Hinreichende Bedingung:

b)  Bestimme die maximale Breite des Reifens
Die maximale Breite ist, wie man in der gegebenen Skizze sieht, durch den Abstand der Schnittstellen gegeben. Dafür setzt du die Funktionsterme der Funktionen
Bestimme die maximale Breite des Reifens
Die maximale Breite ist, wie man in der gegebenen Skizze sieht, durch den Abstand der Schnittstellen gegeben. Dafür setzt du die Funktionsterme der Funktionen  und
und  gleich und löst die Gleichung nach
gleich und löst die Gleichung nach  auf.
auf.
![\(\begin{array}[t]{rll}
f_0(x)&=&g_0(x) \\[5pt]
0,7x^2&=&-5x^4+2,496 &\quad&\scriptsize\mid\; -0,7x^2\\[5pt]
0&=&-5x^4-0,7x^2+2,496 \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/b259de378f46dd542813ae0ca3fa901c9a8397d037a30938152e0ff17bf94277_light.svg) Mit einer Substitution
Mit einer Substitution  erhältst du mit der
erhältst du mit der  -Formel zwei Lösungen für
-Formel zwei Lösungen für  :
:
![\(\begin{array}[t]{rll}
0&=&-5x^4-0,7x^2+2,496 &\;& \text{sub}:x^2=u \\[5pt]
0&=&-5u^2-0,7u+2,496 &\quad&\scriptsize\mid\; :(-5)\\[5pt]
0&=&u^2+0,14u-0,4992 \\[5pt]
u_{1/2}&=&-\dfrac{0,14}{2}\pm\sqrt{\left(\dfrac{0,14}{2}\right)^2+0,4992}\\[5pt]
&=&-0,07\pm\sqrt{0,0049+0,4992}\\[5pt]
&=&-0,07\pm\sqrt{0,5041}\\[5pt]
u_1&=&-0,07+0,71\\[5pt]
&=&0,64\\[5pt]
u_2&=&-0,07-0,71\\[5pt]
&=&-0,78\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/a6bc87ba56c1caaecbf4f51f13a1e7bd03ff26d0060e60dc9912615fedd9e98f_light.svg) Eine Resubstitution liefert dir die entsprechenden
Eine Resubstitution liefert dir die entsprechenden  -Werte:
-Werte:
![\(\begin{array}[t]{rll}
u_1&=&0,64 &\;& \text{resub}:x=\pm\sqrt{u} \\[5pt]
x_1&=&0,8\\[5pt]
x_2&=&-0,8\\[5pt]
u_2&=&-0,78&\;& \text{resub}:x=\pm\sqrt{u} \\[5pt]
x_{3/4}&=&\pm\sqrt{-0,78} &\;&\text{keine reelle Lösung} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/baaf627b6d79152b66b1456277555163c7ff30e0b7442ddc56719fee5d2d88de_light.svg) Du erhältst zwei reelle Lösungen
Du erhältst zwei reelle Lösungen  und
und  . Der Abstand der Stellen ist die Reifenbreite
. Der Abstand der Stellen ist die Reifenbreite  . Eine Längeneinheit entspricht einem Zentimeter. Der Reifen ist an der breitesten Stelle
. Eine Längeneinheit entspricht einem Zentimeter. Der Reifen ist an der breitesten Stelle  cm breit.
cm breit.
 Bestimme die Größe des Winkels, unter dem Metallfelge und Gummitmantel beim Reifen
Bestimme die Größe des Winkels, unter dem Metallfelge und Gummitmantel beim Reifen  aufeinander treffen
Um die Größe des Winkels, der von Metallfelge und Gummimantel eingeschlossen wird, zu bestimmen, musst du zunächst die Steigung der beiden Funktionen an dieser Stelle bestimmen. Die Steigung an der jeweiligen Stelle ist durch den Wert der Ableitung an dieser Stelle gegeben. Die Größe des Winkels einer Kurve zur
aufeinander treffen
Um die Größe des Winkels, der von Metallfelge und Gummimantel eingeschlossen wird, zu bestimmen, musst du zunächst die Steigung der beiden Funktionen an dieser Stelle bestimmen. Die Steigung an der jeweiligen Stelle ist durch den Wert der Ableitung an dieser Stelle gegeben. Die Größe des Winkels einer Kurve zur  -Achse ist gegeben durch:
-Achse ist gegeben durch:
 Wobei
Wobei  die Steigung an der Stelle ist.
die Steigung an der Stelle ist.
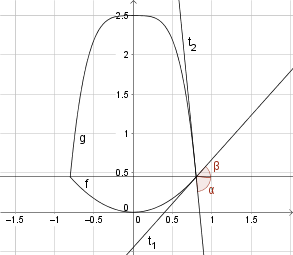 In der Skizze siehst du die beiden Winkel, die zusammen den gesuchten Winkel ergeben. Der Winkel
In der Skizze siehst du die beiden Winkel, die zusammen den gesuchten Winkel ergeben. Der Winkel  ist negativ, weil er nach unten zeigt. Um die Größe des Winkels zwischen zwei Kurven zu erhalten, musst du die Differenz der Winkelgrößen bilden:
ist negativ, weil er nach unten zeigt. Um die Größe des Winkels zwischen zwei Kurven zu erhalten, musst du die Differenz der Winkelgrößen bilden:
 1. Schritt: Steigung bestimmen
1. Schritt: Steigung bestimmen
![\(\begin{array}[t]{rll}
f_0(x)&=&0,7x^2 \\[5pt]
f‘_0(x)&=&1,4x\\[5pt]
f‘_0(0,8)&=&1,12\\[5pt]
m_1&=&1,12\\[5pt]
\\[5pt]
g_0(x)&=&-5x^4+2,496\\[5pt]
g‘_0(x)&=&-20x^3\\[5pt]
g‘_0(0,8)&=&-20\cdot (0,8)^3\\[5pt]
g‘_0(0,8)&=&-10,24\\[5pt]
m_2&=&-10,24\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/8009af93e8a61e6b201d465f010cd26cb60954179011f8220295f50330cc2283_light.svg) 2. Schritt: Schnittwinkel bestimmen
2. Schritt: Schnittwinkel bestimmen
![\(\begin{array}[t]{rll}
\gamma &=& \left|\tan^{-1}(1,12)-\tan^{-1}(-10,24)\right| \\[5pt]
&\approx&\left|48,24^{\circ}-(-84,42^{\circ})\right|\\[5pt]
&=&132,66^{\circ}\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/012306f8cc5396e1508476d8ed35fa2530a11819a98f93d79f5565879cba5e74_light.svg) Der Schnittwinkel, unter dem Metallfelge und Gummimantel aufeinander treffen, ist in etwa
Der Schnittwinkel, unter dem Metallfelge und Gummimantel aufeinander treffen, ist in etwa  groß.
groß.
 Bestimme den Flächeninhalt von
Bestimme den Flächeninhalt von 
 ist die Querschnittsfläche des Reifens. Die Querschnittsfläche ist die Fläche zwischen den Graphen der zwei Funktionen
ist die Querschnittsfläche des Reifens. Die Querschnittsfläche ist die Fläche zwischen den Graphen der zwei Funktionen  und
und  . Der Flächeninhalt zwischen zwei Kurven ist:
. Der Flächeninhalt zwischen zwei Kurven ist:
 Die Integrationsgrenzen sind die Schnittstellen der beiden Funktionen
Die Integrationsgrenzen sind die Schnittstellen der beiden Funktionen  und
und  .
Das Integral kannst du mit deinem Taschenrechner bestimmen:
.
Das Integral kannst du mit deinem Taschenrechner bestimmen:
![\(\begin{array}[t]{rll}
Q_0&=& \left|\displaystyle\int_{-0,8}^{0,8}f_0(x)-g_0(x)\;\mathrm dx\right|\\[5pt]
&=&\left|\displaystyle\int_{-0,8}^{0,8}0,7x^2+5x^4-2,496\;\mathrm dx\right|\\[5pt]
&\approx&\left|-3,1\right|\\[5pt]
&=&3,1\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/eb276fc84395ca3fea0189e45a83d72220a22f9b6f4d1d10b5b2a5a72f7e97d8_light.svg) Der Flächeninhalt beträgt in etwa
Der Flächeninhalt beträgt in etwa  Begünde, warum der Flächeninhalt
Begünde, warum der Flächeninhalt  unabhängig von
unabhängig von  ist
Der Parameter
ist
Der Parameter  verschiebt die Graphen und damit die Fläche in Richtung der positiven
verschiebt die Graphen und damit die Fläche in Richtung der positiven  -Achse. Da die beiden Funktionen um die gleiche Konstante
-Achse. Da die beiden Funktionen um die gleiche Konstante  verschoben werden, ändert sich am Flächeninhalt nichts. Das kannst du auch zeigen, indem du dir das Integral anschaust:
verschoben werden, ändert sich am Flächeninhalt nichts. Das kannst du auch zeigen, indem du dir das Integral anschaust:
![\(\begin{array}[t]{rll}
Q_a&=& \left|\displaystyle\int_{-0,8}^{0,8}f_a(x)-g_a(x)\;\mathrm dx\right|\\[5pt]
&=&\left|\displaystyle\int_{-0,8}^{0,8}0,7x^2+a+5x^4-a-2,496\;\mathrm dx\right|\\[5pt]
&=&\left|\displaystyle\int_{-0,8}^{0,8}0,7x^2+5x^4-2,496\;\mathrm dx\right|\\[5pt]
&=&3,1\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/32d927984e82f74df034ee76d7cbf210d6ea558c4f103196032dd2733009cee5_light.svg) Wie du siehst, fällt der Parameter
Wie du siehst, fällt der Parameter  aus dem Integral. Der Flächeninhalt ist also unabhängig von
aus dem Integral. Der Flächeninhalt ist also unabhängig von  .
.

c)  Bestimme das Volumen des Reifens
Bestimme das Volumen des Reifens  Hier sollst du das Volumen des Reifens
Hier sollst du das Volumen des Reifens  bestimmen. Der Reifen entsteht durch die Rotation der Fläche
bestimmen. Der Reifen entsteht durch die Rotation der Fläche  um die
um die  -Achse. Das Volumen eines Rotationskörpers ist:
-Achse. Das Volumen eines Rotationskörpers ist:
 Die Integrationsgrenzen sind die Schnittstellen der Funktionen
Die Integrationsgrenzen sind die Schnittstellen der Funktionen  und
und  .
.
![\(\begin{array}[t]{rll}
V_{30}&=&\pi\cdot\left|\displaystyle\int_{-0,8}^{0,8}(f_{30}(x))^2-(g_{30}(x))^2\;\mathrm dx\right|\\[5pt]
&=&\pi\cdot \left|\displaystyle\int_{-0,8}^{0,8}(0,7x^2+30)^2-(-5x^4+32,496)^2\;\mathrm dx\right|\\[5pt]
&\approx&\pi\cdot 193,3\\[5pt]
&\approx&607,4\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/7d1403d1a1523f5bea8f6191b39e0dfd5c80ee25e24f0838f3cb7fe932a99ed3_light.svg) Das Volumen des Reifens
Das Volumen des Reifens  beträgt in etwa
beträgt in etwa  .
.
 Erkläre warum das Volumen des Reifens nicht unabhängig von
Erkläre warum das Volumen des Reifens nicht unabhängig von  ist
Hier steht im Integral nicht die Differenz der Funktionen
ist
Hier steht im Integral nicht die Differenz der Funktionen  und
und  , sondern die Differenz der Quadrate der Funktionen. Dadurch bleiben Terme, die abhängig von
, sondern die Differenz der Quadrate der Funktionen. Dadurch bleiben Terme, die abhängig von  sind, im Integral stehen. Das kannst du auch mathematisch zeigen:
sind, im Integral stehen. Das kannst du auch mathematisch zeigen:
![\(\begin{array}[t]{rll}
V_a&=& \pi\cdot\left|\displaystyle\int_{-0,8}^{0,8}(f_a(x))^2-(g_a(x))^2\;\mathrm dx\right| \\[5pt]
&=& \pi\cdot\left|\displaystyle\int_{-0,8}^{0,8}(f_0(x)+a)^2-(g_0(x)+a)^2\;\mathrm dx\right| \\[5pt]
&=&\pi\cdot\left|\displaystyle\int_{-0,8}^{0,8}f_0^2+2\cdot f_0(x)\cdot a+a^2-g_0(x)^2-2\cdot g_0(x) \cdot a -a^2\;\mathrm dx\right| \\[5pt]
&=&\pi\cdot\left|\displaystyle\int_{-0,8}^{0,8}f_0^2+2\cdot f_0(x)\cdot a-g_0(x)^2-2\cdot g_0(x) \cdot a \;\mathrm dx\right| \\[5pt]
&=&V_0+\pi\cdot\left|\displaystyle\int_{-0,8}^{0,8}2a\cdot (f_0(x)- g_0(x)) \;\mathrm dx\right| \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/549f67fcfd9a37d7a80af2ae90ede9fea3c3d9360751f142b42065b20f3111d2_light.svg) Wie du siehst, bleiben Terme, die von
Wie du siehst, bleiben Terme, die von  abhängig sind, stehen.
abhängig sind, stehen.
d)  Beschreibe wie der Punkt
Beschreibe wie der Punkt  bestimmt wird
Hier ist ein Punkt
bestimmt wird
Hier ist ein Punkt  gegeben. Es soll ein Punkt
gegeben. Es soll ein Punkt  auf dem Graphen der Funktion
auf dem Graphen der Funktion  im Intervall
im Intervall ![\([-0,8\,;\,0,8]\)](https://www.schullv.de/resources/formulas/df01b32eb3e18aa2686979a2c1e90b3759ceba0ae18f35a668334810670d6076_light.svg) gefunden werden, für den die Länge der Strecke
gefunden werden, für den die Länge der Strecke  maximal ist.
Die Länge der Strecke
maximal ist.
Die Länge der Strecke  beschreibt den Abstand der Punkte
beschreibt den Abstand der Punkte  und
und  . Der Abstand ist:
. Der Abstand ist:
![\(\begin{array}[t]{rll}
d(x)=\left|\overline{AB}\right|&=&\sqrt{(0,4-x)^2+(2,368-f_0(x))^2}\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/2fc99c0e437bcc832bd1235ce79308511924f0726b788e320d804711f5bdb5a5_light.svg) Setzt man den Funktionsterm von
Setzt man den Funktionsterm von  in die Gleichung ein, erhält man einen Funktionsterm für die Länge der Strecke
in die Gleichung ein, erhält man einen Funktionsterm für die Länge der Strecke  in Abhängigkeit von
in Abhängigkeit von  . Da stetige Funktionen auf kompakten Mengen Maxima und Minima annehmen, hat die Funktion
. Da stetige Funktionen auf kompakten Mengen Maxima und Minima annehmen, hat die Funktion  im Intervall
im Intervall ![\([-0,8\,;\,0,8]\)](https://www.schullv.de/resources/formulas/df01b32eb3e18aa2686979a2c1e90b3759ceba0ae18f35a668334810670d6076_light.svg) ein Maximum. Das Maximum bestimmt man, indem man durch die notwendige Bedingung
ein Maximum. Das Maximum bestimmt man, indem man durch die notwendige Bedingung  eine Extremstelle
eine Extremstelle  findet. Für diese Extremstelle überprüft man die hinreichende Bedingung für Maxima
findet. Für diese Extremstelle überprüft man die hinreichende Bedingung für Maxima  . Setzt man das bestimmte
. Setzt man das bestimmte  in den Punkt
in den Punkt  ein, erhält man die Koordinaten des Punktes
ein, erhält man die Koordinaten des Punktes  .
.