Hilfsmittelfreier Teil

HMF 1 - Analysis (Pool 1)

Für jeden Wert von $a\,(a\in \mathbb{R}, a\neq 0)$ ist eine Funktion $f_a$ durch $f_a(x)=a\cdot x^6-x^4\,\,(x\in\mathbb{R})$ gegeben.

1.1 Bestimme diejenigen Werte von $a$ , für die $f_a$ mehr als eine Nullstelle hat.

(3P)

1.2 Für genau einen Wert von $a$ hat $f_a$ an der Stelle $x=1$ ein Minimum. Bestimme diesen Wert von $a$ .

(2P)

Muster aus schwarzen und weißen Kästchen in einem Raster.

HMF 2 - Analysis (Pool 1)

Gegeben ist die Funktionenschar $f_k$ mit $f_k(x)=(x-k) \cdot \mathrm{e}^{\frac{1}{2}x}$ für $k\gt 0$ und $x\in \mathbb{R}$ .

2.1 Berechne den Schnittpunkt des Graphen von $f_k$ mit der $x$ -Achse.

(2P)

2.2 Die Skizze zeigt die Graphen der Funktionen $f_3$ und $f_4$ .
Kreuze in der folgenden Tabelle an, welche der Terme den Inhalt des markierten Flächenstücks $A$ richtig angeben und welche nicht.

Grafik eines Koordinatensystems mit einer Funktion und beschrifteten Punkten.

Term	richtig	falsch
$\left\|\displaystyle\int_{d}^{b} f_4(x)\;\mathrm dx -\displaystyle\int_{c}^{a}f_3(x)\;\mathrm dx\right\|$
$\left\|\displaystyle\int_{0}^{a} f_4(x)\;\mathrm dx -\displaystyle\int_{0}^{b}f_3(x)\;\mathrm dx\right\|$
$\left\|\displaystyle\int_{0}^{a} f_3(x)\;\mathrm dx -\displaystyle\int_{0}^{b}f_4(x)\;\mathrm dx\right\|$
$\displaystyle\int_{0}^{b} f_4(x)\;\mathrm dx -\displaystyle\int_{0}^{a}f_3(x)\;\mathrm dx$
$\displaystyle\int_{0}^{a} f_3(x)\;\mathrm dx -\displaystyle\int_{0}^{b}f_4(x)\;\mathrm dx$
$\displaystyle\int_{0}^{b}\left\|f_3(x)\;- f_4(x)\right\|\;\mathrm dx$

(3P)

HMF 3 - Analysis (Pool 2)

Gegeben ist die Funktion $f$ mit $f(x)=x^3-6\cdot x^2+11\cdot x-6\,\,\,\,(x\in\mathbb{R})$ .

3.1 Weise nach, dass der Wendepunkt des Graphen von $f$ auf der Geraden mit der Gleichung $y=x-2$ liegt.

(3P)

3.2 Der Graph von $f$ wird verschoben. Der Punkt $(2\mid 0)$ des Graphen der Funktion $f$ besitzt nach der Verschiebung die Koordinaten $(3\mid 2)$ . Der verschobene Graph gehört zu einer Funktion $h$ .
Gib eine Gleichung von $h$ an.

(2P)

HMF 4 - Analytische Geometrie (Pool 1)

4.1 Gegeben seien die Vektoren $\vec{u}$ , $\vec{v}$ und $\vec{w}\in \mathbb{R}^3$ und die reellen Zahlen $r$ und $t$ . Kreuze in der folgenden Tabelle an, ob es sich bei dem Ausdruck um einen Vektor oder um eine Zahl handelt, oder ob der Ausdruck nicht definiert ist.

Ausdruck	Vektor	Zahl	nicht definiert
$\left(\vec{u}\circ \vec{v}\right)+\vec{w}$
$\left\|\vec{u}\right\|^2-\left\|\vec{w}\right\|^2$
$\left(\vec{u}\times \vec{v}\right)-(r\cdot t)\cdot \vec{w}$
$\left(\vec{u}\circ \vec{u}\right)+\left(r-t\right)^2$
$\left(r \cdot \vec{u}\right)\circ \left(t \times \vec{u}\times \vec{v}\right)$
$\vec{u}\times \left(\left(\vec{w}-\vec{v})\times (\vec{u}-\vec{v}\right)\right)$

(3P)

4.2 Gegeben seien die Punkte $A$ , $B$ und $C$ , die nicht auf einer gemeinsamen Geraden liegen.
Gib eine Gleichung der Ebene $E$ , die die Punkte $A$ , $B$ und $C$ enthält, in allgemeiner Form an.
Gib einen Vektor, der orthogonal zu dieser Ebene ist und die Länge $1$ hat, in allgemeiner Form an.

(2P)

HMF 5 - Analytische Geometrie (Pool 1)

Die Gerade $g$ verläuft durch die Punkte $A(0\mid 1\mid 2)$ und $B(2\mid 5\mid 6)$ .

5.1 Zeige, dass die Punkte $A$ und $B$ den Abstand $6$ haben.
Die Punkte $C$ und $D$ liegen auf $g$ und haben von $A$ jeweils den Abstand $12$ .
Bestimme die Koordinaten von $C$ und $D$ .

(3P)

5.2 Die Punkte $A$ , $B$ und $E(1\mid 2\mid 5)$ sollen mit einem Punkt die Eckpunkte eines Parallelogramms bilden. Für die Lage des vierten Eckpunktes gibt es mehrere Möglichkeiten.
Gib für zwei dieser Möglichkeiten die Koordinaten des vierten Eckpunktes an.

(2P)

HMF 6 - Analytische Geometrie (Pool 2)

Gegeben ist eine Kugel $K$ um den Ursprung durch $K:\vec{x}\,^2 =144$ , eine Gerade $g$ mit $g:\vec{x}=s\cdot \begin{pmatrix}2\\-2\\1\end{pmatrix}$ und eine Ebene $E$ mit $E:3x_1+2x_2-2x_3=0$ .

6.1 Berechne die Schnittpunkte der Kugel $K$ und der Geraden $g$ .

(3P)

6.2 Bestimme den Mittelpunkt und den Radius des Schnittkreises der Kugel $K$ mit der Ebene $E$ .

(2P)

HMF 7 - Stochastik (Pool 1)

$50\,\%$ der Studierenden, die sich zu einer Klausur anmelden, sind Wiederholer. Kurz vor der Prüfung treten $28\,\%$ der Wiederholer und $12\,\%$ der anderen Prüflinge von der Klausur zurück.
Es wird ein angemeldeter Studierender zufällig ausgewählt. Verwende folgende Bezeichnungen:

W:	Der Prüfling ist Wiederholer.
Z:	Der Prüfling tritt von der Klausur zurück.

7.1 Erstelle zu diesem Sachverhalt ein vollständig beschriftetes Baumdiagramm mit allen Pfadwahrscheinlichkeiten.

(3P)

7.2 Berechne die Wahrscheinlichkeit dafür, dass ein zufällig auszuwählender Prüfling Wiederholer ist, unter der Bedingung, dass er an der Prüfung teilgenommen hat.

(2P)

HMF 8 - Stochastik (Pool 1)

Balkendiagramm mit Werten für verschiedene k, zeigt PP(x-k) in Abhängigkeit von k.

Für ein Zufallsexperiment wird eine Zufallsvariable $X$ festgelegt, welche die drei Werte $-2$ , $1$ und $2$ annehmen kann. In der Abbildung ist die Wahrscheinlichkeitsverteilung von $X$ dargestellt.

8.1 Ermittle mithilfe der Abbildung den Erwartungswert der Zufallsvariablen $X$ .

(2P)

8.2 Das Zufallsexperiment wird zweimal durchgeführt. Dabei wird jeweils der Wert der Zufallsvariablen $X$ notiert.
Bestimme die Wahrscheinlichkeit dafür, dass die Summe dieser beiden Werte negativ ist.

(3P)

HMF 1 - Analysis (Pool 1)

Hier ist eine Funktion $f_a$ durch eine Gleichung gegeben:

$\begin{array}[t]{rll} f_a(x)=a\cdot x^6-x^4 \end{array}$

1.1
$\blacktriangleright$ Bestimme $a$ , sodass $f_a$ mehr als eine Nullstelle hat

Um Nullstellen einer Funktion zu bestimmen, mussst du sie mit Null gleichsetzen und nach $x$ auflösen.

$\begin{array}[t]{rll} f_a(x)&=&0 \\[5pt] a\cdot x^6 - x^4 &=& 0 \\[5pt] (a\cdot x^2 -1)\cdot x^4 &=& 0\\[5pt] \end{array}$

Mit dem Satz vom Nullprodukt siehst du, dass bei $x^4=0\rightarrow x=0$ eine Nullstelle ist. Für eine weitere Nullstelle musst du den anderen Term auflösen:

$\begin{array}[t]{rll} a\cdot x^2 -1 &=& 0 &\quad& \scriptsize \mid +1\\[5pt] a\cdot x^2 &=& 1 &\quad& \scriptsize \mid :a \\[5pt] x^2 &=& \dfrac{1}{a} &\quad& \scriptsize \mid \pm\sqrt{\;} \\[5pt] x &=& \pm\sqrt{\frac{1}{a}} \\[5pt] \end{array}$

Die zweite Nullstelle liegt bei $x=\pm\sqrt{\frac{1}{a}}$ . Da der Term in der Wurzel positiv sein muss, und man nicht durch Null teilen kann, muss gelten $a>0$ .

1.2
$\blacktriangleright$ Bestimme $a$ , sodass $f_a$ an der Stelle $x=1$ ein Minimum hat

Um zu zeigen, dass eine Funktion $f$ an einer Stelle $x_1$ ein Minimum hat, müssen zwei Bedingungen erfüllt sein:

$f‘(x)=0$ : Die notwendige Bedingung zeigt, dass eine Extrem- oder Sattelstelle vorliegt

$f‘‘(x)>0$ : Die hinreichende Bedingung zeigt, dass die Extremstelle ein Minimum ist

Um die Bedingungen zu zeigen, gehst du in 4 Schritten vor:

Ableitungen bilden

1. Ableitung mit Null gleichsetzen und nach $x$ auflösen

Nullstellen mit $x=1$ gleichsetzen und nach $a$ auflösen

Überprüfen der 2. Bedingung

1. Schritt: Ableitungen von $f$ bilden

$\begin{array}[t]{rll} f_a(x) &=& a\cdot x^6 - x^4 \\[5pt] f_a‘(x) &=& 6a\cdot x^5 - 4\cdot x^3 \\[5pt] f_a‘‘(x) &=& 30a\cdot x^4 - 12 \cdot x^2 \\[5pt] \end{array}$

2. Schritt: notwendige Bedingung anwenden

$\begin{array}[t]{rll} f_a‘(x)&=&0 \\[5pt] 6a\cdot x^5 - 4\cdot x^3 &=& 0 &\quad& \scriptsize \mid\; :x^3\\[5pt] 6a\cdot x^2 -4 &=& 0 &\quad& \scriptsize \mid\; +4\\[5pt] 6a\cdot x^2 &=& 4 &\quad& \scriptsize \mid\; :6a \\[5pt] x^2 &=& \dfrac{2}{3}a &\quad& \scriptsize \mid\; \pm\sqrt{\;} \\[5pt] x_{1/2} &=& \pm \sqrt{\dfrac{2}{3a}} \\[5pt] \end{array}$

Du weißt, dass $f$ an den Stellen $x_{1/2} = \pm \sqrt{\dfrac{2}{3a}}$ Nullstellen hat.

3. Schritt: Nullstellen mit $x=1$ gleichsetzen:

Das Minimum soll an der Stelle $x=1$ liegen, daher benötigst du nur die positive Lösung:

$\begin{array}[t]{rll} x_1 &=& 1 \\[5pt] + \sqrt{\dfrac{2}{3a}} &=& 1 &\quad& \scriptsize \mid\; (\,)^2\\[5pt] \dfrac{2}{3a} &=& 1 &\quad& \scriptsize \mid\; \cdot 3a \\[5pt] 2 &=& 3a &\quad& \scriptsize \mid\; :3 \\[5pt] \dfrac{2}{3}&=& a \\[5pt] \end{array}$

$f$ hat für $a=\dfrac{2}{3}$ an der Stelle $x=1$ eine Extremstelle.

4. Schritt Überprüfe 2. Bedingung:

Abschließend musst du $a=\dfrac{2}{3}$ und $x=1$ in die zweite Ableitung einsetzen und überprüfen, ob der Wert der 2. Ableitung an dieser Stelle größer als Null ist:

$\begin{array}[t]{rll} f_a‘‘(x) &=& 30a\cdot x^4 - 12 \cdot x^2 \\[5pt] f_{\frac{2}{3}}‘‘(1) &=& 30\cdot \dfrac{2}{3} \cdot 1 - 12 \cdot 1 \\[5pt] &=& 20 -12 \\[5pt] &=& 8 > 0 \\[5pt] \end{array}$

Somit sind alle Bedingungen erfüllt. Für $a=\dfrac{2}{3}$ hat $f$ an der Stelle $x=1$ ein Minimum.

HMF 2 - Analysis (Pool 1)

Hier ist eine Funktionenschar $f_k$ mit einer Gleichung angegeben:

$\begin{array}[t]{rll} f_k(x)&=&(x-k) \cdot \mathrm e^{\frac{1}{2}x} \\[5pt] \end{array}$

2.1
$\blacktriangleright$ Berechne den Schnittpunkt mit der $x$ -Achse

Um den Schnittpunkt der Funktionenschar mit der $x$ -Achse zu bestimmen, musst du den Funktionsterm mit Null gleichsetzen und nach $x$ auflösen:

$\begin{array}[t]{rll} f_k(x)&=&0 \\[5pt] (x-k) \cdot \mathrm e^{\frac{1}{2}x} &=& 0 \\[5pt] \end{array}$

Der Satz vom Nullprodukt sagt, dass ein Produkt Null ist wenn mindestens einer der Faktor Null ist. Die Exponentialfunktion ist stets echt größer Null. Somit muss $(x-k)$ gleich Null sein:

$\begin{array}[t]{rll} x-k &=&0 \quad \scriptsize \mid\; +k\\[5pt] x&=& k \\[5pt] \end{array}$

Der Schnittpunkt des Graphen mit der $x$ -Achse ist im Punkt $S(k\,|\,0)$ .

2.2
$\blacktriangleright$ Welche Terme beschreiben den Flächeninhalt

In dieser Aufgabe sollst du angeben, welche Terme den Flächeninhalt der gezeigten Fläche richtig beschreibt. Dazu überlegst du dir zunächst wie der Flächeninhalt bestimmt wird und vergleichst deinen Term mit den gegebenen Termen:

Flächeninhalt bestimmen

Für den Flächeninhalt $A$ braucht man zunächst die Fläche $A_1$ zwischen dem Graphen der Funktion $f_4$ und den Koordinatenachsen:

$\begin{array}[t]{rll} A_1 &=& \displaystyle\int_{0}^{b}|f_4(x)|\;\mathrm dx \end{array}$

Davon muss man die Fläche $A_2$ zwischen dem Graphen der Funktion $f_3$ und den Koordinatenachsen abziehen:

$\begin{array}[t]{rll} A_2 &=& \displaystyle\int_{0}^{a}|f_3(x)|\;\mathrm dx \\[5pt] A &=& \displaystyle\int_{0}^{b}|f_4(x)|\;\mathrm dx - \displaystyle\int_{0}^{a}|f_3(x)|\;\mathrm dx \\[5pt] \end{array}$

Der 3. und 5. Term liefern das richtige Ergebnis. Der 5. Term

$\begin{array}[t]{rll} \displaystyle\int_{0}^{a}f_3(x)\;\mathrm dx - \displaystyle\int_{0}^{b}f_4(x)\;\mathrm dx \\[5pt] \end{array}$

liefert das richtige Ergebnis, weil beide Integrale einen negativen Wert haben, allerdings wird der betragsmäßig größere Wert vom kleineren abgezogen, weshalb der Wert des Terms positiv ist. Der 3. Term ist gleich dem 5. Term mit zusätzlichen Betragsstrichen. Da der 5. Term bereits positiv ist ändert sich durch die Betragsstriche nichts. Alle anderen Terme liefern kein richtiges Ergebnis.

HMF 3 - Analysis (Pool 2)

Die Funktion $f$ ist gegeben durch die Funktionsgleichung:

$\begin{array}[t]{rll} f(x) &=& x^3 - 6\cdot x^2 + 11 \cdot x -6 \\[5pt] \end{array}$

3.1
$\blacktriangleright$ Zeige, dass der Wendepunkt auf der Geraden $y=x-2$ liegt

Hier sollst du zeigen, dass der Wendepunkt der Funktion $f$ auf der Geraden mit der Gleichung $y=x-2$ liegt. Die zwei Bedingungen für einen Wendepunkt sind:

$f‘‘(x) = 0$ Notwendige Bedingung: Die zweite Ableitung muss Null sein.

$f‘‘‘(x) \neq 0$ Hinreichende Bedingung: Die dritte Ableitung muss ungleich Null sein.

Du gehst hier in 4 Schritten vor.

Ableitungen bilden

Zweite Ableitungen mit Null gleichsetzen

2. Bedingung überprüfen und vollständige Koordinaten des Wendepunkt bestimmen

Überprüfe, ob der Wendepunkt auf der Geraden liegt

1. Schritt: Ableitungen bilden

Zunächst bildest du die ersten drei Ableitungen der Funktion $f$ :

$\begin{array}[t]{rll} f(x) &=& x^3 - 6\cdot x^2 + 11 \cdot x -6 \\[5pt] f‘(x) &=& 3\cdot x^2 -12 \cdot x +11 \\[5pt] f‘‘(x) &=& 6 \cdot x -12 \\[5pt] f‘‘‘(x) &=& 6 \\[5pt] \end{array}$

2. Schritt: Zweite Ableitung Null setzen und nach $x$ auflösen

Du musst nun die 2. Ableitung mit Null gleichsetzen und anschließend nach $x$ auflösen.

$\begin{array}[t]{rll} f‘‘(x) &=& 0 \\[5pt] 6 \cdot x -12 &=& 0 &\quad& \scriptsize \mid\; +12\\[5pt] 6 \cdot x &=& 12 &\quad& \scriptsize \mid\; :6\\[5pt] x &=& 2 \\[5pt] \end{array}$

An der Stelle $x=2$ muss der Wendepunkt liegen.

3. Schritt: Hinreichende Bedingung überprüfen

Die dritte Ableitung $f‘‘‘(x)=6$ ist immer größer Null, damit ist die Bedingung erfüllt. Die $y$ -Koordinate des Wendepunkts kann bestimmt werden, wenn der Funktionsterm von $f$ an der Stelle $x=2$ ausgewertet wird:

$\begin{array}[t]{rll} f(2) &=& 2^3 -6 \cdot 2^2 +11 \cdot 2 -6 \\[5pt] &=& 0 \\[5pt] \end{array}$

Der Wendepunkt ist $W(2\,|\,0)$ .

4. Schritt: Überprüfe, ob der Wendepunkt auf der Geraden liegt

Um zu überprüfen, ob der Punkt auf der Geraden liegt, setzt du $x$ - und $y$ -Koordinate in die Geradengleichung ein und überprüfst ob die Gleichung erfüllt ist:

$\begin{array}[t]{rll} y &=& x - 2 \\[5pt] 0 &=& 2 - 2 \\[5pt] 0 &=& 0 \\[5pt] \end{array}$

Die Geradengleichung ist erfüllt, somit liegt der Wendepunkt $W$ auf der Geraden.

3.2
$\blacktriangleright$ Verschiebung des Graphen von $\boldsymbol{f}$

Der Graph von $f$ wird so verschoben, dass der Punkt $(2\,|\,0)$ danach die Koordinaten $(3\,|\,2)$ hat. Der verschobene Graph gehört zur Funktion $h$ , die du bestimmen sollst.

Der Graph der Funktion $g_1$

$\begin{array}[t]{rll} g_1(x) &=& f(x-a) \\[5pt] \end{array}$

geht durch Verschiebung des Graphen von $f$ um $a$ Einheiten entlang der positiven $x$ -Achse hervor.

Der Graph der Funktion $g_2$

$\begin{array}[t]{rll} g_2(x) &=& f(x)+b \\[5pt] \end{array}$

geht durch Verschiebung des Graphen von $f$ um $b$ Einheiten entlang der positiven $y$ -Achse hervor.

Hier wird der Punkt um eine Einheit in positiver $x$ -Richtung und um zwei Einheiten in positiver $y$ -Richtung verschoben. Das heißt, die Konstante sind $a=1$ und $b=2$ . Der Funktionsterm von $h$ ergibt sich nun:

$\begin{array}[t]{rll} h(x) &=& f(x-1) + 2 \\[5pt] &=& (x-1)^3 -6 \cdot (x-1)^2 + 11 \cdot (x-1) -6 + 2\\[5pt] &=& x^3 -3\cdot x^2 +3\cdot x -1 -6\cdot x^2 +12\cdot x -6 + 11\cdot x -11 -6 +2 \\[5pt] &=& x^3 -9 \cdot x^2 + 26 \cdot x -22 \\[5pt] \end{array}$

Die Gleichung für $h$ kannst du als $h(x) =(x-1)^3 -6 \cdot (x-1)^2 + 11 \cdot (x-1) -4$ oder $h(x) = x^3 -9 \cdot x^2 + 26 \cdot x -22$ angeben.

HMF 4 - Analytische Geometrie (Pool 1)

4.1
$\blacktriangleright$ Bestimme was Ausdruck beschreibt

Hier sind mit drei Vektoren $\vec{u}$ , $\vec{v}$ und $\vec{w}$ und zwei reellen Zahlen $r$ und $t$ verschiedene Ausdrücke beschrieben. Du sollst zu jedem Ausdruck sagen, ob es ein Vektor ist, eine Zahl ist oder ob der Ausdruck nicht definiert ist. Das Rechenzeichen $\circ$ ist das Skalarprodukt, wenn es zwischen zwei Vektoren steht, ist das Ergebnis eine reelle Zahl. Das Rechenzeichen $\times$ ist das Kreuzprodukt, wenn es zwischen zwei Vektoren steht, ist das Ergebnis ein Vektor. Betragsstriche $|\vec{a}|$ machen aus einem Vektor eine reelle Zahl. Du gehst alle Ausdrücke nacheinander durch:

Ausdruck	Vektor	Zahl	nicht definiert
$(\vec{u}\circ\vec{v}) + \vec{w}$			X
$\|\vec{u}\|^2 - \|\vec{w}\|^2$		X
$(\vec{u} \times \vec{v}) - (r\cdot t) \cdot \vec{w}$	X
$(\vec{u}\circ\vec{u}) + (r-t)^2$		X
$(r \cdot \vec{u}) \circ(t\times \vec{u} \times \vec{v})$			X
$\vec{u} \times ((\vec{w}- \vec{v})\times ( \vec{u}- \vec{v}))$	X

4.2
$\blacktriangleright$ Bestimmen einer Ebene

Hier sind drei Punkt $A$ , $B$ und $C$ gegeben. Sie liegen nicht auf einer gemeinsamen Geraden, und bilden deshalb eine Ebene. Du sollst die zugehörige Ebenengleichung angeben.

1. Ebenengleichung in Parameterform

Hier ist es sinnvoll die Parameterform zu betrachten:

$E_P: \vec{x} = \vec{p} + s\cdot \vec{u} + t \cdot \vec{v}$

Der Vektor $\vec{p}$ ist der Stützvektor. Der Ortsvektor eines der gegebenen Punkte, bildet den Stützvektor. Die Vektoren $\vec{u}$ und $\vec{v}$ sind die Spannvektoren der Ebene. Du bildest sie als Differenz zwischen den Ortsvektoren verschiedener Punkte.

Stützvektor

Als Stützvektor kannst du den Ortsvektor vom Punkt $A$ verwenden:

$\begin{array}[t]{rll} \vec{p} = \overrightarrow{OA}\\[5pt] \end{array}$

Spannvektoren

Als Spannvektor verwendest du die Differenz der Punkte $A$ $B$ und $A$ $C$ :

$\begin{array}[t]{rll} \vec{u} &=& \overrightarrow{OB}-\overrightarrow{OA} &=& \overrightarrow{AB}\\[5pt] \vec{v} &=& \overrightarrow{OC}-\overrightarrow{OA} &=& \overrightarrow{AC}\\[5pt] \end{array}$

Ebenengleichung

Du kannst jetzt die Ebenengleichung angeben:

$\begin{array}[t]{rll} E_P: \vec{x} = \overrightarrow{OA} + s\cdot \overrightarrow{AB} + t\cdot \overrightarrow{AC}\\[5pt] \end{array}$

$\blacktriangleright$ Bestimme den Normaleneinheitsvektoren

Desweiteren sollst du einen Vektor bestimmen, der senkrecht zur Ebene ist und die Länge 1 hat, also einen Normalenvektor der Länge 1. Den Vektor bildest du mit dem Kreuzprodukt der beiden Spannvektoren der Ebene. Damit er die Länge 1 hat, musst du das Kreuzprodukt durch den Betrag des Kreuzprodukts teilen:

$\begin{array}[t]{rll} \vec{n} =\dfrac{\overrightarrow{AB} \times \overrightarrow{AC}}{|\overrightarrow{AB} \times \overrightarrow{AC}|} \end{array}$

HMF 5 - Analytische Geometrie (Pool 1)

Eine Gerade $g$ verläuft durch die Punkte $A\,(0\,|\,1\,|\,2)$ und $B\,(2\,|\,5\,|\,6)$ .

5.1
$\blacktriangleright$ Zeige, dass der Abstand zwischen $\boldsymbol{A}$ und $\boldsymbol{B}$ gleich 6 ist

Um den Abstand zwischen zwei Punkten zu bestimmen, berechnest du die Länge des Verbindungsvektors zwischen den Punkten. Die Länge des Verbindungsvektors, also der Abstand ist:

$\begin{array}[t]{rll} d &=& \left|\begin{pmatrix}0\\1\\2\\\end{pmatrix}-\begin{pmatrix}2\\5\\6\\\end{pmatrix}\right| \\[5pt] &=& \sqrt{(0-2)^2+(1-5)^2+(2-6)^2}\\[5pt] &=& \sqrt{4+16+16}\\[5pt] &=& \sqrt{36} = 6 \\[5pt] \end{array}$

Damit hast du gezeigt, dass die Punkte $A$ und $B$ den Abstand 6 haben.

$\blacktriangleright$ Bestimme die Koordinaten der Punkte $\boldsymbol{C}$ und $\boldsymbol{D}$

Die Punkte $C$ und $D$ liegen ebenfalls auf der Gerade $g$ . Beide haben den Abstand 12 vom Punkt $A$ . Nun sollst du die Koordinaten der Punkte bestimmen. Der Vektor $\overrightarrow{AB}$ hat die Länge 6, da die Punkte $A$ und $B$ den Abstand 6 haben. Zudem verläuft er parallel zur Geraden $g$ . Wenn man den Vektor $\overrightarrow{AB}$ zwei Mal zum Vektor $\vec{A}$ addiert oder subtrahiert, erhalt man den Ortsvektor der Punkte $C$ und $D$ :

$\begin{array}[t]{rll} \overrightarrow{OC}&=& \overrightarrow{OA} + 2\cdot \overrightarrow{AB} \\[5pt] &=& \begin{pmatrix}0\\1\\2\end{pmatrix} + 2\cdot \begin{pmatrix}2-0\\5-1\\6-2\end{pmatrix} \\[5pt] &=& \begin{pmatrix}0\\1\\2\end{pmatrix} + \begin{pmatrix}4\\8\\8\end{pmatrix} \\[5pt] &=& \begin{pmatrix}4\\9\\10\end{pmatrix} \\[5pt] \overrightarrow{OD}&=& \overrightarrow{OA} - 2\cdot \overrightarrow{AB} \\[5pt] &=& \begin{pmatrix}0\\1\\2\end{pmatrix} - 2\cdot \begin{pmatrix}2-0\\5-1\\6-2\end{pmatrix} \\[5pt] &=& \begin{pmatrix}0\\1\\2\end{pmatrix} - \begin{pmatrix}4\\8\\8\end{pmatrix} \\[5pt] &=& \begin{pmatrix}-4\\-7\\-6\end{pmatrix} \\[5pt] \end{array}$

Die Koordinaten sind $C\,(4\,|\,9\,|\,10)$ und $D\,(-4\,|\,-7\,|\,-6)$ .

5.2
$\blacktriangleright$ Bilde mit den Punkten $\boldsymbol{A}$ , $\boldsymbol{B}$ und $\boldsymbol{E}$ ein Parallelogram

Die Punkte $A$ , $B$ und $E\,(1\,|\,2\,|\,5)$ und ein vierter Punkt $P$ sollen ein Parallelogramm bilden. Ein Parallelogramm hat zwei wichtige Eigenschaften:

Gegenüberliegende Seiten sind parallel

Gegenüberliegende Seiten sind gleichlang

Die zweite Eigenschaft folgt aus der ersten, ist allerdings sehr nützlich. Es gibt mehrere Möglichkeiten mit den gegebenen Punkten ein Parallelogramm zu bilden. Eine Skizze zeigt dir zwei Mögliche Punkte $P_1$ und $P_2$ .

1. Parallelogramm

Das schwarze Parallelogramm wir aus den Punkten $A$ , $B$ , $E$ und $P_1$ gebildet. Die Koordinaten des Punkts $P_1$ findest du, indem du vom Ortsvektor von $E$ den Verbindungsvektor $\overrightarrow{AB}$ subtrahierst:

$\begin{array}[t]{rll} \overrightarrow{OP} &=& \overrightarrow{OE}-\overrightarrow{AB} \\[5pt] &=& \begin{pmatrix}1\\2\\5\end{pmatrix}-\begin{pmatrix}2\\4\\4\end{pmatrix}\\[5pt] &=& \begin{pmatrix}-1\\-2\\1\end{pmatrix} \\[5pt] \end{array}$

Die Koordinaten des Punkts $P_1$ sind somit $P_1\,(-1\,|\,-2\,|\,1)$ .

2. Parallelogramm

Das grüne Parallelogramm wir aus den Punkten $A$ , $B$ , $E$ und $P_2$ gebildet. Die Koordinaten des Punkts $P_2$ findest du, indem du vom Ortsvektor von $B$ den Verbindungsvektor $\overrightarrow{AE}$ subtrahierst:

$\begin{array}[t]{rll} \overrightarrow{OP} &=& \overrightarrow{OB}-\overrightarrow{AE} \\[5pt] &=& \begin{pmatrix}2\\5\\6\end{pmatrix}-\begin{pmatrix}1-0\\2-1\\5-2\end{pmatrix}\\[5pt] &=& \begin{pmatrix}2\\5\\6\end{pmatrix}-\begin{pmatrix}1\\1\\3\end{pmatrix}\\[5pt] &=& \begin{pmatrix}1\\4\\3\end{pmatrix} \end{array}$

Die Koordinaten des Punkts $P_2$ sind somit $P_2\,(1\,|\,4\,|\,3)$ .

HMF 6 - Analytische Geometrie (Pool 2)

Hier sind eine Kugel $K$ , eine Gerade $g$ und eine Ebene $E$ gegeben. Der Kreismittelpunkt ist im Ursprung $O(0\,|\,0\,|\,0)$ , der Radius ist $r_K=\sqrt{144}=12$

6.1
$\blacktriangleright$ Bestimme die Schnittpunkte zwischen Kugel $K$ und Gerade $g$

Hier sind eine Kreis- und eine Geradengleichung gegeben. Um die Schnittpunkt zu erhalten, setzt du die Geradengleichung in die Kreisgleichung ein und löst den Term nach $s$ auf.

$\begin{array}[t]{rll} \left( s\cdot\begin{pmatrix}2\\-2\\1\\\end{pmatrix} \right)^2 &=& 144 \\[5pt] s^2\cdot (4+4+1) &=& 144 \\[5pt] 9 \cdot s^2 &=& 144 &\quad&\scriptsize\mid :9 \\[5pt] s^2 &=& 16 &\quad& \scriptsize \mid \pm\sqrt{\;} \\[5pt] s &=& \pm 4 \\[5pt] \end{array}$

Jetzt kannst du die beiden Werte für $s$ in die Geradengleichung einsetzen und du erhältst die Schnittpunkte:

$\begin{array}[t]{rll} \overrightarrow{OS_1} &=& 4 \cdot \begin{pmatrix}2\\-2\\1\end{pmatrix}\\[5pt] &=& \begin{pmatrix}8\\-8\\4\end{pmatrix} \\[5pt] \overrightarrow{OS_2} &=& -4 \cdot \begin{pmatrix}2\\-2\\1\end{pmatrix}\\[5pt] &=& \begin{pmatrix}-8\\8\\-4\end{pmatrix} \end{array}$

Die Koordinaten der Schnittpunkte sind $S_1\,(8\,|\,-8\,|\,4)$ und $S_2\,(-8\,|\,8\,|\,-4)$ .

6.2
$\blacktriangleright$ Schnittkreis der Kugel $\boldsymbol{K}$ mit der Ebene $\boldsymbol{E}$

Zunächst musst du den Abstand $d$ der Kugelmitte von der Ebene $E$ bestimmen. Der Kugelmittelpunkt liegt im Ursprung $O(0\,|\,0\,|\,0)$ , da der Urspung auch in der Ebene $E$ liegt, ist der Abstand Null.

Da der berechnete Abstand Null ist, ist der Radius des Schnittkreises gleich dem Radius der Kugel:

$\begin{array}[t]{rll} r_s = r_k = 12 \\[5pt] \end{array}$

Der Kreismittelpunkt ist ebenfalls identisch mit dem Kugelmittelpunkt $M_S (0\,|\,0\,|\,0)$ , weil der Abstand Null ist.

HMF 7 - Stochastik (Pool 1)

7.1
$\blacktriangleright$ Baumdiagramm

Hier sollst du ein Baumdiagramm zeichnen, das den Sachverhalt vollständig erfasst. Es handelt sich um ein zweistufiges Zufallsexperiment. In der ersten Stufe erfolgt die Anmeldung zur Prüfung bei der sich zeigt, ob man die Prüfung wiederholt oder zum ersten Mal schreibt. In der zweiten Stufe erfolgt ein möglicher Rücktritt von der Prüfung.

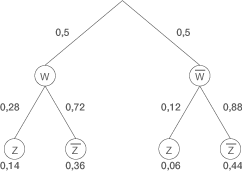
Diagramm eines Entscheidungsbaums mit Wahrscheinlichkeiten an den Knoten.

7.2
$\blacktriangleright$ Bestimme die Wahrscheinlichkeit, dass ein Prüfling Wiederholer ist

Hier musst du die bedingte Wahrscheinlichkeit berechnen, dass ein Prüfungsteilnehmer Wiederholer ist. Dazu verwendest du den Satz von Bayes. Du erhältst die Wahrscheinlichkeit, indem du die Wahrscheinlichkeit, dass ein Wiederholer an der Prüfung teilnimmt, durch die Gesamtwahrscheinlichkeit teilst, dass ein Prüfling an der Prüfung teilnimmt.

1. Wahrscheinlichkeit, dass ein Wiederholer nicht zurücktritt

Für die Wahrscheinlichkeit $P(A)$ musst du die Wahrscheinlichkeiten für Wiederholer $W$ mit der Wahrscheinlichkeit nicht zurückgetreten $\overline{Z}$ multiplizieren:

$\begin{array}[t]{rll} P(A) &=& P(W) \cdot P(\overline{Z}) \\[5pt] &=& 0,5 \cdot 0,72 \\[5pt] &=& 0,36 \end{array}$

Die Wahrscheinlichkeit, dass ein Wiederholer zur Prüfung antritt ist 36%.

2. Wahrscheinlichkeit, dass ein Prüfling nicht zurücktritt

Die Wahrscheinlichkeit, dass ein Prüfling nicht zurücktritt, bildet sich aus der Summe der Wahrscheinlichkeiten, dass ein Wiederholer nicht zurücktritt und der Wahrscheinlichkeit, dass ein nicht Wiederholer nicht zurücktritt. Ersteres hast du bereits berechnet. Für den zweiten Fall multiplizierst du die Wahrscheinlichkeit für nicht Wiederholer $\overline{W}$ und nicht zurück getreten $\overline{Z}$ :

$\begin{array}[t]{rll} P(B) &=& P(\overline{W}) \cdot P(\overline{Z}) \\[5pt] &=& 0,5 \cdot 0,88 \\[5pt] &=& 0,44 \\[5pt] \end{array}$

Die Summe der beiden Wahrscheinlichkeiten $P(A)$ und $P(B)$ ist 80%.

3. Wahrscheinlichkeit berechnen

Jetzt kannst du die Wahrscheinlichkeit bestimmen, dass ein zufälliger Prüfling an der Klausur teilnimmt und Wiederholer ist:

$\begin{array}[t]{rll} P(C) &=& \dfrac{P(A)}{P(B)}\\[5pt] &=& \dfrac{0,36}{0,8}\\[5pt] &=& 0,45 \\[5pt] \end{array}$

Die Wahrscheinlichkeit beträgt somit 45%.

HMF 8 - Stochastik (Pool 1)

8.1
$\blacktriangleright$ Bestimme den Erwartungswert

In der Abbildung auf dem Aufgabenblatt sind alle möglichen Werte einer Zufallsvariable mit zugehöriger Wahrscheinlichkeit gegeben. Um den Erwartungswert $\mu$ einer Zufallsvarible $X$ zu bestimmen, musst du die Summe aller möglichen Ereignisse $k$ multipliziert mit der jeweiligen Wahrscheinlichkeit $P(X=k)$ bilden:

$\begin{array}[t]{rll} \mu &=& 2\cdot P(X=2)+ 1\cdot P(X=1) -2 \cdot P(X=-2) \\[5pt] &=& 2\cdot 0,5 + 1 \cdot 0,25 - 2 \cdot 0,25 \\[5pt] &=& 1 + 0,25 -0,5 \\[5pt] &=& 0,75 \end{array}$

Der Erwartungswert der Zufallsvarible $X$ ist $\mu= 0,75$ .

8.2
$\blacktriangleright$ Bestimme die Wahrscheinlichkeit, dass die Zufallsvariable negativ ist

Du sollst die Wahrscheinichkeit $P(n)$ bestimmen , dass die Summe der jeweiligen Zufallsvariablen negativ ist. Dazu musst du alle Fälle betrachten, für die die Summe negativ wird. Es gibt drei mögliche Szenarien:

Das Experiment liefert zweimal $k = -2$

Das Experiment liefert zuerst $k = -2$ , dann $k=1$

Das Experiment liefert zuerst $k = 1$ , dann $k=-2$

Jetzt musst du die jeweiligen Wahrscheinlichkeiten bestimmen und summieren.

1. Wahrscheinlichkeiten berechnen

Die Wahrscheinlichkeit, dass das Experiment zweimal $k=-2$ liefert:

$\begin{array}[t]{rll} P(A) &=& P(X = -2) \cdot P(X=-2) \\[5pt] &=& 0,25 \cdot 0,25 \\[5pt] &=& 0,0625 \end{array}$

Die Wahrscheinlichkeit, dass das Experiment einmal $k=-2$ und einmal $k=1$ liefert:

$\begin{array}[t]{rll} P(B) &=& P(X = -2) \cdot P(X=1) \\[5pt] &=& 0,25 \cdot 0,25 \\[5pt] &=& 0,0625 \end{array}$

2. Wahrscheinlichkeiten summieren

Abschließend musst du die Summe der Wahrscheinlichkeiten bilden:

$\begin{array}[t]{rll} P(n) &=& P(A) + 2\cdot P(B) \\[5pt] &=& 0,0625 + 2 \cdot 0,0625 \\[5pt] &=& 0,1875 \\[5pt] \end{array}$

Die Wahrscheinlichkeit, dass die Summe der Zufallsvariablen aus zwei Zufallsexperimenten negativ ist, ist $P(n)=18,75\%$ .