Analysis 2

Aufgabe 2: Analysis

Eine Schülerin ist an einem grippalen Infekt erkrankt. Die Funktion $f$ mit

$f(t)=4t\cdot\;\mathrm{e}^{-0,5t}+36,6$ ; $t\geq0$

modelliert ihre Körpertemperatur während des Infektes. Dabei gibt $t$ die Zeit in Tagen nach Auftreten des Infektes und $f(t)$ die Körpertemperatur in $^{\circ}\text{C}$ an.
Es gilt $f‘(t)=(4-2t)\cdot\;\mathrm{e}^{-0,5t}$ .

Berechne die höchste Körpertemperatur der Schülerin während des Infektes.
Berechne die Koordinaten des Wendepunktes $W$ des Graphen von $f$ und interpretiere diese im Sachzusammenhang.
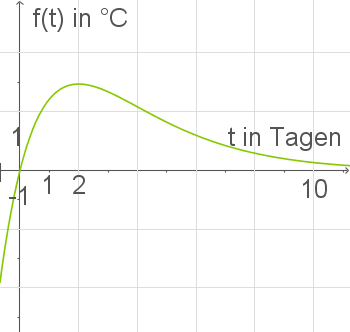
Skizziere den Graphen der Funktion $d$ mit $d(t)=4t\cdot\;\mathrm{e}^{-0,5t}$ im Intervall $[0;10]$ und beschreibe die Bedeutung der Funktion $d$ im Sachzusammenhang.

(14P)

Bestimme mittels Integration eine Stammfunktion von $f$ .
Berechne die durchschnittliche Körpertemperatur der Schülerin innerhalb der ersten Woche des Infektes.
Es gibt eine Temperatur, die zu einem bestimmten Zeitpunkt und dann genau zwei Tage später erneut erreicht wird. Bestimme diese Temperatur und die Zeitpunkte, an denen sie erreicht wird.

(12P)

Die zeitlichen Verläufe der Körpertemperatur anderer Personen während eines Infektes können durch die Funktionenschar $h_k$ mit

$h_k(t)=\dfrac{2}{k}\cdot\;t\cdot\;\mathrm{e}^{-kt}+36,6$ ; $k\gt 0$

modelliert werden.

Jeder Graph der Schar hat einen Hochpunkt $H_k$ . Bestimme die Koordinaten dieses Hochpunktes.

$\left[\text{Kontrolle:}\;H_k\left(\dfrac{1}{k}\;|\;\dfrac{2}{ek^2}+36,6\right)\right]$

Der Krankheitsverlauf wird kritisch, wenn das Maximum der Körpertemperatur $41^{\circ}\text{C}$ oder mehr erreicht. Bestimme diejenigen Werte des Parameters $k$ , für die der Krankheitsverlauf kritisch wird.

(10P)

Es soll der größte $y$ -Achsenabschnitt bestimmt werden, den eine Tangente an den Graphen von $f$ haben kann. Leite eine Zielfunktion für diese Extremwertaufgabe her.

(4P)

$\blacktriangleright$ Maximale Körpertemperatur bestimmen

Gesucht ist die maximale Körpertemperatur der Schülerin, die durch die Funktion $f$ modelliert wird. Deine Aufgabe besteht darin die Koordinaten des Maximums zu ermitteln.
Wenn $x$ eine Maximumstelle ist, so gilt:

$f‘(t)=0$

$f‘‘(t) \lt 0$

Ermittle also zuerst eine Stelle, die das erste Kriterium erfüllt und überprüfe, ob diese Stelle auch dem zweiten Kriterium genügt. Setze diese Stelle anschließend in die Funktion $f$ ein, um den Wert der Körpertemperatur zu diesem Zeitpunkt zu ermitteln.

Setze $f‘$ gleich null und löse die Gleichung nach $t$ auf.

$\begin{array}[t]{rll} 0 &=& f‘(t) \\[5pt] 0 &=& (4-2t) \cdot \mathrm e^{-0,5t} \\[5pt] \end{array}$

Da die $\mathrm e$ -Funktion für keinen Wert von $t$ null wird, kannst du beide Seiten der Gleichung durch $\mathrm e^{-0,5t}$ teilen.

$\begin{array}[t]{rll} 0 &=& (4-2t) \\[5pt] t &=& 2 \end{array}$

Prüfe nun, ob diese Stelle das zweite Kriterium erfüllt. Leite dafür $f‘$ mithilfe der Produktregel nacht $t$ ab.

$\begin{array}[t]{rll} f‘‘(t)&=& -2 \cdot \mathrm e^{-0,5t} -0,5 \cdot (4-2t) \cdot \mathrm e^{-0,5t} \\[5pt] f‘‘(2)&\approx& -0,74 \lt 0 \end{array}$

Somit handelt es sich um ein Maximum, d.h. die höchste Körpertemperatur wird nach $2$ Tagen erreicht. Setze $t=2$ in die ursprüngliche Gleichung ein, um die $y$ -Koordinate zu ermitteln.

$\begin{array}[t]{rll} f(2)&=& 4 \cdot 2 \cdot \mathrm e^{-0,5 \cdot 2} + 36,6 \\[5pt] &\approx& 39,54. \end{array}$

Die Höchsttemperatur von $39,54°$ wird also nach $2$ Tagen erreicht.

$\blacktriangleright$ Koordinaten des Wendepunkts berechnen

Du musst nun die Koordinaten des Wendepunkts der Funktion $f$ bestimmen. Eine Wendestelle lässt sich dabei wie folgt charakterisieren:

Ist $f$ eine Funktion, die dreimal stetig differenzierbar ist, und $(x_W \mid f(x_W))$ sind die Koordinaten eines Wendepunkts, so gilt

$f‘‘(x_W) = 0$

$f‘‘‘(x_W) \neq 0$

Als erstes bestimmst du eine Stelle, die das erste Kriterium erfüllt. Dafür benötigst du die zweite Ableitung $f‘‘$ , die du schon in der ersten Teilaufgabe bestimmt hast. Setze sie gleich null und löse sie nach $t$ auf.

$\begin{array}[t]{rll} 0 &=& f‘‘(t) \\[5pt] 0 &=& -2 \cdot \mathrm e^{-0,5t} -0,5 \cdot (4-2t) \cdot \mathrm e^{-0,5t} &\quad \scriptsize \mid\;\text{Klammere } \mathrm -e^{-0,5t} \text{ aus} \\[5pt] 0 &=& - \mathrm e^{-0,5t} \cdot (2 + 0,5 \cdot (4 - 2t) ) \end{array}$

Da die $\mathrm e$ -Funktion keine Nullstelle besitzt, kannst du die Gleichung durch $-e^{-0,5t}$ teilen.

$\begin{array}[t]{rll} 0 &=& (2 + 0,5 \cdot (4 - 2t) ) \\[5pt] 0 &=& 2 + 2 - t \\[5pt] t &=& 4 \end{array}$

Prüfe nun mit dem zweiten Kriterium, ob diese Stelle auch eine Wendestelle ist. Leite die Funktion $f‘‘$ mithilfe der Produkt- und Kettenregel nach $t$ ab und setze $t=4$ ein.

$\begin{array}[t]{rll} f‘‘‘(t) &=& \mathrm e^{-0,5t} + \mathrm e^{-0,5t} + 0,25 \cdot (4-2t) \cdot \mathrm e^{-0,5t} \\[5pt] f‘‘‘(4) &=& \mathrm e^{-0,5 \cdot 4} + \mathrm e^{-0,5 \cdot 4} + 0,25 \cdot (4-2 \cdot 4) \cdot \mathrm e^{-0,5 \cdot 4} \\[5pt] f‘‘‘(4) &=& 2 \mathrm e^{-2} - \mathrm e^{-2} \\[5pt] f‘‘‘(4) &=& \mathrm e^{-2} \neq 0 \end{array}$

Somit erfüllt $t=4$ die Kriterien einer Wendestelle. Setze $t=4$ in die ursprüngliche Funktion ein, um die $y$ -Koordinate zu erhalten.

$\begin{array}[t]{rll} f(4) &=& 4 \cdot 4 \cdot \mathrm e^{-0,5 \cdot 4} +36,6; \\[5pt] &\approx& 38,77 \end{array}$

Demnach sind die Koordinaten der Wendestelle gegeben durch $(4 \mid 38,77).$

$\blacktriangleright$ Bedeutung des Wendepunkts erklären

Ein Wendepunkt ist ein Punkt, an dem der Funktionsgraph sein Krümmungsverhalten ändert. In diesem Fall hast du eine Rechts-links-Wendestelle, da $f‘‘‘(4) > 0$ ist. Demnach handelt es sich um eine Stelle minimalen Anstiegs, d.h. am vierten Tag fällt die Körpertemperatur der Schülerin am meisten.

$\blacktriangleright$ Skizze des Graphen der Funktion $\boldsymbol{d}$ erstellen und in Sachzusammenhang einordnen

Diese Funktion beschreibt den Verlauf der Körpertemperatur der Schülerin, die über der normalen Körpertemperatur von $36,6 \, °\text{C}$ liegt. Nach $2$ Tagen ist die Körpertemperatur um ca. $2,94 \, °\text{C}$ gestiegen. Danach beginnt sie wieder zu sinken, sodass sie nach $10$ Tagen schon wieder sehr nah an $0 \, °\text{C}$ ist.

Zeichne die Stellen, die dir schon bekannt sind, in das Schaubild ein. Außerdem weißt du, dass zwischen dem Ursprung und dem Hochpunkt die Funktion monoton steigend ist und ab dem Hochpunkt monoton fallend. Dabei konvergiert die Funktion für $x \rightarrow \infty$ gegen $0.$

Diagramm einer Funktion mit Temperatur in °C über Zeit in Tagen, dargestellt durch eine grüne Kurve.

Abb. 1: Funktion $d$ im Intervall $[0; \, 10]$

$\blacktriangleright$ Stammfunktion von $\boldsymbol{f}$ bestimmen

Bestimme eine Stammfunktion von $f$ , indem du eine Funktion $F$ herleitest, die abgeleitet $f$ ergibt.

$\begin{array}[t]{rll} F(t) &=& \int f(t) \, \text{ dt} \\[5pt] &=& \int 4t \cdot \mathrm e^{-0,5t} + 36,6 \, \text{ dt} \\[5pt] \end{array}$

Um dieses unbestimmte Integral zu bestimmen, benötigst du die Formel für die partielle Integration:

$\int f‘(x) \cdot g(x) \text{ dx} = f(x) \cdot g(x) - \int f(x) \cdot g‘(x) \text{ dx}$

Dabei sind $f$ und $g$ differenzierbare Funktionen.

$\begin{array}[t]{rll} F(t) &=& \int 4t \cdot \mathrm e^{-0,5t} + 36,6 \, \text{ dt} \\[5pt] &=& 36,6t + 4 \cdot \int \underbrace{t}_{:=g} \cdot \underbrace{\mathrm e^{-0,5t}}_{:=f‘} \, \text{ dt} \\[5pt] &=& 36,6t + 4 \cdot \big[ -2 \cdot \mathrm e^{-0,5t} \cdot t - \int -2 \cdot \mathrm e^{-0,5t} \cdot 1 \text{ dt} \big] \\[5pt] &=& 36,6t + 4 \cdot \big[ -2 \cdot \mathrm e^{-0,5t} \cdot t - 4 \cdot \mathrm e^{-0,5t} \text{ dt} \big] \\[5pt] &=& 36,6t - 8 t \cdot \mathrm e^{-0,5t} - 16 \cdot \mathrm e^{-0,5t} \end{array}$

Eine Stammfunktion von $f$ ist also gegeben durch $F(t) = 36,6t - 8 t \cdot \mathrm e^{-0,5t} - 16 \cdot \mathrm e^{-0,5t}$ . Um sicher zu gehen, kannst du diese Funktion nach $t$ ableiten und prüfen, ob sie wirklich $f$ ergibt.

$\blacktriangleright$ Durchschnittliche Körpertemperatur der Schülerin berechnen

Berechne die durchschnittliche Körpertemperatur $\overline{f}$ der Schülerin in der ersten Woche, indem du die Funktion $f$ im gefragten Zeitraum $[0; \, 7]$ integrierst und anschließend durch die Länge dieses Intervalls teilst.

$\begin{array}[t]{rll} \overline{f} &=& \dfrac{\int_{0}^7 f(t) \text{ dt}}{7} \\[5pt] &=& \dfrac{F(7) - F(0)}{7} \\[5pt] &=& \dfrac{36,6 \cdot 7 - 8 \cdot 7 \cdot \mathrm e^{-0,5 \cdot 7} - 16 \cdot \mathrm e^{-0,5 \cdot 7} - 36,6 \cdot 0 + 8 \cdot 0 \cdot \mathrm e^{-0,5 \cdot 0} + 16 \cdot \mathrm e^{-0,5 \cdot 0}}{7} \\[5pt] &\approx& 38,58 \end{array}$

Die durchschnittliche Körpertemperatur der Schülerin während der ersten $7$ Tage liegt also bei ca. $38,58 \, °\text{C}$ .

$\blacktriangleright$ Stammfunktion von $\boldsymbol{f}$ bestimmen

Du sollst nun die Temperatur bestimmen, die zu einem bestimmten Zeitpunkt auftritt und dann nach genau zwei Tagen erneut erreicht wird. Formuliere diesen Sachverhalt mithilfe einer Gleichung, die von $t$ abhängt und löse die Gleichung nach $t$ auf. Es muss gelten:

$\begin{array}[t]{rll} f(t) &=& f(t+2) \\[5pt] 4t \cdot \mathrm e^{-0,5t} + 36,6 &=& 4 \cdot (t+2) \cdot \mathrm e^{-0,5 \cdot (t+2)} + 36,6 &\quad \scriptsize \mid\ -36,6; \, :4 \mathrm e^{-0,5t} \\[5pt] t &=&(t+2) \cdot \mathrm e^{-1} \\[5pt] t &=& t \cdot \mathrm e^{-1} + 2 \cdot \mathrm e^{-1} &\quad \scriptsize \mid\ -t \cdot \mathrm e^{-1} \\[5pt] t - t \cdot \mathrm e^{-1} &=& 2 \cdot \mathrm e^{-1} \\[5pt] t \cdot (1- \mathrm e^{-1}) &=& 2 \cdot \mathrm e^{-1} &\quad \scriptsize \mid\ :(1- 4 \mathrm e^{-1}) \\[5pt] t &=& \dfrac{2 \cdot \mathrm e^{-1}}{1- \mathrm e^{-1}} \\[5pt] t &=& \dfrac{2}{\mathrm e- 1} \end{array}$

Setze nun den Wert $t = \dfrac{2}{e-1}$ in die Funktion $f$ ein, um die Körpertemperatur zu diesem Zeitpunkt zu erhalten.

$\begin{array}[t]{rll} f(\dfrac{2}{e-1})&=& 4 \cdot \dfrac{2}{e-1} \cdot \mathrm e^{-0,5 \cdot \frac{2}{e-1}} + 36,6 \\[5pt] &\approx& 39,20 \end{array}$

Zum Zeitpunkt $t_1 = \dfrac{2}{e-1}$ hat die Schülerin eine Körpertemperatur von ca. $39,2 \, ° \text{C}$ . Genau zwei Tage später, also zum Zeitpunkt $t_2 = \dfrac{2}{e-1} + 2$ , wird erneut diese Temperatur erreicht.

$\blacktriangleright$ Hochpunkt $\boldsymbol{H_k}$ bestimmen

Die Verläufe der Körpertemperaturen anderer Personen werden durch die Funktionenschar $h_k$ modelliert. Deine Aufgabe besteht darin den Hochpunkt, also die maximale Temperatur dieser Funktionenschar zu bestimmen. Gehe dabei genauso vor wie du bei allen anderen Funktionen vorgehst, um das Maximum zu bestimmen. Behandle $k \gt 0$ als Konstante. Folgende Kriterien für ein Maximum an der Stelle $x$ müssen dabei erfüllt sein:

$h‘(x)=0$

$h‘‘(x) \lt 0$

Für die erste Ableitung von $h$ gilt mit der Produktregel:

$\begin{array}[t]{rll} h_k ‘(t) &=& \dfrac{2}{k} \cdot (\mathrm e^{-k \cdot t} - k \cdot t \cdot \mathrm e^{-k \cdot t} )\\[5pt] \end{array}$

Setze $h_k‘$ gleich null:

$\begin{array}[t]{rll} 0 &=& \dfrac{2}{k} \cdot (\mathrm e^{-k \cdot t} - k \cdot t \cdot \mathrm e^{-k \cdot t} ) \\[5pt] &=& \dfrac{2}{k} \cdot \mathrm e^{-k \cdot t} \cdot (1 - k \cdot t) \end{array}$

Da die $\mathrm e$ -Funktion keine Nullstellen haben kann, ist die einzig mögliche Nullstelle der ersten Ableitung $t_1 = \dfrac{1}{k}.$ Prüfe mit dem zweiten Kriterium, ob es sich um ein Maximum handelt:

$\begin{array}[t]{rll} h_k‘‘(t)&=& \dfrac{2}{k} \cdot (-k \cdot \mathrm e^{-k \cdot t} - k \cdot \mathrm e^{-k \cdot t} + k^2 \cdot t \cdot \mathrm e^{-kt})\\[5pt] &=& 2 \cdot \mathrm e^{-k \cdot t} \cdot (-2 + k \cdot t ) \\[5pt] h_k‘‘(\dfrac{1}{k}) &=& 2 \cdot \mathrm e^{-k \cdot \frac{1}{k}} \cdot (-2 + k \cdot \dfrac{1}{k} ) \\[5pt] &=& -2 \cdot \mathrm e^{-1} \\[5pt] &\lt & 0 \end{array}$

Demnach handelt es sich bei $t_1 = \dfrac{1}{k}$ um ein Maximum. Setze $t_1$ in $h$ ein, um die $y$ -Kordinate des Hochpunkts zu erhalten:

$\begin{array}[t]{rll} h_k(t) &=& \dfrac{2}{k} \cdot \dfrac{1}{k} \cdot \mathrm e^{-k \cdot \frac{1}{k}} +36,6 \\[5pt] &=& \dfrac{2}{\mathrm e \cdot k^2} +36,6 \end{array}$

Die Koordinaten des Hochpunkts sind folglich $H_k\left(\dfrac{1}{k} \mid \dfrac{2}{\mathrm e k^2} +36,6\right).$

$\blacktriangleright$ kritischen Wert von $\boldsymbol{k}$ bestimmen

Sobald die Körpertemperatur größer als $41 \, ° \text{C}$ wird, ist der Krankheitsverlauf als kritisch zu betrachten. Bestimme die $k$ für die der Krankheitsverlauf kritisch wird, indem du die $y$ -Koordinate des Hochpunkts berechnest, für die der Wert größer als $41 \, ° \text{C}$ ist. Denn wenn die $y$ -Koordinate des Hochpunkts größer als $41 \, ° \text{C}$ ist, weißt du automatisch, dass die Körpertemperatur in einem bestimmten Zeitraum über $41 \, ° \text{C}$ ist.

$\begin{array}[t]{rll} 41 &\leq& \dfrac{2}{\mathrm e \cdot k^2} + 36,6 &\quad \scriptsize \mid\ \cdot \mathrm e \cdot k^2\\[5pt] 41 \cdot \mathrm e \cdot k^2 &\leq& 2+36,6\cdot \mathrm e \cdot k^2 &\quad \scriptsize \mid\ -36,6\cdot \mathrm e \cdot k^2\\[5pt] 4,4\cdot \mathrm e\cdot k^2&\leq& 2&\quad \scriptsize \mid\ :4,4\cdot \mathrm e \\[5pt] k^2 &\leq& \dfrac{1}{2,2 \cdot \mathrm e } \end{array}$

Diese Ungleichung ist genau dann erfüllt, wenn $k$ zwischen $k_1 = -\sqrt{\dfrac{1}{2,2 \cdot \mathrm e}}$ und $k_2 = \sqrt{\dfrac{1}{2,2 \cdot \mathrm e}}$ liegt. Da aber nach Voraussetzung $k \gt 0$ gilt, wird der Krankheitsverlauf genau dann kritisch, wenn $k$ im Intervall $(0; \, \sqrt{\dfrac{1}{2,2 \cdot \mathrm e}}]$ liegt.

$\blacktriangleright$ Größten $\boldsymbol{y}$ -Achsenabschnitt bestimmen

Gesucht ist in dieser Aufgabe der größte $\boldsymbol{y}$ -Achsenabschnitt $c$ einer Tangente der Funktion $f$ in einem Punkt $(t \mid f(t))$ mit $t \geq 0.$ Eine Tangente wird durch die Tangentengleichung

$y = m \cdot x + c$

beschrieben. Dabei ist $m$ die Steigung der Tangente und $c$ der $y$ -Achsenabschnitt.

Da es sich um eine Tangente an einem Punkt $(t \mid f(t))$ handelt, ist die Steigung $m$ gebene durch $m = f‘(t).$ Weiterhin geht die Tangente durch den Punkt $(t \mid f(t))$ , sodass $x = t$ und $y = f(t)$ ist. Setze diese Werte in die Tangentengleichung ein und löse diese Gleichung nach $c$ auf. Da es sich in diesem Fall nicht um eine Zahl $c$ handelt, sondern um eine Funktion deren Maximum bestimmt werden soll, wähle anstatt $c$ die Bezeichnung $c(t)$ . Dabei ist $c(t)$ die Zielfunktion.

$\begin{array}[t]{rll} y &=& m \cdot x + c \\[5pt] f(t) &=& f‘(t) \cdot t + c(t) &\quad \scriptsize \mid\ -f‘(t) \cdot t \\[5pt] c(t) &=& f(t) - f‘(t) \cdot t \\[5pt] c‘(t) &=& f‘(t) - f‘(t) - t \cdot f‘‘(t) \\[5pt] c‘(t) &=& - t \cdot f‘‘(t) \end{array}$

Die zweite Ableitung $f‘‘$ hast du schon in Teilaufgabe a) bestimmt. Setze nun $c‘(t)$ gleich $0$ , um die Extremstellen von $c‘$ zu bestimmen.

$\begin{array}[t]{rll} 0 &=& - t \cdot f‘‘(t) \\[5pt] 0 &=& -t \cdot (-2 \mathrm e^{-0,5t} - 0,5 \cdot (4-2t) \cdot \mathrm e^{-0,5 t}) &\quad \scriptsize \mid\ :(-e^{0,5 t}) \\[5pt] 0 &=& t \cdot (2 + 0,5 \cdot (4-2t)) \\[5pt] 0 &=& t \cdot (4-t) \end{array}$

Somit sind $t_1 = 0$ und $t_2 = 4$ zwei mögliche Extremstellen. Überprüfe nun, um welche Art von Extremstellen es sich handelt. Falls es sich um ein Maximum handelt, muss gelten:

$c‘‘(t) \lt 0$

Die zweite Ableitung von $c$ bestimmst du dabei mithilfe der Produktregel:

$\begin{array}[t]{rll} c‘‘(t)&=& -f‘‘(t) - t \cdot f‘‘‘(t) \\[5pt] &=& 2 \cdot \mathrm e^{-0,5t} + 0,5 \cdot (4-2t) \cdot \mathrm e^{-0,5t} \\[5pt] & & - t \cdot (\mathrm e^{-0,5t} + \mathrm e^{-0,5t} + 0,25 \cdot (4-2t) \cdot \mathrm e^{-0,5t}) \end{array}$

Bei der ersten Stelle $x_1$ kannst du anhand der Skizze sofort erkennen, dass es sich nicht um ein Maximum handeln kann, was durch das Einsetzen von $t_1$ in $c‘‘$ bestätigt wird:

$\begin{array}[t]{rll} c‘‘(0) &=& 2 \cdot \mathrm e^{-0,5 \cdot 0} + 0,5 \cdot (4-2 \cdot 0) \cdot \mathrm e^{-0,5 \cdot 0} \\[5pt] &=& 4 \\[5pt] &\gt & 0 \end{array}$

Setze nun $t_2$ in $c‘‘$ ein:

$\begin{array}[t]{rll} c‘‘(4)&=& 2 \cdot \mathrm e^{-0,5 \cdot 4} + 0,5 \cdot (4-2 \cdot 4) \cdot \mathrm e^{-0,5 \cdot 4} \\[5pt] & & - 4 \cdot (2 \cdot \mathrm e^{-0,5 \cdot 4} + 0,25 \cdot (4-2 \cdot 4) \cdot \mathrm e^{-0,5 \cdot 4}) \end{array}$

Ohne es explizit ausrechnen zu müssen erkennst du, dass $c‘‘(4) \lt 0$ ist und es sich somit um ein Maximum handelt.

$\begin{array}[t]{rll} c(4) &=& 4 \cdot 4 \cdot \mathrm e^{-0,5 \cdot 4} + 36,6 - 4 \cdot (4-2 \cdot 4) \cdot \mathrm e^{-0,5 \cdot 4} \\[5pt] &=& 16 \cdot \mathrm e^{-2} + 36,6 +16 \cdot \mathrm e^{-2} \\[5pt] &\approx& 40,93 \end{array}$

Der maximale $y$ -Achsenabschnitt beträgt somit $40,93 \, ° \text{C.}$

Bildnachweise [nach oben]

[1]