Lerninhalte in Mathe

Abi-Aufgaben (WTR)

Abi-Aufgaben (CAS)

Digitales Schulbuch

Inhaltsverzeichnis

Analysis 1

Aufgabe 1: Analysis

Zwischen zwei Orten $A$ und $B$ befindet sich ein Tal mit einem tiefsten Punkt $T$ . Der Querschnitt des Tals kann durch den Graphen einer ganzrationalen Funktion $f$ dritten Grades beschrieben werden, wobei $f(x)$ die Höhe über dem Meeresspiegel in Kilometern angibt. Im dargestellten Koordinatensystem entspricht eine Einheit einem Kilometer in der Wirklichkeit. Die Orte $A$ und $B$ sowie der Tiefpunkt $T$ haben die Koordinaten $A(0 \mid 0,2), B(1 \mid 0,3)$ und $T(0,5 \mid 0,13)$ .

undefined

Abb. 1

Der Graph der Funktion $f$ ist zusätzlich in Abb. 2 vergrößert dargestellt.

a)

a1)

Leite eine Gleichung der Funktion $f$ her.

(5 BE)

a2)

Bestimme die Stelle, an der der Querschnitt des Tals eine Höhe von $240\,\text{m}$ über dem Meeresspiegel aufweist, und bestimme die Steigung an dieser Stelle.

(2 BE)

a3)

Eine Person wandert von $A$ nach $T$ . Bestimme das durchschnittliche und das maximale Gefälle auf diesem Weg.

(7 BE)

Als Touristenattraktion soll zwischen den Punkten $A$ und $B$ eine Hängebrücke errichtet werden. Der Verlauf der Hängebrücke kann durch den Graphen einer Funktion $g$ mit $g(x) = 0,2x^2 − 0,1 x + 0,2$ beschrieben werden.

b)

b1)

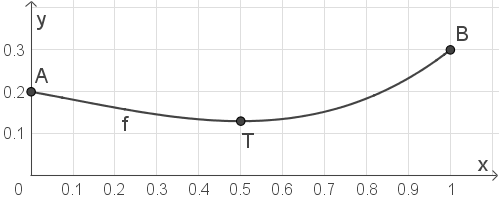
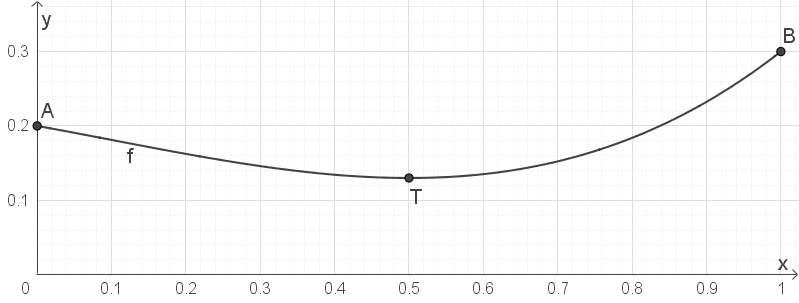
Ergänze die Wertetabelle und zeichne den Graphen.

(4 BE)

b2)

Berechne den Winkel $\alpha$ zwischen dem Verlauf der Hängebrücke und dem Querschnitt des Tals im Punkt $B$ .

(3 BE)

c)

c1)

Es gibt Punkte auf der Hängebrücke, deren Höhe über dem Boden $50\,\text{m}$ beträgt. Zeichne diese Punkte ein.

(2 BE)

c2)

Ermittle rechnerisch die größte Höhe der Hängebrücke über dem Boden.

Die Länge $L$ des Graphen der Funktion $g$ über dem Intervall $[a;b]$ kann durch

$L = \displaystyle\int_{a}^{b} \sqrt{1 + (g‘(x))^2} \mathrm dx$

berechnet werden.

(5 BE)

c3)

Berechne die Länge der Hängebrücke.

(2 BE)

c4)

Begründe, dass

$\displaystyle\int_{0}^{b} \sqrt{1 + (g‘(x))^2} \mathrm dx$ $\gt$ $\sqrt{b^2 + (g(b) - g(0))^2}$ für alle $0 \lt b \leq 1$

gilt.

(3 BE)

d)

Auch die auf $\mathbb{R}$ definierte Funktion

$h$ mit $h(x) = \dfrac{1}{2} \cdot (e^x + e^{-x})$

kann zur Beschreibung von Hängebrücken verwendet werden. Es gilt $h‘‘(x) = h(x)$ .

d1)

Weise rechnerisch nach, dass $(h(x))^2 - (h‘(x))^2 = 1$ gilt.

(4 BE)

d2)

Leite her, dass $\displaystyle\int_{a}^{b} \sqrt{1 + (h‘(x))^2} \mathrm dx = h‘(b) - h‘(a)$ ist.

(3 BE)

Material

$x$	$g(x)$
$0$
$0,1$	$0,192$
$0,2$
$0,3$
$0,4$
$0,5$
$0,6$
$0,7$
$0,8$
$0,9$	$0,272$
$1$

undefined

Abb. 2

a)

a1)

$\blacktriangleright$ Funktionsgleichung herleiten

Bei $f$ handelt es sich um eine ganzrationale Funktion dritten Grades:

$\begin{array}[t]{rll} f(x) &=& ax^3 +bx^2 +cx +d \\[5pt] f‘(x) &=& 3ax^2 +2bx + c \end{array}$

Mit den Koordinaten aus dem Aufgabentext folgt:

$f(0) = 0,2$
$f(1) = 0,3$
$f(0,5) = 0,13$
$f‘(0,5) = 0$

Es ergibt sich folgendes Gleichungssystem:

$\begin{array}{lrll} \text{I}\quad& 0,2...\\[10pt] \text{II}\quad& 0,3... \\[10pt] \text{III}\quad&0,13... \\[10pt] \text{IV}\quad& 0 ... \\[5pt] \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Aus dem Gleichungssystem der letzten drei Gleichungen erhältst du dann:

$a=0,4$
$b= -0,12$
$c= -0,18$
$d= 0,2$

Eine Gleichung von $f$ lautet also:

$f(x)= 0,4x^3 -0,12x^2 -0,18x +0,2.$

a2)

$\blacktriangleright$ Stelle mit der Höhe bestimmen

$x\approx 0,9129$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

An der Stelle $x\approx 0,9129$ beträgt die Höhe über dem Meeresspiegel ca. $240\,\text{m}.$

$\blacktriangleright$ Steigung bestimmen

$f‘(0,9129)\approx 0,601$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

An der Stelle, an der die Höhe über dem Meeresspiegel ca. $240\,\text{m}$ beträgt, beträgt die Steigung ca. $60,1\,\%.$

a3)

$\blacktriangleright$ Durchschnittliches Gefälle bestimmen

$\begin{array}[t]{rll} \overline{m} &=& \dfrac{0,13 - 0,2}{0,5-0} \\[5pt] &=& \dfrac{-0,07}{0,5} \\[5pt] &=& -0,14 \end{array}$

Auf dem Weg von $A$ nach $T$ beträgt das durchschnittliche Gefälle $14\,\%.$

$\blacktriangleright$ Maximales Gefälle bestimmen

Gesucht ist der kleinste Funktionswert von $f‘$ im Intervall $[0;0,5].$

1. Schritt: Ableitungsfunktionen bestimmen

$\begin{array}[t]{rll} f‘(x) &= ... \\[5pt] f‘‘(x) &= ... \\[5pt] f‘‘‘(x) &= ... \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

2. Schritt: Notwendiges Kriterium für Extremstellen anwenden

$x=0,1$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

3. Schritt: Hinreichendes Kriterium überprüfen

$f‘‘‘(0,1) = 2,4$

An der Stelle $x=0,1$ besitzt $f‘$ also ein lokales Minimum.

4. Schritt: Funktionswerte der Intervallränder vergleichen

$\begin{array}[t]{rll} f‘(0,1) &=& -0,192 \\[10pt] f‘(0) &=& -0,18 \\[10pt] f‘(0,5) &=& 0 \\[10pt] \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Das globale Minimum von $f‘$ liegt also an der Stelle $x=0,1.$ Das maximale Gefälle auf dem Weg von $A$ nach $T$ beträgt $19,2\,\%.$

b)

b1)

$\blacktriangleright$ Wertetabelle und Graph ergänzen

$x$	$g(x)$
$0$	$0,2$
$0,1$	$0,192$
$0,2$	$0,188$
$0,3$	$0,188$
$0,4$	$0,192$
$0,5$	$0,2$
$0,6$	$0,212$
$0,7$	$0,228$
$0,8$	$0,248$
$0,9$	$0,272$
$1$	$0,3$

undefined

Abb. 1: Einzeichnen des Graphen von $g$

b2)

$\blacktriangleright$ Winkel berechnen

Ermittle die jeweiligen Steigungswinkel der beiden Graphen:

$\alpha_1\approx 37,95^{\circ}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Für die Hängebrücke folgt:

$\alpha_2\approx 16,70^{\circ}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Es ist

$\alpha_1-\alpha_2 \approx 21,25^{\circ}.$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Der Winkel zwischen dem Verlauf der Hängebrücke und dem Querschnitt des Tals beträgt ca. $21,25^{\circ}.$

c)

c1)

$\blacktriangleright$ Punkte einzeichnen

undefined

Abb. 2: Einzeichnen der Punkte mit einem Abstand von $50\,\text{m}$

c2)

$\blacktriangleright$ Größte Höhe über dem Boden ermitteln

Die Höhe der Hängebrücke über dem Boden kann durch folgende Differenzenfunktion beschrieben werden:

$h(x)=-0,4x^3 +0,32x^2 +0,08x$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Gesucht ist nun der maximale Funktionswert von $h$ im Intervall $[0;1]:$

1. Schritt: Ableitungsfunktionen bestimmen

$\begin{array}[t]{rll} h‘(x) &= -1,2x^2 +0,64x +0,08 \\[5pt] h‘‘(x) &= -2,4x +0,64 \end{array}$

2. Schritt: Notwendiges Kriterium für Extremstellen anwenden

$\begin{array}[t]{rll} h‘(x) &=& 0 \\[5pt] x_1 &\approx& -0,105\\[5pt] x_2 &\approx& 0,638 \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

$x_1$ liegt außerhalb des betrachteten Bereichs. Also wird im Folgenden nur $x_2$ betrachtet:

3. Schritt: Hinreichendes Kriterium überprüfen

$h‘‘(0,638) \lt 0$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

An der Stelle $x \approx 0,638$ besitzt $h$ also ein lokales Maximum.

4. Schritt: Funktionswerte der Intervallränder vergleichen

$\begin{array}[t]{rll} h(0,638) &\approx& 0,077 \\[5pt] h(0) &=& 0 \\[5pt] h(1) &=& 0 \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Die größte Höhe der Hängebrücke über dem Boden beträgt also ca. $77\,\text{m}.$

c3)

$\blacktriangleright$ Länge der Hängebrücke berechnen

$L_H\approx 1,012$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Die Hängebrücke ist ca. $1012\,\text{m}$ lang.

c4)

$\blacktriangleright$ Ungleichung begründen

Mit $\displaystyle\int_{0}^{b}\sqrt{1+(g‘(x))^2}\;\mathrm dx$ wird die Länge der Hängebrücke vom Punkt $A$ bis zum Punkt $P(b\mid g(b))$ berechnet.
Mit $\sqrt{b^2+(g(b)-g(0))^2}$ wird nach dem Satz des Pythagoras die Länge der direkten geradlinigen Verbindungsstrecke zwischen $A$ und $P(b\mid g(b))$ berechnet.
Da die Brücke nicht geradelinig verläuft, ist sie Länger als die direkte geradlinige Verbindungsstrecke zwischen den beiden betrachteten Punkten.

d)

d1)

$\blacktriangleright$ Gleichung rechnerisch nachweisen

$h‘(x)=...$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Dann folgt:

$(h(x))^2 - (h‘(x))^2 ...$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

d2)

$\blacktriangleright$ Gleichung herleiten

Es ist:

$(h(x))^2 = 1 +(h‘(x))^2$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Einsetzen liefert:

$\displaystyle\int_{a}^{b}\sqrt{1+(h‘(x))^2}\;\mathrm dx = ...$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen