Analysis 2

Eine Glasvase wird durch einen Rotationskörper modelliert, der durch die Rotation von zwei Funktionsgraphen um die $x$ -Achse entsteht (siehe Abbildung).

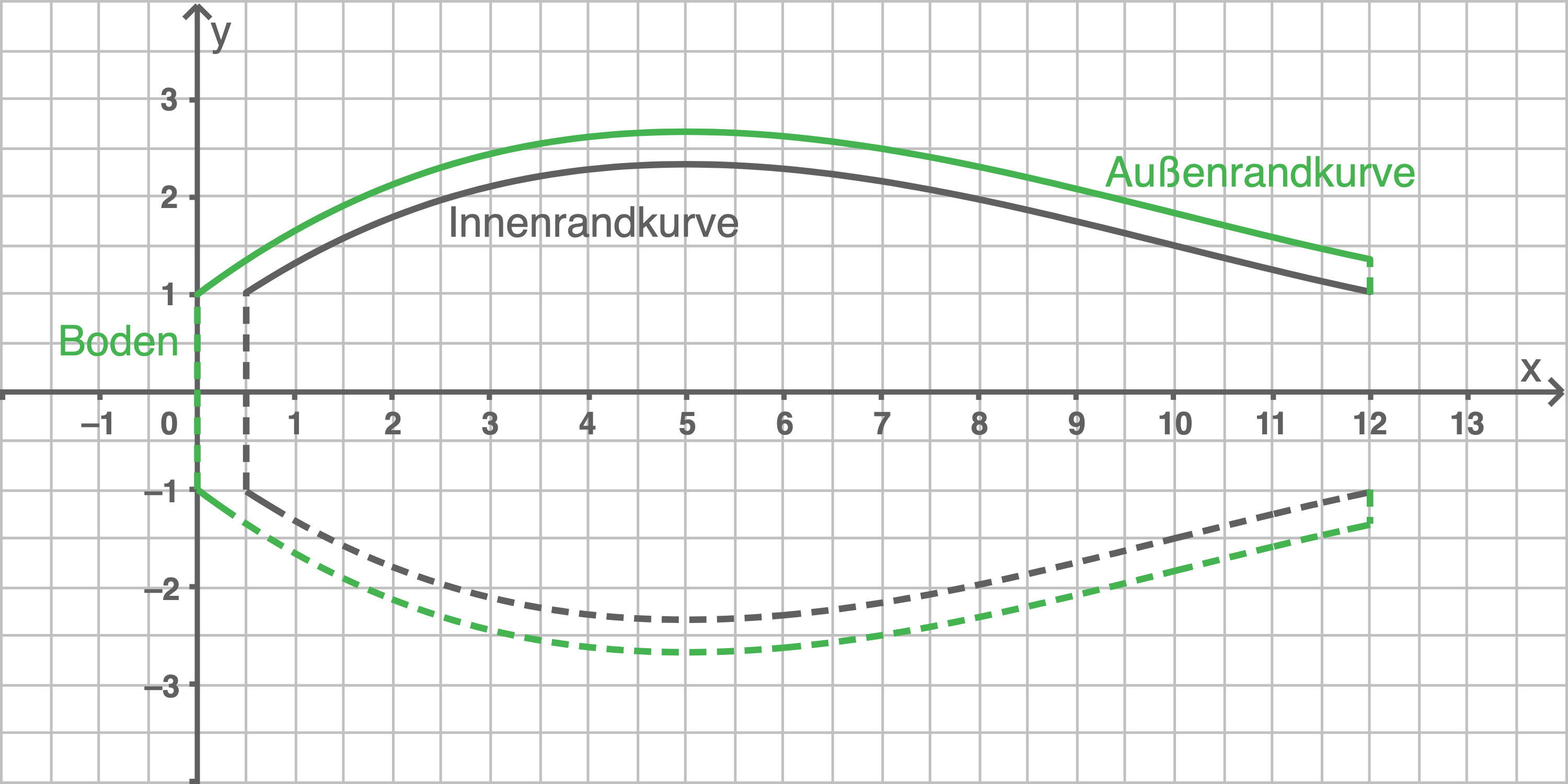
Gitter-Koordinatensystem mit zwei oberen Kurven (grün Außenrandkurve, grau Innenrandkurve), gestrichelte untere Kurven, x- und y-Achse

Eine Längeneinheit im Modell entspricht einem Zentimeter in der Wirklichkeit.

Die Außenrandkurve in der Abbildung wird im Intervall $[0 ; 12]$ beschrieben durch den Graphen einer ganzrationalen Funktion $f$ mit $f(x)=a x^3+b x^2+c x+1,$ wobei $a, b$ und $c$ reelle Zahlen sind.

Der Graph der Funktion $f$ hat an der Stelle $x=5$ einen Hochpunkt. An der Stelle $x=10$ hat der Graph einen Wendepunkt und die Steigung $-\frac{1}{4}.$

a1)

Leite einen Funktionsterm von $f$ her.

$\left[\text{zur Kontrolle: } f(x)=\dfrac{1}{300} x^3-\dfrac{1}{10} x^2+\dfrac{3}{4} x+1 \right]$

(6 BE)

a2)

Begründe, dass der Graph der Funktion $f$ an allen Stellen $x$ mit $x \leq 0$ rechtsgekrümmt ist.

(2 BE)

a3)

Die Vase steht aufrecht in einer geschlossenen zylinderförmigen Verpackung, so dass der Boden der Vase auf deren kreisförmiger Grundfläche steht. Der Radius und die Höhe der zylinderförmigen Verpackung sind so klein wie möglich gewählt.
Berechne den Inhalt der Außenfläche der Verpackung. Vernachlässige dabei die Dicke des Verpackungsmaterials.

(4 BE)

Die Innenrandkurve in der Abbildung wird im Intervall $[0,5 ; 12]$ beschrieben durch den Graphen der Funktion $g$ mit

$g(x)=\dfrac{1}{300} x^3-\dfrac{1}{10} x^2+\dfrac{3}{4} x+\dfrac{2}{3}.$

b1)

Im Rahmen einer Aufgabe im Sachkontext wird die folgende Berechnung durchgeführt:

$\pi \cdot \displaystyle\int_{0,5}^{0,5+h}(g(x))^2 \;\text{d} x=120 \quad$ $\Rightarrow \quad h \approx 9,58$

Formuliere eine passende Aufgabenstellung.

(2 BE)

b2)

Ein Kubikzentimeter Glas hat eine Masse von $2,5$ Gramm.
Berechne die Masse der leeren Vase.

(5 BE)

Im Folgenden wird die Schar der Funktionen $h_k$ mit

$h_k(x)=k x \cdot \text{e}^{-k x+1}+3$ mit $k\gt0$

betrachtet. Für die erste Ableitungsfunktion $\(h_k$ gilt:

$\(h_k$

c1)

Jede Funktion $h_k$ hat genau eine Extremstelle.
Zeige, dass dies die Stelle $x=\frac{1}{k}$ ist.

(2 BE)

c2)

Jede Funktion $h_k$ hat genau eine Wendestelle. Es gibt einen Wert für $k$ , so dass die Extremstelle und die Wendestelle von $h_k$ den Abstand $5$ haben.
Bestimme diesen Wert für $k.$

(5 BE)

c3)

Der Graph von $h_k$ hat in seinem Schnittpunkt mit der $y$ -Achse eine positive Steigung.
Bestimme alle Werte für $k,$ so dass der Schnittwinkel des Graphen von $h_k$ und der $y$ -Achse eine Größe von mindestens $45^{\circ}$ und höchstens $60^{\circ}$ hat.

(4 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

a1)

Ableitung $\(\boldsymbol{f$ aufstellen

$\(f$

Ableitung $\(\boldsymbol{f$ aufstellen

$\(f$

Aus dem Aufgabentext geht folgendes hervor:

$\(\begin{array}{lrll} \text{I}\quad&f$

Somit folgt:

$\begin{array}{lrll} \text{I}\quad&75a+10b+c&=& 0 &\quad \\ \text{II}\quad&60a+2b&=& 0 &\quad \\ \text{III}\quad&300a+20b+c&=& -\frac{1}{4}&\quad \end{array}$

Somit folgt aus Gleichung $\text{II}:$

$\begin{array}[t]{rlll} 60a+2b&=&0 &\mid\;-2b \\[5pt] 60a&=&-2b &\mid\; :60 \\[5pt] a&=&-\dfrac{1}{30}b \end{array}$

Einsetzen von $a=-\frac{1}{30}b$ in Gleichung $\text{I}$ liefert:

$\begin{array}[t]{rlll} 75\cdot\left(-\dfrac{1}{30}b\right)+10b+c&=& 0&\mid\; -7,5b \\[5pt] c &=& -7,5b \end{array}$

Einsetzen von $a=-\frac{1}{30}b$ und $c=-7,5b$ in Gleichung $\text{III}$ liefert:

$\begin{array}[t]{rlll} 300\cdot\left(-\dfrac{1}{30}b\right)+20b-7,5b &=& -\dfrac{1}{4}&\mid\; :\dfrac{5}{2} \\[5pt] b&=& -\dfrac{1}{10} \end{array}$

Für $a$ folgt:

$\begin{array}[t]{rlll} a &=& -\dfrac{1}{30}\cdot\left(-\dfrac{1}{10}\right)& \\[5pt] &=& \dfrac{1}{300} \end{array}$

Für $c$ folgt:

$\begin{array}[t]{rlll} c &=& -7,5\cdot\left(-\dfrac{1}{10}\right) \\[5pt] &=& \dfrac{3}{4} \end{array}$

Durch Einsetzen von $a,b$ und $c$ in $f(x)$ folgt:

$f(x)=\dfrac{1}{300} x^3-\dfrac{1}{10} x^2+\dfrac{3}{4} x+1$

a2)

Die Funktion $f$ dritten Grades hat genau eine Wendestelle bei $x=10.$ Das bedeutet, dass sich dort die Krümmung des Graphen ändert. Auf der Abbildung sieht man, dass der Graph für $x\lt10$ nach rechts gekrümmt ist, also auch für $x \leq 0.$

a3)

Die breiteste Stelle der Vase ist bei $x=5.$ Für den Radius ergibt sich somit:

$\begin{array}[t]{rlll} f(5) &=& \dfrac{1}{300} \cdot5^3-\dfrac{1}{10} \cdot5^2+\dfrac{3}{4} \cdot5+1&\mid\; \\[5pt] &=& \dfrac{8}{3} \end{array}$

Die Höhe der Vase und damit der Verpackung beträgt $h=12.$

Die Außenfläche der Verpackung ergibt sich aus dem Flächeninhalt des Mantels plus dem Flächeninhalt der beiden Deckel.

$\begin{array}[t]{rlll} A_V &=& A_M+2A_D \\[5pt] &=& 2\pi \cdot r\cdot h+2\cdot\pi r^2 \\[5pt] &=& 2\pi\cdot\dfrac{8}{3}\cdot12+2\pi\cdot\left(\dfrac{8}{3}\right)^2 \\[5pt] &\approx& 245,7 \end{array}$

Somit beträgt der Inhalt der Außenfläche der Verpackung etwa $245,7 \; \text{cm}^2.$

b1)

Die Vase wird mit $120\;\text{cm}^3$ Wasser aufgefüllt. Bestimme die Füllhöhe.

b2)

Der Flächeninhalt eines Rotationskörpers berechnet man mit $\pi\cdot\displaystyle\int_{a}^{b}f(x)^2\;\mathrm dx.$ Um das Volumen des Glases zu erhalten, muss der Flächeninhalt unter $g(x)$ vom Flächeninhalt unter $f(x)$ abgezogen werden. Somit folgt:

$\begin{array}[t]{rlll} V &=& \pi\cdot\displaystyle\int_{0}^{12}f(x)^2\;\mathrm dx-\pi\cdot\displaystyle\int_{0,5}^{12}g(x)^2\;\mathrm dx \\[5pt] &=& \pi\cdot\displaystyle\int_{0}^{12}\left(\frac{1}{300} x^3-\frac{1}{10} x^2+\frac{3}{4} x+1\right)^2\;\mathrm dx-\pi\cdot\displaystyle\int_{0,5}^{12}\left(\frac{1}{300} x^3-\frac{1}{10} x^2+\frac{3}{4} x+\frac{2}{3}\right)^2\;\mathrm dx \\[5pt] &=& \pi\cdot\displaystyle\int_{0}^{12}\dfrac{x^6}{90000}-\dfrac{x^5}{1500}+\dfrac{3 x^4}{200}-\dfrac{43 x^3}{300}+\dfrac{29 x^2}{80}+\dfrac{3 x}{2}+1\;\mathrm dx-\pi\cdot\displaystyle\int_{0,5}^{12}\dfrac{x^6}{90000}-\dfrac{x^5}{1500}+\dfrac{3 x^4}{200}-\dfrac{131 x^3}{900}+\dfrac{103 x^2}{240}+x+\dfrac{4}{9}\;\mathrm dx \\[5pt] &=& \pi\cdot\left[\dfrac{x^6}{90000}-\dfrac{x^5}{1500}+\dfrac{3 x^4}{200}-\dfrac{43 x^3}{300}+\dfrac{29 x^2}{80}+\dfrac{3 x}{2}+1\right]_0^{12} - \pi\cdot \left[\dfrac{x^6}{90000}-\dfrac{x^5}{1500}+\dfrac{3 x^4}{200}-\dfrac{131 x^3}{900}+\dfrac{103 x^2}{240}+x+\dfrac{4}{9}\right]_{0,5}^{12} \\[5pt] &=& \pi\cdot\left(\left(\left(\dfrac{12^6}{90000}-\dfrac{12^5}{1500}+\dfrac{3 \cdot12^4}{200}-\dfrac{43\cdot 12^3}{300}+\dfrac{29 \cdot12^2}{80}+\dfrac{3 \cdot12}{2}+1\right)-\left(0\right)\right)-\left(\left(\dfrac{12^6}{90000}-\dfrac{12^5}{1500}+\dfrac{3 \cdot12^4}{200}-\dfrac{131 \cdot12^3}{900}+\dfrac{103 \cdot12^2}{240}+12+\dfrac{4}{9}\right)-\left(\dfrac{0,5^6}{90000}-\dfrac{0,5^5}{1500}+\dfrac{3 \cdot0,5^4}{200}-\dfrac{131 \cdot0,5^3}{900}+\dfrac{103 \cdot0,5^2}{240}+0,5+\dfrac{4}{9}\right)\right)\right)\\[5pt] &=& 50,7 \end{array}$

Damit folgt:

$\begin{array}[t]{rlll} m &=& 50,7 \cdot 2,5 \\[5pt] &=& 126,8 \end{array}$

Somit hat das Glas eine Masse von $126,8\;\text{g}.$

c1)

$\(\boldsymbol{h$ setzen

$\(\begin{array}[t]{rlll} h$

Da die $\mathrm{e}$ -Funktion stets ungleich Null ist, folgt mit dem Satz des Nullprodukts:

$\begin{array}[t]{rlll} k-k^2x &=& 0 &\mid\; -k \\[5pt] -k^2x &=& -k &\mid\; :(-k^2) \\[5pt] x &=& \dfrac{1}{k} \end{array}$

Aus der Aufgabenstellung folgt, dass die hinreichende Bedingung nicht überprüft werden muss.
Somit hat jeder Graph der Funktion $h_k$ die Extremstelle $x=\frac{1}{k}.$

c2)

Ableitung $\(\boldsymbol{h$ aufstellen

$\(\begin{array}[t]{rlll} h$

$\(\boldsymbol{h$ setzen

$\(\begin{array}[t]{rlll} h$

Aus der Aufgabenstellung folgt, dass die hinreichende Bedingung nicht überprüft werden muss.

Abstand zwischen Wendestelle und Extremstelle gleich $\boldsymbol{5}$ setzen

$\begin{array}[t]{rlll} \dfrac{2}{k}-\dfrac{1}{k} &=& 5 \\[5pt] \dfrac{1}{k} &=& 5 &\mid\; \cdot k \\[5pt] 1 &=& 5k &\mid\; :5 \\[5pt] \dfrac{1}{5} &=& k \end{array}$

Wenn $k=\frac{1}{5}$ ist, haben die Wendestelle und Extremstelle von $h_k$ einen Abstand von $5.$

c3)

Der Graph von $h_k$ hat an der Stelle $x=0$ den Steigungswinkel $\alpha$ mit $\(\tan (\alpha)=h_k$ Damit folgt:

$k=\dfrac{\tan\left(\alpha\right)}{\text{e}}$

Es muss gelten $30^{\circ} \leq \alpha \leq 45^{\circ}.$

Da der Tangens zwischen $30^\circ$ und $40^\circ$ streng monoton steigt, folgt für $k:$

$\begin{array}[t]{rlll} \dfrac{\tan\left(30^\circ\right)}{\text{e}}&\leq& k &\leq& \dfrac{\tan\left(45^\circ\right)}{\text{e}}\\[5pt] \dfrac{\sqrt{3}}{3\text{e}} &\leq& k &\leq&\dfrac{1}{\text{e}} \end{array}$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?