Aufgabe 3
In Abbildung 1 ist ein regelmäßiges Tetraeder 
mit den Eckpunkten 
und 
in einem kartesischen Koordinatensystem abgebildet.
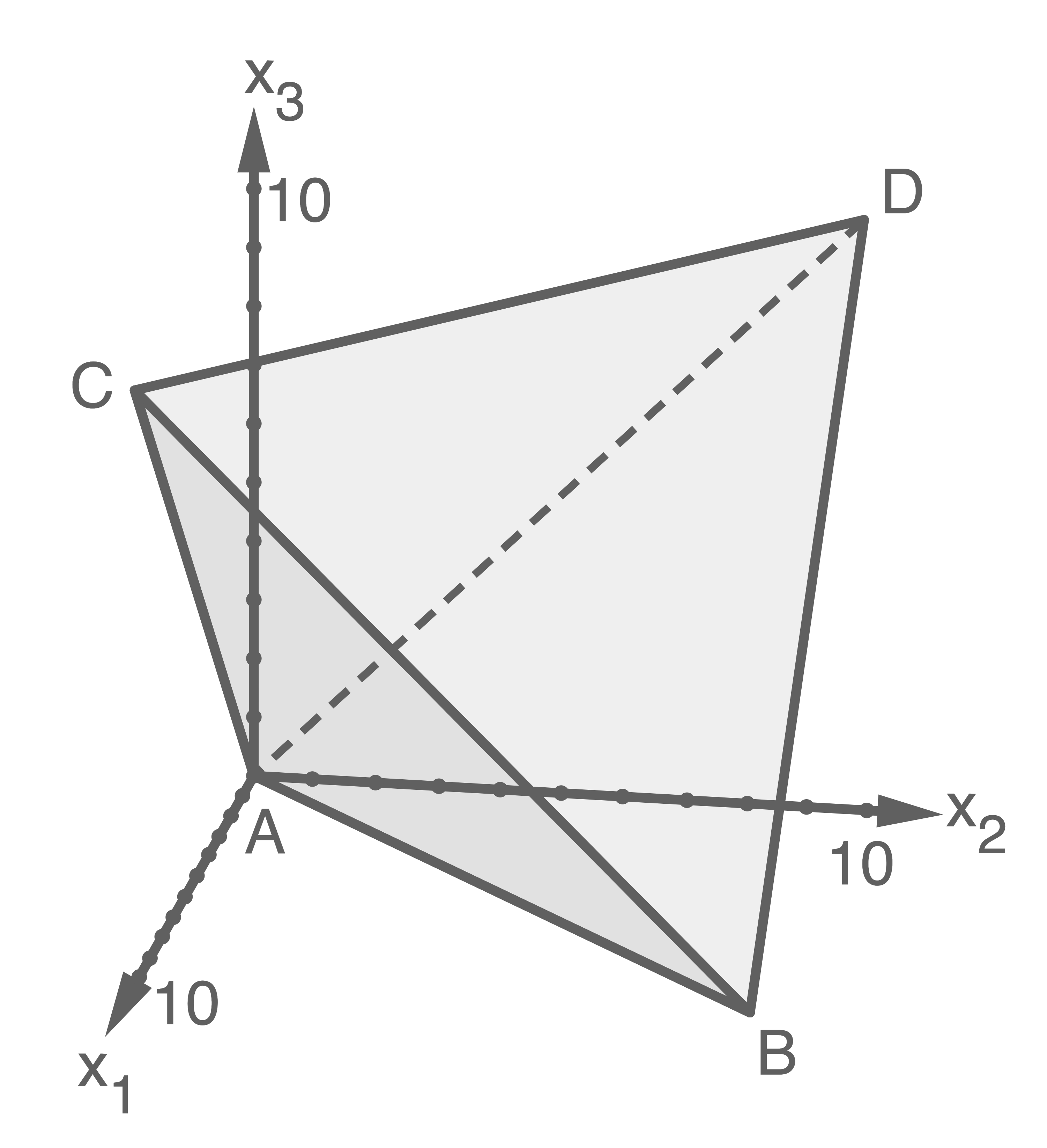
Abbildung 1
a)
(1)
Zeige, dass das Dreieck 
gleichseitig ist.
(2)
Bestimme den Flächeninhalt des Dreiecks und den Oberflächeninhalt des Tetraeders .
(3)
Gib die Koordinaten der Eckpunkte eines Würfels mit dem Volumen 
an, der das Tetraeder enthält.
(4 + 4 + 4 Punkte)
b)
(1)
Stelle eine Koordinatengleichung der Ebene 
auf, in der das Dreieck liegt.
[Mögliche Lösung: 
]
(2)
Stelle die Dreiecksfläche in einer Parameterform dar.
(3)
Bestimme das Volumen des Tetraeders .
(4 + 3 + 4 Punkte)
Abbildung 2
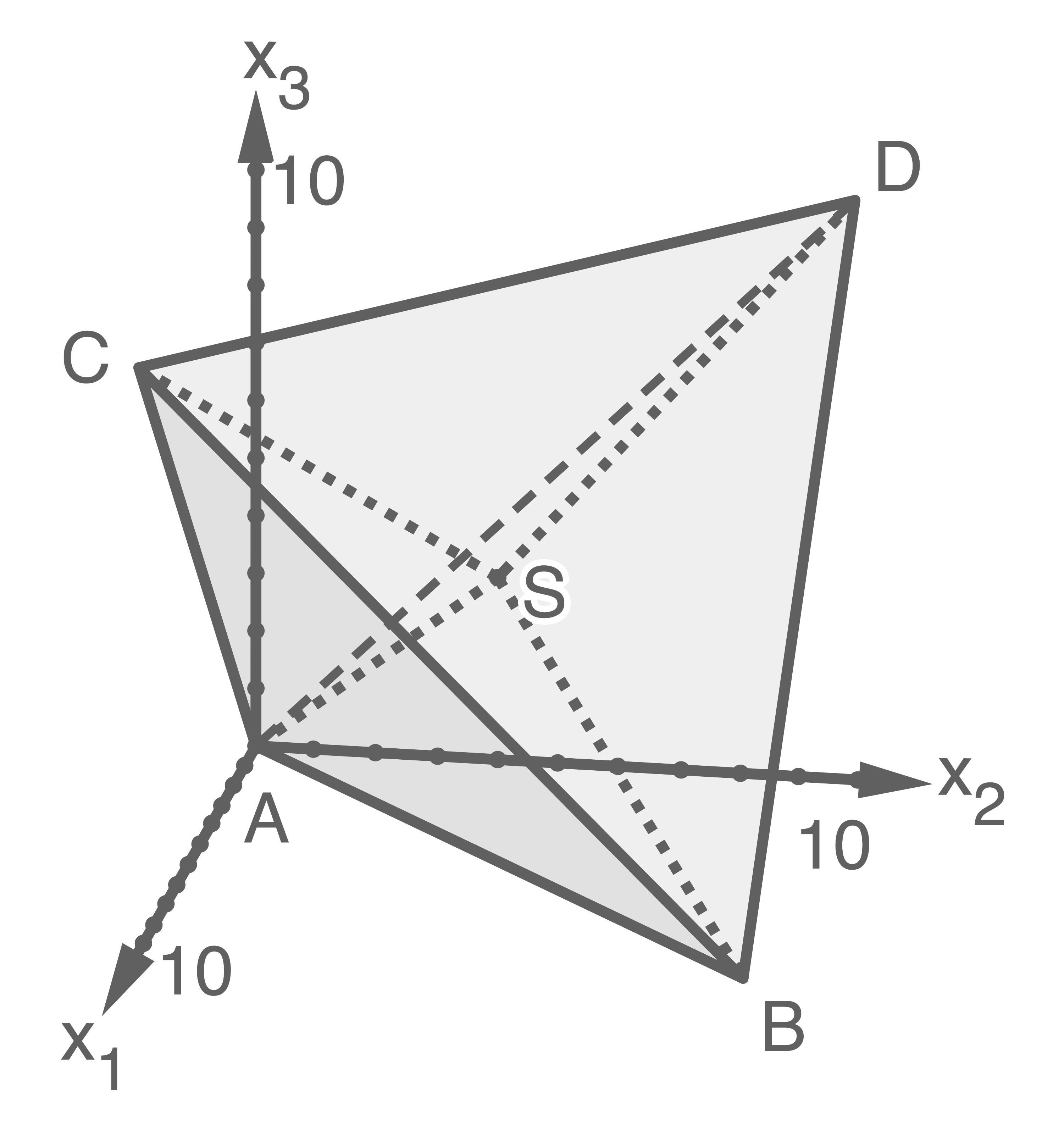
Abbildung 3
c)
Das Dreieck 
liegt in der Ebene 
,
das Dreieck
liegt in der Ebene 
und
das Dreieck
liegt in der Ebene 
das Dreieck
das Dreieck
(1)
Berechne die Größe des Winkels zwischen den Ebenen 
und 
.
(2)
Bestimme die Lösung des linearen Gleichungssystems
und interpretiere die Lösung im Sachzusammenhang.
(3 + 4 Punkte)
d)
Im Folgenden werden unterschiedlich große Drahtkantenmodelle von regelmäßigen Tetraedern in Seifenlauge getaucht. Um dies zu modellieren, wird im Folgenden ein regelmäßiges Tetraeder 
mit dem Eckpunkt 
und den variablen Eckpunkten 
, 
und 
mit 
betrachtet. Dieses Tetraeder hat den Oberflächeninhalt 
.
Taucht man diesen Körper in Seifenlauge, so bilden sich bei dessen Herausnahme im Inneren des Körpers Flächen aus Seifenhaut. Die Seifenhaut besteht aus sechs kongruenten gleichschenkligen Dreiecken mit einem gemeinsamen Eckpunkt, der durch den von 
abhängigen Punkt 
modelliert wird.
Jedes dieser Dreiecke hat den Flächeninhalt 
(1)
Bestimme, um wie viel Prozent der Gesamtflächeninhalt der Seifenhaut kleiner ist als der Oberflächeninhalt 
des Tetraeders.
(2)
Das Dreieck 
liegt in der Ebene 
.
Bestimme rechnerisch die Koordinaten des Fußpunktes 
des Lotes von 
auf die Ebene .
Zur Kontrolle: 
(3)
Auf der Strecke 
liegt der Punkt 
Die sechs Flächen aus Seifenhaut teilen das Tetraeder 
in vier volumengleiche Pyramiden. Diese Pyramiden haben die gemeinsame Spitze und jeweils eine der vier Seitenflächen des Tetraeders 
als Grundfläche.
Bestimme rechnerisch unter Verwendung von die Koordinaten von .
(3 + 4 + 3 Punkte)
a)
(1)
(2)
Es gilt: ![\(\overline{AB}=\overline{AC} =10 \;\text{[LE]}\)](https://mathjax.schullv.de/03c437893cf7221886ed50f2ca5f29e6740fa8256aa696b916150887f19e00dc?color=5a5a5a)
Das Dreieck ist gleichseitig und rechtwinklig, womit sich die Seitenlänge 
mit dem Satz des Pythagoras ergibt:
![\(\begin{array}[t]{rll}
\mid \overline{AB} \mid^2&=& 10^2 +10^2 &\quad \scriptsize \\[5pt]
\mid \overline{AB} \mid^2 &=& 2\cdot 100 &\quad \scriptsize \mid\;\sqrt{\;} \\[5pt]
\overline{AB} &=& \sqrt{2} \cdot 10 \;\text{[LE]}
\end{array}\)](https://mathjax.schullv.de/450dd22e21748f6840d19c1481248b1ae6454ab4d5a30a7ee86d81ea4ee51ad2?color=5a5a5a)
Die Höhe des Dreiecks ergibt sich zu ![\(0,5 \cdot 10 \cdot \sqrt{2} \cdot \sqrt{3} =5 \cdot \sqrt{6} \;\text{[LE]}.\)](https://mathjax.schullv.de/a5b0c5eda36464069618e30c6ef6f4d0a9912f21ce1223fad07f68931608aa2f?color=5a5a5a)
Daraus folgt 
![\(= 50 \cdot \sqrt{3} \;\text{[FE]}.\)](https://mathjax.schullv.de/8d56d3f6ee103efa4d5cd9948366abf612b691c75a3b1fa2424502d40c107fd8?color=5a5a5a)
Damit ergibt sich ![\(O_{\text{Tetraeder}}= 4 \cdot A_{\text{Dreieck}}= 200 \cdot \sqrt{3} \;\text{[FE]}.\)](https://mathjax.schullv.de/c254a5e30233f981df550370e4c36395cb63c8007c4e721ff10dc3dc8c3dc3ff?color=5a5a5a)
(3)
Ein Würfel mit sechs Seiten und einem Volumen von 
hat Seitenlängen von jeweils 
Deshalb sind die Koordinaten der Punkte:
b)
(1)
Normalenvektor ermitteln
Ein Normalenvektor der Ebene, in welcher das Dreieck liegt, kann mithilfe des Kreuzprodukts zweier Vektoren der Ebene berechnet werden.
![\(\begin{array}[t]{rll}
\overrightarrow{AB}\times \overrightarrow{AC}&=&\pmatrix{10\\10\\0} \times \pmatrix{10\\0\\10} &\\[5pt]
&=& \pmatrix{10\cdot 10-0\cdot 0\\0\cdot 10-10\cdot 10\\10\cdot 0-10\cdot 10} &\\[5pt]
&=& 100\cdot \pmatrix{1\\-1\\-1}
\end{array}\)](https://mathjax.schullv.de/d200c27273b2f2acd8f4d95b065c71b679a5b66d9296d097a059315e81c3310a?color=5a5a5a)
Durch Einsetzen von 
und eines Normalenvektors von in die allgemeine Koordinatengleichung folgt:
![\(\begin{array}[t]{rll}
1\cdot 0 -1\cdot 0 -1\cdot 0&=& c& \\[5pt]
0&=&c
\end{array}\)](https://mathjax.schullv.de/6c99d03ed5a91c95c03062c1ca4b2b8612d8dbb73a22461500ac239426427521?color=5a5a5a)
Eine Ebenengleichung von ist somit gegeben durch :
(2)
Eine Parameterform der Dreiecksfläche lautet:
Dreicksfläche : 
mit 
und 
.
(3)
Die Höhe des Tetraeders entspricht dem Abstand des Punktes 
von der Ebene 
.
Es folgt:
![\(\begin{array}[t]{rll}
V_{\text{Tetraeder}}&=& \dfrac{1}{3} \cdot 50\cdot \sqrt{3} \cdot \dfrac{20}{3} \cdot \sqrt{3} & \\[5pt]
&=& \dfrac{1000}{3} \; [\text{VE}]
\end{array}\)](https://mathjax.schullv.de/b5b0885632edaa8263d6b3570305bb50a6573890ceae3e8fb977fe121cf6cb0d?color=5a5a5a)
c)
(1)
Für den Winkel 
zwischen den Ebenen und gilt:
![\(\begin{array}[t]{rll}
\cos (\alpha)&=& \dfrac{|n_I\circ n_J|}{|n_I|\cdot |n_J|}& \\[5pt]
\cos (\alpha) &=& \dfrac{\left|\pmatrix{0\\-1\\1} \circ \pmatrix{1\\0\\1} \right|} {\left| \pmatrix{0\\-1\\1}\right| \cdot \left| \pmatrix {1\\0\\1}\right|}& \\[5pt]
\cos (\alpha) &=&\dfrac{1}{2} & \\[5pt]
\alpha &=& 60 ^{\circ} & \\[5pt]
\end{array}\)](https://mathjax.schullv.de/cb1c6a9cbd3fe79b5cc405c752c980282e7f00bf7488d86da2921e01ed364c39?color=5a5a5a)
(2)
Der Taschenrechner liefert 
als Lösung des linearen Gleichungssystems.
Der Punkt 
ist ein gemeinsamer Punkt der Ebenen 
, und und damit der gemeinsame Punkt 
der sechs kongruenten gleichschenkligen Dreiecke aus der Seifenhaut.
d)
(1)
Die Seifenhaut hat einen Gesamtflächeninhalt von 
Aus 
folgt, dass der Gesamtflächeninhalt der Seifenhaut um ca. 
kleiner ist als der Oberflächeninhalt des Tetraeders.
(2)
(3)