Wahlpflichtteil
1
Gegeben ist für jede positive reelle Zahl  die in
die in  definierte Funktion
definierte Funktion  mit
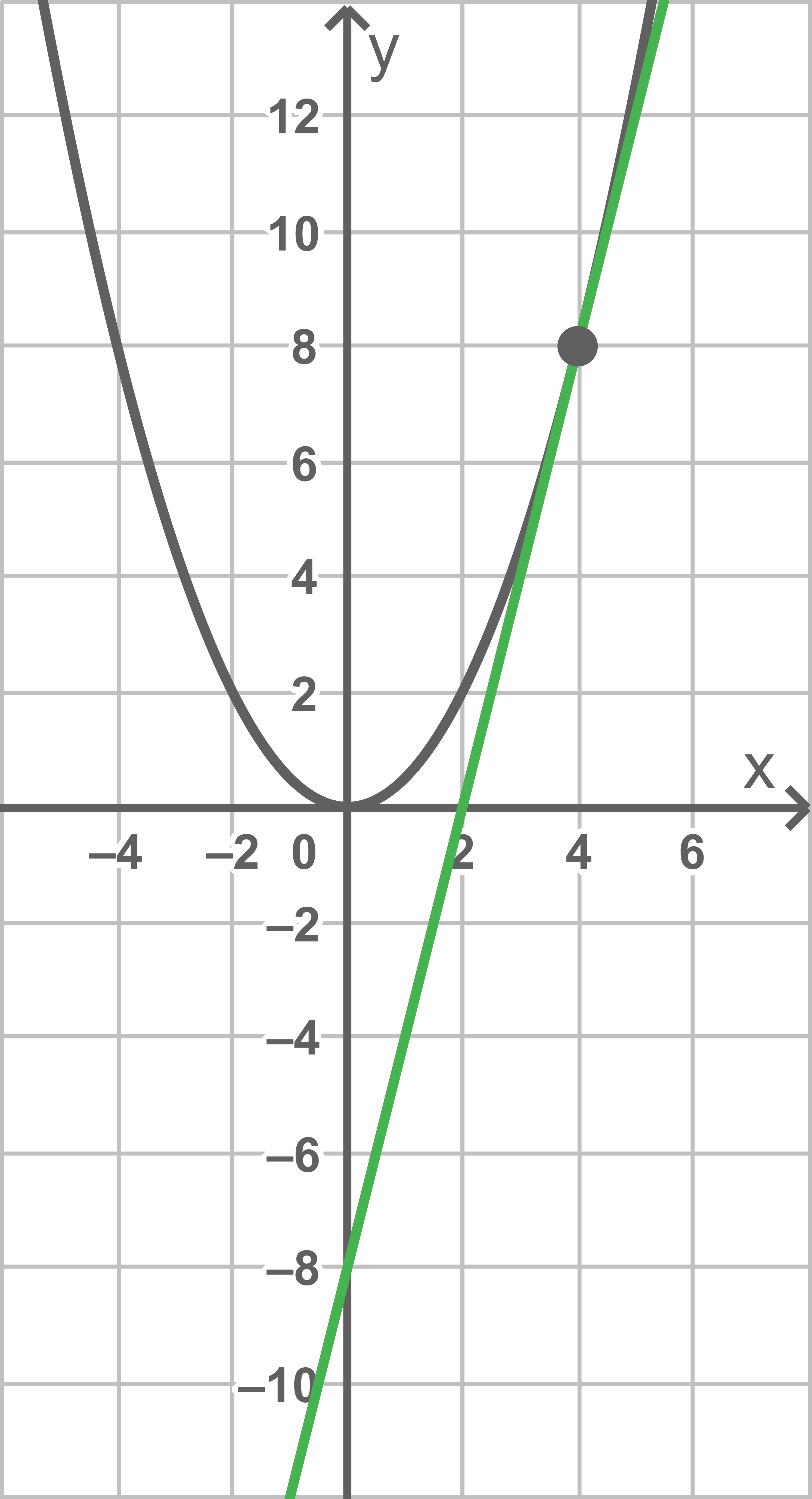
mit  Abbildung 1 zeigt den Graphen von
Abbildung 1 zeigt den Graphen von  sowie die Tangente
sowie die Tangente  an den Graphen von
an den Graphen von  im Punkt
im Punkt  .
.

(1)
Gib anhand Abbildung 1 eine Gleichung der Tangente  an.
an.
(2)
Weise nach, dass für jeden Wert  die Tangente an den Graphen von
die Tangente an den Graphen von  im Punkt
im Punkt  die
die  -Achse im Punkt
-Achse im Punkt  schneidet.
schneidet.
(1 + 4 Punkte)
2
Betrachtet wird die Schar der in  definierten Funktionen
definierten Funktionen  mit
mit  und
und  . Für jeden Wert von
. Für jeden Wert von  besitzt die Funktion
besitzt die Funktion  genau eine Extremstelle.
genau eine Extremstelle.
(1)
Begründe, dass der Graph von  für
für  unterhalb der
unterhalb der  -Achse verläuft.
-Achse verläuft.
(2)
Die Abbildungen 2 und 3 zeigen jeweils einen Graphen der Schar. Einer der beiden Graphen gehört zu einem positiven Wert von  Entscheide, welcher Graph dies ist, und begründe deine Entscheidung.
Entscheide, welcher Graph dies ist, und begründe deine Entscheidung.
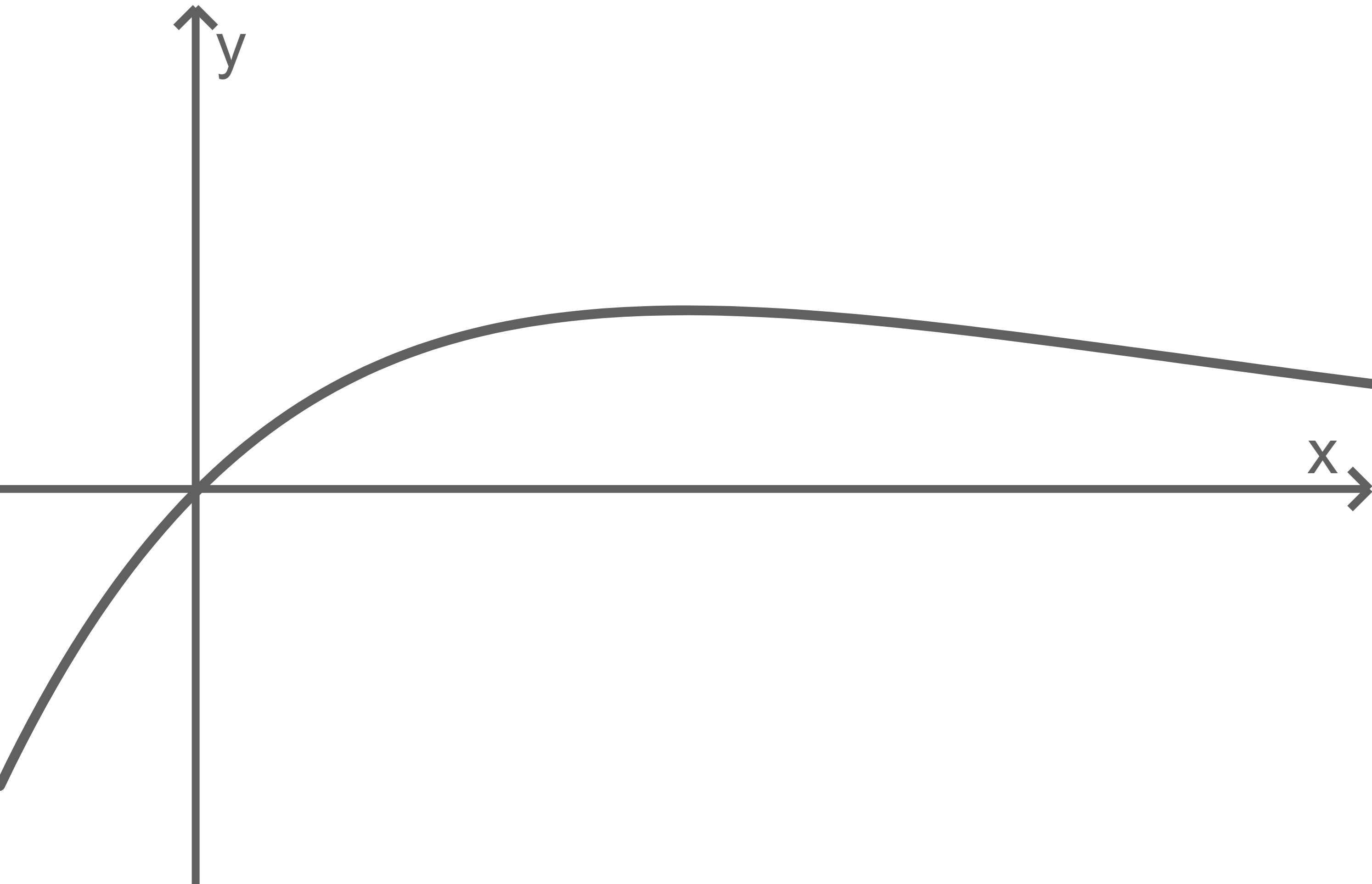
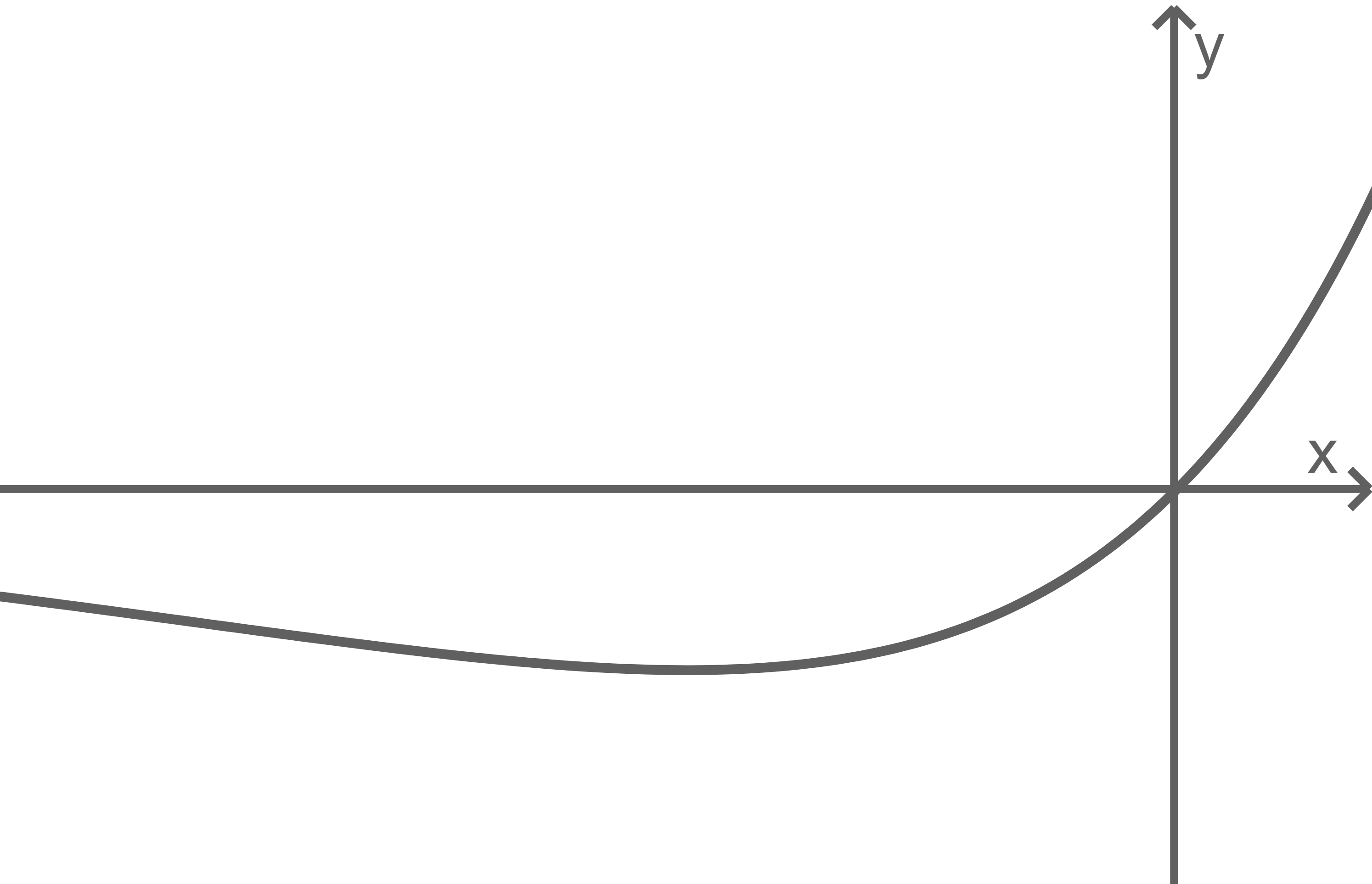

Abb. 2

Abb. 3
(2 + 3 Punkte)
3
Gegeben ist die Schar der Ebenen  mit
mit 
(1)
Ermittle denjenigen Wert von  für den
für den  parallel zur Gerade mit der Gleichung
parallel zur Gerade mit der Gleichung  und
und  verläuft.
verläuft.
(2)
Prüfe, ob die Ebene mit der Gleichung  zur Schar gehört.
zur Schar gehört.
(2 + 3 Punkte)
4
Die Punkte  und
und  sind Eckpunkte eines Parallelogramms
sind Eckpunkte eines Parallelogramms  dessen Diagonalen sich im Punkt
dessen Diagonalen sich im Punkt  schneiden.
schneiden.
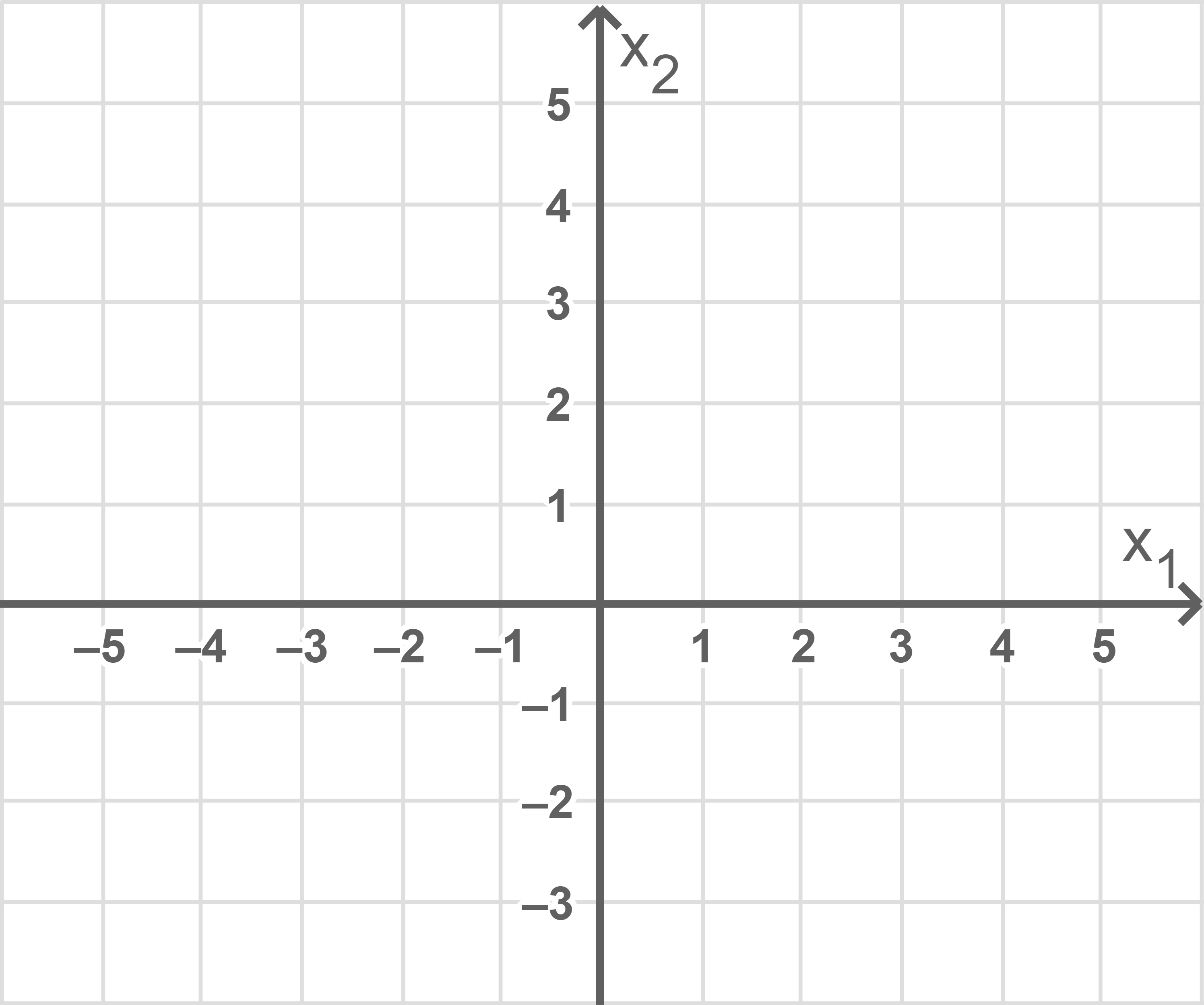
(1)
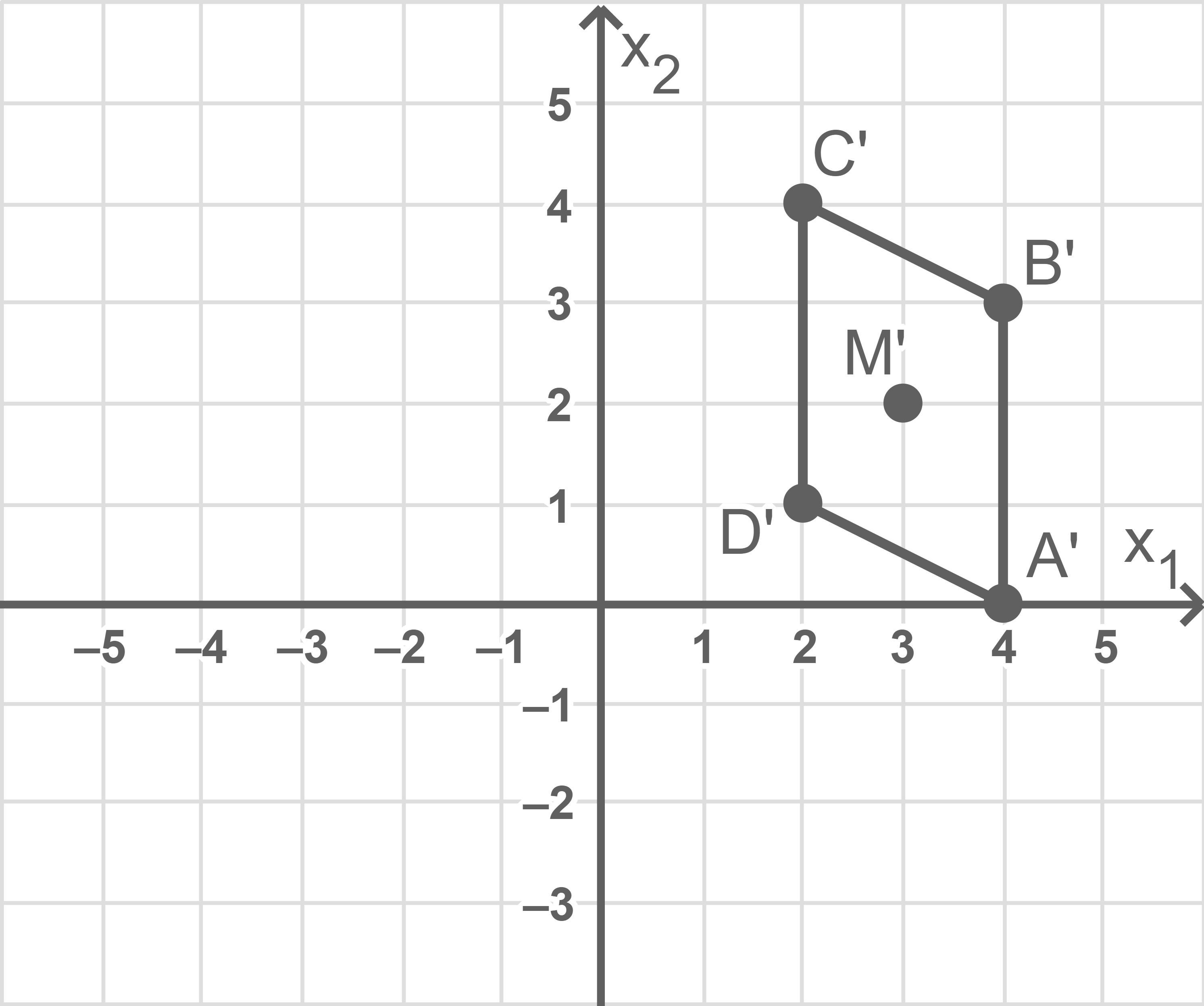
Verschiebt man jeden der Punkte  und
und  parallel zur
parallel zur  -Achse in die
-Achse in die  -Ebene, so ergeben sich die Punkte
-Ebene, so ergeben sich die Punkte  bzw.
bzw.  Das Viereck
Das Viereck  ist ein Parallelogramm, dessen Diagonalen sich im Punkt
ist ein Parallelogramm, dessen Diagonalen sich im Punkt  schneiden.
Zeichne
schneiden.
Zeichne  und
und  in Abbildung 4 ein.
in Abbildung 4 ein.

Abb. 4
(2)
Berechne den Wert des Skalarprodukts  und beurteile, ob der Winkel zwischen den Vektoren
und beurteile, ob der Winkel zwischen den Vektoren  und
und  kleiner ist als
kleiner ist als 
(3 + 2 Punkte)
5
Abbildung 5 zeigt den Graphen der Dichtefunktion einer normalverteilten Zufallsgröße  mit dem Erwartungswert
mit dem Erwartungswert 
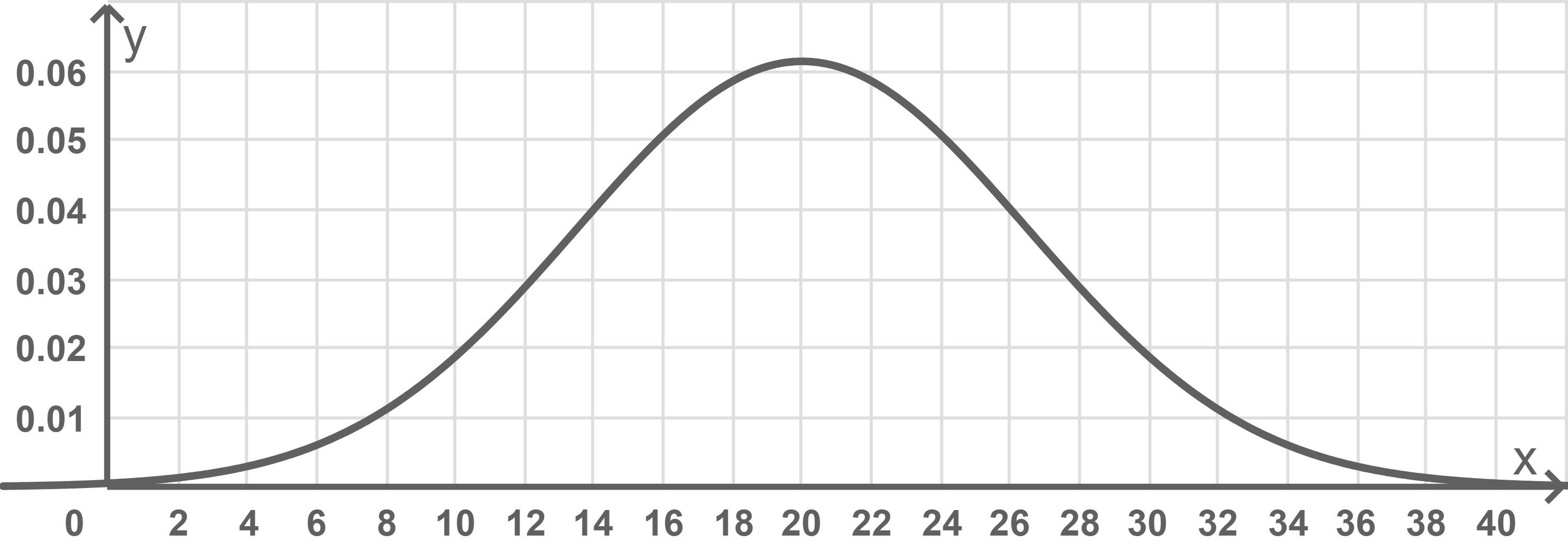

Abb. 5
(1)
Gib die Wahrscheinlichkeit dafür an, dass  den Wert
den Wert  annimmt.
annimmt.
(2)
Gesucht ist die Wahrscheinlichkeit für das Ereignis


somit gilt:
„ nimmt einen Wert an, der um mehr als
nimmt einen Wert an, der um mehr als  von
von  abweicht“
abweicht“
Erläutere die Überlegungen, die zur folgenden Bestimmung der gesuchten Wahrscheinlichkeit führen:
somit gilt:
(1 + 4 Punkte)
6
Ein Tetraeder, das mit den Augenzahlen  und
und  beschriftet ist, wird zum Würfeln verwendet. Das Tetraeder wurde so manipuliert, dass die Augenzahlen nicht alle mit der gleichen Wahrscheinlichkeit auftreten.
beschriftet ist, wird zum Würfeln verwendet. Das Tetraeder wurde so manipuliert, dass die Augenzahlen nicht alle mit der gleichen Wahrscheinlichkeit auftreten.
(1)
Die Augenzahl  tritt mit einer Wahrscheinlichkeit von
tritt mit einer Wahrscheinlichkeit von  auf.
Beschreibe in diesem Kontext ein Ereignis, dessen Wahrscheinlichkeit mit dem folgenden Ausdruck berechnet werden kann:
auf.
Beschreibe in diesem Kontext ein Ereignis, dessen Wahrscheinlichkeit mit dem folgenden Ausdruck berechnet werden kann:


(2)
Mit dem Tetraeder wird dreimal gewürfelt. Die Wahrscheinlichkeitsverteilung der Zufallsgröße  „Anzahl der Einsen" ist in der folgenden Tabelle dargestellt:
„Anzahl der Einsen" ist in der folgenden Tabelle dargestellt:
Berechne den Erwartungswert der Zufallsgröße  und die Wahrscheinlichkeit für das Auftreten der Augenzahl
und die Wahrscheinlichkeit für das Auftreten der Augenzahl 
(2 + 3 Punkte)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
(1)
Die Tangente  gegeben durch die Gleichung
gegeben durch die Gleichung  hat eine positive Steigung, einen
hat eine positive Steigung, einen  -Achsenabschnitt von
-Achsenabschnitt von  und schneidet die
und schneidet die  -Achse bei
-Achse bei  Für die Steigung
Für die Steigung  folgt somit:
folgt somit:
 Somit ergibt sich die Gleichung
Somit ergibt sich die Gleichung 
(2)
Die allgemeine Gleichung der Tangente ist gegeben durch  Für die Ableitung von
Für die Ableitung von  gilt:
gilt:
 Somit folgt
Somit folgt  und
und  Einsetzen der Koordinaten des Punktes
Einsetzen der Koordinaten des Punktes  an dem die Tangente den Graphen berührt, in die Gleichung der Tangente liefert somit:
an dem die Tangente den Graphen berührt, in die Gleichung der Tangente liefert somit:
![\(\begin{array}[t]{rll}
au^2&=& 2au\cdot u + n &\quad \scriptsize \mid\;-2au^2 \\[5pt]
-au^2&=& n
\end{array}\)](https://www.schullv.de/resources/formulas/5df801975510f229ceff9b9066f5a52503c1acb122790bf410cf8868cdb32494_light.svg) Somit gilt
Somit gilt  und die Tangente schneidet die
und die Tangente schneidet die  -Achse damit im Punkt
-Achse damit im Punkt 
2
(1)
Da stets  gilt, folgt für
gilt, folgt für  immer
immer  Somit verläuft der Graph von
Somit verläuft der Graph von  in diesem Fall unterhalb der
in diesem Fall unterhalb der  -Achse.
-Achse.
(2)
Für  gilt:
gilt:
![\(\begin{array}[t]{rll}
\lim\limits_{x\to+\infty}h_a(x)&=&\left(\lim\limits_{x\to+\infty}x\right) \cdot \left(\lim\limits_{x\to+\infty}\mathrm e^{a\cdot x}\right) \\[5pt]
&=&(+\infty)\cdot(+\infty)\\[5pt]
&=&+\infty
\end{array}\)](https://www.schullv.de/resources/formulas/93a1fc94612295ba00abee22b06ae322abb7c25259b739593677251a6b6f0b8a_light.svg) Da die Funktion
Da die Funktion  laut Aufgabenstellung für alle Werte von
laut Aufgabenstellung für alle Werte von  genau eine Extremstelle besitzt, fällt der Graph in Abbildung 1 für steigende Werte von
genau eine Extremstelle besitzt, fällt der Graph in Abbildung 1 für steigende Werte von  weiter. Somit zeigt Abbildung 2 den Graphen der Schar mit positivem Wert von
weiter. Somit zeigt Abbildung 2 den Graphen der Schar mit positivem Wert von 
3
(1)
Ein Normalenvektor  der Ebene
der Ebene  lässt sich aus der Ebenengleichung wie folgt ablesen:
lässt sich aus der Ebenengleichung wie folgt ablesen:
 Für den gesuchten Wert von
Für den gesuchten Wert von  folgt somit:
folgt somit:
![\(\begin{array}[t]{rll}
\pmatrix{2a\\-4\\a-2}\circ\pmatrix{-1\\0\\1}&=&0 \\[5pt]
-2a+a-2&=&0 &\quad \scriptsize \mid\;+a\\[5pt]
-2&=&a
\end{array}\)](https://www.schullv.de/resources/formulas/0d84c87b1bc1f09a4c52cfbd170b335d9334c2d473665b30528db1ae4f322c75_light.svg)
(2)
Ein Normalenvektor der betrachteten Ebene lässt sich wie folgt ablesen:
 Damit die Ebene zur Ebenenschar gehört, muss ein
Damit die Ebene zur Ebenenschar gehört, muss ein  existieren, sodass gilt:
existieren, sodass gilt:
 Aus der zweiten Zeile folgt
Aus der zweiten Zeile folgt  Somit ergibt sich folgendes Gleichungssystem:
Somit ergibt sich folgendes Gleichungssystem:
 Gleichung
Gleichung  liefert
liefert  Da
Da  ergibt, liefert einsetzen von
ergibt, liefert einsetzen von  in Gleichung
in Gleichung  einen Widerspruch. Somit besitzt das Gleichungssystem keine Lösung und die betrachtete Ebene gehört damit nicht zur Schar.
einen Widerspruch. Somit besitzt das Gleichungssystem keine Lösung und die betrachtete Ebene gehört damit nicht zur Schar.
4
(1)
(2)
Da das Skalarprodukt negativ ist, ist der Winkel zwischen den beiden Vektoren nicht kleiner als  sondern größer.
sondern größer.
5
(1)
Da die Zufallsgröße normalverteilt ist, gilt 
(2)
Der Inhalt der Fläche unter dem Graphen der Dichtefunktion zwischen  und
und  kann näherungsweise als Balken mit Breite
kann näherungsweise als Balken mit Breite  und Höhe
und Höhe  betrachtet werden, das heißt es gilt:
betrachtet werden, das heißt es gilt:
 Da der Graph symmetrisch zum Erwartungswert liegt, das heißt symmetrisch zu
Da der Graph symmetrisch zum Erwartungswert liegt, das heißt symmetrisch zu  folgt damit insgesamt der zweite Rechenschritt:
folgt damit insgesamt der zweite Rechenschritt:
6
(1)
„Bei zehn hintereinander ausgeführten Würfen des Tetraeders wird weniger als dreimal die Augenzahl  geworfen.“
geworfen.“
(2)
Für den Erwartungswert von  folgt:
Für die Wahrscheinlichkeit
folgt:
Für die Wahrscheinlichkeit  für das Auftreten der Augenzahl
für das Auftreten der Augenzahl  gilt:
gilt:
![\(\begin{array}[t]{rll}
(1-p)^3&=&\dfrac{27}{125} &\quad \scriptsize \mid\;\sqrt[3]{\;} \\[5pt]
1-p&=&\dfrac{3}{5} &\quad \scriptsize \mid\;-1 \\[5pt]
-p&=&-\dfrac{2}{5} &\quad \scriptsize \mid\;\cdot(-1) \\[5pt]
p&=&\dfrac{2}{5}
\end{array}\)](https://www.schullv.de/resources/formulas/cb99960c0fe6c4f5a262463ffda34acecc63b7658f8efec76ac47fcc18bbee44_light.svg)