Aufgabe 2
Das Jagdverhalten von Raubkatzen in der freien Wildbahn ist gekennzeichnet durch eine hohe Anfangsbeschleunigung. Darauf folgt eine kurze Phase mit annähernd konstanter Geschwindigkeit, bevor die Geschwindigkeit wieder abfällt.
Die Geschwindigkeit eines Tigers bei einem Jagdvorgang aus der Ruheposition heraus wird für zunächst ohne Berücksichtigung der Phase mit konstanter Geschwindigkeit modelliert. Dazu wird für
zunächst ohne Berücksichtigung der Phase mit konstanter Geschwindigkeit modelliert. Dazu wird für  die Funktion
die Funktion  mit
mit

 verwendet. Dabei gibt
verwendet. Dabei gibt  die Zeit seit Verlassen der Ruheposition in Sekunden und
die Zeit seit Verlassen der Ruheposition in Sekunden und  die Geschwindigkeit in
die Geschwindigkeit in  an.
an.
 beibehalten. Hat er seine Beute bis dahin nicht gefasst, muss er den Jagdvorgang abbrechen. In einem konkreten Fall wittert ein Beutetier den Tiger und ergreift die Flucht. Als der Tiger seine Ruheposition verlässt, ist das Beutetier
beibehalten. Hat er seine Beute bis dahin nicht gefasst, muss er den Jagdvorgang abbrechen. In einem konkreten Fall wittert ein Beutetier den Tiger und ergreift die Flucht. Als der Tiger seine Ruheposition verlässt, ist das Beutetier  entfernt und hat seine konstante Fluchtgeschwindigkeit von
entfernt und hat seine konstante Fluchtgeschwindigkeit von  bereits erreicht.
bereits erreicht.
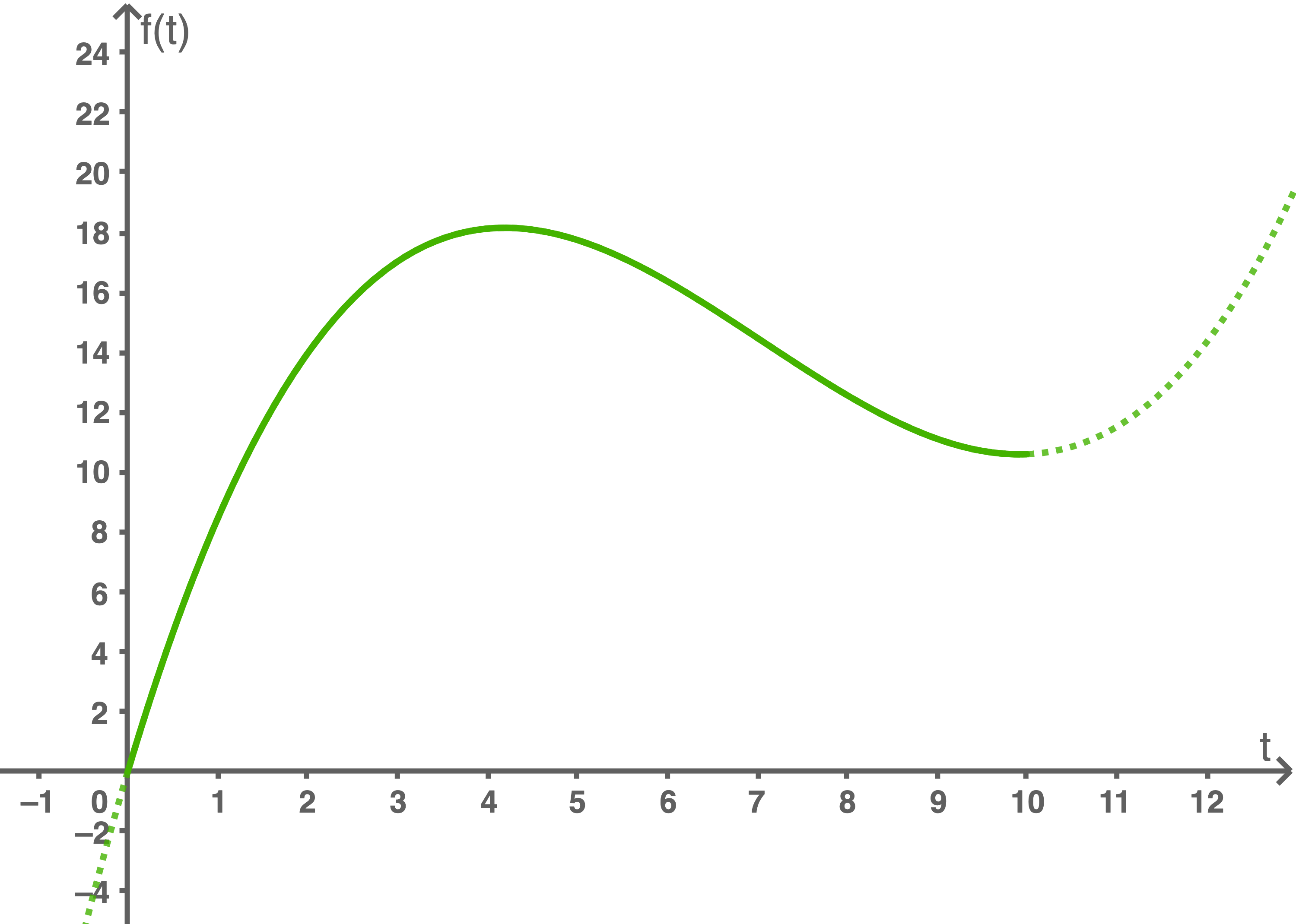
Die Geschwindigkeit eines Tigers bei einem Jagdvorgang aus der Ruheposition heraus wird für

Abbildung 1
a)
(1)
Gib den Funktionswert von  für
für  an und interpretiere diesen Wert im Sachzusammenhang.
an und interpretiere diesen Wert im Sachzusammenhang.
(2)
Weise rechnerisch nach, dass der Tiger seine Maximalgeschwindigkeit von ca.  ungefähr
ungefähr  Sekunden nach Verlassen der Ruheposition erreicht, und gib die Maximalgeschwindigkeit in
Sekunden nach Verlassen der Ruheposition erreicht, und gib die Maximalgeschwindigkeit in  an.
an.
(3 + 8 Punkte)
b)
Ermittle das Zeitintervall, in dem die Geschwindigkeit des Tigers mindestens  beträgt.
beträgt.
(4 Punkte)
c)
(1)
Berechne  und erläutere die Bedeutung dieses Wertes im Sachzusammenhang.
und erläutere die Bedeutung dieses Wertes im Sachzusammenhang.
Wenn ein Tiger seine Maximalgeschwindigkeit erreicht hat, dann kann er diese für höchstens
(2)
Untersuche, ob der Tiger unter diesen Bedingungen das Beutetier einholen kann.
(6 + 5 Punkte)
d)
Im Folgenden wird das Jagdverhalten anderer Raubkatzen mit einem veränderten Modell betrachtet, das durch einen Parameter  für konkrete Raubkatzen spezifiziert werden kann. Die Geschwindigkeiten dieser Raubkatzen aus der Ruheposition heraus werden für
für konkrete Raubkatzen spezifiziert werden kann. Die Geschwindigkeiten dieser Raubkatzen aus der Ruheposition heraus werden für  näherungsweise durch Funktionen der Schar
näherungsweise durch Funktionen der Schar  mit
mit
 , mit
, mit 
 ,
,  ,
,  beschrieben. Dabei gibt weiterhin
beschrieben. Dabei gibt weiterhin  die Zeit seit Verlassen der Ruheposition in Sekunden und
die Zeit seit Verlassen der Ruheposition in Sekunden und  die Geschwindigkeit in
die Geschwindigkeit in  an.
Es ist
an.
Es ist  für
für  und
und 
(1)
Ermittle rechnerisch die Maximalgeschwindigkeit der Raubkatzen in Abhängigkeit vom Parameter  . Auf eine Betrachtung der Randwerte kann dabei verzichtet werden.
[Zur Kontrolle: Die Hochpunkte der Schar sind
. Auf eine Betrachtung der Randwerte kann dabei verzichtet werden.
[Zur Kontrolle: Die Hochpunkte der Schar sind  .]
.]
(2)
Eine konkrete Raubkatze legt ab dem Verlassen der Ruheposition eine Strecke von  zurück und benötigt dafür
zurück und benötigt dafür  Gehe davon aus, dass die Funktion
Gehe davon aus, dass die Funktion  den Geschwindigkeitsverlauf auf dieser Strecke modelliert.
Ermittle mit dem Modell der Funktion
den Geschwindigkeitsverlauf auf dieser Strecke modelliert.
Ermittle mit dem Modell der Funktion  die Maximalgeschwindigkeit, die diese Raubkatze auf dieser Strecke erreicht hat.
die Maximalgeschwindigkeit, die diese Raubkatze auf dieser Strecke erreicht hat.
Ohne Nachweis darf benutzt werden, dass mit
mit  eine Stammfunktion von
eine Stammfunktion von  ist.
ist.
Ohne Nachweis darf benutzt werden, dass
(8 + 6 Punkte)
a)
(1)
(2)
1. Schritt: Notwendige Bedingung für Extremstellen anwenden
![\(\begin{array}[t]{rll}
f](https://www.schullv.de/resources/formulas/b34a20b4fbc5fec1c585d760f72fe8282ba05e5fd7ee814434052502561100e3_light.svg) Mit dem GTR folgt:
Mit dem GTR folgt:
 TI 84-PLUS
TI 84-PLUS
 Casio fx-CG
Daraus ergeben sich
Casio fx-CG
Daraus ergeben sich  und
und  .
2. Schritt: Hinreichende Bedingung für Extremstellen anwenden
.
2. Schritt: Hinreichende Bedingung für Extremstellen anwenden

 Das Maximum liegt an
Das Maximum liegt an  3. Schritt: Funktionswert bestimmen
3. Schritt: Funktionswert bestimmen
 Somit hat der Tiger nach ca. 4,2 Sekunden seine Maximalgeschwindigkeit von ca.
Somit hat der Tiger nach ca. 4,2 Sekunden seine Maximalgeschwindigkeit von ca.  erreicht.
erreicht.
2nd  trace (calc)
trace (calc)  2: zero
2: zero
F5 (G-Solv)  F1: ROOT
F1: ROOT
b)
Der GTR liefert für die Gleichung  die Lösungen
die Lösungen  ,
,  und
und  .
Der Zeitpunkt
.
Der Zeitpunkt  liegt außerhalb des betrachteten Zeitraums.
Aus dem Verlauf des Graphen von
liegt außerhalb des betrachteten Zeitraums.
Aus dem Verlauf des Graphen von  folgt, dass das gesuchte Zeitintervall ca.
folgt, dass das gesuchte Zeitintervall ca.  nach dem Verlassen der Ruheposition beginnt und ca.
nach dem Verlassen der Ruheposition beginnt und ca.  nach dem Verlassen der Ruheposition endet.
nach dem Verlassen der Ruheposition endet.
c)
(1)
Berechnung
Eine Stammfunktion von  ist beispielsweise
ist beispielsweise 
Damit gilt .
Wert erläutern
Der Tiger legt in den ersten
.
Wert erläutern
Der Tiger legt in den ersten  der Modellierung eine Strecke von ca.
der Modellierung eine Strecke von ca.  zurück.
zurück.
Damit gilt
(2)
Der Tiger erreicht nach ca.  seine Maximalgeschwindigkeit. In diesem Zeitraum legt er ca.
seine Maximalgeschwindigkeit. In diesem Zeitraum legt er ca.  zurück.
Danach läuft er mit seiner Maximalgeschwindigkeit von
zurück.
Danach läuft er mit seiner Maximalgeschwindigkeit von  weiter.
weiter.
Die Strecke, die der Tiger in Sekunden nach Verlassen der Ruheposition zurücklegt, hat für
Sekunden nach Verlassen der Ruheposition zurücklegt, hat für  eine Länge von
eine Länge von  In diesem Zeitraum von
In diesem Zeitraum von  Sekunden wächst die Entfernung des Beutetiers zur Ruheposition des Tigers auf
Sekunden wächst die Entfernung des Beutetiers zur Ruheposition des Tigers auf  Die lineare Gleichung
Die lineare Gleichung  hat als einzige Lösung
hat als einzige Lösung  .
Der Tiger müsste seine Maximalgeschwindigkeit daher ca. 15,7 Sekunden beibehalten, um die Beute einzuholen. Er würde die Jagd abbrechen, da er die Beute unter diesen Bedingungen nicht einholen kann.
.
Der Tiger müsste seine Maximalgeschwindigkeit daher ca. 15,7 Sekunden beibehalten, um die Beute einzuholen. Er würde die Jagd abbrechen, da er die Beute unter diesen Bedingungen nicht einholen kann.
Die Strecke, die der Tiger in
d)
(1)
Erste und zweite Ableitung bilden:
 .
.
 1. Schritt: Notwendige Bedingung für Extremstellen anwenden
1. Schritt: Notwendige Bedingung für Extremstellen anwenden
![\(\begin{array}[t]{rll}
g_u](https://www.schullv.de/resources/formulas/bab4925187fa5af428fdbd81c574c5e4dc2e03512e401e5bc7d44fff70bcc72e_light.svg) Wegen
Wegen  und
und  folgt
folgt  2. Schritt: Hinreichende Bedingung für Extremstellen anwenden
2. Schritt: Hinreichende Bedingung für Extremstellen anwenden
 .
An der Stelle
.
An der Stelle  liegt folglich ein Hochpunkt vor.
Wegen
liegt folglich ein Hochpunkt vor.
Wegen  , ergeben sich die Hochpunkte der Schar mit
, ergeben sich die Hochpunkte der Schar mit  .
Die Maximalgeschwindigkeit der Raubkatze beträgt somit
.
Die Maximalgeschwindigkeit der Raubkatze beträgt somit  .
.
(2)
Mit dem solve-Befehl des GTRs folgt:  Da die Maximalgeschwindigkeit für diesen Wert von
Da die Maximalgeschwindigkeit für diesen Wert von  nach
nach  Sekunden angenommen wird, die Raubkatze jedoch schon nach 6 Sekunden am Ende der betrachteten Strecke ist, erreicht die Raubkatze ihre Maximalgeschwindigkeit auf dieser Strecke nach 6 Sekunden.
Die Maximalgeschwindigkeit folgt mit
Sekunden angenommen wird, die Raubkatze jedoch schon nach 6 Sekunden am Ende der betrachteten Strecke ist, erreicht die Raubkatze ihre Maximalgeschwindigkeit auf dieser Strecke nach 6 Sekunden.
Die Maximalgeschwindigkeit folgt mit  .
.