Aufgabe 1
Ein Ölfeld wird seit Beginn des Jahres 1990 mit Bohrungen in mehreren Erdöl führenden Schichten erschlossen. Die momentane Förderrate1 aus diesem Ölfeld im Zeitraum von Anfang 1990 bis Ende 2009 kann im Intervall [0;20] durch die Funktion  mit der Gleichung
mit der Gleichung
 modelliert werden.
modelliert werden.
Dabei wird als Maßzahl zur Einheit 1 Jahr und
als Maßzahl zur Einheit 1 Jahr und  als Maßzahl zur Einheit 1.000 Tonnen pro Jahr aufgefasst. Der Zeitpunkt
als Maßzahl zur Einheit 1.000 Tonnen pro Jahr aufgefasst. Der Zeitpunkt  entspricht dem Beginn des Jahres 1990.
entspricht dem Beginn des Jahres 1990.
Der Graph von ist in der Abbildung 1 in dem für die Modellierung zu betrachtenden Intervall dargestellt.
ist in der Abbildung 1 in dem für die Modellierung zu betrachtenden Intervall dargestellt.
Dabei wird
Der Graph von
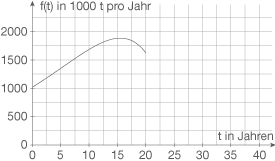
1Im Folgenden wird vereinfachend nur der Begriff der Förederrate verwendet, wobei durchgehend die momentane Förderrate gemeint und zu betrachten ist.
a)
Bestimmen Sie rechnerisch den Zeitpunkt im betrachteten Zeitraum von Anfang 1990 bis Ende 2009, zu dem die Förderrate maximal ist, und berechnen Sie den Maximalwert.
![\([\text{Zur Kontrolle: }f‘(t)=(62-4t)\cdot \mathrm e^{0,1\cdot t}]\)](https://www.schullv.de/resources/formulas/05c31716c5fcb97b60c5848ae2b10b2904001538e19f8649c78d05f3071a051c_light.svg)
(11P)
b)
Die Menge des Erdöls, das seit dem Beginn der Ölförderung Anfang 1990 bis zu einem beliebigem Zeitpunkt  des betrachteten Zeitraums aus dem Ölfeld gefördert wurde, wird durch eine Funktion
des betrachteten Zeitraums aus dem Ölfeld gefördert wurde, wird durch eine Funktion  , beschrieben.
, beschrieben.
- Bestimmen Sie eine Gleichung dieser Funktion M.
[Zur Kontrolle: Eine Stammfunktion der Funktionist die Funktion
mit der Gleichung
.]
- Berechnen Sie die gesamte Fördermenge aus dem Ölfeld von Anfang 1990 bis Ende 2009.
- Ermitteln Sie die Einnahmen aus dem Verkauf des im Jahr 2007 geförderten Erdöls, wenn man von einem Verkaufspreis von 56 Euro pro Barrel im Jahr 2007 ausgeht.
1 Barrel Erdöl (ca. 159 Liter) wiegt ca. 137 kg.
(8P + 3P + 6P)
Seit Anfang des Jahres 2010 schwächt sich der Rückgang der Förderrate ab. Diese soll im Intervall ![\([20;40]\)](https://www.schullv.de/resources/formulas/9483f51a86da482ba01ec6da51d1e0d63a918967cac0e186269cc7f02e64a3a8_light.svg) daher durch die Funktion
daher durch die Funktion  mit der Gleichung
mit der Gleichung
 modelliert werden. Dabei wird wieder
modelliert werden. Dabei wird wieder  als Maßzahl zur Einheit 1 Jahr und
als Maßzahl zur Einheit 1 Jahr und  als Maßzahl zur Einheit 1.000 Tonnen pro Jahr aufgefasst. Der Zeitpunkt
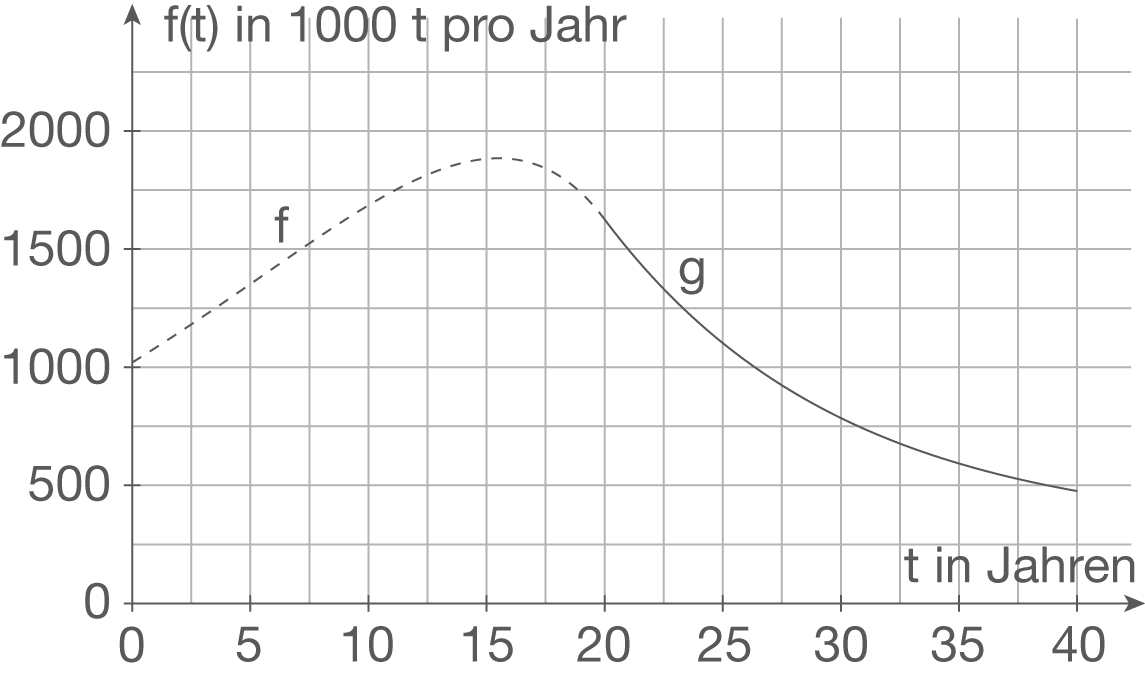
als Maßzahl zur Einheit 1.000 Tonnen pro Jahr aufgefasst. Der Zeitpunkt  entspricht dem Beginn des Jahres 2010. Die Abbildung 2 auf Seite 2 stellt die Graphen der Funktionen
entspricht dem Beginn des Jahres 2010. Die Abbildung 2 auf Seite 2 stellt die Graphen der Funktionen  und
und  in den jeweils für die Modellierung zu betrachtenden Intervallen dar.
in den jeweils für die Modellierung zu betrachtenden Intervallen dar.
c)
- Begründen Sie anhand des Funktionterms von
, warum die Funktion
die Förderrate nicht über einen längeren Zeitraum sinnvoll beschreiben könnte.
- Der Betreiber kalkuliert, dass die Ölförderung für ihn nur wirtschaftlich ist, wenn innerhalb eines Kalenderjahres mindestens 600.000 Tonnen Öl gefördert werden.
Bestimmen Sie das letzte Kalenderjahr, für das die Ölförderung wirtschaftlich sein wird.
[Zur Kontrolle: Die Fördermenge im IntervallT; T +1
.
, lässt sich durch
ermitteln.]

(4P + 10P)
d)
Durch die Funktion  mit der Gleichung
mit der Gleichung
 wird die Förderrate von Anfang 1990 bis Ende 2029 beschrieben. Folgende Angaben dürfen ohne Nachweis verwendet werden:
wird die Förderrate von Anfang 1990 bis Ende 2029 beschrieben. Folgende Angaben dürfen ohne Nachweis verwendet werden:
- Begründen Sie, dass die Funktion
an der Stelle
differenzierbar ist, und entscheiden Sie, ob
dort zweimal differenzierbar ist.
- Begründen Sie, dass
an der Stelle
ein lokales Minimum besitzt.
[Hinweis:darf ohne Nachweis verwendet werden.]
(4P + 4P)
a)
 Maximale Förderrate bestimmen
Die momentane Förderrate aus einem Ölfeld im Zeitraum von 1990 bis 2009 wird im Intervall
Maximale Förderrate bestimmen
Die momentane Förderrate aus einem Ölfeld im Zeitraum von 1990 bis 2009 wird im Intervall ![\(\left[0;20\right]\)](https://www.schullv.de/resources/formulas/2fb45bd1f03fc888bbb9b42d34f330fe350022f99e9f9ee6f7033ab8f18ba841_light.svg) wird durch die Funktion
wird durch die Funktion  mit dem Term
mit dem Term
 modelliert. Dabei gibt die Variable
modelliert. Dabei gibt die Variable  das Jahr und
das Jahr und  die geförderte Menge an Erdöl zur Einheit 1.000 Tonnen pro Jahr an.
die geförderte Menge an Erdöl zur Einheit 1.000 Tonnen pro Jahr an.
Deine Aufgabe ist es rechnerisch den Zeitpunkt zu bestimmen, an dem die Förderrate maximal wird und weiterhin den entsprechenden Maximalwert anzugeben.
Das heißt, du kannst den Hochpunkt der Funktion
zu bestimmen, an dem die Förderrate maximal wird und weiterhin den entsprechenden Maximalwert anzugeben.
Das heißt, du kannst den Hochpunkt der Funktion  bestimmen. Denn dessen
bestimmen. Denn dessen  -Koordinate entspricht dem gesuchten Zeitpunkt, an dem die Förderrate maximal wird und die
-Koordinate entspricht dem gesuchten Zeitpunkt, an dem die Förderrate maximal wird und die  -Koordinate gibt den Maximalwert an.
Um die Koordinaten angeben zu können, musst du zunächst die notwendige und hinreichende Bedingung für Maximalstellen überprüfen.
-Koordinate gibt den Maximalwert an.
Um die Koordinaten angeben zu können, musst du zunächst die notwendige und hinreichende Bedingung für Maximalstellen überprüfen.
Bei einer Maximalstelle der Funktion
der Funktion  müssen folgende Bedingungen erfüllt sein:
müssen folgende Bedingungen erfüllt sein:
 . Hast du diese bestimmt, so kannst du die bestimmte Stelle in den Funktionsterm von
. Hast du diese bestimmt, so kannst du die bestimmte Stelle in den Funktionsterm von  einsetzen und erhältst den zugehörigen Funktionswert an dieser Maximalstelle.
1. Schritt: Notwendige Bedingung überprüfen
Um die notwendige Bedingung einer Maximalstelle der Funktion
einsetzen und erhältst den zugehörigen Funktionswert an dieser Maximalstelle.
1. Schritt: Notwendige Bedingung überprüfen
Um die notwendige Bedingung einer Maximalstelle der Funktion  zu überprüfen, benötigst du zunächst die erste Ableitungsfunktion der Funktion
zu überprüfen, benötigst du zunächst die erste Ableitungsfunktion der Funktion  .
.
Diese erhältst du, indem du die Produktregel anwendest: Für die notwendige Bedingung einer Maximalstelle muss
Für die notwendige Bedingung einer Maximalstelle muss  gelten. Setze also den Funktionsterm der ersten Ableitung
gelten. Setze also den Funktionsterm der ersten Ableitung  gleich Null und ermittle alle potentiellen Werte, für die diese Gleichung erfüllt wird:
gleich Null und ermittle alle potentiellen Werte, für die diese Gleichung erfüllt wird:
 An dieser Stelle kannst du den Satz vom Nullprodukt anwenden. Da der Term
An dieser Stelle kannst du den Satz vom Nullprodukt anwenden. Da der Term  für keinen Wert für
für keinen Wert für  gleich Null werden kann, kannst du diesen vernachlässigen.
gleich Null werden kann, kannst du diesen vernachlässigen.
 Damit hast du eine potentielle Maximalstelle an
Damit hast du eine potentielle Maximalstelle an  ermittelt und kannst für diese Stelle nun das hinreichende Kriterium überprüfen.
ermittelt und kannst für diese Stelle nun das hinreichende Kriterium überprüfen.
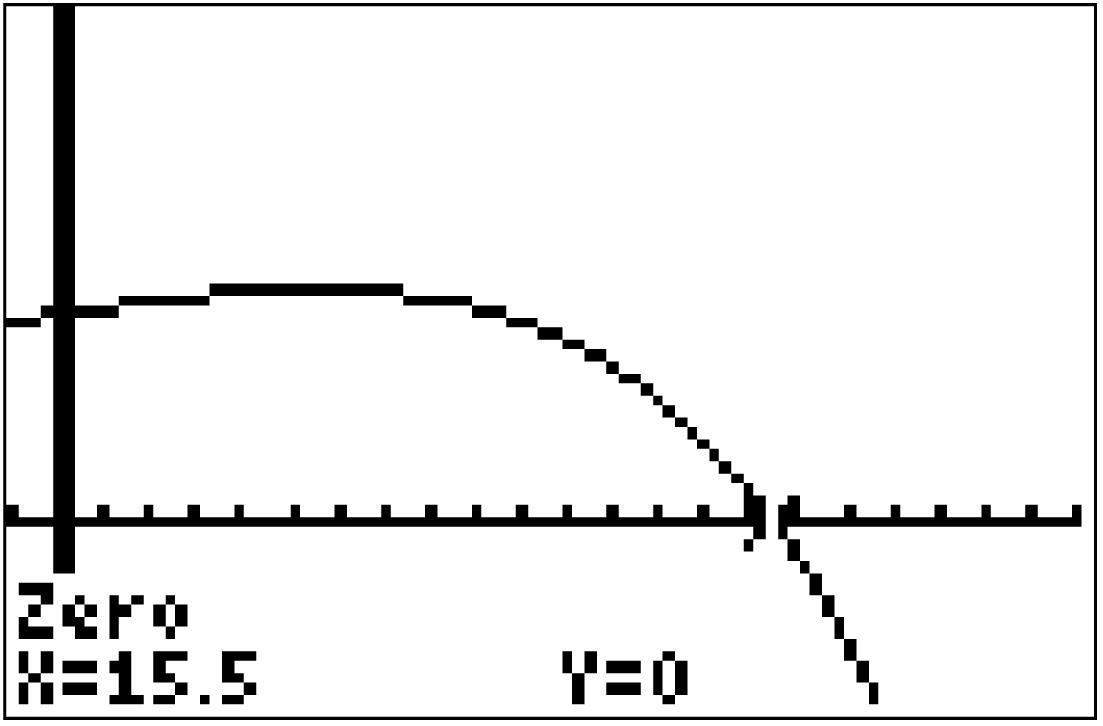 Alternativ bietet es sich auch an, die potentielle Maximalstelle mit dem GTR zu bestimmen:
Alternativ bietet es sich auch an, die potentielle Maximalstelle mit dem GTR zu bestimmen:
Gib dazu den Term der ersten Ableitungsfunktion an und lass deren Schaubild im Graph-Modus anzeigen. Wähle dann unter
an und lass deren Schaubild im Graph-Modus anzeigen. Wähle dann unter
den Befehl zum Bestimmen einer Nullstelle aus und bestätige mit Enter.
Der GTR liefert dir eine potentielle Maximalstelle an  .
2. Schritt: Hinreichende Bedingung überprüfen
Damit eine Maximalstelle vorliegt, muss weiterhin die hinreichende Bedingung
.
2. Schritt: Hinreichende Bedingung überprüfen
Damit eine Maximalstelle vorliegt, muss weiterhin die hinreichende Bedingung  erfüllt werden. Das heißt, du benötigst zunächst die zweite Ableitung der Funktion
erfüllt werden. Das heißt, du benötigst zunächst die zweite Ableitung der Funktion  . Diese erhältst du, indem du den Term von
. Diese erhältst du, indem du den Term von  erneut mit Hilfe der Produktregel ableitest:
erneut mit Hilfe der Produktregel ableitest:
 Überprüfe nun, ob
Überprüfe nun, ob  erfüllt wird:
erfüllt wird:
 Das liefert dir, dass ebenfalls die hinreichende Bedingung erfüllt ist und damit, dass an
Das liefert dir, dass ebenfalls die hinreichende Bedingung erfüllt ist und damit, dass an  eine Maximalstelle vorliegt.
3. Schritt: Koordinaten des Hochpunktes angeben
Aus den Berechnungen zuvor weißt du, dass sich an der Stelle
eine Maximalstelle vorliegt.
3. Schritt: Koordinaten des Hochpunktes angeben
Aus den Berechnungen zuvor weißt du, dass sich an der Stelle  ein Hochpunkt befindet. Damit hast du die
ein Hochpunkt befindet. Damit hast du die  -Koordinate des Hochpunktes bereits ermittelt. Die
-Koordinate des Hochpunktes bereits ermittelt. Die  -Koordinate erhältst du, indem du
-Koordinate erhältst du, indem du  in den Funktionsterm von
in den Funktionsterm von  einsetzt und berechnest:
einsetzt und berechnest:

 Alternativ kannst du den Funktionswert an der Stelle
Alternativ kannst du den Funktionswert an der Stelle  auch mit Hilfe des GTR bestimmen. Gib dazu die Funktion
auch mit Hilfe des GTR bestimmen. Gib dazu die Funktion  im Graph-Modus an und lass deren Graph anzeigen.
Den Funktionswert an besagter Stelle
im Graph-Modus an und lass deren Graph anzeigen.
Den Funktionswert an besagter Stelle  erhältst du über folgende Befehlsfolge:
erhältst du über folgende Befehlsfolge:
Die Koordinaten des Hochpunktes  lauten
lauten  .
.
Das heißt, zum Zeitpunkt wird die Förderrate maximal mit einem Maximalwert von
wird die Förderrate maximal mit einem Maximalwert von  Tonnen pro Jahr.
Tonnen pro Jahr.
Deine Aufgabe ist es rechnerisch den Zeitpunkt
Bei einer Maximalstelle
- Notwendige Bedingung:
- Hinreichende Bedingung:
Diese erhältst du, indem du die Produktregel anwendest:

Gib dazu den Term der ersten Ableitungsfunktion
|
menu |

|
menu |
Das heißt, zum Zeitpunkt
b)
 Bestimmen einer Gleichung für die Funktion
Bestimmen einer Gleichung für die Funktion  Die Funktion
Die Funktion  soll die Menge des Erdöls beschreiben, die seit 1990 bis zu einem beliebig betrachtete Zeitpunkt
soll die Menge des Erdöls beschreiben, die seit 1990 bis zu einem beliebig betrachtete Zeitpunkt  für
für ![\(t \in \left[0;20\right]\)](https://www.schullv.de/resources/formulas/fc3d5915b22c89369087dc8d6e556770dc2016bfa97b60098ada5484aba5a704_light.svg) aus dem Ölfeld gefördert wurde.
aus dem Ölfeld gefördert wurde.
Da die zuvor betrachtete Funktion die momentane Förderrate des Erdöls beschreibt, entspricht die Funktion
die momentane Förderrate des Erdöls beschreibt, entspricht die Funktion  gerade einer Stammfunktion von
gerade einer Stammfunktion von  .
Das heißt, um den Term der Funktion
.
Das heißt, um den Term der Funktion  zu bestimmen, kannst du die Funktion
zu bestimmen, kannst du die Funktion  über dem Intervall
über dem Intervall ![\(\left[0;20\right]\)](https://www.schullv.de/resources/formulas/2fb45bd1f03fc888bbb9b42d34f330fe350022f99e9f9ee6f7033ab8f18ba841_light.svg) integrieren.
integrieren.
Beachte, dass du bei einer Integration eine Integrationskonstante erhältst.
Um an dieser Stelle eine Stammfunktion von zu erhalten, kannst du partielle Integration verwenden:
zu erhalten, kannst du partielle Integration verwenden:
Wähle in diesem Fall:
 die Menge des Erdöls bis zu einem beliebigen Zeitpunkt
die Menge des Erdöls bis zu einem beliebigen Zeitpunkt  beschreibt, wird die obere Grenze des Integrals gleich
beschreibt, wird die obere Grenze des Integrals gleich  gesetzt und ist damit veränderbar.
gesetzt und ist damit veränderbar.
In unserem Fall muss also und
und  gelten. Einsetzen in die oben angeführte Formel liefert dir das gesuchte Integral von
gelten. Einsetzen in die oben angeführte Formel liefert dir das gesuchte Integral von  :
:
![\(\begin{array}{r@{\;\;}l@{\hspace{1cm}}l}
M(t)=&\displaystyle\int_{0}^{t} h‘(t) \cdot g(t)\mathrm{d}t&\\
=& h(t) \cdot g(t) - h(0)\cdot g(0)-\displaystyle\int_{0}^{t} h(t) \cdot g‘(t)\mathrm{d}t&\\
=& 10 \cdot \mathrm{e}^{0,1 \cdot t} \cdot (1.020 -40 \cdot t) - 10 \cdot \mathrm{e}^{0,1 \cdot 0} \cdot (1.020 -40 \cdot 0) -\displaystyle\int_{0}^{t} 10 \cdot \mathrm{e}^{0,1 \cdot t} \cdot (-40) \mathrm{d}t&\\
=& (10.200 -400 \cdot t) \cdot \mathrm{e}^{0,1 \cdot t} - 10.200 \cdot \mathrm{e}^{0} -\displaystyle\int_{0}^{t} -400 \cdot \mathrm{e}^{0,1 \cdot t} \mathrm{d}t&\\
=& (10.200 -400 \cdot t) \cdot \mathrm{e}^{0,1 \cdot t} - 10.200 -\left[ -4.000 \cdot \mathrm{e}^{0,1 \cdot t}\right]_0^t&\\
=& (10.200 -400 \cdot t) \cdot \mathrm{e}^{0,1 \cdot t} - 10.200 - \left( -4.000 \cdot \mathrm{e}^{0,1 \cdot t}\right) + \left( -4.000 \cdot \mathrm{e}^{0}\right) +C &\\
=& (14.200 -400 \cdot t) \cdot \mathrm{e}^{0,1 \cdot t} - 14.200 +C &\\
\end{array}\)](https://www.schullv.de/resources/formulas/951238f594e771a0aa17fae5ab7a5da96677216192c5c3fac79974828e4de66b_light.svg) Ein möglicher Term zur Funktion
Ein möglicher Term zur Funktion  bzw. der Term einer Stammfunktion zur Funktion
bzw. der Term einer Stammfunktion zur Funktion  ist gegeben durch:
ist gegeben durch:
 .
.
 Berechnen der gesamten Fördermenge
Zuvor hast du den Term der Funktion
Berechnen der gesamten Fördermenge
Zuvor hast du den Term der Funktion  ermittelt, die die gesamte geförderte Menge Erdöl von Beginn der Förderung bis zu einem beliebigen Zeitpunkt
ermittelt, die die gesamte geförderte Menge Erdöl von Beginn der Förderung bis zu einem beliebigen Zeitpunkt  beschreibt.
beschreibt.
In der Aufgabenstellung wird nun verlangt, die gesamte Fördermenge von 1990 (Beginn) bis 2009 zu bestimmen, also die gesamte Menge, die im Intervall![\(\left[0;20\right]\)](https://www.schullv.de/resources/formulas/2fb45bd1f03fc888bbb9b42d34f330fe350022f99e9f9ee6f7033ab8f18ba841_light.svg) gefördert wird. Diese Menge entspricht folglich gerade
gefördert wird. Diese Menge entspricht folglich gerade  :
:
 Alternativ kannst du die gesamt geförderte Menge an Erdöl auch mit Hilfe des GTR bestimmen.
Alternativ kannst du die gesamt geförderte Menge an Erdöl auch mit Hilfe des GTR bestimmen.
 Wechsle in den Graph-Modus und und lass den Graphen der Funktion
Wechsle in den Graph-Modus und und lass den Graphen der Funktion  zeichnen. Da die gesamte geförderte Erdölmenge gerade dem Integral der Funktion
zeichnen. Da die gesamte geförderte Erdölmenge gerade dem Integral der Funktion  über dem Intervall
über dem Intervall ![\(\left[0;20\right]\)](https://www.schullv.de/resources/formulas/2fb45bd1f03fc888bbb9b42d34f330fe350022f99e9f9ee6f7033ab8f18ba841_light.svg) entspricht, kannst du folgenden Befehl auswählen:
entspricht, kannst du folgenden Befehl auswählen:
Gib die untere Grenze 0 sowie die obere Grenze 20 an und bestätige mit Enter.
Im Zeitraum von 1990 bis 2009 werden  Tonnen Erdöl gefördert.
Tonnen Erdöl gefördert.
 Einnahmen aus dem Verkauf im Jahr 2007 bestimmen
Im Jahr 2007 beträgt der Verkaufspreis 56 Euro pro Barrel Erdöl. Ein Barrel wiegt ungefähr 137 kg. Deine Aufgabe ist es, die Einnahmen im Jahr 2007 zu bestimmen.
Einnahmen aus dem Verkauf im Jahr 2007 bestimmen
Im Jahr 2007 beträgt der Verkaufspreis 56 Euro pro Barrel Erdöl. Ein Barrel wiegt ungefähr 137 kg. Deine Aufgabe ist es, die Einnahmen im Jahr 2007 zu bestimmen.
Um diese Einnahmen zu bestimmen, kannst du wie folgt vorgehen:![\(\left[17;18 \right]\)](https://www.schullv.de/resources/formulas/2f49e546f59b9d50d81bdc25dfde6c83472a7db5f80ab671785bc59fa63c274c_light.svg) dargestellt.
dargestellt.
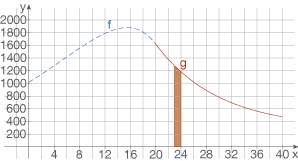 Die rot markierte Fläche entspricht gerade
Die rot markierte Fläche entspricht gerade  :
:
![\(\begin{array}{r@{\;\;}l@{\hspace{1cm}}l}
M(18)-M(17)=& (14.200 -400 \cdot 18) \cdot \mathrm{e}^{0,1 \cdot 18} - 14.200 - \left[ (14.200 -400 \cdot 18) \cdot \mathrm{e}^{0,1 \cdot 18} - 14.200 \right] &\\
=& 7.000 \cdot \mathrm{e}^{1,8} - 7.400 \cdot \mathrm{e}^{1,7} &\\
\approx& 1840,32&\\
\end{array}\)](https://www.schullv.de/resources/formulas/2e21ff450ac17cb521b12a95479e3f71f114d019a2d4b4080378dcebf4243c92_light.svg) Im Jahr 2007 werden also
Im Jahr 2007 werden also  Tonnen Erdöl gefördert.
Alternativ kannst du das Integral auch mit Hilfe des GTR bestimmen.
Tonnen Erdöl gefördert.
Alternativ kannst du das Integral auch mit Hilfe des GTR bestimmen.
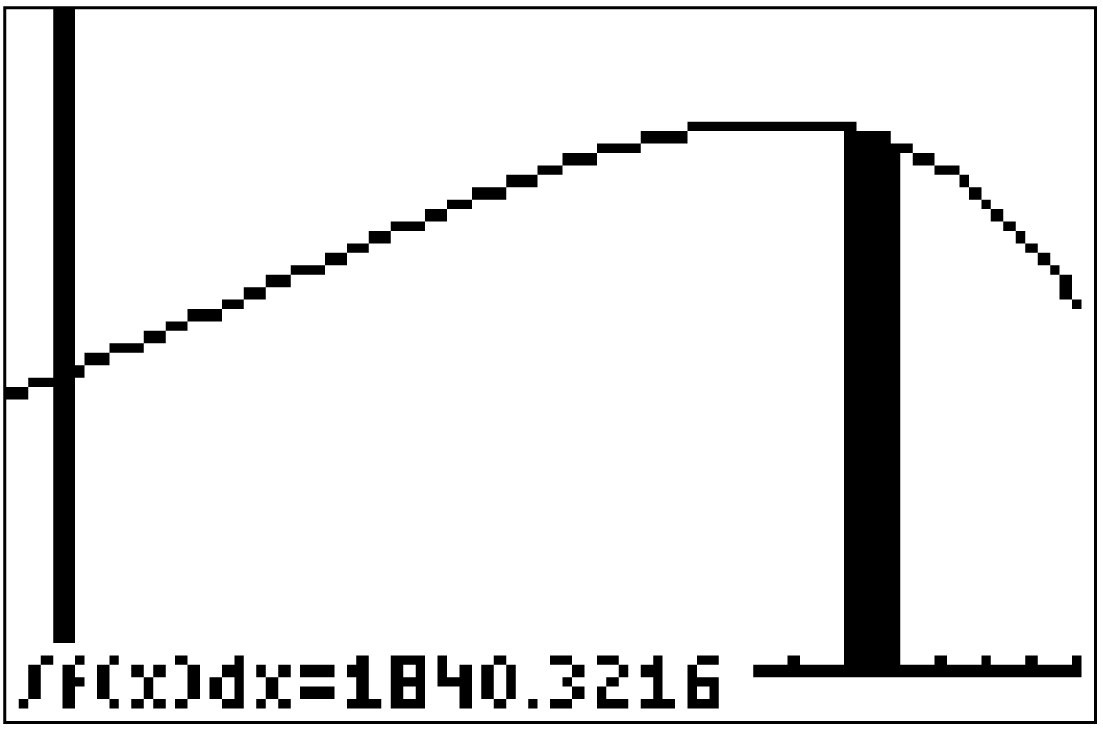 Wechsle in den Graph-Modus und und lass den Graphen zur Funktion
Wechsle in den Graph-Modus und und lass den Graphen zur Funktion  zeichnen. Da die gesamte geförderte Erdölmenge im Jahr 2007 gerade dem Integral der Funktion
zeichnen. Da die gesamte geförderte Erdölmenge im Jahr 2007 gerade dem Integral der Funktion  über dem Intervall
über dem Intervall ![\(\left[17;18\right]\)](https://www.schullv.de/resources/formulas/23297b463e6755b46e2b4c404105b75cd2be949765be868294f2c212dbad1f58_light.svg) entspricht, kannst du folgenden Befehl auswählen:
entspricht, kannst du folgenden Befehl auswählen:
Gib die untere Grenze 17 sowie die obere Grenze 18 an und bestätige mit Enter.
Im Jahr 2007 werden  Tonnen Erdöl gefördert.
2. Schritt: Geförderte Menge in Barrels umrechnen
Da die Menge an gefördertem Erdöl in Barrels gemessen wird, kannst du folgende Umrechnung vornehmen:
Tonnen Erdöl gefördert.
2. Schritt: Geförderte Menge in Barrels umrechnen
Da die Menge an gefördertem Erdöl in Barrels gemessen wird, kannst du folgende Umrechnung vornehmen:
 Im Jahr 2007 werden also
Im Jahr 2007 werden also  Barrels an Erdöl verkauft.
3. Schritt: Einnahmen aus dem Jahr 2007 bestimmen
Im Jahr 2007 liegt der Verkaufspreis eines Barrels bei einem Preis von 56 Euro. Damit folgt:
Barrels an Erdöl verkauft.
3. Schritt: Einnahmen aus dem Jahr 2007 bestimmen
Im Jahr 2007 liegt der Verkaufspreis eines Barrels bei einem Preis von 56 Euro. Damit folgt:
 Es werden also
Es werden also  Euro im Jahr 2007 durch den Verkauf des Erdöls eingenommen.
Euro im Jahr 2007 durch den Verkauf des Erdöls eingenommen.
Da die zuvor betrachtete Funktion
Beachte, dass du bei einer Integration eine Integrationskonstante erhältst.
Um an dieser Stelle eine Stammfunktion von
|
|
In unserem Fall muss also
In der Aufgabenstellung wird nun verlangt, die gesamte Fördermenge von 1990 (Beginn) bis 2009 zu bestimmen, also die gesamte Menge, die im Intervall

|
menu |
Um diese Einnahmen zu bestimmen, kannst du wie folgt vorgehen:
- Bestimme zunächst die geförderte Menge an Erdöl im Jahr 2007. Das Jahr 2007 wird im Schaubild durch das Intervall
dargestellt. Diese Menge entspricht dem Integral:
ist die im Jahr 2007 gewonnene Menge an Erdöl in 1.000 Tonnen. Dividiere diese Menge mit 137 kg, um die Anzahl der Barrels zu erhalten.
- Multipliziere die Anzahl der Barrels mit dem Verkaufspreis von 56 Euro, um die Einnahmen zu erhalten.


|
menu |
c)
 Begründen, warum
Begründen, warum  für einen langen Zeitraum nicht sinnvoll wäre
Die momentane Förderrate ab dem Jahr 2010 wird im Intervall
für einen langen Zeitraum nicht sinnvoll wäre
Die momentane Förderrate ab dem Jahr 2010 wird im Intervall ![\(\left(\left.20;40\right]\right.\)](https://www.schullv.de/resources/formulas/30d871595acdf6c7899bc11b2ad117356c98d4d7a4e19e6565348514245b4fca_light.svg) durch die Funktion
durch die Funktion  mit dem Term
mit dem Term
 modelliert. Dabei gibt die Variable
modelliert. Dabei gibt die Variable  das Jahr und
das Jahr und  die geförderte Menge an Erdöl zur Einheit 1.000 Tonnen pro Jahr an.
die geförderte Menge an Erdöl zur Einheit 1.000 Tonnen pro Jahr an.
Begründe, warum es nicht sinnvoll wäre mittels Funktion die Förderrate über einen größeren Zeitraum zu beschreiben.
Dazu kannst du die Funktion
die Förderrate über einen größeren Zeitraum zu beschreiben.
Dazu kannst du die Funktion  für
für  untersuchen. Liegt beispielsweise ein Grenzwert größer Null vor, so würde das bedeuten, dass das Ölfeld nie erschöpft werden könnte, was nicht möglich ist.
Dazu kannst du die Terme
untersuchen. Liegt beispielsweise ein Grenzwert größer Null vor, so würde das bedeuten, dass das Ölfeld nie erschöpft werden könnte, was nicht möglich ist.
Dazu kannst du die Terme  und
und  separat betrachten.
separat betrachten.
 Das liefert dir, dass die Funktion
Das liefert dir, dass die Funktion  für
für  gegen den Wert
gegen den Wert  konvergiert. Das heißt, dass die momentane Förderrate nie unter diesen Wert fällt und damit, dass das Ölfeld nie erschöpft werden würde. Da das nicht möglich ist, kannst du annehmen, dass
konvergiert. Das heißt, dass die momentane Förderrate nie unter diesen Wert fällt und damit, dass das Ölfeld nie erschöpft werden würde. Da das nicht möglich ist, kannst du annehmen, dass  die momentane Förderrate über einen längeren Zeitraum nicht sinnvoll modelliert.
die momentane Förderrate über einen längeren Zeitraum nicht sinnvoll modelliert.
 Letztes Jahr bestimmen, in welchem die Erdölförderung wirtschaftlich ist
Laut Angaben ist die Erdölförderung nur dann wirtschaftlich, wenn innerhalb eines Kalenderjahres mindestens
Letztes Jahr bestimmen, in welchem die Erdölförderung wirtschaftlich ist
Laut Angaben ist die Erdölförderung nur dann wirtschaftlich, wenn innerhalb eines Kalenderjahres mindestens  Tonnen Öl gefördert wird. Bestimme das Jahr, in dem das zum Letzten mal der Fall ist.
Tonnen Öl gefördert wird. Bestimme das Jahr, in dem das zum Letzten mal der Fall ist.
Die Funktion beschreibt die momentane Förderrate im Intervall
beschreibt die momentane Förderrate im Intervall ![\(\left(\left.20;40\right]\right.\)](https://www.schullv.de/resources/formulas/30d871595acdf6c7899bc11b2ad117356c98d4d7a4e19e6565348514245b4fca_light.svg) . Ihre Stammfunktion
. Ihre Stammfunktion  stellt folglich die geförderte Menge an Erdöl dar.
stellt folglich die geförderte Menge an Erdöl dar.
Um also das Jahr zu bestimmen, in dem die gesamte geförderte Erdölmenge zum letzten Mal mehr als 600.000 Tonnen beträgt, kannst du folgendermaßen vorgehen: bestimmen
Die Stammfunktion
bestimmen
Die Stammfunktion  zur Funktion
zur Funktion  beschreibt die Menge an Erdöl, die ab 2010 bis zu einem beliebigen Zeitpunkt gefördert wird. Da die Menge von einschließlich
beschreibt die Menge an Erdöl, die ab 2010 bis zu einem beliebigen Zeitpunkt gefördert wird. Da die Menge von einschließlich  bis zu einem beliebigem Zeitpunkt beschrieben werden soll, entspricht die untere Grenze 20 und die obere Grenze
bis zu einem beliebigem Zeitpunkt beschrieben werden soll, entspricht die untere Grenze 20 und die obere Grenze  , da sie veränderbar sein soll. Du kannst
, da sie veränderbar sein soll. Du kannst  wie folgt bestimmen:
wie folgt bestimmen:
![\(\begin{array}{r@{\;\;}l@{\hspace{1cm}}l}
G(t)=&\displaystyle\int_{20}^{t} g(t)\;\mathrm{d}t &\\
=&\displaystyle\int_{20}^{t} 180 \cdot \mathrm{e}^{4-0,1 \cdot t}+ 40 \cdot \mathrm{e}^2\;\mathrm{d}t &\\
=&\left[ -1.800 \cdot \mathrm{e}^{4-0,1 \cdot t}+ 40 \cdot t \cdot \mathrm{e}^2\right]_{20}^{t} &\\
=& -1.800 \cdot \mathrm{e}^{4-0,1 \cdot t}+ 40 \cdot t \cdot \mathrm{e}^2 - \left( -1.800 \cdot \mathrm{e}^{4-0,1 \cdot 20}+ 40 \cdot 20 \cdot \mathrm{e}^2 \right) &\\
=& -1.800 \cdot \mathrm{e}^{4-0,1 \cdot t}+ 40 \cdot t \cdot \mathrm{e}^2 +1.800 \cdot \mathrm{e}^{2}- 800 \cdot \mathrm{e}^2 &\\
=& -1.800 \cdot \mathrm{e}^{4-0,1 \cdot t}+ 40 \cdot t \cdot \mathrm{e}^2 +1.000 \cdot \mathrm{e}^{2} &\\
\end{array}\)](https://www.schullv.de/resources/formulas/659df0b4855b2ae07ef331027083006993732cf40ec5cbb9b252cfb57a39f511_light.svg) 2. Schritt: Geförderte Erdölmenge innerhalb eines Jahres berechnen
Zuvor hast du eine Stammfunktion
2. Schritt: Geförderte Erdölmenge innerhalb eines Jahres berechnen
Zuvor hast du eine Stammfunktion  bestimmt, die die gesamte geförderte Menge an Erdöl ab Beginn 2010 bis zu einem beliebigen Zeitpunkt modelliert. Die Menge an Erdöl, die innerhalb eines Kalenderjahres gefördert wird, entspricht gerade der Differenz
bestimmt, die die gesamte geförderte Menge an Erdöl ab Beginn 2010 bis zu einem beliebigen Zeitpunkt modelliert. Die Menge an Erdöl, die innerhalb eines Kalenderjahres gefördert wird, entspricht gerade der Differenz  für
für  .
.
Einsetzen in den Term der Stammfunktion liefert dir die Menge in 1.000 Tonnen pro Jahr:
liefert dir die Menge in 1.000 Tonnen pro Jahr:
![\(\begin{array}{r@{\;\;}l@{\hspace{1cm}}l}
G(t+1)-G(t)=& -1.800 \cdot \mathrm{e}^{4-0,1 \cdot (t+1)}+ 40 \cdot (t+1) \cdot \mathrm{e}^2 +1.000 \cdot \mathrm{e}^{2} &\\
&- \left[ -1.800 \cdot \mathrm{e}^{4-0,1 \cdot t}+ 40 \cdot t \cdot \mathrm{e}^2 +1.000 \cdot \mathrm{e}^{2} \right]&\\
=& -1.800 \cdot \mathrm{e}^{4-0,1 \cdot t -0,1}+ 40 \cdot t \cdot \mathrm{e}^2+40 \cdot \mathrm{e}^2 +1.000 \cdot \mathrm{e}^{2} &\\
&+1.800 \cdot \mathrm{e}^{4-0,1 \cdot t}- 40 \cdot t \cdot \mathrm{e}^2 -1.000 \cdot \mathrm{e}^{2} &\\
=& -1.800 \cdot \mathrm{e}^{4-0,1 \cdot t -0,1}+40 \cdot \mathrm{e}^2 +1.800 \cdot \mathrm{e}^{4-0,1 \cdot t} &\\
=& 1.800 \cdot \mathrm{e}^{4-0,1 \cdot t}\left(1- \mathrm{e}^{-0,1}\right) + 40 \cdot \mathrm{e}^2 &\\
\end{array}\)](https://www.schullv.de/resources/formulas/69c12dc9476016f16ee8e5d19364c05b0ece3243c45bd7ec0c560f400a4213ab_light.svg) Die geförderte Erdölmenge innerhalb eines Jahres beträgt
Die geförderte Erdölmenge innerhalb eines Jahres beträgt  in 1.000 Tonnen.
3. Schritt: Letztes Jahr bestimmen, in dem die Ölförderung wirtschaftlich ist
Damit die Ölförderung wirtschaftlich ist, sollen mindestens 600.000 Tonnen Erdöl innerhalb eines Kalenderjahres gefördert werden.
in 1.000 Tonnen.
3. Schritt: Letztes Jahr bestimmen, in dem die Ölförderung wirtschaftlich ist
Damit die Ölförderung wirtschaftlich ist, sollen mindestens 600.000 Tonnen Erdöl innerhalb eines Kalenderjahres gefördert werden.
Das heißt, es muss folgende Ungleichung erfüllt werden: Diese Ungleichung kannst du nach
Diese Ungleichung kannst du nach  auflösen:
auflösen:
 Das liefert dir, dass
Das liefert dir, dass  gelten muss, damit die Ölförderung wirtschaftlich bleibt. Das heißt, das Kalenderjahr 2024 (entspricht 34 auf der
gelten muss, damit die Ölförderung wirtschaftlich bleibt. Das heißt, das Kalenderjahr 2024 (entspricht 34 auf der  -Achse) ist das letzte Jahr, in dem die Ölförderung mindestens 600.000 Tonnen beträgt.
-Achse) ist das letzte Jahr, in dem die Ölförderung mindestens 600.000 Tonnen beträgt.
Alternativ kannst du das Jahr auch mit Hilfe des GTR bestimmen.
Interpretiere dazu den Term und
und  als neue Funktionen und lass diese im Graph-Modus zeichnen.
als neue Funktionen und lass diese im Graph-Modus zeichnen.
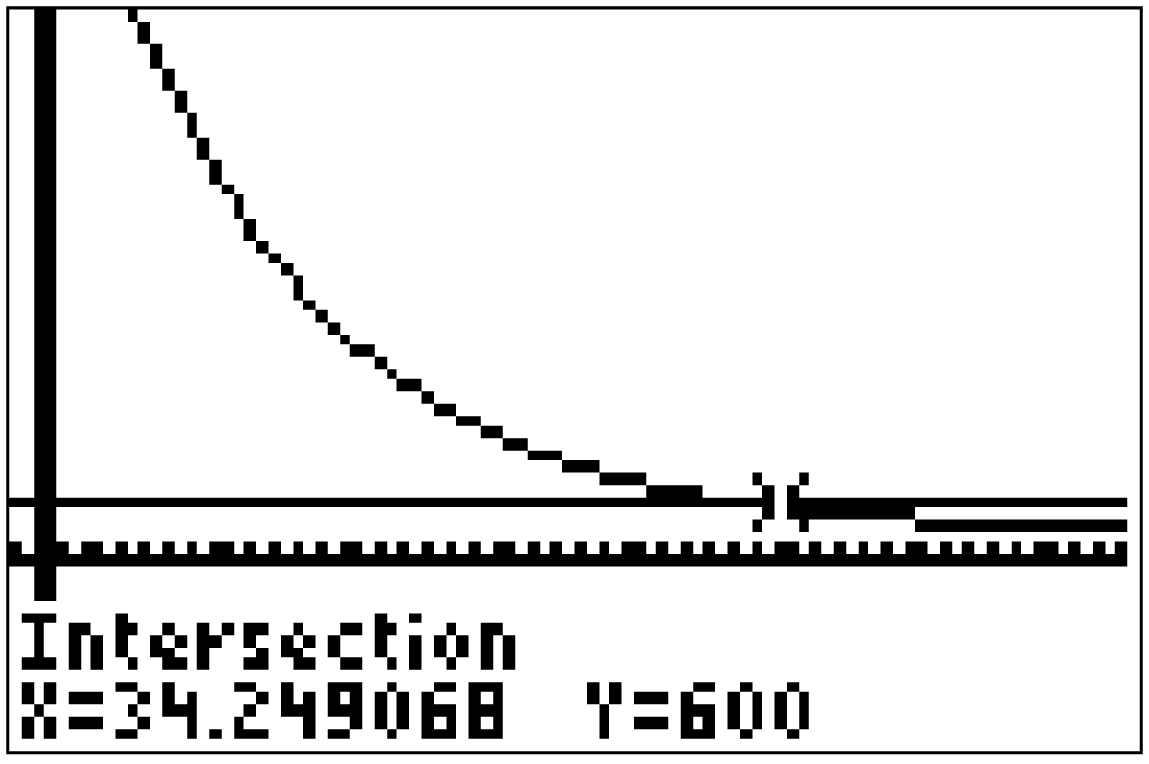 Die Relation
Die Relation  ist solange erfüllt, bis der Funktionswert des ersten Terms kleiner als 600 wird. Das heißt, wir suchen den Schnittpunkt der beiden angezeigten Funktionen. Diesen erhältst du über die Befehlsfolge:
ist solange erfüllt, bis der Funktionswert des ersten Terms kleiner als 600 wird. Das heißt, wir suchen den Schnittpunkt der beiden angezeigten Funktionen. Diesen erhältst du über die Befehlsfolge:
Das liefert dir, dass  gelten muss, damit die Ölförderung wirtschaftlich bleibt. Das heißt, das Kalenderjahr 2024 (entspricht 34 auf der
gelten muss, damit die Ölförderung wirtschaftlich bleibt. Das heißt, das Kalenderjahr 2024 (entspricht 34 auf der  -Achse) ist das letzte Jahr, in dem die Ölförderung mindestens 600.000 Tonnen beträgt.
-Achse) ist das letzte Jahr, in dem die Ölförderung mindestens 600.000 Tonnen beträgt.
Begründe, warum es nicht sinnvoll wäre mittels Funktion
- Für
konvergiert
gegen Null.
- Für
bleibt der Term
unverändert.
Die Funktion
Um also das Jahr zu bestimmen, in dem die gesamte geförderte Erdölmenge zum letzten Mal mehr als 600.000 Tonnen beträgt, kannst du folgendermaßen vorgehen:
- Bestimme eine Stammfunktion
der Funktion
. Es gilt
.
- Berechne die gesamt geförderte Erdölmenge innerhalb eines Jahres, indem du
berechnest. Dieser Term ist abhängig von der Variablen
, die das gesuchte Jahr angibt.
- Löse die Ungleichung
nach
auf, um das gesuchte Jahr zu bestimmen.
Einsetzen in den Term der Stammfunktion
Das heißt, es muss folgende Ungleichung erfüllt werden:
Alternativ kannst du das Jahr auch mit Hilfe des GTR bestimmen.
Interpretiere dazu den Term

|
menu |
d)
 Begründen, dass
Begründen, dass  an der Stelle
an der Stelle  differenzierbar ist
Die Funktion
differenzierbar ist
Die Funktion  setzt sich aus den zuvor betrachteten Funktionen
setzt sich aus den zuvor betrachteten Funktionen  und
und  zusammen:
zusammen:
![\(h(t)=\begin{cases} f(t)=(1.020 -40 \cdot t) \cdot \mathrm{e}^{0,1 \cdot t}, & t\in \left[0;20\right] \\
g(t)=180 \cdot \mathrm{e}^{4-0,1 \cdot t}+ 40 \cdot \mathrm{e}^2, & t\in \left(\left.20;40\right]\right.\end{cases}\)](https://www.schullv.de/resources/formulas/ad4f76eb8ef4e84f699191d83adc9709e4d155c3178b41a019b7cfc6e972d7dc_light.svg) Deine Aufgabe ist es, zu zeigen, dass die Funktion
Deine Aufgabe ist es, zu zeigen, dass die Funktion  an der Stelle
an der Stelle  differenzierbar ist.
differenzierbar ist.
Eine Funktion ist an einer Stelle differenzierbar, wenn gilt:
differenzierbar, wenn gilt:
 überprüfen
Damit die Funktion
überprüfen
Damit die Funktion  an der Stelle
an der Stelle  differenzierbar ist, muss sie an dieser Stelle stetig sein:
differenzierbar ist, muss sie an dieser Stelle stetig sein:
 und
und  an der Stelle
an der Stelle  überein.
2. Schritt: Ableitungen an der Stelle
überein.
2. Schritt: Ableitungen an der Stelle  überprüfen
Damit die Funktion
überprüfen
Damit die Funktion  tatsächlich differenzierbar ist, musst du weiterhin überprüfen, ob die Ableitungen der Funktionen
tatsächlich differenzierbar ist, musst du weiterhin überprüfen, ob die Ableitungen der Funktionen  und
und  an dieser Stelle übereinstimmen.
an dieser Stelle übereinstimmen.
 ist an der Stelle
ist an der Stelle  differenzierbar.
differenzierbar.
 Entscheiden, ob
Entscheiden, ob  an der Stelle
an der Stelle  zweimal differenzierbar ist
Soll die Funktion
zweimal differenzierbar ist
Soll die Funktion  an der Stelle
an der Stelle  zweimal differenzierbar sein, so muss die Ableitungsfunktion der Funktion
zweimal differenzierbar sein, so muss die Ableitungsfunktion der Funktion  an dieser Stelle differenzierbar sein. Analog zur Vorgehensweise vom Aufgabenteil zuvor kannst du dann annehmen, dass für zweimal differenzierbar zusätzlich gelten muss:
an dieser Stelle differenzierbar sein. Analog zur Vorgehensweise vom Aufgabenteil zuvor kannst du dann annehmen, dass für zweimal differenzierbar zusätzlich gelten muss:
 gilt.
Im Aufgabentext werden die folgenden Angaben gemacht:
gilt.
Im Aufgabentext werden die folgenden Angaben gemacht:
 und
und  an der Stelle
an der Stelle  nicht übereinstimmen. Das heißt, dass die Funktion
nicht übereinstimmen. Das heißt, dass die Funktion  an der Stelle
an der Stelle  nicht zweimal differenzierbar ist.
nicht zweimal differenzierbar ist.
 Begründen, dass
Begründen, dass  an der Stelle
an der Stelle  ein Minimum besitzt
Wie du vorher aber nachgewiesen hast, ist die Funktion
ein Minimum besitzt
Wie du vorher aber nachgewiesen hast, ist die Funktion  an der Stelle
an der Stelle  nicht differenzierbar. Das heißt, du kannst die notwendige und hinreichende Bedingung für Minimalstellen nicht prüfen.
nicht differenzierbar. Das heißt, du kannst die notwendige und hinreichende Bedingung für Minimalstellen nicht prüfen.
Um zu begründen, dass die Funktion an der Stelle
an der Stelle  ein lokales Minimum besitzt, musst du zeigen, dass
ein lokales Minimum besitzt, musst du zeigen, dass  in einer Umgebung von
in einer Umgebung von  kleiner als alle anderen Funktionswerte von
kleiner als alle anderen Funktionswerte von  ist.
ist.
Das kannst du nachweisen, indem du zeigst, dass auf dem Intervall
auf dem Intervall ![\(\left[0;20\right]\)](https://www.schullv.de/resources/formulas/2fb45bd1f03fc888bbb9b42d34f330fe350022f99e9f9ee6f7033ab8f18ba841_light.svg) überprüfen:
Die Funktion
überprüfen:
Die Funktion  wird auf dem Intervall
wird auf dem Intervall ![\(\left[0;20\right]\)](https://www.schullv.de/resources/formulas/2fb45bd1f03fc888bbb9b42d34f330fe350022f99e9f9ee6f7033ab8f18ba841_light.svg) durch den Term der Funktion
durch den Term der Funktion  beschrieben.
beschrieben.
Es gilt . Um zu zeigen, dass das einem lokalen Minimum entspricht, kannst du zeigen, dass die Funktion
. Um zu zeigen, dass das einem lokalen Minimum entspricht, kannst du zeigen, dass die Funktion  monoton fallend ist.
Soll die Funktion
monoton fallend ist.
Soll die Funktion  monoton fallend sein, so muss gelten:
monoton fallend sein, so muss gelten:
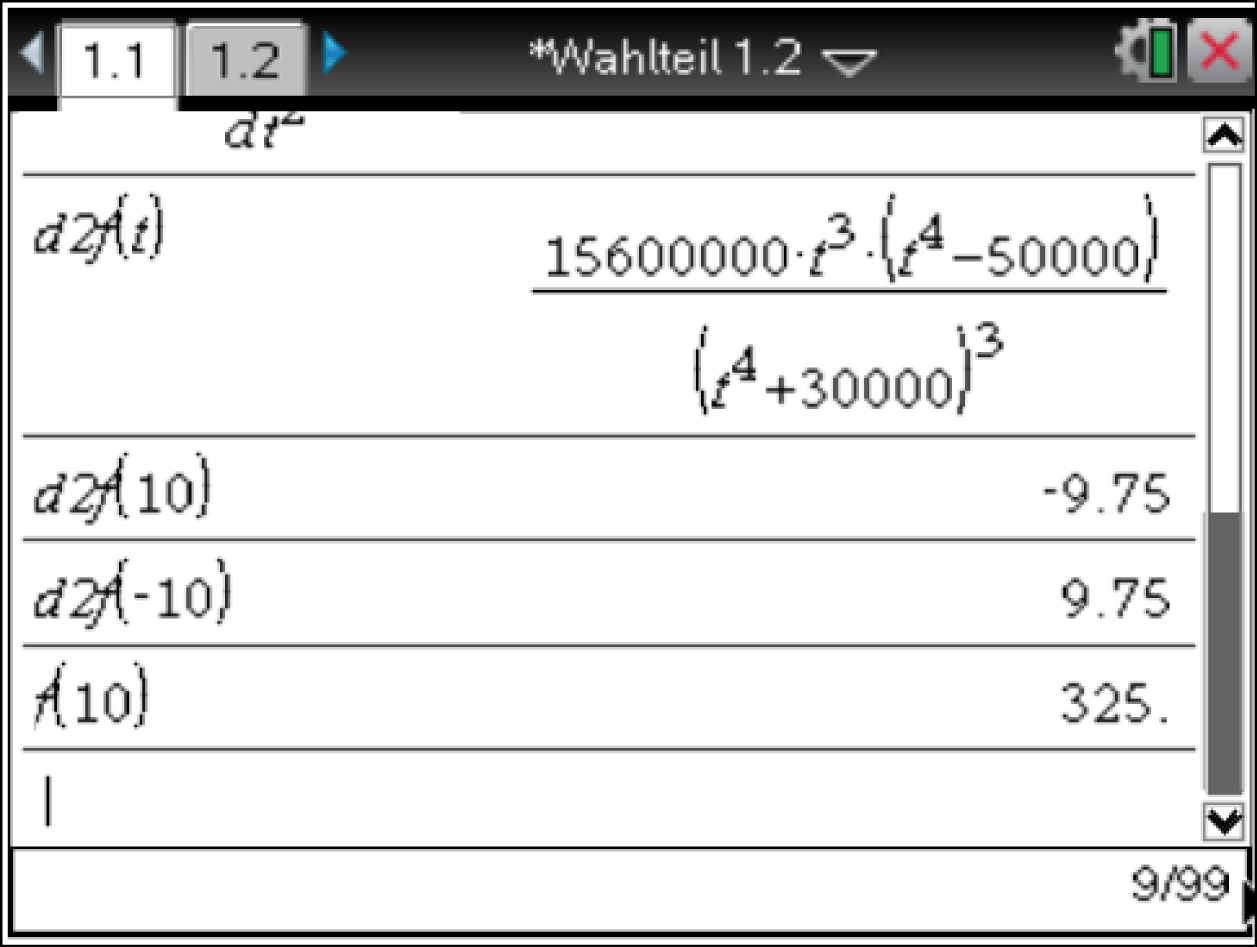
Im Aufgabentext ist angegeben, dass die zweite Ableitungsfunktion durch  gegeben ist, was du ohne Nachweis annehmen darfst. Wir überprüfen nun auf monoton fallend:
gegeben ist, was du ohne Nachweis annehmen darfst. Wir überprüfen nun auf monoton fallend:
 Hier kannst du verwenden, dass der Term
Hier kannst du verwenden, dass der Term  niemals kleiner gleich Null wird. Du kannst diesen Term zur weiteren Betrachtung folglich vernachlässigen.
niemals kleiner gleich Null wird. Du kannst diesen Term zur weiteren Betrachtung folglich vernachlässigen.
 Das liefert dir, dass die Funktion
Das liefert dir, dass die Funktion  für
für  bzw. auf dem Intervall
bzw. auf dem Intervall ![\(\left[5,5;20\right]\)](https://www.schullv.de/resources/formulas/1f9d52c6e8940ea9e966340755c92add39b904ec714c23b81520de56e524bc79_light.svg) monoton fallend ist. Das heißt, auf dem Intervall
monoton fallend ist. Das heißt, auf dem Intervall ![\(\left[0;5,5\right]\)](https://www.schullv.de/resources/formulas/4dff467da747712b1763ae22dbd73c3ef3f36616dec9cc81f6a9898edcae7f09_light.svg) ist sie dahingegen monoton steigend. Es ist also möglich, dass sich ein weiteres lokales Minimum auf dem gesamten Intervall
ist sie dahingegen monoton steigend. Es ist also möglich, dass sich ein weiteres lokales Minimum auf dem gesamten Intervall ![\(\left[0;20\right]\)](https://www.schullv.de/resources/formulas/2fb45bd1f03fc888bbb9b42d34f330fe350022f99e9f9ee6f7033ab8f18ba841_light.svg) befindet.
2. Schritt:
befindet.
2. Schritt:  auf dem Intervall
auf dem Intervall ![\(\left(\left.20;40\right]\right.\)](https://www.schullv.de/resources/formulas/30d871595acdf6c7899bc11b2ad117356c98d4d7a4e19e6565348514245b4fca_light.svg) überprüfen:
Die Funktion
überprüfen:
Die Funktion  wird auf dem Intervall
wird auf dem Intervall ![\(\left(\left.20;40\right]\right.\)](https://www.schullv.de/resources/formulas/30d871595acdf6c7899bc11b2ad117356c98d4d7a4e19e6565348514245b4fca_light.svg) durch den Term der Funktion
durch den Term der Funktion  beschrieben.
beschrieben.
Es gilt . Um zu zeigen, dass das dem lokalen Minimum entspricht, kannst du zeigen, dass die Funktion
. Um zu zeigen, dass das dem lokalen Minimum entspricht, kannst du zeigen, dass die Funktion  monoton steigend ist.
Soll die Funktion
monoton steigend ist.
Soll die Funktion  monoton steigend sein, so muss gelten:
monoton steigend sein, so muss gelten:
Im Aufgabentext ist angegeben, dass die zweite Ableitungsfunktion durch  gegeben ist, was du ohne Nachweis annehmen darfst. Wir überprüfen nun auf monoton steigend:
gegeben ist, was du ohne Nachweis annehmen darfst. Wir überprüfen nun auf monoton steigend:
 Hier kannst du verwenden, dass der Term
Hier kannst du verwenden, dass der Term  niemals kleiner gleich Null wird. Da der Faktor 1,8 weiterhin positiv ist, kannst du festhalten, dass die Funktion
niemals kleiner gleich Null wird. Da der Faktor 1,8 weiterhin positiv ist, kannst du festhalten, dass die Funktion  auf dem gesamten Intervall
auf dem gesamten Intervall ![\(\left(\left.20;40\right]\right.\)](https://www.schullv.de/resources/formulas/30d871595acdf6c7899bc11b2ad117356c98d4d7a4e19e6565348514245b4fca_light.svg) positiv ist. Damit ist
positiv ist. Damit ist  auf
auf ![\(\left(\left.20;40\right]\right.\)](https://www.schullv.de/resources/formulas/30d871595acdf6c7899bc11b2ad117356c98d4d7a4e19e6565348514245b4fca_light.svg) monoton steigend.
monoton steigend.
Folglich befindet sich an der kleinste Funktionswert.
Insgesamt folgt dann, dass sich wegen
der kleinste Funktionswert.
Insgesamt folgt dann, dass sich wegen  an
an  ein lokales Minimum befindet.
ein lokales Minimum befindet.
Eine Funktion ist an einer Stelle
- Die Funktionswerte von
und
stimmen an der Stelle
überein.
- Die Ableitungen von
und
stimmen an der Stelle
überein.
- Die Funktionswerte von
und
stimmen an der Stelle
überein.
- Die Ableitungen von
und
stimmen an der Stelle
überein.
Um zu begründen, dass die Funktion
Das kannst du nachweisen, indem du zeigst, dass
monoton fallend auf dem Intervall
ist und dass
monoton steigend auf dem Intervall
ist
Es gilt
|
|
Es gilt
|
|
Folglich befindet sich an
a)
 Maximale Förderrate bestimmen
Die momentane Förderrate aus einem Ölfeld im Zeitraum von 1990 bis 2009 wird im Intervall
Maximale Förderrate bestimmen
Die momentane Förderrate aus einem Ölfeld im Zeitraum von 1990 bis 2009 wird im Intervall ![\(\left[0;20\right]\)](https://www.schullv.de/resources/formulas/2fb45bd1f03fc888bbb9b42d34f330fe350022f99e9f9ee6f7033ab8f18ba841_light.svg) wird durch die Funktion
wird durch die Funktion  mit dem Term
mit dem Term
 modelliert. Dabei gibt die Variable
modelliert. Dabei gibt die Variable  das Jahr und
das Jahr und  die geförderte Menge an Erdöl zur Einheit 1.000 Tonnen pro Jahr an.
die geförderte Menge an Erdöl zur Einheit 1.000 Tonnen pro Jahr an.
Deine Aufgabe ist es rechnerisch den Zeitpunkt zu bestimmen, an dem die Förderrate maximal wird und weiterhin den entsprechenden Maximalwert anzugeben.
Das heißt, du kannst den Hochpunkt der Funktion
zu bestimmen, an dem die Förderrate maximal wird und weiterhin den entsprechenden Maximalwert anzugeben.
Das heißt, du kannst den Hochpunkt der Funktion  bestimmen. Denn dessen
bestimmen. Denn dessen  -Koordinate entspricht dem gesuchten Zeitpunkt, an dem die Förderrate maximal wird und die
-Koordinate entspricht dem gesuchten Zeitpunkt, an dem die Förderrate maximal wird und die  -Koordinate gibt den Maximalwert an.
Um die Koordinaten angeben zu können, musst du zunächst die notwendige und hinreichende Bedingung für Maximalstellen überprüfen.
-Koordinate gibt den Maximalwert an.
Um die Koordinaten angeben zu können, musst du zunächst die notwendige und hinreichende Bedingung für Maximalstellen überprüfen.
Bei einer Maximalstelle der Funktion
der Funktion  müssen folgende Bedingungen erfüllt sein:
müssen folgende Bedingungen erfüllt sein:
 . Hast du diese bestimmt, so kannst du die bestimmte Stelle in den Funktionsterm von
. Hast du diese bestimmt, so kannst du die bestimmte Stelle in den Funktionsterm von  einsetzen und erhältst den zugehörigen Funktionswert an dieser Maximalstelle.
1. Schritt: Notwendige Bedingung überprüfen
Um die notwendige Bedingung einer Maximalstelle der Funktion
einsetzen und erhältst den zugehörigen Funktionswert an dieser Maximalstelle.
1. Schritt: Notwendige Bedingung überprüfen
Um die notwendige Bedingung einer Maximalstelle der Funktion  zu überprüfen, benötigst du zunächst die erste Ableitungsfunktion der Funktion
zu überprüfen, benötigst du zunächst die erste Ableitungsfunktion der Funktion  .
.
Diese erhältst du, indem du die Produktregel anwendest: Für die notwendige Bedingung einer Maximalstelle muss
Für die notwendige Bedingung einer Maximalstelle muss  gelten. Setze also den Funktionsterm der ersten Ableitung
gelten. Setze also den Funktionsterm der ersten Ableitung  gleich Null und ermittle alle potentiellen Werte, für die diese Gleichung erfüllt wird:
gleich Null und ermittle alle potentiellen Werte, für die diese Gleichung erfüllt wird:
 An dieser Stelle kannst du den Satz vom Nullprodukt anwenden. Da der Term
An dieser Stelle kannst du den Satz vom Nullprodukt anwenden. Da der Term  für keinen Wert für
für keinen Wert für  gleich Null werden kann, kannst du diesen vernachlässigen.
gleich Null werden kann, kannst du diesen vernachlässigen.
 Damit hast du eine potentielle Maximalstelle an
Damit hast du eine potentielle Maximalstelle an  ermittelt und kannst für diese Stelle nun das hinreichende Kriterium überprüfen.
ermittelt und kannst für diese Stelle nun das hinreichende Kriterium überprüfen.
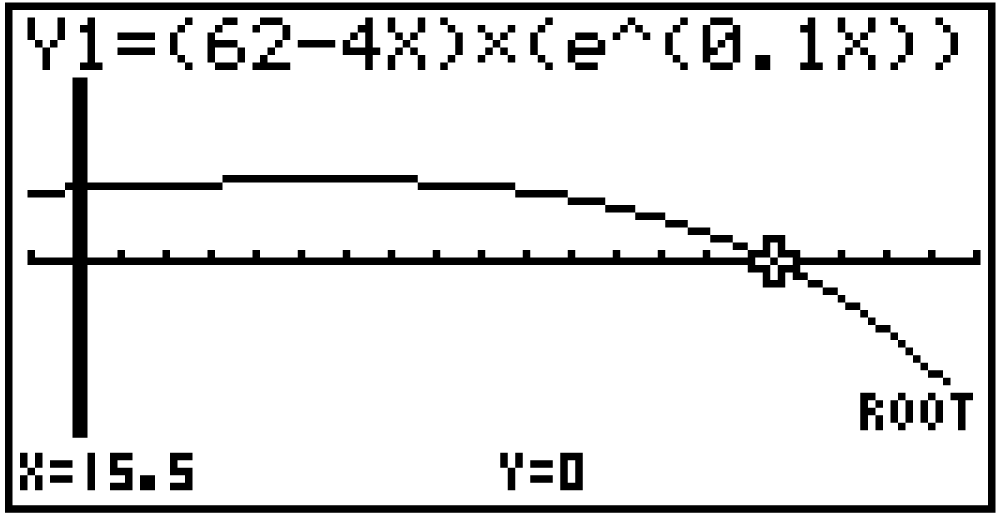 Alternativ bietet es sich auch an, die potentielle Maximalstelle mit dem GTR zu bestimmen:
Alternativ bietet es sich auch an, die potentielle Maximalstelle mit dem GTR zu bestimmen:
Gib dazu den Term der ersten Ableitungsfunktion an und lass deren Schaubild im Graph-Modus anzeigen. Wähle dann unter
an und lass deren Schaubild im Graph-Modus anzeigen. Wähle dann unter
den Befehl zum Bestimmen einer Nullstelle aus und bestätige mit EXE.
Der GTR liefert dir eine potentielle Maximalstelle an  .
2. Schritt: Hinreichende Bedingung überprüfen
Damit eine Maximalstelle vorliegt, muss weiterhin die hinreichende Bedingung
.
2. Schritt: Hinreichende Bedingung überprüfen
Damit eine Maximalstelle vorliegt, muss weiterhin die hinreichende Bedingung  erfüllt werden. Das heißt, du benötigst zunächst die zweite Ableitung der Funktion
erfüllt werden. Das heißt, du benötigst zunächst die zweite Ableitung der Funktion  . Diese erhältst du, indem du den Term von
. Diese erhältst du, indem du den Term von  erneut mit Hilfe der Produktregel ableitest:
erneut mit Hilfe der Produktregel ableitest:
 Überprüfe nun, ob
Überprüfe nun, ob  erfüllt wird:
erfüllt wird:
 Das liefert dir, dass ebenfalls die hinreichende Bedingung erfüllt ist und damit, dass an
Das liefert dir, dass ebenfalls die hinreichende Bedingung erfüllt ist und damit, dass an  eine Maximalstelle vorliegt.
3. Schritt: Koordinaten des Hochpunktes angeben
Aus den Berechnungen zuvor weißt du, dass sich an der Stelle
eine Maximalstelle vorliegt.
3. Schritt: Koordinaten des Hochpunktes angeben
Aus den Berechnungen zuvor weißt du, dass sich an der Stelle  ein Hochpunkt befindet. Damit hast du die
ein Hochpunkt befindet. Damit hast du die  -Koordinate des Hochpunktes bereits ermittelt. Die
-Koordinate des Hochpunktes bereits ermittelt. Die  -Koordinate erhältst du, indem du
-Koordinate erhältst du, indem du  in den Funktionsterm von
in den Funktionsterm von  einsetzt und berechnest:
einsetzt und berechnest:

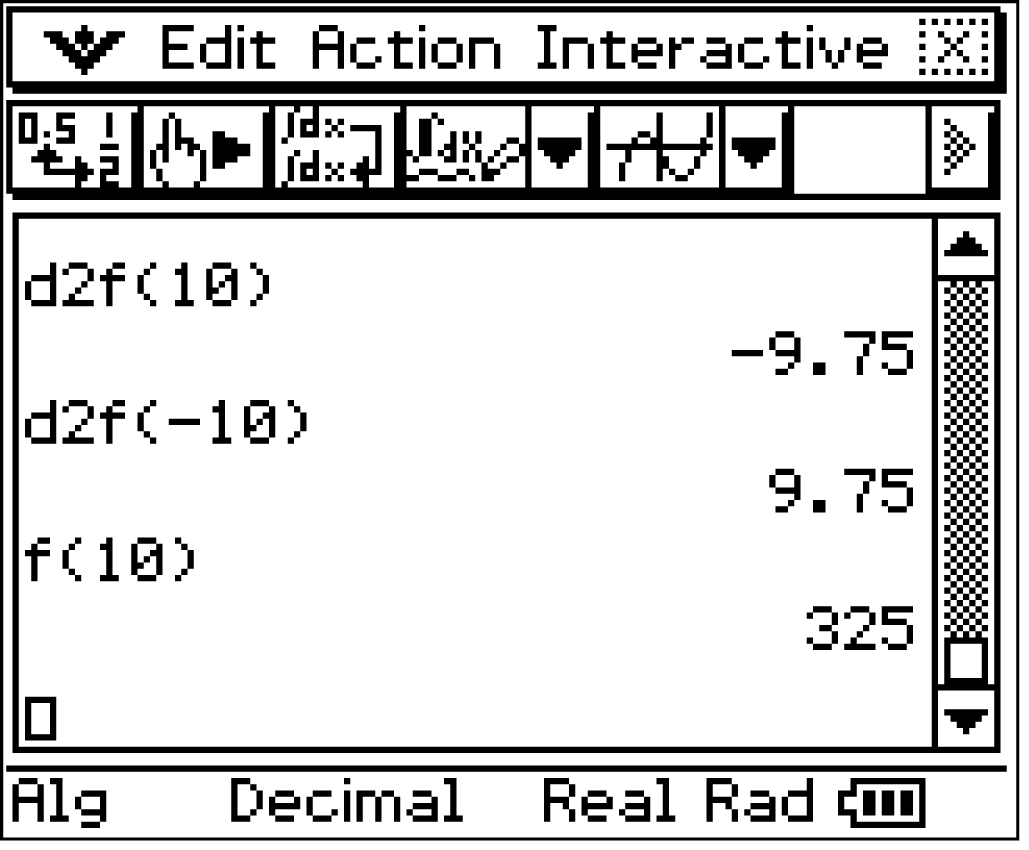 Alternativ kannst du den Funktionswert an der Stelle
Alternativ kannst du den Funktionswert an der Stelle  auch mit Hilfe des GTR bestimmen. Gib dazu die Funktion
auch mit Hilfe des GTR bestimmen. Gib dazu die Funktion  im Graph-Modus an und lass deren Graph anzeigen.
Den Funktionswert an besagter Stelle
im Graph-Modus an und lass deren Graph anzeigen.
Den Funktionswert an besagter Stelle  erhältst du über folgende Befehlsfolge:
erhältst du über folgende Befehlsfolge:
Die Koordinaten des Hochpunktes  lauten
lauten  .
.
Das heißt, zum Zeitpunkt wird die Förderrate maximal mit einem Maximalwert von
wird die Förderrate maximal mit einem Maximalwert von  Tonnen pro Jahr.
Tonnen pro Jahr.
Deine Aufgabe ist es rechnerisch den Zeitpunkt
Bei einer Maximalstelle
- Notwendige Bedingung:
- Hinreichende Bedingung:
Diese erhältst du, indem du die Produktregel anwendest:
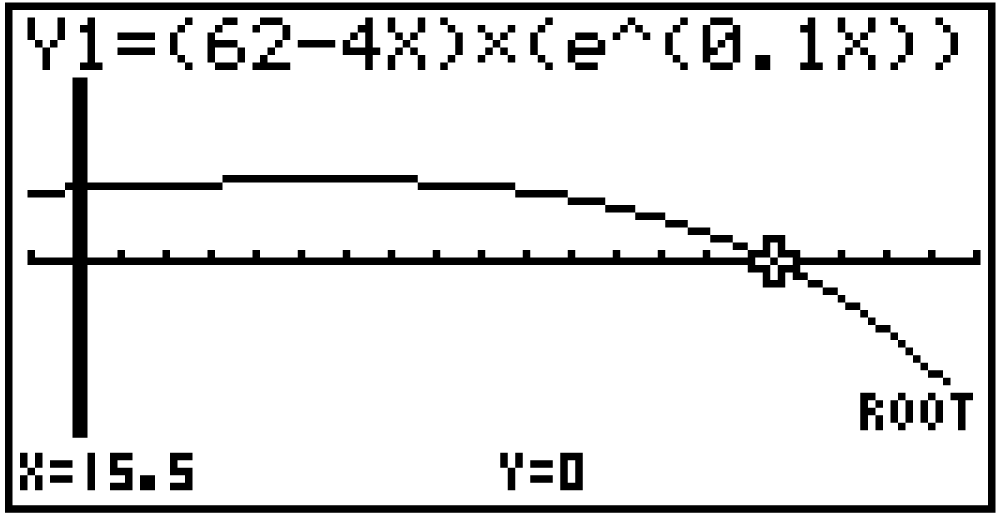
Gib dazu den Term der ersten Ableitungsfunktion
|
G-Solve |

|
G-Solve |
Das heißt, zum Zeitpunkt
b)
 Bestimmen einer Gleichung für die Funktion
Bestimmen einer Gleichung für die Funktion  Die Funktion
Die Funktion  soll die Menge des Erdöls beschreiben, die seit 1990 bis zu einem beliebig betrachtete Zeitpunkt
soll die Menge des Erdöls beschreiben, die seit 1990 bis zu einem beliebig betrachtete Zeitpunkt  für
für ![\(t \in \left[0;20\right]\)](https://www.schullv.de/resources/formulas/fc3d5915b22c89369087dc8d6e556770dc2016bfa97b60098ada5484aba5a704_light.svg) aus dem Ölfeld gefördert wurde.
aus dem Ölfeld gefördert wurde.
Da die zuvor betrachtete Funktion die momentane Förderrate des Erdöls beschreibt, entspricht die Funktion
die momentane Förderrate des Erdöls beschreibt, entspricht die Funktion  gerade einer Stammfunktion von
gerade einer Stammfunktion von  .
Das heißt, um den Term der Funktion
.
Das heißt, um den Term der Funktion  zu bestimmen, kannst du die Funktion
zu bestimmen, kannst du die Funktion  über dem Intervall
über dem Intervall ![\(\left[0;20\right]\)](https://www.schullv.de/resources/formulas/2fb45bd1f03fc888bbb9b42d34f330fe350022f99e9f9ee6f7033ab8f18ba841_light.svg) integrieren.
integrieren.
Beachte, dass du bei einer Integration eine Integrationskonstante erhältst.
Um an dieser Stelle eine Stammfunktion von zu erhalten, kannst du partielle Integration verwenden:
zu erhalten, kannst du partielle Integration verwenden:
Wähle in diesem Fall:
 die Menge des Erdöls bis zu einem beliebigen Zeitpunkt
die Menge des Erdöls bis zu einem beliebigen Zeitpunkt  beschreibt, wird die obere Grenze des Integrals gleich
beschreibt, wird die obere Grenze des Integrals gleich  gesetzt und ist damit veränderbar.
gesetzt und ist damit veränderbar.
In unserem Fall muss also und
und  gelten. Einsetzen in die oben angeführte Formel liefert dir das gesuchte Integral von
gelten. Einsetzen in die oben angeführte Formel liefert dir das gesuchte Integral von  :
:
![\(\begin{array}{r@{\;\;}l@{\hspace{1cm}}l}
M(t)=&\displaystyle\int_{0}^{t} h‘(t) \cdot g(t)\mathrm{d}t&\\
=& h(t) \cdot g(t) - h(0)\cdot g(0)-\displaystyle\int_{0}^{t} h(t) \cdot g‘(t)\mathrm{d}t&\\
=& 10 \cdot \mathrm{e}^{0,1 \cdot t} \cdot (1.020 -40 \cdot t) - 10 \cdot \mathrm{e}^{0,1 \cdot 0} \cdot (1.020 -40 \cdot 0) -\displaystyle\int_{0}^{t} 10 \cdot \mathrm{e}^{0,1 \cdot t} \cdot (-40) \mathrm{d}t&\\
=& (10.200 -400 \cdot t) \cdot \mathrm{e}^{0,1 \cdot t} - 10.200 \cdot \mathrm{e}^{0} -\displaystyle\int_{0}^{t} -400 \cdot \mathrm{e}^{0,1 \cdot t} \mathrm{d}t&\\
=& (10.200 -400 \cdot t) \cdot \mathrm{e}^{0,1 \cdot t} - 10.200 -\left[ -4.000 \cdot \mathrm{e}^{0,1 \cdot t}\right]_0^t&\\
=& (10.200 -400 \cdot t) \cdot \mathrm{e}^{0,1 \cdot t} - 10.200 - \left( -4.000 \cdot \mathrm{e}^{0,1 \cdot t}\right) + \left( -4.000 \cdot \mathrm{e}^{0}\right) +C &\\
=& (14.200 -400 \cdot t) \cdot \mathrm{e}^{0,1 \cdot t} - 14.200 +C &\\
\end{array}\)](https://www.schullv.de/resources/formulas/951238f594e771a0aa17fae5ab7a5da96677216192c5c3fac79974828e4de66b_light.svg) Ein möglicher Term zur Funktion
Ein möglicher Term zur Funktion  bzw. der Term einer Stammfunktion zur Funktion
bzw. der Term einer Stammfunktion zur Funktion  ist gegeben durch:
ist gegeben durch:
 .
.
 Berechnen der gesamten Fördermenge
Zuvor hast du den Term der Funktion
Berechnen der gesamten Fördermenge
Zuvor hast du den Term der Funktion  ermittelt, die die gesamte geförderte Menge Erdöl von Beginn der Förderung bis zu einem beliebigen Zeitpunkt
ermittelt, die die gesamte geförderte Menge Erdöl von Beginn der Förderung bis zu einem beliebigen Zeitpunkt  beschreibt.
beschreibt.
In der Aufgabenstellung wird nun verlangt, die gesamte Fördermenge von 1990 (Beginn) bis 2009 zu bestimmen, also die gesamte Menge, die im Intervall![\(\left[0;20\right]\)](https://www.schullv.de/resources/formulas/2fb45bd1f03fc888bbb9b42d34f330fe350022f99e9f9ee6f7033ab8f18ba841_light.svg) gefördert wird. Diese Menge entspricht folglich gerade
gefördert wird. Diese Menge entspricht folglich gerade  :
:
 Alternativ kannst du die gesamt geförderte Menge an Erdöl auch mit Hilfe des GTR bestimmen.
Alternativ kannst du die gesamt geförderte Menge an Erdöl auch mit Hilfe des GTR bestimmen.
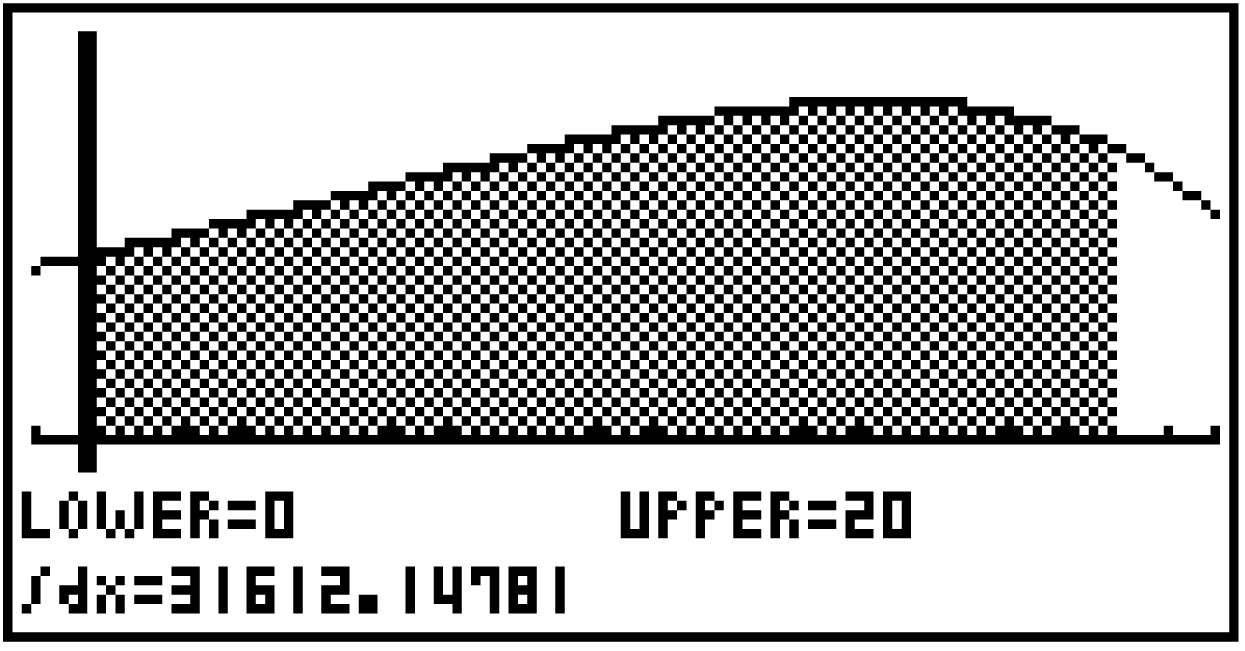 Wechsle in den Graph-Modus und und lass den Graphen der Funktion
Wechsle in den Graph-Modus und und lass den Graphen der Funktion  zeichnen. Da die gesamte geförderte Erdölmenge gerade dem Integral der Funktion
zeichnen. Da die gesamte geförderte Erdölmenge gerade dem Integral der Funktion  über dem Intervall
über dem Intervall ![\(\left[0;20\right]\)](https://www.schullv.de/resources/formulas/2fb45bd1f03fc888bbb9b42d34f330fe350022f99e9f9ee6f7033ab8f18ba841_light.svg) entspricht, kannst du folgenden Befehl auswählen:
entspricht, kannst du folgenden Befehl auswählen:
Gib die untere Grenze 0 sowie die obere Grenze 20 an und bestätige mit EXE.
Im Zeitraum von 1990 bis 2009 werden  Tonnen Erdöl gefördert.
Tonnen Erdöl gefördert.
 Einnahmen aus dem Verkauf im Jahr 2007 bestimmen
Im Jahr 2007 beträgt der Verkaufspreis 56 Euro pro Barrel Erdöl. Ein Barrel wiegt ungefähr 137 kg. Deine Aufgabe ist es, die Einnahmen im Jahr 2007 zu bestimmen.
Einnahmen aus dem Verkauf im Jahr 2007 bestimmen
Im Jahr 2007 beträgt der Verkaufspreis 56 Euro pro Barrel Erdöl. Ein Barrel wiegt ungefähr 137 kg. Deine Aufgabe ist es, die Einnahmen im Jahr 2007 zu bestimmen.
Um diese Einnahmen zu bestimmen, kannst du wie folgt vorgehen:![\(\left[17;18 \right]\)](https://www.schullv.de/resources/formulas/2f49e546f59b9d50d81bdc25dfde6c83472a7db5f80ab671785bc59fa63c274c_light.svg) dargestellt.
dargestellt.
 Die rot markierte Fläche entspricht gerade
Die rot markierte Fläche entspricht gerade  :
:
![\(\begin{array}{r@{\;\;}l@{\hspace{1cm}}l}
M(18)-M(17)=& (14.200 -400 \cdot 18) \cdot \mathrm{e}^{0,1 \cdot 18} - 14.200 - \left[ (14.200 -400 \cdot 18) \cdot \mathrm{e}^{0,1 \cdot 18} - 14.200 \right] &\\
=& 7.000 \cdot \mathrm{e}^{1,8} - 7.400 \cdot \mathrm{e}^{1,7} &\\
\approx& 1840,32&\\
\end{array}\)](https://www.schullv.de/resources/formulas/2e21ff450ac17cb521b12a95479e3f71f114d019a2d4b4080378dcebf4243c92_light.svg) Im Jahr 2007 werden also
Im Jahr 2007 werden also  Tonnen Erdöl gefördert.
Alternativ kannst du das Integral auch mit Hilfe des GTR bestimmen.
Tonnen Erdöl gefördert.
Alternativ kannst du das Integral auch mit Hilfe des GTR bestimmen.
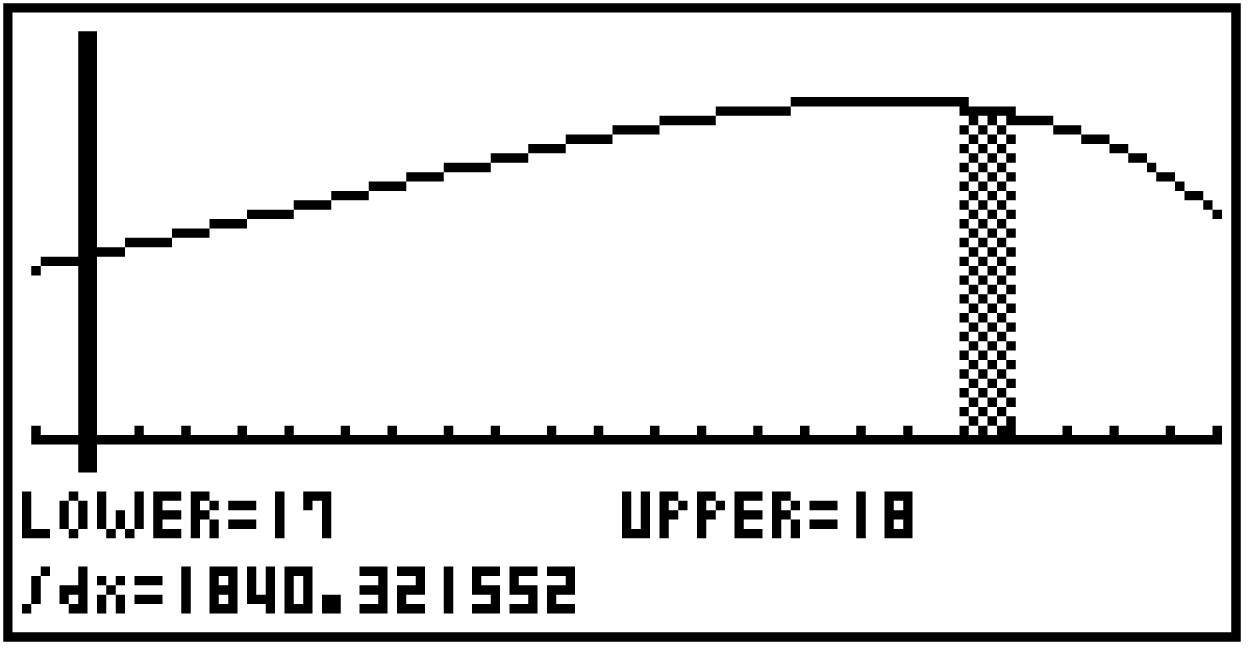 Wechsle in den Graph-Modus und und lass den Graphen zur Funktion
Wechsle in den Graph-Modus und und lass den Graphen zur Funktion  zeichnen. Da die gesamte geförderte Erdölmenge im Jahr 2007 gerade dem Integral der Funktion
zeichnen. Da die gesamte geförderte Erdölmenge im Jahr 2007 gerade dem Integral der Funktion  über dem Intervall
über dem Intervall ![\(\left[17;18\right]\)](https://www.schullv.de/resources/formulas/23297b463e6755b46e2b4c404105b75cd2be949765be868294f2c212dbad1f58_light.svg) entspricht, kannst du folgenden Befehl auswählen:
entspricht, kannst du folgenden Befehl auswählen:
Gib die untere Grenze 17 sowie die obere Grenze 18 an und bestätige mit EXE.
Im Jahr 2007 werden  Tonnen Erdöl gefördert.
2. Schritt: Geförderte Menge in Barrels umrechnen
Da die Menge an gefördertem Erdöl in Barrels gemessen wird, kannst du folgende Umrechnung vornehmen:
Tonnen Erdöl gefördert.
2. Schritt: Geförderte Menge in Barrels umrechnen
Da die Menge an gefördertem Erdöl in Barrels gemessen wird, kannst du folgende Umrechnung vornehmen:
 Im Jahr 2007 werden also
Im Jahr 2007 werden also  Barrels an Erdöl verkauft.
3. Schritt: Einnahmen aus dem Jahr 2007 bestimmen
Im Jahr 2007 liegt der Verkaufspreis eines Barrels bei einem Preis von 56 Euro. Damit folgt:
Barrels an Erdöl verkauft.
3. Schritt: Einnahmen aus dem Jahr 2007 bestimmen
Im Jahr 2007 liegt der Verkaufspreis eines Barrels bei einem Preis von 56 Euro. Damit folgt:
 Es werden also
Es werden also  Euro im Jahr 2007 durch den Verkauf des Erdöls eingenommen.
Euro im Jahr 2007 durch den Verkauf des Erdöls eingenommen.
Da die zuvor betrachtete Funktion
Beachte, dass du bei einer Integration eine Integrationskonstante erhältst.
Um an dieser Stelle eine Stammfunktion von
|
|
In unserem Fall muss also
In der Aufgabenstellung wird nun verlangt, die gesamte Fördermenge von 1990 (Beginn) bis 2009 zu bestimmen, also die gesamte Menge, die im Intervall

|
G-Solve |
Um diese Einnahmen zu bestimmen, kannst du wie folgt vorgehen:
- Bestimme zunächst die geförderte Menge an Erdöl im Jahr 2007. Das Jahr 2007 wird im Schaubild durch das Intervall
dargestellt. Diese Menge entspricht dem Integral:
ist die im Jahr 2007 gewonnene Menge an Erdöl in 1.000 Tonnen. Dividiere diese Menge mit 137 kg, um die Anzahl der Barrels zu erhalten.
- Multipliziere die Anzahl der Barrels mit dem Verkaufspreis von 56 Euro, um die Einnahmen zu erhalten.


|
G-Solve |
c)
 Begründen, warum
Begründen, warum  für einen langen Zeitraum nicht sinnvoll wäre
Die momentane Förderrate ab dem Jahr 2010 wird im Intervall
für einen langen Zeitraum nicht sinnvoll wäre
Die momentane Förderrate ab dem Jahr 2010 wird im Intervall ![\(\left(\left.20;40\right]\right.\)](https://www.schullv.de/resources/formulas/30d871595acdf6c7899bc11b2ad117356c98d4d7a4e19e6565348514245b4fca_light.svg) durch die Funktion
durch die Funktion  mit dem Term
mit dem Term
 modelliert. Dabei gibt die Variable
modelliert. Dabei gibt die Variable  das Jahr und
das Jahr und  die geförderte Menge an Erdöl zur Einheit 1.000 Tonnen pro Jahr an.
die geförderte Menge an Erdöl zur Einheit 1.000 Tonnen pro Jahr an.
Begründe, warum es nicht sinnvoll wäre mittels Funktion die Förderrate über einen größeren Zeitraum zu beschreiben.
Dazu kannst du die Funktion
die Förderrate über einen größeren Zeitraum zu beschreiben.
Dazu kannst du die Funktion  für
für  untersuchen. Liegt beispielsweise ein Grenzwert größer Null vor, so würde das bedeuten, dass das Ölfeld nie erschöpft werden könnte, was nicht möglich ist.
Dazu kannst du die Terme
untersuchen. Liegt beispielsweise ein Grenzwert größer Null vor, so würde das bedeuten, dass das Ölfeld nie erschöpft werden könnte, was nicht möglich ist.
Dazu kannst du die Terme  und
und  separat betrachten.
separat betrachten.
 Das liefert dir, dass die Funktion
Das liefert dir, dass die Funktion  für
für  gegen den Wert
gegen den Wert  konvergiert. Das heißt, dass die momentane Förderrate nie unter diesen Wert fällt und damit, dass das Ölfeld nie erschöpft werden würde. Da das nicht möglich ist, kannst du annehmen, dass
konvergiert. Das heißt, dass die momentane Förderrate nie unter diesen Wert fällt und damit, dass das Ölfeld nie erschöpft werden würde. Da das nicht möglich ist, kannst du annehmen, dass  die momentane Förderrate über einen längeren Zeitraum nicht sinnvoll modelliert.
die momentane Förderrate über einen längeren Zeitraum nicht sinnvoll modelliert.
 Letztes Jahr bestimmen, in welchem die Erdölförderung wirtschaftlich ist
Laut Angaben ist die Erdölförderung nur dann wirtschaftlich, wenn innerhalb eines Kalenderjahres mindestens
Letztes Jahr bestimmen, in welchem die Erdölförderung wirtschaftlich ist
Laut Angaben ist die Erdölförderung nur dann wirtschaftlich, wenn innerhalb eines Kalenderjahres mindestens  Tonnen Öl gefördert wird. Bestimme das Jahr, in dem das zum Letzten mal der Fall ist.
Tonnen Öl gefördert wird. Bestimme das Jahr, in dem das zum Letzten mal der Fall ist.
Die Funktion beschreibt die momentane Förderrate im Intervall
beschreibt die momentane Förderrate im Intervall ![\(\left(\left.20;40\right]\right.\)](https://www.schullv.de/resources/formulas/30d871595acdf6c7899bc11b2ad117356c98d4d7a4e19e6565348514245b4fca_light.svg) . Ihre Stammfunktion
. Ihre Stammfunktion  stellt folglich die geförderte Menge an Erdöl dar.
stellt folglich die geförderte Menge an Erdöl dar.
Um also das Jahr zu bestimmen, in dem die gesamte geförderte Erdölmenge zum letzten Mal mehr als 600.000 Tonnen beträgt, kannst du folgendermaßen vorgehen: bestimmen
Die Stammfunktion
bestimmen
Die Stammfunktion  zur Funktion
zur Funktion  beschreibt die Menge an Erdöl, die ab 2010 bis zu einem beliebigen Zeitpunkt gefördert wird. Da die Menge von einschließlich
beschreibt die Menge an Erdöl, die ab 2010 bis zu einem beliebigen Zeitpunkt gefördert wird. Da die Menge von einschließlich  bis zu einem beliebigem Zeitpunkt beschrieben werden soll, entspricht die untere Grenze 20 und die obere Grenze
bis zu einem beliebigem Zeitpunkt beschrieben werden soll, entspricht die untere Grenze 20 und die obere Grenze  , da sie veränderbar sein soll. Du kannst
, da sie veränderbar sein soll. Du kannst  wie folgt bestimmen:
wie folgt bestimmen:
![\(\begin{array}{r@{\;\;}l@{\hspace{1cm}}l}
G(t)=&\displaystyle\int_{20}^{t} g(t)\;\mathrm{d}t &\\
=&\displaystyle\int_{20}^{t} 180 \cdot \mathrm{e}^{4-0,1 \cdot t}+ 40 \cdot \mathrm{e}^2\;\mathrm{d}t &\\
=&\left[ -1.800 \cdot \mathrm{e}^{4-0,1 \cdot t}+ 40 \cdot t \cdot \mathrm{e}^2\right]_{20}^{t} &\\
=& -1.800 \cdot \mathrm{e}^{4-0,1 \cdot t}+ 40 \cdot t \cdot \mathrm{e}^2 - \left( -1.800 \cdot \mathrm{e}^{4-0,1 \cdot 20}+ 40 \cdot 20 \cdot \mathrm{e}^2 \right) &\\
=& -1.800 \cdot \mathrm{e}^{4-0,1 \cdot t}+ 40 \cdot t \cdot \mathrm{e}^2 +1.800 \cdot \mathrm{e}^{2}- 800 \cdot \mathrm{e}^2 &\\
=& -1.800 \cdot \mathrm{e}^{4-0,1 \cdot t}+ 40 \cdot t \cdot \mathrm{e}^2 +1.000 \cdot \mathrm{e}^{2} &\\
\end{array}\)](https://www.schullv.de/resources/formulas/659df0b4855b2ae07ef331027083006993732cf40ec5cbb9b252cfb57a39f511_light.svg) 2. Schritt: Geförderte Erdölmenge innerhalb eines Jahres berechnen
Zuvor hast du eine Stammfunktion
2. Schritt: Geförderte Erdölmenge innerhalb eines Jahres berechnen
Zuvor hast du eine Stammfunktion  bestimmt, die die gesamte geförderte Menge an Erdöl ab Beginn 2010 bis zu einem beliebigen Zeitpunkt modelliert. Die Menge an Erdöl, die innerhalb eines Kalenderjahres gefördert wird, entspricht gerade der Differenz
bestimmt, die die gesamte geförderte Menge an Erdöl ab Beginn 2010 bis zu einem beliebigen Zeitpunkt modelliert. Die Menge an Erdöl, die innerhalb eines Kalenderjahres gefördert wird, entspricht gerade der Differenz  für
für  .
.
Einsetzen in den Term der Stammfunktion liefert dir die Menge in 1.000 Tonnen pro Jahr:
liefert dir die Menge in 1.000 Tonnen pro Jahr:
![\(\begin{array}{r@{\;\;}l@{\hspace{1cm}}l}
G(t+1)-G(t)=& -1.800 \cdot \mathrm{e}^{4-0,1 \cdot (t+1)}+ 40 \cdot (t+1) \cdot \mathrm{e}^2 +1.000 \cdot \mathrm{e}^{2} &\\
&- \left[ -1.800 \cdot \mathrm{e}^{4-0,1 \cdot t}+ 40 \cdot t \cdot \mathrm{e}^2 +1.000 \cdot \mathrm{e}^{2} \right]&\\
=& -1.800 \cdot \mathrm{e}^{4-0,1 \cdot t -0,1}+ 40 \cdot t \cdot \mathrm{e}^2+40 \cdot \mathrm{e}^2 +1.000 \cdot \mathrm{e}^{2} &\\
&+1.800 \cdot \mathrm{e}^{4-0,1 \cdot t}- 40 \cdot t \cdot \mathrm{e}^2 -1.000 \cdot \mathrm{e}^{2} &\\
=& -1.800 \cdot \mathrm{e}^{4-0,1 \cdot t -0,1}+40 \cdot \mathrm{e}^2 +1.800 \cdot \mathrm{e}^{4-0,1 \cdot t} &\\
=& 1.800 \cdot \mathrm{e}^{4-0,1 \cdot t}\left(1- \mathrm{e}^{-0,1}\right) + 40 \cdot \mathrm{e}^2 &\\
\end{array}\)](https://www.schullv.de/resources/formulas/69c12dc9476016f16ee8e5d19364c05b0ece3243c45bd7ec0c560f400a4213ab_light.svg) Die geförderte Erdölmenge innerhalb eines Jahres beträgt
Die geförderte Erdölmenge innerhalb eines Jahres beträgt  in 1.000 Tonnen.
3. Schritt: Letztes Jahr bestimmen, in dem die Ölförderung wirtschaftlich ist
Damit die Ölförderung wirtschaftlich ist, sollen mindestens 600.000 Tonnen Erdöl innerhalb eines Kalenderjahres gefördert werden.
in 1.000 Tonnen.
3. Schritt: Letztes Jahr bestimmen, in dem die Ölförderung wirtschaftlich ist
Damit die Ölförderung wirtschaftlich ist, sollen mindestens 600.000 Tonnen Erdöl innerhalb eines Kalenderjahres gefördert werden.
Das heißt, es muss folgende Ungleichung erfüllt werden: Diese Ungleichung kannst du nach
Diese Ungleichung kannst du nach  auflösen:
auflösen:
 Das liefert dir, dass
Das liefert dir, dass  gelten muss, damit die Ölförderung wirtschaftlich bleibt. Das heißt, das Kalenderjahr 2024 (entspricht 34 auf der
gelten muss, damit die Ölförderung wirtschaftlich bleibt. Das heißt, das Kalenderjahr 2024 (entspricht 34 auf der  -Achse) ist das letzte Jahr, in dem die Ölförderung mindestens 600.000 Tonnen beträgt.
-Achse) ist das letzte Jahr, in dem die Ölförderung mindestens 600.000 Tonnen beträgt.
Alternativ kannst du das Jahr auch mit Hilfe des GTR bestimmen.
Interpretiere dazu den Term und
und  als neue Funktionen und lass diese im Graph-Modus zeichnen.
als neue Funktionen und lass diese im Graph-Modus zeichnen.
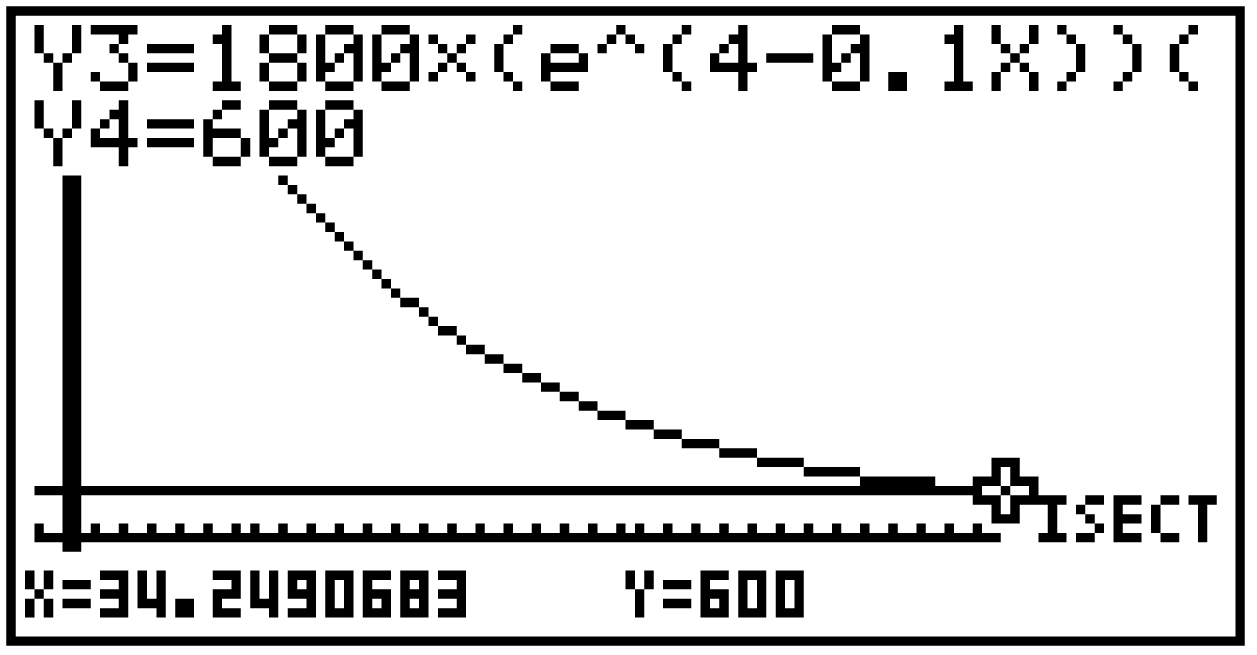 Die Relation
Die Relation  ist solange erfüllt, bis der Funktionswert des ersten Terms kleiner als 600 wird. Das heißt, wir suchen den Schnittpunkt der beiden angezeigten Funktionen. Diesen erhältst du über die Befehlsfolge:
ist solange erfüllt, bis der Funktionswert des ersten Terms kleiner als 600 wird. Das heißt, wir suchen den Schnittpunkt der beiden angezeigten Funktionen. Diesen erhältst du über die Befehlsfolge:
Das liefert dir, dass  gelten muss, damit die Ölförderung wirtschaftlich bleibt. Das heißt, das Kalenderjahr 2024 (entspricht 34 auf der
gelten muss, damit die Ölförderung wirtschaftlich bleibt. Das heißt, das Kalenderjahr 2024 (entspricht 34 auf der  -Achse) ist das letzte Jahr, in dem die Ölförderung mindestens 600.000 Tonnen beträgt.
-Achse) ist das letzte Jahr, in dem die Ölförderung mindestens 600.000 Tonnen beträgt.
Begründe, warum es nicht sinnvoll wäre mittels Funktion
- Für
konvergiert
gegen Null.
- Für
bleibt der Term
unverändert.
Die Funktion
Um also das Jahr zu bestimmen, in dem die gesamte geförderte Erdölmenge zum letzten Mal mehr als 600.000 Tonnen beträgt, kannst du folgendermaßen vorgehen:
- Bestimme eine Stammfunktion
der Funktion
. Es gilt
.
- Berechne die gesamt geförderte Erdölmenge innerhalb eines Jahres, indem du
berechnest. Dieser Term ist abhängig von der Variablen
, die das gesuchte Jahr angibt.
- Löse die Ungleichung
nach
auf, um das gesuchte Jahr zu bestimmen.
Einsetzen in den Term der Stammfunktion
Das heißt, es muss folgende Ungleichung erfüllt werden:
Alternativ kannst du das Jahr auch mit Hilfe des GTR bestimmen.
Interpretiere dazu den Term

|
G-Solve |
d)
 Begründen, dass
Begründen, dass  an der Stelle
an der Stelle  differenzierbar ist
Die Funktion
differenzierbar ist
Die Funktion  setzt sich aus den zuvor betrachteten Funktionen
setzt sich aus den zuvor betrachteten Funktionen  und
und  zusammen:
zusammen:
![\(h(t)=\begin{cases} f(t)=(1.020 -40 \cdot t) \cdot \mathrm{e}^{0,1 \cdot t}, & t\in \left[0;20\right] \\
g(t)=180 \cdot \mathrm{e}^{4-0,1 \cdot t}+ 40 \cdot \mathrm{e}^2, & t\in \left(\left.20;40\right]\right.\end{cases}\)](https://www.schullv.de/resources/formulas/ad4f76eb8ef4e84f699191d83adc9709e4d155c3178b41a019b7cfc6e972d7dc_light.svg) Deine Aufgabe ist es, zu zeigen, dass die Funktion
Deine Aufgabe ist es, zu zeigen, dass die Funktion  an der Stelle
an der Stelle  differenzierbar ist.
differenzierbar ist.
Eine Funktion ist an einer Stelle differenzierbar, wenn gilt:
differenzierbar, wenn gilt:
 überprüfen
Damit die Funktion
überprüfen
Damit die Funktion  an der Stelle
an der Stelle  differenzierbar ist, muss sie an dieser Stelle stetig sein:
differenzierbar ist, muss sie an dieser Stelle stetig sein:
 und
und  an der Stelle
an der Stelle  überein.
2. Schritt: Ableitungen an der Stelle
überein.
2. Schritt: Ableitungen an der Stelle  überprüfen
Damit die Funktion
überprüfen
Damit die Funktion  tatsächlich differenzierbar ist, musst du weiterhin überprüfen, ob die Ableitungen der Funktionen
tatsächlich differenzierbar ist, musst du weiterhin überprüfen, ob die Ableitungen der Funktionen  und
und  an dieser Stelle übereinstimmen.
an dieser Stelle übereinstimmen.
 ist an der Stelle
ist an der Stelle  differenzierbar.
differenzierbar.
 Entscheiden, ob
Entscheiden, ob  an der Stelle
an der Stelle  zweimal differenzierbar ist
Soll die Funktion
zweimal differenzierbar ist
Soll die Funktion  an der Stelle
an der Stelle  zweimal differenzierbar sein, so muss die Ableitungsfunktion der Funktion
zweimal differenzierbar sein, so muss die Ableitungsfunktion der Funktion  an dieser Stelle differenzierbar sein. Analog zur Vorgehensweise vom Aufgabenteil zuvor kannst du dann annehmen, dass für zweimal differenzierbar zusätzlich gelten muss:
an dieser Stelle differenzierbar sein. Analog zur Vorgehensweise vom Aufgabenteil zuvor kannst du dann annehmen, dass für zweimal differenzierbar zusätzlich gelten muss:
 gilt.
Im Aufgabentext werden die folgenden Angaben gemacht:
gilt.
Im Aufgabentext werden die folgenden Angaben gemacht:
 und
und  an der Stelle
an der Stelle  nicht übereinstimmen. Das heißt, dass die Funktion
nicht übereinstimmen. Das heißt, dass die Funktion  an der Stelle
an der Stelle  nicht zweimal differenzierbar ist.
nicht zweimal differenzierbar ist.
 Begründen, dass
Begründen, dass  an der Stelle
an der Stelle  ein Minimum besitzt
Wie du vorher aber nachgewiesen hast, ist die Funktion
ein Minimum besitzt
Wie du vorher aber nachgewiesen hast, ist die Funktion  an der Stelle
an der Stelle  nicht differenzierbar. Das heißt, du kannst die notwendige und hinreichende Bedingung für Minimalstellen nicht prüfen.
nicht differenzierbar. Das heißt, du kannst die notwendige und hinreichende Bedingung für Minimalstellen nicht prüfen.
Um zu begründen, dass die Funktion an der Stelle
an der Stelle  ein lokales Minimum besitzt, musst du zeigen, dass
ein lokales Minimum besitzt, musst du zeigen, dass  in einer Umgebung von
in einer Umgebung von  kleiner als alle anderen Funktionswerte von
kleiner als alle anderen Funktionswerte von  ist.
ist.
Das kannst du nachweisen, indem du zeigst, dass auf dem Intervall
auf dem Intervall ![\(\left[0;20\right]\)](https://www.schullv.de/resources/formulas/2fb45bd1f03fc888bbb9b42d34f330fe350022f99e9f9ee6f7033ab8f18ba841_light.svg) überprüfen:
Die Funktion
überprüfen:
Die Funktion  wird auf dem Intervall
wird auf dem Intervall ![\(\left[0;20\right]\)](https://www.schullv.de/resources/formulas/2fb45bd1f03fc888bbb9b42d34f330fe350022f99e9f9ee6f7033ab8f18ba841_light.svg) durch den Term der Funktion
durch den Term der Funktion  beschrieben.
beschrieben.
Es gilt . Um zu zeigen, dass das einem lokalen Minimum entspricht, kannst du zeigen, dass die Funktion
. Um zu zeigen, dass das einem lokalen Minimum entspricht, kannst du zeigen, dass die Funktion  monoton fallend ist.
Soll die Funktion
monoton fallend ist.
Soll die Funktion  monoton fallend sein, so muss gelten:
monoton fallend sein, so muss gelten:
Im Aufgabentext ist angegeben, dass die zweite Ableitungsfunktion durch  gegeben ist, was du ohne Nachweis annehmen darfst. Wir überprüfen nun auf monoton fallend:
gegeben ist, was du ohne Nachweis annehmen darfst. Wir überprüfen nun auf monoton fallend:
 Hier kannst du verwenden, dass der Term
Hier kannst du verwenden, dass der Term  niemals kleiner gleich Null wird. Du kannst diesen Term zur weiteren Betrachtung folglich vernachlässigen.
niemals kleiner gleich Null wird. Du kannst diesen Term zur weiteren Betrachtung folglich vernachlässigen.
 Das liefert dir, dass die Funktion
Das liefert dir, dass die Funktion  für
für  bzw. auf dem Intervall
bzw. auf dem Intervall ![\(\left[5,5;20\right]\)](https://www.schullv.de/resources/formulas/1f9d52c6e8940ea9e966340755c92add39b904ec714c23b81520de56e524bc79_light.svg) monoton fallend ist. Das heißt, auf dem Intervall
monoton fallend ist. Das heißt, auf dem Intervall ![\(\left[0;5,5\right]\)](https://www.schullv.de/resources/formulas/4dff467da747712b1763ae22dbd73c3ef3f36616dec9cc81f6a9898edcae7f09_light.svg) ist sie dahingegen monoton steigend. Es ist also möglich, dass sich ein weiteres lokales Minimum auf dem gesamten Intervall
ist sie dahingegen monoton steigend. Es ist also möglich, dass sich ein weiteres lokales Minimum auf dem gesamten Intervall ![\(\left[0;20\right]\)](https://www.schullv.de/resources/formulas/2fb45bd1f03fc888bbb9b42d34f330fe350022f99e9f9ee6f7033ab8f18ba841_light.svg) befindet.
2. Schritt:
befindet.
2. Schritt:  auf dem Intervall
auf dem Intervall ![\(\left(\left.20;40\right]\right.\)](https://www.schullv.de/resources/formulas/30d871595acdf6c7899bc11b2ad117356c98d4d7a4e19e6565348514245b4fca_light.svg) überprüfen:
Die Funktion
überprüfen:
Die Funktion  wird auf dem Intervall
wird auf dem Intervall ![\(\left(\left.20;40\right]\right.\)](https://www.schullv.de/resources/formulas/30d871595acdf6c7899bc11b2ad117356c98d4d7a4e19e6565348514245b4fca_light.svg) durch den Term der Funktion
durch den Term der Funktion  beschrieben.
beschrieben.
Es gilt . Um zu zeigen, dass das dem lokalen Minimum entspricht, kannst du zeigen, dass die Funktion
. Um zu zeigen, dass das dem lokalen Minimum entspricht, kannst du zeigen, dass die Funktion  monoton steigend ist.
Soll die Funktion
monoton steigend ist.
Soll die Funktion  monoton steigend sein, so muss gelten:
monoton steigend sein, so muss gelten:
Im Aufgabentext ist angegeben, dass die zweite Ableitungsfunktion durch  gegeben ist, was du ohne Nachweis annehmen darfst. Wir überprüfen nun auf monoton steigend:
gegeben ist, was du ohne Nachweis annehmen darfst. Wir überprüfen nun auf monoton steigend:
 Hier kannst du verwenden, dass der Term
Hier kannst du verwenden, dass der Term  niemals kleiner gleich Null wird. Da der Faktor 1,8 weiterhin positiv ist, kannst du festhalten, dass die Funktion
niemals kleiner gleich Null wird. Da der Faktor 1,8 weiterhin positiv ist, kannst du festhalten, dass die Funktion  auf dem gesamten Intervall
auf dem gesamten Intervall ![\(\left(\left.20;40\right]\right.\)](https://www.schullv.de/resources/formulas/30d871595acdf6c7899bc11b2ad117356c98d4d7a4e19e6565348514245b4fca_light.svg) positiv ist. Damit ist
positiv ist. Damit ist  auf
auf ![\(\left(\left.20;40\right]\right.\)](https://www.schullv.de/resources/formulas/30d871595acdf6c7899bc11b2ad117356c98d4d7a4e19e6565348514245b4fca_light.svg) monoton steigend.
monoton steigend.
Folglich befindet sich an der kleinste Funktionswert.
Insgesamt folgt dann, dass sich wegen
der kleinste Funktionswert.
Insgesamt folgt dann, dass sich wegen  an
an  ein lokales Minimum befindet.
ein lokales Minimum befindet.
Eine Funktion ist an einer Stelle
- Die Funktionswerte von
und
stimmen an der Stelle
überein.
- Die Ableitungen von
und
stimmen an der Stelle
überein.
- Die Funktionswerte von
und
stimmen an der Stelle
überein.
- Die Ableitungen von
und
stimmen an der Stelle
überein.
Um zu begründen, dass die Funktion
Das kannst du nachweisen, indem du zeigst, dass
monoton fallend auf dem Intervall
ist und dass
monoton steigend auf dem Intervall
ist
Es gilt
|
|
Es gilt
|
|
Folglich befindet sich an