Aufgabe 6
Die Nutzung von sozialen Netzwerken wird immer beliebter. Dabei nutzen immer mehr Jugendliche verschiedene soziale Netzwerke. Es wird davon ausgegangen, dass  aller Jugendlichen das (fiktive) soziale Netzwerk „Freundschaftsbuch“ nutzen.
aller Jugendlichen das (fiktive) soziale Netzwerk „Freundschaftsbuch“ nutzen.
Dieser Prozentsatz soll im Folgenden als Wahrscheinlichkeit dafür verwendet werden, dass eine zufällig befragte jugendliche Person „Freundschaftsbuch“ nutzt.
Bildnachweise [nach oben]
Tabelle 2: Kumulierte Binomialverteilung für n=10 und n=20
Tabelle 3: Kumulierte Binomialverteilung für n=50
Tabelle 4: Kumulierte Binomialverteilung für n=100
Bei grau unterlegtem Eingang, d.h.  , gilt:
, gilt:  abgelesener Wert
Tabelle 5: Normalverteilung
abgelesener Wert
Tabelle 5: Normalverteilung


Beispiele für den Gebrauch:


 Die Nutzung von sozialen Netzwerken wird immer beliebter. Dabei nutzen immer mehr Jugendliche verschiedene soziale Netzwerke. Es wird davon ausgegangen, dass
Die Nutzung von sozialen Netzwerken wird immer beliebter. Dabei nutzen immer mehr Jugendliche verschiedene soziale Netzwerke. Es wird davon ausgegangen, dass  aller Jugendlichen das (fiktive) soziale Netzwerk „Freundschaftsbuch“ nutzen.
aller Jugendlichen das (fiktive) soziale Netzwerk „Freundschaftsbuch“ nutzen.
Dieser Prozentsatz soll im Folgenden als Wahrscheinlichkeit dafür verwendet werden, dass eine zufällig befragte jugendliche Person „Freundschaftsbuch“ nutzt.
Tabelle 5: Normalverteilung


Beispiele für den Gebrauch:


 Tabelle 2: Kumulierte Binomialverteilung für n=10 und n=20
Tabelle 2: Kumulierte Binomialverteilung für n=10 und n=20
Tabelle 3: Kumulierte Binomialverteilung für n=50
Tabelle 4: Kumulierte Binomialverteilung für n=100
Bei grau unterlegtem Eingang, d.h.  , gilt:
, gilt:  abgelesener Wert
Bildnachweise [nach oben]
abgelesener Wert
Bildnachweise [nach oben]
Dieser Prozentsatz soll im Folgenden als Wahrscheinlichkeit dafür verwendet werden, dass eine zufällig befragte jugendliche Person „Freundschaftsbuch“ nutzt.
a)
Berechne die Wahrscheinlichkeit, dass von  zufällig ausgewählten Jugendlichen
zufällig ausgewählten Jugendlichen
(1)
genau  Jugendliche „Freundschaftsbuch“ nutzen,
Jugendliche „Freundschaftsbuch“ nutzen,
(2P)
(2)
höchstens  Jugendliche „Freundschaftsbuch“ nutzen,
Jugendliche „Freundschaftsbuch“ nutzen,
(3P)
(3)
die Anzahl der jugendlichen Nutzer, die „Freundschaftsbuch“ nutzen, einem Wert entspricht, der sich um maximal  vom Erwartungswert unterscheidet.
vom Erwartungswert unterscheidet.
(5P)
b)
Ermittle (ggf. durch Probieren), welche positive Anzahl an Jugendlichen mindestens zufällig ausgewählt werden muss, damit man mit einer Wahrscheinlichkeit von höchstens  maximal einen Jugendlichen antrifft, der „Freundschaftsbuch“ nutzt.
maximal einen Jugendlichen antrifft, der „Freundschaftsbuch“ nutzt.
(6P)
c)
In einer Schule gibt es zur schulinternen Kommunikation ein eigenes Netzwerk, das sowohl von Jugendlichen genutzt wird, die „Freundschaftsbuch“ nutzen, als auch von Jugendlichen, die „Freundschaftsbuch“ nicht nutzen. Dabei ist in beiden Gruppen der Anteil derjenigen, die das schulinterne Netzwerk nutzen, identisch. Im Folgenden wird dieser Anteil mit  bezeichnet und auch als Wahrscheinlichkeit für den jeweiligen Fall verwendet.
bezeichnet und auch als Wahrscheinlichkeit für den jeweiligen Fall verwendet.
(1)
Zeige, dass man den Anteil der Jugendlichen, die genau eines dieser Netzwerke nutzen, mit Hilfe des Terms  beschreiben kann, und erkläre die einzelnen Bestandteile des Terms.
beschreiben kann, und erkläre die einzelnen Bestandteile des Terms.
(5P)
(2)
Berechne den Anteil aller Jugendlichen, die das schulinterne Netzwerk nutzen, wenn der Anteil der Jugendlichen, die genau eines dieser Netzwerke nutzen, bei  liegt.
liegt.
(2P)
(3)
Berechne für  die Wahrscheinlichkeit, dass eine zufällig ausgewählte jugendliche Person mindestens eines der beiden Netzwerke nutzt.
die Wahrscheinlichkeit, dass eine zufällig ausgewählte jugendliche Person mindestens eines der beiden Netzwerke nutzt.
(3P)
(4)
Eine zufällig ausgewählte jugendliche Person nutzt das schulinterne Netzwerk.
Gib die Wahrscheinlichkeit an, dass sie „Freundschaftsbuch“ nicht nutzt, und erkläre, wieso dieser Wert auch ohne einen Ansatz über bedingte Wahrscheinlichkeiten ermittelt werden kann.
Gib die Wahrscheinlichkeit an, dass sie „Freundschaftsbuch“ nicht nutzt, und erkläre, wieso dieser Wert auch ohne einen Ansatz über bedingte Wahrscheinlichkeiten ermittelt werden kann.
(4P)
d)
Die Schülervertretung möchte, dass der Nutzungsgrad des schulinternen Netzwerks verbessert wird. Dazu soll mit Aktionen das schulinterne Netzwerk bekannter gemacht werden. Nach einem Jahr möchte die Schülervertretung die Vermutung überprüfen, dass der Nutzungsgrad von vormals  gestiegen ist, und möchte dazu
gestiegen ist, und möchte dazu  zufällig ausgewählte Jugendliche der Schule befragen.
zufällig ausgewählte Jugendliche der Schule befragen.
 ergibt sich die Entscheidungsregel: „Verwirf die Nullhypothese, falls
ergibt sich die Entscheidungsregel: „Verwirf die Nullhypothese, falls  oder mehr Jugendliche das schulinterne Netzwerk nutzen.“
oder mehr Jugendliche das schulinterne Netzwerk nutzen.“
(1)
Gib eine geeignete Nullhypothese an und ermittle eine passende Entscheidungsregel auf dem Signifikanzniveau von  .
.
(6P)
(2)
Bei der Befragung kommt heraus, dass  Jugendliche das schulinterne Netzwerk nutzen.
Jugendliche das schulinterne Netzwerk nutzen.
Beurteile die Situation aus Sicht der Schülervertretung.
Zum Signifikanzniveau von Beurteile die Situation aus Sicht der Schülervertretung.
(2P)
(3)
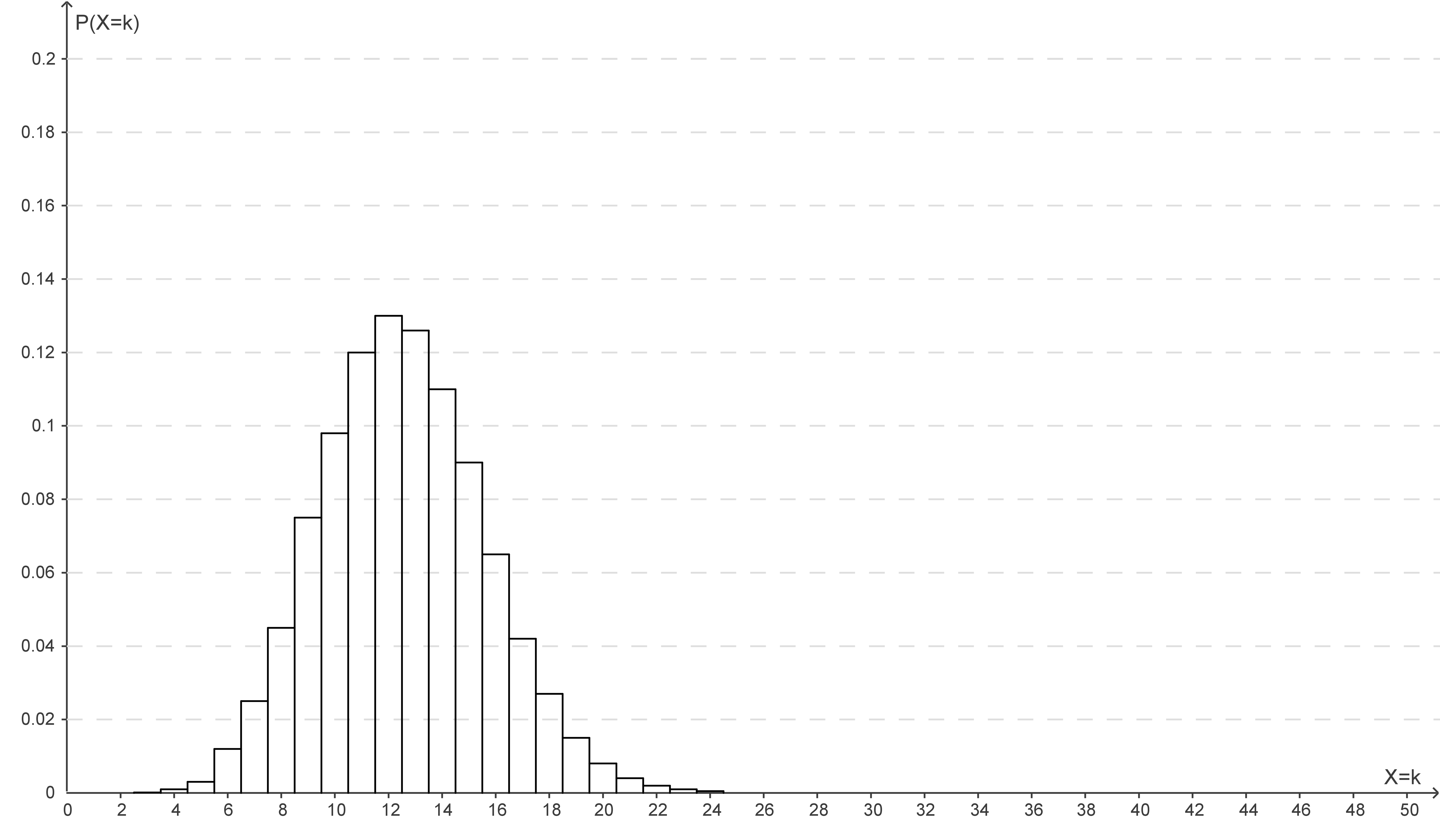
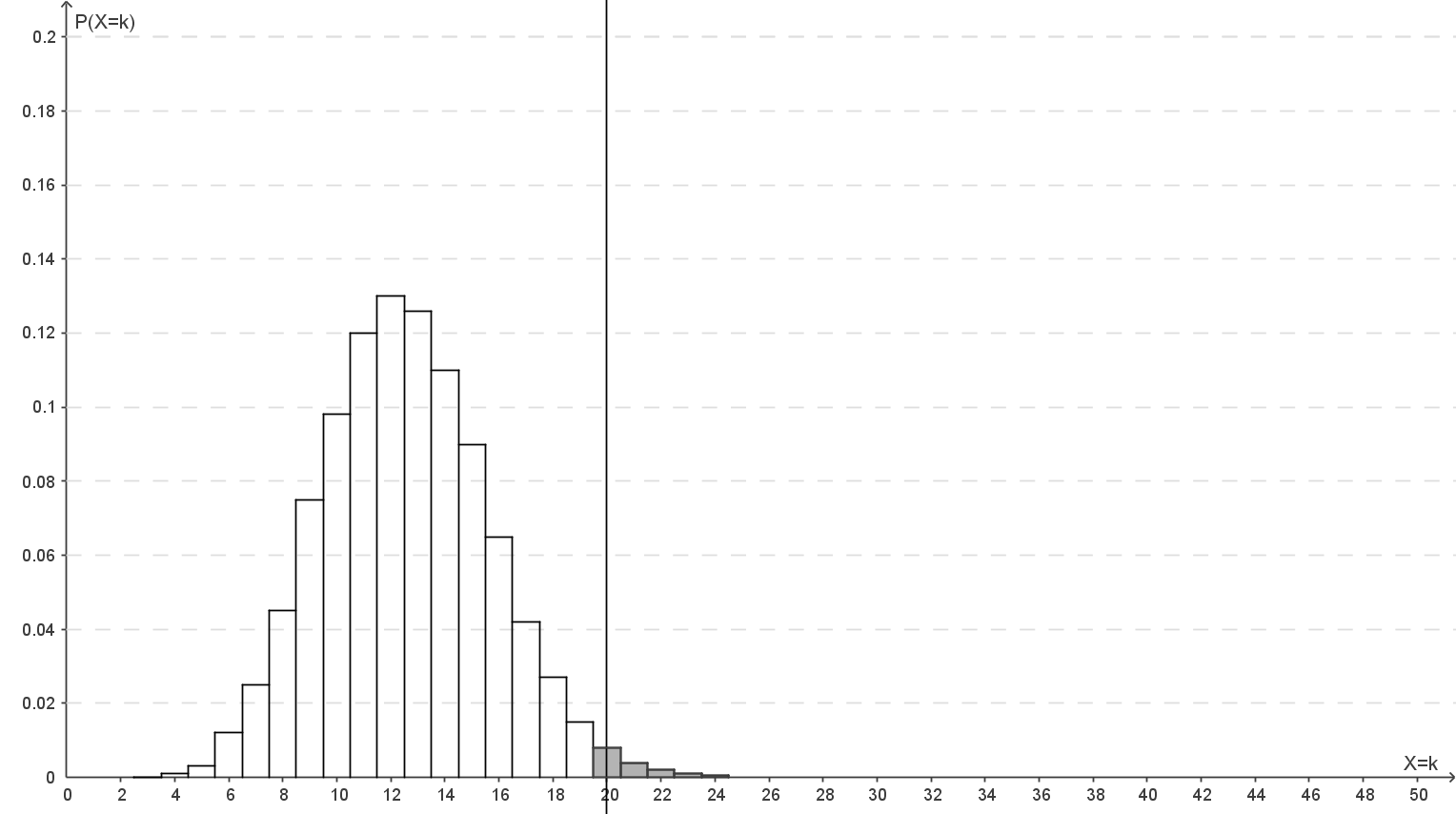
In den Abbildungen 1 - 4 sind die Wahrscheinlichkeiten der jeweils angegebenen Binomialverteilung als Säulen dargestellt. Die Höhe der Säule zum Wert  entspricht dabei
entspricht dabei  .
.
Stelle den Bereich, in dem die Nullhypothese abgelehnt wird, in Abbildung 1 grafisch dar.
Stelle den Bereich, in dem die Nullhypothese abgelehnt wird, in Abbildung 1 grafisch dar.
(3P)
(4)
Beschreibe den Fehler  Art im Sachzusammenhang und berechne die Wahrscheinlichkeit seines Auftretens für den Fall, dass der Nutzungsgrad in Wirklichkeit bei
Art im Sachzusammenhang und berechne die Wahrscheinlichkeit seines Auftretens für den Fall, dass der Nutzungsgrad in Wirklichkeit bei  liegt.
liegt.
(5P)
(5)
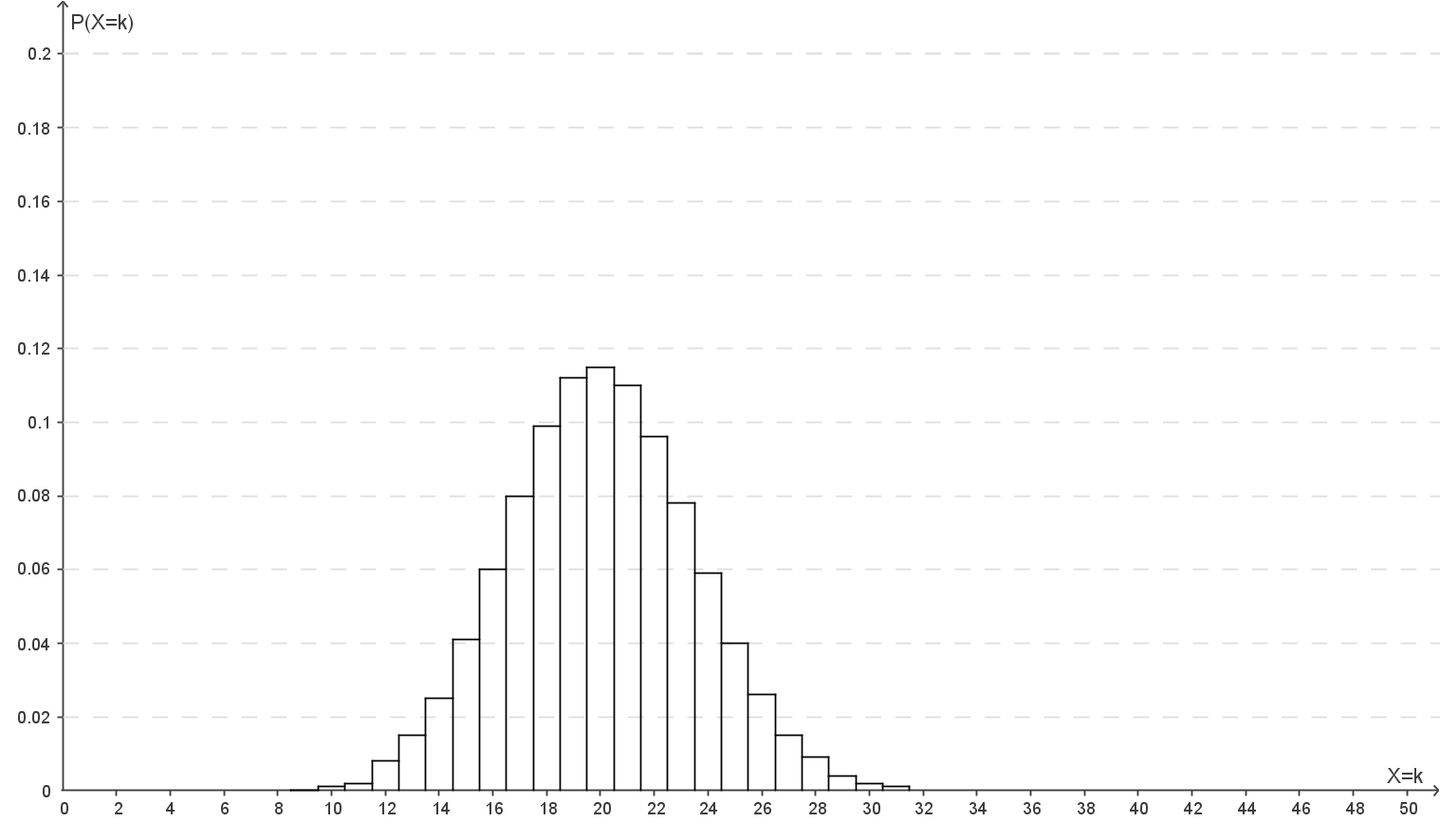
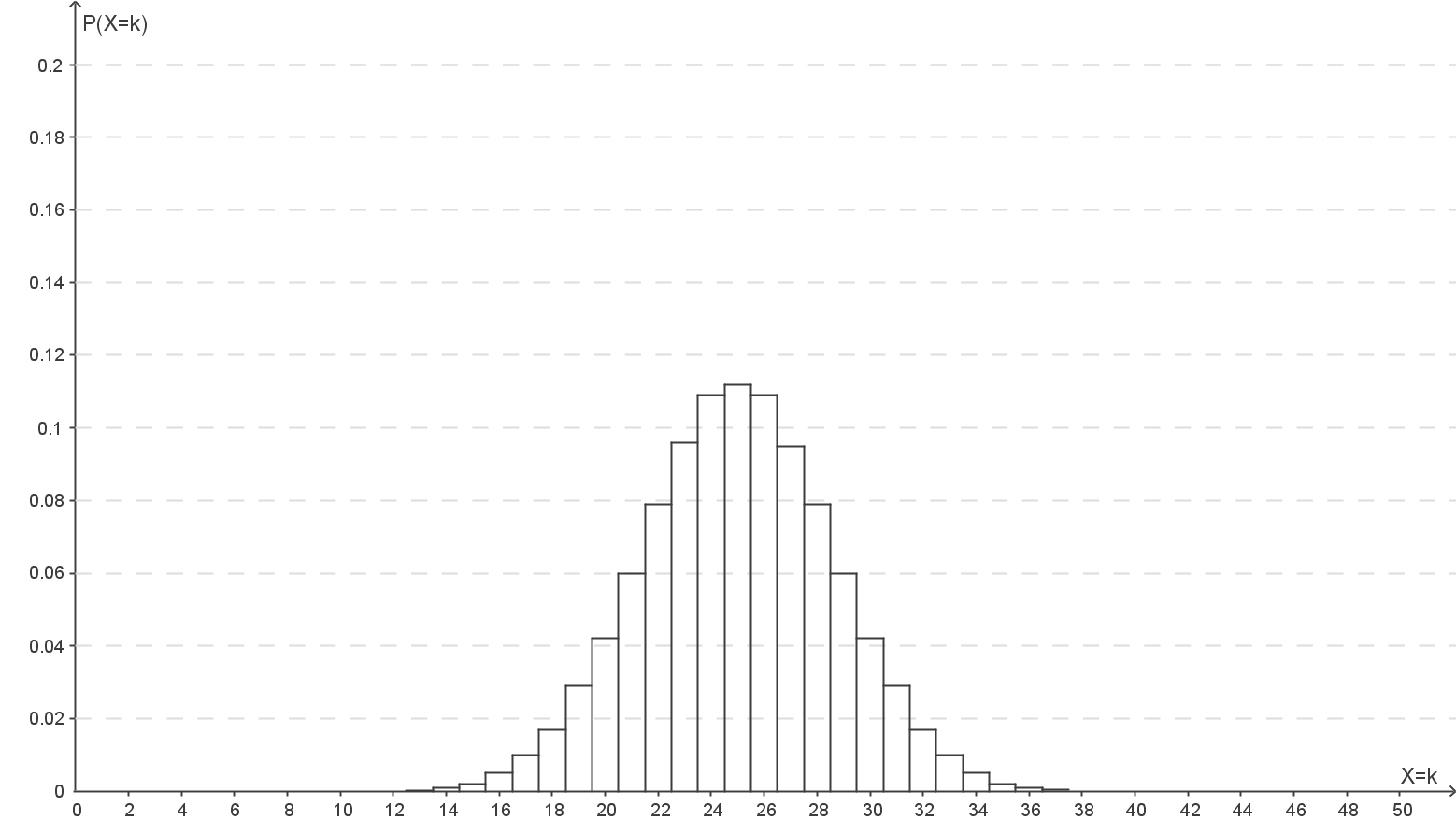
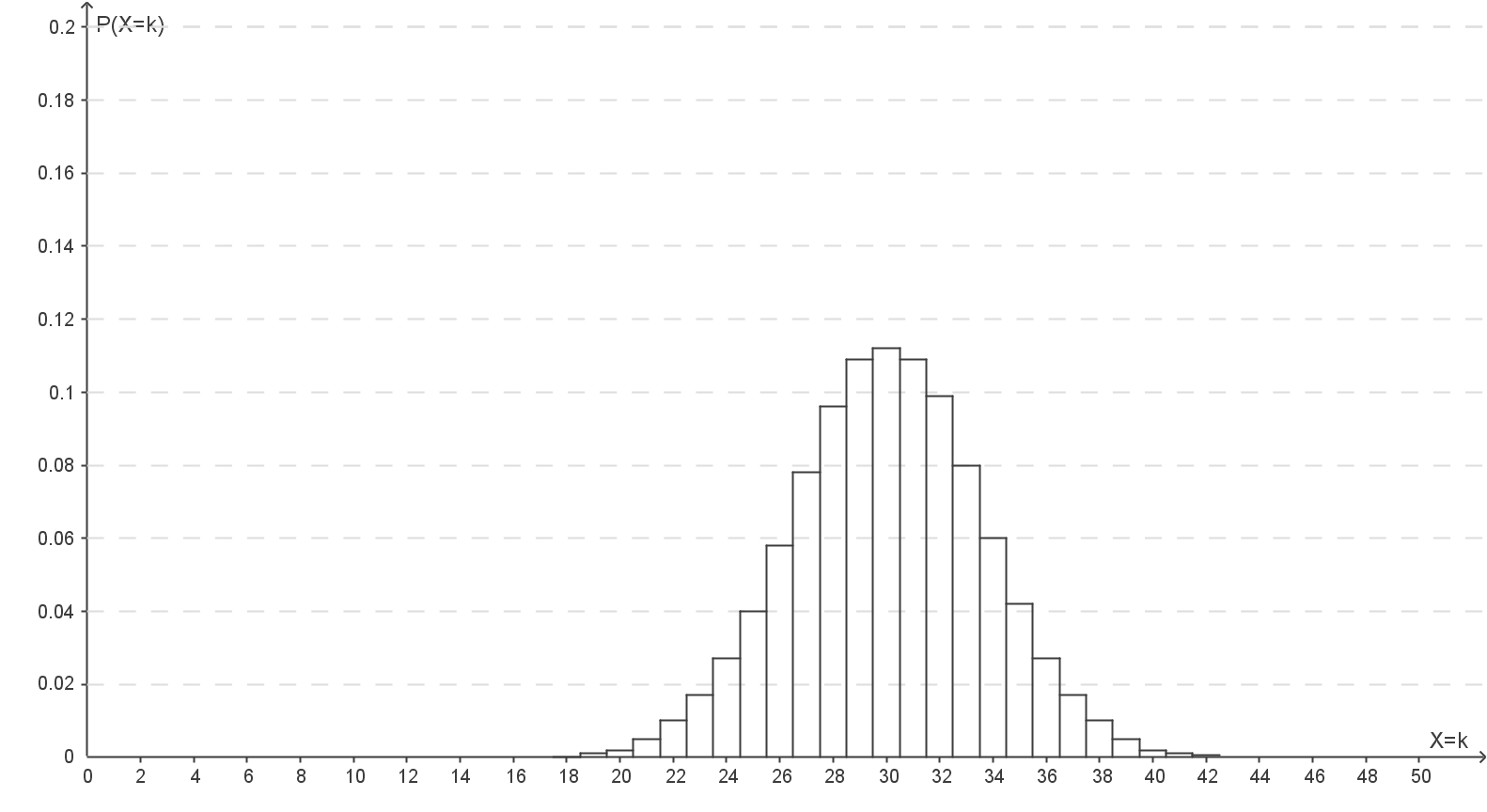
Bei gleich bleibender Entscheidungsregel und steigendem Nutzungsgrad wird die Wahrscheinlichkeit für den Fehler  Art immer kleiner.
Art immer kleiner.
Erkläre, inwieweit dies an den Abbildungen 2 bis 4 abgelesen werden kann.
Erkläre, inwieweit dies an den Abbildungen 2 bis 4 abgelesen werden kann.
(4P)
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
Tabelle 1:  -Regeln für Binomialverteilungen
-Regeln für Binomialverteilungen
Wenn die Laplace-Bedingung erfüllt ist, gelten die
erfüllt ist, gelten die  -Regeln:
-Regeln:
Wenn die Laplace-Bedingung
| n | k | p | k | n | |||||||||
| 0,02 | 0,05 | 0,08 | 0,1 | 0,15 | 0,2 | 0,25 | 0,3 | 0,5 | |||||
| 10 | 0 | 0,8171 | 0,5987 | 0,4344 | 0,3487 | 0,1969 | 0,1074 | 0,0563 | 0,0282 | 0,0010 | 9 | 10 | |
| 1 | 0,9838 | 0,9139 | 0,8121 | 0,7361 | 0,5443 | 0,3758 | 0,2440 | 0,1493 | 0,0107 | 8 | |||
| 2 | 0,9991 | 0,9885 | 0,9599 | 0,9298 | 0,8202 | 0,6778 | 0,5256 | 0,3828 | 0,0547 | 7 | |||
| 3 | 1 | 0,9990 | 0,9942 | 0,9872 | 0,9500 | 0,8791 | 0,7759 | 0,6496 | 0,1719 | 6 | |||
| 4 | 1 | 0,9999 | 0,9994 | 0,9984 | 0,9901 | 0,9672 | 0,9219 | 0,8497 | 0,3770 | 5 | |||
| 5 | 1 | 1 | 1 | 0,9999 | 0,9986 | 0,9936 | 0,9803 | 0,9527 | 0,6230 | 4 | |||
| 6 | 1 | 1 | 1 | 1 | 0,9999 | 0,9991 | 0,9965 | 0,9894 | 0,8281 | 3 | |||
| 7 | 1 | 1 | 1 | 1 | 1 | 0,9999 | 0,9996 | 0,9984 | 0,9453 | 2 | |||
| 8 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9999 | 0,9893 | 1 | |||
| 9 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9990 | 0 | |||
| 20 | 0 | 0,6676 | 0,3585 | 0,1887 | 0,1216 | 0,0388 | 0,0115 | 0,0032 | 0,0008 | 0,0000 | 19 | 20 | |
| 1 | 0,9401 | 0,7358 | 0,5169 | 0,3917 | 0,1756 | 0,0692 | 0,0243 | 0,0076 | 0,0000 | 18 | |||
| 2 | 0,9929 | 0,9245 | 0,7879 | 0,6769 | 0,4049 | 0,2061 | 0,0913 | 0,0355 | 0,0002 | 17 | |||
| 3 | 0,9994 | 0,9841 | 0,9294 | 0,8670 | 0,6477 | 0,4114 | 0,2252 | 0,1071 | 0,0013 | 16 | |||
| 4 | 1 | 0,9974 | 0,9817 | 0,9568 | 0,8298 | 0,6296 | 0,4148 | 0,2375 | 0,0059 | 15 | |||
| 5 | 1 | 0,9997 | 0,9962 | 0,9887 | 0,9327 | 0,8042 | 0,6172 | 0,4164 | 0,0207 | 14 | |||
| 6 | 1 | 1 | 0,9994 | 0,9976 | 0,9781 | 0,9133 | 0,7858 | 0,6080 | 0,0577 | 13 | |||
| 7 | 1 | 1 | 0,9999 | 0,9996 | 0,9941 | 0,9679 | 0,8982 | 0,7723 | 0,1316 | 12 | |||
| 8 | 1 | 1 | 1 | 0,9999 | 0,9987 | 0,9900 | 0,9591 | 0,8867 | 0,2517 | 11 | |||
| 9 | 1 | 1 | 1 | 1 | 0,9998 | 0,9974 | 0,9861 | 0,9520 | 0,4119 | 10 | |||
| 10 | 1 | 1 | 1 | 1 | 1 | 0,9994 | 0,9961 | 0,9829 | 0,5881 | 9 | |||
| 11 | 1 | 1 | 1 | 1 | 1 | 0,9999 | 0,9991 | 0,9949 | 0,7483 | 8 | |||
| 12 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9998 | 0,9987 | 0,8684 | 7 | |||
| 13 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9997 | 0,9423 | 6 | |||
| 14 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9793 | 5 | |||
| 15 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9941 | 4 | |||
| 16 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9987 | 3 | |||
| 17 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9998 | 2 | |||
| n | k | 0,98 | 0,95 | 0,92 | 0,9 | 0,85 | 0,8 | 0,75 | 0,7 | 0,5 | k | n | |
| p | |||||||||||||
|
1
|
||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
3
|
n | k | p | k | n | |||||||||||
|
4
|
0,05 | 0,07 | 0,1 | 0,15 | 1/6 | 0,2 | 0,25 | 0,27 | 0,3 | 1/3 | 0,4 | |||||
|
5
|
50 | 0 | 0,0769 | 0,0266 | 0,0052 | 0,0003 | 0,0001 | 0 | 0 | 0 | 0 | 0 | 0 | 49 | 50 | |
|
6
|
1 | 0,2794 | 0,1265 | 0,0338 | 0,0029 | 0,0012 | 0,0002 | 0 | 0 | 0 | 0 | 0 | 48 | |||
|
7
|
2 | 0,5405 | 0,3108 | 0,1117 | 0,0142 | 0,0066 | 0,0013 | 0,0001 | 0 | 0 | 0 | 0 | 47 | |||
|
8
|
3 | 0,7604 | 0,5327 | 0,2503 | 0,0460 | 0,0238 | 0,0057 | 0,0005 | 0,0002 | 0 | 0 | 0 | 46 | |||
|
9
|
4 | 0,8964 | 0,7290 | 0,4312 | 0,1121 | 0,0643 | 0,0185 | 0,0021 | 0,0008 | 0,0002 | 0 | 0 | 45 | |||
|
10
|
5 | 0,9622 | 0,8650 | 0,6161 | 0,2194 | 0,1388 | 0,0480 | 0,0070 | 0,0030 | 0,0007 | 0,0001 | 0 | 44 | |||
|
11
|
6 | 0,9882 | 0,9417 | 0,7702 | 0,3613 | 0,2506 | 0,1034 | 0,0194 | 0,0089 | 0,0025 | 0,0005 | 0 | 43 | |||
|
12
|
7 | 0,9968 | 0,978 | 0,8779 | 0,5188 | 0,3911 | 0,1904 | 0,0453 | 0,0228 | 0,0073 | 0,0017 | 0,0001 | 42 | |||
|
13
|
8 | 0,9992 | 0,9927 | 0,9421 | 0,6681 | 0,5421 | 0,3073 | 0,0916 | 0,0503 | 0,0183 | 0,0050 | 0,0002 | 41 | |||
|
14
|
9 | 0,9998 | 0,9978 | 0,9755 | 0,7911 | 0,6830 | 0,4437 | 0,1637 | 0,0979 | 0,0402 | 0,0127 | 0,0008 | 40 | |||
|
15
|
10 | 1 | 0,9994 | 0,9906 | 0,8801 | 0,7986 | 0,5836 | 0,2622 | 0,1701 | 0,0789 | 0,0284 | 0,0022 | 39 | |||
|
16
|
11 | 1 | 0,9999 | 0,9968 | 0,9372 | 0,8827 | 0,7107 | 0,3816 | 0,2671 | 0,1390 | 0,0570 | 0,0057 | 38 | |||
|
17
|
12 | 1 | 1 | 0,9990 | 0,9699 | 0,9373 | 0,8139 | 0,5110 | 0,3837 | 0,2229 | 0,1035 | 0,0133 | 37 | |||
|
18
|
13 | 1 | 1 | 0,9997 | 0,9868 | 0,9693 | 0,8894 | 0,6370 | 0,5099 | 0,3279 | 0,1715 | 0,0280 | 36 | |||
|
19
|
14 | 1 | 1 | 0,9999 | 0,9947 | 0,9862 | 0,9393 | 0,7481 | 0,6331 | 0,4468 | 0,2612 | 0,054 | 35 | |||
|
20
|
15 | 1 | 1 | 1 | 0,9981 | 0,9943 | 0,9692 | 0,8369 | 0,7425 | 0,5692 | 0,3690 | 0,0955 | 34 | |||
|
21
|
16 | 1 | 1 | 1 | 0,9993 | 0,9978 | 0,9856 | 0,9017 | 0,8311 | 0,6839 | 0,4868 | 0,1561 | 33 | |||
|
22
|
17 | 1 | 1 | 1 | 0,9998 | 0,9992 | 0,9937 | 0,9449 | 0,8966 | 0,7822 | 0,6046 | 0,2369 | 32 | |||
|
23
|
18 | 1 | 1 | 1 | 0,9999 | 0,9997 | 0,9975 | 0,9713 | 0,9410 | 0,8594 | 0,7126 | 0,3356 | 31 | |||
|
24
|
19 | 1 | 1 | 1 | 1 | 0,9999 | 0,9991 | 0,9861 | 0,9686 | 0,9152 | 0,8036 | 0,4465 | 30 | |||
|
25
|
20 | 1 | 1 | 1 | 1 | 1 | 0,9997 | 0,9937 | 0,9845 | 0,9522 | 0,8741 | 0,5610 | 29 | |||
|
26
|
21 | 1 | 1 | 1 | 1 | 1 | 0,9999 | 0,9974 | 0,9929 | 0,9749 | 0,9244 | 0,6701 | 28 | |||
|
27
|
22 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9990 | 0,9969 | 0,9877 | 0,9576 | 0,7660 | 27 | |||
|
28
|
23 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9996 | 0,9988 | 0,9944 | 0,9778 | 0,8438 | 26 | |||
|
29
|
24 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9999 | 0,9996 | 0,9976 | 0,9892 | 0,9022 | 25 | |||
|
30
|
25 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9998 | 0,9991 | 0,9951 | 0,9427 | 24 | |||
|
31
|
26 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9997 | 0,9979 | 0,9686 | 23 | |||
|
32
|
27 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9999 | 0,9992 | 0,9840 | 22 | |||
|
33
|
28 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9997 | 0,9924 | 21 | |||
|
34
|
29 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9999 | 0,9966 | 20 | |||
|
35
|
30 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9986 | 19 | |||
|
36
|
31 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9995 | 18 | |||
|
37
|
32 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9998 | 17 | |||
|
38
|
33 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9999 | 16 | |||
|
39
|
n | k | 0,95 | 0,93 | 0,9 | 0,85 | 5/6 | 0,8 | 0,75 | 0,73 | 0,7 | 2/3 | 0,6 | k | n | |
|
40
|
||||||||||||||||
|
1
|
||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
3
|
n | k | p | k | n | |||||||||||
|
4
|
0,05 | 0,07 | 0,1 | 0,15 | 1/6 | 0,2 | 0,25 | 0,27 | 0,3 | 1/3 | 0,4 | |||||
|
5
|
100 | 0 | 0,0059 | 0,0007 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 99 | 100 | |
|
6
|
1 | 0,0371 | 0,0060 | 0,0003 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 98 | |||
|
7
|
2 | 0,1183 | 0,0258 | 0,0019 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 97 | |||
|
8
|
3 | 0,2578 | 0,0744 | 0,0078 | 0,0001 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 96 | |||
|
9
|
4 | 0,4360 | 0,1632 | 0,0237 | 0,0004 | 0,0001 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 95 | |||
|
10
|
5 | 0,6160 | 0,2914 | 0,0576 | 0,0016 | 0,0004 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 94 | |||
|
11
|
6 | 0,7660 | 0,4443 | 0,1172 | 0,0047 | 0,0013 | 0,0001 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 93 | |||
|
12
|
7 | 0,8720 | 0,5988 | 0,2061 | 0,0122 | 0,0038 | 0,0003 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 92 | |||
|
13
|
8 | 0,9369 | 0,7340 | 0,3209 | 0,0275 | 0,0095 | 0,0009 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 91 | |||
|
14
|
9 | 0,9718 | 0,8380 | 0,4513 | 0,0551 | 0,0213 | 0,0023 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 90 | |||
|
15
|
10 | 0,9885 | 0,9092 | 0,5832 | 0,0994 | 0,0427 | 0,0057 | 0,0001 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 89 | |||
|
16
|
11 | 0,9957 | 0,9531 | 0,7030 | 0,1635 | 0,0777 | 0,0126 | 0,0004 | 0,0001 | 0,0000 | 0,0000 | 0,0000 | 88 | |||
|
17
|
12 | 0,9985 | 0,9776 | 0,8018 | 0,2473 | 0,1297 | 0,0253 | 0,0010 | 0,0002 | 0,0000 | 0,0000 | 0,0000 | 87 | |||
|
18
|
13 | 0,9995 | 0,9901 | 0,8761 | 0,3474 | 0,2000 | 0,0469 | 0,0025 | 0,0006 | 0,0001 | 0,0000 | 0,0000 | 86 | |||
|
19
|
14 | 0,9999 | 0,9959 | 0,9274 | 0,4572 | 0,2874 | 0,0804 | 0,0054 | 0,0014 | 0,0002 | 0,0000 | 0,0000 | 85 | |||
|
20
|
15 | 1 | 0,9984 | 0,9601 | 0,5683 | 0,3877 | 0,1285 | 0,0111 | 0,0033 | 0,0004 | 0,0000 | 0,0000 | 84 | |||
|
21
|
16 | 1 | 0,9994 | 0,9794 | 0,6725 | 0,4942 | 0,1923 | 0,0211 | 0,0068 | 0,0010 | 0,0001 | 0,0000 | 83 | |||
|
22
|
17 | 1 | 0,9998 | 0,9900 | 0,7633 | 0,5994 | 0,2712 | 0,0376 | 0,0133 | 0,0022 | 0,0002 | 0,0000 | 82 | |||
|
23
|
18 | 1 | 0,9999 | 0,9954 | 0,8372 | 0,6965 | 0,3621 | 0,0630 | 0,0243 | 0,0045 | 0,0005 | 0,0000 | 81 | |||
|
24
|
19 | 1 | 1 | 0,9980 | 0,8935 | 0,7803 | 0,4602 | 0,0995 | 0,0420 | 0,0089 | 0,0011 | 0,0000 | 80 | |||
|
25
|
20 | 1 | 1 | 0,9992 | 0,9337 | 0,8481 | 0,5595 | 0,1488 | 0,0684 | 0,0165 | 0,0024 | 0,0000 | 79 | |||
|
26
|
21 | 1 | 1 | 0,9997 | 0,9607 | 0,8998 | 0,6540 | 0,2114 | 0,1057 | 0,0288 | 0,0048 | 0,0000 | 78 | |||
|
27
|
22 | 1 | 1 | 0,9999 | 0,9779 | 0,9369 | 0,7389 | 0,2864 | 0,1552 | 0,0479 | 0,0091 | 0,0001 | 77 | |||
|
28
|
23 | 1 | 1 | 1 | 0,9881 | 0,9621 | 0,8109 | 0,3711 | 0,2172 | 0,0755 | 0,0164 | 0,0003 | 76 | |||
|
29
|
24 | 1 | 1 | 1 | 0,9939 | 0,9783 | 0,8686 | 0,4617 | 0,2909 | 0,1136 | 0,0281 | 0,0006 | 75 | |||
|
30
|
25 | 1 | 1 | 1 | 0,9970 | 0,9881 | 0,9125 | 0,5535 | 0,3737 | 0,1631 | 0,0458 | 0,0012 | 74 | |||
|
31
|
26 | 1 | 1 | 1 | 0,9986 | 0,9938 | 0,9442 | 0,6417 | 0,4620 | 0,2244 | 0,0715 | 0,0024 | 73 | |||
|
32
|
27 | 1 | 1 | 1 | 0,9994 | 0,9969 | 0,9658 | 0,7224 | 0,5516 | 0,2964 | 0,1066 | 0,0046 | 72 | |||
|
33
|
28 | 1 | 1 | 1 | 0,9997 | 0,9985 | 0,9800 | 0,7925 | 0,6379 | 0,3768 | 0,1524 | 0,0084 | 71 | |||
|
34
|
29 | 1 | 1 | 1 | 0,9999 | 0,9993 | 0,9888 | 0,8505 | 0,7172 | 0,4623 | 0,2093 | 0,0148 | 70 | |||
|
35
|
30 | 1 | 1 | 1 | 1 | 0,9997 | 0,9939 | 0,8962 | 0,7866 | 0,5491 | 0,2766 | 0,0248 | 69 | |||
|
36
|
31 | 1 | 1 | 1 | 1 | 0,9999 | 0,9969 | 0,9307 | 0,8446 | 0,6331 | 0,3525 | 0,0398 | 68 | |||
|
37
|
32 | 1 | 1 | 1 | 1 | 1 | 0,9984 | 0,9554 | 0,8909 | 0,7107 | 0,4344 | 0,0615 | 67 | |||
|
38
|
33 | 1 | 1 | 1 | 1 | 1 | 0,9993 | 0,9724 | 0,9261 | 0,7793 | 0,5188 | 0,0913 | 66 | |||
|
39
|
34 | 1 | 1 | 1 | 1 | 1 | 0,9997 | 0,9836 | 0,9518 | 0,8371 | 0,6019 | 0,1303 | 65 | |||
|
40
|
35 | 1 | 1 | 1 | 1 | 1 | 0,9999 | 0,9906 | 0,9697 | 0,8839 | 0,6803 | 0,1795 | 64 | |||
|
41
|
36 | 1 | 1 | 1 | 1 | 1 | 0,9999 | 0,9948 | 0,9817 | 0,9201 | 0,7511 | 0,2386 | 63 | |||
|
42
|
37 | 1 | 1 | 1 | 1 | 1 | 1,0000 | 0,9973 | 0,9893 | 0,9470 | 0,8123 | 0,3068 | 62 | |||
|
43
|
38 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9986 | 0,9940 | 0,9660 | 0,8630 | 0,3822 | 61 | |||
|
44
|
39 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9993 | 0,9968 | 0,9790 | 0,9034 | 0,4621 | 60 | |||
|
45
|
40 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9997 | 0,9983 | 0,9875 | 0,9341 | 0,5433 | 59 | |||
|
46
|
41 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9999 | 0,9992 | 0,9928 | 0,9566 | 0,6225 | 58 | |||
|
47
|
42 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9999 | 0,9996 | 0,9960 | 0,9724 | 0,6967 | 57 | |||
|
48
|
43 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9998 | 0,9979 | 0,9831 | 0,7635 | 56 | |||
|
49
|
44 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9999 | 0,9989 | 0,9900 | 0,8211 | 55 | |||
|
50
|
45 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9995 | 0,9943 | 0,8689 | 54 | |||
|
51
|
46 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9997 | 0,9969 | 0,9070 | 53 | |||
|
52
|
47 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9999 | 0,9983 | 0,9362 | 52 | |||
|
53
|
48 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9999 | 0,9991 | 0,9577 | 51 | |||
|
54
|
49 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9996 | 0,9729 | 50 | |||
|
55
|
50 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9998 | 0,9832 | 49 | |||
|
56
|
51 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9999 | 0,9900 | 48 | |||
|
57
|
52 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9942 | 47 | |||
|
58
|
53 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9968 | 46 | |||
|
59
|
n | k | 0,95 | 0,93 | 0,9 | 0,85 | 5/6 | 0,8 | 0,75 | 0,73 | 0,7 | 2/3 | 0,6 | k | n | |
|
60
|
||||||||||||||||
|
2
|
||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
3
|
z | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|
4
|
0,0 | 0,5000 | 0,5040 | 0,5080 | 0,5120 | 0,5160 | 0,5199 | 0,5239 | 0,5279 | 0,5319 | 0,5359 | |
|
5
|
0,1 | 0,5398 | 0,5438 | 0,5478 | 0,5517 | 0,5557 | 0,5596 | 0,5636 | 0,5675 | 0,5714 | 0,5753 | |
|
6
|
0,2 | 0,5793 | 0,5832 | 0,5871 | 0,5910 | 0,5948 | 0,5987 | 0,6026 | 0,6064 | 0,6103 | 0,6141 | |
|
7
|
0,3 | 0,6179 | 0,6217 | 0,6255 | 0,6293 | 0,6331 | 0,6368 | 0,6406 | 0,6443 | 0,6480 | 0,6517 | |
|
8
|
0,4 | 0,6554 | 0,6591 | 0,6628 | 0,6664 | 0,6700 | 0,6736 | 0,6772 | 0,6808 | 0,6844 | 0,6879 | |
|
9
|
0,5 | 0,6915 | 0,6950 | 0,6985 | 0,7019 | 0,7054 | 0,7088 | 0,7123 | 0,7157 | 0,7190 | 0,7224 | |
|
10
|
0,6 | 0,7257 | 0,7291 | 0,7324 | 0,7357 | 0,7389 | 0,7422 | 0,7454 | 0,7486 | 0,7517 | 0,7549 | |
|
11
|
0,7 | 0,7580 | 0,7611 | 0,7642 | 0,7673 | 0,7704 | 0,7734 | 0,7764 | 0,7794 | 0,7823 | 0,7852 | |
|
12
|
0,8 | 0,7881 | 0,7910 | 0,7939 | 0,7967 | 0,7995 | 0,8023 | 0,8051 | 0,8078 | 0,8106 | 0,8133 | |
|
13
|
0,9 | 0,8159 | 0,8186 | 0,8212 | 0,8238 | 0,8264 | 0,8289 | 0,8315 | 0,8340 | 0,8365 | 0,8389 | |
|
14
|
1,0 | 0,8413 | 0,8438 | 0,8461 | 0,8485 | 0,8508 | 0,8531 | 0,8554 | 0,8577 | 0,8599 | 0,8621 | |
|
15
|
1,1 | 0,8643 | 0,8665 | 0,8686 | 0,8708 | 0,8729 | 0,8749 | 0,8770 | 0,8790 | 0,8810 | 0,8830 | |
|
16
|
1,2 | 0,8849 | 0,8869 | 0,8888 | 0,8907 | 0,8925 | 0,8944 | 0,8962 | 0,8980 | 0,8997 | 0,9015 | |
|
17
|
1,3 | 0,9032 | 0,9049 | 0,9066 | 0,9082 | 0,9099 | 0,9115 | 0,9131 | 0,9147 | 0,9162 | 0,9177 | |
|
18
|
1,4 | 0,9192 | 0,9207 | 0,9222 | 0,9236 | 0,9251 | 0,9265 | 0,9279 | 0,9292 | 0,9306 | 0,9319 | |
|
19
|
1,5 | 0,9332 | 0,9345 | 0,9357 | 0,9370 | 0,9382 | 0,9394 | 0,9406 | 0,9418 | 0,9429 | 0,9441 | |
|
20
|
1,6 | 0,9452 | 0,9463 | 0,9474 | 0,9484 | 0,9495 | 0,9505 | 0,9515 | 0,9525 | 0,9535 | 0,9545 | |
|
21
|
1,7 | 0,9554 | 0,9564 | 0,9573 | 0,9582 | 0,9591 | 0,9599 | 0,9608 | 0,9616 | 0,9625 | 0,9633 | |
|
22
|
1,8 | 0,9641 | 0,9649 | 0,9656 | 0,9664 | 0,9671 | 0,9678 | 0,9686 | 0,9693 | 0,9699 | 0,9706 | |
|
23
|
1,9 | 0,9713 | 0,9719 | 0,9726 | 0,9732 | 0,9738 | 0,9744 | 0,9750 | 0,9756 | 0,9761 | 0,9767 | |
|
24
|
2,0 | 0,9772 | 0,9778 | 0,9783 | 0,9788 | 0,9793 | 0,9798 | 0,9803 | 0,9808 | 0,9812 | 0,9817 | |
|
25
|
2,1 | 0,9821 | 0,9826 | 0,9830 | 0,9834 | 0,9838 | 0,9842 | 0,9846 | 0,9850 | 0,9854 | 0,9857 | |
|
26
|
2,2 | 0,9861 | 0,9864 | 0,9868 | 0,9871 | 0,9875 | 0,9878 | 0,9881 | 0,9884 | 0,9887 | 0,9890 | |
|
27
|
2,3 | 0,9893 | 0,9896 | 0,9898 | 0,9901 | 0,9904 | 0,9906 | 0,9909 | 0,9911 | 0,9913 | 0,9916 | |
|
28
|
2,4 | 0,9918 | 0,9920 | 0,9922 | 0,9925 | 0,9927 | 0,9929 | 0,9931 | 0,9932 | 0,9934 | 0,9936 | |
|
29
|
2,5 | 0,9938 | 0,9940 | 0,9941 | 0,9943 | 0,9945 | 0,9946 | 0,9948 | 0,9949 | 0,9951 | 0,9952 | |
|
30
|
2,6 | 0,9953 | 0,9955 | 0,9956 | 0,9957 | 0,9959 | 0,9960 | 0,9961 | 0,9962 | 0,9963 | 0,9964 | |
|
31
|
2,7 | 0,9965 | 0,9966 | 0,9967 | 0,9968 | 0,9969 | 0,9970 | 0,9971 | 0,9972 | 0,9973 | 0,9974 | |
|
32
|
2,8 | 0,9974 | 0,9975 | 0,9976 | 0,9977 | 0,9977 | 0,9978 | 0,9979 | 0,9979 | 0,9980 | 0,9981 | |
|
33
|
2,9 | 0,9981 | 0,9982 | 0,9982 | 0,9983 | 0,9984 | 0,9984 | 0,9985 | 0,9985 | 0,9986 | 0,9986 | |
|
34
|
3,0 | 0,9987 | 0,9987 | 0,9987 | 0,9988 | 0,9988 | 0,9989 | 0,9989 | 0,9989 | 0,9990 | 0,9990 | |
|
35
|
3,1 | 0,9990 | 0,9991 | 0,9991 | 0,9991 | 0,9992 | 0,9992 | 0,9992 | 0,9992 | 0,9993 | 0,9993 | |
|
36
|
3,2 | 0,9993 | 0,9993 | 0,9994 | 0,9994 | 0,9994 | 0,9994 | 0,9994 | 0,9995 | 0,9995 | 0,9995 | |
|
37
|
3,3 | 0,9995 | 0,9995 | 0,9995 | 0,9996 | 0,9996 | 0,9996 | 0,9996 | 0,9996 | 0,9996 | 0,9997 | |
|
38
|
3,4 | 0,9997 | 0,9997 | 0,9997 | 0,9997 | 0,9997 | 0,9997 | 0,9997 | 0,9997 | 0,9997 | 0,9998 | |
|
39
|
3,5 | 0,9998 | 0,9998 | 0,9998 | 0,9998 | 0,9998 | 0,9998 | 0,9998 | 0,9998 | 0,9998 | 0,9998 | |
|
40
|
3,6 | 0,9998 | 0,9998 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | |
|
41
|
3,7 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | |
|
42
|
3,8 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 |
Dieser Prozentsatz soll im Folgenden als Wahrscheinlichkeit dafür verwendet werden, dass eine zufällig befragte jugendliche Person „Freundschaftsbuch“ nutzt.
a)
Berechne die Wahrscheinlichkeit, dass von  zufällig ausgewählten Jugendlichen
zufällig ausgewählten Jugendlichen
(1)
genau  Jugendliche „Freundschaftsbuch“ nutzen,
Jugendliche „Freundschaftsbuch“ nutzen,
(2P)
(2)
höchstens  Jugendliche „Freundschaftsbuch“ nutzen,
Jugendliche „Freundschaftsbuch“ nutzen,
(3P)
(3)
die Anzahl der jugendlichen Nutzer, die „Freundschaftsbuch“ nutzen, einem Wert entspricht, der sich um maximal  vom Erwartungswert unterscheidet.
vom Erwartungswert unterscheidet.
(5P)
b)
Ermittle (ggf. durch Probieren), welche positive Anzahl an Jugendlichen mindestens zufällig ausgewählt werden muss, damit man mit einer Wahrscheinlichkeit von höchstens  maximal einen Jugendlichen antrifft, der „Freundschaftsbuch“ nutzt.
maximal einen Jugendlichen antrifft, der „Freundschaftsbuch“ nutzt.
(6P)
c)
In einer Schule gibt es zur schulinternen Kommunikation ein eigenes Netzwerk, das sowohl von Jugendlichen genutzt wird, die „Freundschaftsbuch“ nutzen, als auch von Jugendlichen, die „Freundschaftsbuch“ nicht nutzen. Dabei ist in beiden Gruppen der Anteil derjenigen, die das schulinterne Netzwerk nutzen, identisch. Im Folgenden wird dieser Anteil mit  bezeichnet und auch als Wahrscheinlichkeit für den jeweiligen Fall verwendet.
bezeichnet und auch als Wahrscheinlichkeit für den jeweiligen Fall verwendet.
(1)
Zeige, dass man den Anteil der Jugendlichen, die genau eines dieser Netzwerke nutzen, mit Hilfe des Terms  beschreiben kann, und erkläre die einzelnen Bestandteile des Terms.
beschreiben kann, und erkläre die einzelnen Bestandteile des Terms.
(5P)
(2)
Berechne den Anteil aller Jugendlichen, die das schulinterne Netzwerk nutzen, wenn der Anteil der Jugendlichen, die genau eines dieser Netzwerke nutzen, bei  liegt.
liegt.
(2P)
(3)
Berechne für  die Wahrscheinlichkeit, dass eine zufällig ausgewählte jugendliche Person mindestens eines der beiden Netzwerke nutzt.
die Wahrscheinlichkeit, dass eine zufällig ausgewählte jugendliche Person mindestens eines der beiden Netzwerke nutzt.
(3P)
(4)
Eine zufällig ausgewählte jugendliche Person nutzt das schulinterne Netzwerk.
Gib die Wahrscheinlichkeit an, dass sie „Freundschaftsbuch“ nicht nutzt, und erkläre, wieso dieser Wert auch ohne einen Ansatz über bedingte Wahrscheinlichkeiten ermittelt werden kann.
Gib die Wahrscheinlichkeit an, dass sie „Freundschaftsbuch“ nicht nutzt, und erkläre, wieso dieser Wert auch ohne einen Ansatz über bedingte Wahrscheinlichkeiten ermittelt werden kann.
(4P)
d)
Die Schülervertretung möchte, dass der Nutzungsgrad des schulinternen Netzwerks verbessert wird. Dazu soll mit Aktionen das schulinterne Netzwerk bekannter gemacht werden. Nach einem Jahr möchte die Schülervertretung die Vermutung überprüfen, dass der Nutzungsgrad von vormals  gestiegen ist, und möchte dazu
gestiegen ist, und möchte dazu  zufällig ausgewählte Jugendliche der Schule befragen.
zufällig ausgewählte Jugendliche der Schule befragen.
 ergibt sich die Entscheidungsregel: „Verwirf die Nullhypothese, falls
ergibt sich die Entscheidungsregel: „Verwirf die Nullhypothese, falls  oder mehr Jugendliche das schulinterne Netzwerk nutzen.“
oder mehr Jugendliche das schulinterne Netzwerk nutzen.“
(1)
Gib eine geeignete Nullhypothese an und ermittle eine passende Entscheidungsregel auf dem Signifikanzniveau von  .
.
(6P)
(2)
Bei der Befragung kommt heraus, dass  Jugendliche das schulinterne Netzwerk nutzen.
Jugendliche das schulinterne Netzwerk nutzen.
Beurteile die Situation aus Sicht der Schülervertretung.
Zum Signifikanzniveau von Beurteile die Situation aus Sicht der Schülervertretung.
(2P)
(3)
In den Abbildungen 1 - 4 sind die Wahrscheinlichkeiten der jeweils angegebenen Binomialverteilung als Säulen dargestellt. Die Höhe der Säule zum Wert  entspricht dabei
entspricht dabei  .
.
Stelle den Bereich, in dem die Nullhypothese abgelehnt wird, in Abbildung 1 grafisch dar.
Stelle den Bereich, in dem die Nullhypothese abgelehnt wird, in Abbildung 1 grafisch dar.
(3P)
(4)
Beschreibe den Fehler  Art im Sachzusammenhang und berechne die Wahrscheinlichkeit seines Auftretens für den Fall, dass der Nutzungsgrad in Wirklichkeit bei
Art im Sachzusammenhang und berechne die Wahrscheinlichkeit seines Auftretens für den Fall, dass der Nutzungsgrad in Wirklichkeit bei  liegt.
liegt.
(5P)
(5)
Bei gleich bleibender Entscheidungsregel und steigendem Nutzungsgrad wird die Wahrscheinlichkeit für den Fehler  Art immer kleiner.
Art immer kleiner.
Erkläre, inwieweit dies an den Abbildungen 2 bis 4 abgelesen werden kann.
Erkläre, inwieweit dies an den Abbildungen 2 bis 4 abgelesen werden kann.
(4P)
|
2
|
||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
3
|
z | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|
4
|
0,0 | 0,5000 | 0,5040 | 0,5080 | 0,5120 | 0,5160 | 0,5199 | 0,5239 | 0,5279 | 0,5319 | 0,5359 | |
|
5
|
0,1 | 0,5398 | 0,5438 | 0,5478 | 0,5517 | 0,5557 | 0,5596 | 0,5636 | 0,5675 | 0,5714 | 0,5753 | |
|
6
|
0,2 | 0,5793 | 0,5832 | 0,5871 | 0,5910 | 0,5948 | 0,5987 | 0,6026 | 0,6064 | 0,6103 | 0,6141 | |
|
7
|
0,3 | 0,6179 | 0,6217 | 0,6255 | 0,6293 | 0,6331 | 0,6368 | 0,6406 | 0,6443 | 0,6480 | 0,6517 | |
|
8
|
0,4 | 0,6554 | 0,6591 | 0,6628 | 0,6664 | 0,6700 | 0,6736 | 0,6772 | 0,6808 | 0,6844 | 0,6879 | |
|
9
|
0,5 | 0,6915 | 0,6950 | 0,6985 | 0,7019 | 0,7054 | 0,7088 | 0,7123 | 0,7157 | 0,7190 | 0,7224 | |
|
10
|
0,6 | 0,7257 | 0,7291 | 0,7324 | 0,7357 | 0,7389 | 0,7422 | 0,7454 | 0,7486 | 0,7517 | 0,7549 | |
|
11
|
0,7 | 0,7580 | 0,7611 | 0,7642 | 0,7673 | 0,7704 | 0,7734 | 0,7764 | 0,7794 | 0,7823 | 0,7852 | |
|
12
|
0,8 | 0,7881 | 0,7910 | 0,7939 | 0,7967 | 0,7995 | 0,8023 | 0,8051 | 0,8078 | 0,8106 | 0,8133 | |
|
13
|
0,9 | 0,8159 | 0,8186 | 0,8212 | 0,8238 | 0,8264 | 0,8289 | 0,8315 | 0,8340 | 0,8365 | 0,8389 | |
|
14
|
1,0 | 0,8413 | 0,8438 | 0,8461 | 0,8485 | 0,8508 | 0,8531 | 0,8554 | 0,8577 | 0,8599 | 0,8621 | |
|
15
|
1,1 | 0,8643 | 0,8665 | 0,8686 | 0,8708 | 0,8729 | 0,8749 | 0,8770 | 0,8790 | 0,8810 | 0,8830 | |
|
16
|
1,2 | 0,8849 | 0,8869 | 0,8888 | 0,8907 | 0,8925 | 0,8944 | 0,8962 | 0,8980 | 0,8997 | 0,9015 | |
|
17
|
1,3 | 0,9032 | 0,9049 | 0,9066 | 0,9082 | 0,9099 | 0,9115 | 0,9131 | 0,9147 | 0,9162 | 0,9177 | |
|
18
|
1,4 | 0,9192 | 0,9207 | 0,9222 | 0,9236 | 0,9251 | 0,9265 | 0,9279 | 0,9292 | 0,9306 | 0,9319 | |
|
19
|
1,5 | 0,9332 | 0,9345 | 0,9357 | 0,9370 | 0,9382 | 0,9394 | 0,9406 | 0,9418 | 0,9429 | 0,9441 | |
|
20
|
1,6 | 0,9452 | 0,9463 | 0,9474 | 0,9484 | 0,9495 | 0,9505 | 0,9515 | 0,9525 | 0,9535 | 0,9545 | |
|
21
|
1,7 | 0,9554 | 0,9564 | 0,9573 | 0,9582 | 0,9591 | 0,9599 | 0,9608 | 0,9616 | 0,9625 | 0,9633 | |
|
22
|
1,8 | 0,9641 | 0,9649 | 0,9656 | 0,9664 | 0,9671 | 0,9678 | 0,9686 | 0,9693 | 0,9699 | 0,9706 | |
|
23
|
1,9 | 0,9713 | 0,9719 | 0,9726 | 0,9732 | 0,9738 | 0,9744 | 0,9750 | 0,9756 | 0,9761 | 0,9767 | |
|
24
|
2,0 | 0,9772 | 0,9778 | 0,9783 | 0,9788 | 0,9793 | 0,9798 | 0,9803 | 0,9808 | 0,9812 | 0,9817 | |
|
25
|
2,1 | 0,9821 | 0,9826 | 0,9830 | 0,9834 | 0,9838 | 0,9842 | 0,9846 | 0,9850 | 0,9854 | 0,9857 | |
|
26
|
2,2 | 0,9861 | 0,9864 | 0,9868 | 0,9871 | 0,9875 | 0,9878 | 0,9881 | 0,9884 | 0,9887 | 0,9890 | |
|
27
|
2,3 | 0,9893 | 0,9896 | 0,9898 | 0,9901 | 0,9904 | 0,9906 | 0,9909 | 0,9911 | 0,9913 | 0,9916 | |
|
28
|
2,4 | 0,9918 | 0,9920 | 0,9922 | 0,9925 | 0,9927 | 0,9929 | 0,9931 | 0,9932 | 0,9934 | 0,9936 | |
|
29
|
2,5 | 0,9938 | 0,9940 | 0,9941 | 0,9943 | 0,9945 | 0,9946 | 0,9948 | 0,9949 | 0,9951 | 0,9952 | |
|
30
|
2,6 | 0,9953 | 0,9955 | 0,9956 | 0,9957 | 0,9959 | 0,9960 | 0,9961 | 0,9962 | 0,9963 | 0,9964 | |
|
31
|
2,7 | 0,9965 | 0,9966 | 0,9967 | 0,9968 | 0,9969 | 0,9970 | 0,9971 | 0,9972 | 0,9973 | 0,9974 | |
|
32
|
2,8 | 0,9974 | 0,9975 | 0,9976 | 0,9977 | 0,9977 | 0,9978 | 0,9979 | 0,9979 | 0,9980 | 0,9981 | |
|
33
|
2,9 | 0,9981 | 0,9982 | 0,9982 | 0,9983 | 0,9984 | 0,9984 | 0,9985 | 0,9985 | 0,9986 | 0,9986 | |
|
34
|
3,0 | 0,9987 | 0,9987 | 0,9987 | 0,9988 | 0,9988 | 0,9989 | 0,9989 | 0,9989 | 0,9990 | 0,9990 | |
|
35
|
3,1 | 0,9990 | 0,9991 | 0,9991 | 0,9991 | 0,9992 | 0,9992 | 0,9992 | 0,9992 | 0,9993 | 0,9993 | |
|
36
|
3,2 | 0,9993 | 0,9993 | 0,9994 | 0,9994 | 0,9994 | 0,9994 | 0,9994 | 0,9995 | 0,9995 | 0,9995 | |
|
37
|
3,3 | 0,9995 | 0,9995 | 0,9995 | 0,9996 | 0,9996 | 0,9996 | 0,9996 | 0,9996 | 0,9996 | 0,9997 | |
|
38
|
3,4 | 0,9997 | 0,9997 | 0,9997 | 0,9997 | 0,9997 | 0,9997 | 0,9997 | 0,9997 | 0,9997 | 0,9998 | |
|
39
|
3,5 | 0,9998 | 0,9998 | 0,9998 | 0,9998 | 0,9998 | 0,9998 | 0,9998 | 0,9998 | 0,9998 | 0,9998 | |
|
40
|
3,6 | 0,9998 | 0,9998 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | |
|
41
|
3,7 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | |
|
42
|
3,8 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 | 0,9999 |
Tabelle 1:  -Regeln für Binomialverteilungen
-Regeln für Binomialverteilungen
Wenn die Laplace-Bedingung erfüllt ist, gelten die
erfüllt ist, gelten die  -Regeln:
-Regeln:
Wenn die Laplace-Bedingung
| n | k | p | k | n | |||||||||
| 0,02 | 0,05 | 0,08 | 0,1 | 0,15 | 0,2 | 0,25 | 0,3 | 0,5 | |||||
| 10 | 0 | 0,8171 | 0,5987 | 0,4344 | 0,3487 | 0,1969 | 0,1074 | 0,0563 | 0,0282 | 0,0010 | 9 | 10 | |
| 1 | 0,9838 | 0,9139 | 0,8121 | 0,7361 | 0,5443 | 0,3758 | 0,2440 | 0,1493 | 0,0107 | 8 | |||
| 2 | 0,9991 | 0,9885 | 0,9599 | 0,9298 | 0,8202 | 0,6778 | 0,5256 | 0,3828 | 0,0547 | 7 | |||
| 3 | 1 | 0,9990 | 0,9942 | 0,9872 | 0,9500 | 0,8791 | 0,7759 | 0,6496 | 0,1719 | 6 | |||
| 4 | 1 | 0,9999 | 0,9994 | 0,9984 | 0,9901 | 0,9672 | 0,9219 | 0,8497 | 0,3770 | 5 | |||
| 5 | 1 | 1 | 1 | 0,9999 | 0,9986 | 0,9936 | 0,9803 | 0,9527 | 0,6230 | 4 | |||
| 6 | 1 | 1 | 1 | 1 | 0,9999 | 0,9991 | 0,9965 | 0,9894 | 0,8281 | 3 | |||
| 7 | 1 | 1 | 1 | 1 | 1 | 0,9999 | 0,9996 | 0,9984 | 0,9453 | 2 | |||
| 8 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9999 | 0,9893 | 1 | |||
| 9 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9990 | 0 | |||
| 20 | 0 | 0,6676 | 0,3585 | 0,1887 | 0,1216 | 0,0388 | 0,0115 | 0,0032 | 0,0008 | 0,0000 | 19 | 20 | |
| 1 | 0,9401 | 0,7358 | 0,5169 | 0,3917 | 0,1756 | 0,0692 | 0,0243 | 0,0076 | 0,0000 | 18 | |||
| 2 | 0,9929 | 0,9245 | 0,7879 | 0,6769 | 0,4049 | 0,2061 | 0,0913 | 0,0355 | 0,0002 | 17 | |||
| 3 | 0,9994 | 0,9841 | 0,9294 | 0,8670 | 0,6477 | 0,4114 | 0,2252 | 0,1071 | 0,0013 | 16 | |||
| 4 | 1 | 0,9974 | 0,9817 | 0,9568 | 0,8298 | 0,6296 | 0,4148 | 0,2375 | 0,0059 | 15 | |||
| 5 | 1 | 0,9997 | 0,9962 | 0,9887 | 0,9327 | 0,8042 | 0,6172 | 0,4164 | 0,0207 | 14 | |||
| 6 | 1 | 1 | 0,9994 | 0,9976 | 0,9781 | 0,9133 | 0,7858 | 0,6080 | 0,0577 | 13 | |||
| 7 | 1 | 1 | 0,9999 | 0,9996 | 0,9941 | 0,9679 | 0,8982 | 0,7723 | 0,1316 | 12 | |||
| 8 | 1 | 1 | 1 | 0,9999 | 0,9987 | 0,9900 | 0,9591 | 0,8867 | 0,2517 | 11 | |||
| 9 | 1 | 1 | 1 | 1 | 0,9998 | 0,9974 | 0,9861 | 0,9520 | 0,4119 | 10 | |||
| 10 | 1 | 1 | 1 | 1 | 1 | 0,9994 | 0,9961 | 0,9829 | 0,5881 | 9 | |||
| 11 | 1 | 1 | 1 | 1 | 1 | 0,9999 | 0,9991 | 0,9949 | 0,7483 | 8 | |||
| 12 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9998 | 0,9987 | 0,8684 | 7 | |||
| 13 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9997 | 0,9423 | 6 | |||
| 14 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9793 | 5 | |||
| 15 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9941 | 4 | |||
| 16 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9987 | 3 | |||
| 17 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9998 | 2 | |||
| n | k | 0,98 | 0,95 | 0,92 | 0,9 | 0,85 | 0,8 | 0,75 | 0,7 | 0,5 | k | n | |
| p | |||||||||||||
|
1
|
||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
3
|
n | k | p | k | n | |||||||||||
|
4
|
0,05 | 0,07 | 0,1 | 0,15 | 1/6 | 0,2 | 0,25 | 0,27 | 0,3 | 1/3 | 0,4 | |||||
|
5
|
50 | 0 | 0,0769 | 0,0266 | 0,0052 | 0,0003 | 0,0001 | 0 | 0 | 0 | 0 | 0 | 0 | 49 | 50 | |
|
6
|
1 | 0,2794 | 0,1265 | 0,0338 | 0,0029 | 0,0012 | 0,0002 | 0 | 0 | 0 | 0 | 0 | 48 | |||
|
7
|
2 | 0,5405 | 0,3108 | 0,1117 | 0,0142 | 0,0066 | 0,0013 | 0,0001 | 0 | 0 | 0 | 0 | 47 | |||
|
8
|
3 | 0,7604 | 0,5327 | 0,2503 | 0,0460 | 0,0238 | 0,0057 | 0,0005 | 0,0002 | 0 | 0 | 0 | 46 | |||
|
9
|
4 | 0,8964 | 0,7290 | 0,4312 | 0,1121 | 0,0643 | 0,0185 | 0,0021 | 0,0008 | 0,0002 | 0 | 0 | 45 | |||
|
10
|
5 | 0,9622 | 0,8650 | 0,6161 | 0,2194 | 0,1388 | 0,0480 | 0,0070 | 0,0030 | 0,0007 | 0,0001 | 0 | 44 | |||
|
11
|
6 | 0,9882 | 0,9417 | 0,7702 | 0,3613 | 0,2506 | 0,1034 | 0,0194 | 0,0089 | 0,0025 | 0,0005 | 0 | 43 | |||
|
12
|
7 | 0,9968 | 0,978 | 0,8779 | 0,5188 | 0,3911 | 0,1904 | 0,0453 | 0,0228 | 0,0073 | 0,0017 | 0,0001 | 42 | |||
|
13
|
8 | 0,9992 | 0,9927 | 0,9421 | 0,6681 | 0,5421 | 0,3073 | 0,0916 | 0,0503 | 0,0183 | 0,0050 | 0,0002 | 41 | |||
|
14
|
9 | 0,9998 | 0,9978 | 0,9755 | 0,7911 | 0,6830 | 0,4437 | 0,1637 | 0,0979 | 0,0402 | 0,0127 | 0,0008 | 40 | |||
|
15
|
10 | 1 | 0,9994 | 0,9906 | 0,8801 | 0,7986 | 0,5836 | 0,2622 | 0,1701 | 0,0789 | 0,0284 | 0,0022 | 39 | |||
|
16
|
11 | 1 | 0,9999 | 0,9968 | 0,9372 | 0,8827 | 0,7107 | 0,3816 | 0,2671 | 0,1390 | 0,0570 | 0,0057 | 38 | |||
|
17
|
12 | 1 | 1 | 0,9990 | 0,9699 | 0,9373 | 0,8139 | 0,5110 | 0,3837 | 0,2229 | 0,1035 | 0,0133 | 37 | |||
|
18
|
13 | 1 | 1 | 0,9997 | 0,9868 | 0,9693 | 0,8894 | 0,6370 | 0,5099 | 0,3279 | 0,1715 | 0,0280 | 36 | |||
|
19
|
14 | 1 | 1 | 0,9999 | 0,9947 | 0,9862 | 0,9393 | 0,7481 | 0,6331 | 0,4468 | 0,2612 | 0,054 | 35 | |||
|
20
|
15 | 1 | 1 | 1 | 0,9981 | 0,9943 | 0,9692 | 0,8369 | 0,7425 | 0,5692 | 0,3690 | 0,0955 | 34 | |||
|
21
|
16 | 1 | 1 | 1 | 0,9993 | 0,9978 | 0,9856 | 0,9017 | 0,8311 | 0,6839 | 0,4868 | 0,1561 | 33 | |||
|
22
|
17 | 1 | 1 | 1 | 0,9998 | 0,9992 | 0,9937 | 0,9449 | 0,8966 | 0,7822 | 0,6046 | 0,2369 | 32 | |||
|
23
|
18 | 1 | 1 | 1 | 0,9999 | 0,9997 | 0,9975 | 0,9713 | 0,9410 | 0,8594 | 0,7126 | 0,3356 | 31 | |||
|
24
|
19 | 1 | 1 | 1 | 1 | 0,9999 | 0,9991 | 0,9861 | 0,9686 | 0,9152 | 0,8036 | 0,4465 | 30 | |||
|
25
|
20 | 1 | 1 | 1 | 1 | 1 | 0,9997 | 0,9937 | 0,9845 | 0,9522 | 0,8741 | 0,5610 | 29 | |||
|
26
|
21 | 1 | 1 | 1 | 1 | 1 | 0,9999 | 0,9974 | 0,9929 | 0,9749 | 0,9244 | 0,6701 | 28 | |||
|
27
|
22 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9990 | 0,9969 | 0,9877 | 0,9576 | 0,7660 | 27 | |||
|
28
|
23 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9996 | 0,9988 | 0,9944 | 0,9778 | 0,8438 | 26 | |||
|
29
|
24 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9999 | 0,9996 | 0,9976 | 0,9892 | 0,9022 | 25 | |||
|
30
|
25 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9998 | 0,9991 | 0,9951 | 0,9427 | 24 | |||
|
31
|
26 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9997 | 0,9979 | 0,9686 | 23 | |||
|
32
|
27 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9999 | 0,9992 | 0,9840 | 22 | |||
|
33
|
28 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9997 | 0,9924 | 21 | |||
|
34
|
29 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9999 | 0,9966 | 20 | |||
|
35
|
30 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9986 | 19 | |||
|
36
|
31 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9995 | 18 | |||
|
37
|
32 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9998 | 17 | |||
|
38
|
33 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9999 | 16 | |||
|
39
|
n | k | 0,95 | 0,93 | 0,9 | 0,85 | 5/6 | 0,8 | 0,75 | 0,73 | 0,7 | 2/3 | 0,6 | k | n | |
|
40
|
||||||||||||||||
|
1
|
||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
3
|
n | k | p | k | n | |||||||||||
|
4
|
0,05 | 0,07 | 0,1 | 0,15 | 1/6 | 0,2 | 0,25 | 0,27 | 0,3 | 1/3 | 0,4 | |||||
|
5
|
100 | 0 | 0,0059 | 0,0007 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 99 | 100 | |
|
6
|
1 | 0,0371 | 0,0060 | 0,0003 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 98 | |||
|
7
|
2 | 0,1183 | 0,0258 | 0,0019 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 97 | |||
|
8
|
3 | 0,2578 | 0,0744 | 0,0078 | 0,0001 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 96 | |||
|
9
|
4 | 0,4360 | 0,1632 | 0,0237 | 0,0004 | 0,0001 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 95 | |||
|
10
|
5 | 0,6160 | 0,2914 | 0,0576 | 0,0016 | 0,0004 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 94 | |||
|
11
|
6 | 0,7660 | 0,4443 | 0,1172 | 0,0047 | 0,0013 | 0,0001 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 93 | |||
|
12
|
7 | 0,8720 | 0,5988 | 0,2061 | 0,0122 | 0,0038 | 0,0003 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 92 | |||
|
13
|
8 | 0,9369 | 0,7340 | 0,3209 | 0,0275 | 0,0095 | 0,0009 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 91 | |||
|
14
|
9 | 0,9718 | 0,8380 | 0,4513 | 0,0551 | 0,0213 | 0,0023 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 90 | |||
|
15
|
10 | 0,9885 | 0,9092 | 0,5832 | 0,0994 | 0,0427 | 0,0057 | 0,0001 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 89 | |||
|
16
|
11 | 0,9957 | 0,9531 | 0,7030 | 0,1635 | 0,0777 | 0,0126 | 0,0004 | 0,0001 | 0,0000 | 0,0000 | 0,0000 | 88 | |||
|
17
|
12 | 0,9985 | 0,9776 | 0,8018 | 0,2473 | 0,1297 | 0,0253 | 0,0010 | 0,0002 | 0,0000 | 0,0000 | 0,0000 | 87 | |||
|
18
|
13 | 0,9995 | 0,9901 | 0,8761 | 0,3474 | 0,2000 | 0,0469 | 0,0025 | 0,0006 | 0,0001 | 0,0000 | 0,0000 | 86 | |||
|
19
|
14 | 0,9999 | 0,9959 | 0,9274 | 0,4572 | 0,2874 | 0,0804 | 0,0054 | 0,0014 | 0,0002 | 0,0000 | 0,0000 | 85 | |||
|
20
|
15 | 1 | 0,9984 | 0,9601 | 0,5683 | 0,3877 | 0,1285 | 0,0111 | 0,0033 | 0,0004 | 0,0000 | 0,0000 | 84 | |||
|
21
|
16 | 1 | 0,9994 | 0,9794 | 0,6725 | 0,4942 | 0,1923 | 0,0211 | 0,0068 | 0,0010 | 0,0001 | 0,0000 | 83 | |||
|
22
|
17 | 1 | 0,9998 | 0,9900 | 0,7633 | 0,5994 | 0,2712 | 0,0376 | 0,0133 | 0,0022 | 0,0002 | 0,0000 | 82 | |||
|
23
|
18 | 1 | 0,9999 | 0,9954 | 0,8372 | 0,6965 | 0,3621 | 0,0630 | 0,0243 | 0,0045 | 0,0005 | 0,0000 | 81 | |||
|
24
|
19 | 1 | 1 | 0,9980 | 0,8935 | 0,7803 | 0,4602 | 0,0995 | 0,0420 | 0,0089 | 0,0011 | 0,0000 | 80 | |||
|
25
|
20 | 1 | 1 | 0,9992 | 0,9337 | 0,8481 | 0,5595 | 0,1488 | 0,0684 | 0,0165 | 0,0024 | 0,0000 | 79 | |||
|
26
|
21 | 1 | 1 | 0,9997 | 0,9607 | 0,8998 | 0,6540 | 0,2114 | 0,1057 | 0,0288 | 0,0048 | 0,0000 | 78 | |||
|
27
|
22 | 1 | 1 | 0,9999 | 0,9779 | 0,9369 | 0,7389 | 0,2864 | 0,1552 | 0,0479 | 0,0091 | 0,0001 | 77 | |||
|
28
|
23 | 1 | 1 | 1 | 0,9881 | 0,9621 | 0,8109 | 0,3711 | 0,2172 | 0,0755 | 0,0164 | 0,0003 | 76 | |||
|
29
|
24 | 1 | 1 | 1 | 0,9939 | 0,9783 | 0,8686 | 0,4617 | 0,2909 | 0,1136 | 0,0281 | 0,0006 | 75 | |||
|
30
|
25 | 1 | 1 | 1 | 0,9970 | 0,9881 | 0,9125 | 0,5535 | 0,3737 | 0,1631 | 0,0458 | 0,0012 | 74 | |||
|
31
|
26 | 1 | 1 | 1 | 0,9986 | 0,9938 | 0,9442 | 0,6417 | 0,4620 | 0,2244 | 0,0715 | 0,0024 | 73 | |||
|
32
|
27 | 1 | 1 | 1 | 0,9994 | 0,9969 | 0,9658 | 0,7224 | 0,5516 | 0,2964 | 0,1066 | 0,0046 | 72 | |||
|
33
|
28 | 1 | 1 | 1 | 0,9997 | 0,9985 | 0,9800 | 0,7925 | 0,6379 | 0,3768 | 0,1524 | 0,0084 | 71 | |||
|
34
|
29 | 1 | 1 | 1 | 0,9999 | 0,9993 | 0,9888 | 0,8505 | 0,7172 | 0,4623 | 0,2093 | 0,0148 | 70 | |||
|
35
|
30 | 1 | 1 | 1 | 1 | 0,9997 | 0,9939 | 0,8962 | 0,7866 | 0,5491 | 0,2766 | 0,0248 | 69 | |||
|
36
|
31 | 1 | 1 | 1 | 1 | 0,9999 | 0,9969 | 0,9307 | 0,8446 | 0,6331 | 0,3525 | 0,0398 | 68 | |||
|
37
|
32 | 1 | 1 | 1 | 1 | 1 | 0,9984 | 0,9554 | 0,8909 | 0,7107 | 0,4344 | 0,0615 | 67 | |||
|
38
|
33 | 1 | 1 | 1 | 1 | 1 | 0,9993 | 0,9724 | 0,9261 | 0,7793 | 0,5188 | 0,0913 | 66 | |||
|
39
|
34 | 1 | 1 | 1 | 1 | 1 | 0,9997 | 0,9836 | 0,9518 | 0,8371 | 0,6019 | 0,1303 | 65 | |||
|
40
|
35 | 1 | 1 | 1 | 1 | 1 | 0,9999 | 0,9906 | 0,9697 | 0,8839 | 0,6803 | 0,1795 | 64 | |||
|
41
|
36 | 1 | 1 | 1 | 1 | 1 | 0,9999 | 0,9948 | 0,9817 | 0,9201 | 0,7511 | 0,2386 | 63 | |||
|
42
|
37 | 1 | 1 | 1 | 1 | 1 | 1,0000 | 0,9973 | 0,9893 | 0,9470 | 0,8123 | 0,3068 | 62 | |||
|
43
|
38 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9986 | 0,9940 | 0,9660 | 0,8630 | 0,3822 | 61 | |||
|
44
|
39 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9993 | 0,9968 | 0,9790 | 0,9034 | 0,4621 | 60 | |||
|
45
|
40 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9997 | 0,9983 | 0,9875 | 0,9341 | 0,5433 | 59 | |||
|
46
|
41 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9999 | 0,9992 | 0,9928 | 0,9566 | 0,6225 | 58 | |||
|
47
|
42 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9999 | 0,9996 | 0,9960 | 0,9724 | 0,6967 | 57 | |||
|
48
|
43 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9998 | 0,9979 | 0,9831 | 0,7635 | 56 | |||
|
49
|
44 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9999 | 0,9989 | 0,9900 | 0,8211 | 55 | |||
|
50
|
45 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9995 | 0,9943 | 0,8689 | 54 | |||
|
51
|
46 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9997 | 0,9969 | 0,9070 | 53 | |||
|
52
|
47 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9999 | 0,9983 | 0,9362 | 52 | |||
|
53
|
48 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9999 | 0,9991 | 0,9577 | 51 | |||
|
54
|
49 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9996 | 0,9729 | 50 | |||
|
55
|
50 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9998 | 0,9832 | 49 | |||
|
56
|
51 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9999 | 0,9900 | 48 | |||
|
57
|
52 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9942 | 47 | |||
|
58
|
53 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0,9968 | 46 | |||
|
59
|
n | k | 0,95 | 0,93 | 0,9 | 0,85 | 5/6 | 0,8 | 0,75 | 0,73 | 0,7 | 2/3 | 0,6 | k | n | |
|
60
|
||||||||||||||||
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
a)
(1)
(2)
2nd  DISTR
DISTR  B:binomcdf.
B:binomcdf.
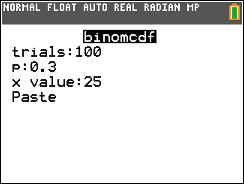 Abb. 1: Eingetragene Daten
Abb. 1: Eingetragene Daten
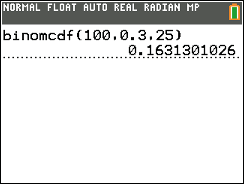 Abb. 2: Ergebnis
Abb. 2: Ergebnis
(3)
Wahrscheinlichkeit für eine Abweichung zum Erwartungswert
In dieser Teilaufgabe sollst du die Wahrscheinlichkeit dafür berechnen, dass sich die Anzahl der Jugendlichen, die Freundschaftsbuch nutzen, um maximal den Wert  vom Erwartungswert unterscheidet. Bestimme also zunächst den Erwartungswert. Da in dieser Aufgabe die Wahrscheinlichkeit, dass ein Jugendlicher Freundschaftsbuch nutzt, konstant bleibt, berechnet sich der Erwartungswert wie folgt:
vom Erwartungswert unterscheidet. Bestimme also zunächst den Erwartungswert. Da in dieser Aufgabe die Wahrscheinlichkeit, dass ein Jugendlicher Freundschaftsbuch nutzt, konstant bleibt, berechnet sich der Erwartungswert wie folgt:
 Da in dieser Aufgabe die Wahrscheinlichkeit bei
Da in dieser Aufgabe die Wahrscheinlichkeit bei  liegt und insgesamt
liegt und insgesamt  Jugendliche befragt werden, liegt der Erwartungswert bei
Jugendliche befragt werden, liegt der Erwartungswert bei
![\(\begin{array}[t]{rll}
E(X)&=& p \cdot n \\[5pt]
&=& 0,3 \cdot 100 \\[5pt]
&=&30
\end{array}\)](https://www.schullv.de/resources/formulas/3d5b0f53f8fa51b8d75cbd0a4faa87e99d1ddabfc842dd5f2d0ea5a94788db57_light.svg) Deshalb ist zu erwarten, dass von
Deshalb ist zu erwarten, dass von  befragten Jugendlichen
befragten Jugendlichen  Jugendliche Freundschaftsbuch nutzen. Somit lautet die gesuchte Wahrscheinlichkeit
Jugendliche Freundschaftsbuch nutzen. Somit lautet die gesuchte Wahrscheinlichkeit  , dies gibt also die Wahrscheinlichkeit dafür an, dass die Anzahl der Jugendlichen, die Freundschaftsbuch nutzen mindestens
, dies gibt also die Wahrscheinlichkeit dafür an, dass die Anzahl der Jugendlichen, die Freundschaftsbuch nutzen mindestens  und höchstens
und höchstens  beträgt.
beträgt.
 Lösungsweg A: Tabelle
Die Wahrscheinlichkeiten kannst du der Tabelle für die kumulierte Binomialverteilung entnehmen.
Die Wahrscheinlichkeit dafür, dass mindestens 25 und höchstens 35 Jugendliche Freundschaftsbuch nutzen, beträgt
Lösungsweg A: Tabelle
Die Wahrscheinlichkeiten kannst du der Tabelle für die kumulierte Binomialverteilung entnehmen.
Die Wahrscheinlichkeit dafür, dass mindestens 25 und höchstens 35 Jugendliche Freundschaftsbuch nutzen, beträgt  .
.
 Lösungsweg B: GTR
Die Wahrscheinlichkeiten kannst du nun wie oben mittels dem binomcdf-Befehl deines GTR bestimmen.
Die Wahrscheinlichkeit dafür, dass mindestens 25 und höchstens 35 Jugendliche Freundschaftsbuch nutzen, beträgt somit
Lösungsweg B: GTR
Die Wahrscheinlichkeiten kannst du nun wie oben mittels dem binomcdf-Befehl deines GTR bestimmen.
Die Wahrscheinlichkeit dafür, dass mindestens 25 und höchstens 35 Jugendliche Freundschaftsbuch nutzen, beträgt somit  .
.
b)
c)
(1)
(2)
(3)
(4)
d)
(1)
Der Ablehnungsbereich hat daher die Form
(2)
(3)
(4)
(5)
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
a)
(1)
(2)
2nd  DISTR
DISTR  B:binomcdf.
B:binomcdf.
 Abb. 1: Eingetragene Daten
Abb. 1: Eingetragene Daten
 Abb. 2: Ergebnis
Abb. 2: Ergebnis
(3)
Wahrscheinlichkeit für eine Abweichung zum Erwartungswert
In dieser Teilaufgabe sollst du die Wahrscheinlichkeit dafür berechnen, dass sich die Anzahl der Jugendlichen, die Freundschaftsbuch nutzen, um maximal den Wert  vom Erwartungswert unterscheidet. Bestimme also zunächst den Erwartungswert. Da in dieser Aufgabe die Wahrscheinlichkeit, dass ein Jugendlicher Freundschaftsbuch nutzt, konstant bleibt, berechnet sich der Erwartungswert wie folgt:
vom Erwartungswert unterscheidet. Bestimme also zunächst den Erwartungswert. Da in dieser Aufgabe die Wahrscheinlichkeit, dass ein Jugendlicher Freundschaftsbuch nutzt, konstant bleibt, berechnet sich der Erwartungswert wie folgt:
 Da in dieser Aufgabe die Wahrscheinlichkeit bei
Da in dieser Aufgabe die Wahrscheinlichkeit bei  liegt und insgesamt
liegt und insgesamt  Jugendliche befragt werden, liegt der Erwartungswert bei
Jugendliche befragt werden, liegt der Erwartungswert bei
![\(\begin{array}[t]{rll}
E(X)&=& p \cdot n \\[5pt]
&=& 0,3 \cdot 100 \\[5pt]
&=&30
\end{array}\)](https://www.schullv.de/resources/formulas/a1f180083ad3457beba49534309f238b4dbef513f49338ab1416ab29d039f69b_light.svg) Deshalb ist zu erwarten, dass von
Deshalb ist zu erwarten, dass von  befragten Jugendlichen
befragten Jugendlichen  Jugendliche Freundschaftsbuch nutzen. Somit lautet die gesuchte Wahrscheinlichkeit
Jugendliche Freundschaftsbuch nutzen. Somit lautet die gesuchte Wahrscheinlichkeit  , dies gibt also die Wahrscheinlichkeit dafür an, dass die Anzahl der Jugendlichen, die Freundschaftsbuch nutzen mindestens
, dies gibt also die Wahrscheinlichkeit dafür an, dass die Anzahl der Jugendlichen, die Freundschaftsbuch nutzen mindestens  und höchstens
und höchstens  beträgt.
beträgt.
 Lösungsweg A: Tabelle
Die Wahrscheinlichkeiten kannst du der Tabelle für die kumulierte Binomialverteilung entnehmen.
Die Wahrscheinlichkeit dafür, dass mindestens 25 und höchstens 35 Jugendliche Freundschaftsbuch nutzen, beträgt
Lösungsweg A: Tabelle
Die Wahrscheinlichkeiten kannst du der Tabelle für die kumulierte Binomialverteilung entnehmen.
Die Wahrscheinlichkeit dafür, dass mindestens 25 und höchstens 35 Jugendliche Freundschaftsbuch nutzen, beträgt  .
.
 Lösungsweg B: GTR
Die Wahrscheinlichkeiten kannst du nun wie oben mittels dem binomcdf-Befehl deines GTR bestimmen.
Die Wahrscheinlichkeit dafür, dass mindestens 25 und höchstens 35 Jugendliche Freundschaftsbuch nutzen, beträgt somit
Lösungsweg B: GTR
Die Wahrscheinlichkeiten kannst du nun wie oben mittels dem binomcdf-Befehl deines GTR bestimmen.
Die Wahrscheinlichkeit dafür, dass mindestens 25 und höchstens 35 Jugendliche Freundschaftsbuch nutzen, beträgt somit  .
.
b)
c)
(1)
(2)
(3)
(4)
d)
(1)
Der Ablehnungsbereich hat daher die Form
(2)
(3)
(4)
(5)
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
a)
(1)
(2)
OPTN  F5:STAT
F5:STAT  F3:DIST
F3:DIST  F5:BINOMIAL
F5:BINOMIAL  F2:Bcd.
F2:Bcd.
 Abb. 1: Ergebnis Teil 1
Abb. 1: Ergebnis Teil 1
 Abb. 2: Ergebnis Teil 2
Abb. 2: Ergebnis Teil 2
(3)
Wahrscheinlichkeit für eine Abweichung zum Erwartungswert
In dieser Teilaufgabe sollst du die Wahrscheinlichkeit dafür berechnen, dass sich die Anzahl der Jugendlichen, die Freundschaftsbuch nutzen, um maximal den Wert  vom Erwartungswert unterscheidet. Bestimme also zunächst den Erwartungswert. Da in dieser Aufgabe die Wahrscheinlichkeit, dass ein Jugendlicher Freundschaftsbuch nutzt, konstant bleibt, berechnet sich der Erwartungswert wie folgt:
vom Erwartungswert unterscheidet. Bestimme also zunächst den Erwartungswert. Da in dieser Aufgabe die Wahrscheinlichkeit, dass ein Jugendlicher Freundschaftsbuch nutzt, konstant bleibt, berechnet sich der Erwartungswert wie folgt:
 Da in dieser Aufgabe die Wahrscheinlichkeit bei
Da in dieser Aufgabe die Wahrscheinlichkeit bei  liegt und insgesamt
liegt und insgesamt  Jugendliche befragt werden, liegt der Erwartungswert bei
Jugendliche befragt werden, liegt der Erwartungswert bei
![\(\begin{array}[t]{rll}
E(X)&=& p \cdot n \\[5pt]
&=& 0,3 \cdot 100 \\[5pt]
&=&30
\end{array}\)](https://www.schullv.de/resources/formulas/a1f180083ad3457beba49534309f238b4dbef513f49338ab1416ab29d039f69b_light.svg) Deshalb ist zu erwarten, dass von
Deshalb ist zu erwarten, dass von  befragten Jugendlichen
befragten Jugendlichen  Jugendliche Freundschaftsbuch nutzen. Somit lautet die gesuchte Wahrscheinlichkeit
Jugendliche Freundschaftsbuch nutzen. Somit lautet die gesuchte Wahrscheinlichkeit  , dies gibt also die Wahrscheinlichkeit dafür an, dass die Anzahl der Jugendlichen, die Freundschaftsbuch nutzen mindestens
, dies gibt also die Wahrscheinlichkeit dafür an, dass die Anzahl der Jugendlichen, die Freundschaftsbuch nutzen mindestens  und höchstens
und höchstens  beträgt.
beträgt.
 Lösungsweg A: Tabelle
Die Wahrscheinlichkeiten kannst du der Tabelle für die kumulierte Binomialverteilung entnehmen.
Die Wahrscheinlichkeit dafür, dass mindestens 25 und höchstens 35 Jugendliche Freundschaftsbuch nutzen, beträgt
Lösungsweg A: Tabelle
Die Wahrscheinlichkeiten kannst du der Tabelle für die kumulierte Binomialverteilung entnehmen.
Die Wahrscheinlichkeit dafür, dass mindestens 25 und höchstens 35 Jugendliche Freundschaftsbuch nutzen, beträgt  .
.
 Lösungsweg B: GTR
Die Wahrscheinlichkeiten kannst du nun wie oben mittels dem binomcdf-Befehl deines GTR bestimmen.
Die Wahrscheinlichkeit dafür, dass mindestens 25 und höchstens 35 Jugendliche Freundschaftsbuch nutzen, beträgt somit
Lösungsweg B: GTR
Die Wahrscheinlichkeiten kannst du nun wie oben mittels dem binomcdf-Befehl deines GTR bestimmen.
Die Wahrscheinlichkeit dafür, dass mindestens 25 und höchstens 35 Jugendliche Freundschaftsbuch nutzen, beträgt somit  .
.
b)
c)
(1)
(2)
(3)
(4)
d)
(1)
Der Ablehnungsbereich hat daher die Form
(2)
(3)
(4)
(5)