Teil A: Ohne Hilfsmittel
a)
Gegeben ist die Funktion  durch die Gleichung
durch die Gleichung


(1)
Bestimme die erste Ableitung.
 Zur Kontrolle:
Zur Kontrolle: 
Ohne Nachweis kann im Folgenden benutzt werden:
(2)
Weise nach, dass ein lokaler Hochpunkt existiert und gib die Koordinaten des Hochpunktes an.
(2 + 4 Punkte)
b)
Gegeben ist die Funktion  durch die Gleichung
durch die Gleichung


 In der Abbildung 1 ist der Graph der Funktion
In der Abbildung 1 ist der Graph der Funktion  dargestellt.
dargestellt.


Abbildung 1
(1)
Berechne den Inhalt der gefärbten Fläche. Die Nullstellen von  darfst du dabei in der Abbildung ablesen.
darfst du dabei in der Abbildung ablesen.
(2)
Der Graph der Funktion  schließt mit der
schließt mit der  -Achse eine Fläche ein. Der Inhalt dieser Fläche soll durch einen Term beschrieben werden.
-Achse eine Fläche ein. Der Inhalt dieser Fläche soll durch einen Term beschrieben werden.
Entscheide für jeden der folgenden Terme und
und  , ob er dazu geeignet ist oder nicht.
, ob er dazu geeignet ist oder nicht.





Entscheide für jeden der folgenden Terme
(3 + 3 Punkte)
c)
Die Punkte 

 sind Eckpunkte des Dreiecks
sind Eckpunkte des Dreiecks  mit
mit 
 und
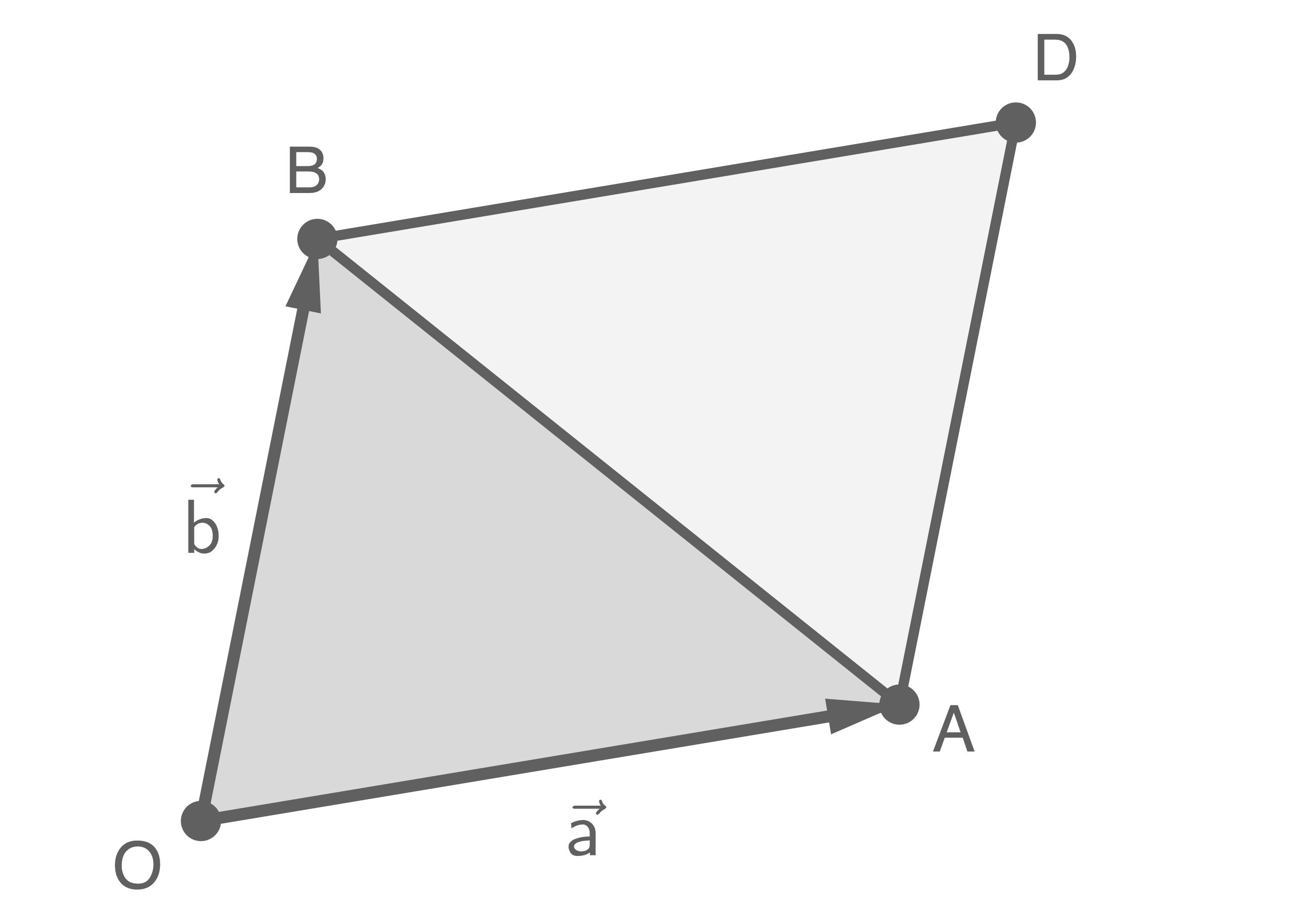
und  In der Abbildung 2 wird das Dreieck
In der Abbildung 2 wird das Dreieck  mithilfe eines Punktes
mithilfe eines Punktes  zu einem Parallelogramm
zu einem Parallelogramm  ergänzt. Es ist
ergänzt. Es ist  und
und 
 besteht aus den Punkten des Randes und allen Punkten im Inneren.
besteht aus den Punkten des Randes und allen Punkten im Inneren.
Das Dreieck ist bestimmt durch die Gleichung
ist bestimmt durch die Gleichung






Abbildung 2 (nicht maßstabsgerechte Skizze)
(1)
Gib die Koordinaten des Punktes  an.
an.
Das Dreieck Das Dreieck
(2)
Prüfe, ob der Punkt  mit
mit  ein Punkt des Dreiecks ist.
ein Punkt des Dreiecks ist.
(2 + 4 Punkte)
d)
(1)
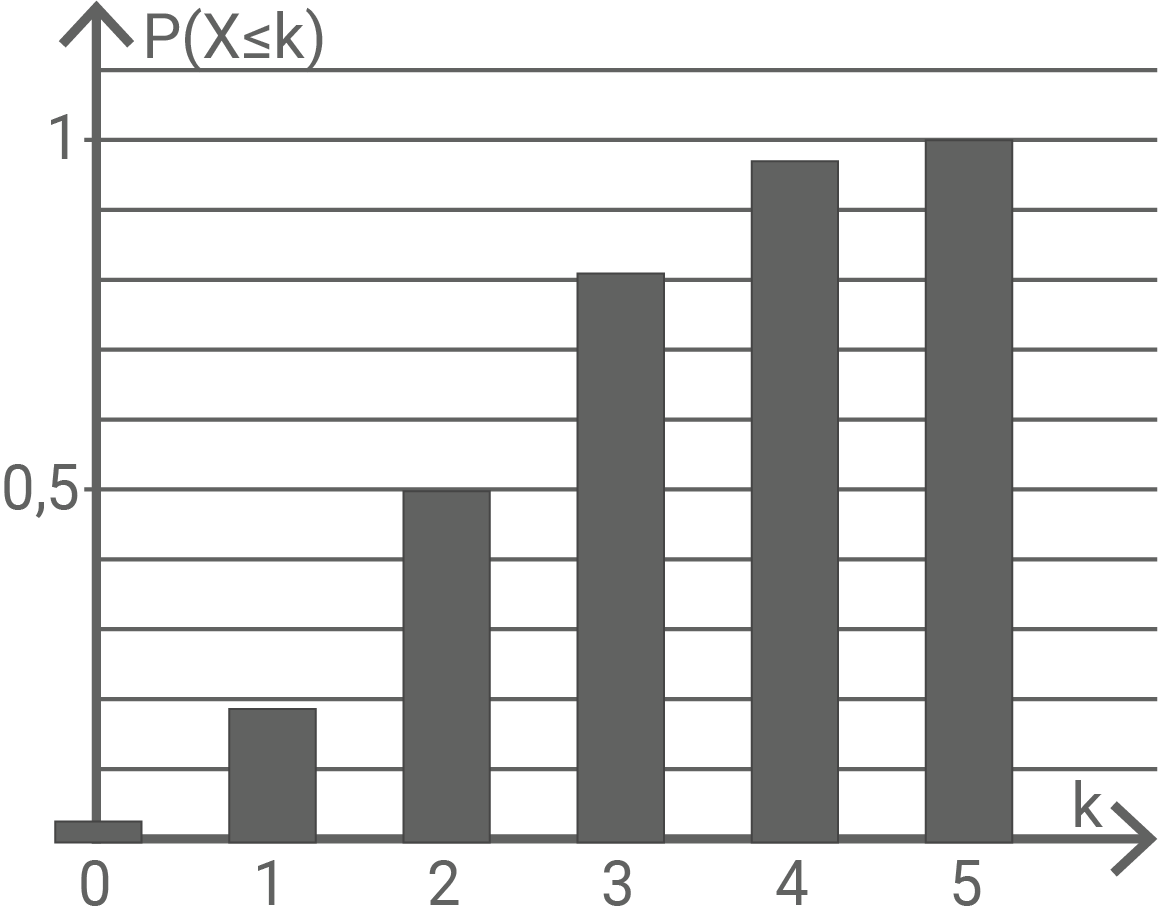
Die Abbildung 3 zeigt kumulierte Werte der Wahrscheinlichkeitsverteilung einer binomialverteilten Zufallsgröße  mit dem Parameter
mit dem Parameter 
Zeichne in die Abbildung 3 den zu gehörenden Wert ein und ermittle näherungsweise die Wahrscheinlichkeit dafür, dass
gehörenden Wert ein und ermittle näherungsweise die Wahrscheinlichkeit dafür, dass  den Wert
den Wert  annimmt.
annimmt.
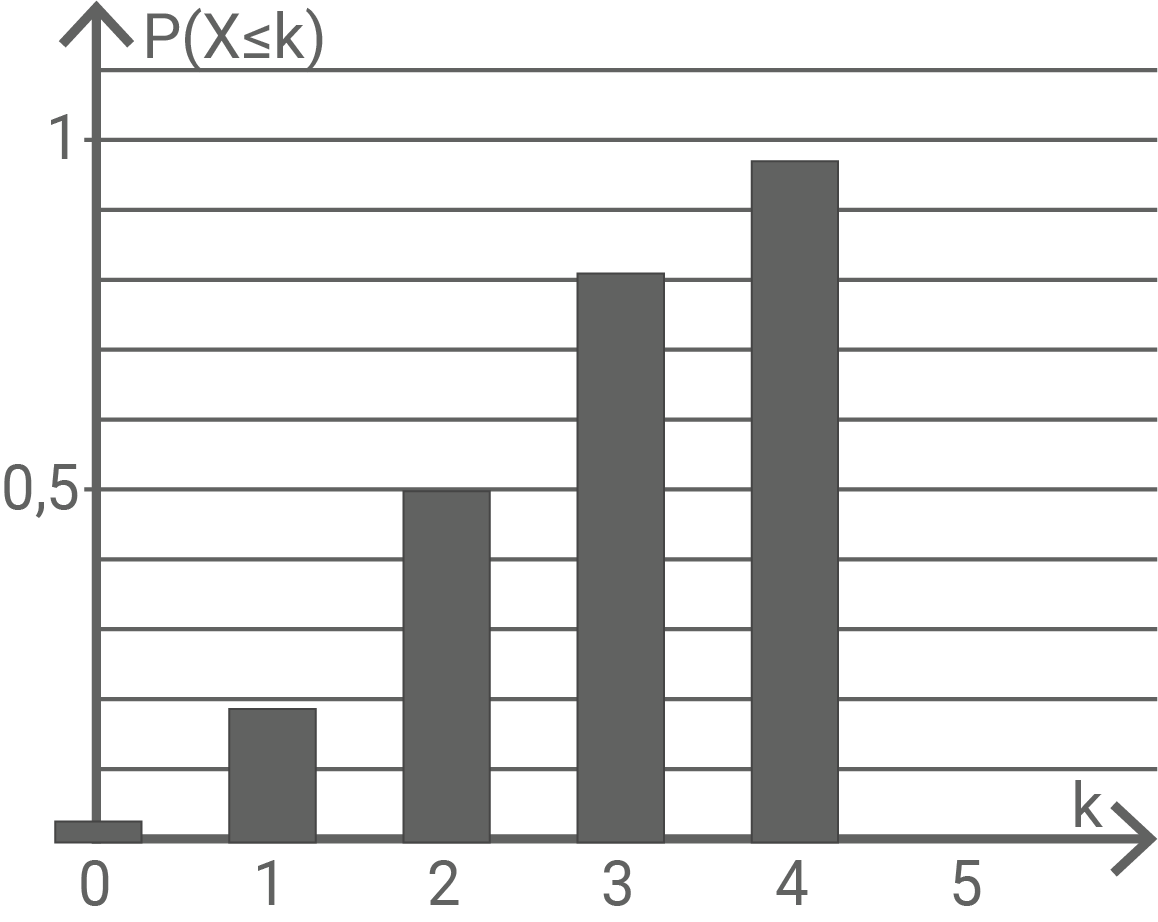
Zeichne in die Abbildung 3 den zu

Abbildung 3
(2)
Betrachtet wird eine binomialverteilte Zufallsgröße  mit den Parametern
mit den Parametern  und
und  Es gilt:
Es gilt: 
Berechne den Wert von
Berechne den Wert von
(3 + 3 Punkte)
a)
(1)
Mit der Produkt- und Kettenregel folgt:
(2)
1. Schritt: Notwendiges Kriterium für Extremstellen anwenden
![\( \begin{array}[t]{rll}
f](https://www.schullv.de/resources/formulas/6a4b96ec394c818402fc3f2dcd15c139a5693f3a28454c628584dc78ed314231_light.svg) Da stets
Da stets  gilt, folgt mit dem Satz vom Nullprodukt
gilt, folgt mit dem Satz vom Nullprodukt  und
und 
![\( \begin{array}[t]{rll}
-\frac{1}{2}x_2 +1 &=& 0 &\quad \scriptsize \mid\; -1 \\[5pt]
-\frac{1}{2}x_2 &=& -1 &\quad \scriptsize \mid\; \cdot (-2) \\[5pt]
x_2 &=& 2
\end{array}\)](https://www.schullv.de/resources/formulas/51e329dbe4a3f0b32de10a99fd6f882163de7054c6b1ab04222843b3efcdd090_light.svg) 2. Schritt: Hinreichendes Kriterium für Extremstellen anwenden
2. Schritt: Hinreichendes Kriterium für Extremstellen anwenden
![\( \begin{array}[t]{rll}
f](https://www.schullv.de/resources/formulas/0569ddb3508f218b1a202f5d22002537f3d7881d507e3cd0f04146af48fbf377_light.svg) An der Stelle
An der Stelle  besitzt der Graph von
besitzt der Graph von  also einen lokalen Hochpunkt.
3. Schritt:
also einen lokalen Hochpunkt.
3. Schritt:  -Koordinate berechnen
-Koordinate berechnen
![\( \begin{array}[t]{rll}
f(2)&=& \frac{1}{2}\cdot 2^2 \cdot \mathrm e^{-2+2} \\[5pt]
&=& 2
\end{array}\)](https://www.schullv.de/resources/formulas/bd015724252efcbb4ccf5149eef34c248822292f6ef250f7a4cac61028e822e7_light.svg) Die Koordinaten des lokalen Hochpunkts lauten also
Die Koordinaten des lokalen Hochpunkts lauten also 
b)
(1)
Die Nullstellen von  werden aus der Abbildung abgelesen und lauten:
werden aus der Abbildung abgelesen und lauten:

 Der Inhalt der schraffierten Fläche beträgt
Der Inhalt der schraffierten Fläche beträgt 
(2)
Die Fläche, die der Graph von  mit der
mit der  -Achse einschließt besteht aus drei Teilflächen. Zwei der Teilflächen liegen unterhalb der
-Achse einschließt besteht aus drei Teilflächen. Zwei der Teilflächen liegen unterhalb der  -Achse. Das zugehörige Integral hat einen negativen Wert. Es muss also der Betrag der jeweiligen Integrale zur Berechnung verwendet werden.
-Achse. Das zugehörige Integral hat einen negativen Wert. Es muss also der Betrag der jeweiligen Integrale zur Berechnung verwendet werden.
Das wird in Term und
und  berücksichtigt, aber nicht in Term
berücksichtigt, aber nicht in Term  da dort lediglich über das Gesamtergebnis der Betrag gebildet wird.
Term
da dort lediglich über das Gesamtergebnis der Betrag gebildet wird.
Term  und
und  sind zur Beschreibung des Flächeninhalts geeignet, Term
sind zur Beschreibung des Flächeninhalts geeignet, Term  ist nicht geeignet.
ist nicht geeignet.
Das wird in Term
c)
(1)
(2)
d)