Aufgabe 3
Aufgabenstellung
Für jede positive reelle Zahl  sind eine Funktion
sind eine Funktion  mit der Gleichung
mit der Gleichung
 ,
,  , und eine Funktion
, und eine Funktion  mit der Gleichung
mit der Gleichung
 ,
,  , gegeben.
, gegeben.
Die Graphen von und
und  sind in der Abbildung 1 dargestellt.
sind in der Abbildung 1 dargestellt.
 Abbildung 1
Es sei nun
Abbildung 1
Es sei nun  eine beliebige positive reelle Zahl.
eine beliebige positive reelle Zahl.
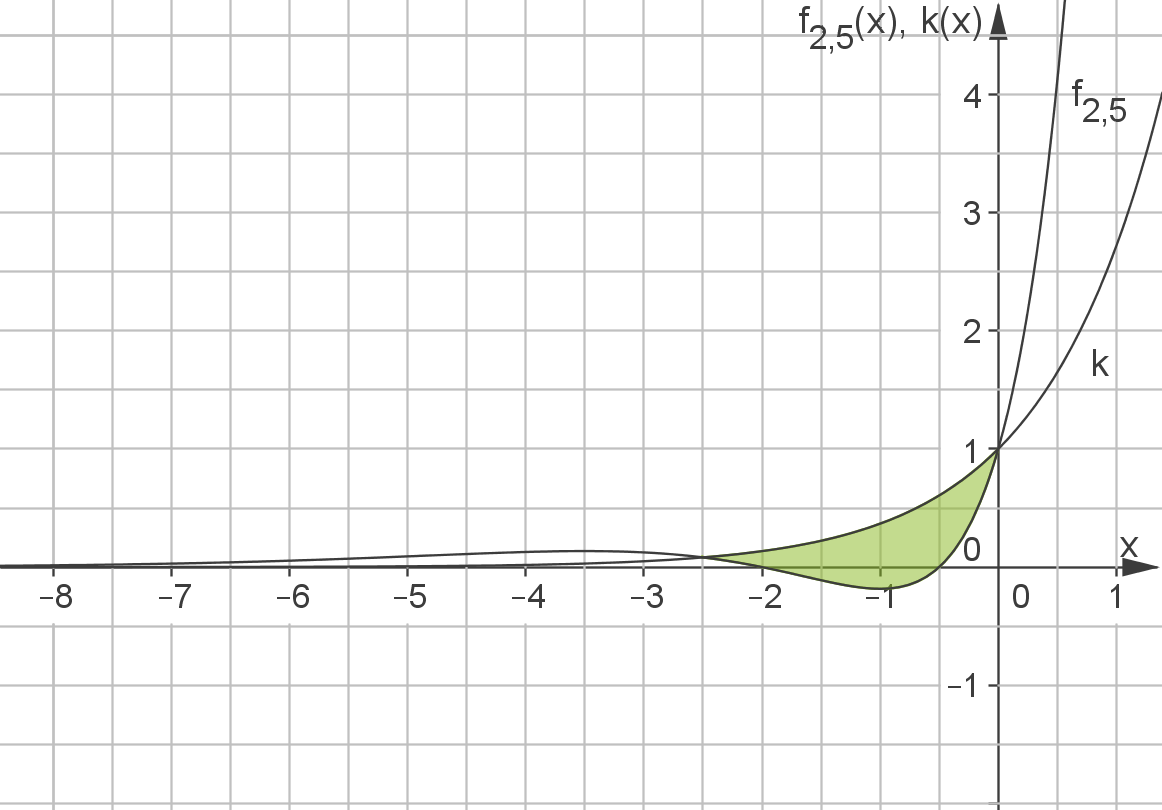 Abbildung 1
Abbildung 1
Die Graphen von
 Abbildung 1
Abbildung 1
a) (1) Ermittle das Intervall auf der  -Achse, für das der Graph der Funktion
-Achse, für das der Graph der Funktion  unterhalb der
unterhalb der  -Achse verläuft.
-Achse verläuft.
[Zur Kontrolle: Das gesuchte Intervall ist![\( ]-1-a;-1[\)](https://www.schullv.de/resources/formulas/31dc663b740091dc6eb536e781d8ab8ced390457b30397c696f8764b15063fa4_light.svg) .]
.]
[Zur Kontrolle: Das gesuchte Intervall ist
(5P)
(2) Zeige: Es gilt  für alle
für alle  .
.
(5P)
(3) Bestimme die Stellen, an denen die Funktion  ein lokales Maximum bzw. Minimum besitzt.
ein lokales Maximum bzw. Minimum besitzt.
(6P)
b) (1) Bestimme dasjenige  , für das die Funktion
, für das die Funktion  genau eine Nullstelle hat.
genau eine Nullstelle hat.
(5P)
(2) Berechne die zugehörige Nullstelle.
(3P)
c) Betrachte nun die Funktion  mit der Gleichung
mit der Gleichung  ,
,  , und die Funktion
, und die Funktion  mit der Gleichung
mit der Gleichung  ,
,  .
.
(1) Ermittle mit Hilfe eines Integrationsverfahrens eine Stammfunktion der Funktion  .
.
[Zur Kontrolle: Zum Beispiel ist die Funktion mit der Gleichung
mit der Gleichung
 eine Stammfunktion von
eine Stammfunktion von  .]
.]
[Zur Kontrolle: Zum Beispiel ist die Funktion
(6P)
(2) Berechne in Abhängigkeit von  den Inhalt
den Inhalt  der Fläche, die von den Graphen der Funktionen
der Fläche, die von den Graphen der Funktionen  und
und  eingeschlossen wird.
eingeschlossen wird.
[Zur Kontrolle: ]
]
[Zur Kontrolle:
(6P)
d) Für  erhält man die Funktion
erhält man die Funktion  mit der Gleichung
mit der Gleichung
 ,
,  .
.
(1) Ermittle mit Hilfe von c) (1) eine Stammfunktion der Funktion  .
.
[Zur Kontrolle: Zum Beispiel ist die Funktion mit der Gleichung
mit der Gleichung
 eine Stammfunktion von
eine Stammfunktion von  .]
.]
[Zur Kontrolle: Zum Beispiel ist die Funktion
(4P)
(2) Berechne den Inhalt der Fläche, die von dem Graphen der Funktion  und der
und der  -Achse eingeschlossen wird.
-Achse eingeschlossen wird.
[Zur Kontrolle: Der gesuchte Flächeninhalt beträgt ungefähr [FE]]
[FE]]
[Zur Kontrolle: Der gesuchte Flächeninhalt beträgt ungefähr
(6P)
(3) In der Abbildung 2 ist die Fläche eingefärbt, die von den Graphen der Funktionen  und
und  eingeschlossen wird.
eingeschlossen wird.
Die -Achse teilt diese Fläche.
-Achse teilt diese Fläche.
Berechne das Verhältnis der größeren zur kleineren Teilfläche.
Die
Berechne das Verhältnis der größeren zur kleineren Teilfläche.
(4P)
 Abbildung 1
Abbildung 1
a)(1)
 Gesuchtes Intervall ermitteln
Anhand von Abbildung 1 erkennst du, dass der Graph von
Gesuchtes Intervall ermitteln
Anhand von Abbildung 1 erkennst du, dass der Graph von  eine nach oben geöffnete Parabel ist. Da der Koeffizient von
eine nach oben geöffnete Parabel ist. Da der Koeffizient von  unabhängig von
unabhängig von  ist, ist auch
ist, ist auch  eine nach oben geöffnete Parabel. Somit musst du noch die Nullstellen der Funktionsgleichung von
eine nach oben geöffnete Parabel. Somit musst du noch die Nullstellen der Funktionsgleichung von  bestimmen, welche dir die Grenzen des gesuchten Intervalls liefern.
Setze den Funktionsterm von
bestimmen, welche dir die Grenzen des gesuchten Intervalls liefern.
Setze den Funktionsterm von  gleich Null, um mögliche Nullstellen zu ermitteln:
gleich Null, um mögliche Nullstellen zu ermitteln:
![\(\begin{array}[t]{rll}
p_a(x)\stackrel{!}=& 0
\\[5pt]
x^2 + (a+2) \cdot x +a +1=&0
\end{array}\)](https://www.schullv.de/resources/formulas/d5026860141199450f7c8ddce533d8c0c5842a59a8297062275164c7baeac6fd_light.svg) Hier kannst du entweder die PQ-Formel oder die Mitternachtsformel verwenden, um die Nullstellen zu bestimmen.
Hier kannst du entweder die PQ-Formel oder die Mitternachtsformel verwenden, um die Nullstellen zu bestimmen.
 Lösungsweg A: PQ-Formel
Du kannst
Lösungsweg A: PQ-Formel
Du kannst  und
und  direkt ablesen. Damit erhältst du die Nullstellen:
direkt ablesen. Damit erhältst du die Nullstellen:
![\(\begin{array}{rll}
x_{1,2} =& - \dfrac{a+2}{2} \pm \sqrt{\left( {\frac{a+2}{2}} \right)^2 - \left(a +1\right)} &\mid\; 1. \text{ Binomische Formel}
\\[5pt]
x_{1,2} =& -\dfrac{a}{2}-1 \pm \sqrt {\frac{a^2 + 4 \cdot a +4}{4} - \left(\frac{4 \cdot a+4}{4}\right)}\\[5pt]
x_{1,2} =& -\dfrac{a}{2}-1 \pm \sqrt {\frac{a^2 + 4 \cdot a +4 -4 \cdot a -4}{4}}\\[5pt]
x_{1,2} =& -\dfrac{a}{2}-1 \pm \sqrt {\frac{a^2}{4}}
\\[5pt]
x_{1,2} =& -\dfrac{a}{2}-1 \pm \dfrac{a}{2}
\end{array}\)](https://www.schullv.de/resources/formulas/4b7248d789aceabcf11b6f2868a53f768d87ebf8d8412f47540d059052385edf_light.svg) Die Nullstellen der Funktion
Die Nullstellen der Funktion  sind also
sind also  und
und  .
.
 Lösungsweg B: Mitternachtsformel
Du kannst die Mitternachtsformel hier direkt anwenden, wobei
Lösungsweg B: Mitternachtsformel
Du kannst die Mitternachtsformel hier direkt anwenden, wobei  ,
,  und
und  :
:
![\(\begin{array}[t]{rll}
x_{1,2} =& \dfrac{{ - (a+2) \pm \sqrt {(a+2)^2 - 4 \cdot 1 \cdot (a+1)} }}{{2\cdot 1}}\\[5pt]
x_{1,2} =&\dfrac{{ -a-2 \pm \sqrt {a^2 + 4 \cdot a +4 - 4 \cdot a -4} }}{{2}}\\[5pt]
x_{1,2} =& -\dfrac{a}{2}-1 \pm \dfrac{\sqrt{a^2}}{2} \\[5pt]
x_{1,2} =& -\dfrac{a}{2}-1 \pm \dfrac{a}{2}
\end{array}\)](https://www.schullv.de/resources/formulas/8a2cea6b9b55e1eeb5178190d95b35622f2af1031f422c952b0c47d7171414e5_light.svg) Die Nullstellen der Funktion
Die Nullstellen der Funktion  sind also
sind also  und
und  .
Da die Nullstellen nicht mehr im gesuchten Intervall
.
Da die Nullstellen nicht mehr im gesuchten Intervall  liegen (der Graph soll unterhalb der
liegen (der Graph soll unterhalb der  -Achse liegen), folgt für
-Achse liegen), folgt für  :
:
![\(I=\left] -1-a; -1 \right[\)](https://www.schullv.de/resources/formulas/b3768a59a7c8974efc5ead52f5dce439a01dffbf66a47238fb1f8d629f3c3469_light.svg) .
a)(2)
.
a)(2)
 Gleichung für
Gleichung für  zeigen
Leite
zeigen
Leite  mit Hilfe der Produktregel ab und forme um, damit du die gesuchte Form von
mit Hilfe der Produktregel ab und forme um, damit du die gesuchte Form von  erhältst.
erhältst.
![\(\begin{array}[t]{rll}
f‘_a(x)=&\left( 2 \cdot x +a \right) \cdot \mathrm e^x + \left( x^2 + a \cdot x +1 \right) \cdot \mathrm e^x &\mid\; \mathrm e^x \text{ ausklammern}
\\[5pt]
=&\left( 2 \cdot x +a + x^2 + a \cdot x +1\right) \cdot \mathrm e^x
\\[5pt]
=&\left( x^2 + (a+2) \cdot x +a+1\right) \cdot \mathrm e^x
\\[5pt]
=& p_a(x) \cdot \mathrm e^x
\end{array}\)](https://www.schullv.de/resources/formulas/f00197b2fc6dfe12ca6c3bad5f7ee42b20ebcedadfd577621097e9ecc7afb596_light.svg) Damit hast du die Behauptung gezeigt.
a)(3)
Damit hast du die Behauptung gezeigt.
a)(3)
 Lokale Extremstellen von
Lokale Extremstellen von  bestimmen
Gesucht sind die Extremstellen der Funktion
bestimmen
Gesucht sind die Extremstellen der Funktion  . Um eine Extremstelle
. Um eine Extremstelle  einer Funktion
einer Funktion  zu bestimmen, musst du Folgendes überprüfen:
zu bestimmen, musst du Folgendes überprüfen:
 aus den beiden vorangegangenen Aufgabenteilen.
1. Schritt: Notwendige Bedingung überprüfen
Setze den Funktionsterm der
aus den beiden vorangegangenen Aufgabenteilen.
1. Schritt: Notwendige Bedingung überprüfen
Setze den Funktionsterm der  Ableitung
Ableitung  gleich Null, um mögliche Nullstellen zu bestimmen.
gleich Null, um mögliche Nullstellen zu bestimmen.  hast du dabei schon im Aufgabenteil (2) bestimmt.
hast du dabei schon im Aufgabenteil (2) bestimmt.
![\(\begin{array}[t]{rll}
f_a‘(x) \stackrel{!}=&0 &\mid\; f_a‘ \text{ aus Aufgabenteil (2) einsetzen}
\\[5pt]
p_a(x) \cdot \mathrm e^x=&0
\end{array}\)](https://www.schullv.de/resources/formulas/80a612b25df4edd659a130a51de9ebe119ad5bd58e9b5d76596d420970e56201_light.svg) Der Satz vom Nullprodukt liefert dir nun, dass das Produkt genau dann gleich Null ist, wenn einer der beiden Faktoren gleich Null ist. Da
Der Satz vom Nullprodukt liefert dir nun, dass das Produkt genau dann gleich Null ist, wenn einer der beiden Faktoren gleich Null ist. Da  ist, betrachte nur noch
ist, betrachte nur noch  :
Aus dem Aufgabenteil (1) kennst du die Nullstellen von
:
Aus dem Aufgabenteil (1) kennst du die Nullstellen von  bereits:
bereits:
 und
und  .
2. Schritt: 2. Ableitung von
.
2. Schritt: 2. Ableitung von  ermitteln
Die Funktionsgleichung von
ermitteln
Die Funktionsgleichung von  ist
ist  . Mit der Produktregel erhältst du:
. Mit der Produktregel erhältst du:
![\(\begin{array}[t]{rll}
f_a‘‘(x) =& \left( 2 \cdot x +a +2 \right) \cdot \mathrm e^x + \left( x^2 + (a+2) \cdot x +a+1 \right) \cdot \mathrm e^x &\mid\; \mathrm e^x \text{ ausklammern}
\\[5pt]
=&\left( 2 \cdot x +a +2 + x^2 + (a+2) \cdot x +a+1 \right) \cdot \mathrm e^x
\\[5pt]
=&\left(x^2 + (a+4) \cdot x +2 \cdot a+3 \right) \cdot \mathrm e^x
\end{array}\)](https://www.schullv.de/resources/formulas/35610c4c958e3dbe1e639e6b46a0f1085d4ae765fe97f2d5a6d025fdb3e3c407_light.svg) 3. Schritt: Hinreichende Bedingung überprüfen
Überprüfe nun das Vorzeichen von
3. Schritt: Hinreichende Bedingung überprüfen
Überprüfe nun das Vorzeichen von  an den gefundenen Nullstellen
an den gefundenen Nullstellen  und
und  . Daraus kannst du die Art der Extremstelle folgern.
. Daraus kannst du die Art der Extremstelle folgern.
![\(\begin{array}[t]{rll}
f_a‘‘(x_1)=&f_a‘‘(-a-1)=\left((-a-1)^2 + (a+4) \cdot (-a-1) +2 \cdot a+3 \right) \cdot \mathrm e^{(-a-1)}
\\[5pt]
=&\left(a^2 + 2 \cdot a +1 - a^2 -a -4 \cdot a-4+2 \cdot a+3 \right) \cdot \mathrm e^{(-a-1)}
\\[5pt]
=&\left(-a \right) \cdot \mathrm e^{(-a-1)} \lt 0
\end{array}\)](https://www.schullv.de/resources/formulas/561ee8db9957c9913ad120b72cccde91a3c319cb63de7e09dbc6a0c9c72ef3a8_light.svg)
![\(\begin{array}[t]{rll}
f_a‘‘(x_2)=&f_a‘‘(-1)=\left((-1)^2 + (a+4) \cdot (-1) +2a+3 \right) \cdot \mathrm e^{(-1)}
\\[5pt]
=&\left(1 + -a -4 +2 \cdot a+3 \right) \cdot \mathrm e^{(-1)}
\\[5pt]
=&a \cdot \mathrm e^{(-1)} \gt 0
\end{array}\)](https://www.schullv.de/resources/formulas/34c3ce329d49d29c2a61f6f83c1915a37d719292cca8f7a4c7ec45d684297550_light.svg) Damit hat die Funktion an der Stelle
Damit hat die Funktion an der Stelle  ein lokales Maximum und an der Stelle
ein lokales Maximum und an der Stelle  ein lokales Minimum.
ein lokales Minimum.
- Notwendige Bedingung:
- Hinreichende Bedingung:
Hochpunkt des Graphen von
an der Stelle
.
Tiefpunkt des Graphen von
an der Stelle
- Oder: Vorzeichen-Wechsel der ersten Ableitung:
Wert der ersten Ableitung vonvor der Stelle
positiv und nach
negativ
Hochpunkt des Graphen.
Wert der ersten Ableitung vonvor der Stelle
negativ und nach
positiv
Tiefpunkt des Graphen.
b)(1)
 Gesuchtes
Gesuchtes  ermitteln
Du sollst das
ermitteln
Du sollst das  ermitteln, für das
ermitteln, für das  genau eine Nullstelle hat. Bestimme dazu mit dem Satz vom Nullprodukt die Form einer Nullstelle von
genau eine Nullstelle hat. Bestimme dazu mit dem Satz vom Nullprodukt die Form einer Nullstelle von  . Nutze auch die PQ-Formel oder die Mitternachtsformel. Damit die Nullstelle eindeutig ist, muss die Diskriminante der Nullstelle gleich Null sein.
1. Schritt: Nullstellen von
. Nutze auch die PQ-Formel oder die Mitternachtsformel. Damit die Nullstelle eindeutig ist, muss die Diskriminante der Nullstelle gleich Null sein.
1. Schritt: Nullstellen von  bestimmen
Die Funktionsgleichung von
bestimmen
Die Funktionsgleichung von  lautet:
lautet:  .
Da
.
Da  ist, liefert dir der Satz vom Nullprodukt, dass du noch
ist, liefert dir der Satz vom Nullprodukt, dass du noch  betrachten musst:
betrachten musst:
 Hier kannst du entweder die PQ-Formel oder die Mitternachtsformel verwenden, um die Nullstellen zu bestimmen.
Hier kannst du entweder die PQ-Formel oder die Mitternachtsformel verwenden, um die Nullstellen zu bestimmen.
 Lösungsweg A: PQ-Formel
Du kannst
Lösungsweg A: PQ-Formel
Du kannst  und
und  direkt ablesen. Damit erhältst du die Nullstellen:
direkt ablesen. Damit erhältst du die Nullstellen:
![\(\begin{array}{rll}
x_{1,2} =& - \dfrac{a}{2} \pm \sqrt{\left( {\frac{a}{2}} \right)^2 - 1 }
\\[5pt]
x_{1,2} =& -\dfrac{a}{2} \pm \sqrt {\frac{a^2}{4} - 1}
\\[5pt]
x_{1,2} =& -\dfrac{a}{2} \pm \dfrac{\sqrt {a^2 -4}}{2}
\end{array}\)](https://www.schullv.de/resources/formulas/5ecade4d6673f1483bb139348ea27cfff0df22c052390f1a722137cac3ef8411_light.svg) Die Nullstellen der Funktion
Die Nullstellen der Funktion  sind also
sind also  und
und  .
.
 Lösungsweg B: Mitternachtsformel
Du kannst die Mitternachtsformel hier direkt anwenden, wobei
Lösungsweg B: Mitternachtsformel
Du kannst die Mitternachtsformel hier direkt anwenden, wobei  ,
,  und
und  :
:
![\(\begin{array}[t]{rll}
x_{1,2} =& \dfrac{{ - a \pm \sqrt {(a)^2 - 4 \cdot 1 \cdot (1)} }}{{2\cdot 1}}\\[5pt]
x_{1,2} =&- \dfrac{ a}{2}\pm \dfrac{\sqrt {a^2 -4} }{2}
\end{array}\)](https://www.schullv.de/resources/formulas/1b6cde641e16fb226fe78bb6a6c83f62cc6921976442df815c44a1b63e20db64_light.svg) Die Nullstellen der Funktion
Die Nullstellen der Funktion  sind also
sind also  und
und  .
2. Schritt:
.
2. Schritt:  bestimmen
Damit die Nullstelle nun eindeutig ist, musst du das
bestimmen
Damit die Nullstelle nun eindeutig ist, musst du das  bestimmen, für das der Wurzelterm der Nullstelle gleich Null ist:
bestimmen, für das der Wurzelterm der Nullstelle gleich Null ist:
![\(\begin{array}[t]{rll}
\dfrac{\sqrt {a^2 -4} }{2}\stackrel{!}{=}& 0&\scriptsize \mid\; (\;)^2
\\[5pt]
\dfrac{a^2 -4 }{4}=& 0&\scriptsize \mid\; \cdot 4
\\[5pt]
a^2 -4 =& 0&\scriptsize \mid\; +4
\\[5pt]
a^2 =& 4&\scriptsize \mid\; \sqrt{\;}
\\[5pt]
|\, a\,| =& 2
\end{array}\)](https://www.schullv.de/resources/formulas/38fc8f1a81ffa947a78396bd52375eca9b372c874ca19300d01d58a970873910_light.svg) Da in der Aufgabenstellung
Da in der Aufgabenstellung  gefordert ist, erhältst du:
Für
gefordert ist, erhältst du:
Für  besitzt
besitzt  genau eine Nullstelle.
b)(2)
genau eine Nullstelle.
b)(2)
 Berechnen der zugehörigen Nullstelle
Du kennst aus dem vorigen Aufgabenteil bereits die Form einer Nullstelle von
Berechnen der zugehörigen Nullstelle
Du kennst aus dem vorigen Aufgabenteil bereits die Form einer Nullstelle von  in Abhängigkeit von
in Abhängigkeit von  . Setze nun das ermittelte
. Setze nun das ermittelte  ein, um die gesuchte Nullstelle zu berechnen.
ein, um die gesuchte Nullstelle zu berechnen.
![\(\begin{array}[t]{rll}
x_{1,2} =&- \dfrac{ a}{2}\pm \dfrac{\sqrt {a^2 -4} }{2}&\scriptsize \mid\; a=2 \text{ einsetzen}
\\[5pt]
x_{1,2} =&- \dfrac{ 2}{2}\pm \dfrac{\sqrt {2^2 -4} }{2} &\scriptsize \mid\; \dfrac{\sqrt {2^2 -4} }{2}=0
\\[5pt]
x_1 =&- 1
\end{array}\)](https://www.schullv.de/resources/formulas/0b9848bcecbdc0c9b260de5f68988868da600fd58372aaad5b6941c592e9c4f5_light.svg) Die zugehörige Nullstelle lautet
Die zugehörige Nullstelle lautet  .
.
c)(1)
 Stammfunktion von
Stammfunktion von  ermitteln
Der Funktionsterm von
ermitteln
Der Funktionsterm von  ist ein Produkt. Wähle also die partielle Integration als Integrationsverfahren. Dabei gilt:
ist ein Produkt. Wähle also die partielle Integration als Integrationsverfahren. Dabei gilt:
 Fasse als
Fasse als  diejenige Funktion auf, die leicht zu integrieren ist und als
diejenige Funktion auf, die leicht zu integrieren ist und als  die Funktion, die beim Ableiten vereinfacht wird:
die Funktion, die beim Ableiten vereinfacht wird:
![\(\begin{array}[t]{rllrl}
u‘(x)=& \mathrm e^x &\qquad& v‘(x)=&2 \cdot x +a
\\[5pt]
u(x)=&\mathrm e^x & \qquad&v(x)=&x^2 +a \cdot x
\end{array}\)](https://www.schullv.de/resources/formulas/93f9d7e91e7bcfe8344b68b7a939d4fd25240db55bcacad7aee71c727101a7b2_light.svg) Einsetzen ergibt:
Einsetzen ergibt:
![\(\begin{array}[t]{rll}
\displaystyle\int h_a \;\mathrm dx=&\mathrm e^x \cdot \left( x^2 +a \cdot x\right) - \displaystyle\int \mathrm e^x \cdot \left(2 \cdot x +a\right) \;\mathrm dx
\end{array}\)](https://www.schullv.de/resources/formulas/c87454717bdec364bbec8fc90e196084c78b5be1b97641b8b6ee3bc94d1b6b42_light.svg) Berechne nun das neu erhaltene Integral ebenfalls mit der partiellen Integration:
Berechne nun das neu erhaltene Integral ebenfalls mit der partiellen Integration:
![\(\begin{array}[t]{rllrl}
u‘(x)=& \mathrm e^x &\qquad& v‘(x)=&2
\\[5pt]
u(x)=&\mathrm e^x & \qquad&v(x)=&2 \cdot x +a
\end{array}\)](https://www.schullv.de/resources/formulas/140c212fc8ee5aeca3a01ffee458562df143efc739c7b1a0d66ef144e307778f_light.svg) Einsetzen ergibt:
Einsetzen ergibt:
![\(\begin{array}[t]{rll}
\displaystyle\int \mathrm e^x \cdot \left(2 \cdot x +a\right) \;\mathrm dx=&\mathrm e^x \cdot \left( 2 \cdot x +a \right) - \displaystyle\int \mathrm e^x \cdot 2 \;\mathrm dx
\\[5pt]
=& \left( 2 \cdot x +a \right) \cdot \mathrm e^x - 2 \cdot \displaystyle\int \mathrm e^x \;\mathrm dx & \scriptsize \mid\; \displaystyle\int \mathrm e^x \;\mathrm dx = \mathrm e^x + c
\\[5pt]
=& \left( 2 \cdot x +a \right) \cdot \mathrm e^x - 2 \cdot \mathrm e^x - c
\end{array}\)](https://www.schullv.de/resources/formulas/bfffcd85882a57a94a96def66bf3028b6da03c82a743c9c8ee977b7d38ca5a93_light.svg) Für
Für  ist
ist  eine Stammfunktion von
eine Stammfunktion von  . Damit kannst du eine Stammfunktion von
. Damit kannst du eine Stammfunktion von  berechnen:
berechnen:
![\(\begin{array}[t]{rll}
\displaystyle\int h_a \;\mathrm dx=&\mathrm e^x \cdot \left( x^2 +a \cdot x\right) - \displaystyle\int \mathrm e^x \cdot \left(2 \cdot x +a\right) \;\mathrm dx & \scriptsize \mid\; \text{Berechnete Stammfunktion einsetzen}
\\[5pt]
=& \mathrm e^x \cdot \left( x^2 +a \cdot x\right) - \left(\left( 2 \cdot x +a \right) \cdot \mathrm e^x - 2 \cdot \mathrm e^x \right)
\\[5pt]
=&\mathrm e^x \cdot \left( x^2 +a \cdot x\right) - \left( 2 \cdot x +a \right) \cdot \mathrm e^x + 2 \cdot \mathrm e^x & \scriptsize \mid\; \mathrm e^x \text{ ausklammern}
\\[5pt]
=& \left(\left( x^2 +a \cdot x\right) - \left( 2 \cdot x +a \right) + 2 \right) \cdot \mathrm e^x
\\[5pt]
=& \left( x^2 +(a-2) \cdot x + 2 -a \right) \cdot \mathrm e^x
\end{array}\)](https://www.schullv.de/resources/formulas/b4bfa34d2624c1121ff961769135b4c31cb827a800eaa753c97fb72882f61ea4_light.svg) Somit ist
Somit ist  eine Stammfunktion von
eine Stammfunktion von  .
c)(2)
.
c)(2)
 Flächeninhalt
Flächeninhalt  berechnen
Du sollst den Flächeninhalt
berechnen
Du sollst den Flächeninhalt  der Fläche, die von den Graphen der Funktionen
der Fläche, die von den Graphen der Funktionen  und
und  eingeschlossen wird, berechnen.
eingeschlossen wird, berechnen.
 mit den Schnittstellen der beiden Funktionen als Grenzen liefert dir
mit den Schnittstellen der beiden Funktionen als Grenzen liefert dir  :
:
 1. Schritt: Integrationsgrenzen bestimmen
Setze die Funktionsterme von
1. Schritt: Integrationsgrenzen bestimmen
Setze die Funktionsterme von  und
und  gleich, um die Schnittstellen der beiden Funktionen zu erhalten:
gleich, um die Schnittstellen der beiden Funktionen zu erhalten:
![\(\begin{array}[t]{rll}
f_a\stackrel{!}{=}&k & \scriptsize \mid\; \text{einsetzen}
\\[5pt]
\left(x^2 + a \cdot x +1\right) \cdot \mathrm e^x=& \mathrm e^x
\end{array}\)](https://www.schullv.de/resources/formulas/1a6ec54b8d1ed9ea7b629b517333096d81182955eea5af68ba1ef9e27291b075_light.svg) Da
Da  , kannst du hier durch
, kannst du hier durch  teilen:
teilen:
![\(\begin{array}[t]{rll}
\left(x^2 + a \cdot x +1\right) \cdot \mathrm e^x=& \mathrm e^x & \scriptsize \mid\; : \, \mathrm e^x
\\[5pt]
\left(x^2 + a \cdot x +1\right) =& 1 & \scriptsize \mid\; -1
\\[5pt]
x^2 + a \cdot x =& 0 & \scriptsize \mid\; x \text{ ausklammern}
\\[5pt]
\left( x + a\right) \cdot x =& 0
\end{array}\)](https://www.schullv.de/resources/formulas/e33d5a5e47f957b2da597fd4c451229eca45f896eb7fc39524b92c63a5942c01_light.svg) Der Satz vom Nullprodukt liefert die beiden Nullstellen
Der Satz vom Nullprodukt liefert die beiden Nullstellen  und
und  .
Somit lautet die untere Integrationsgrenze
.
Somit lautet die untere Integrationsgrenze  und die obere
und die obere  .
2. Schritt:
.
2. Schritt:  berechnen
Mit dem Hauptsatz der Integralrechnung ergibt sich:
berechnen
Mit dem Hauptsatz der Integralrechnung ergibt sich:
![\(\begin{array}[t]{rll}
A(a)=& \left| \, \displaystyle\int_{-a}^{0} h_a(x) \;\mathrm dx \, \right|
\\[5pt]
=& \left| \, H_a(0) - H_a(-a) \, \right|
\\[5pt]
=& \left|\,\left( 0^2 +(a-2) \cdot 0 + 2 -a \right) \cdot \mathrm e^0 - \left( (-a)^2 +(a-2) \cdot (-a) + 2 -a \right) \cdot \mathrm e^{-a}\,\right|
\\[5pt]
=&\left|\, 2-a - \left( a^2 +(a-2) \cdot (-a) + 2 -a \right) \cdot \mathrm e^{-a}\,\right|
\\[5pt]
=&\left|\, 2-a - \left( a^2 - a^2 + 2 \cdot a + 2 -a \right) \cdot \mathrm e^{-a}\,\right|
\\[5pt]
=&\left| \,2-a - \left( a+2 \right) \cdot \mathrm e^{-a}\,\right|
\end{array}\)](https://www.schullv.de/resources/formulas/f8a752e9f4a15a68e181679287d67e7975e6d99b7a4d3500516e2a0bcf33c7ed_light.svg) Der gesuchte Flächeninhalt beträgt
Der gesuchte Flächeninhalt beträgt  .
.
- Nutze dazu die Funktion
, die in der Aufgabenstellung als Differenz von
und
definiert wird.
- Eine Stammfunktion
hast du bereits im ersten Aufgabenteil berechnet.
- Die Grenzen der eingeschlossenen Fläche erhältst du, indem du die beiden Stellen
und
, an denen sich die Funktionen schneiden, berechnest.
d)(1)
 Stammfunktion von
Stammfunktion von  ermitteln
Du sollst eine Stammfunktion von
ermitteln
Du sollst eine Stammfunktion von  mit Hilfe der Aufgabe c)(1) ermitteln. Du kennst bereits eine Stammfunktion von
mit Hilfe der Aufgabe c)(1) ermitteln. Du kennst bereits eine Stammfunktion von  und kannst eine Stammfunktion von
und kannst eine Stammfunktion von  berechnen. In der Aufgabenstellung von c) hast du Folgendes gegeben:
berechnen. In der Aufgabenstellung von c) hast du Folgendes gegeben:
 Forme dies nach
Forme dies nach  um und setze
um und setze  ein:
ein:
 Für eine Stammfunktion von
Für eine Stammfunktion von  gilt:
gilt:
![\(\begin{array}[t]{rll}
\displaystyle\int k(x)\;\mathrm dx=& \displaystyle\int \mathrm e^x \;\mathrm dx
\\[5pt]
=&\mathrm e^x +c
\end{array}\)](https://www.schullv.de/resources/formulas/77b56a1e27b2f200cc2319b79468fe4bee6cab63d8cd9c8fab36bac48ef86b84_light.svg) Für
Für  ist
ist  eine Stammfunktion von
eine Stammfunktion von  .
Mit dem Hauptsatz der Integralrechnung und der Linearität des Integrals ergibt sich:
.
Mit dem Hauptsatz der Integralrechnung und der Linearität des Integrals ergibt sich: ![\(\begin{array}[t]{rll}
\displaystyle\int f_{2,5}(x) \;\mathrm dx=& \displaystyle\int\left( h_{2,5}(x)+ k(x)\right) \;\mathrm dx
\\[5pt]
=& \displaystyle\int h_{2,5}(x) \;\mathrm dx + \displaystyle\int k(x)\;\mathrm dx
\\[5pt]
=&H_{2,5}(x) + K(x)
\\[5pt]
=& \left( x^2 +(2,5-2) \cdot x + 2 -2,5 \right) \cdot \mathrm e^x + \mathrm e^x
\\[5pt]
=& \left( x^2 + 0,5 \cdot x -0,5 \right) \cdot \mathrm e^x + \mathrm e^x & \scriptsize \mid\; \mathrm e^x \text{ ausklammern}
\\[5pt]
=& \left( x^2 + 0,5 \cdot x -0,5 + 1\right) \cdot \mathrm e^x
\\[5pt]
=& \left( x^2 + 0,5 \cdot x + 0,5 \right) \cdot \mathrm e^x
\end{array}\)](https://www.schullv.de/resources/formulas/bb948974e4c9b36a32920811f4389033bee4cf550fb462e5f8afc1b70332e7e3_light.svg) Also ist
Also ist  eine Stammfunktion von
eine Stammfunktion von  .
d)(2)
.
d)(2)
 Gesuchten Flächeninhalt berechnen
Der Flächeninhalt, der vom Graphen von
Gesuchten Flächeninhalt berechnen
Der Flächeninhalt, der vom Graphen von  und der
und der  -Achse eingeschlossen wird, ist gesucht.
-Achse eingeschlossen wird, ist gesucht.
 mit den Nullstellen von
mit den Nullstellen von  als Integrationsgrenzen liefert dir also den Flächeninhalt der eingeschlossenen Fläche.
1. Schritt: Integrationsgrenzen bestimmen
Aus der Lösung von Aufgabe b)(1) erhältst du die Nullstellen von
als Integrationsgrenzen liefert dir also den Flächeninhalt der eingeschlossenen Fläche.
1. Schritt: Integrationsgrenzen bestimmen
Aus der Lösung von Aufgabe b)(1) erhältst du die Nullstellen von  :
Die Nullstellen der Funktion
:
Die Nullstellen der Funktion  sind
sind  und
und  .
Einsetzen von
.
Einsetzen von  ergibt:
ergibt:
![\(\begin{array}[t]{rll}
x_1=&-\dfrac{\left(\frac{5}{2}\right)}{2} - \dfrac{\sqrt {\left(\frac{5}{2}\right)^2 -4} }{2}
\\[5pt]
=&-\dfrac{5}{4} - \dfrac{\sqrt {\frac{25}{4} -\frac{16}{4}} }{2}
\\[5pt]
=&-\dfrac{5}{4} - \dfrac{\sqrt {\frac{9}{4}} }{2}
\\[5pt]
=&-\dfrac{5}{4} - \dfrac{3}{4}
\\[5pt]
=&-2
\end{array}\)](https://www.schullv.de/resources/formulas/6bbf93843d04314e4c3f1154f6446b9de24df4b0cb93c13ea4b632342ed0852b_light.svg) und
und
![\(\begin{array}[t]{rll}
x_2=&-\dfrac{\left(\frac{5}{2}\right)}{2} + \dfrac{\sqrt {\left(\frac{5}{2}\right)^2 -4} }{2}
\\[5pt]
=&-\dfrac{5}{4} + \dfrac{\sqrt {\frac{25}{4} -\frac{16}{4}} }{2}
\\[5pt]
=&-\dfrac{5}{4} + \dfrac{\sqrt {\frac{9}{4}} }{2}
\\[5pt]
=&-\dfrac{5}{4} + \dfrac{3}{4}
\\[5pt]
=& -\dfrac{1}{2}
\end{array}\)](https://www.schullv.de/resources/formulas/e25f8ea474cfdcd3277eb9914bc672a0e66a7fb2bb87219a510b3ceef1fd3975_light.svg) Damit sind
Damit sind  und
und  die Integrationsgrenzen.
2. Schritt: Eingeschlossene Fläche berechnen
Mit dem Hauptsatz der Integralrechnung folgt:
die Integrationsgrenzen.
2. Schritt: Eingeschlossene Fläche berechnen
Mit dem Hauptsatz der Integralrechnung folgt:
![\(\begin{array}[t]{rll}
\left|\,\displaystyle\int_{-2}^{-0,5} f_{2,5}\;\mathrm dx\,\right|=& \left|\,F_{2,5}(-0,5) - F_{2,5}(-2)\,\right|
\\[5pt]
=& \left|\,\left( (-0,5)^2 + 0,5 \cdot (-0,5) + 0,5 \right) \cdot \mathrm e^{-0,5} - \left( (-2)^2 + 0,5 \cdot (-2) + 0,5 \right) \cdot \mathrm e^{-2}\,\right|
\\[5pt]
=& \left|\,\left( 0,25 -0,25 + 0,5 \right) \cdot \mathrm e^{-0,5} - \left( 4 -1 + 0,5 \right) \cdot \mathrm e^{-2}\,\right|
\\[5pt]
=& \left|\,0,5 \cdot \mathrm e^{-0,5} - 3,5 \cdot \mathrm e^{-2} \,\right|
\\[5pt]
\approx& \left|\, -0,17 \,\right|
\\[5pt]
=& 0,17
\end{array}\)](https://www.schullv.de/resources/formulas/2c43120b6877d0b302c1caece02e79aec224ac7e3fe83a773dcbe76a8709489d_light.svg) Also beträgt der Inhalt der zwischen
Also beträgt der Inhalt der zwischen  -Achse und dem Graphen der Funktion
-Achse und dem Graphen der Funktion  eingeschlossenen Fläche ca.
eingeschlossenen Fläche ca.  Flächeneinheiten.
d)(3)
Flächeneinheiten.
d)(3)
 Verhältnis von größeren zur kleineren Teilfläche berechnen
Um das Verhältnis der beiden Flächen zueinander zu berechnen, benötigst du den Inhalt der beiden Flächen:
Verhältnis von größeren zur kleineren Teilfläche berechnen
Um das Verhältnis der beiden Flächen zueinander zu berechnen, benötigst du den Inhalt der beiden Flächen:
 in
in  ein, um die gesamte schraffierte Fläche zu berechnen:
ein, um die gesamte schraffierte Fläche zu berechnen:
 Damit ergibt sich für den Flächeninhalt der größeren Fläche:
Damit ergibt sich für den Flächeninhalt der größeren Fläche:
 Das Verhältnis von größeren zur kleineren Teilfläche beträgt also:
Das Verhältnis von größeren zur kleineren Teilfläche beträgt also:
 Die größere Fläche ist demnach etwa viermal so groß wie die kleinere Teilfläche.
Die größere Fläche ist demnach etwa viermal so groß wie die kleinere Teilfläche.
- Das Integral einer Funktion gibt dir die Fläche zwischen
-Achse und dem Graphen der Funktion an. Integriere also über
.
- Im ersten Aufgabenteil hast du bereits eine Stammfunktion
von
berechnet.
- Da die Schnittpunkte von
und der
-Achse gerade die Nullstellen der Funktion
sind, liefern diese die Integrationsgrenzen.
- Die Nullstellen von
hast du bereits in der Aufgabe b)(1) berechnet, somit musst du noch
einsetzen.
- Den Inhalt der kleineren Fläche, also von der
-Achse und dem Graphen von
eingeschlossenen Fläche hast du im zweiten Aufgabenteil berechnet, dieser beträgt
Flächeneinheiten.
- Den Inhalt der gesamten schraffierten Fläche erhältst du durch einsetzen von
in
aus der Aufgabe c)(2).
- Der Inhalt der größeren Fläche ergibt sich damit aus der Subtraktion der kleineren Fläche von der gesamten Fläche.