Aufgabe 4
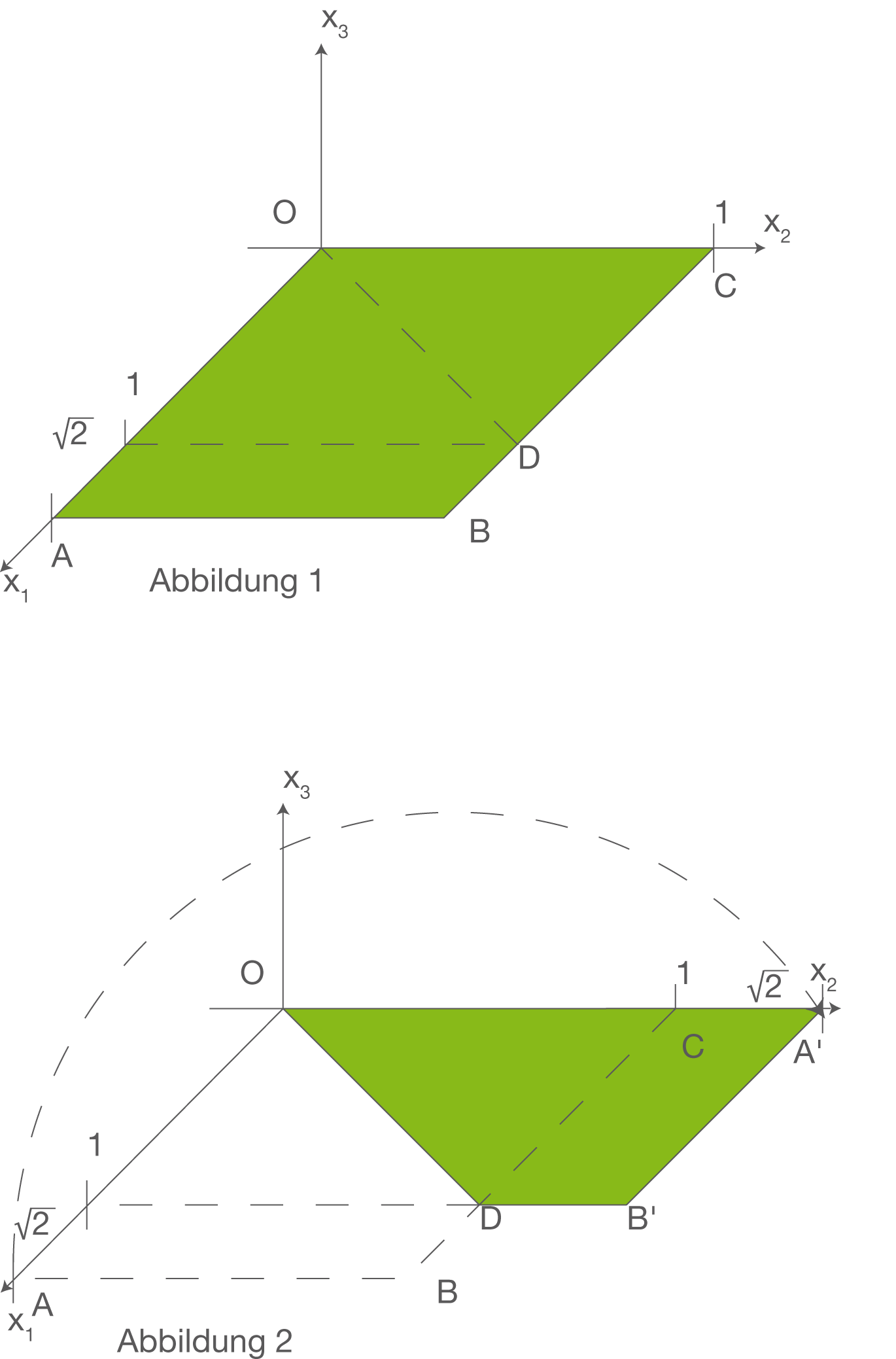
Ein Blatt DIN-A4-Papier liegt in der  -Ebene. Gegeben sind seine Eckpunkte
-Ebene. Gegeben sind seine Eckpunkte
 sowie der Punkt
sowie der Punkt  .1
.1
Das Blatt wird jetzt entlang der Strecke gefaltet. Das Dreieck
gefaltet. Das Dreieck  bleibt dabei fest, während das Viereck
bleibt dabei fest, während das Viereck  in das Viereck
in das Viereck  übergeht, das wieder in der
übergeht, das wieder in der  Ebene liegt. Die Gegebenheiten sind in den folgenden Schrägbildern dargestellt.
Ebene liegt. Die Gegebenheiten sind in den folgenden Schrägbildern dargestellt.
Zur Veranschaulichung kann ein DIN-A4-Blatt entsprechend gefaltet werden.
Das Blatt wird jetzt entlang der Strecke
Zur Veranschaulichung kann ein DIN-A4-Blatt entsprechend gefaltet werden.
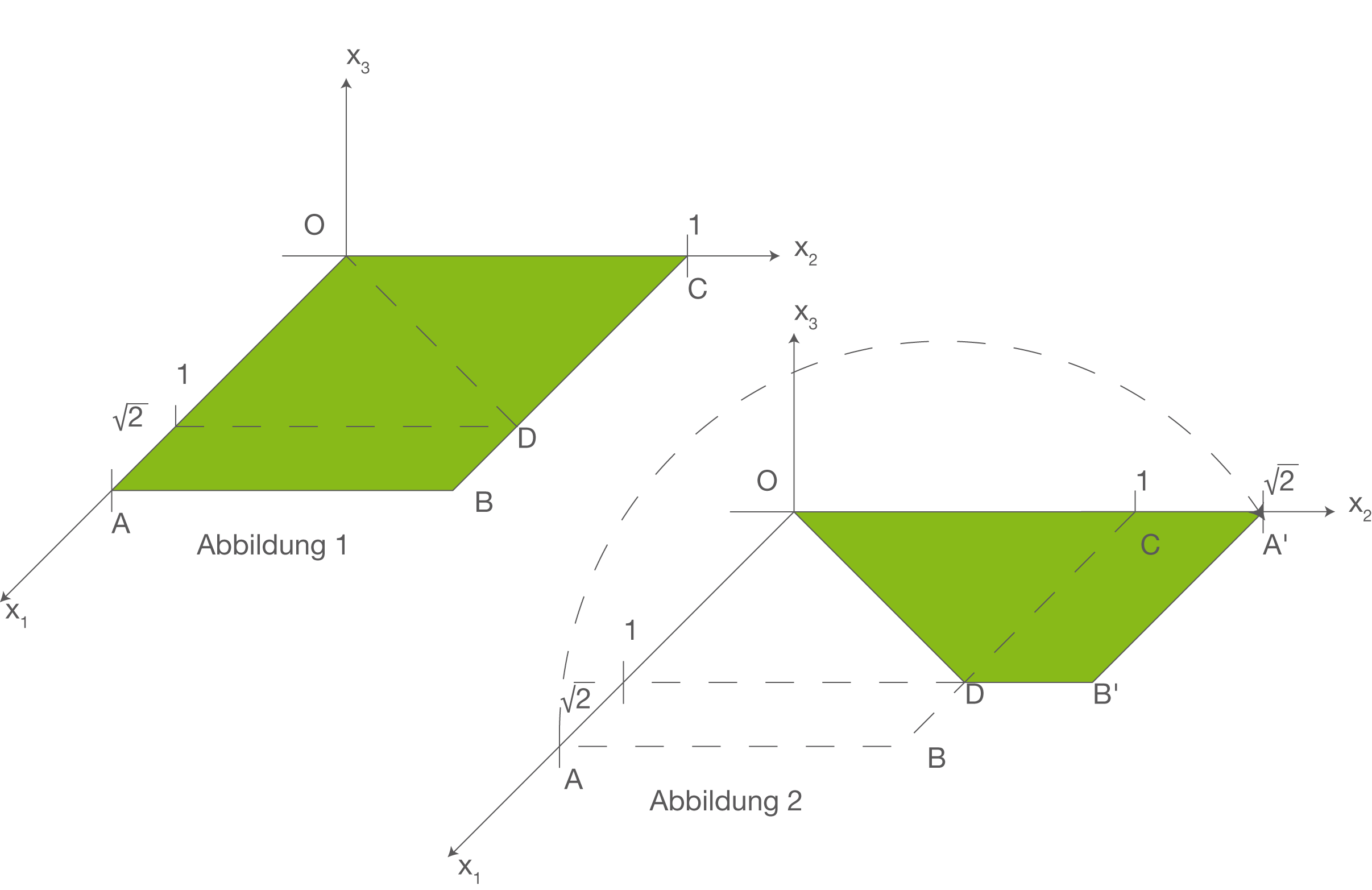
1Als Längeneinheit (LE) wird die Länge der kürzeren Seite des DIN-A4-Blattes verwendet
a)
Bestimmen Sie den Abstand des Punktes B von der Geraden OD.
(8P)
b)
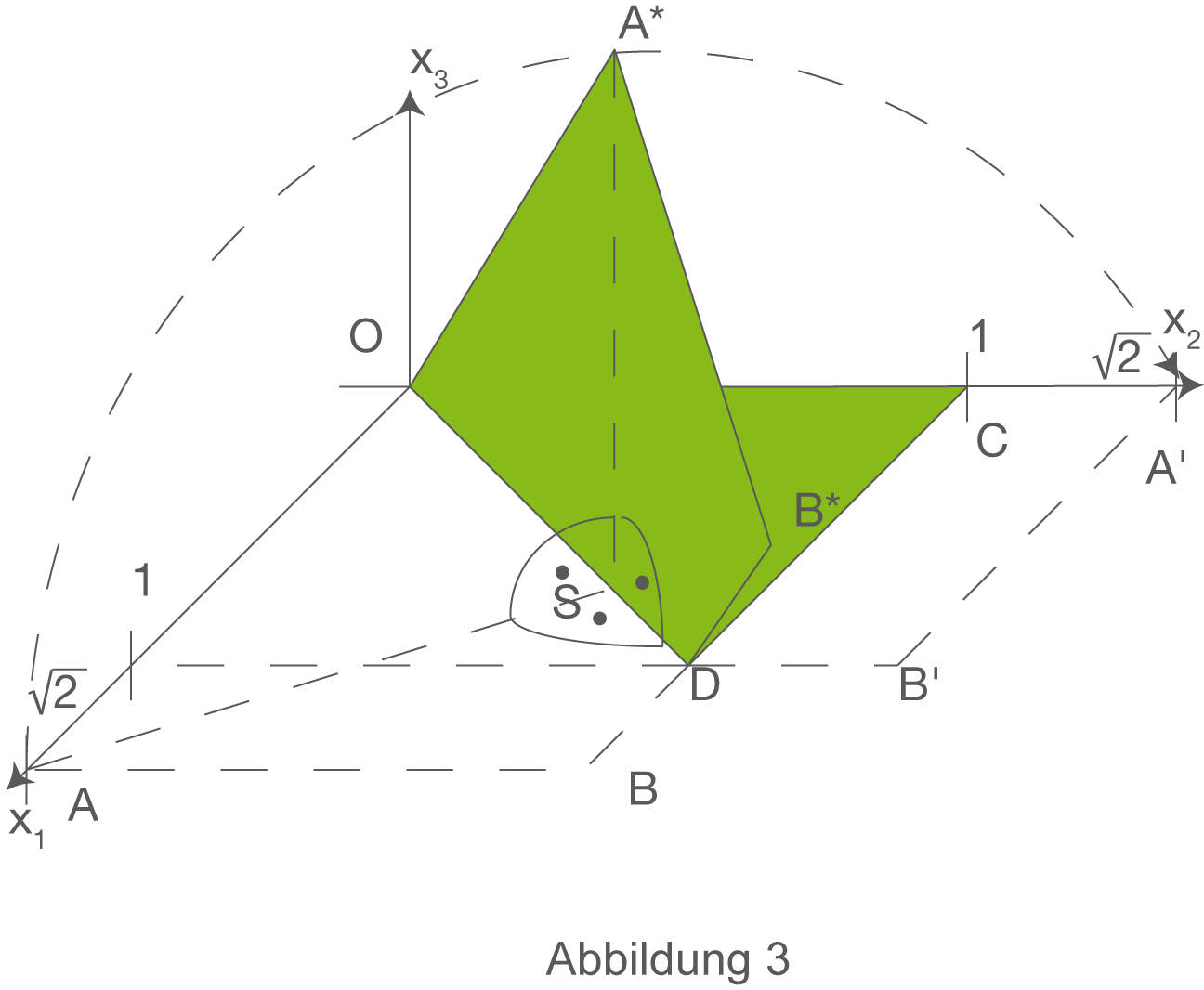
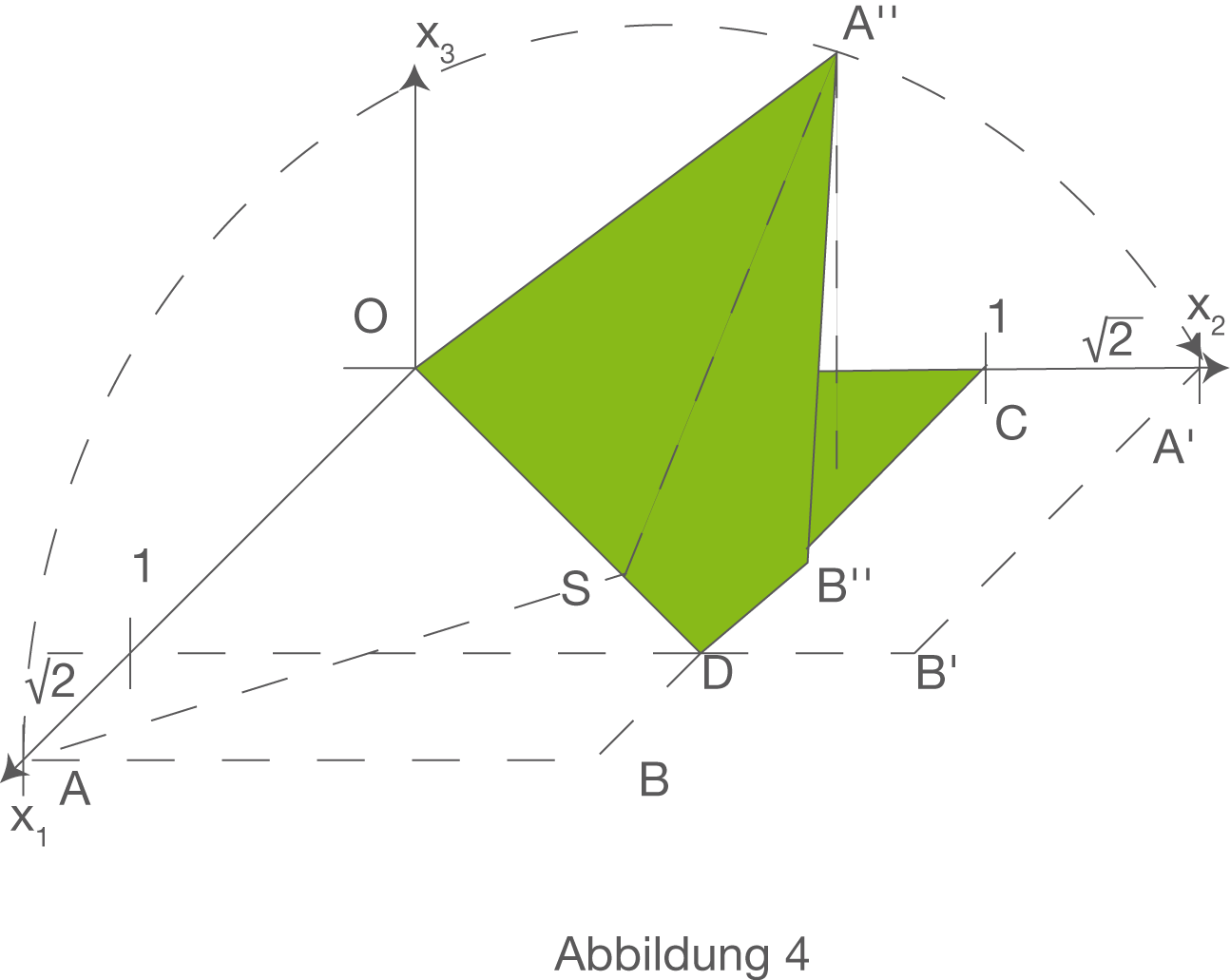
Die Ecke des Blattes, die durch das Falten aus der Position A in die Position A‘ gebracht wird, bewegt sich bei dem Faltvorgang auf einem Halbkreis in einer Ebene E (siehe Abbildung 1 bis 4).
- Leiten Sie je eine Gleichung dieser Ebene E in Parameterform und in Normalenform her.
[Zur Kontrolle eine Koordinatengleichung:]
- Bestimmen Sie die Koordinaten des Schnittpunktes S der Ebene E mit der Geraden OD.
[Zur Kontrolle: S]
(7P + 4P)
Während des Faltvorgangs liegt das beim Falten bewegte Papier-Viereck stets in einer Ebene  der durch
der durch  , gegebenen Ebenenschar. Vorher und nachher liegt es jeweils in der
, gegebenen Ebenenschar. Vorher und nachher liegt es jeweils in der  -Ebene (siehe Abbildung 1 bis 4.)
-Ebene (siehe Abbildung 1 bis 4.)
c)
 gebracht, das in einer sowohl zur
gebracht, das in einer sowohl zur  -Ebene als auch zur Ebene
-Ebene als auch zur Ebene  senkrechten Ebene
senkrechten Ebene  liegt (siehe Abbildung 3).
liegt (siehe Abbildung 3).
- Weisen Sie rechnerisch nach, dass die Gerade OD in jeder Ebene
der Ebenenschar liegt.
- Begründen Sie, dass die Ebene E aus b) senkrecht zu jeder Ebene
, ist.
- Berechnen Sie den Wert des Parameters k, für den
ist.
- Ermitteln Sie die Koordinaten des Punktes
.

(4P + 5P + 3P + 6P)
d)
Während des Faltvorgangs kommt das beim Falten bewegte Papier-Viereck auch in die Position des Vierecks OA‘‘B‘‘D, dessen Punkt A‘‘ in der Ebene  liegt.
liegt.
- Bestimmen Sie die Koordinaten des Punktes A‘‘.
Zur Kontrolle:
- Zeigen Sie, dass das Dreieck OCA‘‘ gleichschenklig rechtwinklig ist.

(7P + 6P)
a)
 Abstand des Punktes
Abstand des Punktes  zur Geraden
zur Geraden  angeben
Ein DIN-A4-Blatt wird entlang der Strecke
angeben
Ein DIN-A4-Blatt wird entlang der Strecke  wie in Abbildung 1 und 2 gefaltet. Bestimme den Abstand des Punktes
wie in Abbildung 1 und 2 gefaltet. Bestimme den Abstand des Punktes  zur Geraden
zur Geraden  .
.
 Der Abstand eines Punktes zu einer Geraden entspricht der kürzesten Strecke, die den Punkt mit der Geraden verbindet.
Der Abstand eines Punktes zu einer Geraden entspricht der kürzesten Strecke, die den Punkt mit der Geraden verbindet.
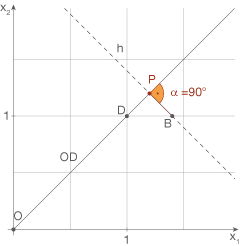 Diese Strecke muss folglich senkrecht auf der Geraden stehen. Daher entspricht der gesuchte Abstand gerade der Länge der Strecke
Diese Strecke muss folglich senkrecht auf der Geraden stehen. Daher entspricht der gesuchte Abstand gerade der Länge der Strecke  .
Um die Länge dieser Strecke
.
Um die Länge dieser Strecke  zu bestimmen, kannst du eine Hilfsgerade
zu bestimmen, kannst du eine Hilfsgerade  so konstruieren, dass sie senkrecht zur Geraden
so konstruieren, dass sie senkrecht zur Geraden  verläuft und den Punkt
verläuft und den Punkt  enthält.
enthält.
Bestimme den Schnittpunkt der Hilfgeraden
der Hilfgeraden  und der Geraden
und der Geraden  .
Hast du diesen bestimmt, so kannst du die Länge der Strecke
.
Hast du diesen bestimmt, so kannst du die Länge der Strecke  mit Hilfe des Betrags bestimmen.
Den Betrag einer Strecke
mit Hilfe des Betrags bestimmen.
Den Betrag einer Strecke  zweier Punkte
zweier Punkte  und
und  kannst du folgendermaßen bestimmen:
kannst du folgendermaßen bestimmen:
1. Schritt: Hilfsgerade  konstruieren
Bevor wir die Geradengleichung für
konstruieren
Bevor wir die Geradengleichung für  angeben können, ist es hilfreich, zuerst die Geradengleichung zu
angeben können, ist es hilfreich, zuerst die Geradengleichung zu  aufzustellen:
aufzustellen:
 Um die Gleichung der Hilfsgeraden
Um die Gleichung der Hilfsgeraden  zu bestimmen, gehen wir zunächst von einer allgemeinen Geradengleichung aus:
zu bestimmen, gehen wir zunächst von einer allgemeinen Geradengleichung aus:
 Dabei ist
Dabei ist  der Stützvektor und
der Stützvektor und  der Richtungsvektor. Für den Stützvektor
der Richtungsvektor. Für den Stützvektor  kannst du die Koordinaten eines Punktes verwenden, der garantiert auf der Geraden
kannst du die Koordinaten eines Punktes verwenden, der garantiert auf der Geraden  liegt. Hier bietet sich beispielweise der Punkt
liegt. Hier bietet sich beispielweise der Punkt  an. Du erhältst also folgenden Stützvektor:
an. Du erhältst also folgenden Stützvektor:
 Soll die Hilfsgerade
Soll die Hilfsgerade  senkrecht zur Geraden
senkrecht zur Geraden  sein, so muss das Skalarprodukt ihrer Richtungsvektoren gleich Null sein. Das heißt, es muss gelten:
sein, so muss das Skalarprodukt ihrer Richtungsvektoren gleich Null sein. Das heißt, es muss gelten:
 Damit das Skalarprodukt gleich Null ist, muss folglich
Damit das Skalarprodukt gleich Null ist, muss folglich  gelten. Du kannst hier jeden beliebigen Wert für
gelten. Du kannst hier jeden beliebigen Wert für  wählen. Da die Gerade
wählen. Da die Gerade  und der Punkt
und der Punkt  in der
in der  Ebene liegen, sollte ebenfalls
Ebene liegen, sollte ebenfalls  gelten.
gelten.
Wir wählen, um die Rechnung möglichst einfach zu halten, und erhalten dann folgende Geradengleichung zur Hilfsgeraden
und erhalten dann folgende Geradengleichung zur Hilfsgeraden  :
:
 2. Schritt: Schnittpunkt
2. Schritt: Schnittpunkt  der Hilfsgeraden
der Hilfsgeraden  mit der Geraden
mit der Geraden  bestimmen
Die Koordinaten des Schnittpunktes
bestimmen
Die Koordinaten des Schnittpunktes  der Hilfsgeraden
der Hilfsgeraden  und der Geraden
und der Geraden  kannst du bestimmen, indem du die beiden Geradengleichungen gleichsetzt:
kannst du bestimmen, indem du die beiden Geradengleichungen gleichsetzt:
 Dadurch erhältst du ein lineares Gleichungssystem, durch welches du Werte für die Parameter
Dadurch erhältst du ein lineares Gleichungssystem, durch welches du Werte für die Parameter  und
und  ermitteln kannst:
ermitteln kannst:

 Es muss also
Es muss also  bzw.
bzw.  gelten. Setze entweder den Parameterwert für
gelten. Setze entweder den Parameterwert für  in die Hilfsgeradengleichung oder den Parameterwert für
in die Hilfsgeradengleichung oder den Parameterwert für  in die Geradengleichung zu
in die Geradengleichung zu  ein. Das liefert dir die Koordinaten von
ein. Das liefert dir die Koordinaten von  .
.
 Jetzt kannst du die Koordinaten des Schnittpunktes
Jetzt kannst du die Koordinaten des Schnittpunktes  vollständig angeben mit:
vollständig angeben mit:
 3 Schritt: Abstand zwischen
3 Schritt: Abstand zwischen  und der Geraden
und der Geraden  berechnen
Zuvor hast du überlegt, dass der Abstand des Punktes
berechnen
Zuvor hast du überlegt, dass der Abstand des Punktes  zur Geraden
zur Geraden  gerade dem Abstand den Punktes
gerade dem Abstand den Punktes  zum Punkt
zum Punkt  entspricht. Berechne also:
entspricht. Berechne also:
 Damit hat der Punkt
Damit hat der Punkt  einen Abstand von
einen Abstand von  LE zur Geraden OD.
LE zur Geraden OD.


Bestimme den Schnittpunkt
|
|
Wir wählen, um die Rechnung möglichst einfach zu halten,
b)
 Gleichung der Ebene
Gleichung der Ebene  in Parameterform angeben
Das Blatt in der
in Parameterform angeben
Das Blatt in der  Ebene wird wie in Abbildung 1 und 2 gefaltet. Beim Faltvorgang „wandert“ der Punkt
Ebene wird wie in Abbildung 1 und 2 gefaltet. Beim Faltvorgang „wandert“ der Punkt  in die Position
in die Position  . Dabei bewegt sich der Punkt entlang eines Halbkreises. Die Ebene
. Dabei bewegt sich der Punkt entlang eines Halbkreises. Die Ebene  soll diesen Halbkreis enthalten und senkrecht zur
soll diesen Halbkreis enthalten und senkrecht zur  Ebene stehen.
Ebene stehen.
 Deine Aufgabe ist es, die Ebenengleichung zur Ebene
Deine Aufgabe ist es, die Ebenengleichung zur Ebene  in Parameterform anzugeben.
in Parameterform anzugeben.
Eine Ebenengleichung in Parameterform sieht wie folgt aus:
Der Vektor  wird Stützvektor genannt,
wird Stützvektor genannt,  und
und  sind die linear unabhängigen Spannvektoren der Ebene
sind die linear unabhängigen Spannvektoren der Ebene  .
Stelle die gesuchten Stütz- und Spannvektoren auf, um eine Ebenengleichung in Parameterform zu erhalten.
1. Schritt: Stützvektor der Ebene
.
Stelle die gesuchten Stütz- und Spannvektoren auf, um eine Ebenengleichung in Parameterform zu erhalten.
1. Schritt: Stützvektor der Ebene  aufstellen
Für den Stützvektor kannst du die Koordinaten eines Punktes verwenden, der garantiert in der Ebene liegt. Hier bietet sich beispielweise der Punkt
aufstellen
Für den Stützvektor kannst du die Koordinaten eines Punktes verwenden, der garantiert in der Ebene liegt. Hier bietet sich beispielweise der Punkt  an. Es ergibt sich also:
an. Es ergibt sich also:
 2. Schritt: Spannvektor
2. Schritt: Spannvektor  der Ebene
der Ebene  aufstellen
Da in der Aufgabenstellung verlangt wird, dass die Ebene
aufstellen
Da in der Aufgabenstellung verlangt wird, dass die Ebene  senkrecht auf der
senkrecht auf der  Ebene steht, kannst du einen der Spannvektoren direkt angeben, der diese Bedingung erfüllt:
Ebene steht, kannst du einen der Spannvektoren direkt angeben, der diese Bedingung erfüllt:
 3. Schritt: Spannvektor
3. Schritt: Spannvektor  der Ebene
der Ebene  aufstellen
Sollen weiterhin die Punkte
aufstellen
Sollen weiterhin die Punkte  und
und  in der Ebene
in der Ebene  enthalten sein, so muss auch ihre Verbindungsstrecke in der Ebene
enthalten sein, so muss auch ihre Verbindungsstrecke in der Ebene  liegen. Das heißt, du kannst den Vektor
liegen. Das heißt, du kannst den Vektor  als zweiten Spannvektor verwenden.
als zweiten Spannvektor verwenden.
 Offensichtlich benötigen wir die Koordinaten des Punktes
Offensichtlich benötigen wir die Koordinaten des Punktes  , um den zweiten Spannvektor angeben zu können. Anhand Abbildung 3 kannst du die Koordinaten ablesen. Der Punkt
, um den zweiten Spannvektor angeben zu können. Anhand Abbildung 3 kannst du die Koordinaten ablesen. Der Punkt  hat die Koordinaten
hat die Koordinaten  . Damit kannst du nun den Vektor
. Damit kannst du nun den Vektor  bestimmen:
bestimmen:
 4. Schritt: Aufgestellte Vektoren in Ebenengleichung einsetzen
Einsetzen des Stützvektors
4. Schritt: Aufgestellte Vektoren in Ebenengleichung einsetzen
Einsetzen des Stützvektors  und der Spannvektoren
und der Spannvektoren  und
und  in die allgemeine Form einer Ebenengleichung in Parameterform liefert dir die gesuchte Gleichung:
in die allgemeine Form einer Ebenengleichung in Parameterform liefert dir die gesuchte Gleichung:

 Gleichung der Ebene
Gleichung der Ebene  in Normalenform angeben
Die Normalenform einer Ebenengleichung kannst du allgemein wie folgt angeben:
in Normalenform angeben
Die Normalenform einer Ebenengleichung kannst du allgemein wie folgt angeben:
Dabei ist  der Stützvektor und
der Stützvektor und  der Normalenvektor der Ebene. Beim Stützvektor kannst du wie zuvor vorgehen: Wähle einen Punkt, der garantiert in der Ebene
der Normalenvektor der Ebene. Beim Stützvektor kannst du wie zuvor vorgehen: Wähle einen Punkt, der garantiert in der Ebene  liegt und verwende dessen Koordinaten für den Stützvektor. Du kannst hier beispielsweise denselben Stützvektor
liegt und verwende dessen Koordinaten für den Stützvektor. Du kannst hier beispielsweise denselben Stützvektor  wählen, den du bereits bei der Parameterform gewählt hast.
wählen, den du bereits bei der Parameterform gewählt hast.
Letztlich benötigst du nur noch den Normalenvektor . Dafür bieten sich zwei Möglichkeiten an:
. Dafür bieten sich zwei Möglichkeiten an:
 Lösungsweg A: Koordinatenform
Eine Ebenengleichung in Koordinatenform ist allgemein von der Form:
Lösungsweg A: Koordinatenform
Eine Ebenengleichung in Koordinatenform ist allgemein von der Form:
Hast du bereits eine Ebenengleichung der Ebene in Parameterform, so kannst du die Koordinatenform ermitteln, indem du die Ebenengleichung in Parameterform mit  ,
,  und
und  wie folgt gleichsetzt:
wie folgt gleichsetzt:
 Daraus erhältst du ein lineares Gleichungssystem, bei welchem du die Parameter
Daraus erhältst du ein lineares Gleichungssystem, bei welchem du die Parameter  und
und  eliminieren musst, um die Koordinatenform zu erhalten.
eliminieren musst, um die Koordinatenform zu erhalten.
 In der Gleichung
In der Gleichung  sind nun beide Parameter eliminiert. Das heißt, die Ebenengleichung zur Ebene
sind nun beide Parameter eliminiert. Das heißt, die Ebenengleichung zur Ebene  in Koordinatenform lautet:
in Koordinatenform lautet:
 Hier kannst du den Normalenvektor direkt ablesen mit:
Hier kannst du den Normalenvektor direkt ablesen mit:

 Lösungsweg B: Kreuzprodukt
Da der Normalenvektor
Lösungsweg B: Kreuzprodukt
Da der Normalenvektor  senkrecht auf beiden Spannvektoren
senkrecht auf beiden Spannvektoren  und
und  stehen soll, kannst du deren Kreuzprodukt bilden:
stehen soll, kannst du deren Kreuzprodukt bilden:
 Da bei einem Normalenvektor nur dessen Richtung und nicht dessen Länge relevant ist, kannst du diesen wie folgt vereinfachen:
Da bei einem Normalenvektor nur dessen Richtung und nicht dessen Länge relevant ist, kannst du diesen wie folgt vereinfachen:

 In allgemeine Normalenform einsetzen:
Da du den Normalenvektor
In allgemeine Normalenform einsetzen:
Da du den Normalenvektor  bestimmt hast und den Stützvektor aus der Parameterform wiederverwenden kannst, ergibt sich folgende Gleichung der Ebene
bestimmt hast und den Stützvektor aus der Parameterform wiederverwenden kannst, ergibt sich folgende Gleichung der Ebene  in Normalenform:
in Normalenform:

 Koordinaten des Schnittpunktes
Koordinaten des Schnittpunktes  bestimmen
Die Gerade
bestimmen
Die Gerade  schneidet die Ebene
schneidet die Ebene  in einem Punkt
in einem Punkt  . Um den Schnittpunkt einer Geraden mit einer Ebene zu ermitteln, kannst du die Geradengleichung komponentenweise in die zuvor bestimme Ebenengleichung in Parameterform einsetzen. Gehe also wie folgt vor:
. Um den Schnittpunkt einer Geraden mit einer Ebene zu ermitteln, kannst du die Geradengleichung komponentenweise in die zuvor bestimme Ebenengleichung in Parameterform einsetzen. Gehe also wie folgt vor:
 mit Ebenengleichung von
mit Ebenengleichung von  gleichsetzen
Komponentenweise Gleichsetzen der Geradengleichung mit der Ebenengleichung von
gleichsetzen
Komponentenweise Gleichsetzen der Geradengleichung mit der Ebenengleichung von  liefert dir folgendes lineares Gleichungssystem, welches du nach
liefert dir folgendes lineares Gleichungssystem, welches du nach  auflösen sollst:
auflösen sollst:
 Du erhältst
Du erhältst  .
2. Schritt: Parameter
.
2. Schritt: Parameter  in Geradengleichung von
in Geradengleichung von  einsetzen
Einsetzen von
einsetzen
Einsetzen von  in die Geradengleichung zu
in die Geradengleichung zu  liefert dir die Koordinaten des Schnittpunktes
liefert dir die Koordinaten des Schnittpunktes  :
:
 Der Schnittpunkt
Der Schnittpunkt  besitzt die Koordinaten
besitzt die Koordinaten  .
.

Eine Ebenengleichung in Parameterform sieht wie folgt aus:
|
|
|
|
Letztlich benötigst du nur noch den Normalenvektor
| A: | Stelle die Ebenengleichung in Koordinatenform auf, denn an dieser kannst du den Normalenvektor direkt ablesen. |
| B: | Da der Normalenvektor senkrecht auf der Ebene |
|
|
- Setze diese Geradengleichung komponentenweise in die Ebenengleichung von
ein und löse nach dem Parameter
auf. Dadurch erhältst du einen Wert für den Parameter
.
- Setze diesen Parameterwert für
anschließend in die Geradengleichung von
ein. Das liefert dir die Koordinaten des gesuchten Schnittpunktes
.
c)
 Nachweisen, dass Gerade
Nachweisen, dass Gerade  in jeder Ebene der Ebenenschar liegt
Während des Faltvorgangs liegt das bewegte Papierviereck immer in einer Ebene der Ebenenschar mit der Ebenengleichung
in jeder Ebene der Ebenenschar liegt
Während des Faltvorgangs liegt das bewegte Papierviereck immer in einer Ebene der Ebenenschar mit der Ebenengleichung
 Weise rechnerisch nach, dass die Gerade
Weise rechnerisch nach, dass die Gerade  in jeder Ebene
in jeder Ebene  liegt.
Willst du zeigen, dass die Gerade
liegt.
Willst du zeigen, dass die Gerade  in jeder Ebene
in jeder Ebene  liegt, so kannst du die Gleichung der Gerade in die Gleichung der Ebenenschar einsetzen. Löse nach deren Parametern
liegt, so kannst du die Gleichung der Gerade in die Gleichung der Ebenenschar einsetzen. Löse nach deren Parametern  und
und  auf. Ergibt sich hierbei eine wahre Aussage für alle
auf. Ergibt sich hierbei eine wahre Aussage für alle  und
und  , so liegt die Gerade
, so liegt die Gerade  in jeder Ebene
in jeder Ebene  .
Die Gleichung der Gerade
.
Die Gleichung der Gerade  hast du zuvor bereits aufgestellt mit:
hast du zuvor bereits aufgestellt mit:
 Komponentenweise Einsetzen liefert dir:
Komponentenweise Einsetzen liefert dir:
 In diese Gleichung kannst du jeden beliebigen Wert für den Parameter
In diese Gleichung kannst du jeden beliebigen Wert für den Parameter  bzw.
bzw.  einsetzen. Das heißt, es liegt immer eine wahre Aussage vor und damit gilt, dass die Gerade
einsetzen. Das heißt, es liegt immer eine wahre Aussage vor und damit gilt, dass die Gerade  in jeder Ebene
in jeder Ebene  liegt.
liegt.
 Nachweisen, dass die Ebene
Nachweisen, dass die Ebene  senkrecht zu jeder Ebene der Ebenenschar ist
Die Ebene
senkrecht zu jeder Ebene der Ebenenschar ist
Die Ebene  hat laut Teilaufgabe b) folgende Ebenengleichung:
hat laut Teilaufgabe b) folgende Ebenengleichung:
 Willst du zeigen, dass die Ebene senkrecht zu jeder Ebene
Willst du zeigen, dass die Ebene senkrecht zu jeder Ebene  ist, so kannst du zeigen, dass die Normalenvektoren
ist, so kannst du zeigen, dass die Normalenvektoren  und
und  senkrecht zueinander sind. Das heißt, ihr Skalarprodukt ist gleich Null.
Die Normalenvektoren
senkrecht zueinander sind. Das heißt, ihr Skalarprodukt ist gleich Null.
Die Normalenvektoren  und
und  der Ebene
der Ebene  und
und  kannst du anhand der Koordinatenform direkt ablesen:
kannst du anhand der Koordinatenform direkt ablesen:
 Bildest du das Skalarprodukt der Normalenvektoren, so erhältst du:
Bildest du das Skalarprodukt der Normalenvektoren, so erhältst du:
 Damit hast du gezeigt, dass das Skalarprodukt der Normalenvektoren für jedes
Damit hast du gezeigt, dass das Skalarprodukt der Normalenvektoren für jedes  gleich Null ist. Folglich steht die Ebene
gleich Null ist. Folglich steht die Ebene  senkrecht auf allen Ebenen der Schar
senkrecht auf allen Ebenen der Schar  .
.
 Parameter
Parameter  für
für  bestimmen, sodass
bestimmen, sodass  gilt
gilt
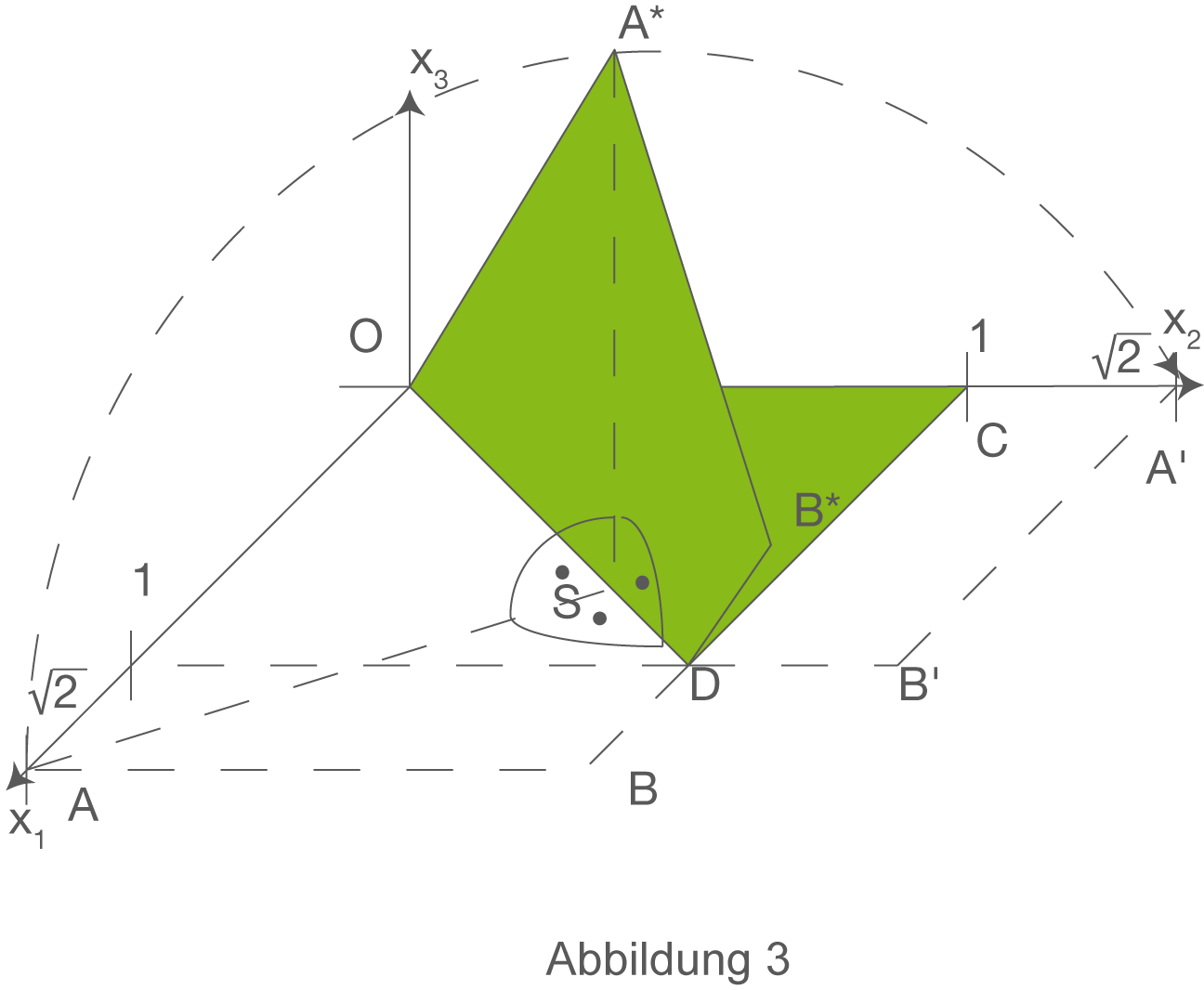 Während des Faltvorgangs nehmen die Punkte
Während des Faltvorgangs nehmen die Punkte  und
und  die Positionen
die Positionen  und
und  ein.
Eine neue Ebene
ein.
Eine neue Ebene  soll nun das daraus entstehende Viereck
soll nun das daraus entstehende Viereck  enthalten. Weiterhin ist
enthalten. Weiterhin ist  eine Ebene der Ebenenschar
eine Ebene der Ebenenschar  und senkrecht zur
und senkrecht zur  Ebene.
Deine Aufgabe ist es, einen Parameterwert für
Ebene.
Deine Aufgabe ist es, einen Parameterwert für  zu ermitteln, sodass
zu ermitteln, sodass  gilt.
Soll
gilt.
Soll  senkrecht zur
senkrecht zur  Ebene sein, kannst du verwenden, dass das Skalarprodukt des Normalenvektors der
Ebene sein, kannst du verwenden, dass das Skalarprodukt des Normalenvektors der  Ebene und des Normalenvektors der Ebene
Ebene und des Normalenvektors der Ebene  gleich Null sein muss. In mathematischen Formeln ausgedrückt heißt das:
gleich Null sein muss. In mathematischen Formeln ausgedrückt heißt das:
Da dir der Normalenvektor  nicht bekannt ist, aber
nicht bekannt ist, aber  eine Ebene der Schar
eine Ebene der Schar  ist, kannst du den Normalenvektor der Ebenenschar
ist, kannst du den Normalenvektor der Ebenenschar  verwenden und so einen passenden Wert für den Parameter
verwenden und so einen passenden Wert für den Parameter  ermitteln.
ermitteln.
 Folglich muss
Folglich muss  gelten, damit die Bedingung erfüllt wird. Das heißt, für
gelten, damit die Bedingung erfüllt wird. Das heißt, für  gilt
gilt  . Die Ebene
. Die Ebene  halt also folgende Ebenengleichung in Koordinatenform:
halt also folgende Ebenengleichung in Koordinatenform:

 Koordinaten des Punktes
Koordinaten des Punktes  ermitteln
Der Punkt
ermitteln
Der Punkt  liegt laut Voraussetzung in den Ebenen
liegt laut Voraussetzung in den Ebenen  und
und  . Folglich muss dieser Punkt ebenfalls auf der Schnittgeraden
. Folglich muss dieser Punkt ebenfalls auf der Schnittgeraden  der Ebenen liegen.
der Ebenen liegen.
Im Punkt schneidet die Ebene
schneidet die Ebene  die Gerade
die Gerade  , an welcher das Blatt gefaltet wird. Durch das Falten bewegt sich der Punkt
, an welcher das Blatt gefaltet wird. Durch das Falten bewegt sich der Punkt  entlang eines Halbkreises um den Punkt
entlang eines Halbkreises um den Punkt  und nimmt entlang dieses Halbkreises die Position
und nimmt entlang dieses Halbkreises die Position  ein. Das heißt, der Punkt
ein. Das heißt, der Punkt  hat den selben Abstand zum Punkt
hat den selben Abstand zum Punkt  wie der gesuchte Punkt
wie der gesuchte Punkt  , es gilt also
, es gilt also  .
.
 Du kann also wie folgt vorgehen, um die Koordinaten des Punktes
Du kann also wie folgt vorgehen, um die Koordinaten des Punktes  zu bestimmen:
zu bestimmen:
 der Ebenen
der Ebenen  und
und  bestimmen
Die Schnittgerade erhältst du, indem du beide Ebenengleichungen in einem linearen Gleichungssystem auflöst.
bestimmen
Die Schnittgerade erhältst du, indem du beide Ebenengleichungen in einem linearen Gleichungssystem auflöst.
 Damit sind die
Damit sind die  - und
- und  -Koordinaten der Geradengleichung fest. Da über die
-Koordinaten der Geradengleichung fest. Da über die  -Koordinate keine Aussage gemacht werden kann, kannst du für diese jeden beliebigen Wert einsetzen. Wir setzen also
-Koordinate keine Aussage gemacht werden kann, kannst du für diese jeden beliebigen Wert einsetzen. Wir setzen also  und erhalten die Gleichung der Schnittgeraden
und erhalten die Gleichung der Schnittgeraden  mit:
mit:
 Da der Punkt
Da der Punkt  auf der Schnittgeraden
auf der Schnittgeraden  liegt, kannst du die Koordinaten des Punktes
liegt, kannst du die Koordinaten des Punktes  in Abhängigkeit vom Parameter
in Abhängigkeit vom Parameter  angeben mit:
angeben mit:
 2. Schritt: Verwenden, dass
2. Schritt: Verwenden, dass  gelten muss
Offensichtlich ist nur noch die
gelten muss
Offensichtlich ist nur noch die  -Koordinate vom Parameter
-Koordinate vom Parameter  abhängig. Einen passenden Wert für
abhängig. Einen passenden Wert für  kannst du mit Hilfe der Bedingung
kannst du mit Hilfe der Bedingung  bestimmen.
Den Betrag
bestimmen.
Den Betrag  kannst du bereits berechnen, da dir die Koordinaten beider Punkte bekannt sind:
kannst du bereits berechnen, da dir die Koordinaten beider Punkte bekannt sind:
 Damit gilt
Damit gilt  und wir können diese Bedingung im Folgenden weiterverwenden:
und wir können diese Bedingung im Folgenden weiterverwenden:
 Damit muss
Damit muss  gelten. Nun kannst du die Koordinaten des Punktes
gelten. Nun kannst du die Koordinaten des Punktes  vollständig angeben:
vollständig angeben: 

|
|
Im Punkt

- Bestimme die Schnittgerade
der Ebenen
und
. (Dadurch erhältst du zunächst die erste und zweite Koordinate von
).
- Verwende, dass
gilt, um die dritte Koordinate zu bestimmen.
d)
 Bestimmen der Koordinaten des Punktes
Bestimmen der Koordinaten des Punktes 
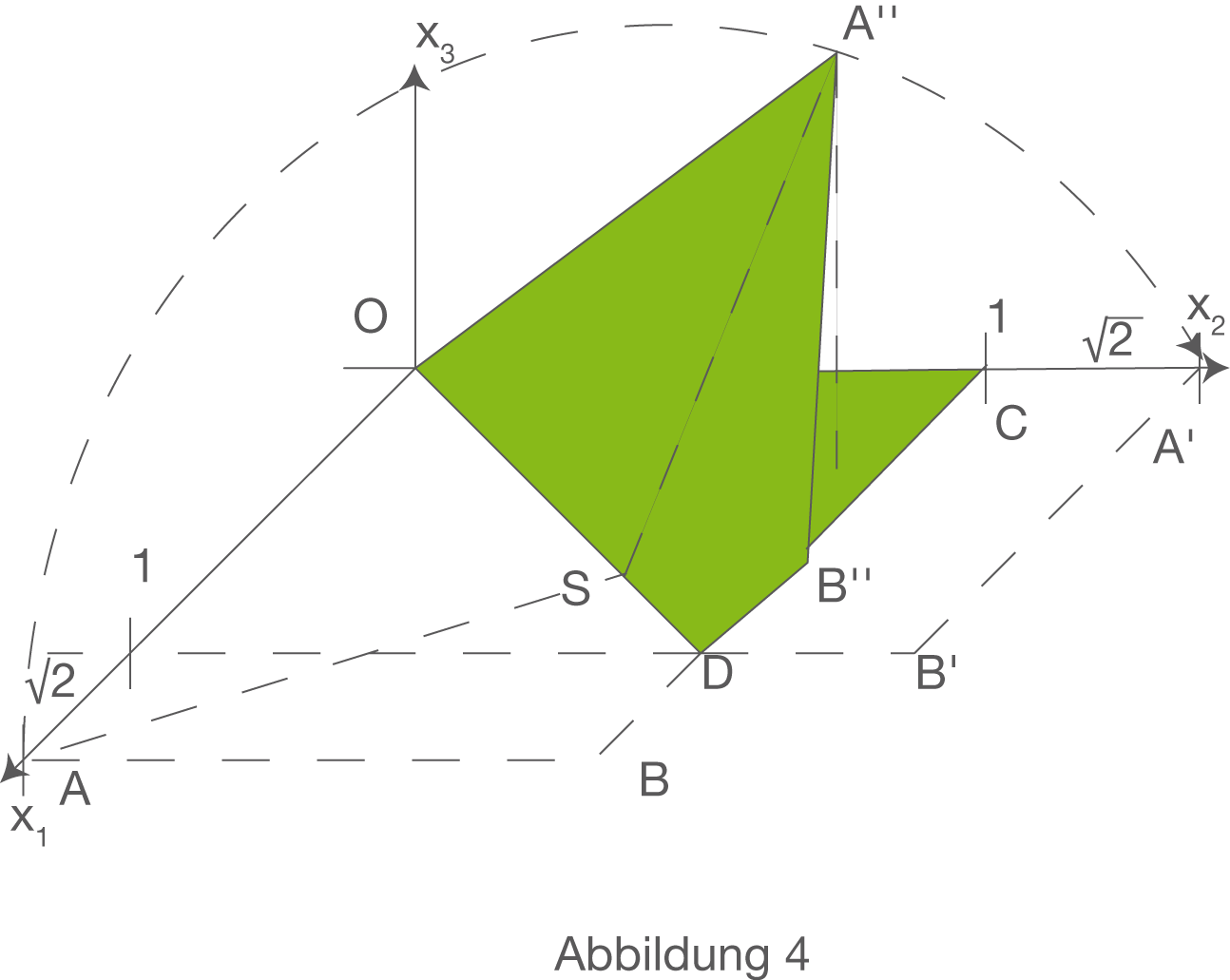 Beim Faltvorgang erreicht das Papierviereck die Position OA‘‘B‘‘D. Die Koordinaten des Punktes
Beim Faltvorgang erreicht das Papierviereck die Position OA‘‘B‘‘D. Die Koordinaten des Punktes  sind teilweise bekant mit:
sind teilweise bekant mit:
 .
Deine Aufgabe ist es, die vollständigen Koordinaten des Punktes
.
Deine Aufgabe ist es, die vollständigen Koordinaten des Punktes  anzugeben.
In einem Aufgabenteil zuvor hast du eine Ebene
anzugeben.
In einem Aufgabenteil zuvor hast du eine Ebene  ermittelt, in der sich der Halbkreis befindet, auf dem sich der Ausgangspunkt
ermittelt, in der sich der Halbkreis befindet, auf dem sich der Ausgangspunkt  entlang bewegt. Diese Ebene hat die folgende Ebenengleichung:
entlang bewegt. Diese Ebene hat die folgende Ebenengleichung:
 Daher muss auch der gesuchte Punkt
Daher muss auch der gesuchte Punkt  in dieser Ebene liegen. Das heißt, der Punkt
in dieser Ebene liegen. Das heißt, der Punkt  liegt auf der Schnittgeraden der Ebene
liegt auf der Schnittgeraden der Ebene  und der Ebene
und der Ebene  .
Weiterhin kannst du verwenden, dass sich durch das Falten der Punkt
.
Weiterhin kannst du verwenden, dass sich durch das Falten der Punkt  entlang eines Halbkreises um den Punkt
entlang eines Halbkreises um den Punkt  bewegt und entlang dieses Halbkreises die Position
bewegt und entlang dieses Halbkreises die Position  einnimmt. Das heißt, der Punkt
einnimmt. Das heißt, der Punkt  hat den selben Abstand zum Punkt
hat den selben Abstand zum Punkt  wie der gesuchte Punkt
wie der gesuchte Punkt  , es gilt also
, es gilt also  .
.
Du kann also wie folgt vorgehen, um die Koordinaten des Punktes zu bestimmen:
zu bestimmen:
 der Ebenen
der Ebenen  und
und  bestimmen
Die Schnittgerade erhältst du, indem du beide Ebenengleichungen in einem linearen Gleichungssystem auflöst.
bestimmen
Die Schnittgerade erhältst du, indem du beide Ebenengleichungen in einem linearen Gleichungssystem auflöst.
 Damit sind die
Damit sind die  - und
- und  -Koordinaten der Geradengleichung fest. Da über die
-Koordinaten der Geradengleichung fest. Da über die  -Koordinate keine Aussage gemacht werden kann, kannst du für diese jeden beliebigen Wert einsetzen. Wir setzen also
-Koordinate keine Aussage gemacht werden kann, kannst du für diese jeden beliebigen Wert einsetzen. Wir setzen also  und erhalten die Gleichung der Schnittgeraden
und erhalten die Gleichung der Schnittgeraden  mit:
mit:
 Da der Punkt
Da der Punkt  auf der Schnittgeraden
auf der Schnittgeraden  liegt, kannst du die Koordinaten des Punktes
liegt, kannst du die Koordinaten des Punktes  in Abhängigkeit vom Parameter
in Abhängigkeit vom Parameter  angeben mit:
angeben mit:
 2. Schritt: Verwenden, dass
2. Schritt: Verwenden, dass  gelten muss
Offensichtlich ist nur noch die
gelten muss
Offensichtlich ist nur noch die  -Koordinate vom Parameter
-Koordinate vom Parameter  abhängig. Einen passenden Wert für
abhängig. Einen passenden Wert für  kannst du mit Hilfe der Bedingung
kannst du mit Hilfe der Bedingung  bestimmen.
Den Betrag
bestimmen.
Den Betrag  hast du bereits zuvor berechnet und es gilt
hast du bereits zuvor berechnet und es gilt  . Wir können diese Bedingung im Folgenden weiterverwenden:
. Wir können diese Bedingung im Folgenden weiterverwenden:
 Damit muss
Damit muss  gelten. Nun kannst du die Koordinaten des Punktes
gelten. Nun kannst du die Koordinaten des Punktes  vollständig angeben:
vollständig angeben: 
 Zeigen, dass das Dreieck
Zeigen, dass das Dreieck  gleichschenklig rechtwinklig ist
Zeige, dass das Dreieck
gleichschenklig rechtwinklig ist
Zeige, dass das Dreieck  rechtwinklig und gleichschenklig ist. Dabei kannst du folgende Eigenschaften verwenden:
rechtwinklig und gleichschenklig ist. Dabei kannst du folgende Eigenschaften verwenden:
 rechtwinklig ist
Ein Dreieck ist rechtwinklig, wenn zwei Kantenvektoren senkrecht aufeinander stehen. Ist das der Fall, so ist ihr Skalarprodukt gleich Null. Gib zunächst die Kantenvektoren
rechtwinklig ist
Ein Dreieck ist rechtwinklig, wenn zwei Kantenvektoren senkrecht aufeinander stehen. Ist das der Fall, so ist ihr Skalarprodukt gleich Null. Gib zunächst die Kantenvektoren  ,
,  und
und  des Dreieck
des Dreieck  an:
an:
 ,
,  und
und  :
:
 und
und  gleich Null. Folglich ist das Dreieck
gleich Null. Folglich ist das Dreieck  rechtwinklig.
Zeigen, dass das Dreieck
rechtwinklig.
Zeigen, dass das Dreieck  gleichschenklig ist
Ein Dreieck ist gleichschenklig, wenn zwei Kanten gleich lang sind. Berechne also die Beträge der Vektoren und überprüfe, ob das der Fall ist:
gleichschenklig ist
Ein Dreieck ist gleichschenklig, wenn zwei Kanten gleich lang sind. Berechne also die Beträge der Vektoren und überprüfe, ob das der Fall ist:
 und
und  gleich lang. Folglich ist das Dreieck
gleich lang. Folglich ist das Dreieck  gleichschenklig.
gleichschenklig.

Du kann also wie folgt vorgehen, um die Koordinaten des Punktes
- Bestimme die Schnittgerade
der Ebenen
und
. (Dadurch erhältst du zunächst die erste Koordinate von
).
- Verwende, dass
gilt, um die dritte Koordinate zu bestimmen.
- Rechtwinklig: Soll das Dreieck
rechtwinklig sein, so kannst du zeigen, dass das Skalarprodukt zweier Kantenvektoren gleich Null ist.
- Gleichschenklig: Damit ein Dreieck gleichschenklig ist, müssen zwei Kanten gleich lang sein. Zeige also, dass der Betrag zweier Kantenvektoren übereinstimmt.
a)
 Abstand des Punktes
Abstand des Punktes  zur Geraden
zur Geraden  angeben
Ein DIN-A4-Blatt wird entlang der Strecke
angeben
Ein DIN-A4-Blatt wird entlang der Strecke  wie in Abbildung 1 und 2 gefaltet. Bestimme den Abstand des Punktes
wie in Abbildung 1 und 2 gefaltet. Bestimme den Abstand des Punktes  zur Geraden
zur Geraden  .
.
 Der Abstand eines Punktes zu einer Geraden entspricht der kürzesten Strecke, die den Punkt mit der Geraden verbindet.
Der Abstand eines Punktes zu einer Geraden entspricht der kürzesten Strecke, die den Punkt mit der Geraden verbindet.
 Diese Strecke muss folglich senkrecht auf der Geraden stehen. Daher entspricht der gesuchte Abstand gerade der Länge der Strecke
Diese Strecke muss folglich senkrecht auf der Geraden stehen. Daher entspricht der gesuchte Abstand gerade der Länge der Strecke  .
Um die Länge dieser Strecke
.
Um die Länge dieser Strecke  zu bestimmen, kannst du eine Hilfsgerade
zu bestimmen, kannst du eine Hilfsgerade  so konstruieren, dass sie senkrecht zur Geraden
so konstruieren, dass sie senkrecht zur Geraden  verläuft und den Punkt
verläuft und den Punkt  enthält.
enthält.
Bestimme den Schnittpunkt der Hilfgeraden
der Hilfgeraden  und der Geraden
und der Geraden  .
Hast du diesen bestimmt, so kannst du die Länge der Strecke
.
Hast du diesen bestimmt, so kannst du die Länge der Strecke  mit Hilfe des Betrags bestimmen.
Den Betrag einer Strecke
mit Hilfe des Betrags bestimmen.
Den Betrag einer Strecke  zweier Punkte
zweier Punkte  und
und  kannst du folgendermaßen bestimmen:
kannst du folgendermaßen bestimmen:
1. Schritt: Hilfsgerade  konstruieren
Bevor wir die Geradengleichung für
konstruieren
Bevor wir die Geradengleichung für  angeben können, ist es hilfreich, zuerst die Geradengleichung zu
angeben können, ist es hilfreich, zuerst die Geradengleichung zu  aufzustellen:
aufzustellen:
 Um die Gleichung der Hilfsgeraden
Um die Gleichung der Hilfsgeraden  zu bestimmen, gehen wir zunächst von einer allgemeinen Geradengleichung aus:
zu bestimmen, gehen wir zunächst von einer allgemeinen Geradengleichung aus:
 Dabei ist
Dabei ist  der Stützvektor und
der Stützvektor und  der Richtungsvektor. Für den Stützvektor
der Richtungsvektor. Für den Stützvektor  kannst du die Koordinaten eines Punktes verwenden, der garantiert auf der Geraden
kannst du die Koordinaten eines Punktes verwenden, der garantiert auf der Geraden  liegt. Hier bietet sich beispielweise der Punkt
liegt. Hier bietet sich beispielweise der Punkt  an. Du erhältst also folgenden Stützvektor:
an. Du erhältst also folgenden Stützvektor:
 Soll die Hilfsgerade
Soll die Hilfsgerade  senkrecht zur Geraden
senkrecht zur Geraden  sein, so muss das Skalarprodukt ihrer Richtungsvektoren gleich Null sein. Das heißt, es muss gelten:
sein, so muss das Skalarprodukt ihrer Richtungsvektoren gleich Null sein. Das heißt, es muss gelten:
 Damit das Skalarprodukt gleich Null ist, muss folglich
Damit das Skalarprodukt gleich Null ist, muss folglich  gelten. Du kannst hier jeden beliebigen Wert für
gelten. Du kannst hier jeden beliebigen Wert für  wählen. Da die Gerade
wählen. Da die Gerade  und der Punkt
und der Punkt  in der
in der  Ebene liegen, sollte ebenfalls
Ebene liegen, sollte ebenfalls  gelten.
gelten.
Wir wählen, um die Rechnung möglichst einfach zu halten, und erhalten dann folgende Geradengleichung zur Hilfsgeraden
und erhalten dann folgende Geradengleichung zur Hilfsgeraden  :
:
 2. Schritt: Schnittpunkt
2. Schritt: Schnittpunkt  der Hilfsgeraden
der Hilfsgeraden  mit der Geraden
mit der Geraden  bestimmen
Die Koordinaten des Schnittpunktes
bestimmen
Die Koordinaten des Schnittpunktes  der Hilfsgeraden
der Hilfsgeraden  und der Geraden
und der Geraden  kannst du bestimmen, indem du die beiden Geradengleichungen gleichsetzt:
kannst du bestimmen, indem du die beiden Geradengleichungen gleichsetzt:
 Dadurch erhältst du ein lineares Gleichungssystem, durch welches du Werte für die Parameter
Dadurch erhältst du ein lineares Gleichungssystem, durch welches du Werte für die Parameter  und
und  ermitteln kannst:
ermitteln kannst:

 Es muss also
Es muss also  bzw.
bzw.  gelten. Setze entweder den Parameterwert für
gelten. Setze entweder den Parameterwert für  in die Hilfsgeradengleichung oder den Parameterwert für
in die Hilfsgeradengleichung oder den Parameterwert für  in die Geradengleichung zu
in die Geradengleichung zu  ein. Das liefert dir die Koordinaten von
ein. Das liefert dir die Koordinaten von  .
.
 Jetzt kannst du die Koordinaten des Schnittpunktes
Jetzt kannst du die Koordinaten des Schnittpunktes  vollständig angeben mit:
vollständig angeben mit:
 3 Schritt: Abstand zwischen
3 Schritt: Abstand zwischen  und der Geraden
und der Geraden  berechnen
Zuvor hast du überlegt, dass der Abstand des Punktes
berechnen
Zuvor hast du überlegt, dass der Abstand des Punktes  zur Geraden
zur Geraden  gerade dem Abstand den Punktes
gerade dem Abstand den Punktes  zum Punkt
zum Punkt  entspricht. Berechne also:
entspricht. Berechne also:
 Damit hat der Punkt
Damit hat der Punkt  einen Abstand von
einen Abstand von  LE zur Geraden OD.
LE zur Geraden OD.


Bestimme den Schnittpunkt
|
|
Wir wählen, um die Rechnung möglichst einfach zu halten,
b)
 Gleichung der Ebene
Gleichung der Ebene  in Parameterform angeben
Das Blatt in der
in Parameterform angeben
Das Blatt in der  Ebene wird wie in Abbildung 1 und 2 gefaltet. Beim Faltvorgang „wandert“ der Punkt
Ebene wird wie in Abbildung 1 und 2 gefaltet. Beim Faltvorgang „wandert“ der Punkt  in die Position
in die Position  . Dabei bewegt sich der Punkt entlang eines Halbkreises. Die Ebene
. Dabei bewegt sich der Punkt entlang eines Halbkreises. Die Ebene  soll diesen Halbkreis enthalten und senkrecht zur
soll diesen Halbkreis enthalten und senkrecht zur  Ebene stehen.
Ebene stehen.
 Deine Aufgabe ist es, die Ebenengleichung zur Ebene
Deine Aufgabe ist es, die Ebenengleichung zur Ebene  in Parameterform anzugeben.
in Parameterform anzugeben.
Eine Ebenengleichung in Parameterform sieht wie folgt aus:
Der Vektor  wird Stützvektor genannt,
wird Stützvektor genannt,  und
und  sind die linear unabhängigen Spannvektoren der Ebene
sind die linear unabhängigen Spannvektoren der Ebene  .
Stelle die gesuchten Stütz- und Spannvektoren auf, um eine Ebenengleichung in Parameterform zu erhalten.
1. Schritt: Stützvektor der Ebene
.
Stelle die gesuchten Stütz- und Spannvektoren auf, um eine Ebenengleichung in Parameterform zu erhalten.
1. Schritt: Stützvektor der Ebene  aufstellen
Für den Stützvektor kannst du die Koordinaten eines Punktes verwenden, der garantiert in der Ebene liegt. Hier bietet sich beispielweise der Punkt
aufstellen
Für den Stützvektor kannst du die Koordinaten eines Punktes verwenden, der garantiert in der Ebene liegt. Hier bietet sich beispielweise der Punkt  an. Es ergibt sich also:
an. Es ergibt sich also:
 2. Schritt: Spannvektor
2. Schritt: Spannvektor  der Ebene
der Ebene  aufstellen
Da in der Aufgabenstellung verlangt wird, dass die Ebene
aufstellen
Da in der Aufgabenstellung verlangt wird, dass die Ebene  senkrecht auf der
senkrecht auf der  Ebene steht, kannst du einen der Spannvektoren direkt angeben, der diese Bedingung erfüllt:
Ebene steht, kannst du einen der Spannvektoren direkt angeben, der diese Bedingung erfüllt:
 3. Schritt: Spannvektor
3. Schritt: Spannvektor  der Ebene
der Ebene  aufstellen
Sollen weiterhin die Punkte
aufstellen
Sollen weiterhin die Punkte  und
und  in der Ebene
in der Ebene  enthalten sein, so muss auch ihre Verbindungsstrecke in der Ebene
enthalten sein, so muss auch ihre Verbindungsstrecke in der Ebene  liegen. Das heißt, du kannst den Vektor
liegen. Das heißt, du kannst den Vektor  als zweiten Spannvektor verwenden.
als zweiten Spannvektor verwenden.
 Offensichtlich benötigen wir die Koordinaten des Punktes
Offensichtlich benötigen wir die Koordinaten des Punktes  , um den zweiten Spannvektor angeben zu können. Anhand Abbildung 3 kannst du die Koordinaten ablesen. Der Punkt
, um den zweiten Spannvektor angeben zu können. Anhand Abbildung 3 kannst du die Koordinaten ablesen. Der Punkt  hat die Koordinaten
hat die Koordinaten  . Damit kannst du nun den Vektor
. Damit kannst du nun den Vektor  bestimmen:
bestimmen:
 4. Schritt: Aufgestellte Vektoren in Ebenengleichung einsetzen
Einsetzen des Stützvektors
4. Schritt: Aufgestellte Vektoren in Ebenengleichung einsetzen
Einsetzen des Stützvektors  und der Spannvektoren
und der Spannvektoren  und
und  in die allgemeine Form einer Ebenengleichung in Parameterform liefert dir die gesuchte Gleichung:
in die allgemeine Form einer Ebenengleichung in Parameterform liefert dir die gesuchte Gleichung:

 Gleichung der Ebene
Gleichung der Ebene  in Normalenform angeben
Die Normalenform einer Ebenengleichung kannst du allgemein wie folgt angeben:
in Normalenform angeben
Die Normalenform einer Ebenengleichung kannst du allgemein wie folgt angeben:
Dabei ist  der Stützvektor und
der Stützvektor und  der Normalenvektor der Ebene. Beim Stützvektor kannst du wie zuvor vorgehen: Wähle einen Punkt, der garantiert in der Ebene
der Normalenvektor der Ebene. Beim Stützvektor kannst du wie zuvor vorgehen: Wähle einen Punkt, der garantiert in der Ebene  liegt und verwende dessen Koordinaten für den Stützvektor. Du kannst hier beispielsweise denselben Stützvektor
liegt und verwende dessen Koordinaten für den Stützvektor. Du kannst hier beispielsweise denselben Stützvektor  wählen, den du bereits bei der Parameterform gewählt hast.
wählen, den du bereits bei der Parameterform gewählt hast.
Letztlich benötigst du nur noch den Normalenvektor . Dafür bieten sich zwei Möglichkeiten an:
. Dafür bieten sich zwei Möglichkeiten an:
 Lösungsweg A: Koordinatenform
Eine Ebenengleichung in Koordinatenform ist allgemein von der Form:
Lösungsweg A: Koordinatenform
Eine Ebenengleichung in Koordinatenform ist allgemein von der Form:
Hast du bereits eine Ebenengleichung der Ebene in Parameterform, so kannst du die Koordinatenform ermitteln, indem du die Ebenengleichung in Parameterform mit  ,
,  und
und  wie folgt gleichsetzt:
wie folgt gleichsetzt:
 Daraus erhältst du ein lineares Gleichungssystem, bei welchem du die Parameter
Daraus erhältst du ein lineares Gleichungssystem, bei welchem du die Parameter  und
und  eliminieren musst, um die Koordinatenform zu erhalten.
eliminieren musst, um die Koordinatenform zu erhalten.
 In der Gleichung
In der Gleichung  sind nun beide Parameter eliminiert. Das heißt, die Ebenengleichung zur Ebene
sind nun beide Parameter eliminiert. Das heißt, die Ebenengleichung zur Ebene  in Koordinatenform lautet:
in Koordinatenform lautet:
 Hier kannst du den Normalenvektor direkt ablesen mit:
Hier kannst du den Normalenvektor direkt ablesen mit:

 Lösungsweg B: Kreuzprodukt
Da der Normalenvektor
Lösungsweg B: Kreuzprodukt
Da der Normalenvektor  senkrecht auf beiden Spannvektoren
senkrecht auf beiden Spannvektoren  und
und  stehen soll, kannst du deren Kreuzprodukt bilden:
stehen soll, kannst du deren Kreuzprodukt bilden:
 Da bei einem Normalenvektor nur dessen Richtung und nicht dessen Länge relevant ist, kannst du diesen wie folgt vereinfachen:
Da bei einem Normalenvektor nur dessen Richtung und nicht dessen Länge relevant ist, kannst du diesen wie folgt vereinfachen:

 In allgemeine Normalenform einsetzen:
Da du den Normalenvektor
In allgemeine Normalenform einsetzen:
Da du den Normalenvektor  bestimmt hast und den Stützvektor aus der Parameterform wiederverwenden kannst, ergibt sich folgende Gleichung der Ebene
bestimmt hast und den Stützvektor aus der Parameterform wiederverwenden kannst, ergibt sich folgende Gleichung der Ebene  in Normalenform:
in Normalenform:

 Koordinaten des Schnittpunktes
Koordinaten des Schnittpunktes  bestimmen
Die Gerade
bestimmen
Die Gerade  schneidet die Ebene
schneidet die Ebene  in einem Punkt
in einem Punkt  . Um den Schnittpunkt einer Geraden mit einer Ebene zu ermitteln, kannst du die Geradengleichung komponentenweise in die zuvor bestimme Ebenengleichung in Parameterform einsetzen. Gehe also wie folgt vor:
. Um den Schnittpunkt einer Geraden mit einer Ebene zu ermitteln, kannst du die Geradengleichung komponentenweise in die zuvor bestimme Ebenengleichung in Parameterform einsetzen. Gehe also wie folgt vor:
 mit Ebenengleichung von
mit Ebenengleichung von  gleichsetzen
Komponentenweise Gleichsetzen der Geradengleichung mit der Ebenengleichung von
gleichsetzen
Komponentenweise Gleichsetzen der Geradengleichung mit der Ebenengleichung von  liefert dir folgendes lineares Gleichungssystem, welches du nach
liefert dir folgendes lineares Gleichungssystem, welches du nach  auflösen sollst:
auflösen sollst:
 Du erhältst
Du erhältst  .
2. Schritt: Parameter
.
2. Schritt: Parameter  in Geradengleichung von
in Geradengleichung von  einsetzen
Einsetzen von
einsetzen
Einsetzen von  in die Geradengleichung zu
in die Geradengleichung zu  liefert dir die Koordinaten des Schnittpunktes
liefert dir die Koordinaten des Schnittpunktes  :
:
 Der Schnittpunkt
Der Schnittpunkt  besitzt die Koordinaten
besitzt die Koordinaten  .
.

Eine Ebenengleichung in Parameterform sieht wie folgt aus:
|
|
|
|
Letztlich benötigst du nur noch den Normalenvektor
| A: | Stelle die Ebenengleichung in Koordinatenform auf, denn an dieser kannst du den Normalenvektor direkt ablesen. |
| B: | Da der Normalenvektor senkrecht auf der Ebene |
|
|
- Setze diese Geradengleichung komponentenweise in die Ebenengleichung von
ein und löse nach dem Parameter
auf. Dadurch erhältst du einen Wert für den Parameter
.
- Setze diesen Parameterwert für
anschließend in die Geradengleichung von
ein. Das liefert dir die Koordinaten des gesuchten Schnittpunktes
.
c)
 Nachweisen, dass Gerade
Nachweisen, dass Gerade  in jeder Ebene der Ebenenschar liegt
Während des Faltvorgangs liegt das bewegte Papierviereck immer in einer Ebene der Ebenenschar mit der Ebenengleichung
in jeder Ebene der Ebenenschar liegt
Während des Faltvorgangs liegt das bewegte Papierviereck immer in einer Ebene der Ebenenschar mit der Ebenengleichung
 Weise rechnerisch nach, dass die Gerade
Weise rechnerisch nach, dass die Gerade  in jeder Ebene
in jeder Ebene  liegt.
Willst du zeigen, dass die Gerade
liegt.
Willst du zeigen, dass die Gerade  in jeder Ebene
in jeder Ebene  liegt, so kannst du die Gleichung der Gerade in die Gleichung der Ebenenschar einsetzen. Löse nach deren Parametern
liegt, so kannst du die Gleichung der Gerade in die Gleichung der Ebenenschar einsetzen. Löse nach deren Parametern  und
und  auf. Ergibt sich hierbei eine wahre Aussage für alle
auf. Ergibt sich hierbei eine wahre Aussage für alle  und
und  , so liegt die Gerade
, so liegt die Gerade  in jeder Ebene
in jeder Ebene  .
Die Gleichung der Gerade
.
Die Gleichung der Gerade  hast du zuvor bereits aufgestellt mit:
hast du zuvor bereits aufgestellt mit:
 Komponentenweise Einsetzen liefert dir:
Komponentenweise Einsetzen liefert dir:
 In diese Gleichung kannst du jeden beliebigen Wert für den Parameter
In diese Gleichung kannst du jeden beliebigen Wert für den Parameter  bzw.
bzw.  einsetzen. Das heißt, es liegt immer eine wahre Aussage vor und damit gilt, dass die Gerade
einsetzen. Das heißt, es liegt immer eine wahre Aussage vor und damit gilt, dass die Gerade  in jeder Ebene
in jeder Ebene  liegt.
liegt.
 Nachweisen, dass die Ebene
Nachweisen, dass die Ebene  senkrecht zu jeder Ebene der Ebenenschar ist
Die Ebene
senkrecht zu jeder Ebene der Ebenenschar ist
Die Ebene  hat laut Teilaufgabe b) folgende Ebenengleichung:
hat laut Teilaufgabe b) folgende Ebenengleichung:
 Willst du zeigen, dass die Ebene senkrecht zu jeder Ebene
Willst du zeigen, dass die Ebene senkrecht zu jeder Ebene  ist, so kannst du zeigen, dass die Normalenvektoren
ist, so kannst du zeigen, dass die Normalenvektoren  und
und  senkrecht zueinander sind. Das heißt, ihr Skalarprodukt ist gleich Null.
Die Normalenvektoren
senkrecht zueinander sind. Das heißt, ihr Skalarprodukt ist gleich Null.
Die Normalenvektoren  und
und  der Ebene
der Ebene  und
und  kannst du anhand der Koordinatenform direkt ablesen:
kannst du anhand der Koordinatenform direkt ablesen:
 Bildest du das Skalarprodukt der Normalenvektoren, so erhältst du:
Bildest du das Skalarprodukt der Normalenvektoren, so erhältst du:
 Damit hast du gezeigt, dass das Skalarprodukt der Normalenvektoren für jedes
Damit hast du gezeigt, dass das Skalarprodukt der Normalenvektoren für jedes  gleich Null ist. Folglich steht die Ebene
gleich Null ist. Folglich steht die Ebene  senkrecht auf allen Ebenen der Schar
senkrecht auf allen Ebenen der Schar  .
.
 Parameter
Parameter  für
für  bestimmen, sodass
bestimmen, sodass  gilt
gilt
 Während des Faltvorgangs nehmen die Punkte
Während des Faltvorgangs nehmen die Punkte  und
und  die Positionen
die Positionen  und
und  ein.
Eine neue Ebene
ein.
Eine neue Ebene  soll nun das daraus entstehende Viereck
soll nun das daraus entstehende Viereck  enthalten. Weiterhin ist
enthalten. Weiterhin ist  eine Ebene der Ebenenschar
eine Ebene der Ebenenschar  und senkrecht zur
und senkrecht zur  Ebene.
Deine Aufgabe ist es, einen Parameterwert für
Ebene.
Deine Aufgabe ist es, einen Parameterwert für  zu ermitteln, sodass
zu ermitteln, sodass  gilt.
Soll
gilt.
Soll  senkrecht zur
senkrecht zur  Ebene sein, kannst du verwenden, dass das Skalarprodukt des Normalenvektors der
Ebene sein, kannst du verwenden, dass das Skalarprodukt des Normalenvektors der  Ebene und des Normalenvektors der Ebene
Ebene und des Normalenvektors der Ebene  gleich Null sein muss. In mathematischen Formeln ausgedrückt heißt das:
gleich Null sein muss. In mathematischen Formeln ausgedrückt heißt das:
Da dir der Normalenvektor  nicht bekannt ist, aber
nicht bekannt ist, aber  eine Ebene der Schar
eine Ebene der Schar  ist, kannst du den Normalenvektor der Ebenenschar
ist, kannst du den Normalenvektor der Ebenenschar  verwenden und so einen passenden Wert für den Parameter
verwenden und so einen passenden Wert für den Parameter  ermitteln.
ermitteln.
 Folglich muss
Folglich muss  gelten, damit die Bedingung erfüllt wird. Das heißt, für
gelten, damit die Bedingung erfüllt wird. Das heißt, für  gilt
gilt  . Die Ebene
. Die Ebene  halt also folgende Ebenengleichung in Koordinatenform:
halt also folgende Ebenengleichung in Koordinatenform:

 Koordinaten des Punktes
Koordinaten des Punktes  ermitteln
Der Punkt
ermitteln
Der Punkt  liegt laut Voraussetzung in den Ebenen
liegt laut Voraussetzung in den Ebenen  und
und  . Folglich muss dieser Punkt ebenfalls auf der Schnittgeraden
. Folglich muss dieser Punkt ebenfalls auf der Schnittgeraden  der Ebenen liegen.
der Ebenen liegen.
Im Punkt schneidet die Ebene
schneidet die Ebene  die Gerade
die Gerade  , an welcher das Blatt gefaltet wird. Durch das Falten bewegt sich der Punkt
, an welcher das Blatt gefaltet wird. Durch das Falten bewegt sich der Punkt  entlang eines Halbkreises um den Punkt
entlang eines Halbkreises um den Punkt  und nimmt entlang dieses Halbkreises die Position
und nimmt entlang dieses Halbkreises die Position  ein. Das heißt, der Punkt
ein. Das heißt, der Punkt  hat den selben Abstand zum Punkt
hat den selben Abstand zum Punkt  wie der gesuchte Punkt
wie der gesuchte Punkt  , es gilt also
, es gilt also  .
.
 Du kann also wie folgt vorgehen, um die Koordinaten des Punktes
Du kann also wie folgt vorgehen, um die Koordinaten des Punktes  zu bestimmen:
zu bestimmen:
 der Ebenen
der Ebenen  und
und  bestimmen
Die Schnittgerade erhältst du, indem du beide Ebenengleichungen in einem linearen Gleichungssystem auflöst.
bestimmen
Die Schnittgerade erhältst du, indem du beide Ebenengleichungen in einem linearen Gleichungssystem auflöst.
 Damit sind die
Damit sind die  - und
- und  -Koordinaten der Geradengleichung fest. Da über die
-Koordinaten der Geradengleichung fest. Da über die  -Koordinate keine Aussage gemacht werden kann, kannst du für diese jeden beliebigen Wert einsetzen. Wir setzen also
-Koordinate keine Aussage gemacht werden kann, kannst du für diese jeden beliebigen Wert einsetzen. Wir setzen also  und erhalten die Gleichung der Schnittgeraden
und erhalten die Gleichung der Schnittgeraden  mit:
mit:
 Da der Punkt
Da der Punkt  auf der Schnittgeraden
auf der Schnittgeraden  liegt, kannst du die Koordinaten des Punktes
liegt, kannst du die Koordinaten des Punktes  in Abhängigkeit vom Parameter
in Abhängigkeit vom Parameter  angeben mit:
angeben mit:
 2. Schritt: Verwenden, dass
2. Schritt: Verwenden, dass  gelten muss
Offensichtlich ist nur noch die
gelten muss
Offensichtlich ist nur noch die  -Koordinate vom Parameter
-Koordinate vom Parameter  abhängig. Einen passenden Wert für
abhängig. Einen passenden Wert für  kannst du mit Hilfe der Bedingung
kannst du mit Hilfe der Bedingung  bestimmen.
Den Betrag
bestimmen.
Den Betrag  kannst du bereits berechnen, da dir die Koordinaten beider Punkte bekannt sind:
kannst du bereits berechnen, da dir die Koordinaten beider Punkte bekannt sind:
 Damit gilt
Damit gilt  und wir können diese Bedingung im Folgenden weiterverwenden:
und wir können diese Bedingung im Folgenden weiterverwenden:
 Damit muss
Damit muss  gelten. Nun kannst du die Koordinaten des Punktes
gelten. Nun kannst du die Koordinaten des Punktes  vollständig angeben:
vollständig angeben: 

|
|
Im Punkt

- Bestimme die Schnittgerade
der Ebenen
und
. (Dadurch erhältst du zunächst die erste und zweite Koordinate von
).
- Verwende, dass
gilt, um die dritte Koordinate zu bestimmen.
d)
 Bestimmen der Koordinaten des Punktes
Bestimmen der Koordinaten des Punktes 
 Beim Faltvorgang erreicht das Papierviereck die Position OA‘‘B‘‘D. Die Koordinaten des Punktes
Beim Faltvorgang erreicht das Papierviereck die Position OA‘‘B‘‘D. Die Koordinaten des Punktes  sind teilweise bekant mit:
sind teilweise bekant mit:
 .
Deine Aufgabe ist es, die vollständigen Koordinaten des Punktes
.
Deine Aufgabe ist es, die vollständigen Koordinaten des Punktes  anzugeben.
In einem Aufgabenteil zuvor hast du eine Ebene
anzugeben.
In einem Aufgabenteil zuvor hast du eine Ebene  ermittelt, in der sich der Halbkreis befindet, auf dem sich der Ausgangspunkt
ermittelt, in der sich der Halbkreis befindet, auf dem sich der Ausgangspunkt  entlang bewegt. Diese Ebene hat die folgende Ebenengleichung:
entlang bewegt. Diese Ebene hat die folgende Ebenengleichung:
 Daher muss auch der gesuchte Punkt
Daher muss auch der gesuchte Punkt  in dieser Ebene liegen. Das heißt, der Punkt
in dieser Ebene liegen. Das heißt, der Punkt  liegt auf der Schnittgeraden der Ebene
liegt auf der Schnittgeraden der Ebene  und der Ebene
und der Ebene  .
Weiterhin kannst du verwenden, dass sich durch das Falten der Punkt
.
Weiterhin kannst du verwenden, dass sich durch das Falten der Punkt  entlang eines Halbkreises um den Punkt
entlang eines Halbkreises um den Punkt  bewegt und entlang dieses Halbkreises die Position
bewegt und entlang dieses Halbkreises die Position  einnimmt. Das heißt, der Punkt
einnimmt. Das heißt, der Punkt  hat den selben Abstand zum Punkt
hat den selben Abstand zum Punkt  wie der gesuchte Punkt
wie der gesuchte Punkt  , es gilt also
, es gilt also  .
.
Du kann also wie folgt vorgehen, um die Koordinaten des Punktes zu bestimmen:
zu bestimmen:
 der Ebenen
der Ebenen  und
und  bestimmen
Die Schnittgerade erhältst du, indem du beide Ebenengleichungen in einem linearen Gleichungssystem auflöst.
bestimmen
Die Schnittgerade erhältst du, indem du beide Ebenengleichungen in einem linearen Gleichungssystem auflöst.
 Damit sind die
Damit sind die  - und
- und  -Koordinaten der Geradengleichung fest. Da über die
-Koordinaten der Geradengleichung fest. Da über die  -Koordinate keine Aussage gemacht werden kann, kannst du für diese jeden beliebigen Wert einsetzen. Wir setzen also
-Koordinate keine Aussage gemacht werden kann, kannst du für diese jeden beliebigen Wert einsetzen. Wir setzen also  und erhalten die Gleichung der Schnittgeraden
und erhalten die Gleichung der Schnittgeraden  mit:
mit:
 Da der Punkt
Da der Punkt  auf der Schnittgeraden
auf der Schnittgeraden  liegt, kannst du die Koordinaten des Punktes
liegt, kannst du die Koordinaten des Punktes  in Abhängigkeit vom Parameter
in Abhängigkeit vom Parameter  angeben mit:
angeben mit:
 2. Schritt: Verwenden, dass
2. Schritt: Verwenden, dass  gelten muss
Offensichtlich ist nur noch die
gelten muss
Offensichtlich ist nur noch die  -Koordinate vom Parameter
-Koordinate vom Parameter  abhängig. Einen passenden Wert für
abhängig. Einen passenden Wert für  kannst du mit Hilfe der Bedingung
kannst du mit Hilfe der Bedingung  bestimmen.
Den Betrag
bestimmen.
Den Betrag  hast du bereits zuvor berechnet und es gilt
hast du bereits zuvor berechnet und es gilt  . Wir können diese Bedingung im Folgenden weiterverwenden:
. Wir können diese Bedingung im Folgenden weiterverwenden:
 Damit muss
Damit muss  gelten. Nun kannst du die Koordinaten des Punktes
gelten. Nun kannst du die Koordinaten des Punktes  vollständig angeben:
vollständig angeben: 
 Zeigen, dass das Dreieck
Zeigen, dass das Dreieck  gleichschenklig rechtwinklig ist
Zeige, dass das Dreieck
gleichschenklig rechtwinklig ist
Zeige, dass das Dreieck  rechtwinklig und gleichschenklig ist. Dabei kannst du folgende Eigenschaften verwenden:
rechtwinklig und gleichschenklig ist. Dabei kannst du folgende Eigenschaften verwenden:
 rechtwinklig ist
Ein Dreieck ist rechtwinklig, wenn zwei Kantenvektoren senkrecht aufeinander stehen. Ist das der Fall, so ist ihr Skalarprodukt gleich Null. Gib zunächst die Kantenvektoren
rechtwinklig ist
Ein Dreieck ist rechtwinklig, wenn zwei Kantenvektoren senkrecht aufeinander stehen. Ist das der Fall, so ist ihr Skalarprodukt gleich Null. Gib zunächst die Kantenvektoren  ,
,  und
und  des Dreieck
des Dreieck  an:
an:
 ,
,  und
und  :
:
 und
und  gleich Null. Folglich ist das Dreieck
gleich Null. Folglich ist das Dreieck  rechtwinklig.
Zeigen, dass das Dreieck
rechtwinklig.
Zeigen, dass das Dreieck  gleichschenklig ist
Ein Dreieck ist gleichschenklig, wenn zwei Kanten gleich lang sind. Berechne also die Beträge der Vektoren und überprüfe, ob das der Fall ist:
gleichschenklig ist
Ein Dreieck ist gleichschenklig, wenn zwei Kanten gleich lang sind. Berechne also die Beträge der Vektoren und überprüfe, ob das der Fall ist:
 und
und  gleich lang. Folglich ist das Dreieck
gleich lang. Folglich ist das Dreieck  gleichschenklig.
gleichschenklig.

Du kann also wie folgt vorgehen, um die Koordinaten des Punktes
- Bestimme die Schnittgerade
der Ebenen
und
. (Dadurch erhältst du zunächst die erste Koordinate von
).
- Verwende, dass
gilt, um die dritte Koordinate zu bestimmen.
- Rechtwinklig: Soll das Dreieck
rechtwinklig sein, so kannst du zeigen, dass das Skalarprodukt zweier Kantenvektoren gleich Null ist.
- Gleichschenklig: Damit ein Dreieck gleichschenklig ist, müssen zwei Kanten gleich lang sein. Zeige also, dass der Betrag zweier Kantenvektoren übereinstimmt.