Aufgabe 1

Aufgabenstellung

Ein Schüler beobachtet in einem Experiment insgesamt sechs Tage lang die Vermehrung von Pantoffeltierchen in einer Nährlösung. Zur Modellierung der Anzahl der Pantoffeltierchen während der ersten drei Tage verwendet er für $0\leq t \leq 3$ die Funktion $N_1$ mit der Gleichung

$N_{1}(t)=500\cdot\mathrm{e}^{0,6\cdot t}$ , $t\in\mathbb{R}$ .

Dabei wird $t$ als Maßzahl zur Einheit 1 Tag und $N_{1}(t)$ als Anzahl der Pantoffeltierchen zum Zeitpunkt $t$ aufgefasst.

Der Graph von $N_1$ ist in der Abbildung 1 dargestellt.

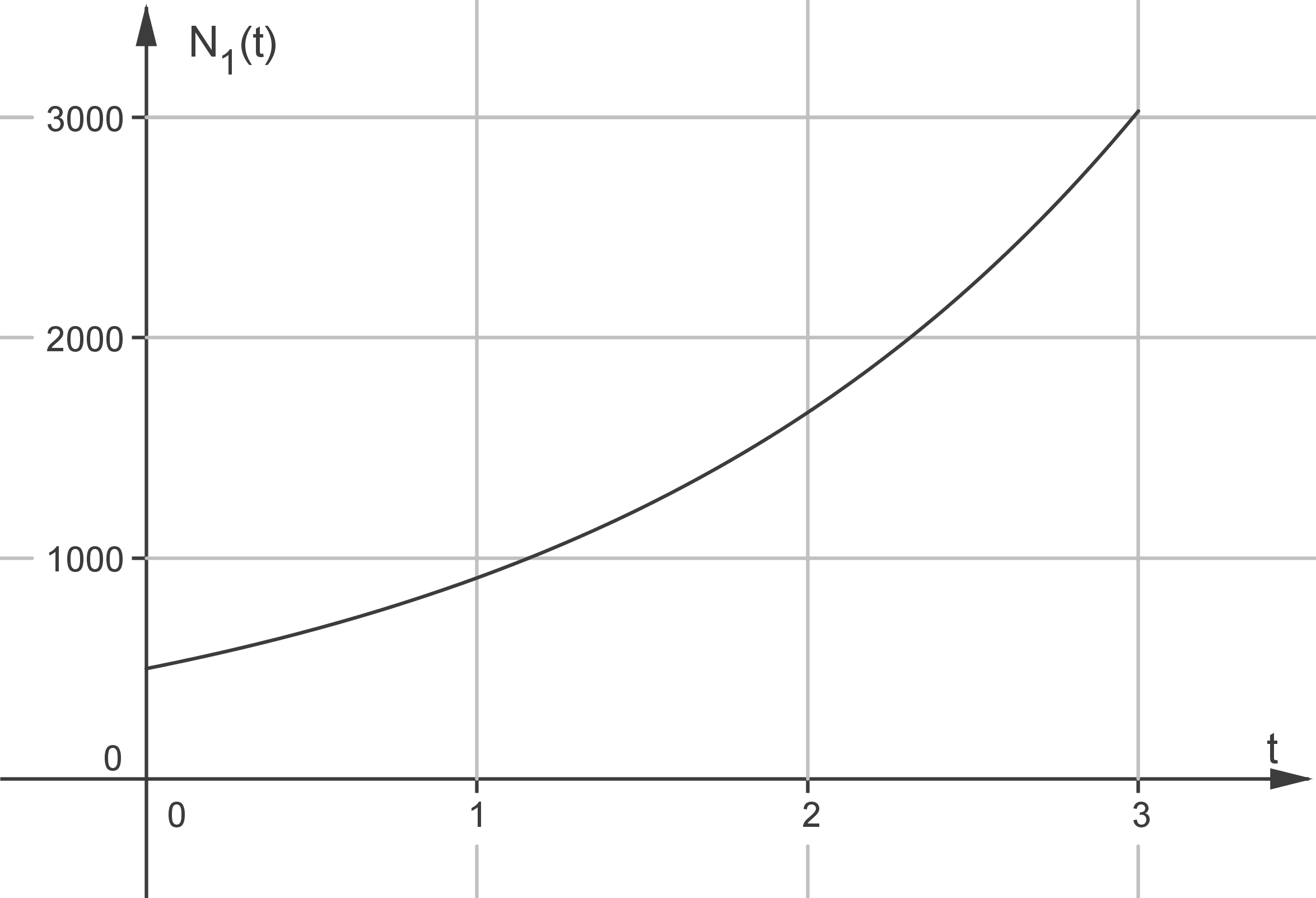Grafik eines Graphen mit einer Kurve, die N(t) über der Zeit t darstellt.

Abbildung 1

a) (1) Berechne den Funktionswert von $N_1$ an der Stelle $t=3$ und interpretiere diesen Wert im Sachzusammenhang.

(2P)

(2) Bestimme rechnerisch den Zeitpunkt, zu dem $2.000$ Pantoffeltierchen in der Nährlösung vorhanden sind.

(3P)

(3) Berechne die durchschnittliche Anzahl von Pantoffeltierchen in der Nährlösung während des ersten halben Tages der Beobachtung.

[Zur Kontrolle: Die durchschnittliche Anzahl von Pantoffeltierchen in der Nährlösung während des ersten halben Tages der Beobachtung beträgt ungefähr $583$ .]

(5P)

(4) Der Schüler berechnet einen Näherungswert für die durchschnittliche Anzahl von Pantoffeltierchen in der Nährlösung während des ersten halben Tages, indem er das arithmetische Mittel der Funktionswerte $N_1(0)$ und $N_1(0,5)$ bildet.

Zeige, dass das arithmetische Mittel der Funktionswerte $N_1(0)$ und $N_1(0,5)$ um weniger als $1\,$ % von dem in (3) berechneten Durchschnitt abweicht.

(4P)

(5) Weise nach, dass die prozentuale Abweichung des arithmetischen Mittels der Funktionswerte $N_1(a)$ und $N_1(a+0,5)$ von der durchschnittlichen Anzahl der Pantoffeltierchen in der Nährlösung in einem Zeitintervall $[a; a+0,5]$ mit $0\leq a\leq 2,5$ unabhängig von $a$ weniger als $1\,$ % beträgt.

(7P)

b) Während der ersten drei Tage (für $0\leq t\leq 3$ ) wird im Modell des Schülers die momentane Änderungsrate der Anzahl der Pantoffeltierchen durch die Funktion $r_1$ mit der Gleichung

$r_{1}(t)=300\cdot\mathrm{e}^{0,6\cdot t}$ , $t\in\mathbb{R}$ ,

beschrieben.

Dabei wird $r_{1}(t)$ als Maßzahl zur Einheit 1 Tier pro Tag aufgefasst.

(1) Für die Funktion $r_1$ und die zugehörige Ableitungsfunktion $r_{1}‘$ gilt für alle $t\in\mathbb{R}$ die Aussage:

$r_{1}(t)>0$ und $r_{1}‘(t)>0.$

[Die Gültigkeit dieser Aussage musst du nicht nachweisen.]

Interpretiere die Bedeutung dieser Aussage im Sachzusammenhang.

(5P)

(2) Ermittle die größte momentane Änderungsrate der Anzahl der Pantoffeltierchen in der Nährlösung in den ersten drei Tagen.

(4P)

c) Bei der weiteren Beobachtung erkennt der Schüler, dass nach etwa drei Tagen die momentane Änderungsrate der Anzahl der Pantoffeltierchen geringer wird. Um die Entwicklung ab dem Zeitpunkt $t=3$ zu prognostizieren, sucht er eine Funktion, für deren momentane Änderungsrate $r_2$ zu jedem Zeitpunkt $t=3+a$ mit $0\leq a\leq 3$ die Gleichung $r_2(3+a)=r_1(3-a)$ gilt.

(1) Interpretiere die Bedeutung der Gleichung $r_2(3+a)=r_1(3-a)$ , $0\leq a\leq 3$ , im Sachzusammenhang.

(3P)

(2) Leite aus der Gleichung $r_1(t)=300\cdot \mathrm{e}^{0,6\cdot t}$ für die momentane Änderungsrate $r_1$ und der Gleichung $r_2(3+a)=r_1(3-a)$ , $0\leq a\leq 3$ , die Gleichung

$r_2(t)=300\cdot \mathrm{e}^{3,6-0,6\cdot t}, 3\leq t \leq 6,$

zur Modellierung der momentanen Änderungsrate der Anzahl der Pantoffeltierchen nach dem dritten Tag her.

(4P)

(3) Ermittle ausgehend von den Funktionen $N_1$ und $r_2$ eine Gleichung der Funktion $N_2$ , durch die die Anzahl der Pantoffeltierchen nach dem dritten Tag bis zum Ende der Beobachtung (also für $3\leq t\leq 6$ ) beschrieben werden kann.

[Zur Kontrolle: $N_2(t)=1.000\cdot \mathrm{e}^{1,8}-500\cdot\mathrm{e}^{3,6-0,6\cdot t}$ .]

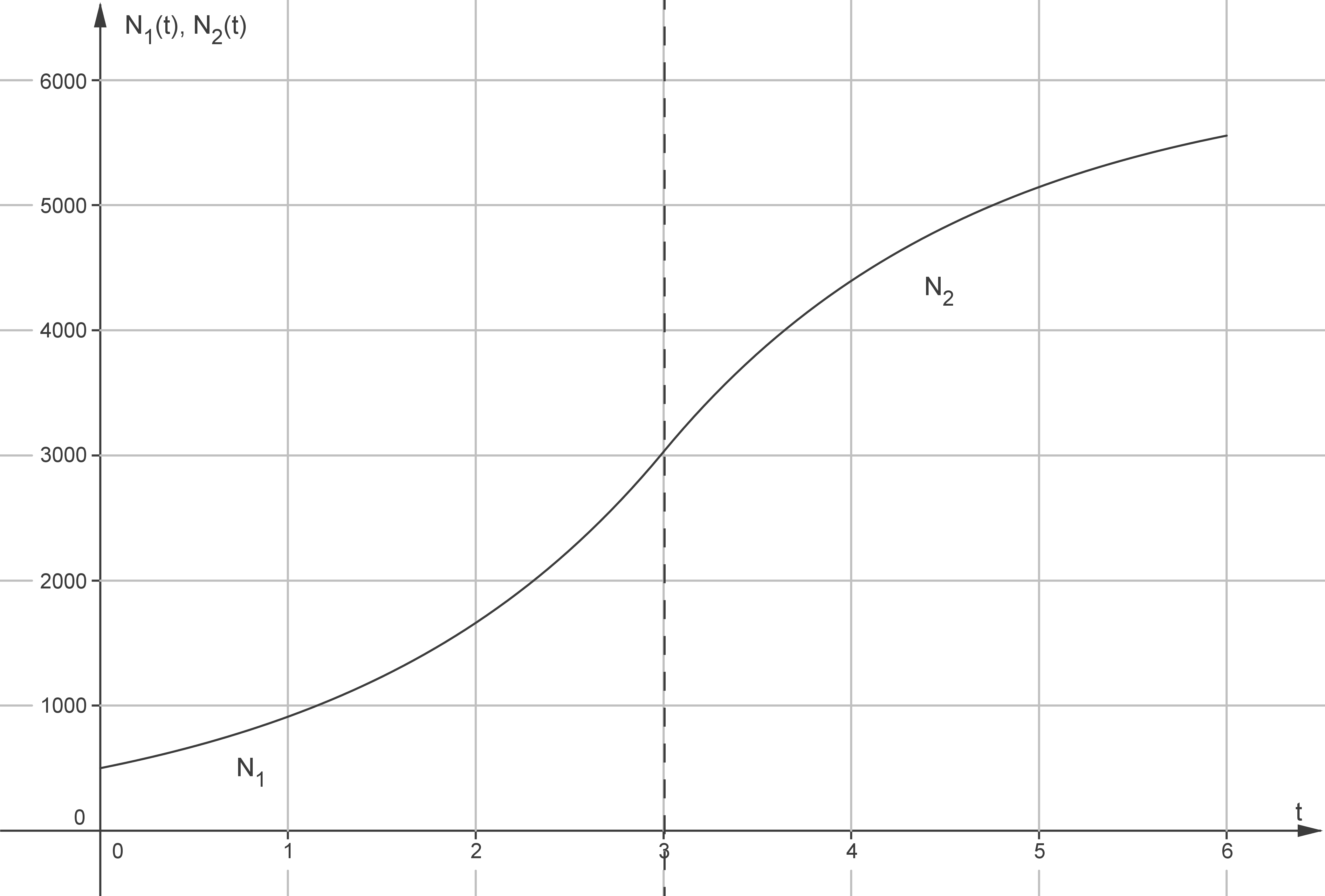Grafik mit zwei Kurven, die die Entwicklung von N1 und N2 über die Zeit t darstellen.

Abbildung 2

(6P)

(4) Erkläre anhand von Abbildung 2, weshalb die folgende Gleichung gilt:

$\displaystyle\int_{0}^{3}\;N_1(t)\mathrm {dt} + \displaystyle\int_{3}^{6}\;N_2(t) \mathrm {dt} =6\cdot N_1(3)$ .

[Die Punktsymmetrie des Graphen zu $(3\mid N_1(3))$ muss nicht nachgewiesen werden.]

(4P)

(5) Der Schüler verwendet die Funktion $N_2$ auch zur Modellierung der Anzahl der Pantoffeltierchen für $t\geq 6$ .

Begründe, dass in diesem Modell die Anzahl der Pantoffeltierchen in der Nährlösung zu keinem Zeitpunkt größer als $6.050$ wird.

(3P)

a)(1)
$\blacktriangleright$ Funktionswert berechnen

Berechne den Funktionswert von $N_1$ an der Stelle $t=3$ durch Einsetzen von $t=3$ in die gegebene Funktionsgleichung von $N_1$ .

$\color{#87c800}{\blacktriangleright\blacktriangleright}$ Lösungsweg A: Lösen per Hand

$\begin{array}[t]{rll} N_1(3)=& 500 \cdot \mathrm e^{0,6 \cdot 3} \\[5pt] =&500 \cdot \mathrm e^{1,8} \\[5pt] \approx& 3.024,82 \end{array}$

Der Funktionswert von $N_1$ an der Stelle $t=3$ ist ca. $3.024,82$ .

$\color{#87c800}{\blacktriangleright\blacktriangleright}$ Lösungsweg B: Lösen mit dem GTR

Definiere in deinem GTR die Funktion $n(t)$ . Werte diese dann an der Stelle $t=3$ aus:

Mathematik-Software zeigt eine Berechnung mit der Formel n(t)=500·e^(0.6·t) und Ergebnis für n(3) an.

Der Funktionswert von $N_1$ an der Stelle $t=3$ ist ca. $3.024,82$ .

$\blacktriangleright$ Funktionswert im Sachzusammenhang interpretieren

Interpretiere den Funktionswert im Sachzusammenhang, indem du dir die Bedeutung der Funktion $N_1$ aus der Aufgabenstellung klar machst.

Der Funktionswert von $N_1$ an der Stelle $t=3$ gibt die Anzahl der Pantoffeltierchen in der Nährlösung am $3.$ Tag des Experiments an.

a)(2)
$\blacktriangleright$ Gesuchten Zeitpunkt bestimmen

Setze den Funktionsterm von $N_1$ gleich $2.000$ und löse nacht $t$ auf, um rechnerisch den Zeitpunkt, an dem $2.000$ Pantoffeltierchen in der Nährlösung enthalten sind, zu bestimmen.

$\begin{array}[t]{rll} N_1(t)\stackrel{!}=& 2.000 \\[5pt] 500 \cdot \mathrm e^{0,6 \cdot t}=&2.000& \scriptsize \mid\; :500 \\[5pt] \mathrm e^{0,6 \cdot t}=&4& \scriptsize \mid\; \ln \\[5pt] 0,6 \cdot t=&\ln(4)& \scriptsize \mid\; 0,6 \\[5pt] t=&\dfrac{\ln(4)}{0,6} \\[5pt] \approx&2,31 \end{array}$

Zum Zeitpunkt $t=2,31$ sind also $2.000$ Pantoffeltierchen in der Nährlösung vorhanden.

a)(3)
$\blacktriangleright$ Durchschnittliche Anzahl berechnen

Gesucht ist die durchschnittliche Anzahl von Pantoffeltierchen in der Nährlösung während des ersten halben Tages der Beobachtung. Die Anzahl der Pantoffeltierchen zum Zeitpunkt $t$ entspricht dem Funktionswert $N_1(t)$ . Berechne also den durchschnittlichen Funktionswert von $N_1$ im Intervall $\left[0;0,5\right]$ . Nutze dazu die Formel für den durchschnittlichen Funktionswert unter einem Graphen einer Funktion $f$ .

Durchschnittlicher Funktionswert im Intervall $[a,b]$ einer Funktion $f$

$\dfrac{1}{b-a} \cdot \displaystyle\int_{a}^{b} f(t) \; \mathrm dt$

Einsetzen der Funktion $N_1(t)$ und des Intervalls $\left[0;0,5\right]$ in die Formel führt auf das gesuchte Ergebnis.

Nutze den Hauptsatz der Integralrechnung:

$\begin{array}[t]{rll} \dfrac{1}{0,5-0} \cdot \displaystyle\int_{0}^{0,5} N_1(t) \mathrm dt=&2 \cdot \displaystyle\int_{0}^{0,5} 500 \cdot \mathrm e^{0,6 \cdot t} \mathrm dt \\[5pt] =&2 \cdot \left[\dfrac{2.500}{3}\cdot \mathrm e^{0,6 \cdot t}\right]_0^{0,5} \\[5pt] =&\dfrac{5.000}{3} \cdot \left(\mathrm e^{0,3}-\mathrm e^0 \right) \\[5pt] \approx&583 \end{array}$

Damit beträgt die durchschnittliche Anzahl an Pantoffeltierchen in der Nährlösung während des ersten halben Tages der Beobachtung ca. $583$ .

a)(4)
$\blacktriangleright$ Geringe Abweichung des arithmetischen Mittels zeigen

Berechne zunächst das arithmetische Mittel der Funktionswerte $N_1(0)$ und $N_1(0,5)$ und setze dieses dann in Verhältnis zu der bereits in (3) berechneten durchschnittlichen Anzahl von Pantoffeltierchen während des ersten halben Tages.

Das arithmetische Mittel der zwei Funktionswerte ergibt sich folgendermaßen:

$\begin{array}[t]{rll} \overline{x}_{\text{arith}}=& \dfrac{N_1(0)+N_1(0,5)}{2} \\[5pt] =& \dfrac{500 \cdot \mathrm e^{0,6 \cdot 0}+500 \cdot \mathrm e^{0,6 \cdot 0,5}}{2} \\[5pt] =&250 \cdot \left(\mathrm e^{0}+\mathrm e^{0,3}\right) \\[5pt] \approx&587 \end{array}$

Setze das arithmetische Mittel in Verhältnis zu der in (3) berechneten durchschnittlichen Anzahl an Pantoffeltierchen während des ersten halben Tages:

$\begin{array}[t]{rll} \dfrac{\left(\dfrac{5.000}{3}\right) \cdot \left(\mathrm e^{0,3}-\mathrm e^0 \right)}{250 \cdot \left(\mathrm e^{0,3}+\mathrm e^{0}\right)} \approx& 0,9926 \end{array}$

Also beträgt die Abweichung der beiden berechneten Werte etwa $1-0,9926=0,0074$ , was $0,74 \%$ entspricht. Damit ist bewiesen, dass das arithmetische Mittel der Funktionswerte $N_1(0)$ und $N_1(0,5)$ weniger als $1\%$ von dem in (3) berechneten Durchschnitt abweicht.

a)(5)
$\blacktriangleright$ Behauptung über die prozentuale Abweichung nachweisen

Berechne zunächst den Durchschnitt aus (3) für das allgemeine Intervall $\left[a; a+0,5\right]$ . Nutze dazu die Formel für den durchschnittlichen Funktionswert in einem bestimmten Intervall einer Funktion und den Hauptsatz der Integralrechnung.

Berechne anschließend das allgemeine arithmetische Mittel der Funktionswerte $N_1(a)$ und $N_1(a+0,5)$ .

Setze dann die beiden berechneten Terme in Verhältnis zueinander und forme um, sodass du $a$ kürzen und die konstante prozentuale Abweichung angeben kannst.

1. Schritt: Allgemeinen Durchschnitt aus (3) berechnen

$\begin{array}[t]{rll} \dfrac{1}{a+0,5-a} \cdot \displaystyle\int_{a}^{a+0,5} N_1(t) \mathrm dt=& \dfrac{1}{0,5} \cdot \displaystyle\int_{a}^{a+0,5} 500 \cdot \mathrm e^{0,6 \cdot t} \mathrm dt \\[5pt] =&2 \cdot \left[\dfrac{2.500}{3}\cdot \mathrm e^{0,6 \cdot t}\right]_a^{a+0,5} \\[5pt] =&\dfrac{5.000}{3} \cdot \left(\mathrm e^{0,6 \cdot (a+0,5)}-\mathrm e^{0,6 \cdot a} \right) \end{array}$

2. Schritt: Arithmetisches Mittel von $\boldsymbol{N_1(a)}$ und $\boldsymbol{N_1(a+0,5)}$ berechnen

$\begin{array}[t]{rll} \dfrac{N_1(a)+N_1(a+0,5)}{2}=& \dfrac{500 \cdot \mathrm e^{0,6 \cdot a}+500 \cdot \mathrm e^{0,6 \cdot (a+0,5)}}{2} \\[5pt] =&250 \cdot \left(\mathrm e^{0,6 \cdot a}+\mathrm e^{0,6 \cdot (a+0,5)}\right) \end{array}$

3. Schritt: Prozentuale Abweichung berechnen

Setze die beiden berechneten Terme nun in Verhältnis zueinander:

$\begin{array}[t]{rll} \dfrac{\left(\dfrac{5.000}{3}\right) \cdot \left(\mathrm e^{0,6 \cdot (a+0,5)}-\mathrm e^{0,6 \cdot a} \right)}{250 \cdot \left(\mathrm e^{0,6 \cdot a}+\mathrm e^{0,6 \cdot (a+0,5)}\right)} =& \dfrac{5.000}{750} \cdot \left(\dfrac{ \mathrm e^{0,6 \cdot (a+0,5)}-\mathrm e^{0,6 \cdot a}}{\mathrm e^{0,6 \cdot a}+\mathrm e^{0,6 \cdot (a+0,5)}}\right)& \scriptsize \mid\; \mathrm e^{0,6 \cdot a} \text{ ausklammern} \\[5pt] =& \dfrac{20}{3} \cdot \left(\dfrac{ \color{red}{\mathrm e^{0,6 \cdot a}} \cdot \left(\mathrm e^{0,6 \cdot 0,5}-1\right)}{\color{red}{\mathrm e^{0,6 \cdot a}} \cdot \left(1+\mathrm e^{0,6 \cdot 0,5}\right)}\right) \\[5pt] =& \dfrac{20}{3} \cdot \left(\dfrac{\mathrm e^{0,3}-1}{\mathrm e^{0,3}+1}\right) \\[5pt] \approx&0,9926 \end{array}$

Damit erhältst du wie in Aufgabe (4):

Die prozentuale Abweichung des arithmetischen Mittels der Funktionswerte $N_1(a)$ und $N_1(a+0,5)$ von der durchschnittlichen Anzahl der Pantoffeltierchen in der Nährlösung in einem Zeitintervall $[a;a+0,5]$ mit $0\leq a \leq 2,5$ beträgt unabhängig von $a$ etwa $1-0,9926=0,0074$ und damit weniger als $1\%$ .

b)(1)
$\blacktriangleright$ Bedeutung der Aussagen im Sachzusammenhang interpretieren

Die momentane Änderungsrate entspricht der Wachstumsgeschwindigkeit der Pantoffeltierchen. Die Ableitung der momentanen Änderungsrate gibt dir Auskunft darüber, wie sich die Wachstumsgeschwindigkeit ändert. Nutze diese Interpretation der beiden Funktionen, um die mathematischen Aussagen auf den Sachzusammenhang zu beziehen.

Aussage	Bedeutung im Sachzusammenhang
$r_1(t)>0:$	Die momentane Änderungsrate ist zu jedem Zeitpunkt des Experiments positiv. Das bedeutet, dass die Wachstumsgeschwindigkeit während der ersten drei Tage immer positiv ist. Deshalb vermehren sich die Pantoffeltierchen zu jeder Zeit innerhalb der ersten drei Tage. Es gibt keinen Zeitpunkt, an dem die Anzahl der Pantoffeltierchen gleich bleibt oder weniger wird.
$r_1‘(t)>0:$	Die Ableitung der momentanen Änderungsrate ist immer positiv. Das bedeutet, dass die Wachstumsgeschwindigkeit im Laufe der Zeit immer größer wird. Also gilt, dass die Anzahl der Pantoffeltierchen umso schneller steigt, je weiter die Zeit vorangeschritten ist.

b)(2)
$\blacktriangleright$ Größte momentane Änderungsrate ermitteln

Um die größte momentane Änderungsrate der Anzahl der Pantoffeltierchen in den ersten drei Tagen zu ermitteln, bestimmst du das Maximum der momentanen Änderungsrate $r_1(t)$ im Intervall $[0,3]$ . Dazu gibt es verschiedene Lösungswege:

$\color{#87c800}{\blacktriangleright\blacktriangleright}$ Lösungsweg A: Argumentation mit Aufgabe b)(1)

Aus der Aufgabenstellung b)(1) kennst du folgende Eigenschaften der momentanen Änderungsrate:

$r_1(t) \gt 0$ und $r_1‘(t) \gt 0$ für alle $t \in \mathbb{R}$ .

Da $r_1‘(t) \gt 0$ , steigt die Änderungsrate im Laufe der Zeit immer weiter an, d.h. je größer $t$ ist, desto größer ist auch die Änderungsrate. Damit kann das Maximum der Änderungsrate nur am rechten Rand des Intervalls $[0;3]$ liegen. Somit liegt die größte momentane Änderungsrate in den ersten drei Tagen an der Stelle $t=3$ und sie beträgt $r_1(3)=300 \cdot \mathrm e^{1,8}\approx 1.814,89$ .

$\color{#87c800}{\blacktriangleright\blacktriangleright}$ Lösungsweg B: Lösen per Hand

Um einen Extrempunkt zu bestimmen, kannst du Folgendes überprüfen:

Notwendige Bedingung

Hinreichende Bedingung

Prüfe zudem, ob ein Extrempunkt auf dem Rand des Intervalls angenommen wird, indem du die Randwerte des Intervalls in die momentane Änderungsrate $r_1(t)$ einsetzt.

1. Schritt: 1. Ableitung von $\boldsymbol{r_1}$ bestimmen

Die Funktionsgleichung von $r_1$ ist in der Aufgabenstellung gegeben. Nutze die Kettenregel beim Ableiten:

$\begin{array}[t]{rll} r_1‘(t)=& 300 \cdot 0,6 \cdot \mathrm e^{0,6 \cdot t} \\[5pt] =&180 \cdot \mathrm e^{0,6 \cdot t} \end{array}$

2. Schritt: Notwendige Bedingung überprüfen

Setze die Funktionsgleichung der 1. Ableitung $r_1‘(t)$ gleich Null, um mögliche Nullstellen zu bestimmen:

$\begin{array}[t]{rll} r_1‘(t)\stackrel{!}=& 0 \\[5pt] 180 \cdot \mathrm e^{0,6 \cdot t}\stackrel{!}=& 0 \end{array}$

Der Satz vom Nullprodukt liefert dir nun, dass $r_1‘(t)$ keine Nullstelle besitzt, da sowohl $180>0$ als auch $\mathrm e^{0,6 \cdot t}>0$ ist.

3. Schritt: Maximum auf dem Rand des Intervalls $\boldsymbol{[0,3]}$ bestimmen

Nehme nun also an, dass die momentane Änderungsrate ihr Maximum im Intervall $[0,3]$ auf dem Rand annimmt. Setze dazu die Stellen $t=0$ und $t=3$ in die Funktionsgleichung von $r_1$ ein.

$r_1(0)=300 \cdot \mathrm e^{0,6 \cdot 0}=300$

$r_1(3)=300 \cdot \mathrm e^{0,6 \cdot 3}=300 \cdot \mathrm e^{1,8}$

Da $r_1(0)=300 < 300 \cdot \mathrm e^{1,8}=r_1(3)$ ist, nimmt die Funktion $r_1$ im Intervall $[0,3]$ ihr Maximum an der Stelle $t=3$ an.

Damit beträgt die größte momentane Änderungsrate der Anzahl der Pantoffeltierchen in der Nährlösung in den ersten drei Tagen gerade $r_1(3)=300 \cdot \mathrm e^{1,8}\approx 1.814,89$ .

$\color{#87c800}{\blacktriangleright\blacktriangleright}$ Lösungsweg C: Lösen mit dem GTR

Wechsle mit deinem GTR in das GRAPH-Menü und speichere dort den Funktionsterm von $r_1$ . Hast du diesen dort eingegeben, dann stelle das Fenster so ein, dass der gewünschte Bereich sichtbar ist.

Wähle dann unter

6: Graph analysieren 3: Maximum

den Befehl zum Bestimmen des Maximums aus und bestätige mit Enter. Gib anschließend deine Intervallgrenzen $t=0$ und $t=3$ ein.

Grafik einer mathematischen Funktion mit Kurve und Koordinaten.

Damit beträgt die größte momentane Änderungsrate der Anzahl der Pantoffeltierchen in der Nährlösung in den ersten drei Tagen etwa $1.810$ .

c)(1)
$\blacktriangleright$ Bedeutung der Gleichung im Sachzusammenhang interpretieren

$r_1$ entspricht der momentanen Änderungsrate ab dem Zeitpunkt $t=0$ bis zum Zeitpunkt $t=3$ . Der Term $3-a$ nimmt für $0\leq a \leq 3$ Werte zwischen $0$ und $3$ an. $r_2$ entspricht der momentanen Änderungsrate ab dem Zeitpunkt $t=3$ . Der Term $3+a$ nimmt für $0\leq a \leq 3$ Werte zwischen $3$ und $6$ an. Nutze diese Eigenschaften, um die Gleichung im Sachzusammenhang zu interpretieren.

Im Sachzusammenhang bedeutet dies, dass die Wachstumsgeschwindigkeit der Anzahl der Pantoffeltierchen im gleichen Abstand vor und nach Tag $3$ ( $t=3$ ) gleich ist. Damit sind die Änderungsraten symmetrisch um den dritten Tag verteilt.

c)(2)
$\blacktriangleright$ Funktionsgleichung von $\boldsymbol{r_2}$ herleiten

Nutze die Gleichung, die $r_2$ in Beziehung zu $r_1$ setzt. Setze dort den gegebenen Funktionsterm von $r_1$ ein. Durch Substituieren von $3+a$ durch $t$ kannst du die gesuchte Funktionsgleichung herleiten.

$\begin{array}[t]{rlll} r_2(3+a)=&r_1(3-a)& 0\leq a \leq 3 & \scriptsize \mid\; \text{Einsetzen der Funktionsgleichung von } r_1 \\[5pt] r_2(3+a)=&300 \cdot \mathrm e^{0,6 \cdot (3-a)}& 0\leq a \leq 3 \end{array}$

Substituiere nun $3+a$ durch $t$ :

$\begin{array}[t]{rll} 3+a=& t& \scriptsize \mid\; -3 \\[5pt] a=&t-3 \end{array}$

Mit der Substitution folgt:

$\begin{array}[t]{rllllll} 0&\leq& a& \leq& 3& \scriptsize \mid\; a=t-3 \\[5pt] 0&\leq& t-3& \leq &3 & \scriptsize \mid\; +3 \\[5pt] 3&\leq& t& \leq& 6 \end{array}$

Wende die Substitution nun auf deine Gleichung für $r_2$ an:

$\begin{array}[t]{rlll} r_2(3+a)=&300 \cdot \mathrm e^{0,6 \cdot (3-a)}& 0\leq a \leq 3 & \scriptsize \mid\; \text{Substituiere } a+3=t \\[5pt] r_2(t)=& 300 \cdot \mathrm e^{0,6 \cdot (3-(t-3))} &3\leq t \leq 6 \\[5pt] =& 300 \cdot \mathrm e^{0,6 \cdot (6-t)} &3\leq t \leq 6 \\[5pt] =& 300 \cdot \mathrm e^{3,6 -0,6 \cdot t} &3\leq t \leq 6 \end{array}$

Damit hast du die gesuchte Funktionsgleichung für die momentane Änderungsrate der Anzahl der Pantoffeltierchen nach dem dritten Tag hergeleitet.

c)(3)
$\blacktriangleright$ Funktionsgleichung von $\boldsymbol{N_2}$ ermitteln

Da $r_2$ die Änderungsrate von $N_2$ ist, ist $N_2$ eine Stammfunktion von $r_2$ . Bestimme zunächst mit dem Hauptsatz der Integralrechnung eine allgemeine Stammfunktion von $r_2$ . Zum Bestimmen der Integrationskonstante kannst du nutzen, dass du die Anzahl der Pantoffeltierchen am dritten Tag sowohl durch $N_1$ als auch durch $N_2$ berechnen kannst.

$\blacktriangleright$ Stammfunktion von $\boldsymbol{r_2}$ bestimmen

Nutze den Hauptsatz der Integralrechnung:

$\begin{array}[t]{rll} N_2(t)=& \displaystyle\int r_2(t) \;\mathrm dt \\[5pt] =&\displaystyle\int 300 \cdot \mathrm e^{3,6 -0,6 \cdot t} \;\mathrm dt \\[5pt] =& -\dfrac{300}{\left(\frac{6}{10}\right)}\cdot \mathrm e^{3,6 -0,6 \cdot t} +c \\[5pt] =& -500 \cdot \mathrm e^{3,6 -0,6 \cdot t} +c \end{array}$

$\blacktriangleright$ Integrationskonstante $\boldsymbol{c}$ bestimmen

Da sowohl $N_1$ als auch $N_2$ die Anzahl der Pantoffeltierchen am Tag $3$ beschreiben, gilt:

$N_1(3)=N_2(3)$

Setze nun die Funktionsterme ein und löse nach $c$ auf:

$\begin{array}[t]{rll} N_1(3)=&N_2(3) & \scriptsize \mid\; \text{Funktionsterme einsetzen} \\[5pt] 500 \cdot \mathrm e^{0,6 \cdot 3} =& -500 \cdot \mathrm e^{3,6 -0,6 \cdot 3} +c \\[5pt] 500 \cdot \mathrm e^{1,8} =& -500 \cdot \mathrm e^{1,8} +c & \scriptsize \mid\; +500 \cdot \mathrm e^{1,8} \\[5pt] 1.000 \cdot \mathrm e^{1,8}=&c \end{array}$

Damit ergibt sich für die Funktionsgleichung von $N_2$ :

$N_2(t)= 1.000 \cdot \mathrm e^{1,8} -500 \cdot \mathrm e^{3,6 -0,6 \cdot t}$

c)(4)
$\blacktriangleright$ Gültigkeit der Gleichung erklären

Mache dir zunächst die graphische Bedeutung der einzelnen Terme der Gleichung klar. Mit der Punktsymmetrie und Abbildung 2 kannst du erklären, warum die Gleichung gilt.

Term	Bedeutung in der Abbildung
$\displaystyle\int_{0}^{3} N_1(t)\;\mathrm dt$	Das Integral gibt die Fläche unter dem Graphen der Funktion $N_1$ von $t=0$ bis $t=3$ an.
$\displaystyle\int_{3}^{6} N_2(t)\;\mathrm dt$	Das Integral gibt die Fläche unter dem Graphen der Funktion $N_2$ von $t=3$ bis $t=6$ an.
$6 \cdot N_1(3)$	Hier wird die Fläche des Rechtecks mit den Seitenlängen $6$ und $N_1(3)$ berechnet.

An folgender Skizze kannst du das gut erkennen:

Graph mit verschiedenen farbigen Flächen und mathematischen Funktionen auf einem Koordinatensystem.

Vergleichst du nun die Fläche der beiden Integrale mit der des Rechtecks, so stellst du Folgendes fest:
Das Flächenstück unter $N_2$ von $t=3$ bis $t=6$ , das noch nicht im Rechteck enthalten ist, entspricht gerade dem fehlenden Flächenstück des Rechtecks, das über der Funktion $N_1$ von $t=0$ bis $t=3$ liegt. Die Punktsymmetrie des Graphen um den Punkt $\left(3 \mid N_1(3) \right)$ liefert dir, dass die beiden Flächenstücke gleich groß sind.

c)(5)
$\blacktriangleright$ Obere Grenze für Anzahl der Pantoffeltierchen begründen

Um zu begründen, dass die Anzahl der Tierchen nicht größer als $6.050$ wird, benötigst du eine Eigenschaft der Exponentialfunktion. Für alle $x \in \mathbb{R}$ gilt: $\mathrm e^x \gt 0$ , somit gilt auch $\mathrm e^{3,6 - 0,6 \cdot t} \gt 0$ für alle $t \in \mathbb{R}$ . Damit gilt auch die Gleichung $500 \cdot \mathrm e^{3,6 - 0,6 \cdot t} \gt 0$ . Die Funktionsgleichung wird folgendermaßen abgeschätzt:

$N_2(t)=1.000 \cdot \mathrm e^{1,8} - 500 \cdot \mathrm e^{3,6 - 0,6 \cdot t} \lt 1.000 \cdot \mathrm e^{1,8} = 6.049,65 \lt 6.050$

Damit hast du gezeigt, dass die Anzahl der Pantoffeltierchen zu keinem Zeitpunkt größer als $6.050$ wird.

a)(1)
$\blacktriangleright$ Funktionswert berechnen

Berechne den Funktionswert von $N_1$ an der Stelle $t=3$ durch Einsetzen von $t=3$ in die gegebene Funktionsgleichung von $N_1$ .

$\color{#87c800}{\blacktriangleright\blacktriangleright}$ Lösungsweg A: Lösen per Hand

$\begin{array}[t]{rll} N_1(3)=& 500 \cdot \mathrm e^{0,6 \cdot 3} \\[5pt] =&500 \cdot \mathrm e^{1,8} \\[5pt] \approx& 3.024,82 \end{array}$

Der Funktionswert von $N_1$ an der Stelle $t=3$ ist ca. $3.024,82$ .

$\color{#87c800}{\blacktriangleright\blacktriangleright}$ Lösungsweg B: Lösen mit dem GTR

Speichere den Funktionsterm von $N_1$ im Graph-Modus deines GTR und lass dir den zugehörigen Graph über anzeigen.

Bestimme dann mit folgendem Befehl den Funktionswert in $t=3$ :

G-Solve F6: F1: Y-Cal

Gib $3$ ein und bestätige mit Enter.

Grafik eines mathematischen Ausdrucks mit einer blauen Kurve und Koordinatenachse.