Analysis 1

Immer mehr Hausbesitzer errichten auf ihren Hausdächern eine Solaranlage, mit der Energie aus Sonnenlicht gewonnen wird.

Mit der in $\mathbb{R}$ definierten Funktion $f$ mit

$f(t)=8 \cdot \mathrm{e}^{-0,1 \cdot(t-13,5)^2}-0,3$

wird die Leistung einer Solaranlage in einem durch das Intervall $\left[t_1 ; t_2\right]$ gegebenen Zeitraum an einem bestimmten Tag modelliert. Dabei sind $t_1$ und $t_2$ die Nullstellen von $f.$

Durch $t$ ist die Zeit in Stunden $(\text{h})$ gegeben, die am betrachteten Tag seit $0$ Uhr vergangen ist. Durch $f(t)$ ist die Leistung der Solaranlage in Kilowatt $(\text{kW})$ gegeben. Es wird angenommen, dass die Leistung der Solaranlage am betrachteten Tag außerhalb des durch $\left[t_1 ; t_2\right]$ gegebenen Zeitraums $0 \; \text{kW}$ beträgt.

In Abbildung 1 ist der Graph der Funktion $f$ dargestellt.

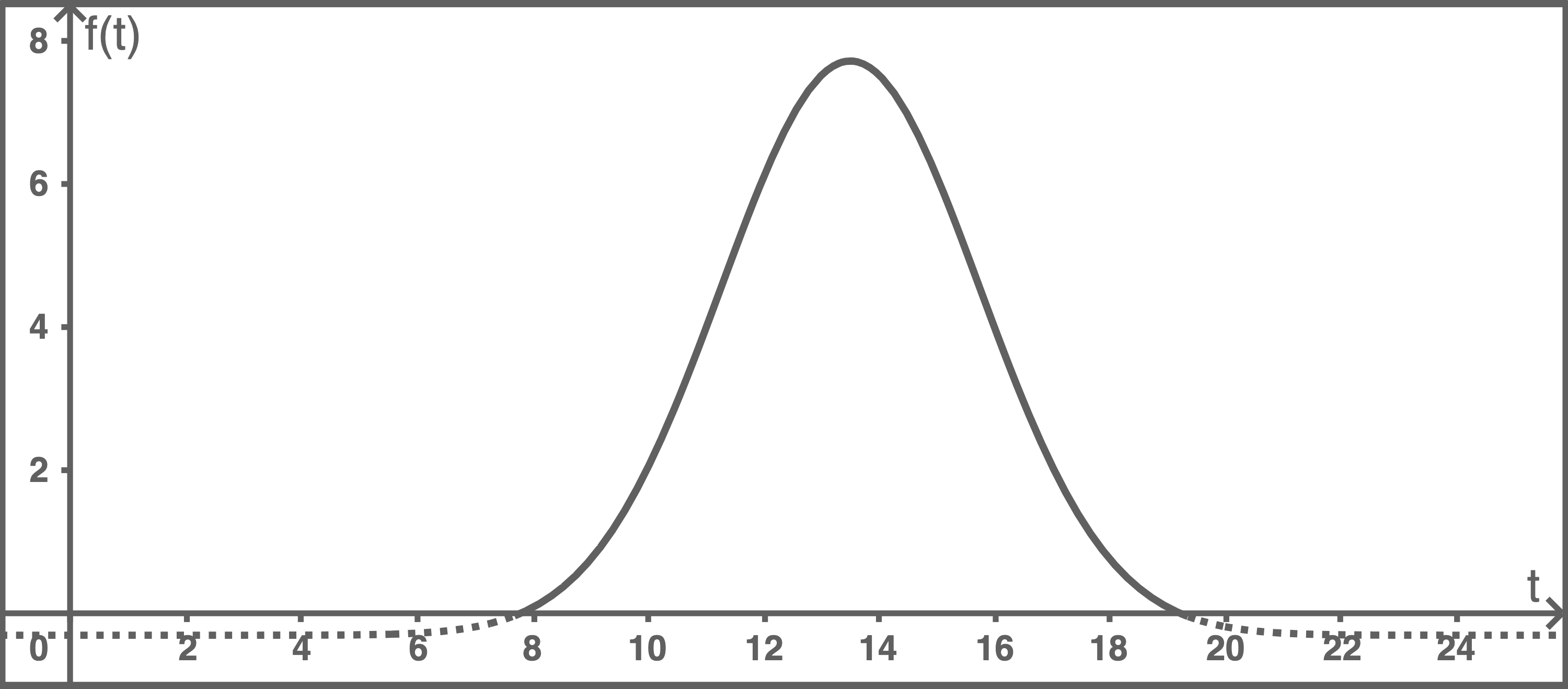
Grafik einer Funktion f(t) mit einer Kurve, die einen Anstieg und Abfall zeigt, auf einem Koordinatensystem.

Abbildung 1

(1)

Gib $f(12)$ an und interpretiere den Wert im Sachzusammenhang.

(2)

Bestimme $t_1$ und $t_2$ gerundet auf zwei Nachkommastellen.

[Zur Kontrolle: Bei Rundung auf eine Nachkommastelle ergibt sich $t_1 \approx 7,8$ und $t_2 \approx 19,2.]$

(3)

(i)

Zeige: $\(f$

(ii)

Untersuche rechnerisch, zu welchem Zeitpunkt am betrachteten Tag die Leistung der Solaranlage maximal ist.

(4)

Bestimme den Zeitpunkt am betrachteten Tag, zu dem die Leistung der Solaranlage am stärksten abnimmt.

(2+2+5+3 Punkte)

Im Folgenden wird die von der Solaranlage aus dem Sonnenlicht gewonnene Energie betrachtet. Die Leistung der Solaranlage ist die Änderungsrate dieser Energie. Die von der Solaranlage gewonnene Energie wird im Folgenden in der Einheit Kilowattstunden $(\text{kWh})$ angegeben.

Weise nach, dass die am betrachteten Tag von $11$ Uhr bis $15$ Uhr gewonnene Energie ungefähr $26,47 \;\text{kWh}$ beträgt.

(2 Punkte)

Mit der Solaranlage werden die elektrischen Geräte des Hauses betrieben. Wenn die Leistung, die diese Geräte benötigen, die von der Solaranlage gelieferte Leistung übersteigt, dann wird die zusätzlich benötigte Energie aus dem städtischen Stromnetz bezogen. Wenn die von den elektrischen Geräten des Hauses benötigte Leistung geringer ist als die von der Solaranlage gelieferte Leistung, dann wird die überschüssige Energie in das städtische Stromnetz eingespeist.

Mit der in $\mathbb{R}$ definierten Funktion $g$ mit

$g(t)=1,4 \cdot\left(t^2-26,3 t+173,3\right) \cdot \mathrm{e}^{-0,1 \cdot(t-13,5)^2}+0,5$

wird für $0 \leq t \leq 24$ für jeden Zeitpunkt des betrachteten Tages die Leistung modelliert, die die elektrischen Geräte des Hauses benötigen.

Durch $t$ ist wieder die Zeit in Stunden $(\text{h})$ gegeben, die am betrachteten Tag seit $0$ Uhr vergangen ist. Durch $g(t)$ ist die von den Geräten des Hauses benötigte Leistung in Kilowatt $(\text{kW})$ gegeben.

Die Situation ist in Abbildung 2 dargestellt.

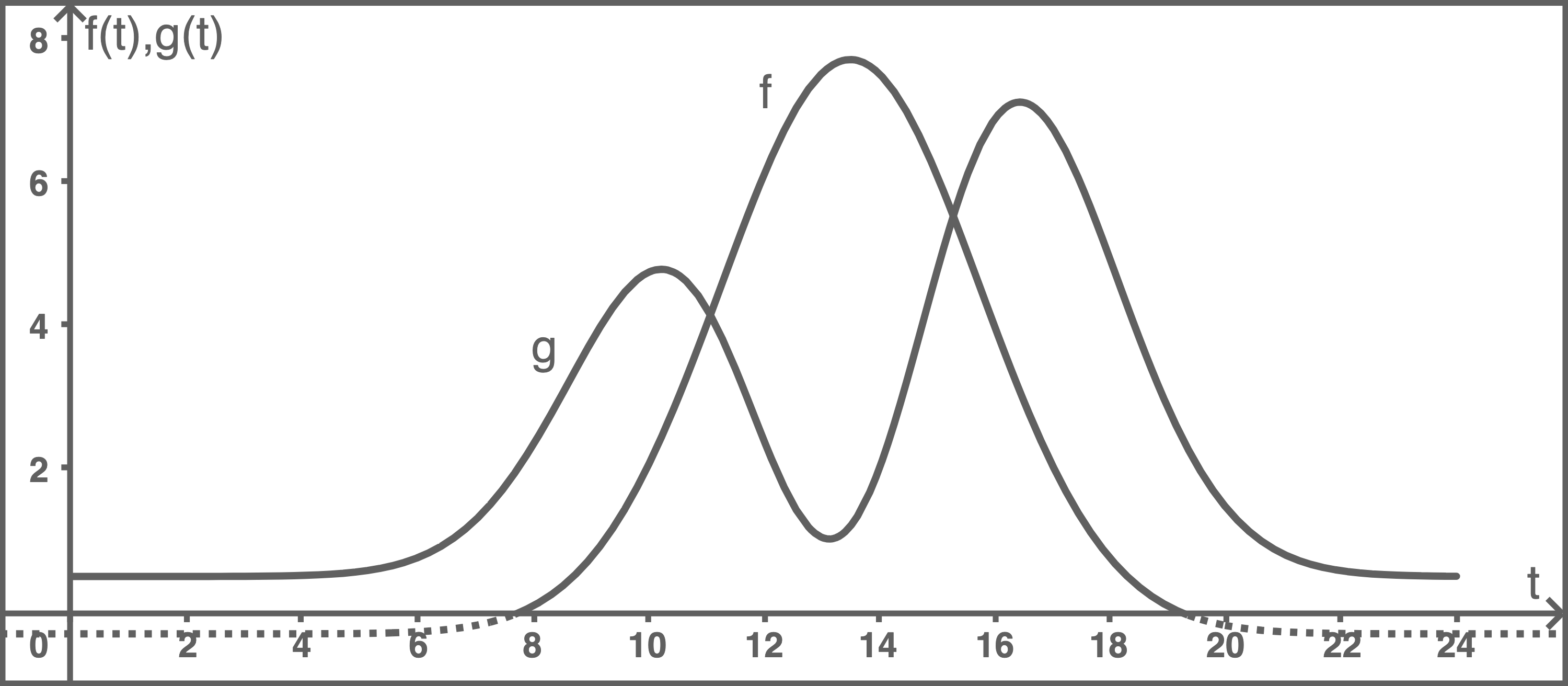
Diagramm mit den Funktionen f(t) und g(t) in Abhängigkeit von t, dargestellt durch zwei Linien.

Abbildung 2

(1)

Bestimme die Länge des Zeitraums am betrachteten Tag, in dem die von den elektrischen Geräten des Hauses benötigte Leistung geringer ist als die von der Solaranlage gelieferte Leistung.

Die am betrachteten Tag gewonnene bzw. genutzte Energie wird in drei Kategorien unterteilt: in das städtische Stromnetz eingespeiste Energie $(\text{E}),$ aus dem städtischen Stromnetz bezogene Energie $(\text{B})$ und selbst gewonnene und genutzte Energie $(\text{G}).$

(2)

(i)

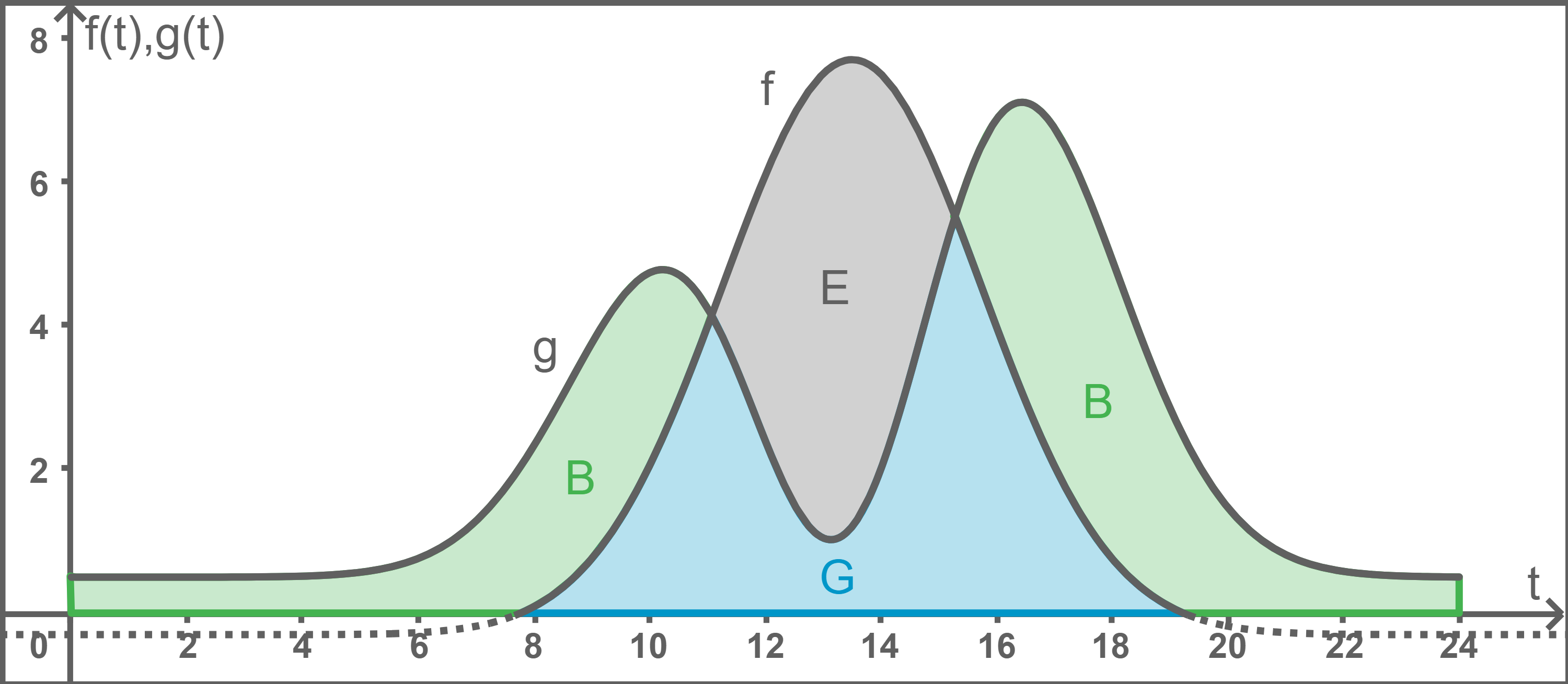
Markiere in Abbildung 2 die Flächenstücke, deren Flächeninhalte den Energien $E, B$ und $G$ entsprechen.

Unterscheide die Markierungen sichtbar.

(ii)

Für jede Kilowattstunde, die der Hausbesitzer in das städtische Stromnetz einspeist, werden ihm $8,3 \;\text{ct}$ gutgeschrieben.

Bestimme den Betrag, der dem Hausbesitzer für den betrachteten Tag gutgeschrieben wird.

(3+6 Punkte)

Der zeitliche Verlauf der von den elektrischen Geräten des Hauses benötigten Leistung ähnelt sich an den meisten Tagen.

Die in $\mathbb{R}$ definierten Funktionen $h_a$ mit

$h_a(t)=a \cdot\left(t^2-26,3 t+173,3\right) \cdot \mathrm{e}^{-0,1 \cdot(t-13,5)^2}+0,5 \text { mit } a\gt0$

werden für $0 \leq t \leq 24$ verwendet, um für verschiedene Tage für jeden Zeitpunkt des jeweiligen Tages die von den Geräten benötigte Leistung zu modellieren.

Dabei ist $t$ die Zeit in Stunden ab $0$ Uhr am jeweiligen Tag und $h_a(t)$ die benötigte Leistung der elektrischen Geräte des Hauses in Kilowatt $(\text{kW}).$

(1)

Gib den Wert des Parameters $a$ an, für den die Funktionen $h_a$ und $g$ übereinstimmen, und beschreibe, wie sich der Parameter $a$ auf den Verlauf des Graphen von $h_a$ auswirkt.

(2)

$H_a$ ist die vom Parameter $a$ abhängige Funktion mit der Gleichung

$H_a(t)=\displaystyle\int_0^t h_a(x) \;\text{d}x, t \in \mathbb{R}$

Interpretiere die Bedeutung von $H_a$ im Sachzusammenhang.

(3)

Durch die Modellierung der Leistung der Solaranlage mit der Funktion $f$ ist im Modell auch die Energie gegeben, die am betrachteten Tag gewonnen wird. Es gibt einen Wert für den Parameter $a,$ für den diese Energie mit der von den elektrischen Geräten des Hauses benötigten Energie übereinstimmt, die sich bei der Modellierung der Leistung mit der Funktion $h_a$ für $0 \leq t \leq 24$ ergibt.

Ermittle diesen Wert von $a.$

(3+2+2 Punkte)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

(1)

Wert angeben

$f(12)\approx6,09$

Im Sachzusammenhang interpretieren

Nach $12$ Stunden hat die Solaranlage ungefähr $6,09\;\text{kW}$ an Leistung geliefert.

(2)

Auflösen nach $t$ von $f(t)=0$ liefert mit dem solve-Befehl des GTR:

$\begin{array}[t]{rlll} t_1&=&7,77 \\[5pt] t_2&=&19,23 \end{array}$

(3)

(i)

Mit der Kettenregel folgt für die erste Ableitung von $f:$

Rechenweg anzeigen

$\( f$

(ii)

Auflösen der notwendigen Bedingung für Extremstellen $\(f$ nach $t$ mit dem solve-Befehl des GTR liefert:

$t=13.5$

Da die Funktion an beiden Intervallgrenzen Nullstellen besitzt und dazwischen positive Werte annimmt, muss die hinreichende Bedingung für Extremstellen nicht überprüft werden. Die Leistung der Solaranlage ist somit nach genau $13,5$ Stunden maximal und beträgt folgenden Wert:

$\begin{array}[t]{rlll} f(13,5)&=&8\mathrm e^{-0,1\cdot(13,5-13,5)^2}-0,3 \\[5pt] &=&7,7\;[\text{kW}] \end{array}$

(4)

Der Zeitpunkt, zu dem die Leistung der Solaranlage am stärksten abnimmt, ist durch den Wendepunkt der Funktion $f$ gegeben, der rechts vom Hochpunkt liegt. Für die zweite Ableitung von $f$ folgt mit dem GTR:

$\(f$ $\cdot\mathrm{e}^{-0,1\cdot\left(t - 13,5\right)^{2}}$

Auflösen der notwendigen Bedingung für Wendestellen $\(f$ nach $t$ mit dem solve-Befehl des GTR liefert:

$\begin{array}[t]{rlll} t_1&=&11,26 \\[5pt] t_2&=&15,74 \end{array}$

Mit Hilfe des Graphen von $f$ kann erkannt werden, dass rechts von dem Hochpunkt ein Wendepunkt vorliegt. Da nur einer der beiden Werte größer als der Wert der Hochstelle von $f$ ist, muss die hinreichende Bedingung für Wendestellen somit nicht überprüft werden.
Der Zeitpunkt, zu dem die Leistung der Solaranlage am stärksten abnimmt, ist damit nach $15,74$ Stunden erreicht.

(1)

Die Leistung der Solaranlage ist die Änderungsrate der Energie. Somit wird die gesuchte Energie durch den Flächeninhalt der Fläche gegeben, die $f$ zwischen $t=11$ und $t=15$ mit der $t$ -Achse einschließt, das heißt durch den folgenden Ausdruck:

$\displaystyle\int_{11}^{15}\left(8 \cdot \mathrm e^{-0,1 \cdot(t-13,5)^2}-0,3\right)\;\mathrm dx$

Der GTR liefert für diesen Ausdruck ca. den Wert $26,47.$ Somit beträgt die am betrachteten Tag von $11$ Uhr bis $15$ Uhr gewonnene Energie ungefähr $26,47\;\mathrm{kWh}.$

(1)

Der Zeitraum, in dem die von den elektrischen Geräten des Hauses benötigte Leistung geringer ist als die von der Solaranlage gelieferte Leistung, ist durch das Intervall gegeben, in dem der Graph von $g$ unter dem Graphen von $f$ verläuft. Auflösen von $f(t)=g(t)$ nach $t$ mit dem solve-Befehl des GTR liefert:

$\begin{array}[t]{rlll} t_1&\approx&11,07 \\[5pt] t_2&\approx&15,28 \end{array}$

Die Länge des gesuchten Zeitraums beträgt somit ca. $15,28-11,07=4,21\;\text{h}.$

(2)

(i)

Grafische Darstellung von Funktionen f(t) und g(t) mit verschiedenen Flächen und Zeitachsen.

(ii)

Integral anzeigen

Berechnen des Integrals mit dem GTR liefert für den gesuchten Betrag insgesamt ca. $141,76\;\text{ct}\approx1,42\,\text{€}.$

(1)

Parameter angeben

$a=1,4$

Auswirkung auf den Graphen beschreiben

Der Parameter $a$ staucht bzw. streckt den Graphen von $h_a$ in $y$ -Richtung.

(2)

Die Funktion $H_a$ gibt an, wieviel Energie die Geräte des Hauses von Beginn des Tages bis zu einem bestimmten Zeitpunkt $t$ am Tag bereits benötigt haben.

(3)

Damit die beiden in der Aufgabenstellung beschriebenen Energien gleich groß sind, muss folgende Gleichung gelten:

$\displaystyle\int_{7,77}^{19,23}f(x)\;\mathrm dx=\displaystyle\int_{0}^{24}h_a(x)\;\mathrm dx$

Auflösen dieser Gleichung nach $a$ mit dem solve-Befehl des GTR liefert $a\approx0,94.$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?