Wahlpflichtteil

Gegeben ist die in $\mathbb{R}$ definierte Funktion $f$ mit $f(x)=\frac{1}{4} x^3-3 x.$

(1)

Es gilt $\(f$

Zeige, dass $2$ eine Extremstelle von $f$ ist.

(2)

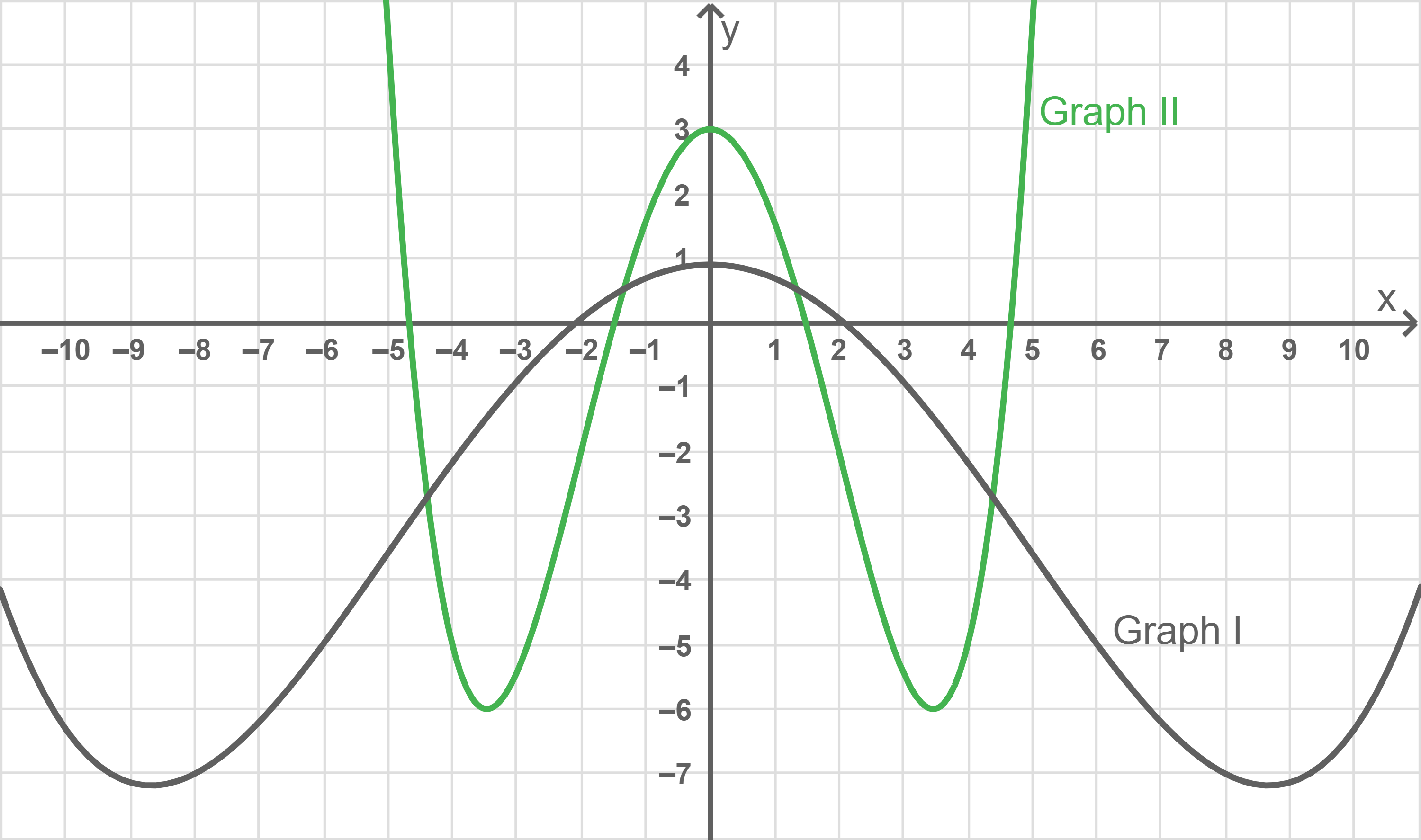
Einer der abgebildeten Graphen I und II ist der Graph einer Stammfunktion von $f.$

Gib diesen Graphen an und begründe deine Angabe.

Abbildung 1

(2+3 Punkte)

Betrachtet werden die in $\mathbb{R}$ definierten Funktionen $f$ und $g.$

Für $x \in \mathbb{R}$ gilt $g(x)=f(x) \cdot \mathrm{e}^{x}.$

(1)

Weise nach, dass die folgende Aussage wahr ist:

Wenn der Graph von $g$ im Punkt $(a \mid g(a))$ mit $a \in \mathbb{R}$ eine waagerechte Tangente besitzt, dann gilt $\(f$

(2)

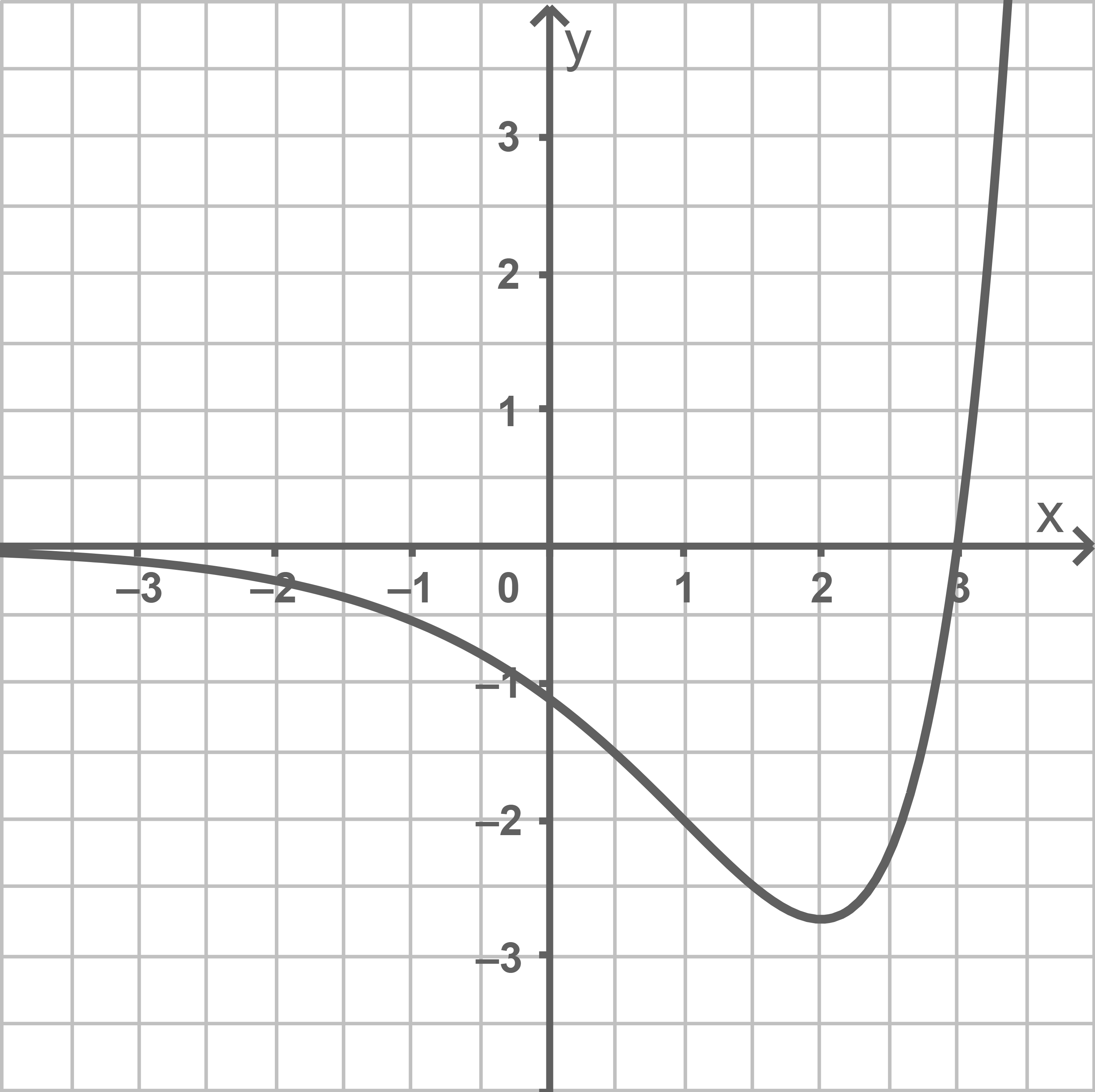
Abbildung 2 stellt den Graphen von $f$ dar.

Zeige mithilfe von Abbildung 2, dass der Graph von $g$ im Punkt $(1 \mid g(1))$ keine waagerechte Tangente besitzt.

Abbildung 2

(3+2 Punkte)

(1)

Gegeben sind zwei Vektoren $\overrightarrow{a}$ und $\overrightarrow{b}$ mit jeweils drei reellen Zahlen als Koordinaten.

Entscheide durch Ankreuzen, ob der jeweilige Ausdruck einen Vektor mit drei Koordinaten darstellt, eine reelle Zahl darstellt oder nicht definiert ist.

Ausdruck	$\color{#fff}{\overrightarrow{a}\circ(\overrightarrow{a}+\overrightarrow{b})}$	$\color{#fff}{\overrightarrow{a}+(\overrightarrow{a}\circ\overrightarrow{b})}$
Vektor mit drei Koordinaten		
reelle Zahl		
nicht definiert		

(2)

Betrachtet wird der Winkel zwischen den Vektoren $\overrightarrow{u}=\pmatrix{2\\3\\0}$ und $\overrightarrow{v_r}=\pmatrix{r\\4\\2}$ mit $r \in \mathbb{R}.$

Ermittle alle Werte von $r,$ für die dieser Winkel eine Größe von mindestens $90^{\circ}$ hat.

(2+3 Punkte)

Gegeben ist die Schar der Ebenen $E_k: k \cdot x+(2-k) \cdot y=k$ mit $k \in \mathbb{R}.$

(1)

Es gibt eine Koordinatenebene, zu der alle Ebenen der Schar senkrecht stehen.

Gib diese an.

(2)

Zeige, dass jeweils zwei verschiedene Ebenen der Schar nicht parallel zueinander sind.

(1+4 Punkte)

Bei einem Spiel wird ein Würfel zweimal geworfen. Die Seiten des Würfels sind mit den Zahlen von $1$ bis $6$ durchnummeriert.

(1)

Begründe, dass die Wahrscheinlichkeit dafür, bei keinem der beiden Würfe die Zahl 3 zu erzielen, $\dfrac{25}{36}$ beträgt.

(2)

Der Einsatz bei diesem Spiel beträgt $2$ Euro. Je nachdem, wie oft dabei die Zahl $3$ erzielt wird, werden folgende Auszahlungen getätigt:

Anzahl der Würfe, bei denen die Zahl 3 erzielt wird	Auszahlung in Euro
$0$	$0$
$1$	$5$
$2$	$x$

Bei wiederholter Durchführung des Spiels ist zu erwarten, dass sich auf lange Sicht Einsätze und Auszahlungen ausgleichen.

Ermittle den Wert von $x.$

(2+3 Punkte)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

(1)

Für die erste Ableitung von $f$ gilt:

$\(\begin{array}[t]{rlll} f$

Einsetzen von $x=2$ liefert:

$\(\begin{array}[t]{rlll} f$

Somit ist die notwendige Bendingung für Extremstellen in $x=2$ erfüllt. Da die hinreichende Bedingung für Extremstellen bereits in der Aufgabenstellung gegeben ist, folgt somit, dass $2$ eine Extremstelle von $f$ ist.

(2)

Da $f$ bei $x=2$ eine Extremstelle besitzt, hat jede Stammfunktion von $f$ bei $x=2$ eine Wendestelle. Aus der Abbildung folgt somit, dass Graph II der Graph einer Stammfunktion von $f$ ist.

(1)

Für die Ableitung von $g$ gilt:

$\(\begin{array}[t]{rlll} g$

Der Graph von $g$ besitzt eine waagerechte Tangente in einem Punkt, wenn die Ableitung von $g$ dort gleich Null ist. Nullsetzen der Ableitung an der Stelle $x=a$ liefert:

$\(\begin{array}[t]{rlll} g$

Da die $\mathrm e$ -Funktion stets ungleich Null ist, folgt mit dem Satz des Nullprodukts $\(f$ und somit $\(f$

(2)

Aus der Abbildung folgt, dass sowohl $\(f$ als auch $f(1)\lt0$ gilt. Somit ist für $a=1$ die Gleichung $\(f$ aus Teilaufgabe 5.1 nicht erfüllt und damit kann der Graph von $g$ im Punkt $(1\mid g(1))$ keine waagerechte Tangente besitzen.

(1)

Ausdruck	$\color{#fff}{\overrightarrow{a}\circ(\overrightarrow{a}+\overrightarrow{b})}$	$\color{#fff}{\overrightarrow{a}+(\overrightarrow{a}\circ\overrightarrow{b})}$
Vektor mit drei Koordinaten		
reelle Zahl		
nicht definiert		

(2)

Der Winkel zwischen den beiden Vektoren beträgt genau dann mindestens $90^\circ,$ wenn das Skalarprodukt Null oder negativ ist. Somit folgt für die gesuchten Werte von $r:$

$\begin{array}[t]{rlll} \pmatrix{2\\3\\0}\circ\pmatrix{r\\4\\2}&\leq&0 \\[5pt] 2r+12&\leq&0 &\mid\;-12 \\[5pt] 2r&\leq&-12 &\mid\;:2 \\[5pt] r&\leq&-6 \end{array}$

(1)

Alle Ebenengleichungen der Schar enthalten $z$ nicht. Somit stehen die Ebenen der Schar senkrecht zur $x$ - $y$ -Ebene.

(2)

Zwei Ebenen $E_{k_1}$ und $E_{k_2}$ der Schar sind parallel genau dann, wenn ihre Normalenvektoren Vielfache voneinander sind:

$\pmatrix{k_1\\2-k_1\\0}=a\cdot\pmatrix{k_2\\2-k_2\\0}$

Aus den ersten beiden Zeilen folgt:

$\begin{array}{lrll} \text{I}\quad&k_1&=& a\cdot k_2 \\ \text{II}\quad&2-k_1&=&a\cdot(2-k_2) \\ \end{array}$

Addieren von $\text{I}$ und $\text{II}$ liefert:

$\begin{array}[t]{rlll} 2&=&2a &\mid\;:2\\[5pt] 1&=&a \end{array}$

Der einzige mögliche Wert ist somit $a=1.$ Für diesen Wert sind die beiden Vektoren allerdings keine Vielfachen voneinander, sondern der gleiche Vektor und gehören somit zur gleichen Ebene. Zwei verschiedene Ebenen der Schar sind damit nicht parallel zueinander.

(1)

Die Wahrscheinlichkeit, bei einem einzelnen Wurf keine 3 zu würfeln, beträgt $\frac{5}{6}.$ Damit beträgt die Wahrscheinlichkeit in beiden Würfen keine 3 zu erzielen $\frac{5}{6}\cdot\frac{5}{6}=\frac{25}{36}.$

(2)

Die Wahrscheinlichkeit, in beiden Würfen eine 3 zu erzielen, beträgt $\frac{1}{6}\cdot\frac{1}{6}=\frac{1}{36}.$ Zusammen mit der Wahrscheinlichkeit aus Teilaufgabe 4.1 ergibt sich somit $1-\frac{26}{36}=\frac{10}{36}$ als Wahrscheinlichkeit für genau eine 3 in zwei Würfen.
Die erwartete Auszahlung pro Spiel soll gleich dem Einsatz, d.h. $2\,\text{€},$ sein. Somit folgt für $x:$

Rechenweg anzeigen

$x=22$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?