Vorschlag B1
Kräfte auf elektrische Ladungen
1
Im Physikunterricht gehören zu den ersten Versuchen zur Elektrizitätslehre Experimente mit geladenen Körpern. Im Folgenden werden elektrisch geladene Luftballons betrachtet.
1.1
Ein Luftballon, dessen Oberfläche mit Metall bedampft ist, und ein Luftballon ohne eine solche Bedampfung werden durch Berühren an einer Stelle elektrisch negativ aufgeladen.
Erkläre den Unterschied, der sich für die Ladungsverteilung aus der Bedampfung der Oberfläche mit Metall ergibt.
(3 BE)
1.2
Ein negativ geladener Luftballon, dessen Oberfläche mit Metall bedampft ist, hängt an einem langen Faden von der Decke. An einem Isolierstiel wird eine ungeladene Metallkugel seitlich in die Nähe des Ballons gehalten. Der Ballon kann weder den Isolierstiel noch die Metallkugel berühren.
Skizziere die sich ergebende Lage von Faden, Ballon und Metallkugel.
Skizziere auch die Ladungsverteilung auf Ballon und Metallkugel.
Erläutere deine Skizze.
(6 BE)
1.3
Zwei gleiche, negativ geladene Luftballons, deren Oberflächen mit Metall bedampft sind, hängen an langen Fäden von der Decke. Die Ballons berühren sich nicht, die Fäden sind aber so lang, dass sich die Ballons grundsätzlich berühren können (Material 1). Der Ballon 1 wird nun vorsichtig mit der Hand berührt und die Hand anschließend wieder weggenommen.
Erkläre, welche Folgen dies hat.
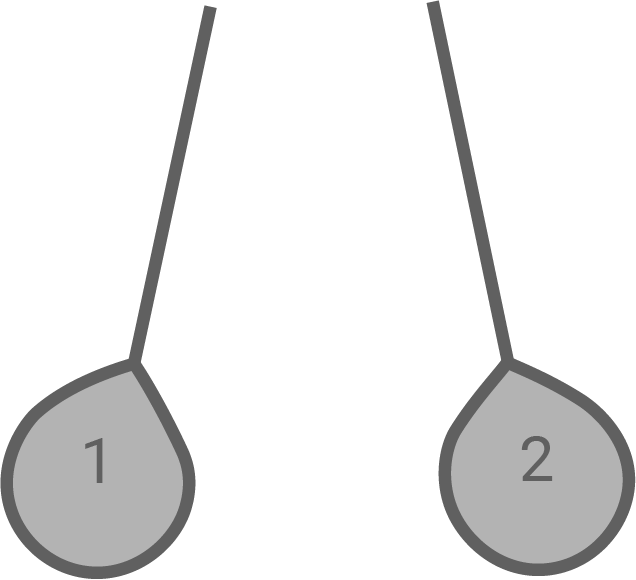
Material 1: Negativ geladene Luftballons mit Metallbedampfung
(5 BE)
2
Die Betrachtung von geladenen Körpern führt zum Begriff des elektrischen Feldes.
An einen luftgefüllten Plattenkondensator aus kreisförmigen Metallplatten, die einen Plattenabstand von 
und einen Radius von jeweils 
besitzen, wird eine Spannung von 
angelegt
und einen Radius von jeweils besitzen, wird eine Spannung von angelegt
2.1
Berechne die Ladung, die im Plattenkondensator gespeichert ist, und die elektrische Feldstärke zwischen den Kondensatorplatten.
(5 BE)
2.2
Beide Kondensatorplatten haben in der Mitte ein winziges Loch. Durch dieses Loch wird ein Elektron mit der Geschwindigkeit von 
geschossen (Material 2).
Begründe, welches der Diagramme in Material 3 die Veränderung der kinetischen Energie des Elektrons im Plattenkondensator in Abhängigkeit von der Flugstrecke 
durch den Plattenkondensator beschreibt.
Berechne die kinetische Energie des Elektrons, nachdem es den Kondensator durchflogen hat.
geschossen (Material 2).
Begründe, welches der Diagramme in Material 3 die Veränderung der kinetischen Energie des Elektrons im Plattenkondensator in Abhängigkeit von der Flugstrecke durch den Plattenkondensator beschreibt.
Berechne die kinetische Energie des Elektrons, nachdem es den Kondensator durchflogen hat.
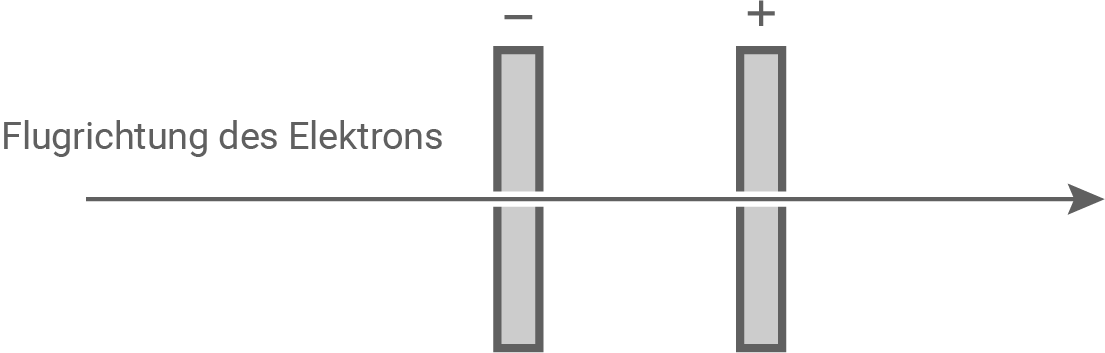
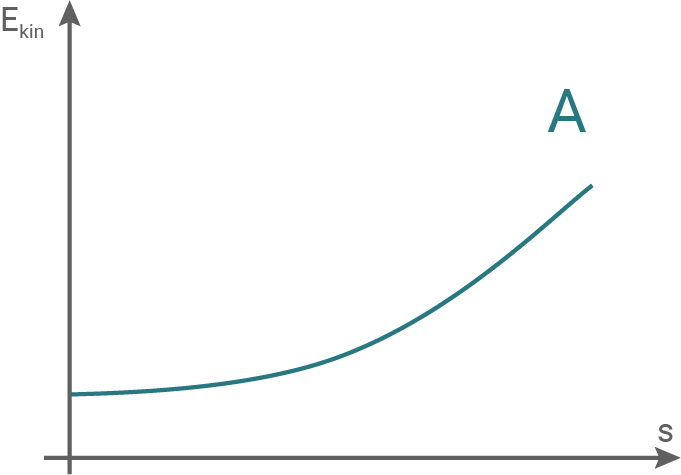
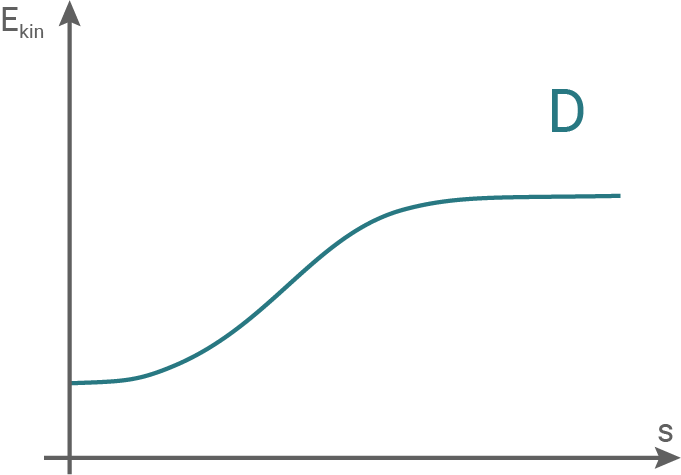
Material 2: Querschnitt durch den Plattenkondensator mit Elektron
Material 3: Mögliche Diagramme für die kinetische Energie des Elektrons
(6 BE)
3
Nicht nur in elektrischen Feldern, auch in magnetischen Feldern wirken auf bewegte elektrische Ladungen Kräfte.
Ein Leiterrahmen der Breite 
wird an eine Spannungsquelle angeschlossen, sodass er von einem Strom durchflossen wird. Hält man den Leiterrahmen in ein Magnetfeld (Material 4), spürt man, wie dieser nach unten gezogen wird.
wird an eine Spannungsquelle angeschlossen, sodass er von einem Strom durchflossen wird. Hält man den Leiterrahmen in ein Magnetfeld (Material 4), spürt man, wie dieser nach unten gezogen wird.
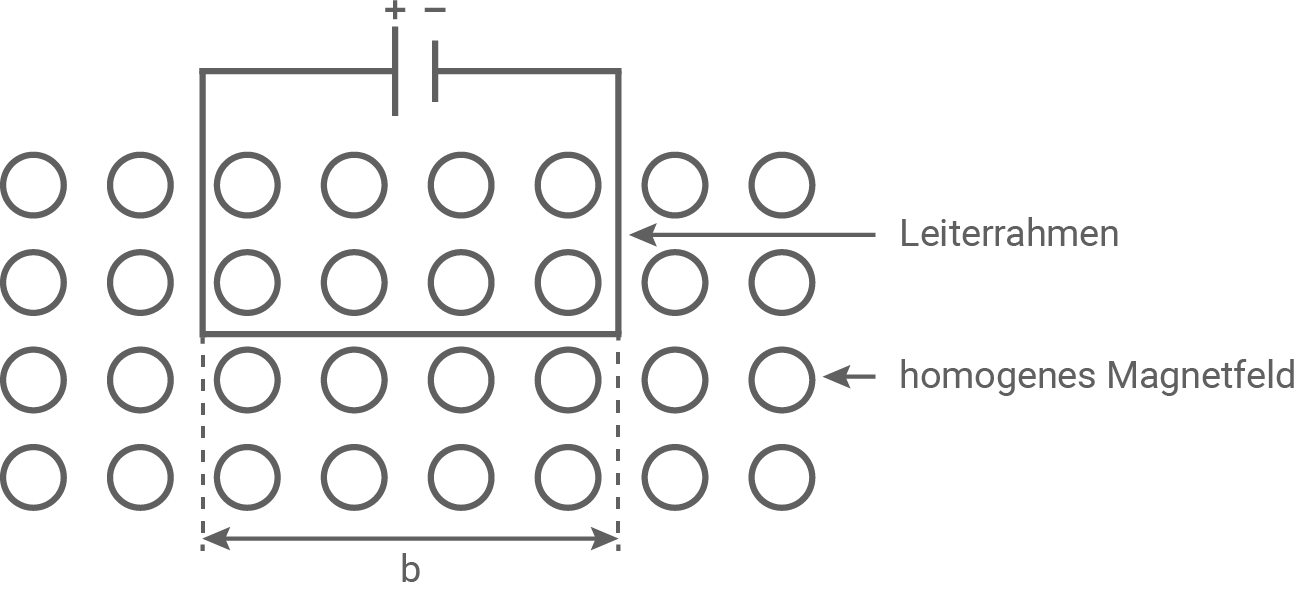
Material 4: Stromdurchflossener Leiterrahmen im homogenen Magnetfeld
3.1
Begründe, welche Richtung die magnetischen Feldlinien in Material 4 besitzen und zeichne diese Richtung ein.
Erläutere, dass man nur die Kraft auf den unteren horizontalen Teil des Leiterrahmens spürt.
(5 BE)
3.2
Die Kraft auf den Leiterrahmen wird in Abhängigkeit von der Stromstärke bestimmt. Die Messergebnisse sind in Material 5 angegeben.
Werte die Daten zeichnerisch und rechnerisch aus. Zur rechnerischen Auswertung kann die letzte Tabellenzeile genutzt werden.
Bestimme mithilfe Ihrer Auswertung und der Breite des Leiterrahmens die magnetische Flussdichte 
des Magnetfelds.
des Magnetfelds.
Material 5: Kraft auf den Leiterrahmen in Abhängigkeit von der Stromstärke
 in  |
 in  |
|
|---|---|---|
| 3,0 | 64 | |
| 5,0 | 107 | |
| 8,0 | 166 | |
| 10,0 | 209 |
(7 BE)
4
Eine Leiterschleife wird gleichförmig mit der Geschwindigkeit 
nach unten in ein homogenes Magnetfeld mit der magnetischen Flussdichte 
abgesenkt (Material 6). Die Leiterschleife besitzt die Länge 
die Breite und den elektrischen Widerstand 
nach unten in ein homogenes Magnetfeld mit der magnetischen Flussdichte abgesenkt (Material 6). Die Leiterschleife besitzt die Länge die Breite und den elektrischen Widerstand
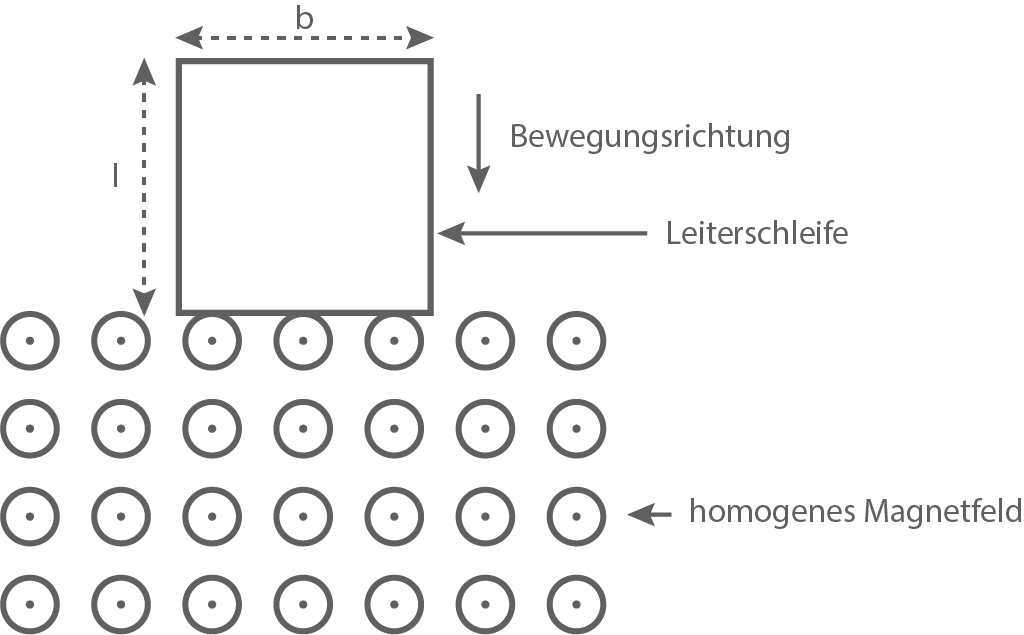
Material 6: Leiterschleife wird in das Magnetfeld bewegt
4.1
Erkläre die physikalischen Vorgänge in der Leiterschleife während des Eintritts in das Magnetfeld und gib die Richtung der entstehenden Elektronenbewegung an.
(4 BE)
4.2
Zum Zeitpunkt 
beginnt die gleichförmige Bewegung der Leiterschleife in das Magnetfeld hinein. Zum Zeitpunkt 
befindet sich die Leiterschleife vollständig im Magnetfeld.
Berechne den Zeitpunkt 
Berechne die elektrische Stromstärke in der Leiterschleife bis zu diesem Zeitpunkt
Erläutere die Auswirkungen auf den Stromfluss in der Leiterschleife, sobald diese vollständig in das magnetische Feld eingetaucht ist.
beginnt die gleichförmige Bewegung der Leiterschleife in das Magnetfeld hinein. Zum Zeitpunkt befindet sich die Leiterschleife vollständig im Magnetfeld.
Berechne den Zeitpunkt
Berechne die elektrische Stromstärke in der Leiterschleife bis zu diesem Zeitpunkt
Erläutere die Auswirkungen auf den Stromfluss in der Leiterschleife, sobald diese vollständig in das magnetische Feld eingetaucht ist.
(6 BE)
4.3
Die Leiterschleife wird über dem Magnetfeld losgelassen, sodass sie im freien Fall in das Magnetfeld eintritt.
Begründe, dass beim Eintritt der Leiterschleife in das Magnetfeld die Beschleunigung, die die Schleife erfährt, abnimmt.
(3 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.1
Ein Luftballon, der nicht mit Metall bedampft ist, gilt als Nichtleiter. Wenn negative elektrische Ladungen auf den Ballon treffen, bleiben sie auf seiner Oberfläche haften und laden ihn elektrisch negativ auf. Durch Influenzladungen kann sich die Verteilung der Ladungen auf dem Ballon verändern, was bedeutet, dass die elektrische Ladung an verschiedenen Stellen unterschiedlich sein kann.
Ein Luftballon, der mit Metall bedampft ist, kann die negativ geladenen Elektronen auf seiner Oberfläche gleichmäßig verteilen, da das Metall die Elektronen leitet. Infolgedessen entsteht eine homogene Ladungsverteilung auf dem Ballon, da die Elektronen sich untereinander durch Abstoßungskräfte gleichmäßig verteilen.
1.2
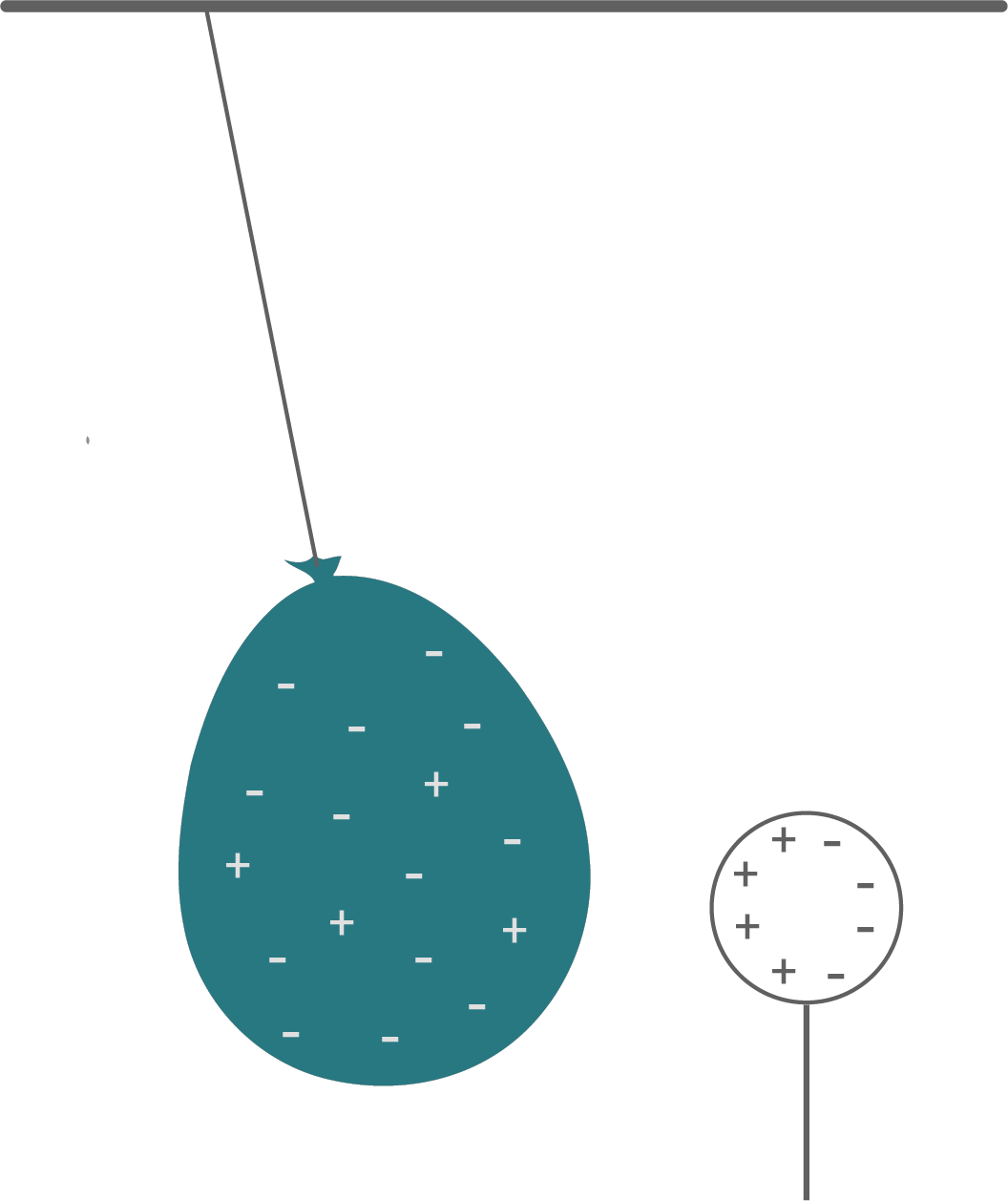
1.3
(1) Beide Ballons sind negativ aufgeladen und stoßen sich aufgrund ihrer gleichen Ladung ab.
(2) Wenn einer der Ballons mit der Hand berührt wird, werden die überschüssigen negativen Ladungsträger abgeleitet und der Ballon wird danach neutral geladen.
(3) Der negativ geladene Ballon erzeugt durch Influenz eine Ladungsverschiebung auf dem neutralen Ballon. Dadurch ziehen sich beide Ballons aufgrund der unterschiedlichen Ladungen an, bis sie sich schließlich berühren. Dies ist ähnlich zur Situation in Aufgabe 1.2, wo die Ladungsverschiebung auf einem nichtmetallischen Ballon aufgrund von Influenz auftritt.
2.1
Es gilt 
und außerdem 
Daraus folgt:
Mit 
und 
folgt:
und außerdem
Daraus folgt:
Mit und folgt:
2.2
Wird das Elektron durch das Loch geschossen und durchfliegt die Kondensatorplatten, so wird es von der negativen Platte abgestoßen und von der positiven Platte angezogen. Dadurch nimmt die Geschwindigkeit des Elektrons zu.
Da es sich um ein homogenes Feld im Plattenkondensator handelt, wird das Elektron auf der Strecke konstant beschleunigt, wodurch die kinetische Energie linear zunimmt.
Es gilt nämlich Folgendes: Beschleunigende Kraft:
ist konstant.
Beschleunigungsarbeit: 
woraus 
folgt.
Der Graph der kinetischen Energie muss also linear verlaufen. Somit beschreibt Diagramm B den Sachverhalt.
Es gilt: 
dabei entspricht 
der kinetischen Energie vor dem Eindringen in den Kondensator und 
der Beschleunigungsarbeit, die beim Durchlaufen der Kondenstorplatten in kinetische Energie umgewandelt wird.
Da es sich um ein homogenes Feld im Plattenkondensator handelt, wird das Elektron auf der Strecke konstant beschleunigt, wodurch die kinetische Energie linear zunimmt.
Es gilt nämlich Folgendes: Beschleunigende Kraft:
ist konstant.
Beschleunigungsarbeit: woraus folgt.
Der Graph der kinetischen Energie muss also linear verlaufen. Somit beschreibt Diagramm B den Sachverhalt.
Es gilt: dabei entspricht der kinetischen Energie vor dem Eindringen in den Kondensator und der Beschleunigungsarbeit, die beim Durchlaufen der Kondenstorplatten in kinetische Energie umgewandelt wird.
![\(\begin{array}[t]{rll}
E _{\text {kin }}&=& E _0+ W_{\text{el}} \\[5pt]
&=&\dfrac{1}{2} m _{ e } \cdot v _0^2+ e \cdot E \cdot d \\[5pt]
&=& \frac{1}{2} \cdot 9,11 \cdot 10^{-31}\;\text{kg} \cdot\left(4 \cdot 10^6 \frac{ \text{m} }{ \text{s}}\right)^2+1,602 \cdot 10^{-19} \text{C}\cdot 60 \text{V} \\[5pt]
&=& 1,7 \cdot 10^{-17} \;\text{J}
\end{array}\)](https://www.schullv.de/resources/formulas/acf4353313d0d88d2bca41d822bf5c6def617dd24ca066d39f872508a65bd167_light.svg)
3.1
Im unteren Teil des Leiterrahmens wirkt eine Kraft nach unten, da eine Kraft den Leiterrahmen nach unten zieht.
Mit der Linke-Hand Regel folgt: Die Feldlinien zeigen aus der Ebene heraus.
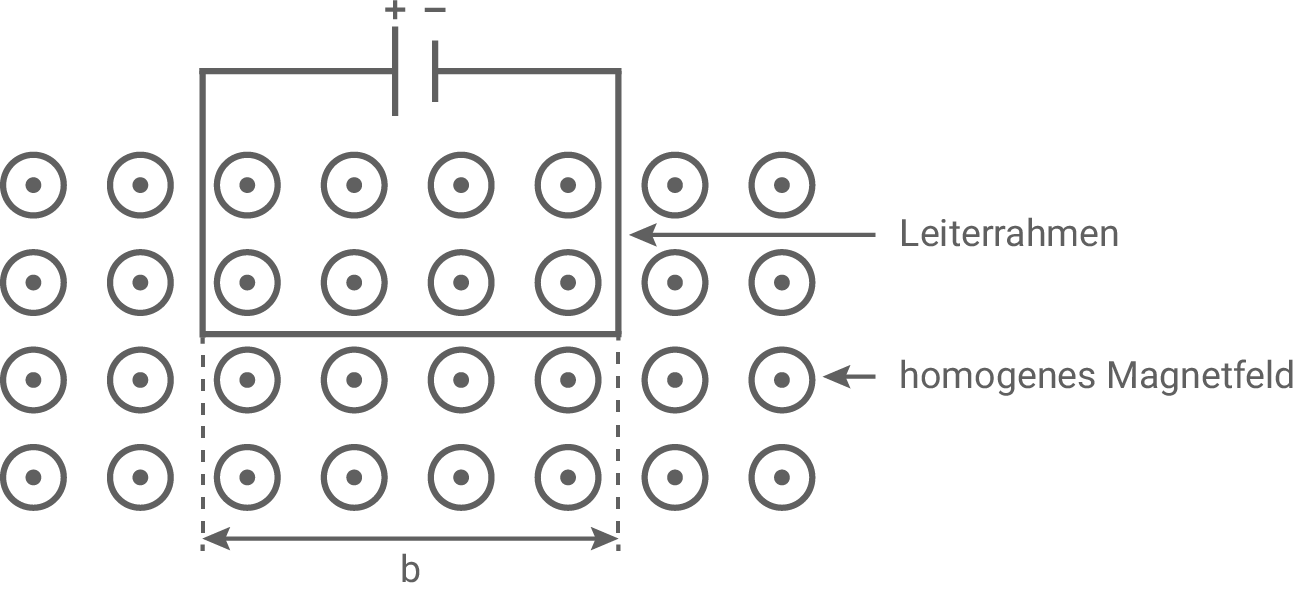Da sich der obere Teil des Leiterrahmens außerhalb des homogenen Magnetfeldes befindet, wird er von keiner Lorentzkraft beeinflusst. Die Kräfte, die auf die rechte und linke Seite des Rahmens im Magnetfeld wirken, sind gleich groß und entgegengesetzt gerichtet. Daraus folgt, dass sich diese Kräfte gegenseitig aufheben. Folglich wird nur der untere horizontale Teil des Leiterrahmens von einer Kraft beeinflusst.
3.2
Zeichnerische Auswertung
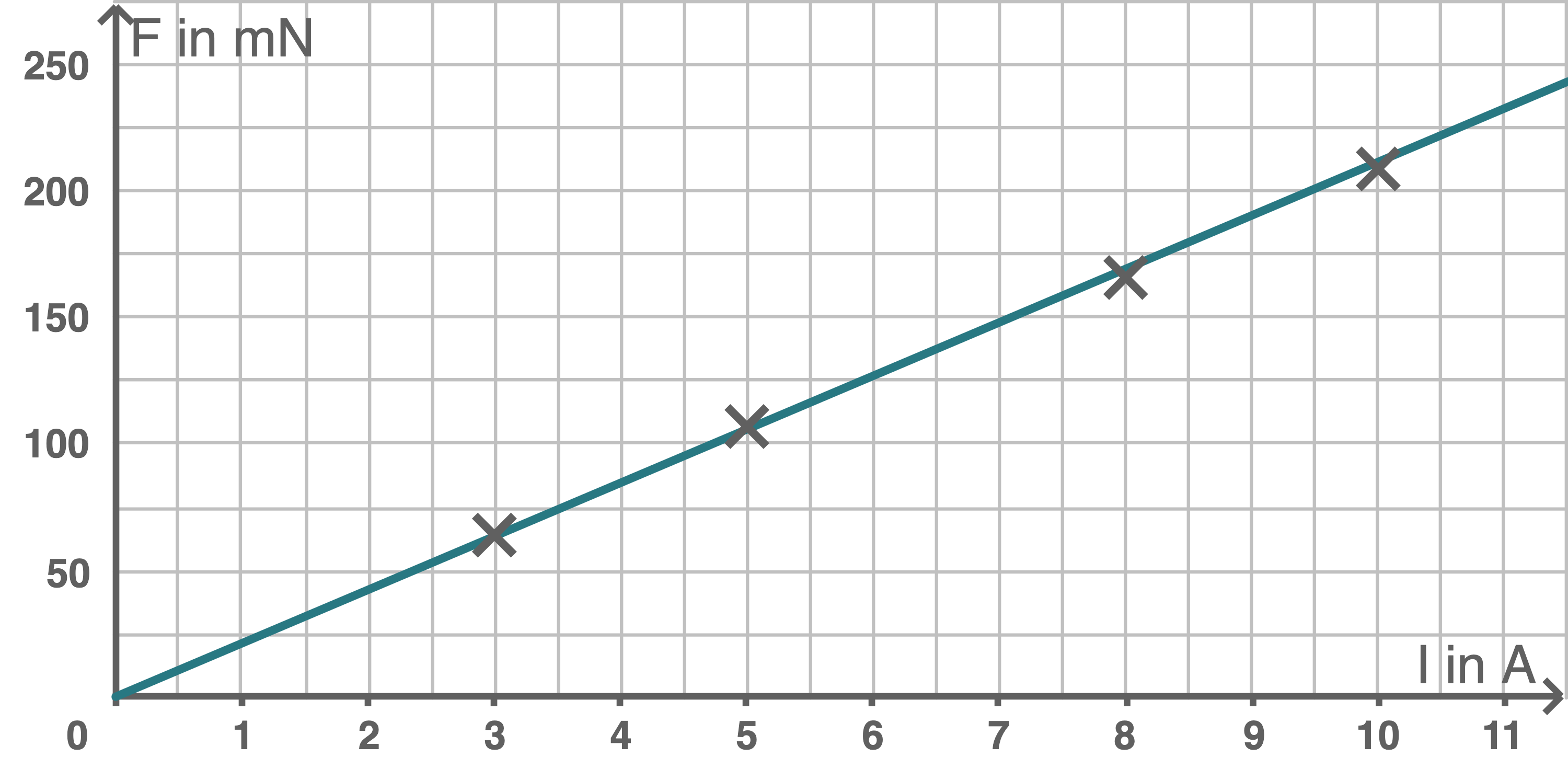Für die Steigung 
der Geraden folgt 
Rechnerische Auswertung
Es folgt:
Magnetische Flussdichte
der Geraden folgt
Rechnerische Auswertung
 in  |
 in |
 in  |
|---|---|---|
| 3,0 | 64 | 21,3 |
| 5,0 | 107 | 21,4 |
| 8,0 | 166 | 20,8 |
| 10,0 | 209 | 20,9 |
Magnetische Flussdichte
![\(\begin{array}[t]{rll}
B&=& \dfrac{ F }{ I \cdot b } \\[5pt]
&=& \dfrac{ F }{ I } \cdot \frac{1}{b} \\[5pt]
&=& m \cdot \frac{1}{B} \\[5pt]
&=& 21,1 \cdot 10^{-3} \frac{\text{N}}{\text{A}} \cdot \frac{1}{0,05 \;\text{m} } \\[5pt]
&=&0,42 \;\text{T}
\end{array}\)](https://www.schullv.de/resources/formulas/467d2676a2566626713ed3e5c78107c2bfcb7f1028e471ad075500de4f00c99b_light.svg)
4.1
Eine Induktionsspannung entsteht, wenn sich der magnetische Fluss durch eine Leiterschleife ändert. Solange die Leiterschleife nicht in das Magnetfeld eintritt oder es vollständig verlässt, gibt es keine induzierte Spannung. Wenn sich die Leiterschleife jedoch teilweise im homogenen Magnetfeld befindet und mit einer konstanten Geschwindigkeit abgesenkt wird, wird eine Spannung induziert. Die Lorentzkraft wirkt auf die freien negativen Ladungsträger (Elektronen) im unteren Teil der Leiterschleife und lenkt sie nach rechts ab. Dadurch entsteht eine Ladungstrennung, bei der sich an der linken Seite der Schleife ein Elektronenmangel und an der rechten Seite ein Elektronenüberschuss befindet. In den senkrechten Teilen der Leiterschleife werden die Elektronen ebenfalls nach rechts abgelenkt, jedoch nur an den Rand des Leiters gedrückt, was vernachlässigt werden kann.
4.2
Zeitpunkt
Da die Leiterschleife mit einer konstanten Geschwindigkeit in das Magnetfeld abgesenkt wird, handelt es sich um eine gleichförmige Bewegung.
Elektrische Stromstärke bis zum Zeitpunkt
![\(\begin{array}[t]{rll}
U _{ ind }&=& - n \cdot \dfrac{\Delta \Phi}{\Delta t } \\[5pt]
&=& - n \cdot \dfrac{ B \cdot \Delta A }{\Delta t } \\[5pt]
&=& B \cdot \dfrac{\Delta A }{\Delta t }
\end{array}\)](https://www.schullv.de/resources/formulas/a2e7a9de9635ca9ddfdcdc45259e64d959e5960a289ecbfcdc17c84ab48ae1cc_light.svg)
Es gilt 
und 
woraus folgt:
Wenn die gesamte Fläche der Leiterschleife im Magnetfeld liegt, bleibt die vom Magnetfeld durchsetzte Fläche konstant. Da es keine zeitliche Änderung gibt, entsteht auch keine Induktionsspannung. Somit fließt auch kein Strom durch die Leiterschleife.
Da die Leiterschleife mit einer konstanten Geschwindigkeit in das Magnetfeld abgesenkt wird, handelt es sich um eine gleichförmige Bewegung.
Elektrische Stromstärke bis zum Zeitpunkt 
![\(\begin{array}[t]{rll}
v&=& \dfrac{\ell}{ t _1} &\quad \scriptsize \mid\;\cdot \ell \\[5pt]
\dfrac{v}{\ell}&=& \dfrac{1}{t_1} \\[5pt]
\dfrac{\ell}{v}&=& t_1 \\[5pt]
t_1 &=&\dfrac{\ell}{v}\\[5pt]
t_1 &=&\dfrac{8 \;\text{cm}}{10 \frac{\text{cm}}{\text{s}}} \\[5pt]
t_1 &=& 0,8 \; \text{s}
\end{array}\)](https://www.schullv.de/resources/formulas/d5bd5b14eef34034ac0f29723f642188c04ecbc26323f40071498f3785afb158_light.svg)
Es gilt und woraus folgt:
Wenn die gesamte Fläche der Leiterschleife im Magnetfeld liegt, bleibt die vom Magnetfeld durchsetzte Fläche konstant. Da es keine zeitliche Änderung gibt, entsteht auch keine Induktionsspannung. Somit fließt auch kein Strom durch die Leiterschleife.
![\(\begin{array}[t]{rll}
U _{ ind} &=& B \cdot \dfrac{\Delta A }{\Delta t } \\[5pt]
&=& - B \cdot \dfrac{\Delta \ell \cdot b }{\Delta t } \\[5pt]
&=& - B \cdot \dfrac{ v \cdot \Delta t \cdot b }{\Delta t } \\[5pt]
&=& - B \cdot v \cdot b\\[5pt]
&=& -0,4 \;\text{T} \cdot 0,10 \frac{\text{m}}{\text{s}} \cdot 0,05 \;\text{m} \\[5pt]
&=& -0,002 \;\text{V}
\end{array}\)](https://www.schullv.de/resources/formulas/8bd3fe452bb3265306274e05ef29e9df27ffe3cd5a72797f9b72cb3a4ee0ef2f_light.svg)
![\(\begin{array}[t]{rll}
U _{ ind } &=& R \cdot I &\quad \scriptsize \mid\; :R\\[5pt]
\dfrac{U _{ ind }}{R}&=& I \\[5pt]
I&=& \dfrac{U _{ ind }}{R} \\[5pt]
&=& \dfrac{0,002\;\text{V} }{0,1 \; \Omega} \\[5pt]
&=& 0,02 \;\text{A}
\end{array}\)](https://www.schullv.de/resources/formulas/011157f2ce24cf0f531d8cc795d88f50c47d17ab3d1cdb62319e777825715d37_light.svg)
4.3
Wenn sich die Leiterschleife in das Magnetfeld hineinbewegt, verändert sich die vom Magnetfeld durchsetzte Fläche und damit auch der magnetische Fluss durch die Leiterschleife. Dadurch wird in der Leiterschleife eine Induktionsspannung induziert, die einen Stromfluss in der Leiterschleife hervorruft. Die Stromrichtung ist bei der gezeigten Magnetfeldrichtung gegen den Uhrzeigersinn. Die Elektronenbewegung aufgrund der induzierten Spannung ruft eine Kraft hervor, die nach oben zeigt und damit der Fallbeschleunigung entgegenwirkt. Die Bremswirkung lässt sich mithilfe der Lenz'schen Regel erklären: Der Induktionsstrom ist stets so gerichtet, dass er der Ursache seiner Entstehung entgegenwirkt.