Vorschlag B2

Kondensatoren, Blitze und Faraday’scher Käfig

Ein luftgefüllter Plattenkondensator $\left(\varepsilon_{ r }=1\right)$ mit vertikal ausgerichteten, quadratischen Platten (Seitenlänge $a =40 \,\text{cm},$ Plattenabstand $d =2\,\text{cm}$ ) wird an eine regelbare Spannungsquelle angeschlossen.

1.1

In einer Messreihe wird die Abhängigkeit der Ladung $Q$ auf einer der Kondensatorplatten von der angelegten Spannung $U$ gemessen (Material 1).

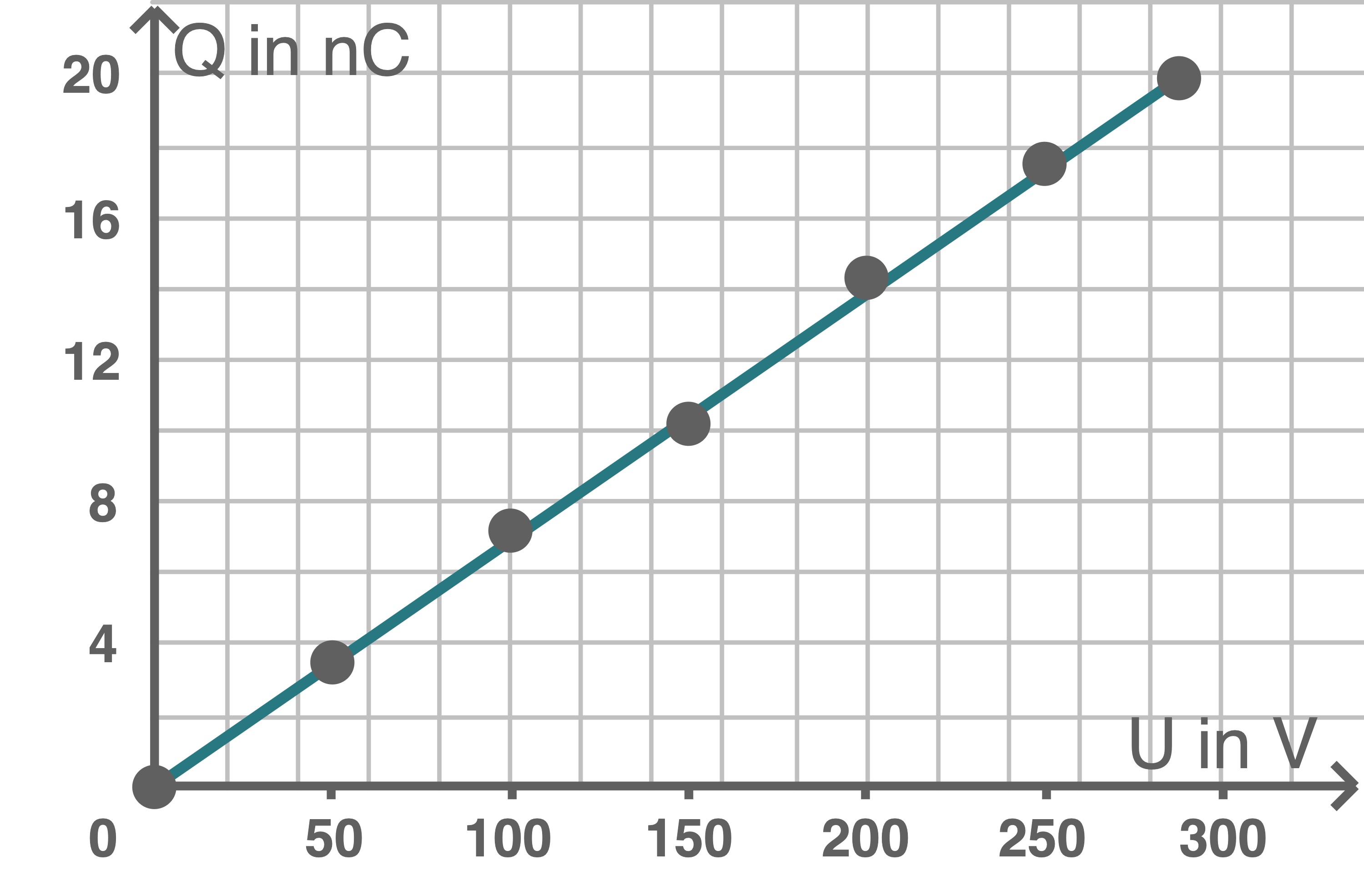
Zeichne die Messwerte in ein $U$ - $Q$ -Diagramm ein und ermittle aus dem Diagramm mithilfe einer Ausgleichsgeraden die Kapazität $C _{\text {graph }}$ des Kondensators.

Berechne aus den Abmessungen des Kondensators die Kapazität $C$ des Kondensators.

Berechne die prozentuale Abweichung von $C _{\text {graph }}$ von $C.$

[zur Kontrolle: $C =7,08 \cdot 10^{-11} \,\text F$ ]

Material 1: Messreihe am Kondensator

$\color{#fff}{\text U}$ in $\color{#fff}{\text V}$	$\color{#fff}{\text Q}$ in $\color{#fff}{\text {nC}}$
0	0
50	3,5
100	7,2
150	10,2
200	14,3
250	17,5

(10 BE)

1.2

Der Plattenkondensator wird nun mit $U =250 \,\text V$ aufgeladen und von der Spannungsquelle getrennt. Der Plattenabstand wird danach auf $4 \,\text{cm}$ erhöht.

Untersuche die quantitativen Auswirkungen dieser Änderung auf die Spannung und die gespeicherte Energie des Kondensators.

(4 BE)

1.3

Der Plattenkondensator wird an die Spannungsquelle mit $U =250 \,\text V$ angeschlossen und der Plattenabstand wird wieder auf $d =2 \,\text{cm}$ eingestellt.

1.3.1

Zwischen die Kondensatorplatten wird eine Polyethylenplatte $\left(\varepsilon_{ r }=2,4\right)$ eingeführt, sodass der gesamte Zwischenraum ausgefüllt ist.

Begründe, dass sich jetzt bei gleicher Spannung eine größere Ladung auf den Platten befindet als im Falle des luftgefüllten Plattenkondensators.

Berechne die Kapazität $C_{\text {Poly }}$ des mit Polyethylen gefüllten Kondensators.

(5 BE)

1.3.2

Die Polyethylenplatte wird entfernt und der Zwischenraum wird von unten zu drei Fünfteln mit einer unbekannten Substanz gefüllt. Der restliche Zwischenraum ist mit Luft ausgefüllt. Dieser teilweise gefüllte Kondensator kann durch eine Parallelschaltung von zwei Kondensatoren beschrieben werden. Skizziere diese Schaltung. Mit der Formel

$\varepsilon_{ r }=\dfrac{5}{3} \cdot \frac{ C _{ T }}{ C }-\dfrac{2}{3}$

kann die Dielektrizitätskonstante $\varepsilon_{ r }$ der unbekannten Substanz berechnet werden. Hierbei ist $C _{ \text T }$ die Kapazität des gesamten Kondensators, der teilweise mit der Substanz gefüllt ist, und $C$ die Kapazität des gesamten nur mit Luft gefüllten Kondensators.

Leite diese Formel her.

Der Kondensator aus Aufgabe 1.1 hat die Kapazität $C =7,08 \cdot 10^{-11} \,\text F.$ Die Kapazität des teilweise gefüllten Kondensators beträgt jetzt $C _{\text T }=1,73 \cdot 10^{-10} \,\text F.$

Berechne den Wert von $\varepsilon_{ r }.$

(8 BE)

Das Material wird nun aus dem Kondensator entfernt, sodass dieser wieder vollständig mit Luft gefüllt ist. Der Plattenabstand beträgt $d =2 \,\text{cm}.$ Der Kondensator wird so gedreht, dass seine Platten horizontal ausgerichtet und mit einer Spannung von $10 \,\text{kV}$ aufgeladen sind. Die obere Platte des Kondensators ist positiv geladen.

In die Mitte des Kondensators wird ein negativ geladenes Tröpfchen der Masse $\text m=2 \cdot 10^{-6} \,\text{kg}$ gebracht, das die Ladung $Q=1,8 \cdot 10^{-12} \,C$ trägt. Das Tröpfchen erfährt eine Gesamtkraft, die nach unten gerichtet ist. Der Auftrieb und die Luftreibung sollen für die weitere Betrachtung vernachlässigt werden.

2.1

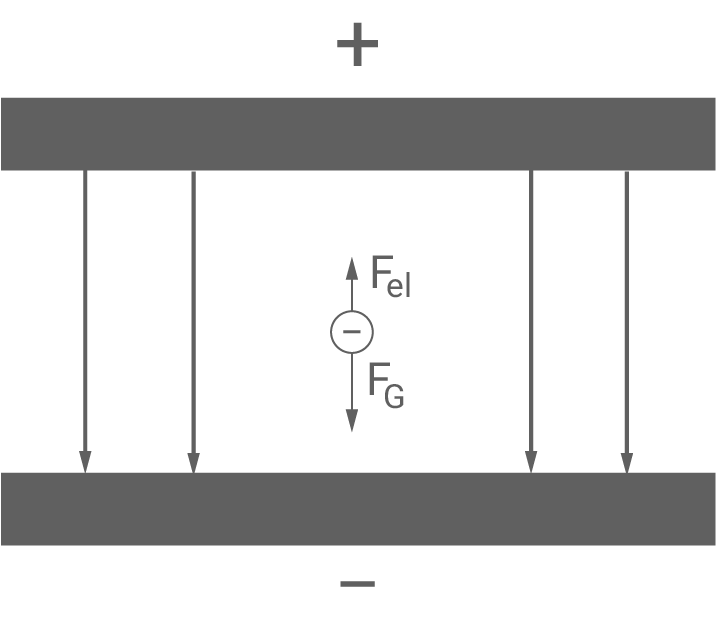
Skizziere das Tröpfchen, die elektrischen Feldlinien innerhalb des Kondensators und die auf das Tröpfchen wirkenden Kräfte mit Beschriftung.

(4 BE)

2.2

Mit der Formel $a = g -\dfrac{ Q \cdot U }{ \text m \cdot d }$ lässt sich die Beschleunigung des Tröpfchens berechnen.

Leite diese Formel her und berechne damit die Beschleunigung.

Bestätige durch eine Einheitenbetrachtung der Formel die Einheit der Beschleunigung.

(8 BE)

2.3

Das fallende Tröpfchen soll nun zwischen den Kondensatorplatten zum Schweben gebracht werden.

Erkläre das experimentelle Vorgehen.

(4 BE)

In einem Labor werden mit einem Hochspannungsgenerator Blitzentladungsphänomene demonstriert. Solche Entladungen werden im Labor zwischen einer negativ geladenen metallischen Spitze an der Decke und einer positiv geladenen Metallplatte am Boden erzeugt. In Material 2 ist der schematische Aufbau des Versuchs dargestellt.

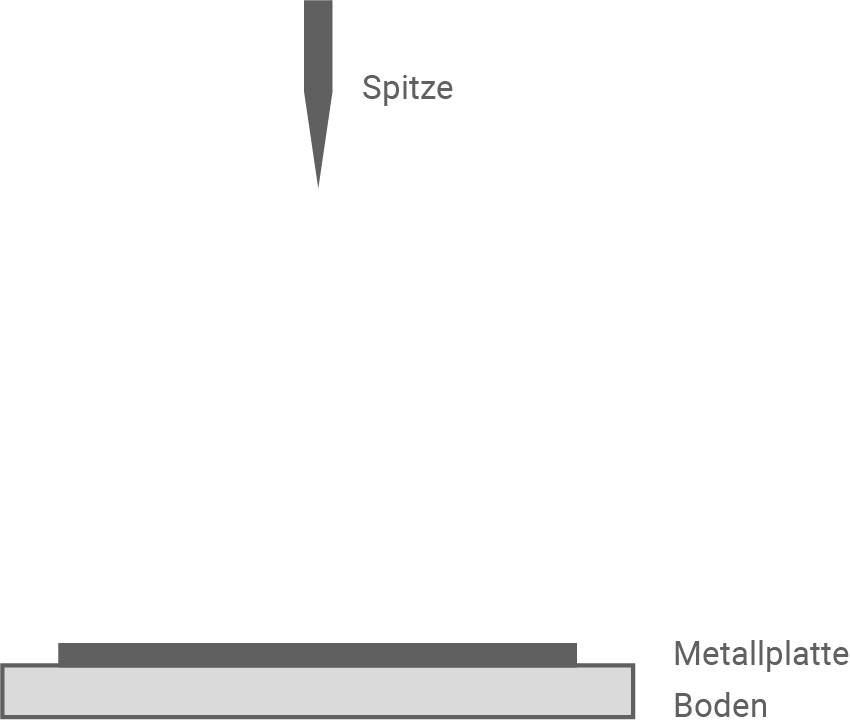
Material 2: Spitze und Boden im Hochspannungslabor

3.1

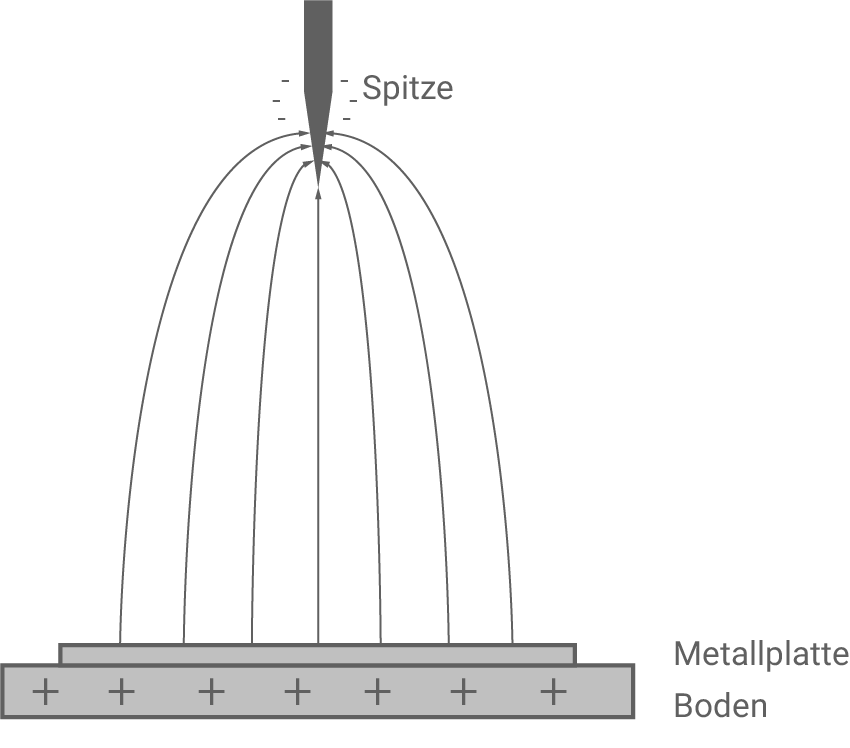
Beschreibe, in welchem Bereich die Feldstärke am größten ist, und skizziere die elektrischen Feldlinien in Material 2.

(3 BE)

3.2

In einem weiteren Versuch wird die Schutzwirkung eines Faraday'schen Käfigs untersucht. Als Testobjekt wird ein Mobiltelefon verwendet, dessen Elektronik durch hohe Spannungen beschädigt wird. Das Mobiltelefon wird in einen kugelförmigen Metallkäfig gelegt, der isoliert unterhalb der Spitze platziert wird. Danach wird zwischen der Spitze und dem Boden eine Hochspannung angelegt. Das Mobiltelefon im Käfig bleibt unbeschädigt, sogar wenn es so platziert wird, dass es die Innenseite des Käfigs berührt.

Erläutere die Schutzwirkung des Faraday'schen Käfigs und auch, dass das Handy die Innenseite des Käfigs unbeschädigt berühren kann.

(4 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

$U$ - $Q$ -Diagramm

Formel zur Bestimmung der Kapazität: $C=\dfrac{Q}{U}$

Die Kapazität lässt sich auch aus der Steigung der Ausgleichsgeraden bestimmen:

$m=\dfrac{\Delta Q}{\Delta U}$ $=\dfrac{14\cdot 10^{-9}\;\text{C}}{200\;\text{V}}$ $=7 \cdot 10^{-11}\;\dfrac{\text{C}}{\text{V}}$ $= 70 \;\text{pF}$

Berechnen der Kapazität mit:

$\begin{array}[t]{rll} C&=& \varepsilon_0 \cdot \varepsilon_r \cdot \dfrac{ A }{ d } \\[5pt] &=& 8,854 \cdot 10^{-12} \dfrac{\text{As} }{ \text{Vm} } \cdot 1 \cdot \dfrac{(0,40 \text{m} )^2}{0,02 \text{m} } \\[5pt] &=&7,1 \cdot 10^{-11} \;\text{F} \end{array}$

Prozentuale Abweichung

$\left|\dfrac{7,0-7,1}{7,1}\right|=0,014=1,4 \%$

1.2

Auswirkung auf die Spannung

Der Plattenkondensator ist von der Ladungsquelle getrennt, somit ist die Ladung auf dem Kondensator konstant.

Es gilt: $d_1=2\cdot d_2$

$C_2=\varepsilon_0 \cdot \varepsilon_r \cdot \dfrac{ A }{ d_2 }$ $=\varepsilon_0 \cdot \varepsilon_r \cdot \dfrac{ A }{ 2\cdot d_1 }$ $=\dfrac{1}{2}\cdot \varepsilon_r \cdot \dfrac{ A }{d_1 }$ $= \dfrac{1}{2}\cdot C_1$

Für die Spannung folgt:

$U_2= \dfrac{Q_2}{C_2}$ $=\dfrac{Q_1}{\frac{1}{2}\cdot C_1}$ $=2\cdot \dfrac{Q_1}{C_1}$ $=2\cdot U_1$ $=2\cdot 250 \;\text{V}=500\;\text{V}$

Auswirkung auf die gespeicherte Energie

Es gilt: $E_{el}=\dfrac{1}{2}\cdot C\cdot U^2$

$E_{el_2}=\dfrac{1}{2}\cdot C_2\cdot U_2^2$ $=\dfrac{1}{2}\cdot \left(\dfrac{1}{2}\cdot C_1 \right)\cdot (2\cdot U_1)^2$ $= \dfrac{1}{2}\cdot 4\cdot \left(\dfrac{1}{2}\cdot C_1\cdot U_1^2 \right)$ $=2\cdot E_{el_1}$

Folgende Werte ergeben sich:

$E_{el_1}=\dfrac{1}{2}\cdot C_1\cdot U_1^2$ $=\dfrac{1}{2}\cdot 7,1\cdot 10^{-11}\;\text{F} \cdot (250 \;\text{V})^2$ $= 2,2\cdot 10^{-6} \;\text{J}$

$E_{el_2}=2\cdot E_{el_1}$ $= 2\cdot 2,2 \;\mu\text{J}$ $4,4 \;\mu\text{J}$

1.3.1

Begründung

Die Polyethylenplatte ist ein Dielektrikum und hat die Eigenschaft, einen elektrischen Dipol auszubilden. Als Isolator besitzt die Platte keine freien Elektronen. Daher können die elektrischen Ladungen innerhalb der Moleküle nur verschoben werden. In diesem Fall drehen sich die Ladungsträger im Dielektrikum so, dass die Elektronen in Richtung der positiv geladenen Kondensatorplatte zeigen. Die Gegenseite, also die positiv geladenen Enden des Dipols, drehen sich in Richtung der negativ geladenen Platte.

Dadurch entsteht in der Polyethylenplatte ein entgegengesetztes elektrisches Feld und die freien Ladungen auf den Kondensatorplatten werden teilweise neutralisiert. Das Ladungsgleichgewicht zwischen den beiden Platten und der Spannungsquelle wird verändert: Die abstoßende Wirkung der Plattenladung auf Ladungen, die von der Spannungsquelle auf die Platten gepumpt werden sollen, wird geringer. Daher kann bei gleich gebliebener Spannung U nun mehr Ladung Q auf die Platten fließen als ohne Verwendung der Polyethylenplatte.

Kapazität berechnen

Mit $\varepsilon_r=2,4$ folgt:

$C_{\text{Poly}} = \varepsilon_0\cdot \varepsilon_r\cdot \dfrac{A}{d}$ $=8,854\cdot 10^{-12} \dfrac{\text{As}}{\text{Vm}}\cdot 2,4\cdot \dfrac{(0,4\;\text{m})^2}{0,02\;\text{m}}$ $= 1,7\cdot 10^{-10} \;\text{F}$ $=0,17\;\text{nF}$

1.3.2

Formel herleiten

Für zwei parallel geschaltete Kondensatoren gilt: $C_{ges}=C+C_S,$ wobei $C_S$ der Kapazität des Kondensators mit der unbekannten Substanz entspricht. Hier gilt $C_{ges}=C_T$

$C_S= \varepsilon_0\cdot \varepsilon_r\cdot \dfrac{A_S}{d},$ wobei $A_S= \dfrac{3}{5} A$ gilt.

$C= \varepsilon_0\cdot \dfrac{A_{\text{Luft}}}{d},$ wobei $A_{\text{Luft}}= \dfrac{2}{5} A$ gilt.

Rechenweg anzeigen

$\varepsilon_r=...$

Werte einsetzen:

$\varepsilon_r=\dfrac{5}{3}\cdot \dfrac{C_T}{C}-\dfrac{2}{3}$ $=\dfrac{5}{3} \cdot \dfrac{1,73 \cdot 10^{-10}\; \text{F} }{7,08 \cdot 10^{-11} \; \text{F} }-\dfrac{2}{3}$ $=3,41$

2.1

2.2

Auf das negativ geladene Tröpfchen wirkt nach unten die Gewichtskraft $F_{ G }$ und nach oben die elektrische Kraft $F_{el}$ . Die auf das Teilchen wirkende Kraft resultiert aus:

$F_{ \text {res } }= F_G- F_{el}$

Es gilt weiterhin:

$F_{\text {res }}= m \cdot a$

$F _{ G }= m \cdot g$ und

$F _{ el }= Q \cdot E = Q \cdot \dfrac{ U }{ d }$

Daraus folgt:

$\begin{array}[t]{rll} F_{\text {res }}&=& F_G- F_{el} \\[5pt] m \cdot a &=&m \cdot g -Q \cdot d\frac{ U }{ d } &\quad \scriptsize \mid\;\cdot m \\[5pt] a&=& g - \dfrac{Q \cdot U }{m\cdot d }& \end{array}$

Einsetzen der Werte:

$a =9,81 \frac{\text{m} }{ \text{s} ^2}-\dfrac{1,8 \cdot 10^{-12}\text{C} \cdot 10 \cdot 10^3 \text{V} }{2 \cdot 10^{-6} \text{kg} \cdot 0,02 \;\text{m} }$ $=9,36 \frac{\text{m} }{ \text{s} ^2}$

Einheitenbetrachtung:

$1 \dfrac{ \text{C} \cdot \text{V} }{ \text{kg} \cdot \text{m} }$ $=1 \dfrac{\text{C} \cdot \frac{ \text{J} }{ \text{C} }}{ \text{kg} \cdot \text{m} }$ $=1 \dfrac{\text{kg}\cdot \text{m} ^2}{ \text{kg} \cdot \text{m} \cdot \text{s} ^2}$ $=1 \dfrac{ \text{m}}{ \text{s} ^2}$

2.3

Das geladene Tröpfchen sinkt im elektrischen Feld des Plattenkondensators nach unten. Wird die Spannung erhöht, so erhöht sich auch das elektrische Feld zwischen den Kondensatorplatten und die Kraft auf das Tröpfchen wird größer.

Dieser Kraft wirkt die Gewichtskraft entgegen. Die Spannung wird so lange erhöht, bis ein Kräftegleichgewicht herrscht. Dann ist die resultierende Kraft gleich Null und das Tröpfchen schwebt.

3.1

3.2

Gelangt ein Faraday’scher Käfig in ein elektrisches Feld, so sammeln sich die Elektronen an der Seite des Metalls, die zum positiven Pol dieses Feldes zeigt. Dadurch herrscht auf dieser Seite ein negativer und auf der anderen Seite ein positiver Ladungsüberschuss und es bildet sich im Inneren des Käfigs ein weiteres elektrisches Feld. Dieses ist dem äußeren Feld entgegengesetzt, wodurch sich die Feldlinien im Hohlraum gegenseitig aufheben.

Es ist sogar möglich, den Käfig von innen zu berühren, ohne dabei einen elektrischen Schlag zu bekommen. Das liegt daran, dass sich die elektrischen Ladungen durch das äußere Feld alle auf der Außenseite des Käfigs befinden; somit kann durch die Berührung kein Strom abfließen.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?