Vorschlag B2

Eigenschaften von Quantenobjekten

Der Fotoeffekt wurde von Wilhelm Hallwachs im Jahre 1888 entdeckt. Für seine Deutung des Fotoeffekts erhielt Albert Einstein den Nobelpreis des Jahres 1921.

1.1

Skizziere und beschrifte einen Versuchsaufbau, mit dem man die maximale kinetische Energie $\text E_{\text{kin }}$ der Fotoelektronen bestimmen kann.

Beschreibe mithilfe der Skizze allgemein die Vorgänge beim Fotoeffekt und erläutere, wie die oben beschriebene Größe bestimmt werden kann.

(7 BE)

1.2

Folgende Formel gilt beim Fotoeffekt: $\text E_{ \text{kin} }=\text E_{ \text{ph} }-\text E_{ \text A }$

Erläutere die drei in der Formel vorkommenden Größen.

(3 BE)

1.3

Eine Fotozelle wird nacheinander mit monochromatischem Licht verschiedener Frequenzen beleuchtet. Erst ab einer Frequenz von $5,52 \cdot 10^{14} \,\text{Hz}$ tritt der Fotoeffekt ein.

Berechne die Austrittsarbeit der Fotozelle und entscheide, welche Fotozelle aus der Tabelle in Material 1 verwendet wurde.

Material 1: Austrittsarbeiten verschiedener Fotozellen

Fotozelle	$\color{#fff}{\text E_{ \text A }}$ in $\color{#fff}{ \text{eV}}$
Fotozelle 1 (AgCsO)	1,04
Fotozelle 2 (Cäsium)	1,94
Fotozelle 3 (Natrium)	2,28
Fotozelle 4 (Zink)	4,34

In Klammern ist das Kathodenmaterial der jeweiligen Fotozellen angegeben.

(3 BE)

1.4

Begründe, dass unterhalb einer Grenzfrequenz selbst bei Erhöhung der Lichtintensität der Fotoeffekt nicht auftritt.

(2 BE)

1.5

Viele Leuchtdioden (LED) senden monochromatisches Licht aus. Die Lichterzeugung kann man als Umkehrung des Fotoeffekts verstehen. Insbesondere besteht ein proportionaler Zusammenhang zwischen der angelegten Spannung, ab der eine LED zu leuchten beginnt (Schwellenspannung, Mindestspannung), und der Frequenz des emittierten Lichts. In Material 2 sind für verschiedene Leuchtdioden die Schwellen für die notwendigen Spannungen angegeben. Die Tabelle enthält auch Spalten zum Eintragen der Ergebnisse von Aufgabe 1.5.1.

Material 2: Daten für verschiedenfarbige LEDs

„Farbe“ der LED	IR	Rot	Grün	UV
$\color{#fff}{U_{\text {Schwelle }}}$ in $\color{#fff}{\text V}$	1,30	1,75	2,30	3,80
$\color{#fff}{\text E_{ \text{el} }}$ in $\color{#fff}{10^{-19} \text J}$
$\color{#fff}{\lambda}$ in $\color{#fff}{\text{nm}}$	939	706	538	322
$\color{#fff}{f}$ in $\color{#fff}{10^{14} \text{Hz}}$

1.5.1

Berechne die elektrische Energie $\text E_{ \text{el} },$ die ein Elektron beim Durchlaufen der Schwellenspannung gewinnt, und berechne aus den Wellenlängen des entstehenden Lichts die zugehörigen Frequenzen $f.$

(4 BE)

1.5.2

Zeichne ein Diagramm, das die Energien $\text E_{\text {el }}$ in Abhängigkeit von den Frequenzen $f$ darstellt, und zeichne eine Ausgleichsgerade durch die Datenpunkte.

(4 BE)

1.5.3

Bestimme die Steigung der Ausgleichsgeraden und erkläre die physikalische Bedeutung dieses Werts.

(4 BE)

Im Folgenden werden die Eigenschaften von Quantenobjekten betrachtet.

2.1

Berechne die Energie und die Masse eines Photons der Wellenlänge von $\lambda=546 \,\text{nm}.$

(4 BE)

2.2

Die Sonne hat eine Strahlungsleistung von $\text P=3,845 \cdot 10^{26} \,\text W.$ Vereinfachend wird angenommen, dass das Sonnenlicht eine mittlere Wellenlänge von $546\,\text{nm}$ besitzt.

Die Anzahl der von der Sonne in der Zeit $t$ emittierten Photonen kann mit der Formel $n=\dfrac{\text P \cdot t \cdot \lambda}{h \cdot c}$ berechnet werden.

Leite diese Formel her.

Berechne die Anzahl der von der Sonne pro Sekunde emittierten Photonen.

(4 BE)

2.3

Im Jahre 1924 hat Louis de Broglie seine bahnbrechenden Hypothesen aufgestellt, die erst drei Jahre später bestätigt werden konnten.

Nenne die De-Broglie-Gleichung und die grundsätzliche Überlegung, die zu dieser Gleichung führte.

Beschreibe, worin die experimentellen Schwierigkeiten der Bestätigung lagen und wie sie gelöst wurden (z.B. durch Clinton Davisson und Lester Germer).

(4 BE)

2.4

Zeige, dass für den Impuls eines Elektrons, welches aus der Ruhe heraus mit einer nicht zu hohen Beschleunigungsspannung $\text U$ beschleunigt wurde, gilt: $p=\sqrt{2 \cdot e \cdot \text U \cdot \text m_{ c }}$ . Dabei ist $e$ die Elementarladung und $\text m_{ e }$ die Masse des Elektrons.

Berechne mithilfe der Formel den Impuls eines mit $5 \,\text{kV}$ beschleunigten Elektrons.

$\big[$ zur Kontrolle: $p=3,82 \cdot 10^{-23} \,\text{Ns} \big]$

(5 BE)

2.5

Das Auflösungsvermögen eines Mikroskops, d.h. der Abstand $\Delta x$ zweier Punkte, die gerade noch als getrennt wahrgenommen werden können, wird durch die Wellenlänge des verwendeten Lichts begrenzt. Hierbei gilt vereinfacht, dass die Wellenlänge höchstens gleich dem Auflösungsvermögen sein darf. Durch die Entwicklung von Elektronenmikroskopen, die sich die Welleneigenschaften von Elektronen zunutze machen, konnte das Auflösungsvermögen deutlich verbessert werden und der Blick in die atomare Welt wurde ermöglicht.

2.5.1

Beurteile, ob die mit $5 \,\text{kV}$ beschleunigten Elektronen zur Betrachtung atomarer Strukturen im Bereich von $1 \,\text{nm}$ geeignet sind.

(3 BE)

2.5.2

Schätze ab, um welchen Faktor sich das Auflösungsvermögen bei einer Beschleunigungsspannung von $5\,\text{kV}$ im Vergleich zu sichtbarem Licht verbessert hat.

(3 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

Als Photoeffekt wird das physikalische Phänomen bezeichnet, dass Licht hinreichend großer Frequenz (bzw. hinreichend kleiner Wellenlänge) Elektronen aus Materialien (z. B. Metallen) herauslösen kann.

Der Fotoeffekt beschreibt die Freisetzung von Elektronen aus Metalloberflächen, wenn diese mit Licht bestrahlt werden. Wenn ein Photon auf ein Metall trifft, kann es ein Hüllelektron eines Metallatoms anregen und dessen Bindungsenergie überwinden, um das Elektron aus dem Metall zu lösen. Die kinetische Energie der Fotoelektronen hängt von der Energie des Photons ab und kann durch die Gegenfeldmethode bestimmt werden. Hierbei wird eine Gegenspannung zwischen der Anode und der Kathode der Fotozelle angelegt, um die Elektronen abzubremsen. Bei steigender Gegenspannung sinkt der Fotostrom, bis schließlich kein Strom mehr fließt, weil alle Elektronen gestoppt wurden. Die maximale kinetische Energie der schnellsten Fotoelektronen kann dann mit der Gleichung $E_{kin, \max}=e\cdot U_G$ berechnet werden, wobei $e$ die Elementarladung und $U_G$ die Gegenspannung ist.

1.2

$E _{\text {kin }}:$ kinetische Energie der Fotoelektronen nach dem Auslösen aus der Metalloberfläche
$E _{ ph }:$ Energie der auf das Metall auftreffenden Photonen, vollständig auf Elektron übertragen
$E _{ A }$ ist die Ablösearbeit um Metall zu verlassen

1.3

Es ist $f _{\text {grenz }}=5,52 \cdot 10^{14} \;\text{Hz}$ gegeben.

Rechenweg anzeigen

$E _{ ph }= 2,28\;\text{eV}$

Somit wurde Fotozelle 3 (Natrium) verwendet.

1.4

Wenn die Intensität des einfallenden Lichts erhöht wird, erhöht sich die Anzahl der Photonen, die pro Zeiteinheit auf die Metallplatte treffen. Wenn sich die Frequenz des Lichts oberhalb der Grenzfrequenz befindet, werden mehr Elektronen aus der Fotokathode ausgelöst. Die Energie der einzelnen Photonen hängt jedoch nur von der Lichtfrequenz ab und ist proportional dazu, gemäß der Formel $E _{ ph }=h \cdot f$ . Daher hat die Erhöhung der Intensität des Lichts keinen Einfluss auf die Energie der Photonen und somit auf den Fotoeffekt, der nur eintritt, wenn die Frequenz oberhalb der Grenzfrequenz liegt, unabhängig von der Lichtintensität.

1.5.1

Es gilt: $E_{e l}=e \cdot U_{\text {Schwelle }}$ und $c=\lambda \cdot f,$ womit folgt:

„Farbe“ der LED	IR	Rot	Grün	UV
$\color{#fff}{U_{\text {Schwelle }}}$ in $\color{#fff}{\text V}$	1,30	1,75	2,30	3,80
$\color{#fff}{\text E_{ \text{el} }}$ in $\color{#fff}{10^{-19} \text J}$	2,1	2,8	3,7	6,1
$\color{#fff}{\lambda}$ in $\color{#fff}{\text{nm}}$	939	706	538	322
$\color{#fff}{f}$ in $\color{#fff}{10^{14} \text{Hz}}$	3,2	4,2	5,6	9,3

1.5.2

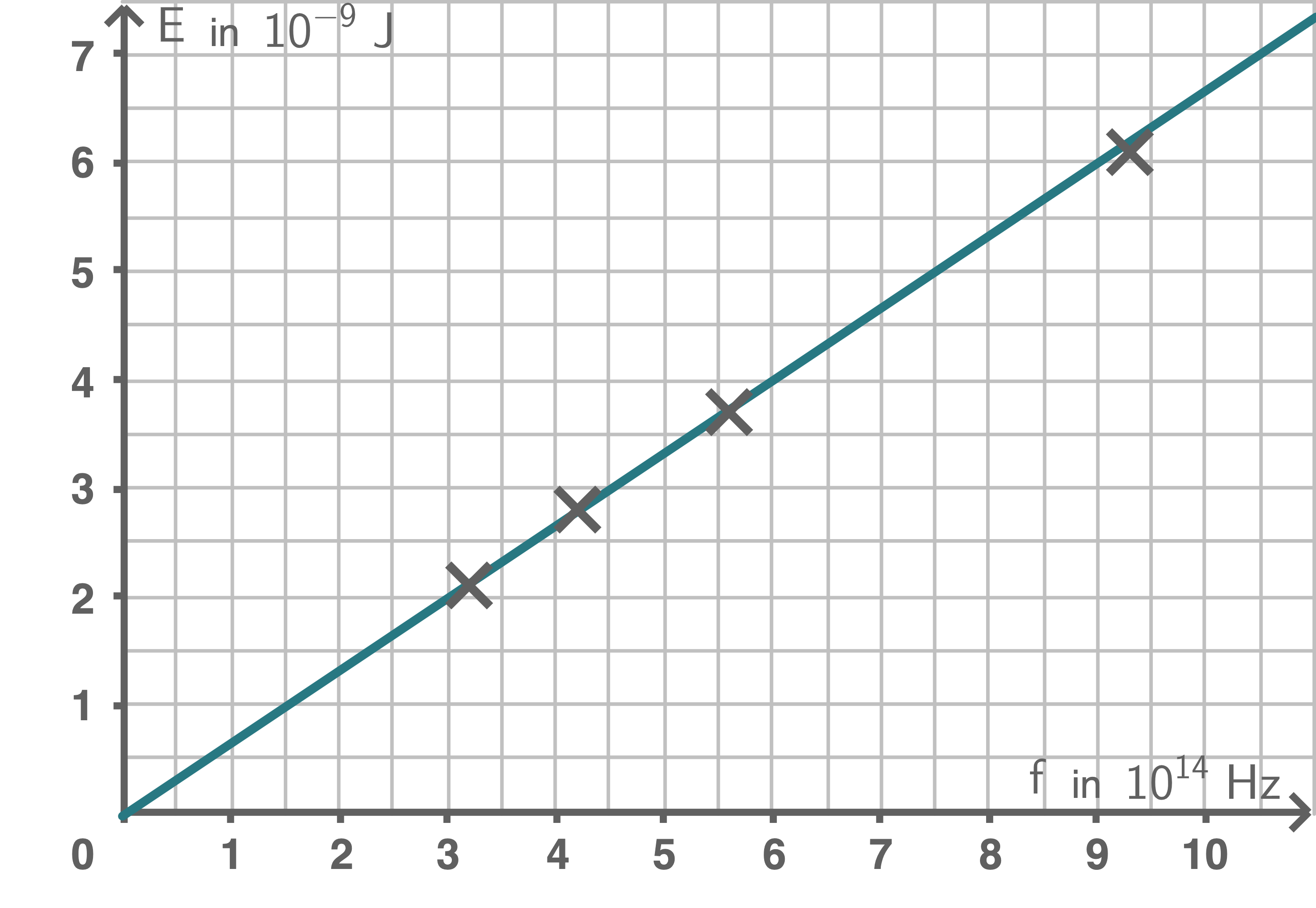
1.5.3

Steigung

$m =\dfrac{\Delta E _{ el }}{\Delta f }$ $=\dfrac{5 \cdot 10^{-19} \;\text{J}}{7,5 \cdot 10^{14} \;\text{Hz} }$ $\approx 6,6 \cdot 10^{-34}\;\text{Js}$

Physikalische Bedeutung

Es gilt: $E _{ el }= m \cdot f,$ woraus $E _{ el } \sim f$ folgt.

Da die Lichterzeugung hier als Umkehrung des Fotoeffekts aufgefasst werden kann, gilt $E _{ el }= E _{ ph }.$

Daraus folgt:

$\begin{array}[t]{rll} E_{e l}&=& E_{p h} \\[5pt] m \cdot f&=& h \cdot f \\[5pt] m&=&h \end{array}$

Somit entspricht die Steigung $m$ ist dem Planck'schen Wirkungsquantum $h.$ Der Literaturwert beträgt $h =6,626 \cdot 10^{-34} \;\text{Js},$ was nahe an der berechneten Steigung $m$ liegt.

2.1

Energie bestimmen

Rechenweg anzeigen

$E_{ ph }= 2,27 \;\text{eV}$

Masse bestimmen

Rechenweg anzeigen

$E_{ph}=4,05 \cdot 10^{-36} \;\text{kg}$

2.2

$\begin{array}[t]{rll} n&=& \dfrac{ E _{ ges }}{ E _{ ph }} \\[5pt] n&=& \dfrac{ P \cdot t }{ h \cdot f } \\[5pt] n&=& \dfrac{ P \cdot t \cdot \lambda}{ h \cdot c } \\[5pt] &=& \dfrac{3,845 \cdot 10^{26}\;\text{W} \cdot 1 \;\text{s} \cdot 546 \cdot 10^{-9} \;\text{m}}{6,626 \cdot 10^{-34} \;\text{Js} \cdot 2,998 \cdot 10^8 \frac{ \text{m} }{ \text{s} }} \\[5pt] &\approx & 1,06 \cdot 10^{45} \end{array}$

2.3

Die De-Broglie-Gleichung lautet $\lambda = \dfrac{h}{p}.$
Dabei entspricht $\lambda$ der Wellenlänge, $h$ das Plancksche Wirkungsquantum und $p$ der Impuls eines Teilchens ist.

Die Überlegung von de Broglie war, dass Teilchen nicht nur als Teilchen, sondern auch als Welle betrachtet werden können. Er schlug vor, dass jedes Teilchen, obwohl es eine Masse hat und somit ein Teilchen ist, auch eine Wellenlänge besitzt, die von seinem Impuls abhängt.

Die experimentellen Schwierigkeiten lagen darin, dass es schwierig war, die Welleneigenschaften von Teilchen zu beobachten. Clinton Davisson und Lester Germer führten 1927 ein Experiment durch, bei dem sie Elektronen durch ein Kristallgitter schossen und auf einem Schirm dahinter ein Interferenzmuster beobachteten. Dieses Muster konnte nur durch die Annahme erklärt werden, dass die Elektronen auch Welleneigenschaften besitzen. Dieses Experiment bestätigte somit die De-Broglie-Hypothese und zeigte, dass Teilchen auch als Wellen betrachtet werden können.

2.4

Herleitung

$\begin{array}[t]{rll} E _{ el }&=& E _{ kin } \\[5pt] e \cdot U &=& \dfrac{1}{2} \cdot m_e \cdot v ^2 \end{array}$

Für den Impuls eines Elektrons gilt:

$\begin{array}[t]{rll} p&=& m_e \cdot v &\quad \scriptsize \mid\;:m_e \\[5pt] \dfrac{p}{m_e}&=& v \\[5pt] v&=& \dfrac{p}{m_e} \end{array}$

Einsetzen und umstellen ergibt:

Rechenweg anzeigen

$p=\sqrt{2\cdot m_e\cdot e \cdot U}$

Impuls eines mit $5 \;\text{kV}$ beschleunigten Elektrons

Rechenweg anzeigen

$p = 3,82 \cdot 10^{-23} \frac{\text{kg} \cdot \text{m}}{\text{s}}$

2.5.1

$\begin{array}[t]{rll} \lambda&=& \dfrac{h}{p} \\[5pt] &=& \dfrac{6,626 \cdot 10^{-34} \;\text{Js} }{3,82 \cdot 10^{-23} \;\text{Ns}} \\[5pt] &=& 1,73 \cdot 10^{-11} \;\text{m} \\[5pt] &=& 0,0173 \;\text{nm} \end{array}$

Da Wellenlänge der Elektronen kleiner als $1 \;\text{nm}$ ist, sind die beschleunigten Elektronen zur zur Betrachtung atomarer Strukturen geeignet.

2.5.2

$\dfrac{\lambda_{\text {violett }}}{\lambda_{ e }}$ $=\dfrac{380 \cdot 10^{-9} \;\text{m} }{1,73 \cdot 10^{-11} \;\text{m} }$ $\approx 22000$

Das Auflösungsvermögen ist um das ca. 22000-fache höher.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?