Vorschlag B3
Fadenpendel
Fadenpendel werden im Physikunterricht als ein Beispiel für harmonische Oszillatoren betrachtet. In den folgenden Aufgaben beschreibt
die momentane Auslenkung des Pendelkörpers aus der Gleichgewichtslage bei seiner Bewegung entlang des Kreisbogens. Der Pendelkörper wird als punktförmig angenommen, die Masse des Fadens ist vernachlässigbar und Reibungskräfte sollen generell vernachlässigt werden. Verwende für den Ortsfaktor 
.
1
In der Physik spielt der Begriff der harmonischen Schwingung eine zentrale Rolle.
1.1
Beschreibe, was man unter dem linearen Kraftgesetz versteht, und gib den Zusammenhang zwischen dem linearen Kraftgesetz und der harmonischen Schwingung an.
(3 BE)
1.2
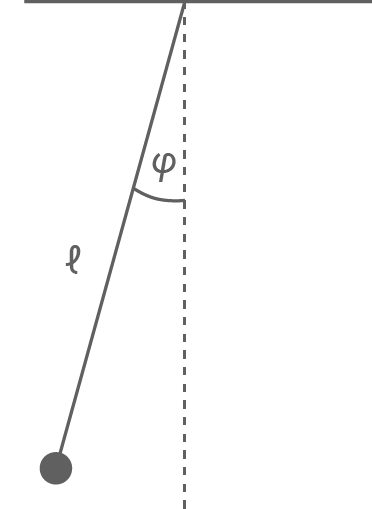
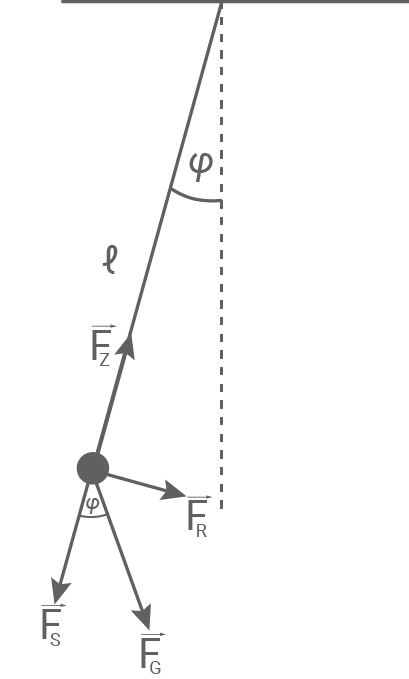
In Material 1 ist ein Fadenpendel dargestellt.
Zeichne in Material 1 die für die Schwingung relevanten Kräfte im richtigen Längenverhältnis ein.
Nenne die Bedingung, damit die Schwingung des Fadenpendels harmonisch ist.
Zeichne in Material 1 die für die Schwingung relevanten Kräfte im richtigen Längenverhältnis ein.
Nenne die Bedingung, damit die Schwingung des Fadenpendels harmonisch ist.
Material 1
Fadenpendel
(4 BE)
1.3
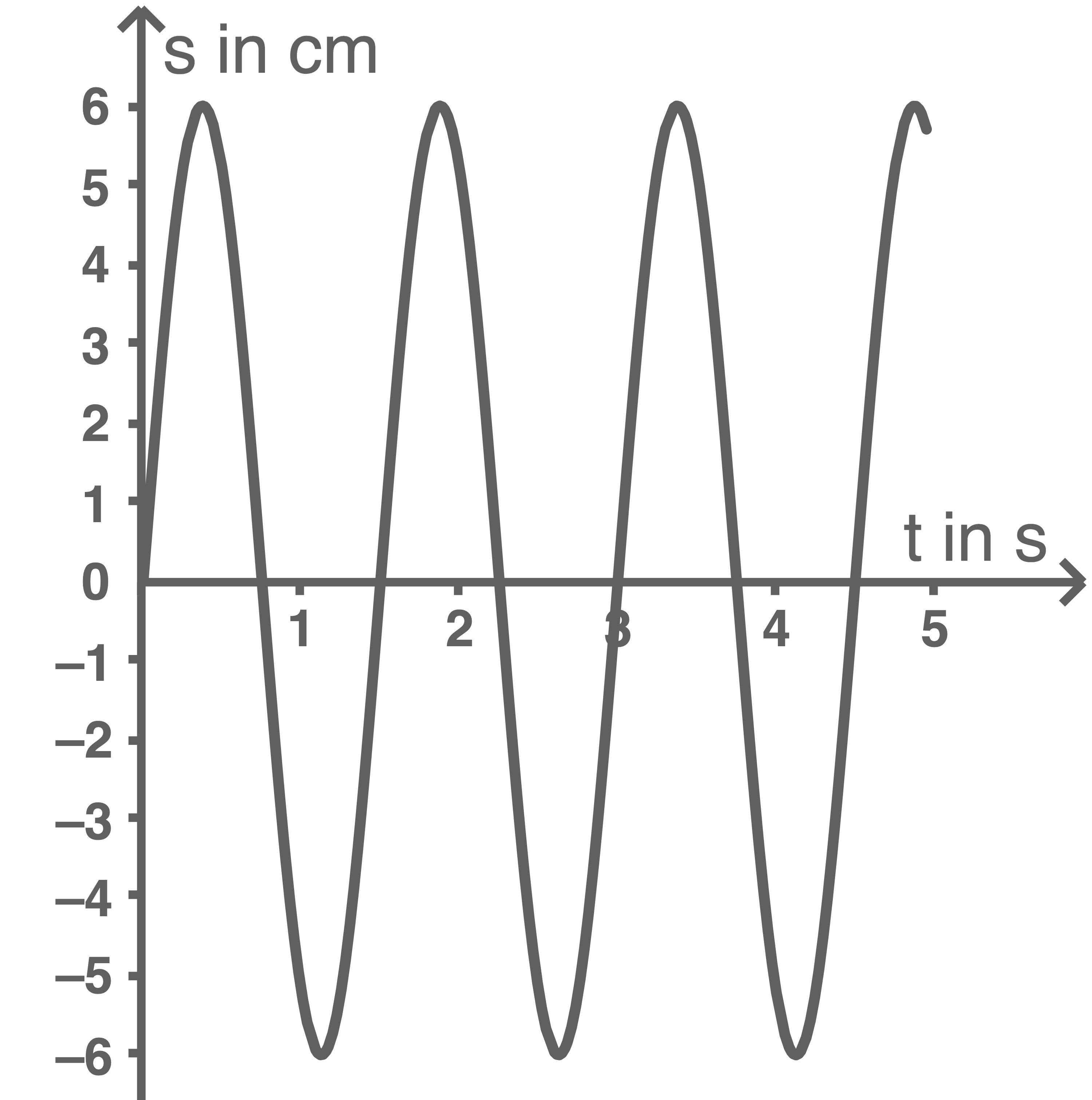
In Material 2 ist die Schwingung eines Fadenpendels grafisch dargestellt.
Bestimme mithilfe von Material 2 die Amplitude
und die Schwingungsdauer 
Gib die zum Graphen passende Schwingungsgleichung an.
Bestimme mithilfe von Material 2 die Amplitude
und die Schwingungsdauer
Gib die zum Graphen passende Schwingungsgleichung an.
Material 2
Zeitlicher Verlauf einer Schwingung
(3 BE)
2
Im Folgenden wird ein Fadenpendel mit der Pendellänge 
betrachtet. Der Pendelkörper besitzt eine Masse von 
Das Pendel wird zur Seite ausgelenkt, sodass der Pendelkörper um 
angehoben wird (Material 3). Nach dem Loslassen führt das Pendel eine Schwingung aus.
betrachtet. Der Pendelkörper besitzt eine Masse von Das Pendel wird zur Seite ausgelenkt, sodass der Pendelkörper um angehoben wird (Material 3). Nach dem Loslassen führt das Pendel eine Schwingung aus.
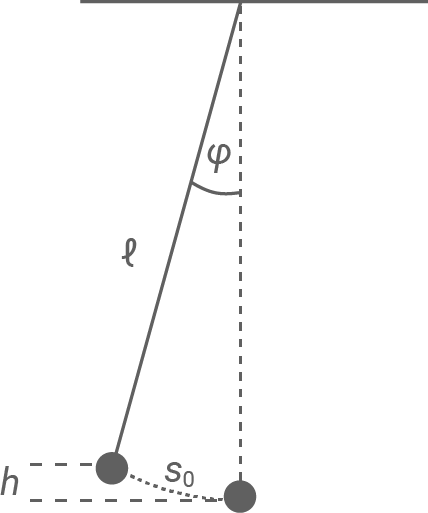
Material 3
Anheben des Pendelkörpers um die Höhe
2.1
Bestimme den maximalen Auslenkwinkel 
der Schwingung und beurteile das Ergebnis im Hinblick darauf, ob die Schwingung harmonisch ist.
Berechne die Schwingungsdauer
und die Amplitude der Schwingung.
[zur Kontrolle: 
]
der Schwingung und beurteile das Ergebnis im Hinblick darauf, ob die Schwingung harmonisch ist.
Berechne die Schwingungsdauer
und die Amplitude der Schwingung.
[zur Kontrolle: ]
(9 BE)
2.2
Beschreibe ausgehend von der maximalen Auslenkung, wie sich der Betrag der Geschwindigkeit des Pendelkörpers und der Betrag der Beschleunigung während einer halben Schwingungsperiode verändern. Beschreibe auch die Energieumwandlungen.
Begründe, warum es nach dem Auslenken und Loslassen des Pendelkörpers zu einer Schwingung kommt und der Pendelkörper nicht in der Gleichgewichtslage stehen bleibt.
Begründe, warum es nach dem Auslenken und Loslassen des Pendelkörpers zu einer Schwingung kommt und der Pendelkörper nicht in der Gleichgewichtslage stehen bleibt.
(9 BE)
2.3
Ermittle den maximalen Beschleunigungsbetrag.
(3 BE)
2.4
Der Betrag der maximalen Geschwindigkeit des Pendelkörpers kann mit der Formel 
berechnet werden. Leite mithilfe der Energieerhaltung diese Formel her und berechne 
berechnet werden. Leite mithilfe der Energieerhaltung diese Formel her und berechne
(5 BE)
2.5
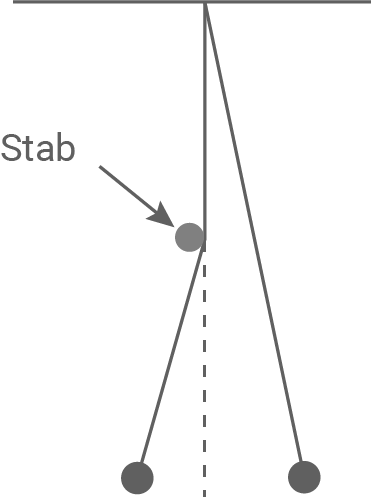
In Material 4a ist ein sogenanntes Hemmungspendel dargestellt. Ein Stab wird so positioniert, dass der Faden in vertikaler Stellung an diesen stößt. Dadurch schwingt das Pendel nach rechts mit der vollen Pendellänge und auf der linken Seite wird durch den Stab die Pendellänge auf die Hälfte verkürzt. Das Pendel wird zur rechten Seite ausgelenkt und zum Zeitpunkt 
losgelassen.
Beurteile, welches Diagramm in Material 4b den zeitlichen Verlauf der entstehenden Schwingung qualitativ richtig darstellt.
losgelassen.
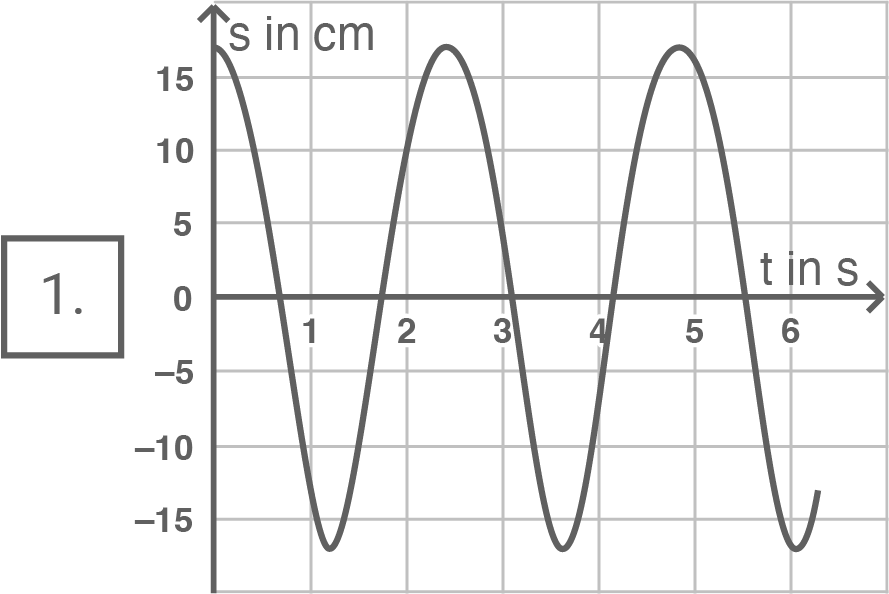
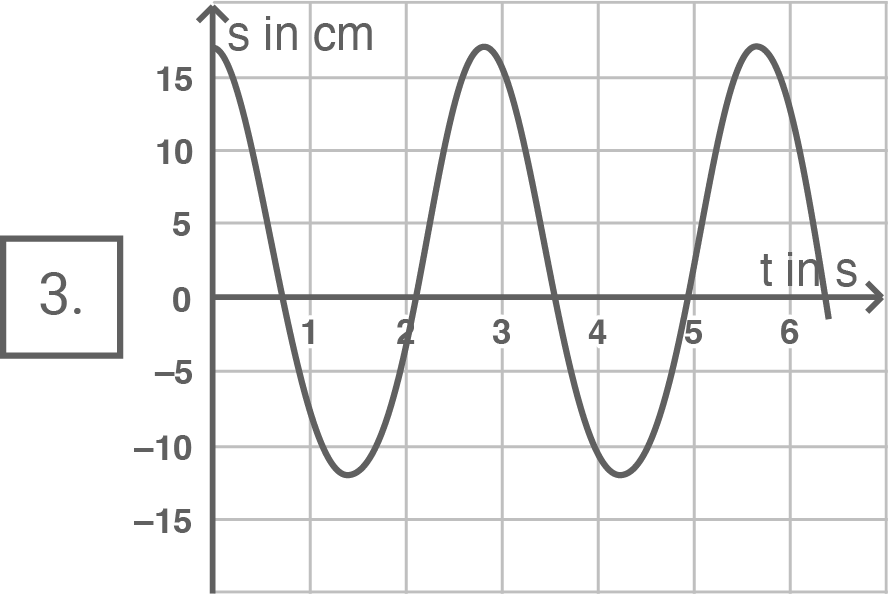
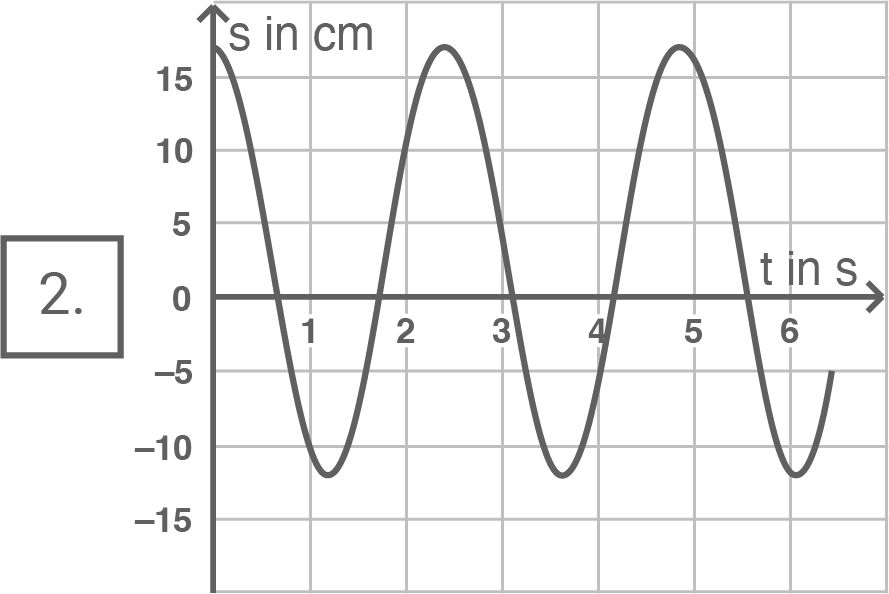
Beurteile, welches Diagramm in Material 4b den zeitlichen Verlauf der entstehenden Schwingung qualitativ richtig darstellt.
Material 4a
Hemmungspendel
Material 4b
Zeitlicher Verlauf der Schwingung des Hemmungspendels
(4 BE)
3
Eine Bleikugel hängt an einem dünnen Stahldraht mit der Länge 
Die Bleikugel wird um 
aus der Ruhelage ausgelenkt und führt dann eine harmonische Schwingung aus. Verändert man die Temperatur 
eines Körpers um 
, so erfährt dieser eine Längenänderung 
, die mithilfe der Formel 
berechnet werden kann. Hierbei ist 
eine Materialkonstante, die als Längenausdehnungskoeffizient bezeichnet wird, und für den verwendeten Stahldraht 
beträgt. Die Temperaturänderung wird in der Einheit 
gemessen.
Die Bleikugel wird um aus der Ruhelage ausgelenkt und führt dann eine harmonische Schwingung aus. Verändert man die Temperatur eines Körpers um , so erfährt dieser eine Längenänderung , die mithilfe der Formel berechnet werden kann. Hierbei ist eine Materialkonstante, die als Längenausdehnungskoeffizient bezeichnet wird, und für den verwendeten Stahldraht beträgt. Die Temperaturänderung wird in der Einheit gemessen.
3.1
Untersuche, wie sich eine Erwärmung des Pendelfadens auf die Schwingungsdauer des Pendels auswirkt.
(2 BE)
3.2
Die Raumtemperatur wird um 
erhöht.
Bestimme die Auswirkung dieser Temperaturerhöhung auf die Anzahl der Schwingungen des Pendels pro Tag, unter der Annahme, dass keine Dämpfung auftritt und es somit möglich ist, dass das Pendel einen ganzen Tag schwingt.
Hinweis: Verwende für die Schwingungsdauer 5 Nachkommastellen.
erhöht.
Bestimme die Auswirkung dieser Temperaturerhöhung auf die Anzahl der Schwingungen des Pendels pro Tag, unter der Annahme, dass keine Dämpfung auftritt und es somit möglich ist, dass das Pendel einen ganzen Tag schwingt.
Hinweis: Verwende für die Schwingungsdauer 5 Nachkommastellen.
(8 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.1
Das lineare Kraftgesetz besagt, dass die Rückstellkraft 
in einem Feder-Masse-System proportional zur Auslenkung ist, ausgedrückt durch das Hooke'sche Gesetz:
Dieses Gesetz führt bei vernachlässigbarer Reibung und kleinen Auslenkungen zu einer harmonischen Schwingung, da die Beschleunigung 
proportional zur Auslenkung ist.
in einem Feder-Masse-System proportional zur Auslenkung ist, ausgedrückt durch das Hooke'sche Gesetz:
Dieses Gesetz führt bei vernachlässigbarer Reibung und kleinen Auslenkungen zu einer harmonischen Schwingung, da die Beschleunigung 
![\(\begin{array}[t]{rll}
F_{\text{R}}&=& -k \cdot s &\quad \scriptsize \mid\; \text{Newtons zweites Gesetz:}\quad F=m\cdot a \\[5pt]
m\cdot a&=& -k \cdot s &\quad \scriptsize \mid\; +k\cdot s \\[5pt]
m\cdot a +k\cdot s&=& 0 &\quad \scriptsize \mid\; \cdot \dfrac{1}{m} \\[5pt]
a +\dfrac{k}{m}\cdot s&=& 0 &\quad \scriptsize \mid\; \omega^2= \dfrac{k}{m} \\[5pt]
a +\omega^2\cdot s&=& 0 &\quad \scriptsize \mid\; \omega^2= \dfrac{k}{m} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/c83def12a24ba2f10a73725e6a3cc0d174fcd517a5e0b261092fc758241c092b_light.svg)
proportional zur Auslenkung ist.
1.2
![\(\begin{array}[t]{rll}
F_{\text{R}}&=& -k \cdot s&\quad \scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/dead5fb506aae19a86a7db27a6b96b8961a488617cbaa51e9f9cb0e0b10735ed_light.svg)
1.3
Die Schwingungsdauer entspricht der zeitlichen Dauer für eine vollständige Schwingung des Fadenpendels, gemessen beispielsweise zwischen aufeinanderfolgenden Maxima oder Minima im 
Diagramm. Zwischen 
und 
durchläuft das Pendel genau zwei Perioden. Die Schwinungsdauer beträgt folgtlich 
Die Amplitude 
ist der Abstand zwischen dem Punkt maximaler Auslenkung und dem Ruhpunkt und beträgt daher 
Für die Schwinungsgleichung ergibt sich damit:
![\(\begin{array}[t]{rll}
s(t)&=& s_0\cdot \sin\left(\dfrac{2 \pi}{T}\cdot t\right) &\quad \scriptsize \\[5pt]
&=& 0,06 \;\text{m} \cdot \sin\left(\dfrac{2 \pi}{1,5 \;\text{s}}\cdot t\right) &\quad \scriptsize \\[5pt]
&=& 0,06 \;\text{m} \cdot \sin\left(\dfrac{4\pi }{3\;\text{s}}\cdot t\right)
\end{array}\)](https://www.schullv.de/resources/formulas/4e4b668f816764ffca005a2ca07cd9ce89fd72ee856bdd9e38c7ba8f0220fc6d_light.svg)
entspricht der zeitlichen Dauer für eine vollständige Schwingung des Fadenpendels, gemessen beispielsweise zwischen aufeinanderfolgenden Maxima oder Minima im Diagramm. Zwischen und durchläuft das Pendel genau zwei Perioden. Die Schwinungsdauer beträgt folgtlich
Die Amplitude ist der Abstand zwischen dem Punkt maximaler Auslenkung und dem Ruhpunkt und beträgt daher
Für die Schwinungsgleichung ergibt sich damit:
2.1
maximalen Auslenkwinkel
Gegeben: 
Gesucht:
Lösung:
Zwischen der Maximalen Auslenkung und der Ruhelage lässt sich ein rechtwinkliges Dreieckbilden, so dass trigonometrische Beziehungen gelten:
![\(\begin{array}[t]{rll}
\cos\left(\varphi\right)&=& \dfrac{\ell-h}{\ell} &\quad \scriptsize \mid\;\cos^{-1}\left(\;\right) \\[5pt]
\varphi&=& \cos^{-1}\left(\dfrac{\ell-h}{\ell}\right)
\end{array}\)](https://www.schullv.de/resources/formulas/36b26bedba9e757e88e86504ca1d5126c0d0fc2e139c9f43d4e8177b6bdf1140_light.svg)
Einsetzen der Werte liefert:
![\(\begin{array}[t]{rll}
\varphi&=& \cos^{-1}\left(\dfrac{\ell-h}{\ell}\right)&\quad \scriptsize\\[5pt]
&=& \cos^{-1}\left(\dfrac{2,000\;\text{m}- 0,7\;\text{cm}}{2,000\;\text{m}}\right) &\quad \scriptsize\\[5pt]
&=& \cos^{-1}\left(\dfrac{2,000\;\text{m}- 0,007\;\text{m}}{2,000\;\text{m}}\right) &\quad \scriptsize\\[5pt]
&=& \cos^{-1}\left(\dfrac{1.993}{2,000}\right) &\quad \scriptsize\\[5pt]
&=& 4,8 ^° &\quad \scriptsize\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/f7f18aa4ffc1719ec26305cad1a759646748850c30ac3bd47cb88ea9da61fdbf_light.svg)
Ein Auslenkwinkel von 
ist klein genug, um die Kleinwinkelnäherung zu rechtfertigen. Daher kann die Schwingung als harmonisch betrachtet werden.
Schwingungsdauer
Gegeben: 
Gesucht:
Lösung:
![\(\begin{array}[t]{rll}
T&=& 2\pi \sqrt{\dfrac{\ell}{g}} &\quad \scriptsize \\[5pt]
&=& 2\pi \cdot \sqrt{\dfrac{2,000\;\text{m}}{9,81 \;\frac{\text{m}}{\text{s}^2}}} &\quad \scriptsize \\[5pt]
&=& 2,84 \;\text{s}
\end{array}\)](https://www.schullv.de/resources/formulas/eaa7d3e814c8d7194ce450740ce4ee391e077018ec5628d788f58a6d697f881e_light.svg)
Amplitude
Gegeben: 
Gesucht:
Lösung: Für die Amplitude einer harmonischen Schwingung kann diese näherungsweise als Gerade angenommen werden. Mit den trigonometrischen Beziehungen gilt:
![\(\begin{array}[t]{rll}
s_0&=&\ell\cdot \sin(\varphi) &\quad \scriptsize \\[5pt]
&=& 2,000\;\text{m} \cdot \sin(4,8^°) &\quad \scriptsize \\[5pt]
&=& 0,167 \;\text{m}
\end{array}\)](https://www.schullv.de/resources/formulas/3ad6494a3dd88076828bb304cd70356ecad4d1267881051ae5b220094bec1d98_light.svg)
Gegeben:
Gesucht:
Lösung:
Zwischen der Maximalen Auslenkung und der Ruhelage lässt sich ein rechtwinkliges Dreieckbilden, so dass trigonometrische Beziehungen gelten:
Einsetzen der Werte liefert:
Ein Auslenkwinkel von ist klein genug, um die Kleinwinkelnäherung zu rechtfertigen. Daher kann die Schwingung als harmonisch betrachtet werden.
Schwingungsdauer
Gegeben:
Gesucht:
Lösung:
Amplitude
Gegeben:
Gesucht:
Lösung: Für die Amplitude einer harmonischen Schwingung kann diese näherungsweise als Gerade angenommen werden. Mit den trigonometrischen Beziehungen gilt:
2.2
maximale Auslenkung
Bei maximaler Auslenkung ist die Geschwindigkeit des Pendelkörpers gleich null, da der Körper kurzzeitig anhält, bevor er in die entgegengesetzte Richtung zu schwingen beginnt, und da er keine kinetische Enrgie hat. Gleichzeitig ist die potenzielle Energie des Körpers maximal, da er sich auf maximaler Höhe befindet. Bei maximaler Auslenkung ist die Rückstellkraft am stärksten, da die Auslenkung am größten ist. Da die Beschleunigung direkt proportional zur Rückstellkraft ist, erreicht die Beschleunigung ebenfalls ihren maximalen Wert.
Weg in die Gleichgewichtslage
Auf dem Weg in die Gleichgewichtslage wandelt der Körper seine potenzielle Energie in kinetische Energie um. Seine Geschwindigkeit nimmt zu, und seine Beschleunigung nimmt ab, je näher er der Gleichgewichtslage ist.
Gleichgewichtslage
In der Gleichgewichtslage hat der Körper maximale Geschwindigkeit und damit maximale kinetische Energie. Die gesamte potenzielle Energie aus der maximalen Auslenkung wurde in kinetische Energie umgewandelt. Seine Beschleunigung ist gleich null.
Weg aus der Gleichgewichtslage
Wenn der Körper die Gleichgewichtslage passiert hat, wandelt er seine kinetische Energie wieder in potenzielle Energie um. Seine Geschwindigkeit nimmt ab, und seine Beschleunigung nimmt zu, bis der Körper wieder die maximale Auslenkung und damit seine maximale Höhe erreicht hat. Hier hat er erneut maximale potenzielle Energie, keine kinetische Energie, seine Geschwindigkeit ist null, aber seine Beschleunigung ist maximal.
Begründung der Schwinung
Nach dem Auslenken und Loslassen des Pendelkörpers entsteht eine Schwingung aufgrund der Gravitationskraft und der elastischen Rückstellkraft des Fadenpendels. Die Gravitationskraft strebt danach, den Körper zur Gleichgewichtslage zu ziehen, während die Rückstellkraft, die durch die Auslenkung erzeugt wird, den Pendelkörper in die entgegengesetzte Richtung beschleunigt. Durch diese Wechselwirkung von Kräften erfolgt eine kontinuierliche Umwandlung zwischen potenzieller und kinetischer Energie, wodurch der Pendelkörper schwingt.
2.3
Für die Beschleunigung gilt:
Wenn das Fadenpendel seine maximale Auslenkung erreicht hat, ist seine Beschleunigung maximal. Aus Material 3 ist abzulesen, dass nach 
das Pendel seine maximale Auslenkung erricht. Einsetzen der Werte liefert:
![\(\begin{array}[t]{rll}
a(t)&=& \dfrac{dv(t)}{dt}&\quad \scriptsize \mid\; v(t) = \dfrac{ds(t)}{dt} \\[5pt]
&=& \dfrac{d^2s(t)}{dt^2} &\quad \scriptsize \mid\;s(t)= s_0\cdot \sin\left(\dfrac{2 \pi}{T}\cdot t\right) \\[5pt]
&=& \dfrac{d^2 \left(s_0\cdot \sin\left(\dfrac{2 \pi}{T}\cdot t\right)\right)}{dt^2} &\quad \scriptsize \mid\; \dfrac{d}{dt} \sin\left(\dfrac{2 \pi}{T}\cdot t\right) \overset{\text{Kettenregel}}{=} \cos\left(\dfrac{2 \pi}{T}\cdot t\right)\cdot \dfrac{2 \pi}{T} \\[5pt]
&=& \dfrac{d \left(s_0\cdot \cos\left(\dfrac{2 \pi}{T}\cdot t\right)\cdot\dfrac{2 \pi}{T}\right)}{dt} &\quad \scriptsize \mid\; \dfrac{d}{dt}\left(\cos\left(\dfrac{2 \pi}{T}\cdot t\right)\right) \overset{\text{Kettenregel}}{=} -\sin\left(\dfrac{2 \pi}{T}\cdot t\right)\cdot \dfrac{2 \pi}{T}\\[5pt]
&=& -s_0\cdot \sin\left(\dfrac{2 \pi}{T}\cdot t\right)\cdot \dfrac{2 \pi}{T} \cdot\dfrac{2 \pi}{T} &\quad \scriptsize \\[5pt]
&=& -\dfrac{4 \pi^2\cdot s_0}{T^2}\cdot \sin\left(\dfrac{2 \pi}{T}\cdot t\right)
\end{array}\)](https://www.schullv.de/resources/formulas/3739fdfb4fbbb00789fb12298a47362e55ee097c4e06bed87129ecbefb660244_light.svg)
das Pendel seine maximale Auslenkung erricht. Einsetzen der Werte liefert:
![\(\begin{array}[t]{rll}
a(t_{a_{\text{max}}})&=& -\dfrac{4 \pi^2\cdot s_0}{T^2}\cdot \sin\left(\dfrac{2 \pi}{T}\cdot t_{a_{\text{max}}}\right)&\quad \scriptsize \mid\;t_{a_{\text{max}}}=\dfrac{1}{4}T \\[5pt]
&=& -\dfrac{4 \pi^2\cdot s_0}{T^2}\cdot \sin\left(\dfrac{2 \pi}{T}\cdot\dfrac{1}{4}T\right)&\quad \scriptsize \\[5pt]
&=& -\dfrac{4 \pi^2\cdot s_0}{T^2}\cdot \sin\left(\dfrac{ \pi}{2}\right)&\quad \scriptsize \\[5pt]
&=& -\dfrac{4 \pi^2\cdot 0,167 \;\text{m}}{2,84^2 \;\text{s}^2}\cdot \sin\left(\dfrac{ \pi}{2}\right)&\quad \scriptsize \\[5pt]
&=& 0,82 \;\dfrac{\text{m}}{\text{s}^2}
\end{array}\)](https://www.schullv.de/resources/formulas/ef3b3a859daf0a8eda57a80c8d5e1ba1079d5f45a67e2d918f54b482a1afb0f6_light.svg)
2.4
![\(\begin{array}[t]{rll}
E_{\text{kin,max}}&=& E_{\text{pot,max}}&\quad \scriptsize \\[5pt]
\dfrac{1}{2}\cdot m\cdot v_{\text{max}}^2&=& m\cdot g\cdot h&\quad \scriptsize \mid\; \cdot \dfrac{2}{m}\\[5pt]
v_{\text{max}}^2&=& 2\cdot g\cdot h \quad \scriptsize \\[5pt]
v_{\text{max}}&=& \sqrt{ 2\cdot g\cdot h}
\end{array}\)](https://www.schullv.de/resources/formulas/d8abdef9b770b6e0a807276aca796d844547c939b336d53023a05fa57a780f68_light.svg)
Einsetzen der Werte liefert:
![\(\begin{array}[t]{rll}
v_{\text{max}}&=& \sqrt{ 2\cdot g\cdot h} &\quad \scriptsize \\[5pt]
&=& \sqrt{ 2\cdot 9,81 \;\dfrac{\text{m}}{\text{s}^2}\cdot 0,007\;\text{m}}&\quad \scriptsize \\[5pt]
&=& 0,37 \;\dfrac{\text{m}}{\text{s}}
\end{array}\)](https://www.schullv.de/resources/formulas/81744f0661bbb0c1159edbc059b89ffe27347a5fa0b2ac5b74c9bc7ac380111d_light.svg)
2.5
Die maximale Auslenkung des beschriebenen Hemmungspendels ist auf der rechten Seite größer als auf der linken Seite, da es auf der linken Seite nur die Hälfte der Fadenlänge zur Verfügung hat. Da das Pendel nach rechts ausgelenkt wird, muss immer das Maximum betragsmäßig weiter von dem Gleichgewicht (s=0) entfernt sein als das Minimum. Aufgrund dieser Information kommen nur Diagramm 2 oder Diagramm 3 in Frage.
Für die Periodendauer der rechten Seite mit Pendellänge 
gilt:
![\(\begin{array}[t]{rll}
T_R&=& 2\cdot \pi\cdot \sqrt{\dfrac{\ell_R}{g}} &\quad \scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/8d448c1b9fb8f69f53807bd6d621d006344e04e291fdd48220d39ff977d50cad_light.svg)
Für die Periodendauer auf der linken Seite mit Pendellänge 
gilt:
![\(\begin{array}[t]{rll}
T_L&=& 2\cdot \pi\cdot \sqrt{\dfrac{\ell_L}{g}} &\quad \scriptsize \\[5pt]
T_L&=& 2\cdot \pi\cdot \sqrt{\dfrac{\ell_R}{2g}} &\quad \scriptsize \\[5pt]
T_L&=& 2\cdot \pi\cdot \sqrt{\dfrac{\ell_R}{g}} \cdot \dfrac{1}{\sqrt{2}} &\quad \scriptsize \\[5pt]
T_L&=& T_R \cdot \dfrac{1}{\sqrt{2}} &\quad \scriptsize \\[5pt]
T_L&\lt& T_R
\end{array}\)](https://www.schullv.de/resources/formulas/ab29ae0bfa4fb75e6ae44814724ef9c4cb838ae7a435a3540791ca918085a96b_light.svg)
Diagramm 2 beschreibt es richtig, da sich hier das Pendel jeweils länger auf der rechten Seite aufhält als auf der linken Seite.
gilt:
Für die Periodendauer auf der linken Seite mit Pendellänge gilt:
Diagramm 2 beschreibt es richtig, da sich hier das Pendel jeweils länger auf der rechten Seite aufhält als auf der linken Seite.
3.1
Für die ursprüngliche Schwingungsdauer gilt:
![\(\begin{array}[t]{rll}
T&=& 2 \pi \cdot \sqrt{\dfrac{\ell}{g}} &\quad \scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/05141de71d435512a78c93762b99c019bc0430a2a9998f162842e3e274cdea66_light.svg)
Für die Schwingungsdauer 
des erwärmten Pendels gilt:
Eine Erwärmung des Pendeldrahts führt zu einer Verlängerung des Drahts. Dies hat zur Folge, dass die Schwingungsdauer des Pendels zunimmt, da der Zähler im Verhältnis 
größer wird, während der Nenner gleich bleibt.
gilt:
Für die Schwingungsdauer des erwärmten Pendels gilt:
Eine Erwärmung des Pendeldrahts führt zu einer Verlängerung des Drahts. Dies hat zur Folge, dass die Schwingungsdauer des Pendels zunimmt, da der Zähler im Verhältnis 
![\(\begin{array}[t]{rll}
T](https://www.schullv.de/resources/formulas/435f2d90557d1a49fd666798b574cb561e29b33caaae5fa5eb7ed778b245eef5_light.svg)
größer wird, während der Nenner gleich bleibt.
3.2
Die Anzahl der Schwingungen 
des erwärmten Pendels verringert sich, da die Dauer für eine Schwingung zunimmt. Für die Änderung der Anzahl der Schwingungen, also die Veränderung im Vergleich zu vor der Erwärmung, gilt:
Das erwärmten Pendels schafft also nur noch 
vond er Anzahl der Schwinungen des nicht erwärmten Pendels. Das erwärmte Pendel schwingt innerhalb von einem Tag Mal:
Das erwärmte Pendel schwingt folglich etwa 60913 Mal innerhalb von einem Tag, während das nicht erwärmte Pendel 
Mal an einem Tag schwingt.
des erwärmten Pendels verringert sich, da die Dauer für eine Schwingung zunimmt. Für die Änderung der Anzahl der Schwingungen, also die Veränderung im Vergleich zu vor der Erwärmung, gilt:
Das erwärmten Pendels schafft also nur noch 
![\(\begin{array}[t]{rll}
\dfrac{n](https://www.schullv.de/resources/formulas/8f64fa9d01484b2cd513f39442bb38d82cd4061152520ff116d08e725b899fe6_light.svg)
vond er Anzahl der Schwinungen des nicht erwärmten Pendels. Das erwärmte Pendel schwingt innerhalb von einem Tag Mal:
Das erwärmte Pendel schwingt folglich etwa 60913 Mal innerhalb von einem Tag, während das nicht erwärmte Pendel 
![\(\begin{array}[t]{rll}
n](https://www.schullv.de/resources/formulas/d55ca5e29ec43ee90f252f82877102b0a25a4acfcc7c435baf6bcdd934cf7e6b_light.svg)
Mal an einem Tag schwingt.