Vorschlag A2
Untersuchungen von Emissions- und Absorptionsspektren
Die sichtbare Oberfläche der Sonne wird als Fotosphäre bezeichnet, die die Energie aus dem Innern der Sonne als kontinuierliches Spektrum nach außen abgibt. Über der Fotosphäre befinden sich die anschließende Chromosphäre und die darüber liegende Korona. Unmittelbar zu Beginn oder vor dem Ende einer totalen Sonnenfinsternis ist für ca. 4 Sekunden nur die leuchtende Schicht der Chromosphäre zu sehen. Spaltet man ihr Licht in seine Wellenlängen auf, so erscheinen helle Linien. Weil diese hellen Linien nur für kurze Zeit aufblitzen, spricht man vom „Flash-Spektrum“. Diese Spektrallinien gehen vor allem auf die Elemente Wasserstoff, Helium und Calcium zurück.
1
Zur Untersuchung des Flash-Spektrums verwendet man ein Gitter mit 
Linien pro Millimeter (Gitterkonstante 
), welches das Licht auf einen im Abstand 
entfernten Schirm beugt.
Linien pro Millimeter (Gitterkonstante ), welches das Licht auf einen im Abstand entfernten Schirm beugt.
1.1
Zeige, dass sich der Abstand 
zwischen dem Hauptmaximum nullter Ordnung und den Maxima der ersten Ordnung für Licht der Wellenlänge 
mithilfe der Kleinwinkelnäherung mit der Formel 
berechnen lässt.
zwischen dem Hauptmaximum nullter Ordnung und den Maxima der ersten Ordnung für Licht der Wellenlänge mithilfe der Kleinwinkelnäherung mit der Formel berechnen lässt.
(4 BE)
1.2
Bei einer totalen Sonnenfinsternis konnte 1868 das bis dahin unbekannte Element Helium in der Chromosphäre nachgewiesen werden.
Berechne mithilfe der Formel aus Aufgabe 1.1 die Wellenlänge der Spektrallinie, die bei der Beobachtung auf dem Schirm als Maximum erster Ordnung im Abstand von
zum Hauptmaximum nullter Ordnung erscheint und gib unter Verwendung von Material 1 die Farbe der Spektrallinie an.
Berechne mithilfe der Formel aus Aufgabe 1.1 die Wellenlänge der Spektrallinie, die bei der Beobachtung auf dem Schirm als Maximum erster Ordnung im Abstand von
zum Hauptmaximum nullter Ordnung erscheint und gib unter Verwendung von Material 1 die Farbe der Spektrallinie an.
Material 1
Tabelle zur Definition von Wellenlängen und FarbenWellenlängenbereich in  |
Farbe |
|---|---|
| 380-420 | Violett |
| 420-490 | Blau |
| 490-570 | Grün |
| 570-600 | Gelb |
| 600-640 | Orange |
| 640-780 | Rot |
(5 BE)
1.3
Die Linien des Flash-Spektrums sind bei der Analyse des Sonnenlichts ohne Sonnenfinsternis als dunkle Absorptionslinien im Sonnenspektrum zu sehen (Material 2), mit Sonnenfinsternis erscheinen sie in der Analyse für kurze Zeit als helle Linien. Die Linien haben zu jedem der betrachteten Zeitpunkte die gleiche Intensität. Bei voller Sonnenstrahlung ist diese Intensität relativ zu den umgebenden Wellenlängenbereichen sehr gering, die Linien erscheinen dunkel. Bei einer Sonnenfinsternis fehlt die Intensität in den umgebenden Wellenlängenbereichen vollständig, somit erscheinen die Linien nun hell.
Erkläre diese Tatsachen und begründe, warum die dunklen Linien nicht vollständig schwarz sind.
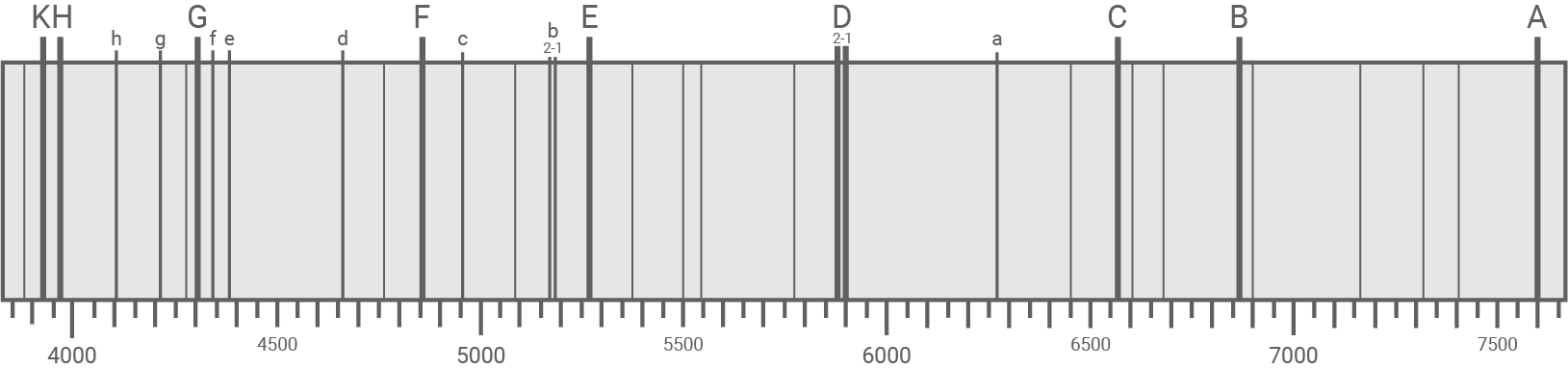Wellenlängenangaben in 
Erkläre diese Tatsachen und begründe, warum die dunklen Linien nicht vollständig schwarz sind.
Material 2
Dunkle Absorptionslinien im Sonnenspektrum
(5 BE)
1.4
Zwei Absorptionslinien aus Material 2 sind auf einfach ionisiertes Calcium aus der Chromosphäre zurückzuführen. Diese Linien entstehen durch Anregungen aus dem Grundzustand auf die eng benachbarten Energiestufen A und B im Termschema von Material 3.
Ermittle mithilfe von Material 3 die Wellenlängen dieser beiden Absorptionslinien und ordne deinen Ergebnissen die entsprechenden Linien in Material 2 zu.
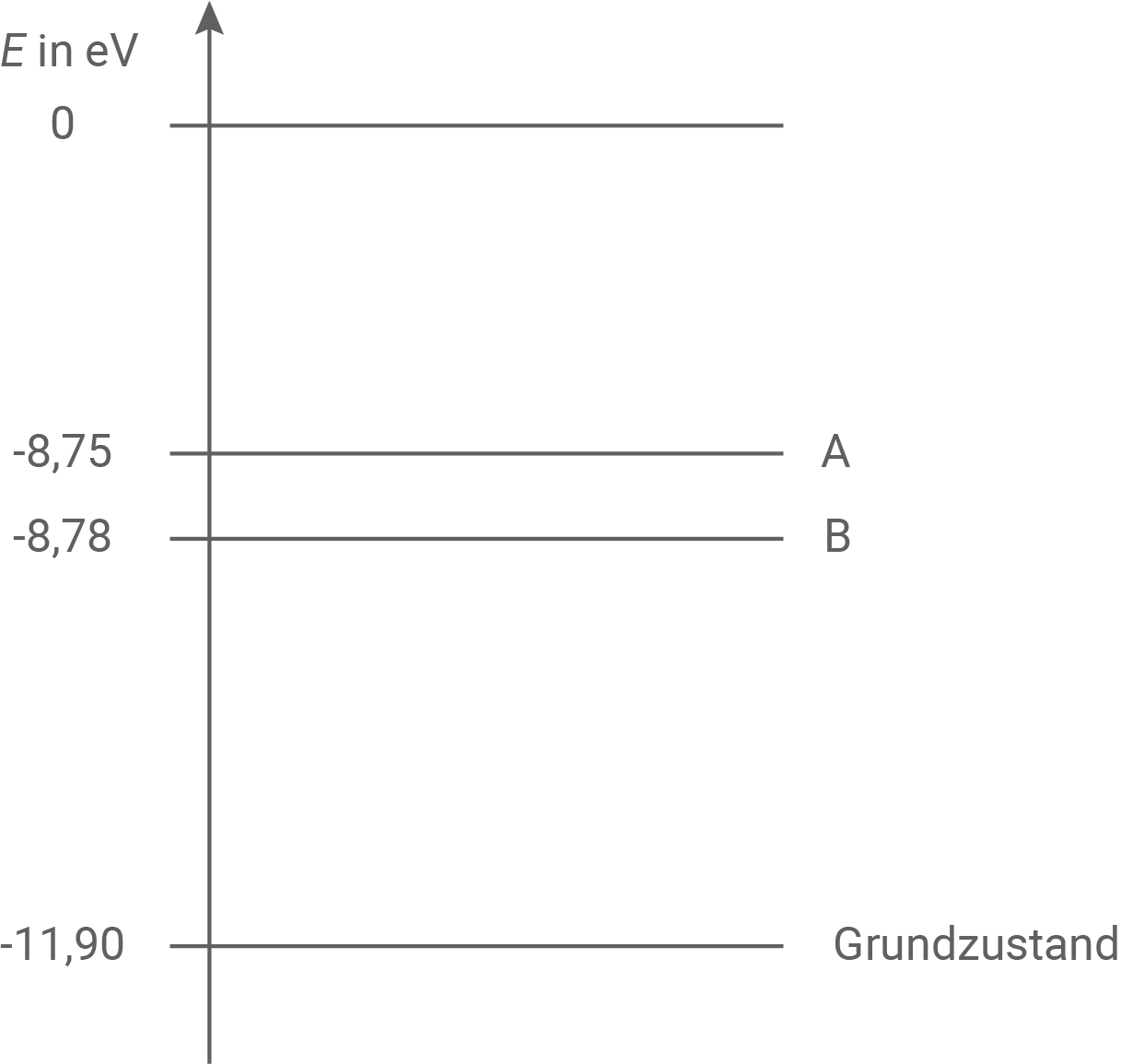Die Darstellung ist nicht maßstabsgerecht.
Ermittle mithilfe von Material 3 die Wellenlängen dieser beiden Absorptionslinien und ordne deinen Ergebnissen die entsprechenden Linien in Material 2 zu.
Material 3
Auszug aus dem Termschema von
(6 BE)
1.5
1869 entdeckte unter anderem Charles Young bei einer weiteren Sonnenfinsternis in der Korona eine Spektrallinie, die auf zwölffach ionisiertes Eisen zurückgeht. Diese starke Ionisierung von Elementen ist in der Chromosphäre und der Fotosphäre nicht zu finden. Erkläre diese Tatsache mithilfe von Material 4.
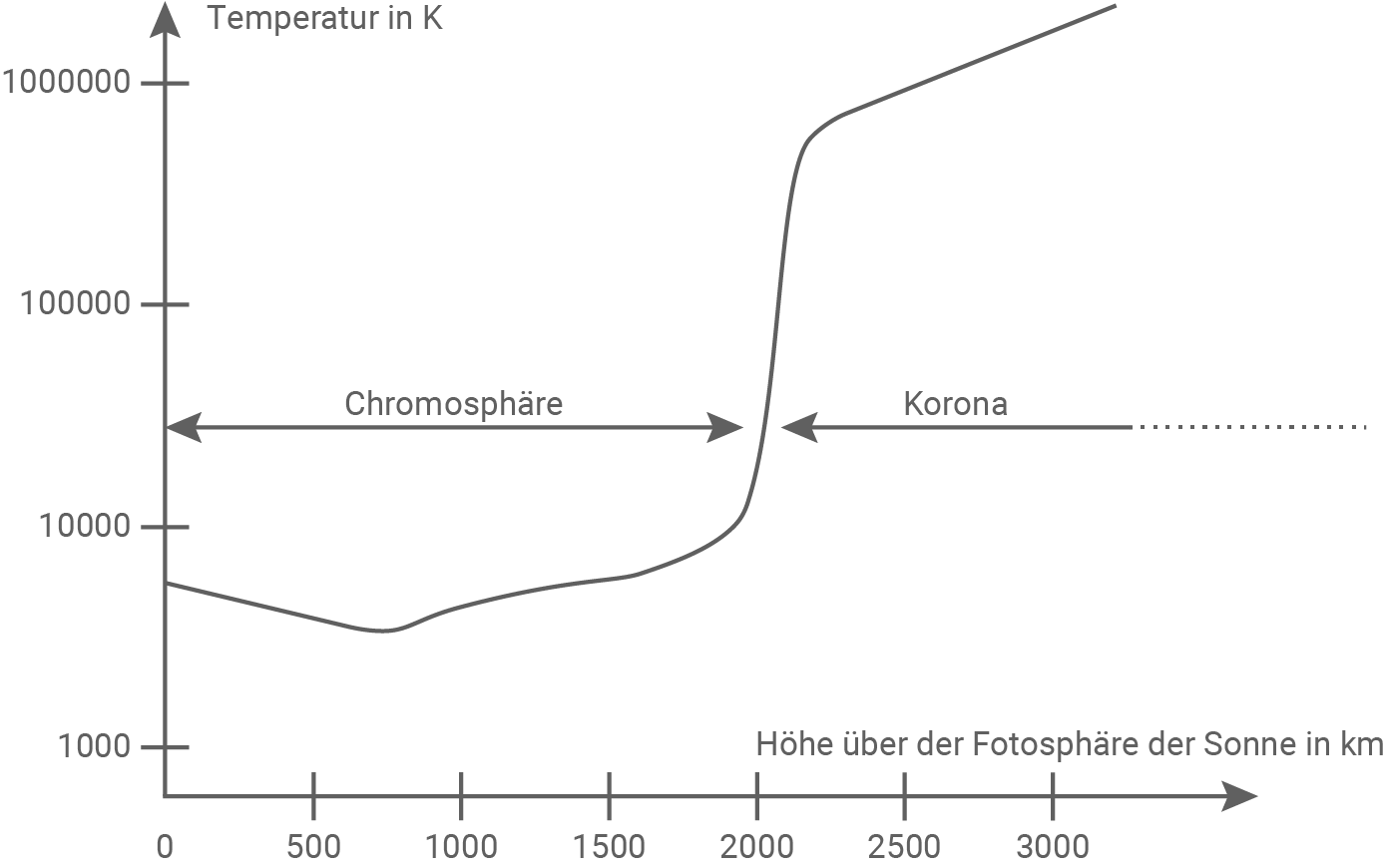Auf der waagrechten Achse sind von innen nach außen die Schichtdicken der Chromosphäre und der Korona aufgetragen, wobei die Korona sehr weit in den Weltraum reicht.
Auf der senkrechten Achse ist die Temperatur in logarithmischer Skalierung aufgetragen.
Material 4
Temperaturverlauf in den äußeren Schichten der Sonne
(3 BE)
2
Zur Bestimmung des Termschemas von Natrium wird eine durchsichtige Kammer mit Natriumdampf gefüllt und mit Elektronen der Energie 
beschossen. Mithilfe eines Detektors wird die Energie der Elektronen nach der Wechselwirkung mit den Natriumatomen bestimmt.
beschossen. Mithilfe eines Detektors wird die Energie der Elektronen nach der Wechselwirkung mit den Natriumatomen bestimmt.
2.1
Berechne die Geschwindigkeit der eingeschossenen Elektronen.
(3 BE)
2.2
Die Natriumatome liegen im Dampf nur im Grundzustand vor, dessen Energie 
beträgt. Die eingeschossenen Elektronen führen Stöße mit den Natriumatomen aus. Vereinfachend wird zunächst angenommen, dass ein Elektron nur mit einem Natriumatom einen Stoß ausführt, bevor es im Detektor registriert wird, und dass Elektronensprünge im Atom ausschließlich von und in den Grundzustand betrachtet werden. Die Energien der Elektronen nach der Wechselwirkung mit den Natriumatomen besitzen die Werte 
und 
beträgt. Die eingeschossenen Elektronen führen Stöße mit den Natriumatomen aus. Vereinfachend wird zunächst angenommen, dass ein Elektron nur mit einem Natriumatom einen Stoß ausführt, bevor es im Detektor registriert wird, und dass Elektronensprünge im Atom ausschließlich von und in den Grundzustand betrachtet werden. Die Energien der Elektronen nach der Wechselwirkung mit den Natriumatomen besitzen die Werte und
2.2.1
Begründe, dass die Elektronen nach der Wechselwirkung nur ganz bestimmte Energiewerte besitzen.
(5 BE)
2.2.2
Zeichne mithilfe der angegebenen Werte ein maßstabsgetreues Termschema von Natrium mit dem Grundzustand und den ersten drei angeregten Zuständen.
Prüfe, ob das Gas durch den Beschuss mit den Elektronen eine oder mehrere Wellenlängen im sichtbaren Bereich abgibt.
Prüfe, ob das Gas durch den Beschuss mit den Elektronen eine oder mehrere Wellenlängen im sichtbaren Bereich abgibt.
(10 BE)
2.2.3
Beurteile, ob ein Elektron beim Durchfliegen des Natriumgases auch mehrere Natriumatome aus dem Grundzustand heraus anregen könnte.
(3 BE)
2.2.4
Der Energiewert des Grundniveaus kann durch den Elektronenbeschuss mit der Energie von nicht ermittelt werden.
Entscheide jeweils begründet, ob eine der folgenden Änderungen zur Ermittlung des Energiewerts des Grundzustands genutzt werden kann.
nicht ermittelt werden.
Entscheide jeweils begründet, ob eine der folgenden Änderungen zur Ermittlung des Energiewerts des Grundzustands genutzt werden kann.
a)
Es werden Elektronen mit einer größeren Energie als 
eingeschossen.
eingeschossen.
b)
Statt Elektronen werden Photonen mit der Energie 
in das Gas geschossen, was der Energiedifferenz zwischen Grundzustand und erstem angeregten Zustand entspricht.
in das Gas geschossen, was der Energiedifferenz zwischen Grundzustand und erstem angeregten Zustand entspricht.
(6 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.1
Aus der Beugungsgleichung folgt:
Mit der Kleinwinkelnäherung gilt 
und es folgt:
![\(\begin{array}[t]{rll}
\tan{\left(\alpha\right)}&=& \dfrac{x}{e} &\quad \scriptsize \mid\;\tan{\left(\alpha\right)} \approx \alpha \\[5pt]
\alpha&=& \dfrac{x}{e}
\end{array}\)](https://www.schullv.de/resources/formulas/ce69cdf31ba2c7be0f30816970ade568e2d15e450436895caf5be1eb0d2ee2ae_light.svg)
Einsetzen in die Beugungsgleichung liefert:
![\(\begin{array}[t]{rll}
g\cdot \sin{\left(\alpha\right)}&=& n\cdot \lambda&\quad \scriptsize \mid\; \text{Kleinwinkelnäherung:} \tan{\left(\alpha\right)} \approx \sin{\left(\alpha\right)} \approx \alpha \\[5pt]
g\cdot \alpha &=& n\cdot \lambda&\quad \scriptsize \mid\; \text{für das erste Maximum der ersten Ordnung :} \;n=1 \\[5pt]
g\cdot \alpha&=& \lambda
\end{array}\)](https://www.schullv.de/resources/formulas/3e38d6817e12c9aa0a1a5e8ee8307bbd8dd578c1802e3d1642e05a91b4e8a372_light.svg)
und es folgt:
Einsetzen in die Beugungsgleichung liefert:
![\(\begin{array}[t]{rll}
g\cdot \alpha&=& \lambda &\quad \scriptsize \mid\;\alpha= \dfrac{x}{e} \\[5pt]
g\cdot \dfrac{x}{e} &=& \lambda &\quad \scriptsize \mid\; \cdot \dfrac{e}{g} \\[5pt]
x &=& \dfrac{\lambda\cdot e}{g} &\quad \scriptsize \mid\; \dfrac{1}{g}= L \\[5pt]
x &=& \lambda\cdot e \cdot L
\end{array}\)](https://www.schullv.de/resources/formulas/ab7e532e001a0c989671cfb5edf7b04a67d0a8bf4c25fea21e183b09f839677f_light.svg)
1.2
Für die Wellenlänge gilt:
![\(\begin{array}[t]{rll}
x &=& \lambda\cdot e \cdot L&\quad \scriptsize \mid\; \cdot \dfrac{1}{e\cdot L} \\[5pt]
\dfrac{x}{e\cdot L}&=& \lambda &\quad \scriptsize \\[5pt]
\lambda&=& \dfrac{x}{e\cdot L}
\end{array}\)](https://www.schullv.de/resources/formulas/fca8650251c0ed1f32cb77b4f23b9e176b3be48585fa931b9acc746e220c1cd4_light.svg)
Einsetzen der Werte liefert:
Die Farbe der Spektrallinie ist gelb.
gilt:
Einsetzen der Werte liefert:
Die Farbe der Spektrallinie ist gelb.
![\(\begin{array}[t]{rll}
\lambda&=& \dfrac{x}{e\cdot L} &\quad \scriptsize \mid\, x=5,29 \; \text{mm} \\[5pt]
&=& \dfrac{ 5,29 \; \text{mm}}{ 90 \; \text{mm}\cdot \; 100 \;\dfrac{\text{Linien}}{\text{mm}}} &\quad \scriptsize \mid\; L=\dfrac{1}{g} = \dfrac{1}{10^{-5} \;\text{m}} = 10^5 \;\text{m}^{-1}\\[5pt]
&=& \dfrac{ 5,29 \; \text{mm}}{ 90 \; \text{mm}\cdot \; 10^5 \;\text{m}^{-1}} &\quad \scriptsize \mid\; 1 \;\text{mm} = 10^{-3} \,\text{m} \\[5pt]
&=& \dfrac{ 5,29\cdot 10^{-3} \,\text{m} }{ 90 \cdot 10^{-3} \,\text{m} \cdot \; 10^5 \;\text{m}^{-1}} &\quad \scriptsize \mid\; 1 \;\text{mm} = 10^{-3} \,\text{m} \\[5pt]
&=& \dfrac{ 5,29 }{ 90 \cdot \; 10^5 \;\text{m}^{-1}} &\quad \scriptsize \mid\; 1 \;\text{mm} = 10^{-3} \,\text{m} \\[5pt]
&=& 0, 0588 \cdot 10^{-5} \;\text{m} &\quad \scriptsize \\[5pt]
&=& 588 \cdot 10^{-9} \;\text{m} &\quad \scriptsize \mid\; 1 \;\text{m} = 10^9 \, \text{nm}\\[5pt]
&=& 588 \, \text{nm} &\quad \scriptsize \mid\; \lambda \in [570 \, \text{nm},600 \, \text{nm}]\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/e55e683a076ea6d79e82a050a0e2acc08cc9880966f29608d82d197490c3f25d_light.svg)
1.3
Die dunklen Absorptionslinien im Sonnenspektrum entstehen, weil die Sonne kontinuierliches Licht abstrahlt, das auf seinem Weg durch die Sonnenatmosphäre von Atomen absorbiert wird. Dies führt dazu, dass einige Wellenlängen im Spektrum fehlen, aber sie sind nicht völlig schwarz, da nicht alle Photonen dieser Wellenlängen absorbiert werden. Einige passieren die Atmosphäre, und thermische Bewegungen der Atome sowie Druckeffekte führen zur Aufhellung und Verbreiterung dieser Linien.
Während einer Sonnenfinsternis blockiert der Mond das Sonnenlicht, was die umgebenden Wellenlängenbereiche nahezu dunkel macht, da keine Sonnenstrahlung vorhanden ist. Dadurch werden die Spektrallinien hervorgehoben und erscheinen hell im Vergleich zur sonst dunklen Umgebung.
1.4
Wellenlänge der beiden Absorptionslinien
Für den Übergang von dem Grundzustand zu der Energiestufe A gilt:
Linien zuordnen
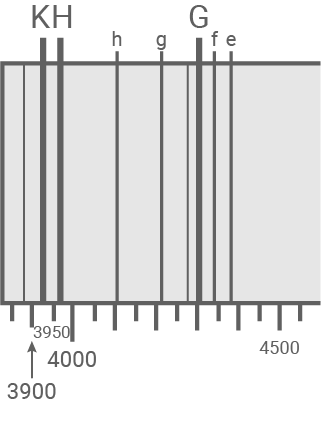
enpricht K, da diese Wellenlänge kleiner als 
ist und aber größer als 
enpricht H, da diese Wellenlänge größer als ist und aber kleiner als 
![\(\begin{array}[t]{rll}
\Delta E&=& h\cdot \dfrac{c}{\lambda_A} &\quad \scriptsize \mid\; \cdot \lambda_A \\[5pt]
\Delta E\cdot \lambda_A&=& h\cdot c &\quad \scriptsize \mid\; \cdot \dfrac{1}{\Delta E} \\[5pt]
\lambda_A&=& \dfrac{h\cdot c}{\Delta E} &\quad \scriptsize \mid\; \Delta E= E_A-E_{\text{Grundzustand}} \\[5pt]
\lambda_A&=& \dfrac{h\cdot c}{E_A-E_{\text{Grundzustand}}} &\quad \scriptsize \\[5pt]
\lambda_A&=& \dfrac{6,626\cdot 10^{-34}\;\text{Js} \cdot 3\cdot 10^8 \dfrac{\text{m} }{\text{s}}}{-8,75 \;\text{eV}-\left(-11,90 \;\text{eV} \right)} &\quad \scriptsize \mid\; 1 \;\text{J}= 6,242\cdot 10^{18} \;\text{eV} \\[5pt]
\lambda_A&=& \dfrac{6,626\cdot 10^{-34}\cdot 6,242\cdot 10^{18} \;\text{eV} \cdot 3\cdot 10^8 \text{m}}{3,15 \;\text{eV}} &\quad \scriptsize \\[5pt]
\lambda_A&=& 39,39\cdot 10^{-8} \;\text{m} &\quad \scriptsize \\[5pt]
\lambda_A&=& 3939 \cdot 10^{-10} \;\text{m}
\end{array}\)](https://www.schullv.de/resources/formulas/4e5f997978685bbc7a931d49ee69bc8ef806bf9bc23a7528a4db7f293a577526_light.svg)
Analog gilt für den Übergang von dem Grundzustand zu der Energiestufe B :
![\(\begin{array}[t]{rll}
\lambda_B&=& \dfrac{h\cdot c}{E_B-E_{\text{Grundzustand}}} &\quad \scriptsize \\[5pt]
&=& \dfrac{6,626\cdot 10^{-34}\cdot 6,242\cdot 10^{18} \;\text{eV} \cdot 3\cdot 10^8 \text{m}}{-8,78 \;\text{eV}-\left(-11,90 \;\text{eV} \right)} &\quad \scriptsize \mid\; 1 \;\text{J}= 6,242\cdot 10^{18} \;\text{eV} \\[5pt]
&=& 39,77 \cdot 10^{-8}\;\text{m}&\quad \scriptsize \\[5pt]
&=& 3977 \cdot 10^{-10}\;\text{m}
\end{array}\)](https://www.schullv.de/resources/formulas/9c3788c1a767259894908fd78c4fb0315a00f72c5d9aa1f3767b11abd3d32046_light.svg)
enpricht K, da diese Wellenlänge kleiner als ist und aber größer als enpricht H, da diese Wellenlänge größer als ist und aber kleiner als
1.5
Die starke Ionisierung von Elementen wie zwölffach ionisiertem Eisen in der Sonnenkorona, im Gegensatz zur Chromosphäre und Fotosphäre, resultiert aus den stark unterschiedlichen Temperaturen in diesen Schichten. Die hohe Temperatur in der Korona ermöglicht die starke Ionisierung, da Elektronen genügend Energie haben, um sich weit von den Atomkernen zu entfernen. Die Chromosphäre und die Fotosphäre haben niedrigere Temperaturen und zeigen daher nicht die gleiche Ionisierung und Spektrallinien.
2.1
Die Geschwindigkeit des Elektrons lässt sich über seine kinetische Energie berechnen. Es gilt: ![\(\begin{array}[t]{rll}
E_{\text{kin}}&=& \dfrac{1}{2}\cdot m_e\cdot v^2&\quad \scriptsize \mid\; \cdot \dfrac{2}{m_e} \\[5pt]
\dfrac{E_{\text{kin}}\cdot 2}{m_e}&=& v^2&\quad \scriptsize \mid\; \sqrt{\;} \\[5pt]
\sqrt{\dfrac{E_{\text{kin}}\cdot 2}{m_e}}&=& v
\end{array}\)](https://www.schullv.de/resources/formulas/f4538155bd5754c8e593ed92a665db679379a2861fcf008f06d93fc9fc86d607_light.svg)
Einsetzen der Werte liefert:
Einsetzen der Werte liefert:
![\(\begin{array}[t]{rll}
v&=&\sqrt{\dfrac{4,7 \;\text{eV} \cdot 2}{9,109⋅10^{−31} \;\text{kg}}} &\quad \scriptsize \mid\; 1 \text{eV} = 1,8·10^{−36} \;\text{kg}\cdot c^2 = 1,8·10^{−36}\cdot 3\cdot 10^8 \;\dfrac{\text{kg}\cdot \text{m}^2}{\text{s}^2} \\[5pt]
&=&\sqrt{\dfrac{4,7 \cdot 1,8·10^{−36}\cdot 3\cdot 10^8 \;\dfrac{\text{kg}\cdot \text{m}^2}{\text{s}^2} \cdot 2}{9,109⋅10^{−31} \;\text{kg}}} &\quad \scriptsize \\[5pt]
&=& \sqrt{5,6 \cdot 10^{3}}\;\dfrac{\text{m}}{\text{s}}&\quad \scriptsize \\[5pt]
&=& 74,6 \;\dfrac{\text{m}}{\text{s}}
\end{array}\)](https://www.schullv.de/resources/formulas/55fbfa70d065ac58a4daefdd967b1cb03675f02fd5f132dacf372c06b3a2df5c_light.svg)
2.2.1
Die Elektronen besitzen nach der Wechselwirkung mit den Natriumatomen nur ganz bestimmte Energiewerte, weil die Stoßprozesse im Modell nur Übergänge zwischen den Elektronenenergien und dem Grundzustand des Natriumatoms berücksichtigen. Nur wenn die Energie der Elektronen genau zu den erlaubten Übergängen passt, werden diese spezifischen Energien beobachtet. Dies führt zu diskreten Energieniveaus nach der Wechselwirkung.
2.2.2
Termschema von Natrium
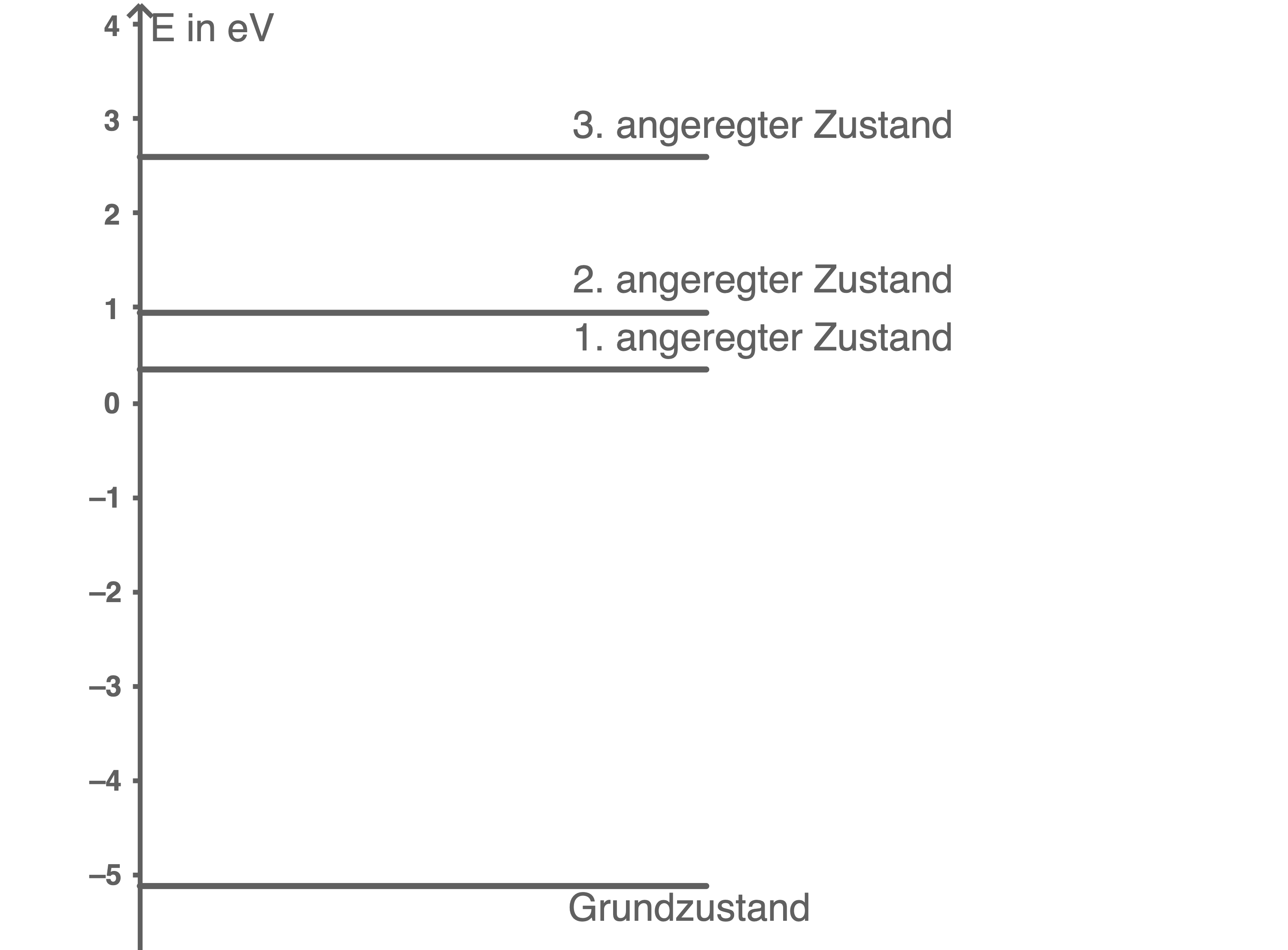Wellenlängen im sichtbaren Bereich
Das menschliche Auge kann Licht mit einer Wellenlänge zwischen 
und 
wahrnehmen. Für die entsprechenden Energiedifferenzen gilt:
![\(\begin{array}[t]{rll}
\Delta E &=& h\cdot \dfrac{c}{\lambda}
\end{array}\)](https://www.schullv.de/resources/formulas/d27be6a34caf83e01b380d15e6871d5444415e7e325e2d1d56a85ef5170b2cf0_light.svg)
Einsetzen der Wellenlängen lifert:
Für die Energiedifferenzen der unterschiedlichen Zustande von Natrium gilt:
1. angeregter Zustand: 
2. angeregter Zustand: 
3. angeregter Zustand: 
Die Energiedifferenzen zwischen den Zuständen liegen alle weit über dem Bereich des sichtbaren Lichts. Daher wird das Gas keine Emission im sichtbaren Bereich aufweisen, da die Elektronen nicht genug Energie haben, um Photonen im sichtbaren Bereich zu emittieren.
und wahrnehmen. Für die entsprechenden Energiedifferenzen gilt:
Einsetzen der Wellenlängen lifert:
Für die Energiedifferenzen der unterschiedlichen Zustande von Natrium gilt:
1. angeregter Zustand: ![\(\begin{array}[t]{rll}
\Delta E_{\text{max}} &=& h\cdot \dfrac{c}{\lambda_{\text{min}}}&\quad \scriptsize \\[5pt]
&=& 4,136\cdot 10^{-15} \;\text{eV s}\cdot \dfrac{3\cdot 10^8 \;\dfrac{\text{m}}{\text{s}}}{380 \;\text{nm}}&\quad \scriptsize \mid\; 1 \;\text{nm} = 10^{-9} \; \text{m} \\[5pt]
&=& 4,136\cdot 10^{-15} \;\text{eV s}\cdot \dfrac{3\cdot 10^8 \;\dfrac{\text{m}}{\text{s}}}{380 \cdot 10^{-9} \; \text{m}}&\quad \scriptsize \\[5pt]
&=& 0,0327 \cdot 10^{-2} \;\text{eV}&\quad \scriptsize \\[5pt]
&=& 3,37 \;\text{eV}
\end{array}\)](https://www.schullv.de/resources/formulas/78288343e9f2c8ad433a87f2d04c888e762e4c5d454b53c8dbd95a53ce0a5a29_light.svg)
![\(\begin{array}[t]{rll}
\Delta E_{\text{min}} &=& h\cdot \dfrac{c}{\lambda_{\text{max}}}&\quad \scriptsize \\[5pt]
&=& 4,136\cdot 10^{-15} \;\text{eV s}\cdot \dfrac{3\cdot 10^8 \;\dfrac{\text{m}}{\text{s}}}{780 \cdot 10^{-9} \; \text{m}}&\quad \scriptsize \\[5pt]
&=& 0,0159 \cdot 10^{-2} \;\text{eV}&\quad \scriptsize \\[5pt]
&=& 1,59 \;\text{eV}
\end{array}\)](https://www.schullv.de/resources/formulas/5cd194641fdbc7dca9e89a1733830e328d755d7e1fe5071035a837eeb50eb5a8_light.svg)
2. angeregter Zustand:
3. angeregter Zustand:
Die Energiedifferenzen zwischen den Zuständen liegen alle weit über dem Bereich des sichtbaren Lichts. Daher wird das Gas keine Emission im sichtbaren Bereich aufweisen, da die Elektronen nicht genug Energie haben, um Photonen im sichtbaren Bereich zu emittieren.
2.2.3
Ein Elektron, das durch Natriumgas fliegt, kann mehrere Natriumatome aus dem Grundzustand anregen. Dies geschieht, wenn die kinetische Energie des Elektrons ausreicht, um die Energiedifferenz zwischen dem Grundzustand der Natriumatome und den angeregten Zuständen zu überwinden. Diese Wechselwirkung hängt von der Energie des Elektrons, der Dichte der Natriumatome und anderen Faktoren ab. Es ist jedoch wichtig zu beachten, dass nicht alle Elektronen die erforderliche Energie haben oder in der Lage sind, die Natriumatome anzuregen.
2.2.4
a)
Nein, das Einschießen von Elektronen mit einer Energie größer als 5, 
ist erforderlich, um Elektronen aus dem Grundzustand in den ersten angeregten Zustand zu heben. Daher hilft diese Methode allein nicht bei der direkten Bestimmung der Energie des Grundzustands.
ist erforderlich, um Elektronen aus dem Grundzustand in den ersten angeregten Zustand zu heben. Daher hilft diese Methode allein nicht bei der direkten Bestimmung der Energie des Grundzustands.
b)
Das Schießen von Photonen mit 
in das Gas kann Elektronen im Natriumatom aus dem Grundzustand in den ersten angeregten Zustand anheben. Wenn die Elektronen vom ersten angeregten Zustand in den Grundzustand zurückkehren, emittieren sie Photonen derselben Energie. Durch die Messung dieser emittierten Photonen kann die Energiedifferenz zwischen dem Grundzustand und dem ersten angeregten Zustand bestimmt werden, was zur Ermittlung des Energiewerts des Grundzustands führt.
in das Gas kann Elektronen im Natriumatom aus dem Grundzustand in den ersten angeregten Zustand anheben. Wenn die Elektronen vom ersten angeregten Zustand in den Grundzustand zurückkehren, emittieren sie Photonen derselben Energie. Durch die Messung dieser emittierten Photonen kann die Energiedifferenz zwischen dem Grundzustand und dem ersten angeregten Zustand bestimmt werden, was zur Ermittlung des Energiewerts des Grundzustands führt.