Vorschlag A2

Optisches Gitter und Betrachtungen zur Lichtgeschwindigkeit

Laut einer Studie können aus den Kokons von Seidenraupen optische Komponenten wie Beugungsgitter hergestellt werden, die sich durch das Einbringen spezieller biologischer Substanzen in ihren optischen Eigenschaften gezielt verändern lassen. Dabei können die Beugungsgitter eine Gitterkonstante von unter einem Mikrometer erreichen.

Zur Ermittlung der Gitterkonstanten $g$ wird ein solches Gitter mit Laserlicht der Wellenlänge $\lambda$ beleuchtet, sodass sich auf einem $e =50 \,\text{cm}$ entfernten Schirm ein Interferenzmuster ergibt.

1.1

Erkläre mithilfe einer Skizze die Entstehung der Interferenzmaxima und leite die Formel $g \cdot \sin \alpha_{ n }= n \cdot \lambda$ zur Bestimmung des $n$ -ten Beugungsmaximums unter dem Winkel $\alpha_{ n }$ her.

(6 BE)

1.2

Zur Bestimmung der Gitterkonstanten wird nacheinander sichtbares Licht verschiedener Wellenlängen verwendet und jeweils der Abstand der beiden Beugungsmaxima erster Ordnung zueinander gemessen. Die Ergebnisse sind in Material 1 dokumentiert.

Material 1: Abstände der beiden Maxima erster Ordnung zueinander

Wellenlänge	Abstand der Maxima erster Ordnung
$\lambda_1=578 \,\text{nm}$	82 cm
$\lambda_2=546 \,\text{nm}$	76 cm
$\lambda_3=436 \,\text{nm}$	54 cm
$\lambda_4=405 \,\text{nm}$	50 cm

1.2.1

Erläutere einen messtechnischen Vorteil, den die Bestimmung des Abstands der beiden Maxima erster Ordnung zueinander im Vergleich zu der Bestimmung des Abstands eines Maximums erster Ordnung zum Maximum nullter Ordnung besitzt.

(2 BE)

1.2.2

Bestimme unter Verwendung aller Messwerte die Gitterkonstante $g.$

Prüfe dafür zunächst, ob die Kleinwinkelnäherung verwendet werden darf.

(6 BE)

1.2.3

Der Hersteller des Gitters gibt an, dass pro Millimeter 1111 Gitterspalte vorhanden sind.

Berechne die prozentuale Abweichung des Ergebnisses aus Aufgabe 1.2.2 von der Angabe des Herstellers.

(3 BE)

1.3

Wird ein Gitter mit der Gitterkonstanten $g =9 \cdot 10^{-7} \,\text m$ mit Licht der Wellenlänge $\lambda_5=550 \,\text{nm}$ und mit Licht der Wellenlänge $\lambda_6=420 \,\text{nm}$ gleichzeitig bestrahlt, so ergibt sich dahinter ein Beugungsmuster aus Streifen zweier verschiedener Farben.

Gib mithilfe von Material 2 die Farben der beiden Wellenlängen an.

Berechne gesondert für jede Farbe die maximale Anzahl der Streifen, die zu beobachten sind, wobei das Maximum nullter Ordnung für jede Farbe einzeln zählt.

Material 2: Sechs Spektralfarbbereiche des Lichts

Farbe	Wellenlängenbereich in $\text{nm}$
Rot	$\approx 770-640$
Orange	$\approx 640-600$
Gelb	$\approx 600-570$
Grün	$\approx 570-490$
Blau	$\approx 490-430$
Violett	$\approx 430-390$

(5 BE)

1.4

Die Gitterkonstanten dieser Gitter können bei der Herstellung einen minimalen Wert von etwa $g =0,125 \,\mu \text m$ erreichen.

Untersuche, ob sichtbares Licht zur genauen Bestimmung dieses minimalen Werts noch geeignet ist.

(2 BE)

1.5

Nenne einen Vorteil, den eine Herstellung einer Gitterstruktur aus Kokon bietet.

(2 BE)

Doppelspalte können ebenfalls bei der Bestrahlung mit Laserlicht Interferenzmuster erzeugen.

2.1

Beschreibe zwei Gemeinsamkeiten und zwei Unterschiede der beiden Interferenzmuster, wenn Gitter und Doppelspalt die gleichen Spaltabstände und vernachlässigbare Spaltbreiten besitzen.

(4 BE)

2.2

Der Abstand der beiden Spalte eines Doppelspalts beträgt im Folgenden $d =100 \,\mu\text m.$ Der Doppelspalt wird mit Licht der Wellenlänge $\lambda=550 \,\text{nm}$ bestrahlt.

Berechne, wie weit sich ein Schirm vom Doppelspalt entfernt befinden muss, damit die beiden Maxima erster Ordnung einen Abstand von $2 \,\text{cm}$ besitzen. Du darfst ohne Nachweis die Kleinwinkelnäherung verwenden.

(4 BE)

2.3

Beschreibe und begründe allgemein zwei Möglichkeiten, durch Veränderung des Experiments den Abstand zweier Maxima erster Ordnung zu vergrößern.

(4 BE)

Die Lichtgeschwindigkeit ist eine grundlegende Naturkonstante. Im Folgenden werden ein historisches Experiment zu ihrer Messung und ein Experiment zur Veranschaulichung ihrer Größenordnung betrachtet.

3.1

Der Physiker Hippolyte Fizeau hat im 19. Jahrhundert die Lichtgeschwindigkeit mit dem Versuchsaufbau aus Material 3 bestimmt. Das Licht einer Lichtquelle wird dabei über einen halbdurchlässigen Spiegel auf den Rand eines sich drehenden Zahnrads gelenkt. Trifft das Licht auf eine Lücke, so kann es das Zahnrad passieren, läuft zu einem weit entfernten Spiegel und wird dort reflektiert. Das Rad wird so schnell gedreht, dass das Licht beim Rücklauf auf den benachbarten Zahnradzahn trifft und der Beobachter Dunkelheit feststellt. Dieser Fall tritt ein, wenn das Zahnrad 720 Zähne (und 720 Lücken) besitzt und 12,6 Umdrehungen pro Sekunde macht.

Berechne, wie lange das Zahnrad für eine Umdrehung braucht, und zeige, dass die Zeit, in der das Zahnrad von der Mitte einer Lücke auf die Mitte des folgenden Zahns weitergelaufen ist, $t =5,51 \cdot 10^{-5} \,s$ beträgt.

Berechne mit diesem Ergebnis und mithilfe von Material 3 einen Messwert für die Lichtgeschwindigkeit.

Berechne die prozentuale Abweichung des Messwerts vom Literaturwert.

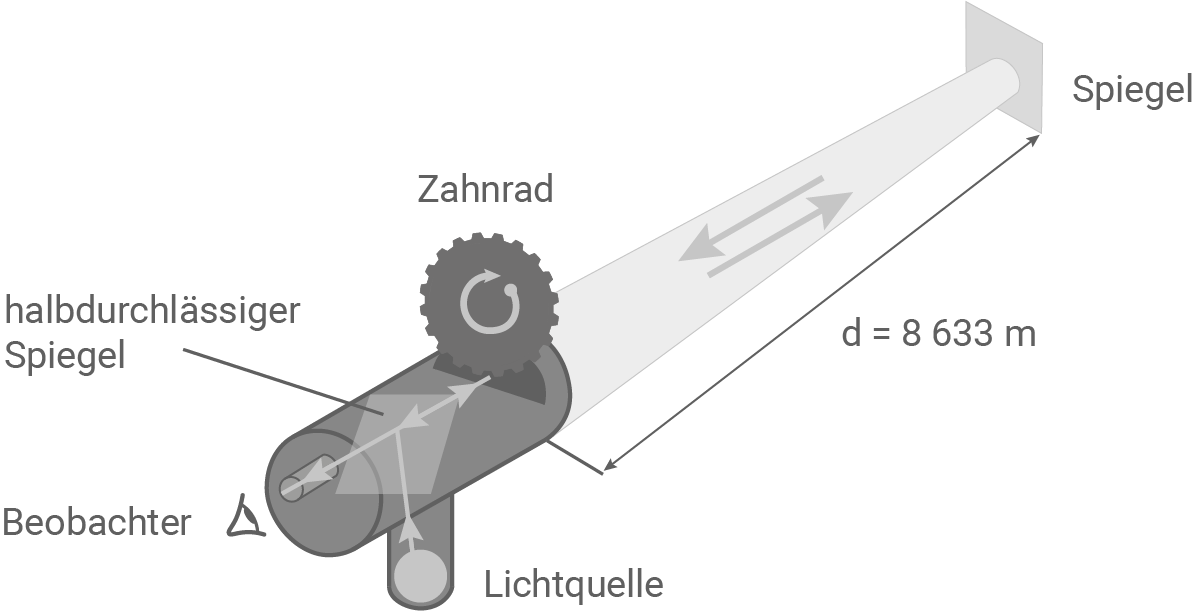
Material 3: Aufbau nach Fizeau

(7 BE)

3.2

Um die Größenordnung der Lichtgeschwindigkeit zu demonstrieren, wird folgendes Experiment geplant: Ein auf der Erde positionierter Laser wird auf einen auf dem Mond aufgestellten Spiegel gerichtet und bestrahlt ihn mit einem Laserpuls der Wellenlänge $\lambda=550 \,\text{nm}.$

Gleichzeitig mit dem Start des Laserpulses wird auf der Erde eine Kugel von einem 10 Meter hohen Turm fallen gelassen. Für die Entfernung von der Erdoberfläche zum Mond soll $384400 \,\text{km}$ angenommen werden.

Untersuche unter Vernachlässigung des Luftwiderstands, ob die Kugel vor der Wiederankunft des Laserpulses auf dem Boden ankommt.

(5 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

Trifft das Licht auf das Gitter, so werden die Lichtwellen nach dem Huygens'schen Prinzip gebeugt. Die gleichphasigen Elementarwellen, die von den Spalten ausgehen interferieren miteinander auf dem Schirm.

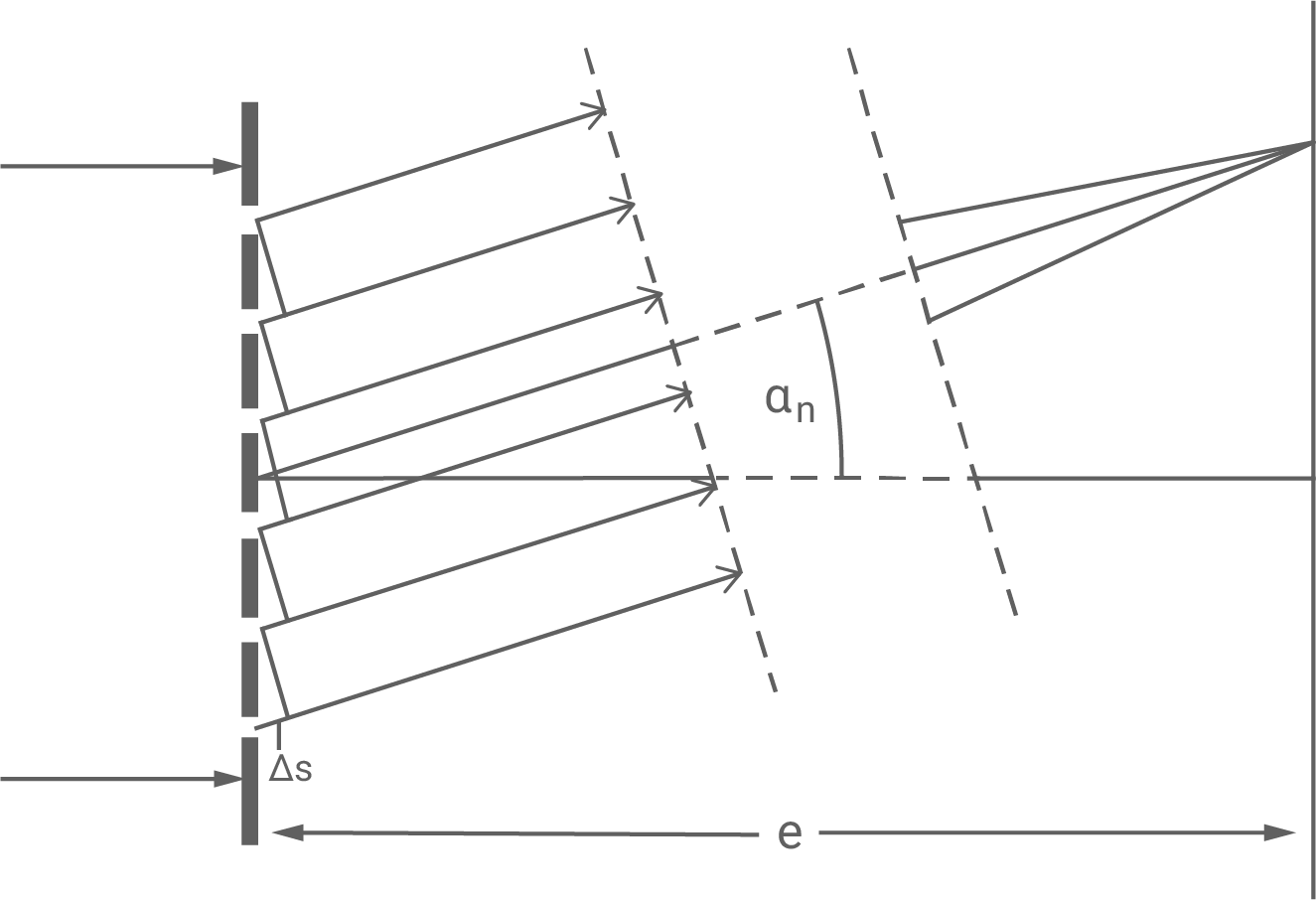Interferieren die Elementarwellen konstruktiv, also mit einem Gangunterschied von $\Delta s =n \cdot \lambda$ mit $n =0 ; 1 ; 2,...),$ so sind unter einem Beugungswinkel von $\alpha_n$ Intensitätsmaxima auf dem Schirm zu sehen.

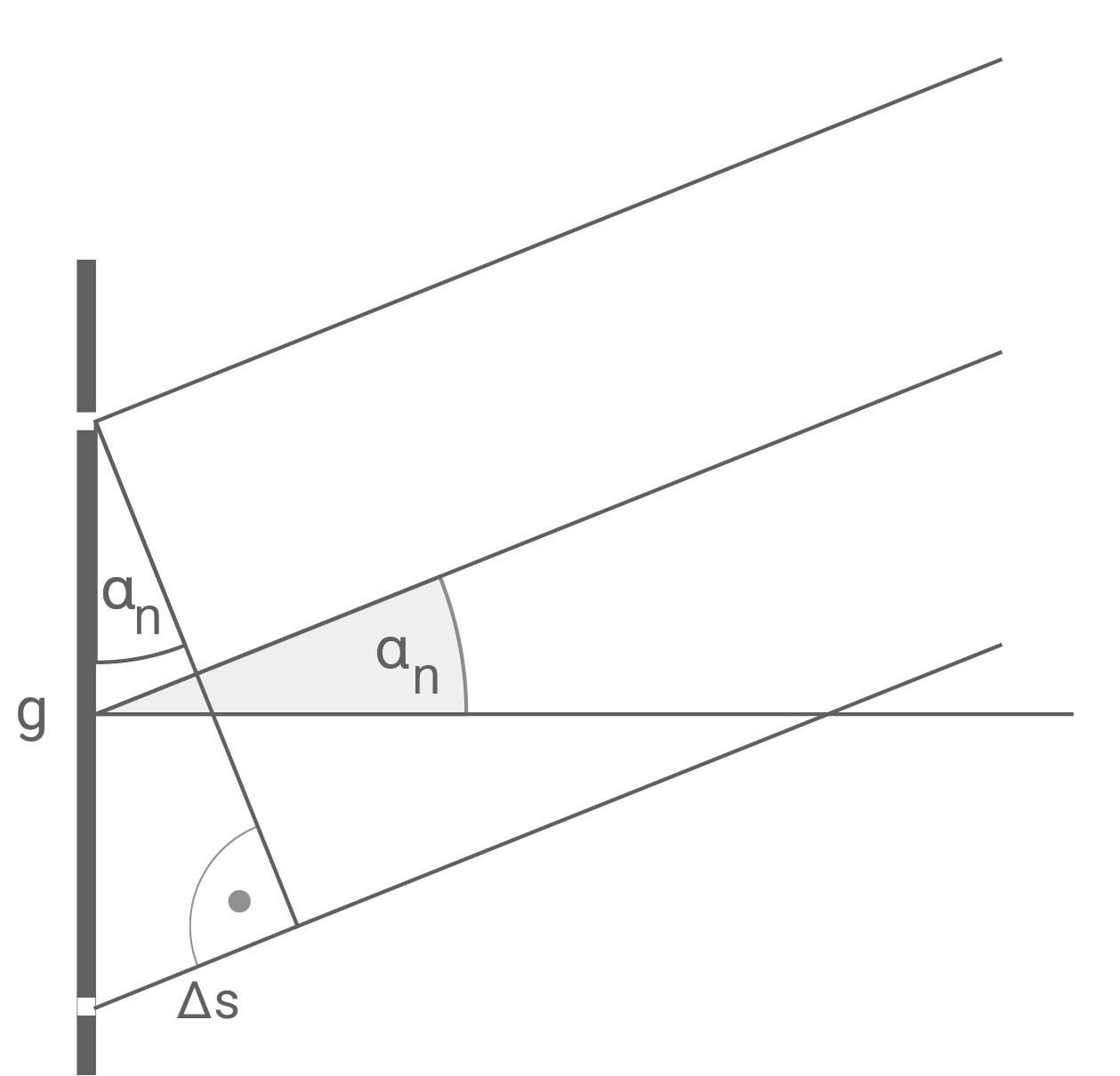Es gilt:

$\begin{array}[t]{rll} \sin (\alpha_n)&=& \dfrac{\Delta s}{g}&\quad \scriptsize \mid\;\cdot g \\[5pt] \sin (\alpha_n)\cdot g &=& \Delta s \\[5pt] \Delta s &=&\sin (\alpha_n)\cdot g \end{array}$

Gleichsetzen der Gleichungen für $\Delta s$ ergibt: $\sin (\alpha_n)\cdot g =n \cdot \lambda$ mit $n=0; 1; 2,..$

1.2.1

Die Interferenzmaxima erster Ordnung sind gleich hell und gut erkennbar. Durch die höhere Messgenauigkeit ergibt sich der messtechnische Vorteil.

Es ist besser bei einer Längenmessung eine größere Entfernung zu bestimmen, da dann der absolute Messfehler konstant ist. Somit sinkt der prozentuale Messfehler für größere Messwerte.

1.2.2

Die Abstände $d_n$ der Maxima vom Maximum 0. Ordnung lassen sich mit $\tan(\alpha_n)=\dfrac{d_n}{e}$ berechnen.

$\alpha_1= \tan^{-1}\left(\dfrac{d_1}{e}\right)$ $=\tan^{-1}\left(\dfrac{\dfrac{82 \;\text{cm}}{2}}{50 \;\text{cm}}\right)$ $=\tan^{-1}(0,82) = 39,4^{\circ}$

Ebenso ergeben sich: $\alpha_2= 37,2^{\circ},$ $\alpha_3= 28,4^{\circ},$ $\alpha_4= 26,6^{\circ}$

Diese Winkel sind alle größer als $5^{\circ}.$ Somit kann die Kleinwinkelnäherung nicht angewendet werden.

Bestimmung der Gitterkonstanten

$\begin{array}[t]{rll} g\cdot \sin(\alpha_n)&=&n \cdot \lambda &\quad \scriptsize \mid\;:\sin(\alpha_n) \\[5pt] g&=& \dfrac{n \cdot \lambda}{\sin(\alpha_n)} \end{array}$

Es folgt:

$g_1= \dfrac{n \cdot \lambda}{\sin(\alpha_1)}$ $= 911\;\text{nm}$

$g_2= \dfrac{n \cdot \lambda}{\sin(\alpha_2)}$ $= 903\;\text{nm}$

$g_3= \dfrac{n \cdot \lambda}{\sin(\alpha_3)}$ $= 917\;\text{nm}$

$g_4= \dfrac{n \cdot \lambda}{\sin(\alpha_4)}$ $= 905\;\text{nm}$

Der Mittelwert folgt mit: $\dfrac{911+903+917+905}{4}\;\text{nm} =909\;\text{nm}$

Somit sollte die gesuchte Gitterkonstante ca. $0,9 \;\mu\text{m}$ entsprechen.

1.2.3

Laut Angabe des Herstellers hat das Gitter eine Gitterkonstante von $g =\dfrac{1 \cdot 10^{-3} \;\text{m}}{1111}=9,001 \cdot 10^{-7} \;\text{m} =900,1 \;\text{nm}$

Prozentuale Abweichung:

$\left|\dfrac{900,1 \;\text{nm} -909 \;\text{nm}}{900,1 \;\text{nm} }\right|=0,010=1,0 \%$

1.3

Farben der Wellenlängen

$\lambda_5 = 550 \;\text{nm}$ entspricht grünem Licht und $\lambda_6 = 420 \;\text{nm}$ entspricht violettem Licht.

Maximale Anzahl der Streifen

Für das grüne Licht gilt:

$\begin{array}[t]{rll} g \cdot \sin (\alpha_n)&=& n \cdot \lambda_5 &\quad \scriptsize \mid\;:g \\[5pt] \sin (\alpha_n)&=& \dfrac{ n \cdot \lambda_5}{g} \\[5pt] \sin (\alpha_n)&=& \dfrac{ n \cdot 550\cdot 10^{-9}\;\text{m}}{9\cdot 10^{-7}\;\text{m}} \end{array}$

Es muss $\sin (\alpha_n) \lt 1$ gelten, da der Ablenkwinkel des Interferenzmaximums höchster Ordnung kleiner als $90^{\circ}$ ist.

Rechenweg anzeigen

$n_{\max}=1$

Bei grünem Licht sind Maxima bis zur ersten Ordnung erkennbar. Insgesamt (mit dem Maximum 0. Ordnung) sind 3 Maxima zu beobachten.

Für das violette Licht gilt:

$\begin{array}[t]{rll} g \cdot \sin (\alpha_n)&=& n \cdot \lambda_6 &\quad \scriptsize \mid\;:g \\[5pt] \sin (\alpha_n)&=& \dfrac{ n \cdot \lambda_6}{g} \\[5pt] \sin (\alpha_n)&=& \dfrac{ n \cdot 420\cdot 10^{-9}\;\text{m}}{9\cdot 10^{-7}\;\text{m}} \end{array}$

Es muss $\sin (\alpha_n) \lt 1$ gelten, da der Ablenkwinkel des Interferenzmaximums höchster Ordnung kleiner als $90^{\circ}$ ist.

Rechenweg anzeigen

$n_{\max}=2$

Bei violettem Licht sind Maxima bis zur zweiten Ordnung erkennbar. Insgesamt (mit dem Maximum 0. Ordnung) sind 5 Maxima zu beobachten.

1.4

$\sin (\alpha_n)$ kann maximal den Wert 1 annehmen. Um $g$ bestimmen zu können, sollten die Maxima 1. Ordnung auf dem Schirm sichtbar sein.

Für $n =1$ und $\sin (\alpha_1)=1$ folgt $g =\lambda$ $=0,125 \;\mu \text{m} =125 \;\text{nm}$

Aus Material 2 folgt, dass sichtbares Licht etwa zwischen $390 \;\text{nm}$ und $770 \;\text{nm}$ liegt und dieses ist somit ungeeignet zur Bestimmung des minimalen Werts.

1.5

Eine Gitterstruktur aus Kokon ist biologisch abbaubar und sehr stabil. Die optischen Eigenschaften können durch biologische Substanzen verändert werden.

2.1

Gemeinsamkeiten

Das Licht wird gebeugt.
Maxima und Minima sind unter gleichem Ausfallwinkel zu beobachten und die Abstände der Maxima und Minima sind gleich.
Wellenlänge des Lichts kann aus dem Abstand zwischen den Hauptmaxima berechnet werden.

Unterschiede

Doppelspalt: 2 Spalte, wodurch ein Teil des einfallenden Lichts ausgeblendet wird.
Gitter: mehrere Spalte, wodurch mehr des einfallendes Lichts die Spalte durchläuft
Maxima beim Gitter sind heller als beim Doppelspalt, denn mehr Licht aus den Einzelspalten kann miteinander interferieren
Größere Gesamtintensität bei Gitter, wegen mehreren Spalten, die zur Interferenz beitragen: Maxima sind schmäler und schärfer abgegrenzt

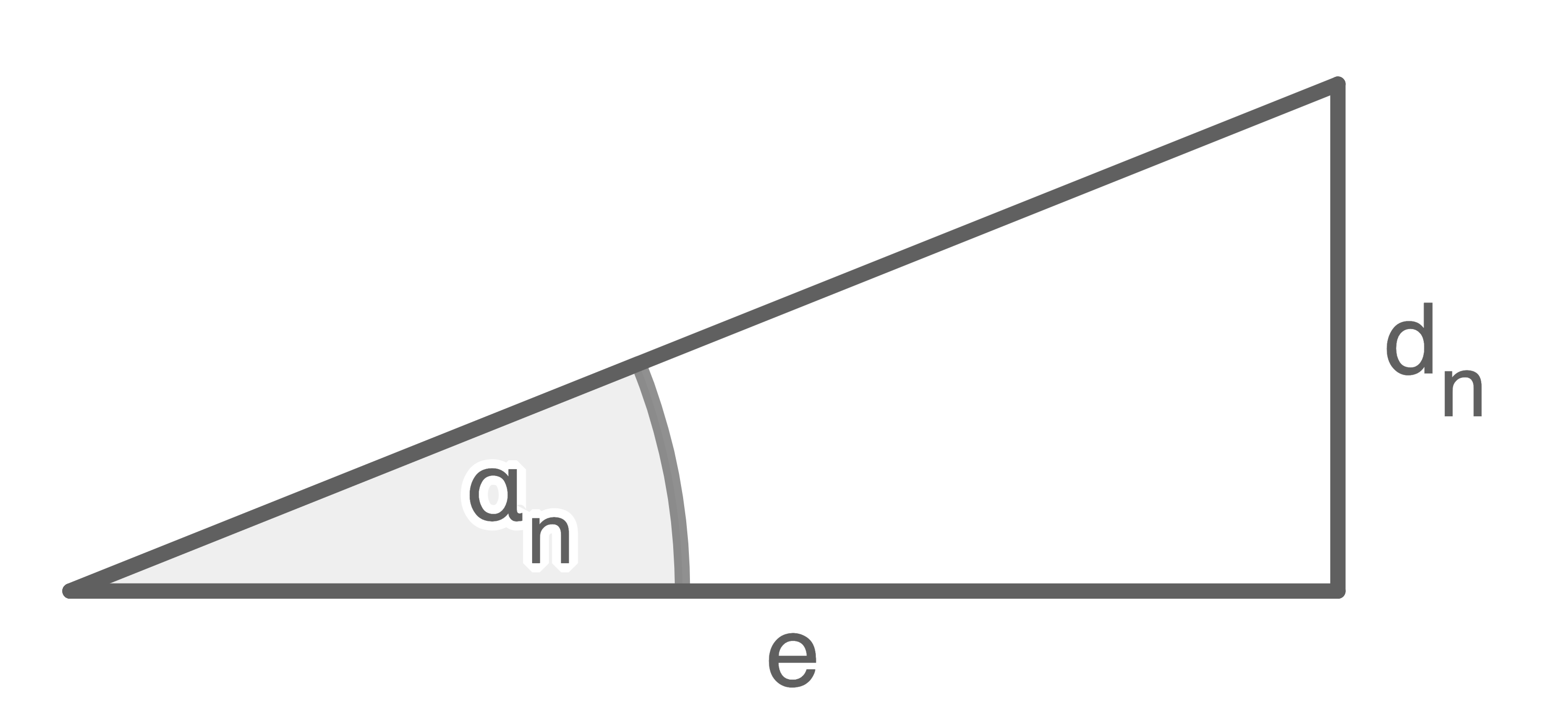
2.2

Es gilt: $d \cdot \sin(\alpha_n) = n \cdot \lambda$ und $\tan (\alpha_n)=\dfrac{d_n}{e}$ mit $n =0,1,2,...$

Kleinwinkelnäherung:

$\begin{array}[t]{rll} \sin(\alpha_n)&=& \tan (\alpha_n) \\[5pt] \dfrac{n \cdot \lambda}{d}&=& \dfrac{d_n}{e} \scriptsize \mid\;\cdot e \;\mid\cdot \dfrac{d}{n \cdot \lambda} \\[5pt] e&=& \dfrac{d}{n \cdot \lambda} \cdot d_n \\[5pt] e&=& \dfrac{100\; \mu \text{m} \cdot 2 \;\text{cm} }{550 \;\text{nm} } \\[5pt] e&=&\dfrac{100 \cdot 10^{-6}\;\text{m} \cdot 2 \cdot 10^{-2}\;\text{m} }{550 \cdot 10^{-9} \;\text{m} } \\[5pt] e&=& 3,6 \;\text{m} \end{array}$

2.3

$\begin{array}[t]{rll} \dfrac{n \cdot \lambda}{d}&=& \dfrac{d_n}{e} &\quad \scriptsize \mid\;\cdot e \\[5pt] \dfrac{n \cdot \lambda}{d}\cdot e&=& d_n \\[5pt] d_n&=& \dfrac{n \cdot \lambda}{d}\cdot e \\[5pt] d_1&=&\dfrac{\lambda}{d}\cdot e \end{array}$

Den Abstand $2d_1$ zweier Maxima erster Ordnung kann folglich vergrößert werden durch:

Verkleinerung des Spaltabstandes $d$
Vergrößerung des Schirmabstandes $e$

3.1

Umlaufzeit für eine Umdrehung

$t=\dfrac{1 \;\text{s}}{12,6}=0,0793 \;\text {s}$

Laufzeit zwischen Zahn und Lücke

Umdrehungen des Zahnrades von einer Lücke zum nächsten Zahn: $\dfrac{1}{2 \cdot 720}=\dfrac{1}{1440}$

$t_2 =\dfrac{1}{1440} \cdot t$ $=\dfrac{1}{1440} \cdot 0,0793 \;\text {s}$ $=5,51 \cdot 10^{-5} \;\text {s}$

Wert für die Lichtgeschwindigkeit

$v= \dfrac{s}{t}$ $=\dfrac{2d}{t}$ $= \dfrac{2\cdot 8633\;\text{m}}{5,51\cdot 10^{-5}\;\text{s}}$ $= 3,13\cdot 10^8 \;\dfrac{\text{m}}{\text{s}}$

Prozentuale Abweichung

Die Lichtgeschwindigkeit beträgt ca. $c= 3,00\cdot 10^8 \;\frac{\text{m}}{\text{s}}.$

$\dfrac{3,13-3,00}{3,00}\approx0,043=4,3 \% \text {. }$

3.2

Zeit, in der Licht von der Erde zum Mond und zurück zu gelangt

Die Bewegung ist geradlinig gleichförmig.

$\begin{array}[t]{rll} c&=& \dfrac{2 \cdot s_{EM}}{t}&\quad \scriptsize \mid\;\cdot t \;\mid:c \\[5pt] t&=&\dfrac{2 \cdot s_{EM}}{c} \\[5pt] t&=& \dfrac{2 \cdot 384400 \cdot 10^3 \;\text{m} }{3,00 \cdot 10^8 \frac{\text{m} }{ \text{s}}} \\[5pt] t&=& 2,56 \;\text{s} \end{array}$

Freier Fall der Kugel

Die Bewegung ist gleichförmig beschleunigt.

$\begin{array}[t]{rll} s&=& \dfrac{1}{2}\cdot g \cdot t^2 &\quad \scriptsize \mid\;\cdot 2 \;\mid\;:g \\[5pt] \dfrac{2\cdot s}{g}&=& t^2 \\[5pt] t^2&=& \dfrac{2\cdot s}{g} &\quad \scriptsize \mid\;\sqrt{\;} \\[5pt] t&=& \sqrt{\dfrac{2 \cdot s }{ g }}\\[5pt] &=& \sqrt{\dfrac{2 \cdot 10 \;\text{m} }{9,81 \frac{\text{m} }{ \;\text{s}^2}}}\\[5pt] &\approx& 1,43 \;\text{s} \end{array}$

Die Kugel fällt auf den Boden, wenn der Laserimpuls ca. den Mond erreicht.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?