Vorschlag A1

Spielgeräte für Groß und Klein

Beschreibe allgemein und unabhängig von einem Sachzusammenhang, was man unter einer mechanischen Schwingung versteht.

Nenne ein Kriterium, mit dem man eine harmonische Schwingung charakterisieren kann.

(2 BE)

1.2

Gib zwei Beispiele für mechanische Schwingungen an und entscheide jeweils, ob man diese Schwingung als harmonisch bezeichnen kann.

(4 BE)

Die Montage und Demontage von Windkraftanlagen erfordern Kräne enormer Höhe (Material 1). Hängt eine Last am Seil des Kranauslegers, so kann man dies vereinfacht als ein Fadenpendel mit einer Punktmasse an einem masselosen Faden ansehen. Auf einer hessischen Baustelle gerät beim Anheben der Last (Gondel einer Windkraftanlage, vgl. rechte Abbildung in Material 1) die Masse $\text m =100 \,t$ in Schwingung. Die Aufhängung des Seils (Material 2) kann dabei zunächst als fest angenommen werden. Zur Überwachung des Krans wird die Bewegung zu jedem Zeitpunkt vermessen. Als im Kran eine Seillänge von $145 \,\text m$ (Abstand vom Aufhängepunkt zur Last) angezeigt wird, stellt man fest, dass sich die angehängte Masse in genau $12 \,s$ von einem Umkehrpunkt zum anderen bewegt. Der horizontale Abstand zwischen diesen Umkehrpunkten beträgt $s _{\text {hor }}=12 \,\text m.$

Für die Fallbeschleunigung soll im Folgenden der Wert $g=9,81 \dfrac{ \text m }{ s ^2}$ verwendet werden.

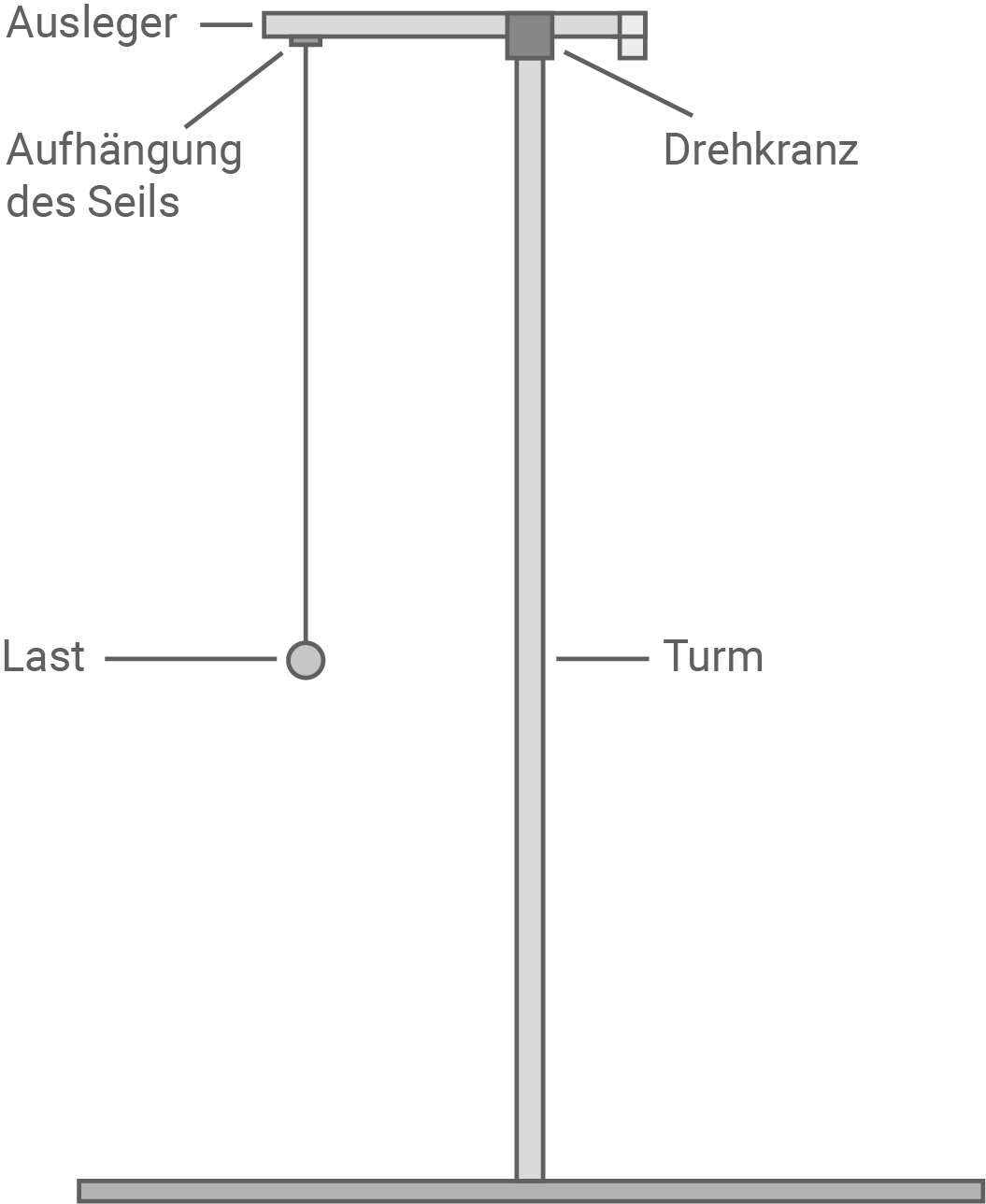
Material 1: Kran bei der Montage einer Windkraftanlage

Material 2: Skizze Kran (mit Vereinfachung ein Seil zum Anheben der Last)

2.1

Berechne ohne Verwendung der Seillänge die Schwingungsdauer des Pendels.

(2 BE)

2.2

Beurteile mithilfe einer geeigneten Rechnung, ob in diesem Fall die Kleinwinkelnäherung verwendet werden darf, und beurteile, ob es sich hier in guter Näherung um eine harmonische Schwingung handelt.

(4 BE)

2.3

Prüfe die obige Angabe der Seillänge durch eine Berechnung aus der Schwingungsdauer.

Berechne die prozentuale Abweichung Ihres Ergebnisses von dem angegebenen Wert und nenne eine mögliche Ursache der Abweichung.

(5 BE)

2.4

Berechne die maximale potenzielle Energie der schwingenden Gondel und ihre Geschwindigkeit beim Durchgang durch die Ruhelage unter der Annahme der Seillänge $\ell=145 \,\text m$ und der oben angegebenen horizontalen Auslenkung. Der Nullpunkt der potenziellen Energie soll durch die Ruhelage festgelegt werden.

(5 BE)

2.5

Die Last wird nun durch Verkürzung der Seillänge angehoben.

Untersuche den Einfluss einer solchen Verkürzung auf die Schwingungsdauer der Last.

Mit dem Kran soll nun die Amplitude der Schwingung im Verlauf der Zeit aktiv verringert werden. Die Seillänge soll hierbei konstant bleiben. Der Ausleger lässt sich mithilfe des Drehkranzes drehen und die Aufhängung des Seils lässt sich entlang des Auslegers verschieben.

Entwickle eine Idee für ein mögliches Vorgehen.

(4 BE)

Bei einem Federbrett, das z.B. bei Kindern für das Training der Körperkoordination verwendet wird, sind zwischen zwei Holzbrettern vier gleichartige Schraubenfedern montiert (Material 3). Belastet man das Federbrett gleichmäßig mit einer Masse von $70 \,\text{kg},$ so verringert sich der Abstand zwischen den Holzbrettern um $5 \,\text{cm}.$ Der Einfluss der Masse der Bretter und der Schraubenfedern soll im Folgenden vernachlässigt werden, die Reibung zunächst noch nicht. Für die Fallbeschleunigung soll der Wert $g=9,81 \dfrac{ \text m }{ s ^2}$ verwendet werden.

Material 3: Federbrett

hessen physik abi gk 2022 aufgabe a1 material 3 pedalo federbrett

3.1

Bestimme die Federkonstante einer einzelnen Schraubenfeder und erläutere den Lösungsweg.

$\bigg[$ zur Kontrolle: $D _{\text {eine Feder }}=3434 \,\dfrac{ \text N }{\text m } \bigg]$

(6 BE)

3.2

Das Federbrett, das mit einer Masse von $70 \,\text {kg}$ gleichmäßig belastet ist, wird nun um weitere $2 \,\text{cm}$ zusammengedrückt und zum Zeitpunkt $t =0 \,s$ losgelassen.

Beschreibe die resultierende Bewegung.

(2 BE)

3.3

Im Folgenden soll die Reibung vernachlässigt werden. Berechne die Schwingungsdauer des mit einer Masse von $70 \,\text{kg}$ belasteten Federbretts.

Entscheide, ob zur Beschreibung der Bewegung aus Aufgabe 3.2 die Schwingungsgleichung in der Form $s(t)=s_0 \cdot \sin (\omega \cdot t)$ oder $s(t)=-s_0 \cdot \cos (\omega \cdot t)$ mit $s _0>0$ verwendet werden muss, und gib die Gleichung mit den konkreten Werten für diesen Fall an.

Skizziere das $t$ - $s$ -Diagramm der Schwingung für $0 s \leq t \leq 1 s.$

(8 BE)

3.4

Untersuche den funktionalen Zusammenhang zwischen der auf das Federbrett aufgelegten Masse und der Schwingungsdauer.

(2 BE)

3.5

Eine als punktförmig angenommene Masse von $35 \,\text{kg}$ wird aus einer Höhe von $h =20 \,\text{cm}$ über dem oberen Holzbrett so auf das unbelastete Federbrett fallen gelassen, dass sie das Federbrett in der Mitte trifft und dort sofort liegen bleibt. Die Masse versetzt das Brett in Schwingung. Hierbei mögliche Energieverluste sollen vernachlässigt werden.

Bestimme die Amplitude der Schwingung und erläutere deinen Lösungsweg.

(6 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

Mechanische Schwingung

Eine mechanische Schwingung beschreibt eine zeitlich periodische Bewegung eines Körpers um dessen Ruhelage. Eine rücktreibende Kraft bringt den Körper stets in die Gleichgewichtslage zurück.

Harmonische Schwingung

Bei einer harmonischen Schwingung ist die rücktreibende Kraft proportional zur Auslenkung und zur Gleichgewichtslage hin gerichtet.
Eine harmonische Schwingung entspricht einem Oszillator, welcher sinusförmig um seine Gleichgewichtslage schwingt und kann somit durch eine sinusförmige Funktion beschrieben werden.

1.2

Beispiele mechanischer Schwingungen:

Federpendel
Feder-Schwere-Pendel
Fadenpendel

Die Körper kehren jeweils nach immer gleichlangen Zeitabschnitten in den gleichen Bewegungszustand zurück.

Schwingungen sind harmonisch für kleine Auslenkungen, wenn der Auslenkwinkel ist kleiner ist als $5^{\circ}.$

2.1

Gegeben: $\; t= 12 \;\text{s}$

Gesucht: $\; T$

Lösung: $\; T=2\cdot t=2\cdot 12 \;\text{s}$ $=24 \;\text{s}$

2.2

Verwendung der Kleinwinkelnäherung beurteilen

Kleinwinkelnäherung:

Näherung bei der $\sin(\alpha)$ durch den Winkel $\alpha$ selbst im Bogenmaß ersetzt wird.
Bietet sich gut für Winkel $\alpha \lt 5^{\circ}$ an.

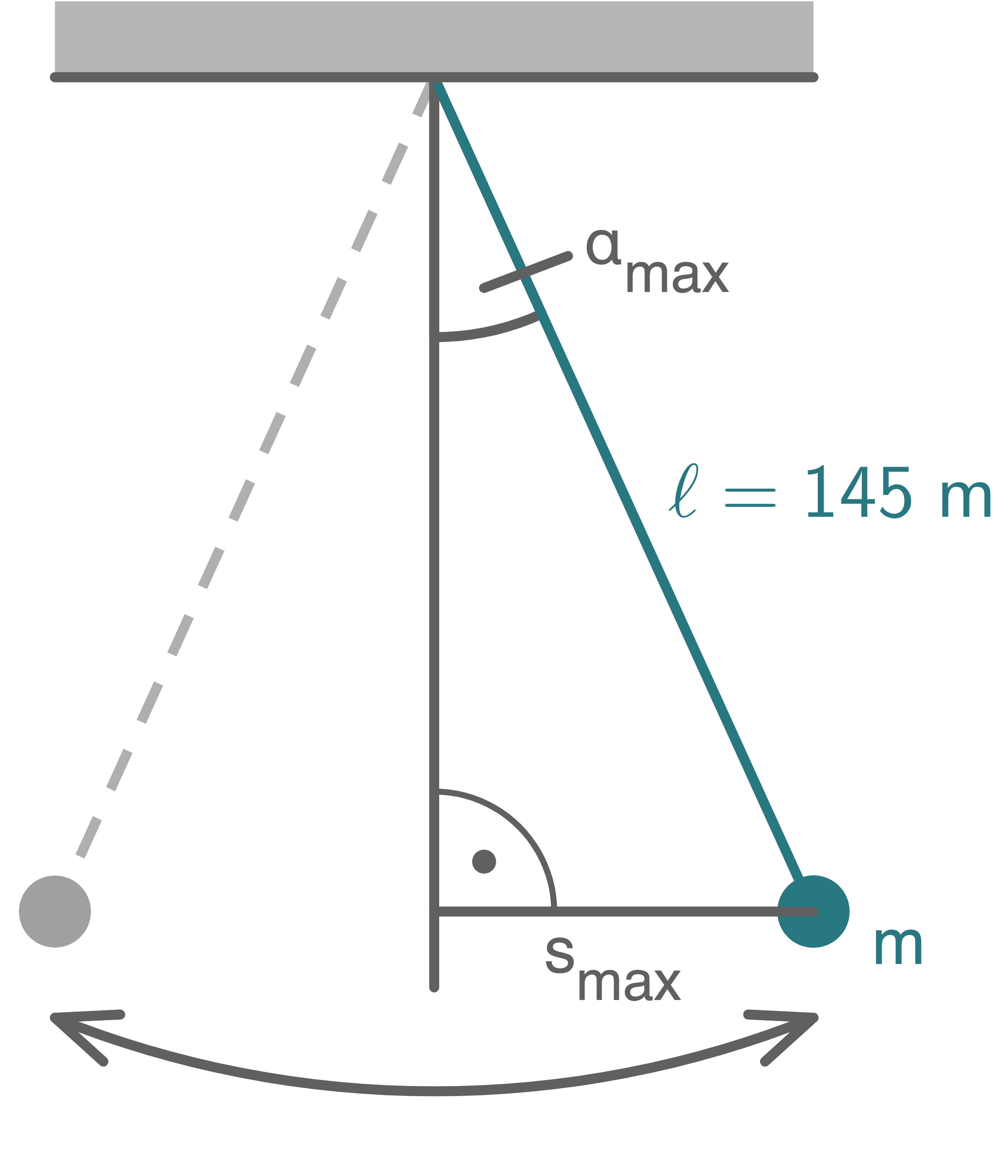
Gegeben: $\;s_{\text{max}}= \dfrac{ s_{\text{hor}}}{2}= 6 \;\text{m},$ $\ell = 145 \;\text{m}$

Gesucht: $\;\alpha_{\text{max}}$

Lösung: Da es sich um ein rechtwinkliges Dreieck handelt, folgt aus der Winkelfunktion:

$\begin{array}[t]{rll} \sin (\alpha_{\max })&=& \frac{\text {Gegenkathete}}{\text { Hypotenuse }} \\[5pt] &=& \dfrac{s_{\max }}{\ell} \\[5pt] &=& \dfrac{6 \; \text{m} }{145\; \text{m}}\\[5pt] \sin (\alpha_{\max })&=& 0,0414 &\quad \scriptsize \mid\;\sin^{-1}\\[5pt] \alpha_{\max }& \approx & 2,37^{\circ} \end{array}$

Hilfsskizze (nicht maßstabsgetreu)

Somit kann die Kleinwinkelnäherung gut verwendet werden.

Harmonische Schwingung beurteilen

Die Auslenkung ist klein genug, weswegen die Bogenlänge der Auslenkung durch $s_{\max}$ angenähert wird.

Für den Betrag der rücktreibenden Kraft $F_R$ gilt:

$\begin{array}[t]{rll} F_R&=&F_G \cdot \sin (\alpha) \\[5pt] &=& F_G \cdot \dfrac{s_{\max}}{\ell} \\[5pt] &=&\dfrac{ m \cdot g }{\ell} \cdot s_{\max} \end{array}$

Für kleine Auslenungen ist die rücktreibende Kraft proportional zur Auslenkung $(F_R \sim s).$

Somit kann der Kran als ein harmonisch schwingendes Fadenpendel gesehen werden.

2.3

Seillänge überprüfen

Gegeben: $T= 24\;\text{s},$ $g$

Gesucht $\ell$

Lösung:

$\begin{array}[t]{rll} T&=& 2 \pi \cdot \sqrt{\dfrac{\ell}{ g }}&\quad \scriptsize \mid\;: 2 \pi \\[5pt] \dfrac{T}{2 \pi}&=& \sqrt{\dfrac{\ell}{ g }} &\quad \scriptsize \mid\;(\;)^2 \\[5pt] \dfrac{T^2}{4 \pi^2}&=& \dfrac{\ell}{ g }&\quad \scriptsize \mid\;\cdot g \\[5pt] \dfrac{T^2}{4 \pi^2}\cdot g&=& \ell \\[5pt] \ell&=&\dfrac{T^2\cdot g }{4 \pi^2} \\[5pt] \ell&=&\dfrac{(24 s )^2 \cdot 9,81 \frac{\text{m}}{\;\text{s}^2}}{4 \pi^2} \\[5pt] &=& 143 \;\text{m} \end{array}$

Prozentuale Abweichung

$\dfrac{145\;\text{m} -143 \;\text{m}}{145 \;\text{m}}$ $=0,014 =1,4 \%$

Mögliche Ursache der Abweichung

Messungenauigkeiten bei der Bestimmung der Seillänge
Messungenauigkeiten bei der Bestimmung der Schwingungsdauer

2.4

Potenzielle Energie der Gondel im Umkehrpunkt:

$E _{pot,\max }= m \cdot g \cdot h$

Für die Höhe $h$ folgt

$\begin{array}[t]{rll} x + h &=& \ell \\[5pt] h&=& \ell -x \end{array}$

$x$ ergibt sich aus den Beziehungen im rechtwinkligen Dreieck:

$\begin{array}[t]{rll} \cos (\alpha_{\max })&=& \dfrac{\text { Ankathete }}{\text { Hypotenuse }}\\[5pt] &=&\dfrac{ x }{\ell} &\quad \scriptsize \mid\;\cdot \ell \\[5pt] \cos (\alpha_{\max })\cdot \ell&=& x \\[5pt] x &=&\ell\cdot \cos (\alpha_{\max }) \end{array}$

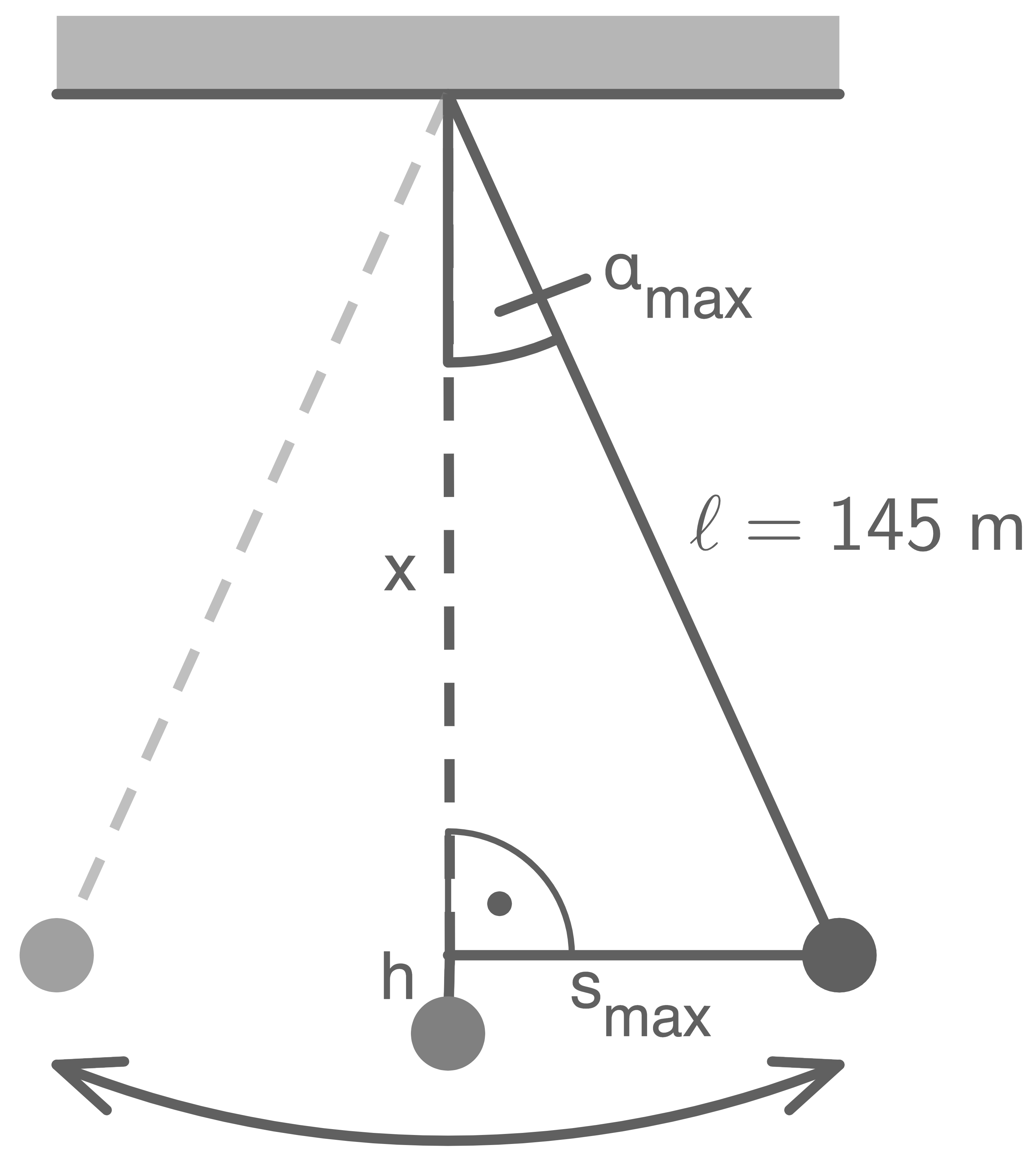
Hilfsskizze

Für die Höhe $h$ folgt somit:

$\begin{array}[t]{rll} h&=& \ell-\ell \cdot \cos \alpha_{\max } \\[5pt] &=& 145 \;\text{m} -145 \;\text{m} \cdot \cos (2,37^{\circ}) \\[5pt] &=& 0,124 \;\text{m} \end{array}$

Daraus ergibt sich die maximale potenzielle Energie zu:

$E _{pot,\max} =100 \cdot 10^3 \;\text{kg} \cdot 9,81 \frac{\text{m}}{\text{s} ^2} \cdot 0,124 \;\text{m}$ $=1,22 \cdot 10^5 \;\text{J} =122 \;\text{kJ}$

Geschwindigkeit beim Durchgang durch die Ruhelage

Beim Durchlaufen der Gleichgewichtslage gilt:

$E _{ kin,\max }=E _{ pot , \max }$

Rechenweg anzeigen

$v _{\max }\approx 1,56 \;\frac{\text{m}}{\text{s}}$

2.5

Einfluss der Verkürzung der Seillänge

Betrachtung der Formel:

$\begin{array}[t]{rll} T&=& 2 \pi \cdot \sqrt{\dfrac{\ell}{g}} \\[5pt] &=& 2 \pi \cdot \dfrac{\sqrt{\ell}}{\sqrt{g}} \\[5pt] &=& 2 \pi \cdot \sqrt{\ell}\cdot \dfrac{1}{\sqrt{g}} \end{array}$

Wird die Seillänge verkürzt, also $\ell$ kleiner, so wird auch $\ell$ kleiner, somit nimmt der gesamte Term einen kleineren Wert an und auch $T$ wird kleiner.

Die Schwingungdauer $T$ des Fadenpendels ist proportional zu $\ell,$ also $T \sim \sqrt{\ell}.$

Daraus folgt: Wenn die Seillänge $\ell$ verkürzt wird, dann verringert sich die Schwingungsdauer $T.$

Verringerung der Amplitude

Wird der Aufhängepunkt des Seils in Richtung der der momentanen Auslenkung der Last verschoben, überlagern sich die Bewegungen längs des Auslenkers und der Drehbewegung senkrecht zum Auslenker. Infolgedessen wird die Gleichgewichtslage des Pendels verschoben in Richtung der momentanen Position. Deswegen wird die rücktreibende Kraft geringer und somit verringert sich die Amplitude der Schwingung.

3.1

Für die Federkonstante gilt: $D=\dfrac{ F }{\Delta s }$

In diesem Fall gilt $F= F_G= m \cdot g.$ Und somit folgt:

$D=\dfrac{ m \cdot g }{\Delta s }=\dfrac{70\;\text{kg} \cdot 9,81 \frac{ \text{m} }{ \text{s} }}{0,05 \; \text{m} }=13734 \; \frac{\text{N} }{ \text{m} }$

Das System besteht aus vier gleichen Federn, auf die sich die Gewichtskraft der Masse gleichmäßig verteilt. Somit entspricht die Federkonstante einer einzelenen Schraubenfeder:

$D_{\text{eine Feder}}=\dfrac{1}{4} \cdot D =\dfrac{1}{4} \cdot 13734 \frac{ N }{ m }=3434 \; \frac{\text{N} }{ \text{m} }$

3.2

Das Federbett wird aus der Ruhelage des unbelasteten Bretts ausgelenkt. Die Ruhelage des belasteten Bretts liegt $5 \;\text{cm}$ unterhalb der Ruhelage des unbelasteten Bretts.

Bei einer Auslenkung um $2 \;\text{cm},$ beginnt eine harmonische Schwingung. Die Schwingung verläuft zunächst nach oben, durch die Ruhelage, bis zum Umkehrpunkt und dann nach unten durch die Ruhelage zum unteren Umkehrpunkt.

Aufgrund der Reibung liegt der obere Umkehrpunkt weniger als $2 \;\text{cm}$ über der neuen Ruhelage. Der Vorgang wiederholt sich, allerdings werden die Schwingungen geringer, bis das Brett schlussendlich in der neuen Ruhelage zum Stillstand kommt.

3.3

$\begin{array}[t]{rll} T&=& 2 \pi \cdot \sqrt{\dfrac{ m }{ D _{ ges }}} \\[5pt] &=& 2 \pi \cdot \sqrt{\dfrac{70\;\text{kg}}{13734 \dfrac{ \text{N}}{ \text{m} }}} \end{array}$

Das belastete Federbrett wird ausgelenkt und im unteren Umkehrpunkt losgelassen. Danach schwingt es nach oben. Der zur Bewegung passende Graph der Sinusfunktion schneidet zunächst die $y$ -Achse in einem Tiefpunkt (unterer Umkehrpunkt), steigt dann monoton, schneidet die $x$ -Achse (Gleichgewichtslage) und steigt dann weiter monoton zum Hochpunkt (oberer Umkehrpunkt). Dies entspricht dem Verlauf des Graphen der zweiten Funktionsgleichung $s ( t )=- s _0 \cdot \cos (\omega \cdot t ) \quad \text { mit } s _0.$

Somit ergibt sich die Schwingungsgleichung zu:

$s(t)=-0,02\;\text{m} \cdot \cos \left(14 \frac{1}{ s } \cdot t \right)$

$t$ - $s$ -Diagramm

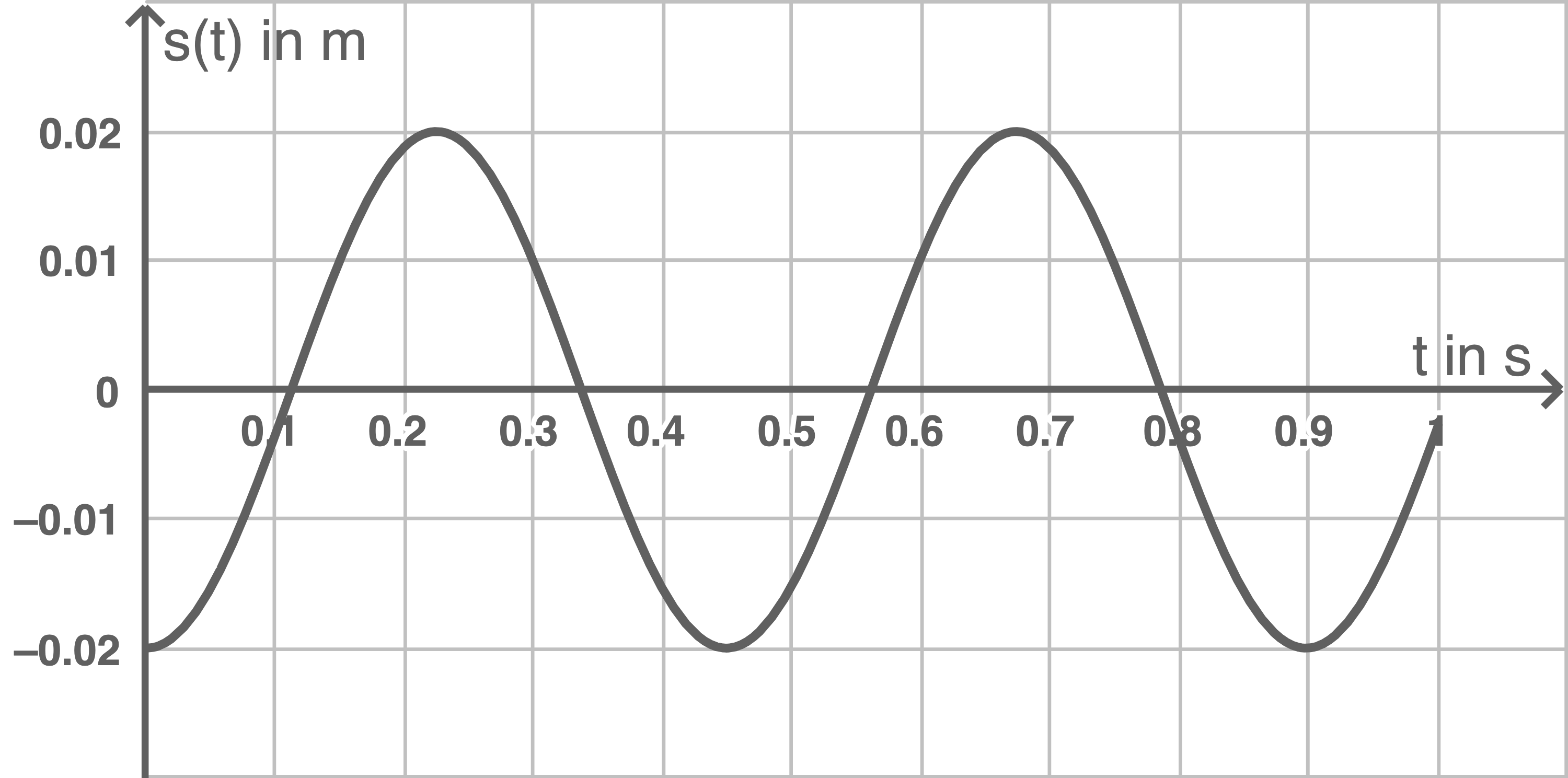
3.4

Es gilt: $T =2 \pi \cdot \sqrt{\frac{ m }{D}}$

Daraus folgt, dass $T$ proportional zu $\sqrt{ m }.$

Daraus folgt $T \sim \sqrt{ m }$ und $m \sim T ^2.$

Folglich ändert sich die aufgelegte Masse quadratisch mit der Schwingungsdauer.

3.5

Im unteren Umkehrpunkt gilt:

$E _{ pot , ges } = E _{\text {Spann }}$

Rechenweg anzeigen

$s _{\max }^2-\dfrac{2\cdot m\cdot g}{D}\cdot s _{\max}$ $=\dfrac{2\cdot m\cdot g\cdot( h) }{D}$

Diese quadratische Gleichung für $s _{\max }$ wird durch quadratische Ergänzung gelöst: Dabei wird auf beiden Seiten der Gleichung den Term $\left(\dfrac{ m \cdot g }{ D }\right)^2$ addiert und die zweite binomische Formel angewandt:

Rechenweg anzeigen

$s _{\max 1,2} =\frac{ m \cdot g }{ D } \pm \sqrt{\frac{2 m \cdot g \cdot h }{ D }+\left(\frac{ m \cdot g }{ D }\right)^2}$

Einsetzen der Werte ergibt:

Rechenweg anzeigen

$s _{\max 1,2}=...$

Daraus folgt: $s _{\max , 1}=0,128 \; \text{m }$ und $s _{\max , 2}=-0,078 \; \text{m }$

Da eine Amplitude nur positive Werte annehmen kann, beträgt die Amplitude $s _{\max }=12,8 \; \text{cm }.$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?