Vorschlag B3
Atommodelle – Termschema von Wasserstoff – Flammenfärbung
1
Von der Antike bis zum Ende des 19. Jahrhunderts bestand die Vorstellung, dass Materie aus massiven, unteilbaren Teilchen, den Atomen (von altgriechisch átomos „unteilbar“), besteht. Erst zu Beginn des 20. Jahrhunderts wurde die Vorstellung vom Aufbau eines Atoms u. a. von den drei Physikern Joseph Thomson, Ernest Rutherford und Niels Bohr grundlegend erweitert.
1.1
Im Material ist die Darstellung eines Atoms nach dem Thomson'schen Atommodell zu sehen.
Beschreibe das Atommodell nach Thomson, das auch als „Rosinenkuchenmodell“ bezeichnet wird.
Atommodell nach Thomson

(2 BE)
1.2
Das Atommodell nach Rutherford wurde durch den folgenden Streuversuch motiviert: Es wurden  -Teilchen (positiv geladene Helium-Atomkerne) auf eine Goldfolie gelenkt. Dabei passierten die meisten
-Teilchen (positiv geladene Helium-Atomkerne) auf eine Goldfolie gelenkt. Dabei passierten die meisten  -Teilchen ungehindert die Folie. Es gab aber auch
-Teilchen ungehindert die Folie. Es gab aber auch  -Teilchen, die seitlich bzw. sogar zurückgestreut wurden.
Erläutere, inwiefern das Thomson'sche Atommodell unzureichend ist, um das Ergebnis des Streuversuchs zu erklären, und gib die Schlussfolgerung aus dem Versuchsergebnis an, die zum Atommodell von Rutherford geführt hat.
-Teilchen, die seitlich bzw. sogar zurückgestreut wurden.
Erläutere, inwiefern das Thomson'sche Atommodell unzureichend ist, um das Ergebnis des Streuversuchs zu erklären, und gib die Schlussfolgerung aus dem Versuchsergebnis an, die zum Atommodell von Rutherford geführt hat.
(4 BE)
1.3
Nenne die Bohr'schen Postulate und gib ein experimentelles Ergebnis an, das mit dem Bohr'schen Atommodell erklärt werden kann.
(6 BE)
2
Aus dem Bohr'schen Atommodell folgt die Formel für die Energieniveaus des Wasserstoffatoms:

2.1
Bestätige mithilfe der Einheiten der Naturkonstanten, dass die Größe  die Einheit einer Energie hat.
die Einheit einer Energie hat.
(4 BE)
2.2
Berechne die niedrigsten 5 Energiezustände eines Wasserstoffatoms in der Einheit  und zeichne das zugehörige Energieniveauschema maßstabsgetreu.
und zeichne das zugehörige Energieniveauschema maßstabsgetreu.
(5 BE)
2.3
Die Spektrallinien der Lyman-Serie entstehen bei Übergängen angeregter Elektronen von einem Energieniveau  in das Energieniveau
in das Energieniveau  Berechne die Energiedifferenzen der drei Übergänge innerhalb der Lyman-Serie, bei denen die Photonen mit den größtmöglichen Wellenlängen emittiert werden, und zeichne die Übergänge in das Energieniveauschema aus Aufgabe 2.2 ein.
Berechne die Energiedifferenzen der drei Übergänge innerhalb der Lyman-Serie, bei denen die Photonen mit den größtmöglichen Wellenlängen emittiert werden, und zeichne die Übergänge in das Energieniveauschema aus Aufgabe 2.2 ein.
(3 BE)
2.4
Wasserstoff-Atome emittieren sichtbares Licht der Wellenlängen  und
und  .
Entscheide, ob diese Spektrallinien zu der Lyman-Serie gehören, und bestimme die Werte der zugehörigen Energieniveaus.
.
Entscheide, ob diese Spektrallinien zu der Lyman-Serie gehören, und bestimme die Werte der zugehörigen Energieniveaus.
(7 BE)
2.5
Ein Wasserstoff-Atom befindet sich im Grundzustand  . Es wird mit Photonen unterschiedlicher Energie bestrahlt:
. Es wird mit Photonen unterschiedlicher Energie bestrahlt: 
 und
und  .
Erörtere, in welchen Fällen eine Reaktion mit dem Wasserstoff-Atom stattfinden kann und welcher Art diese Reaktion jeweils ist.
.
Erörtere, in welchen Fällen eine Reaktion mit dem Wasserstoff-Atom stattfinden kann und welcher Art diese Reaktion jeweils ist.
(6 BE)
2.6
Entfernt man aus der Hülle eines Helium-Atoms ein Elektron, so erhält man ein einfach positiv geladenes  -Ion. Da das
-Ion. Da das  -Ion wie das Wasserstoff-Atom nur ein Hüllenelektron besitzt, kann das Bohr'sche Atommodell angewendet werden.
Begründe, warum die Energie zur vollständigen Ionisation des
-Ion wie das Wasserstoff-Atom nur ein Hüllenelektron besitzt, kann das Bohr'sche Atommodell angewendet werden.
Begründe, warum die Energie zur vollständigen Ionisation des  -Ions größer ist als die Energie zur Ionisation des Wasserstoff-Atoms.
-Ions größer ist als die Energie zur Ionisation des Wasserstoff-Atoms.
(4 BE)
3
Um bei Feuerwerken Flammen zu färben, kommen Stoffe zum Einsatz, die Licht spezifischer Wellenlängen  emittieren, wenn man sie in eine (farblose) Flamme hält. Die Färbung entsteht dadurch, dass Elektronen in einen angeregten Zustand versetzt werden und unter Aussenden eines oder mehrerer Photonen wieder in den Grundzustand zurückkehren. Unter anderem erzeugen Alkalimetalle eine spezifische Flammenfärbung, zum Beispiel Cäsium
emittieren, wenn man sie in eine (farblose) Flamme hält. Die Färbung entsteht dadurch, dass Elektronen in einen angeregten Zustand versetzt werden und unter Aussenden eines oder mehrerer Photonen wieder in den Grundzustand zurückkehren. Unter anderem erzeugen Alkalimetalle eine spezifische Flammenfärbung, zum Beispiel Cäsium  , Lithium
, Lithium  und Kalium
und Kalium  und
und  .
.
3.1
Berechne jeweils die Energien der von Cäsium und Lithium ausgesendeten Photonen in Joule und in Elektronenvolt.
(2 BE)
3.2
Nenne zwei mögliche Erklärungen dafür, dass im Kalium nicht nur eine, sondern zwei Wellenlängen in der spezifischen Flammenfärbung beobachtet werden.
(4 BE)
3.3
Eine Cäsiumplatte (Austrittsarbeit  wird mit gebündeltem Licht einer von Kalium charakteristisch gefärbten Flamme bestrahlt.
Zeige, dass dabei nur eine der Kalium-Wellenlängen den Fotoeffekt im Cäsium auslösen kann.
wird mit gebündeltem Licht einer von Kalium charakteristisch gefärbten Flamme bestrahlt.
Zeige, dass dabei nur eine der Kalium-Wellenlängen den Fotoeffekt im Cäsium auslösen kann.
(3 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.1
Thomson ordnet Teilchen eine innere Struktur zu, welche er mit der eines Rosinenkuchens vergleicht:
- Teig entspricht positiv geladener Masse
- Elektronen (negative Ladung) sind wie Rosinen im Teig verteilt
- Atome sind insgesamt neutral (wie Rosinenkuchen)
1.2
Widersprüche:
- Die meisten
-Teilchen passieren die Folie. Nach Thomson müssten die angenommene positive homogene Atomladung die positiv geladenen
-Teilchen daran hindern, die Atome zu durchdringen, wegen der elektrostatischen Abstoßung.
- Die
-Teilchen werden selten gestreut, in unterschiedlichen Richtungen. Nach Thomson müsste die Streuung wegen der homogenen Verteilung der positiven Ladung verteilt sein bezüglich der Richtung und Intensität.
- Die
-Teilchen werden gestreut, wenn diese einen geringen Anteil Atomvolumen und einen größeren Anteil an Atommasse haben.
- Der größte Teil des Atoms ist leer ist. Darin bewegen sich die Elektronen.
1.3
1. Quantenbedingung:
Die Elektronen laufen auf stabilen Bahnen um den Atomkern. Hierbei bleibt die Energie erhalten. Die Bahnen halten weitere Quantenbedingungen ein und die Energie eines Elektrons kann nur bestimmte Werte annehmen.
2. Frequenzbedingung:
Dass Elektronen die Bahn auf eine höhere wechseln, brauchen sie zusätzliche Energie. Diese folgt durch Absorption, Übergang auf eine höhere Bahn) oder die Elektronen geben Energie durch Emission, um auf eine niedrigere Bahn zu wechseln.
Mit Hilfe eines Photons einer bestimmten Frequenz wird die Energiedifferenz ausgeglichen.
Mit dem Bohr-Modell können drei empirisch gefundenen Serienformeln für Wasserstoff, nämlich die Balmer-, Lyman- und Paschen-Serie, erklärt werden.
2.1
2.2

2.3
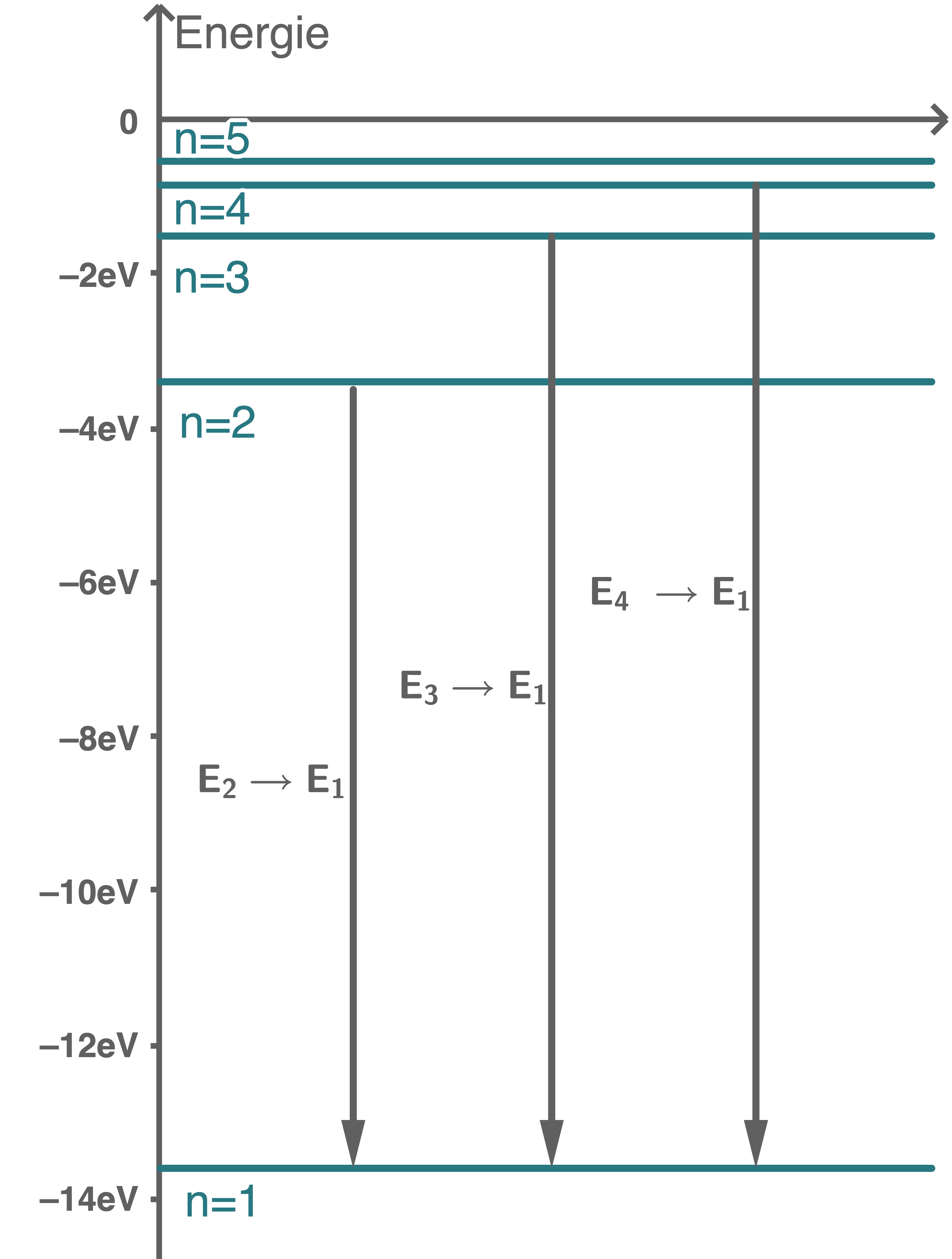
2.4
Es gilt:

 Einsetzen:
Einsetzen:



 Diese Wellenlängen gehören nicht zur Lyman-Serie.
Überprüfung ob die Wellenlängen zur Balmer-Serie gehören:
Diese Wellenlängen gehören nicht zur Lyman-Serie.
Überprüfung ob die Wellenlängen zur Balmer-Serie gehören:





 Die Energiedifferenzen passen ungefähr zu den berechneten Energiedifferenzen.
Die Energiedifferenzen passen ungefähr zu den berechneten Energiedifferenzen.
2.5
Reaktion mit Wasserstoff-Atom: Die Anregungsenergie entspricht genau dem Wert einer Energiedifferenz zwischen zwei Niveaus bzw. die Energie ist größer als die Bindungsenergie des Elektrons.
 Wenn ein Wasserstoff-Atom im Grundzustand mit dieser Energie bestrahlt wird, so passiert nichts. Da die Energie zwischen den Übergangsenergien der beiden Lyman-Übergänge mit
Wenn ein Wasserstoff-Atom im Grundzustand mit dieser Energie bestrahlt wird, so passiert nichts. Da die Energie zwischen den Übergangsenergien der beiden Lyman-Übergänge mit  und
und  liegt, gibt es keine Anregung.
liegt, gibt es keine Anregung.
 Die Energiedifferenz entspricht genau der Energie, die für den Übergang
Die Energiedifferenz entspricht genau der Energie, die für den Übergang  benötigt wird. Das Elektron gelangt in den angeregten Zustand
benötigt wird. Das Elektron gelangt in den angeregten Zustand  da es das Photon absobiert.
da es das Photon absobiert.
 Die Bindungsenergie des Elektrons ist kleiner als die Energie des Photons: Das Atom wird ionisiert und zu einem freien Elektron. Es ergibt sich dadurch die kinetische Energie des Elektrons zu
Die Bindungsenergie des Elektrons ist kleiner als die Energie des Photons: Das Atom wird ionisiert und zu einem freien Elektron. Es ergibt sich dadurch die kinetische Energie des Elektrons zu 

2.6
Das Wasserstoff-Atom hat ein Hüllelektron. Ebenso das Helium-Ion. Die negative Ladung der Hülle ist folglich gleich groß.
Der Kern des Wasserstoff-Atoms besteht aus einem Proton. Der Kern des Helium-Inons besteht aus zwei Protonen und zwei Neutronen. Somit hat das Helium-Ion die doppelte Ladung.
Folglich ist die Bindung des Hüllelektrons an den Heliumkern beim Helium-Ion stärker als an den Wasserstoffkern. Deswegen ist die Ionisierungsenergie des Helium-Ions größer.
3.1
3.2
- Geht das Elektron von einem angeregten Zustand in den Grundzustand über, so kann es in einen metastabilen Zwischenzustand fallen und dann in den Grundzustand. Hierbei sendet es Photon aus, welche kleinere Energien und somit größere Wellenlängen als ein Photon besitzen.
- Eventuell hat das Kalium auch Kalium-Ionen, welche einfach ionisiert sind und wobei das Valenzelektron in der Außenschale fehlt. Kalium-Ionen nehmen andere Energieniveaus an, wodurch Hüllelektronen andere Übergänge erfahren und somit auch Photonen anderer Wellenlängen emittiert werden.
3.3