Vorschlag A2
Hall-Effekt und Induktion in Drehzahlsensoren
In modernen Fahrzeugen findet sich eine Vielzahl von Drehzahlsensoren zum Beispiel für die Bestimmung des richtigen Zündzeitpunkts in einem Benzinmotor oder für die Regelung des Antiblockiersystems (ABS). Das Funktionsprinzip vieler dieser Sensoren beruht auf dem Hall-Effekt, sodass man auch von Hall-Sensoren spricht.
1
Zur Untersuchung der physikalischen Grundlagen des Hall-Effekts wird ein rechteckiges Kupferplättchen mit der Länge  Breite
Breite  und Dicke
und Dicke  verwendet (Material 1). Das Plättchen wird von einem homogenen Magnetfeld durchsetzt, bei dem die Magnetfeldlinien in die Zeichenebene hinein verlaufen.
Die linke Seite des Plättchens ist mit dem Pluspol einer regelbaren Spannungsquelle verbunden, die rechte Seite mit dem Minuspol. Zur Messung der Stromstärke
verwendet (Material 1). Das Plättchen wird von einem homogenen Magnetfeld durchsetzt, bei dem die Magnetfeldlinien in die Zeichenebene hinein verlaufen.
Die linke Seite des Plättchens ist mit dem Pluspol einer regelbaren Spannungsquelle verbunden, die rechte Seite mit dem Minuspol. Zur Messung der Stromstärke  durch das Plättchen wird ein Amperemeter verwendet. Zwischen den beiden Anschlüssen oben und unten wird die Spannung
durch das Plättchen wird ein Amperemeter verwendet. Zwischen den beiden Anschlüssen oben und unten wird die Spannung  gemessen.
gemessen.
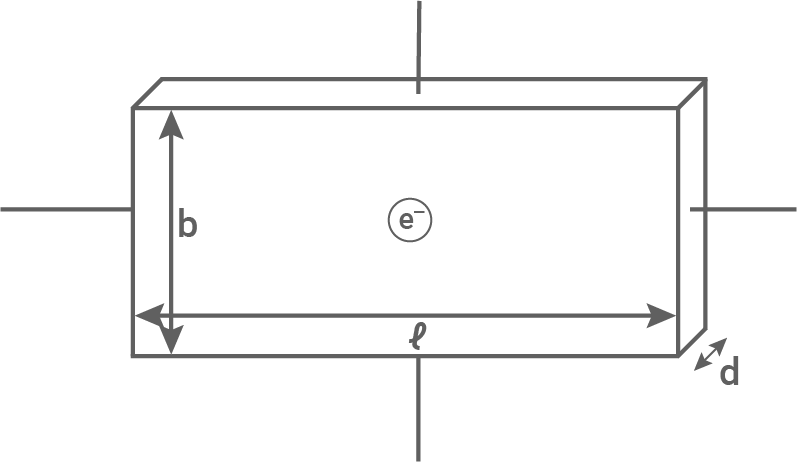
Material 1: Kupferplättchen zur Untersuchung des Hall-Effekts

1.1
Zeichne in Material 1 die fehlenden Leitungen, die Spannungsquelle mit Angabe der Polung, das Amperemeter, das Voltmeter und einige Magnetfeldlinien ein.
(4 BE)
1.2
Zeichne in Material 1 die Kräfte ein, die auf das in der Mitte dargestellte, bewegte Elektron wirken.
Erläutere das Entstehen einer konstanten Hall-Spannung.
(7 BE)
1.3
Dieser Aufbau eignet sich, um die magnetische Flussdichte  des Magnetfelds mit (1)
des Magnetfelds mit (1)  zu bestimmen. Dabei ist
zu bestimmen. Dabei ist  die Hall-Spannung,
die Hall-Spannung,  die Breite des Plättchens und
die Breite des Plättchens und  die konstante Driftgeschwindigkeit der Elektronen.
Leite diese Formel her.
die konstante Driftgeschwindigkeit der Elektronen.
Leite diese Formel her.
(4 BE)
1.4
Mit dem Voltmeter wird eine Hall-Spannung von  bestimmt.
Berechne mit den angegebenen Werten die magnetische Flussdichte
bestimmt.
Berechne mit den angegebenen Werten die magnetische Flussdichte  unter der Annahme, dass die Driftgeschwindigkeit der Elektronen
unter der Annahme, dass die Driftgeschwindigkeit der Elektronen  beträgt.
beträgt.
(3 BE)
2
Die Hall-Spannung  kann mit der Formel (2)
kann mit der Formel (2)  berechnet werden.
berechnet werden.  ist die Hall-Konstante des verwendeten Materials und
ist die Hall-Konstante des verwendeten Materials und  seine Dicke.
seine Dicke.  ist die Stromstärke und
ist die Stromstärke und  die magnetische Flussdichte.
die magnetische Flussdichte.
2.1
Die Gesamtzahl  der freien Elektronen geteilt durch das Volumen
der freien Elektronen geteilt durch das Volumen  des Plättchens ist die Ladungsträgerdichte
des Plättchens ist die Ladungsträgerdichte  des Materials.
Leite die Beziehung
des Materials.
Leite die Beziehung  unter Verwendung der Gleichungen (1) und (2) her.
Zeige mithilfe von Gleichung (2), dass die Hall-Konstante die Einheit
unter Verwendung der Gleichungen (1) und (2) her.
Zeige mithilfe von Gleichung (2), dass die Hall-Konstante die Einheit  hat.
hat.
(7 BE)
2.2
Die Hall-Spannung wird nun mit einem Plättchen aus einem unbekannten Material erzeugt. Die Dicke des Plättchens beträgt  und das Magnetfeld hat eine Flussdichte von
und das Magnetfeld hat eine Flussdichte von  Die Hall-Spannung wird in Abhängigkeit von der Stromstärke gemessen. Die Ergebnisse sind in Material 2a zu sehen.
Ermittle unter Verwendung aller Messwerte und Material 2b, aus welchem Material das Plättchen besteht.
Die Hall-Spannung wird in Abhängigkeit von der Stromstärke gemessen. Die Ergebnisse sind in Material 2a zu sehen.
Ermittle unter Verwendung aller Messwerte und Material 2b, aus welchem Material das Plättchen besteht.
Material 2
a) Messwerttabelle
| Stromstärke |
Hall-Spannung |
|---|---|
| 10 | 112 |
| 15 | 170 |
| 20 | 229 |
| 25 | 281 |
b) Hall-Konstanten verschiedener Materialien
| Material | Hall-Konstante |
|---|---|
| Kupfer | |
| Silber | |
| Aluminium | |
| Bismut | |
| Indiumantimonid | |
| Germanium | |
| Silizium |
(5 BE)
3
Nun soll ein Hall-Sensor betrachtet werden, mit dem die Drehzahl des Blendenrotors gemessen werden kann (Material 3). Wenn sich der Rotor dreht, so bewegen sich die das Magnetfeld abschirmenden Blenden und die Lücken abwechselnd durch den Spalt zwischen Hall-Sensor und Dauermagnet.
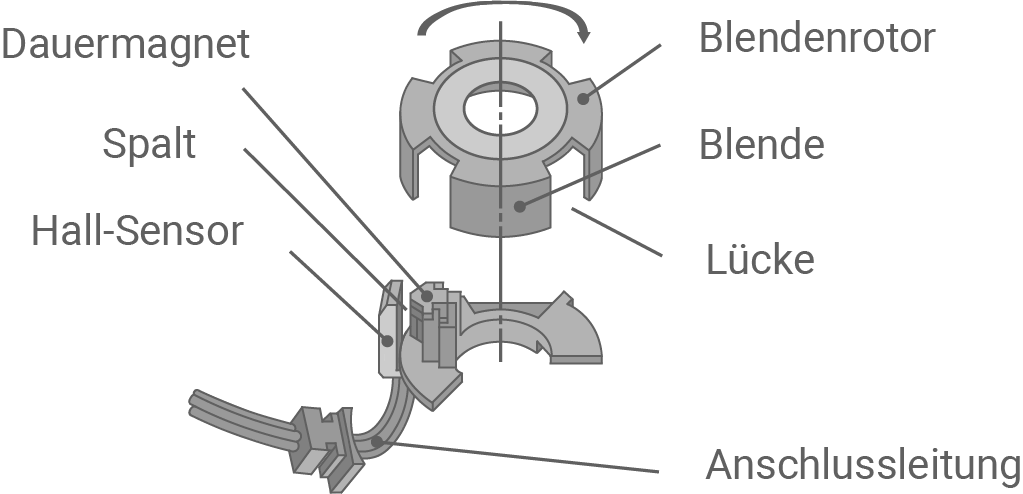 b) Fotografie
b) Fotografie

Material 3: Hall-Sensor mit Blendenrotor
a) Schematischer Aufbau

3.1
Erkläre das Zustandekommen des Verlaufs der Hall-Spannung bei konstanter Drehfrequenz (Material 4), insbesondere auch die Form des Anstiegs und Abfalls der Spannung.
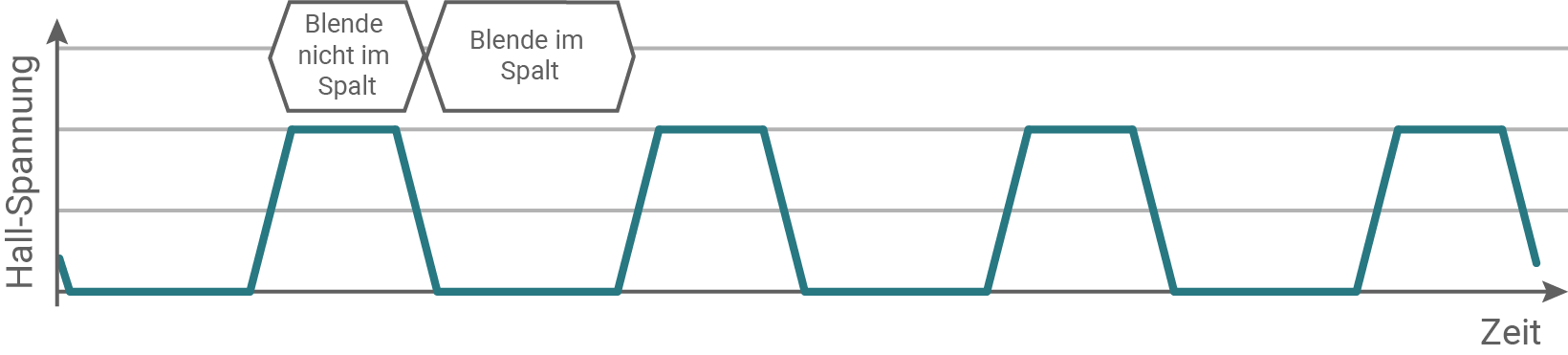
Material 4: Verlauf der Hall-Spannung mit Position der Blenden

(4 BE)
3.2
Die Zeit zwischen zwei aufeinanderfolgenden Anstiegen der Hall-Spannung in Material 4 beträgt  Berechne mithilfe von Material 3 die Drehzahl des Blendenrotors in Umdrehungen pro Minute.
Berechne mithilfe von Material 3 die Drehzahl des Blendenrotors in Umdrehungen pro Minute.
(3 BE)
4
Neben den Hall-Sensoren, die eine Spannungsversorgung benötigen, kommen auch induktive Sensoren zum Einsatz, die keine Spannungsversorgung erfordern.
Induktion tritt auf, wenn eine Leiterschleife im Magnetfeld rotiert (Material 5).
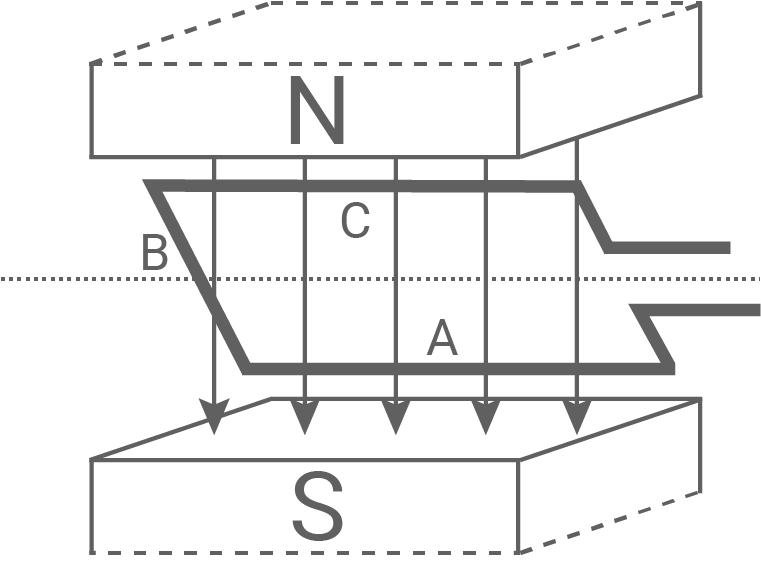
Material 5: Rotierende Leiterschleife im Magnetfeld mit Bezeichnung der Schleifenabschnitte A, B und C

4.1
Erkläre die Entstehung der Induktionsspannung zwischen den Enden der Schleife, indem die Kraft auf jeweils ein Elektron in jedem Leiterstück 
 und
und  betrachten.
betrachten.
(4 BE)
4.2
Die Induktionsspannung, die bei Rotation der Leiterschleife in Material 5 entsteht, ist eine Wechselspannung.
Berechne die maximale Induktionsspannung bei einer Drehfrequenz von  einer magnetischen Flussdichte von
einer magnetischen Flussdichte von  und einer quadratischen Leiterschleife mit der Kantenlänge
und einer quadratischen Leiterschleife mit der Kantenlänge 
(5 BE)
4.3
Bei einem Drehzahlsensor, wie er in Material 6 dargestellt ist, dreht sich ein Zahnrad aus Eisen an einem Eisenkern vorbei, der von einer Induktionsspule umgeben ist. Am anderen Ende des Eisenkerns befindet sich ein Dauermagnet. In der Induktionsspule entsteht eine Wechselspannung, deren Frequenz Rückschlüsse auf die Drehzahl des Zahnrads zulässt.
Erkläre die physikalischen Zusammenhänge, die diesem Messprinzip zugrunde liegen, und erkläre, dass so die Drehzahl bestimmt werden kann.
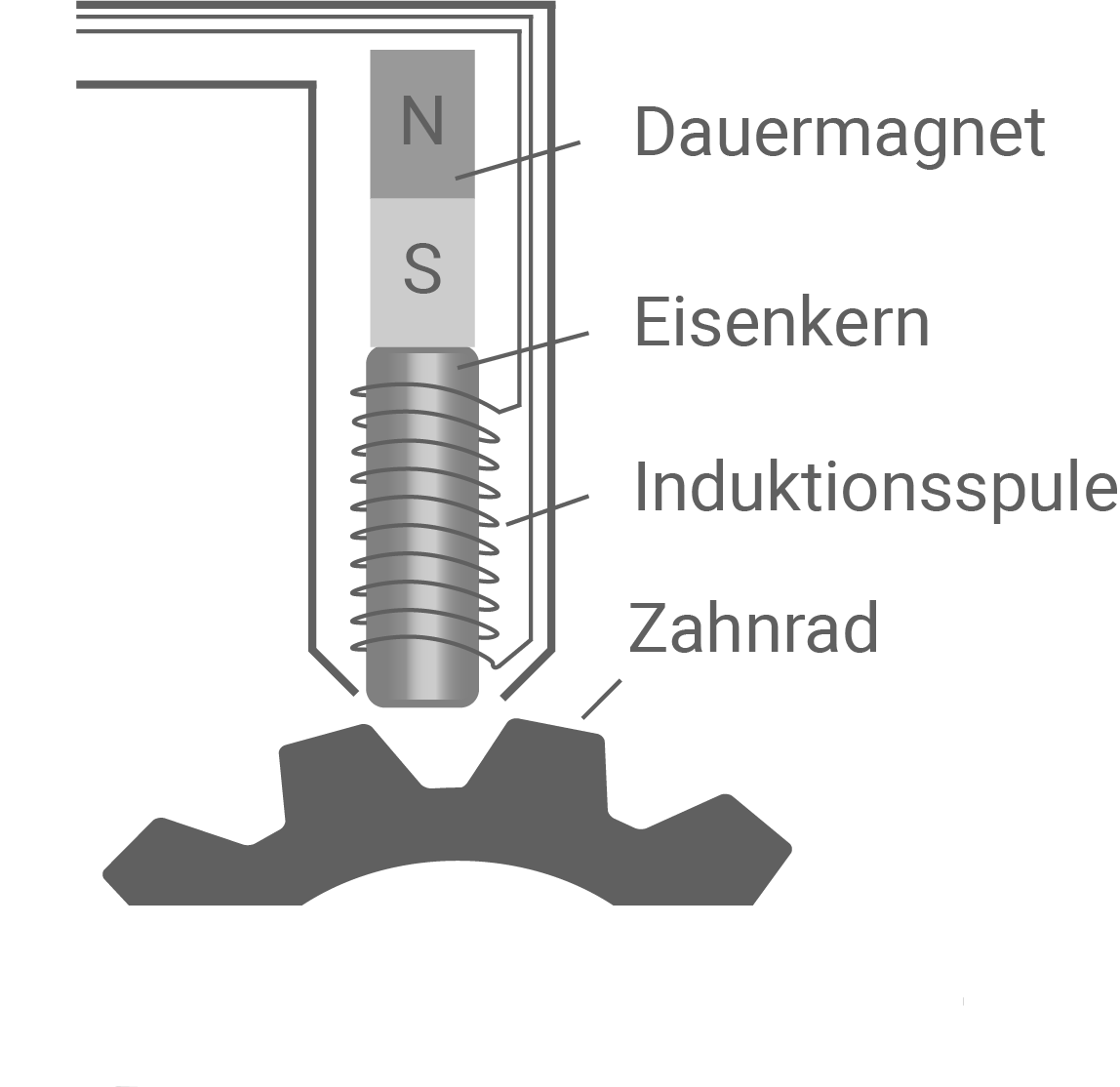
Material 6: Induktiver Drehzahlsensor

(4 BE)
1.1
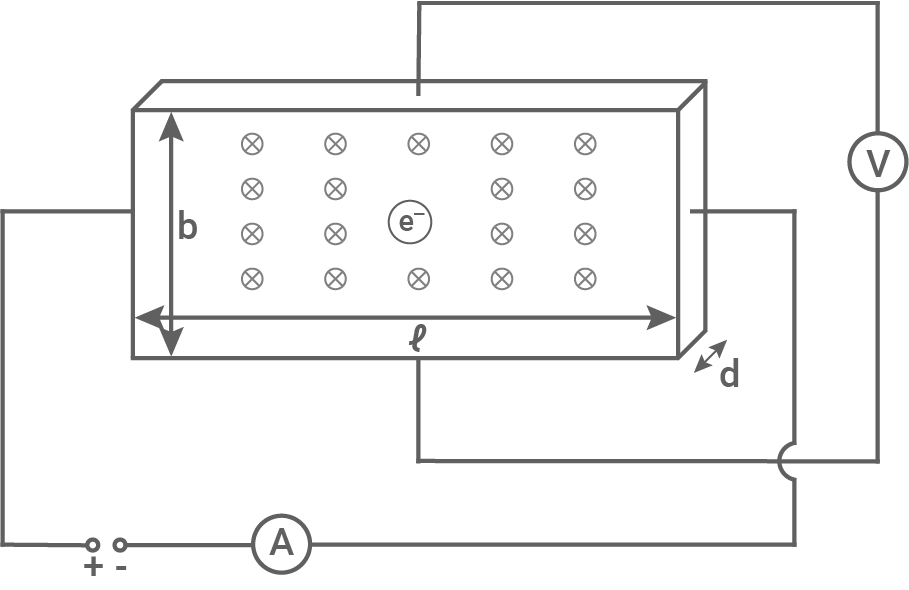
1.2

1.3
1.4
2.1
2.2
Für jedes Messwertpaar lässt sich mit Hilfe von (2) die Hall-Konstante berechnen.
![\(\begin{array}[t]{rll}
U_H&=& R_H \cdot \dfrac{ I \cdot B }{ d } &\quad \scriptsize \mid\;\cdot \dfrac{d }{ I \cdot B} \\[5pt]
\dfrac{U_H\cdot d }{ I \cdot B}&=& R_H\\[5pt]
R_H&=& \dfrac{U_H\cdot d }{ I \cdot B}
\end{array}\)](https://www.schullv.de/resources/formulas/5af13781537f7376d1e1621092727813fb3a195df2bbabffd027743db35f5651_light.svg) Ergänzen der Messwerttabelle:
Ergänzen der Messwerttabelle:
Mittelwert:


 Somit handelt besteht das Plättchen aus Silizium.
Somit handelt besteht das Plättchen aus Silizium.
| Stromstärke |
Hall-Spannung |
Hall-Konstante |
|---|---|---|
| 10 | 112 | 7,9 |
| 15 | 170 | 8,0 |
| 20 | 229 | 8,1 |
| 25 | 281 | 7,9 |
3.1
Der Hall-Sensor ist zusammen mit einem Permanentmagneten auf einer Grundplatte montiert, die sich drehbar in einem Gehäuse befindet. Zwischen dem Sensor und dem Permanentmagneten liegt ein Spalt vor. Der Blendenrotor, der sich dreht, enthält Lücken, durch die das Magnetfeld freigegeben wird, und Blenden, die das Magnetfeld abschatten.
Wenn sich die metallische Blende im Spalt befindet, wird das Magnetfeld des Permanentmagneten abgeschirmt. Dadurch bricht die magnetische Flussdichte zusammen und die Hall-Spannung nimmt ab. Sobald sich wieder eine Lücke zwischen der Hall-Sonde und dem Permanentmagneten befindet, wird das Magnetfeld nicht mehr abgeschirmt und die Hall-Spannung baut sich wieder auf.
Der Blendenrotor dreht sich mit konstanter Geschwindigkeit, sodass die Blenden mit konstanter Geschwindigkeit zwischen der Sonde und dem Magneten vorbeigleiten. Die Hall-Spannung, die gemäß (2) proportional zur magnetischen Flussdichte B ist, nimmt also linear zu, wenn eine Lücke in den Spalt gelangt, und nimmt linear ab, wenn sich eine Blende in den Spalt bewegt.
3.2
4.1
Ein Elektron, das sich in einem magnetischen Feld bewegt, erfährt die Lorentzkraft. Die Richtung dieser Kraft kann mit der Drei-Finger-Regel der linken Hand bestimmt werden. Wenn die Feldlinien des magnetischen Feldes senkrecht zur Bewegungsrichtung des Elektrons stehen, wirkt die Lorentzkraft ebenfalls senkrecht zum Magnetfeld und zur Bewegungsrichtung.
Bei einer rotierenden Leiterschleife entsteht die Bewegung der Elektronen durch die Rotation. Aus diesem Grund wirkt auf die Elektronen in den Leiterstücken A und C eine Kraft, die parallel zum Leiter verläuft. Aufgrund der entgegengesetzten Bewegungsrichtung der Elektronen sind diese Kräfte an A und C immer entgegengesetzt gerichtet. Dadurch entsteht eine Spannung zwischen den Enden der Leiterschleife.
Im Leiterstück B wirkt die Lorentzkraft immer senkrecht zum Leiter. Daher trägt diese Kraft nicht zum Stromfluss in der Schleife be
4.2
4.3
Der Dauermagnet wird verwendet, um den Eisenkern in der Induktionsspule zu magnetisieren, wodurch im Inneren der Spule ein magnetisches Feld entsteht. Wenn sich ein Zahn des Zahnrades gegenüber dem Eisenkern befindet, wird das Magnetfeld verstärkt. Sobald jedoch eine Zahnlücke in die Nähe des Eisenkerns gelangt, wird das Magnetfeld wieder abgeschwächt. Dadurch ändert sich die magnetische Flussdichte im Laufe der Messzeit. Diese Änderung führt zur Induktion einer Spannung in der Induktionsspule. Die Vorzeichenänderung dieser Induktionsspannung hängt von der Änderung der magnetischen Flussdichte ab. Wenn ein Spannungsmessgerät angeschlossen ist, würde es eine Wechselspannung anzeigen. Die Frequenz dieser Wechselspannung wird durch den Wechsel der Zähne und Lücken des Zahnrades bestimmt. Indem man die Anzahl der Zähne des Zahnrades kennt, kann man die Drehzahl des Zahnrades bestimmen.