Vorschlag B1 – Materialprüfungsverfahren mittels Pendelschwingungen

Materialprüfungsverfahren sind in der Industrie nötig, um bestimmte Zertifizierungen zu erhalten. Ein Verfahren zur Prüfung von Oberflächen basiert auf einem Pendel

Im Folgenden soll zunächst ein Fadenpendel der Länge $\ell$ mit einer punktförmigen Masse $m =200 \,\text g$ und der Schwingungsdauer $T =1,40 \, \text{s}$ untersucht werden (Material 1). Es gilt die Kleinwinkelnäherung, sodass von einer harmonischen Schwingung ausgegangen werden kann. Das Pendel wird aus der Ruhelage ausgelenkt und zum Zeitpunkt $t=0 \, \text{s}$ losgelassen. Die Schwingung wird als ungedämpft betrachtet.

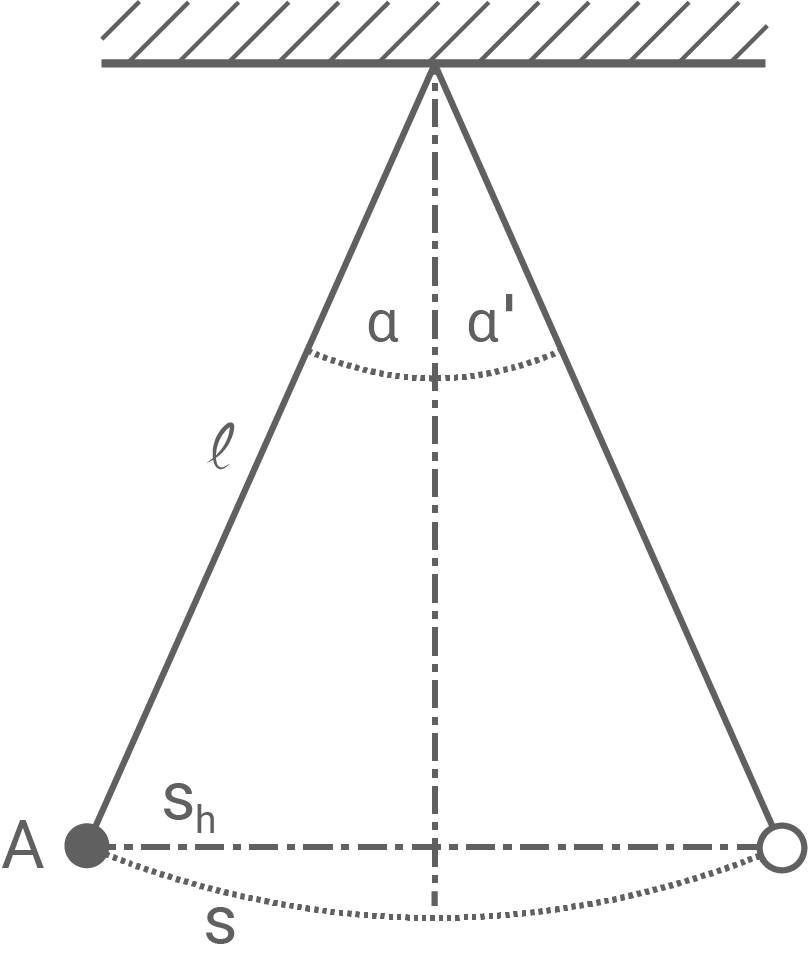
Material 1: Schematische Darstellung eines Fadenpendels

1.1

Zeichne in Material 1 an der mit $A$ gekennzeichneten Stelle die Kraftpfeile der wirkenden Kräfte im richtigen Größenverhältnis ein und beschrifte diese mit den Bezeichnungen Rückstellkraft $\vec{F}_\text R$ , Gewichtskraft $\vec{ F}_\text G$ und Fadenkraft $\vec{ F}_{\ell}.$

(4 BE)

1.2

Zeige, dass bei der Auslenkung des Pendels um die Strecke $s$ für die Rückstellkraft gilt:

$F_\text R=-D \cdot s$

mit der Richtgröße $D=\dfrac{ m \cdot g }{\ell}.$

(5 BE)

1.3

Leite ausgehend von der Formel $F_\text R=-D \cdot s$ aus Aufgabe 1.2 eine Differenzialgleichung für eine ungedämpfte harmonische Schwingung her.

Leite daraus mit einem geeigneten Lösungsansatz das Zeit-Beschleunigung-Gesetz und damit eine Formel zur Berechnung der Schwingungsdauer $T$ eines ungedämpften Fadenpendels her.

(6 BE)

1.4

Berechne die Länge des Pendels und die Amplitude der Schwingung für einen Auslenkungswinkel von $\alpha=6^{\circ}.$

[zur Kontrolle: $\ell=0,487 \,\text m$ ]

(5 BE)

1.5

Erläutere, insbesondere unter Betrachtung der Zeitpunkte $t =0 \; \text{s}, t =\dfrac{1}{4} \,T$ und $t=\dfrac{1}{2} \; T,$ die Energieformen und ihre Umwandlung im Laufe einer halben Schwingung.

(4 BE)

1.6

Berechne die maximale kinetische Energie und die maximale Geschwindigkeit des Pendels unter Verwendung der Werte aus Aufgabe 1.4.

Begründe anhand einer Formel, dass die maximale Geschwindigkeit des Pendels nicht von seiner Masse abhängt.

(7 BE)

1.7

Erkläre qualitativ, wie sich die Schwingungsdauer ändert, wenn das Pendel auf dem Mond schwingen würde.

Beschreibe, wie man den Ortsfaktor des Mondes mithilfe des Pendels bestimmen könnte.

Erkläre, wie man ohne die Verwendung besserer Messgeräte die Genauigkeit der Messung erhöhen könnte.

(4 BE)

Mit einem speziellen Verfahren wird die Oberfläche eines Materials geprüft. Hierbei wird ein genormtes Pendel mit zwei Auflagekugeln aus Edelstahl auf der Probe, deren Oberfläche geprüft werden soll, positioniert (Material 2). Das Pendel wird um einen Winkel $\alpha_{\max , 0}$ ausgelenkt und zum Zeitpunkt $t=0 \, \text{s}$ losgelassen. Die Messung ist mit Abschluss derjenigen vollständigen Schwingung beendet, in der der maximale Auslenkungswinkel erstmals einen Wert $\alpha_{\text {max, Ende}}$ unterschreitet. Die Anzahl der vollständigen Pendelschwingungen bis zu diesem Zeitpunkt wird Pendelhärte der Oberfläche genannt (Information zum Begriff der Pendelhärte siehe Material 3). Dabei beträgt die für die Messung relevante Pendellänge $\ell=0,490 \,\text m$ und die Periodendauer wiederum $T =1,40 \,\text{s}$ . Die Messung beginnt mit einem Auslenkungswinkel von $\alpha_{\max , 0}=6^{\circ}$ und endet nach Unterschreiten des Winkels $\alpha_{\max, \text{Ende}} =3^{\circ}$ . Die Variable $y(t)$ beschreibt die zeitabhängige horizontale Auslenkung des Pendels.

Die Messwerttabelle in Material 4 zeigt die Abhängigkeit der Amplitude $y _{\max }$ von der Zeit während dieser Messung.

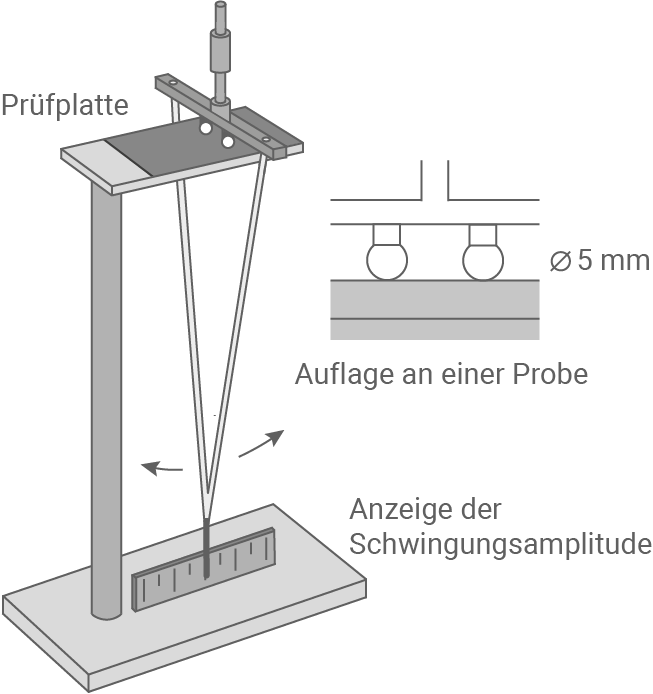
Material 2: Aufbau eines Oberflächenhärtemessgeräts

Material 3: Information zum Begriff der Pendelhärte

Das hier betrachtete Messverfahren wird üblicherweise zur Beurteilung des plastischelastischen Verhaltens von Beschichtungen, also z.B. von Lacken, Farben oder Grundierungen verwendet. Alle Beschichtungen zeigen ein elastisches Materialverhalten und sind somit nicht „hart“ wie man das im ersten Moment denken könnte. Der Begriff der Härte ist auf diesem Gebiet nach DIN 55945 definiert als „der Widerstand einer Beschichtung gegen eine mechanische Einwirkung wie z.B. Druck, Reiben oder Ritzen“. Dazu werden verschiedene Testverfahren genutzt, eines davon basiert auf dem in Material 2 gezeigten Aufbau.

Material 4: Messwerttabelle

$\color{#fff}n$	$\color{#fff}y_{\color{#fff}{\max, n}}$ in $\color{#fff}{\text{m}}$
0	0,051
20	0,044
40	0,038
60	0,033
80	0,028
100	0,024

$n$ : Anzahl der Schwingungen; $y _{\max , n }$ : Amplitude der $n$ -ten Schwingung

2.1

Erkläre unter Beachtung des in Material 2 gezeigten Aufbaus, wie es zu der in Material 4 dargestellten Abnahme der Amplitude mit der Zeit kommt.

(2 BE)

2.2

Bei einer gedämpften harmonischen Schwingung gilt für den zeitlichen Verlauf der horizontalen Auslenkung die Formel

$y(t)=y_{\max , 0} \cdot e^{- k \cdot t } \cdot \cos (\omega \cdot t ) \text {. }$

Begründe, dass für $t = n \cdot T$ die Formel

$k =\dfrac{-\ln \left(\dfrac{ y _{\max , n }}{ y _{\max , 0}}\right)}{ n \cdot T }$

gilt.

Zeige mithilfe dieser Formel und unter Verwendung aller Messwerte, dass die mittlere Dämpfungskonstante (auch Abklingfaktor genannt) $\overline{ k } \approx 5,29 \cdot 10^{-3} \dfrac{1}{ \text s }$ beträgt.

(6 BE)

2.3

Berechne unter Verwendung des Startwerts für $n =0$ in Material 4 die Zeit bis zum Ende der Messung sowie die Pendelhärte der Probe.

(5 BE)

2.4

Für zwei Proben wird die Pendelhärte nach obigem Verfahren bestimmt, dabei werden die Messungen nicht im Vakuum durchgeführt, jedoch unter sonst streng vergleichbaren Bedingungen. Das Pendel ist in einer abgeschirmten Box untergebracht, sodass störender Luftzug verhindert wird.

Erörtere, wie die unvermeidliche Luftreibung die Vergleichbarkeit der Versuchsergebnisse beeinflusst und ob diese Messmethode unter diesen Umständen überhaupt geeignet ist, verschiedene Proben miteinander zu vergleichen.

(2 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

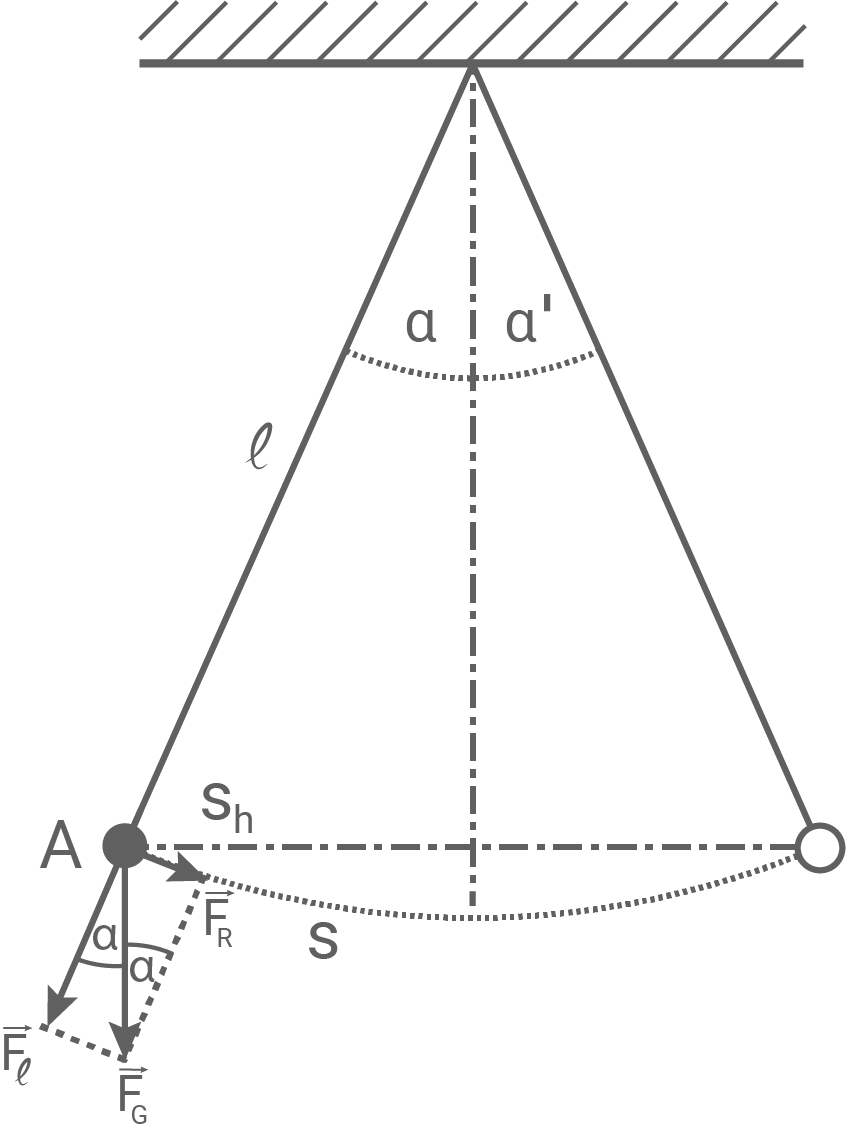
1.2

Für die Rückstellkraft $F_R$ gilt:

$\begin{array}[t]{rll} \sin \left(\alpha\right)&=& -\dfrac{F_R}{F_G}&\quad \scriptsize \mid\; \cdot -F_G \\[5pt] - F_G \cdot \sin \left(\alpha\right)&=& F_R &\quad \scriptsize \mid\; F_G = m\cdot g \\[5pt] - m\cdot g \cdot \sin \left(\alpha\right)&=& F_R &\quad \scriptsize \\[5pt] \end{array}$

Für sehr kleine Winkel kann die gebogene und eigentlich von dem Pendel zurückgelegte Strecke $s$ ungefähr mit der Strecke $s_h$ gleich gesetzt werden, so dass gilt $s_h \approx s.$

$\begin{array}[t]{rll} - m\cdot g \cdot \sin \left(\alpha\right)&=& F_R &\quad \scriptsize \mid\; \sin \alpha=\dfrac{s_{h}}{\ell} \approx \dfrac{s}{\ell} \\[5pt] - m\cdot g \cdot \dfrac{s}{\ell}&=& F_R &\quad \scriptsize \mid\; D=\dfrac{m\cdot g}{\ell} \\[5pt] - D\cdot s&=& F_R &\quad \scriptsize \\[5pt] F_R&=& - D\cdot s \end{array}$

1.3

Differenzialgleichung für eine ungedämpfte harmonische Schwingung

$\begin{array}[t]{rll} F&=& m\cdot a &\quad \scriptsize \mid\; F=F_R \\[5pt] F_R&=& m\cdot a &\quad \scriptsize \\[5pt] - D\cdot s&=& m\cdot a &\quad \scriptsize \mid\; a=\ddot{s}=\dfrac{\text{d}^2 s}{\text{dt}^2} \\[5pt] - D\cdot s&=& m\cdot \ddot{s} &\quad \scriptsize \mid\; \cdot D=\dfrac{m\cdot g}{\ell} \\[5pt] - \dfrac{m\cdot g}{\ell}\cdot s&=& m\cdot \ddot{s} &\quad \scriptsize \mid\; \cdot \dfrac{1}{m} \\[5pt] - \dfrac{g}{\ell}\cdot s&=& \ddot{s} &\quad \scriptsize \mid\; +\dfrac{g}{\ell}\cdot s \\[5pt] s&=& \ddot{s} +\dfrac{g}{\ell}\cdot s &\quad \scriptsize \\[5pt] \end{array}$

Zeit-Beschleunigung-Gesetz

Aus der hergeleiteten Differenzialgleichung folgt:

$\begin{array}[t]{rll} s&=& \ddot{s} +\dfrac{g}{\ell}\cdot s &\quad \scriptsize \mid\; -\dfrac{g}{\ell}\cdot s\\[5pt] - \dfrac{g}{\ell}\cdot s&=& \ddot{s} &\quad \scriptsize \mid\; k=\text{konst}=\dfrac{g}{\ell} \\[5pt] - k\cdot s&=& \ddot{s} &\quad \scriptsize \\[5pt] \end{array}$

Es ist eine Funktion s(t) gesucht, deren zweite Ableitung der Ursprungsfunktion s(t) multipliziert mit einem konstanten Vorfaktor ergibt. Bekannte Funktionen, die diese Bedingung erfüllen, wären beispielsweise die Exponentialfunktion, die Sinusfunktion oder die Kosinusfunktion. Ein möglicher Ansatz für diese Differenzialgleichung mit der gegeben Anfangsbedinung $s(0 \;\text{s})=\text{s}_0$ ist:

$\begin{array}[t]{rll} s(t)&=& s_0\cdot \cos(\omega\cdot t) &\quad \scriptsize \\[5pt] \dot{s}(t)&=& -{s}_0 \cdot \omega \cdot \sin (\omega \cdot {t}) &\quad \scriptsize \\[5pt] \ddot{s}(t)&=& -{s}_0 \cdot \omega^2 \cdot \cos (\omega \cdot {t}) = -\omega^2 \cdot s(t)&\quad \scriptsize \\[5pt] \end{array}$

Bestimmung von $\omega$ durch Einsetzen in die Differenzialgleichung:

$\begin{array}[t]{rll} - \dfrac{g}{\ell}\cdot s(t)&=& \ddot{s}(t) &\quad \scriptsize \mid\; \ddot{s}(t)= - \omega^2 \cdot s(t) \\[5pt] - \dfrac{g}{\ell}\cdot s(t)&=& -\omega^2 \cdot s(t) &\quad \scriptsize \\[5pt] - \dfrac{g}{\ell}&=& -\omega^2 &\quad \scriptsize \mid\; \cdot (-1) \\[5pt] \dfrac{g}{\ell}&=& \omega^2 &\quad \scriptsize \mid\; \sqrt{\;} \\[5pt] \sqrt{\dfrac{g}{\ell}}&=& \omega &\quad \scriptsize \\[5pt] \end{array}$

Die Schwingungsgleichung für das Pendel lautet:

$\begin{array}[t]{rll} s(t)&=& s_0\cdot \cos(\omega\cdot t) &\quad \scriptsize \mid\;\omega=\sqrt{\dfrac{g}{\ell}} \\[5pt] \end{array}$

Das Zeit-Beschleunigungsgesetz erfolgt durch zweimaliges Ableiten nach der Zeit:

$\begin{array}[t]{rll} \ddot{s}(t)&=& -{s}_0 \cdot \omega^2 \cdot \cos (\omega \cdot {t}) &\quad \scriptsize \mid\; \ddot{s}=a \\[5pt] a&=& -{s}_0 \cdot \omega^2 \cdot \cos (\omega \cdot {t}) &\quad \scriptsize \mid\;\omega=\sqrt{\dfrac{g}{\ell}} \\[5pt] \end{array}$

Schwinungsdauer $T$

Es gilt für $\omega:$

$\begin{array}[t]{rll} \omega &=& \dfrac{2 \pi}{T}&\quad \scriptsize \mid\;\cdot T \\[5pt] \omega\cdot T&=& 2 \pi &\quad \scriptsize \mid\; \cdot \dfrac{1}{\omega} \\[5pt] T&=& \dfrac{2 \pi}{\omega} &\quad \scriptsize \mid\; \omega=\sqrt{\dfrac{g}{\ell}} \\[5pt] T&=& \dfrac{2 \pi}{\sqrt{\dfrac{g}{\ell}}} &\quad \scriptsize \\[5pt] T&=& 2 \pi\cdot \sqrt{\dfrac{\ell}{g}} &\quad \scriptsize \\[5pt] \end{array}$

1.4

Gegeben: $T=1,40 \,\text{s} ,$ $\alpha= 6 ^° ,$

Gesucht: $\ell,s_0$

Lösung: Umstellen der hergeleiteten Gleichung aus 1.3 ergibt für die Länge des Pendels $\ell$ :

$\begin{array}[t]{rll} T&=& 2 \pi\cdot \sqrt{\dfrac{\ell}{g}} &\quad \scriptsize \mid\;(\;)^2 \\[5pt] T^2&=& 4 \pi^2\cdot \dfrac{\ell}{g} &\quad \scriptsize \mid\;\cdot \dfrac{g}{4\pi^2} \\[5pt] \dfrac{T^2\cdot g}{4\pi^2}&=& \ell &\quad \scriptsize \\[5pt] \end{array}$

Einsetzen der Werte liefert:

$\begin{array}[t]{rll} \ell &=& \dfrac{T^2\cdot g}{4\pi^2}&\quad \scriptsize \\[5pt] &=&\dfrac{(1,40 \;\text{s})^2\cdot 9,81\;\dfrac{\text{m}}{\text{s}^2}}{4\pi^2} &\quad \scriptsize \\[5pt] &=& 0,487 \;\text{m} &\quad \scriptsize \\[5pt] &=& 48,7 \;\text{cm} \end{array}$

Die Amplitude $s_0$ berechnet sich mithilfe des Kreisumfanges $u$ des Kreises, der die Länge $\ell$ des Pendels als Radius hat.

$\begin{array}[t]{rll} \dfrac{s_0}{u}&=&\dfrac{\alpha}{360 ^\circ} &\quad \scriptsize \mid\;\cdot u \\[5pt] s_0&=&\dfrac{\alpha}{360 ^\circ}\cdot u &\quad \scriptsize \mid\;u=2\pi\cdot \ell\\[5pt] s_0&=&\dfrac{\alpha}{360 ^\circ}\cdot 2\pi\cdot \ell &\quad \scriptsize \\[5pt] \end{array}$

Einsetzen der Werte liefert:

$\begin{array}[t]{rll} s_0&=&\dfrac{\alpha}{360 ^\circ}\cdot 2\pi\cdot \ell &\quad \scriptsize \\[5pt] &=&\dfrac{6 ^\circ}{360 ^\circ}\cdot 2\pi\cdot 48,7 \;\text{cm} &\quad \scriptsize \\[5pt] &=& 5,1 \;\text{cm} &\quad \scriptsize \\[5pt] \end{array}$

1.5

Das Fadenpendel hat kinetische und/oder potentielle Energie, die jeweils während der Bewegung ineinander umgewandelt werden.

$t= 0 \;\text{s}:$

Bei $t= 0 \;\text{s}$ befindet sich das Fadenpendel an seinem Umkehrpunkt, dem Punkt maximaler Auslenkung. Die gesamte Energie besteht aus potentieller Energie $E_{\text {pot }},$ da die Geschwindkigkeit des Pendels an dieser Stelle gleich Null ist und es somit keine kinetische Energie besitzt.

Sobald das Pendel losgelassen wird, wandelt es seine potentielle Energie in kinetische Energie um. Das Pendel bewegt sich folglich mit einer Geschwindikeit $v≠0$ und verliert gleichzeitig an Höhe.

$t= \dfrac{1}{4} \;\text{s}:$

Bei $t= \dfrac{1}{4} \;\text{s}$ geht das Pendel durch seine Ruhelage. Es befindet also in seiner minimalen Höhe $h=0.$ Folglich ist die potentielle Energie gleich Null. Die gesamte potentielle Energie aus dem Umkehrpunkt wurde also in kinetische Energie umgewandelt, so dass diese hier maximal ist. Das Fadenpendel bewegt sich hier mit seiner maximale Geschwindigkeit.

$t= \dfrac{1}{2} \;\text{s}:$

Nachdem das Pendel durch seine Ruhelage geschwungen ist, bewegt es sich weiter in Richtung seines zweiten Umkehrpunktes bei $t= \dfrac{1}{2} \;\text{s}.$ Die Energieverteilung an dem zweiten Umkehrpunkt entspricht der Situation an dem ersten Umkehrpunkt bei $t= 0 \;\text{s}.$ Die gesamte kinetische Energie aus dem Durchgang durch die Ruhelage hat sich in potentielle Energie umgewandelt. Da die Höhe des Pendels der Ausgangshöhe entspricht, sind auch die potentielle Energien beider Umkehrpunkte gleich groß, also Null.

1.6

Gegeben: $\ell=48,7 \,\text{cm},$ $s_h= 5,1 \,\text{cm},$ $m=0,200 \,\text{kg}$

Gesucht: $E_{\text{kin,max}},$ $v_{\text{max}}$

Lösung:

1. Schritt: Herleitung

$\begin{array}[t]{rll} E_{\text {kin,max }}&=& E_{\text {pot,max }}&\quad \scriptsize \\[5pt] E_{\text {kin,max }}&=& m\cdot g\cdot h&\quad \scriptsize \\[5pt] \end{array}$

Die Höhe $h$ entpricht hierbei dem Höhenunterschied zwischen der maximalen Auslenkung und der Ruhelage des Pendels. Zur Berechnung von $h$ darf die Näherung $s_0\approx s_h$ verwendet werden, da es sich um kleine Auslenkungswinkel $\alpha$ handelt. Mit dem Satz des Pythagoras folgt für $h$ :

Rechenweg anzeigen

$h =\ell-\sqrt{\ell^2-s_{h}^2}$

2. Schritt: Maximale kinetische Energie berechnen

Einsetzen des Zusammenhangs von $h$ in die Formel für die maximale kinetische Energie liefert:

Rechenweg anzeigen

$E_{\text {kin,max }}=5,3 \cdot 10^{-3}\;\text{J}$

3. Schritt: Maximalgeschwindigkeit berechnen

$\begin{array}[t]{rll} E_{\text {kin,max }}&=& \dfrac{1}{2}\cdot m\cdot v^2_{\text{max}}&\quad \scriptsize \mid\;\cdot 2 \\[5pt] 2\cdot E_{\text {kin,max }}&=& m\cdot v^2_{\text{max}}&\quad \scriptsize \mid\;\cdot \dfrac{1}{m} \\[5pt] \dfrac{2\cdot E_{\text {kin,max }}}{m}&=& v^2_{\text{max}}&\quad \scriptsize \mid\;\sqrt{\;} \\[5pt] \sqrt{\dfrac{2\cdot E_{\text {kin,max }}}{m}}&=& v_{\text{max}}&\quad \scriptsize \\[5pt] \end{array}$

Einsetzen der Werte liefert:

$\begin{array}[t]{rll} v_{\text{max}}&=& \sqrt{\dfrac{2\cdot E_{\text {kin,max }}}{m}}&\quad \scriptsize \\[5pt] &=& \sqrt{\dfrac{2\cdot 5,3 \cdot 10^{-3}\;\text{J}}{0,200 \;\text{kg}}}&\quad \scriptsize \\[5pt] &=& 0,23 \;\dfrac{\text{m}}{\text{s}}&\quad \scriptsize \\[5pt] \end{array}$

Es gilt:

$\begin{array}[t]{rll} E_{\text {kin,max }}&=& E_{\text {pot,max }}&\quad \scriptsize \\[5pt] \dfrac{1}{2}\cdot m\cdot v^2_{\text{max}}&=& m\cdot g\cdot h&\quad \scriptsize \mid\;\cdot 2 \\[5pt] m\cdot v^2_{\text{max}}&=& 2\cdot m\cdot g\cdot h&\quad \scriptsize \mid\;\cdot \dfrac{1}{m} \\[5pt] v^2_{\text{max}}&=& 2\cdot g\cdot h&\quad \scriptsize \mid\; \sqrt{\;}\\[5pt] v_{\text{max}}&=& \sqrt{2\cdot g\cdot h}&\quad \scriptsize \\[5pt] \end{array}$

Begründung

Da sich die Masse $m$ herauskürzt, ist die Formel für die Geschwindigkeit unabhängig von der Masse des Fadenpendels.

1.7

Pendelschwingung auf dem Mond

Für die Schwinungsdauer $T$ gilt:

$\begin{array}[t]{rll} T&=& 2 \pi\cdot \sqrt{\dfrac{\ell}{g}} &\quad \scriptsize \\[5pt] \end{array}$

Da $g_M$ im Nenner steht, wird $T$ größer für ein kleineres $g_M.$ Somit ist die Schwindungsdauer auf dem Mond größer als auf der Erde.

Ortsfaktorbestimmung

Umstellen nach $g_M$ der Formel für die Schwinungsdauer liefert:

$\begin{array}[t]{rll} T&=& 2 \pi\cdot \sqrt{\dfrac{\ell}{g_M}} &\quad \scriptsize \mid\;\cdot \dfrac{1}{2\pi} \\[5pt] \dfrac{T}{2\pi}&=& \sqrt{\dfrac{\ell}{g_M}} &\quad \scriptsize \mid\; (\;)^2 \\[5pt] \left(\dfrac{T}{2\pi}\right)^2&=& \dfrac{\ell}{g_M} &\quad \scriptsize \mid\; \cdot g_M\\[5pt] \left(\dfrac{T}{2\pi}\right)^2\cdot g_{M}&=& \ell &\quad \scriptsize \mid\; \cdot \dfrac{1}{\left(\dfrac{T}{2\pi}\right)^2} \\[5pt] g_{M}&=& \dfrac{\ell }{\left(\dfrac{T}{2\pi}\right)^2} &\quad \scriptsize \\[5pt] g_{M}&=& \dfrac{\ell }{1}\cdot \dfrac{\left(2\pi\right)^2}{T^2} &\quad \scriptsize \\[5pt] g_{M}&=& \dfrac{\ell\cdot 4\pi^2 }{T^2} &\quad \scriptsize \\[5pt] \end{array}$

Um den Ortsfaktor des Mondes zu bestimmen, wird die Schwinungsdauer experimentell bestimmt. Außerdem die Länge des Pendels gemessen. Mithilfe einer Stoppuhr wird die Schwingungsdauer bestimmt, die das Pendel nach dem Auslenken um einen kleinen Winkel des Pendels aus der Ruhelage benötigt. Die Formel der Schwingungsdauer wird nach $g_M$ umgestellt. Dann die Werte eingesetzt

Genauigkeitserhöhung der Messung

Um den Messfehler zu verringern, bietet es sich an mit einem Mittelwert der Schwinungsdauer zurechnen. Dafür muss das Experiemnt wiederholt werden.

Auch das Verlängern der Pendellänge $\ell$ sorgt für genauere Messungen, da so die Schwinungsdauer erhöht wird und die Zeiten exakter bestimmt werden können.

2.1

Das Abnehmen der Amplitude mit der Zeit ist den Reibungsverlusten und den Verformungsverlusten verschuldet. Durch diese Verluste verringert sich die maximale potentielle Energie und die maximale kinetische Energie mit der Zeit.

Die Reibungsverluste entstehen durch die Reibung an den Auflangepunkten auf der Prüfplatte während der Pendelbewegung. Ein Teil der Bewegungsenergie wird folglich in Wärmeenergie umgewandelt. Auch der Luftwiderstand führt zu Reibungsverlusten durch Umwandlung von Bewegungsenergie in Wärmeenergie.

Die Verformungsverluste entstehen durch die Reaktion des Materials der Prüfplatte auf die mechanische Einwirkung. Ein Teil der Bewegungsenergie wird dabei in Wärmeenergie und Verformungsarbeit umgewandelt.

2.2

Die horizontale Auslenkung $y(t=n\cdot T)$ des Pendels ist nach der Zeit $t=n\cdot T$ nicht mehr gleich der Auslenkung zum Startzeitpunkt $y=(t=0)=y_{\max,0}$ aufgrund der Reibungs- und Verformungsverluste. Für die Auslenkung $y(t)$ nach der Zeit $t=n\cdot T$ gilt folglich für den harmonischen, gedämpften Oszillator:

Rechenweg anzeigen

$k= -\dfrac{\ln\left(\dfrac{y_{\max , n}}{y_{\max , 0}}\right)}{n\cdot T}$

Einsetzen der Werte liefert für die Dämpfungskonstanten $k$ :

$\color{#fff}n$	$\color{#fff}y_{\color{#fff}{\max, n}}$ in $\color{#fff}{\text{m}}$	$\color{#fff}k$ in $\color{#fff}{10^{-3}\dfrac{1}{\text{s}}}$
0	0,051
20	0,044	5,27
40	0,038	5,25
60	0,033	5,18
80	0,028	5,35
100	0,024	5,38

Für den Mittelwert $\overline{k}$ gilt:

Rechenweg anzeigen

$\overline{k}= 5,29 \cdot 10^{-3} \;\dfrac{1}{\text{s}}$

2.3

Es gilt für die horizontale Auslenkung von dem kleinsten Winkel der Messung $\alpha_{\text{max,Ende} }=3^{\circ}:$

$\begin{array}[t]{rll} \sin (\alpha_{\text {max }, \text { Ende }})&=& \dfrac{y_{\text{max,Ende} }}{\ell} &\quad \scriptsize \mid\; \cdot \ell\\[5pt] \sin (\alpha_{\text {max }, \text { Ende }})\cdot \ell&=& y_{\text{max,Ende} } &\quad \scriptsize \\[5pt] \end{array}$

Einsetzen der Werte liefert:

$\begin{array}[t]{rll} y_{\text{max,Ende} }&=&\sin (\alpha_{\text {max }, \text { Ende }})\cdot \ell &\quad \scriptsize \\[5pt] &=& 0,490 \;\text{m} \cdot \sin(3^{\circ}) &\quad \scriptsize \\[5pt] &=& 0,0256 \;\text{m} &\quad \scriptsize \\[5pt] \end{array}$

Es gilt nach Teilaufgabe 2.2:

$\begin{array}[t]{rll} -\dfrac{\ln\left(\dfrac{y_{\max , \text{Ende}}}{y_{\max , 0}}\right)}{n_{\max}\cdot T}&=& \overline{k } &\quad \scriptsize \mid\; \cdot n_{\max}\\[5pt] -\dfrac{\ln\left(\dfrac{y_{\max , \text{Ende}}}{y_{\max , 0}}\right)}{T}&=& \overline{k }\cdot n_{\max} &\quad \scriptsize \mid\; \cdot \dfrac{1}{\overline{k}}\\[5pt] -\dfrac{\ln\left(\dfrac{y_{\max , \text{Ende}}}{y_{\max , 0}}\right)}{T\cdot\overline{k } }&=& n_{\max} &\quad \scriptsize\\[5pt] \end{array}$

Einsetzen der Werte liefert:

$\begin{array}[t]{rll} n_{\max}&=& -\dfrac{\ln\left(\dfrac{y_{\max , \text{Ende}}}{y_{\max , 0}}\right)}{T\cdot\overline{k } } &\quad \scriptsize\\[5pt] &=& -\dfrac{\ln \left(\dfrac{0,0256 \;\text{m}}{0,051 \;\text{m}}\right)}{-5,29 \cdot 10^{-3} \;\dfrac{1}{\text{s}} \cdot 1,40 \;\text{s}} &\quad \scriptsize\\[5pt] &=& 93 \end{array}$

Die Messzeit beträgt folglich:

$\begin{array}[t]{rll} t_{\text{mess}}&=& n_{\max}\cdot T &\quad \scriptsize \\[5pt] &=& 93\cdot 1,40 \;\text{s} &\quad \scriptsize \\[5pt] &=& 130 \;\text{s} \end{array}$

Nach ungefähr $130$ Sekunden ist die Messung fertig.

2.4

Der Einfluss des Luftwiderstands auf die Amplituden der Pendelbewegung ist sehr gering, da der Auslenkungswinkel $\alpha$ sehr klein ist und die Schwingungsdauern $T$ sehr groß sind. Der Luftwiderstand verändert die Ergebnisse unterschiedlicher Proben in etwa gleichem Maße. Folglich ist der Vergleich unterschiedlicher Messungen vertretbar.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?