Vorschlag B3

Stehende Wellen und Doppler-Effekt

Bei Blasinstrumenten werden Luftsäulen im Innern des Instruments zu Schwingungen angeregt. Beispielsweise bringt der Luftstrom, der von einem Musiker in eine Klarinette geblasen wird, das am Mundstück befestigte Blatt zum Schwingen (Material 1). Dies regt die Luftsäule im zylindrischen Klarinettenrohr zu einer stehenden Welle an. Die Klarinette verhält sich dabei vereinfacht wie ein einseitig geschlossenes Rohr, an dessen geschlossenem Ende die Luftsäule zu Schwingungen angeregt wird. Die Schallgeschwindigkeit beträgt $c=340 \,\text m / s.$

Material 1: Klarinette

1.1

Beschreibe allgemein, wodurch eine stehende Welle entsteht.

(2 BE)

1.2

In einem einseitig geschlossenen Rohr der Länge $\text L=65,0 \,\text{cm}$ wird die Luftsäule durch einen Tongenerator mit regelbarer Frequenz zu Schwingungen angeregt.

Erkläre mithilfe von Material 2 (ohne auf eventuelle Phasensprünge einzugehen), dass nur bei bestimmten Frequenzen stehende Schallwellen entstehen und dass für die Frequenz der ersten Oberschwingung die Formel $f_1=\dfrac{3 c}{4 \text L}$ gilt.

Berechne die Frequenzen der Grundschwingung und der ersten beiden Oberschwingungen.

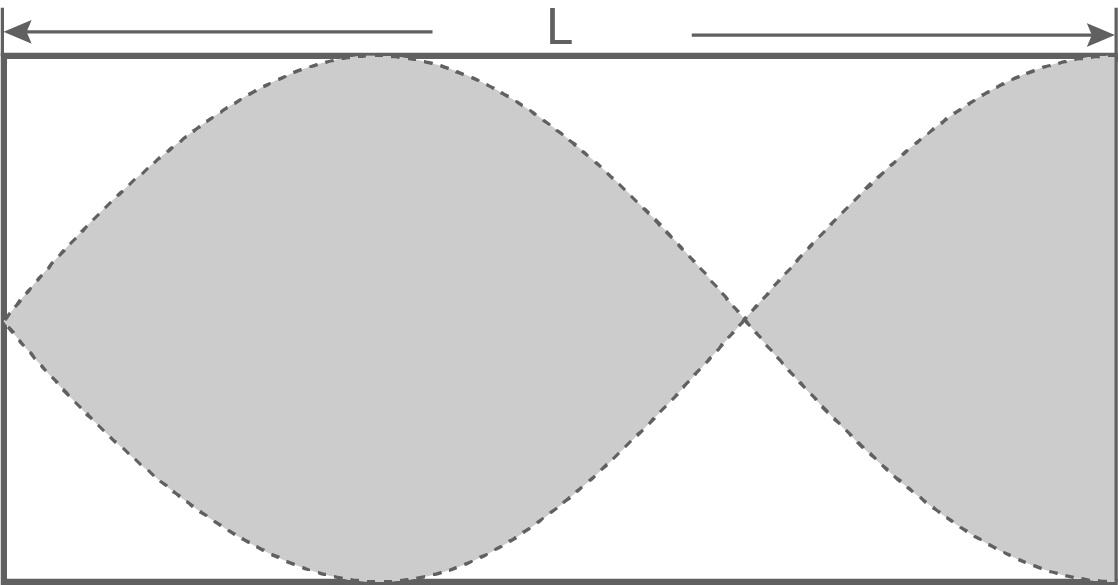
Material 2: Schematische Darstellung der ersten Oberschwingung

(7 BE)

Zwei Rohre mit jeweils einem offenen und einem geschlossenen Ende haben die Längen $\text L_1=65,0 \,\text{cm}$ und $\text L_2=64,0 \,\text{cm}.$ In ihnen wird jeweils die erste Oberschwingung durch Schallwellen gleicher Amplitude angeregt. Ein Empfänger nimmt in einiger Entfernung von den Rohren die Überlagerung der beiden Töne auf. Es ergibt sich das in Material 3 dargestellte Schwingungsbild. Diesem kann eine relativ kleine Frequenz (Schwebungsfrequenz) und eine relativ große Frequenz (Frequenz des Schwebungstons) entnommen werden. Die Schallgeschwindigkeit beträgt weiterhin $c=340 \,\text m / s.$

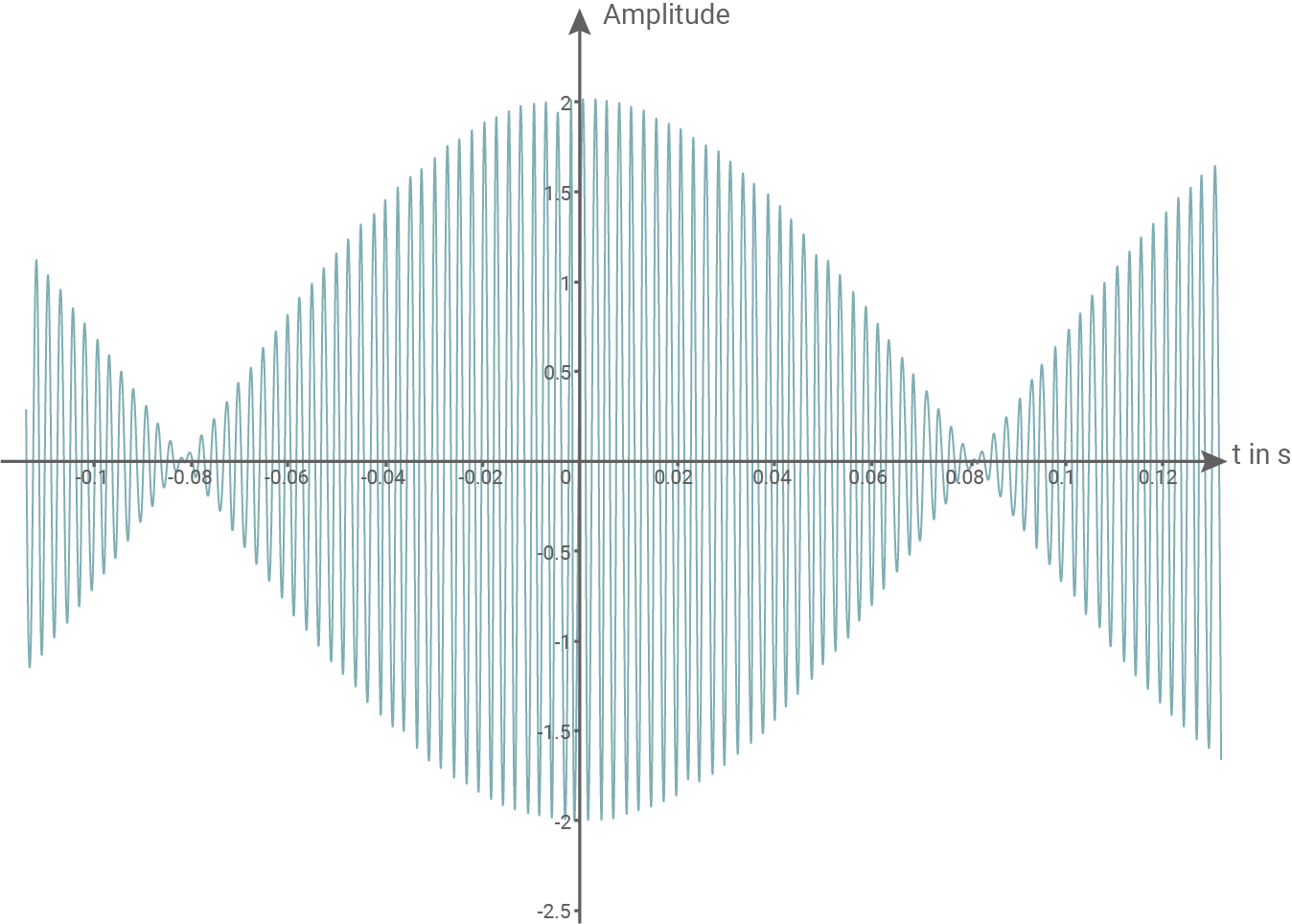
Material 3: Schwingungsbild der überlagerten Töne (Amplitude in relativen Einheiten)

2.1

Erläutere die Entstehung des Schwingungsbilds und bestimme aus Material 3 die Werte für die Schwebungsfrequenz und die Frequenz des Schwebungstons.

(5 BE)

2.2

Berechne die Schwebungsfrequenz aus den oben gegebenen Daten.

Vergleiche quantitativ dieses Ergebnis mit dem Ergebnis aus Aufgabe 2.1.

(6 BE)

2.3

Ein Mensch kann Schwebungsfrequenzen, die größer als $f_{ \text S }=20\,\text{Hz}$ sind, nicht wahrnehmen.

Berechne für $\text L_1=65 \,\text{cm}$ die minimale Länge $\text L_2$ des zweiten Rohrs, damit die Schwebung gerade noch wahrgenommen werden kann.

(4 BE)

Ändert sich der Abstand zwischen einem Sender, der einen Ton bestimmter Frequenz $f$ aussendet, und einem Empfänger während der Dauer des Signals, so registriert der Empfänger einen Ton anderer Frequenz $f^{\prime}.$ Bei diesem sogenannten Doppler-Effekt sind zwei Fälle zu unterscheiden. Bewegt sich im ersten Fall ein Empfänger mit einer Geschwindigkeit $v$ von einem ruhenden Sender weg, so empfängt er einen tieferen Ton. Bewegt sich im zweiten Fall ein Sender mit der Geschwindigkeit $v$ von einem ruhenden Empfänger weg, so lässt sich die Empfängerfrequenz mit folgender Gleichung berechnen, wobei $c=340\,\text m / s$ die Schallgeschwindigkeit ist:

$f^{\prime}=\dfrac{f}{1+\dfrac{\text V}{c}}$

3.1

Erläutere, dass es in beiden Fällen zu einer Änderung der empfangenen Frequenz kommt.

(4 BE)

3.2

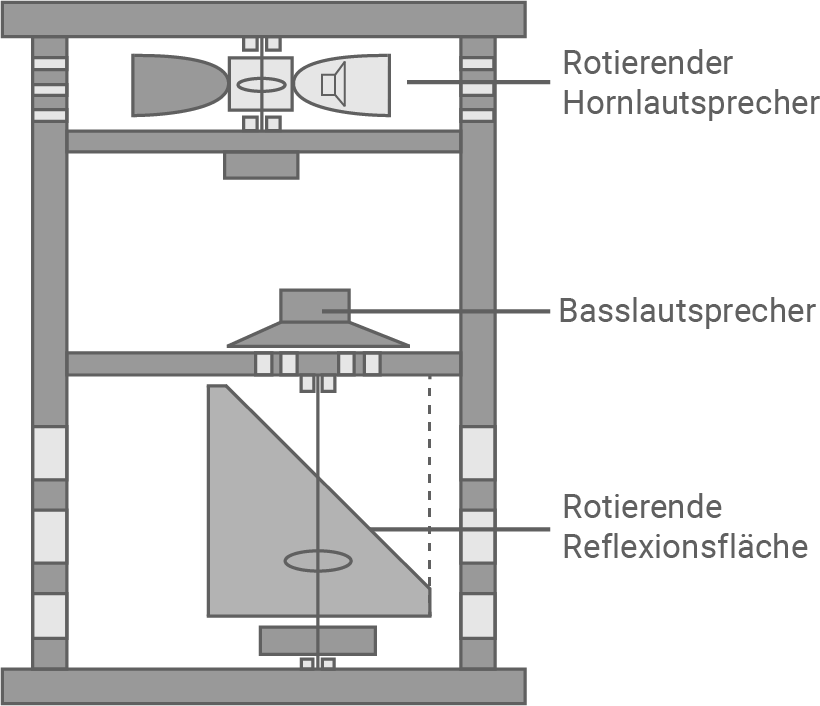
Ein Leslie-Kabinett besteht neben dem Basslautsprechersystem aus zwei rotierenden Hörnern, welche sich im oberen Teil befinden (Material 4). Dabei enthält nur ein Horn einen Lautsprecher. Das andere Horn enthält keinen Lautsprecher, besitzt aber die gleiche Masse.

Wir betrachten zunächst die Rotation des Lautsprechers unter Vernachlässigung der Schallreflexionen an den Wänden. Material 5 zeigt exemplarisch zwei verschiedene Positionen des Lautsprechers während eines Umlaufs sowie einen Zuhörer (Empfänger).

Da der Lautsprecher in ein Horn eingebaut ist, hat er eine bevorzugte Abstrahlrichtung. Abhängig von der Position des Lautsprechers variiert deshalb die Lautstärke, die der Empfänger wahrnimmt. Dieser Effekt wird Tremolo genannt. Außerdem variiert die wahrgenommene Tonhöhe. Dieser Effekt wird Vibrato genannt und durch den Doppler-Effekt hervorgerufen.

Im Folgenden ist die Rotationsfrequenz der Hörner auf $f_{\text {rot }}=100$ Umdrehungen pro Minute eingestellt. Der Lautsprecher befindet sich $0,15 \,\text m$ von der Rotationsachse entfernt und sendet eine Tonfrequenz von $f=880\,\text{Hz}$ aus. Die Schallgeschwindigkeit beträgt $c=340 \,\text m / s.$

Material 4: Leslie-Kabinett

Material 5: Rotierender Lautsprecher (gegen den Uhrzeigersinn)

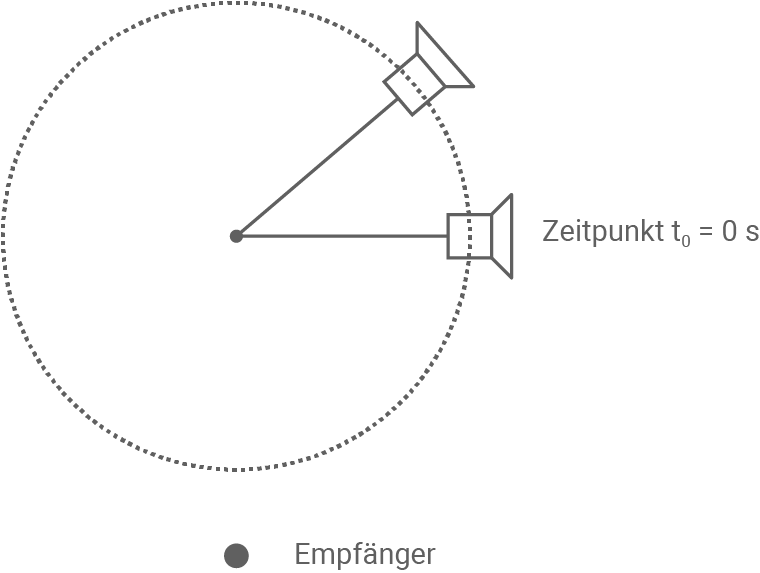hessen physik abi lk 2021 vorschlag b3 material 5 rotierender lautsprecher (gegen der uhrzeigersinn)

Es soll vereinfachend angenommen werden, dass der Empfänger - anders als dargestellt - unendlich weit von dem rotierenden Lautsprecher entfernt ist.

3.2.1

Zeichne bei beiden Positionen des Lautsprechers in Material 5 die Richtung der Geschwindigkeit als Pfeil ein.

Begründe, dass die effektive Geschwindigkeitskomponente, die zum Dopplereffekt beiträgt, durch die Formel $v_{\text {eff }}(t)=v \cdot \cos \left(2 \pi \cdot f_{\text {rot }} \cdot t\right)$ beschrieben werden kann, und deute das wechselnde Vorzeichen von $v_{\text {eff }}(t).$

(8 BE)

3.2.2

Gib einen Term an, der die vom Zuhörer empfangene Frequenz in Abhängigkeit von der Zeit beschreibt, und berechne die maximale und minimale empfangene Frequenz.

Zeichne für zwei volle Lautsprecherumdrehungen ein $\(t-f$ -Diagramm in Material 6.

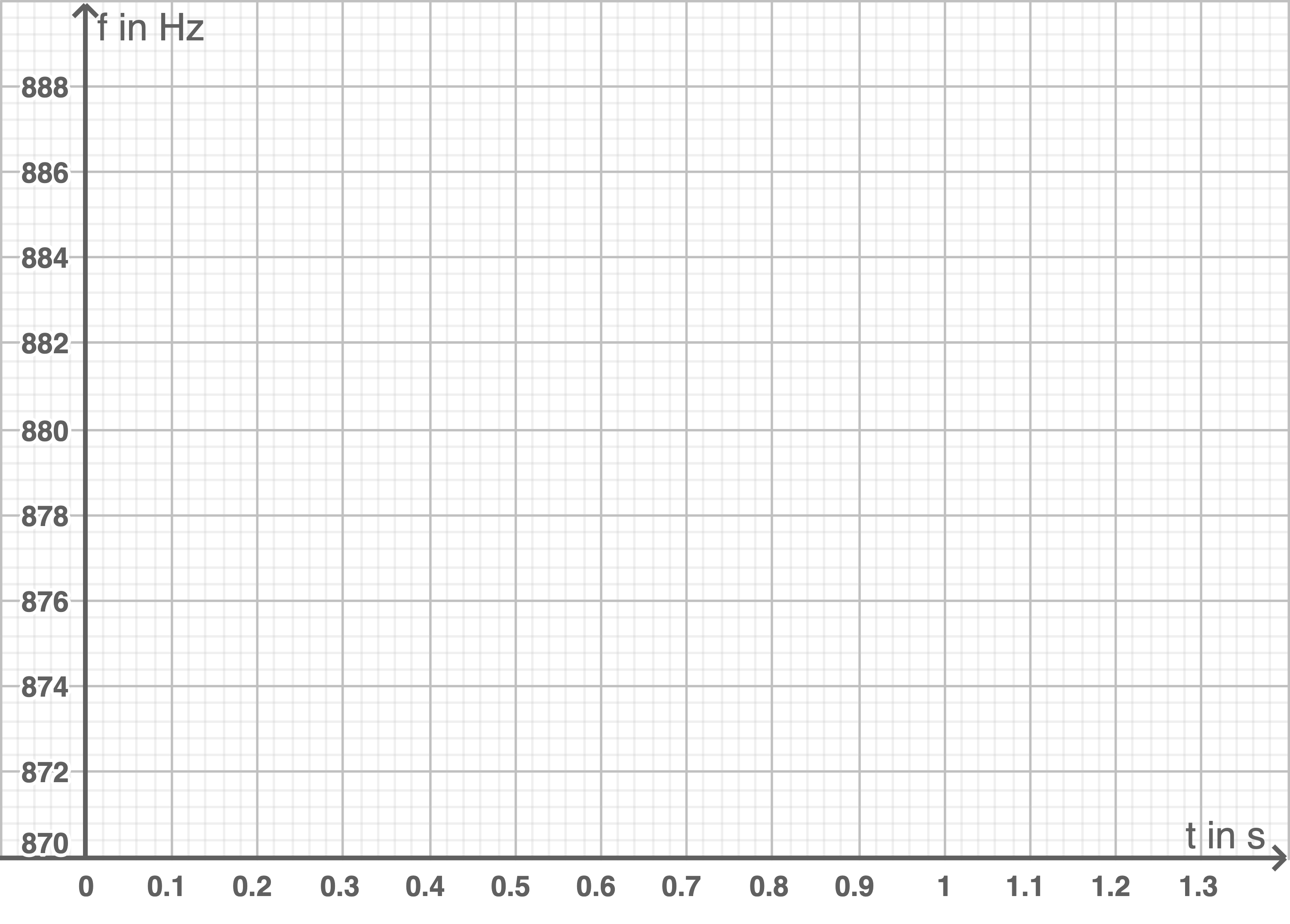
Material 6: Koordinatensystem

(8 BE)

3.2.3

Nimm zu der folgenden Aussage Stellung: „Das Tremolo ist gegenüber dem Vibrato um $90^{\circ}$ phasenverschoben.“

(4 BE)

3.2.4

Zusätzlich wird der Ton des Lautsprechers an den Gehäusewänden oder an Zimmerwänden reflektiert.

Untersuche, welche weiteren Effekte dadurch auftreten können.

(2 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

Eine stehende Welle entsteht durch die Überlagerung von zwei Wellen gleicher Frequenz, Wellenlänge und Amplitude, die in entgegengesetzte Richtungen durch einen begrenzten Raum, wie zum Beispiel ein Rohr oder eine Saite, laufen. Wenn diese beiden Wellen aufeinandertreffen, interferieren sie miteinander und bilden ein Muster von konstruktiven und destruktiven Interferenzen.

1.2

In einem Klarinettenrohr breiten sich Schallwellen aus, welche an beiden Enden reflektiert werden. Dadurch bilden sich stehende Wellen bei passender Rohrlänge aus, die eine passende Länge und Frequenz besitzen.

An der Öffnung der Klarinette entsteht beim Einblasen ein Wellenknoten und am offenen Ende ein Wellenbauch.

In der Abbildung hängt die Länge des Rohrs mit der Wellenlänge über $L= \dfrac{3}{4}\cdot \lambda$ zusammen.

Allgemein gilt: $L=(2n+1)\cdot \dfrac{\lambda_n}{4}$

Außerdem gilt:

$\begin{array}[t]{rll} c&=&\lambda_n\cdot f_n &\quad \scriptsize \mid\; :f_n\\[5pt] \dfrac{c}{f_n}&=&\lambda_n \\[5pt] \lambda_n &=& \dfrac{c}{f_n} \end{array}$

Einsetzen ergibt:

$L= (2n+1) \cdot \dfrac{c}{4\cdot f_n}$

Umstellen nach $f_n$ und einsetzen von $n=1,$ um die Frequenz der ersten Oberschwingung zu erhalten:

$\begin{array}[t]{rll} L&=& (2n+1) \cdot \dfrac{c}{4\cdot f_n} &\quad \scriptsize \mid\; :(2n+1) \\[5pt] \dfrac{L}{2n+1}&=& \dfrac{c}{4\cdot f_n} \\[5pt] \dfrac{c}{4\cdot f_n} &=& \dfrac{L}{2n+1} \\[5pt] \dfrac{4\cdot f_n}{c} &=& \dfrac{2n+1}{L} &\quad \scriptsize \mid\;\cdot c \\[5pt] 4\cdot f_n&=&\dfrac{2n+1}{L}\cdot c &\quad \scriptsize \mid\;:4 \\[5pt] f_n&=& \dfrac{2n+1}{4\cdot L}\cdot c \\[5pt] f_1&=& \dfrac{2\cdot 1+1}{4\cdot L}\cdot c \\[5pt] f_1&=& \dfrac{3c}{4\cdot L} \end{array}$

Frequenzen der Grundschwingung und der ersten beiden Oberschwingungen

Einsetzen von $n=0,1,2$ in $f_n=(2n+1)\cdot \dfrac{c}{4\cdot L}$ ergibt:

$f_0= \dfrac{340 \frac{\text{m}}{\text{s}}}{4\cdot 0,65\;\text{m}}$ $= 131 \;\text{Hz}$

$f_1=3\cdot \dfrac{340 \frac{\text{m}}{\text{s}}}{4\cdot 0,65\;\text{m}}$ $= 3\cdot f_0$ $= 392 \;\text{Hz}$

$f_2=5\cdot \dfrac{340 \frac{\text{m}}{\text{s}}}{4\cdot 0,65\;\text{m}}$ $= 5 \cdot f_0$ $= 654 \;\text{Hz}$

2.1

Schwebung ist der Effekt, der auftritt, wenn sich zwei harmonische Schwingungen mit ähnlichen Frequenzen überlagern und eine resultierende Schwingung mit der Frequenz des Schwebungstons erzeugen. Die Lautstärke dieser resultierenden Schwingung schwankt mit der Schwebungsfrequenz, da sich die Amplitude periodisch verstärkt und abschwächt.

$f_S=\dfrac{1}{0,16 \;\text{s}}=6,25 \;\text{Hz}$

Aus Material 3 werden im Intervall $[0;0,8]$ insgesamt 32 Schwingungen abgelesen. Daraus folgt die Frequenz des Schwebungstons mit $f= \dfrac{32}{0,08 \;\text{s}}$ $= 400 \;\text{Hz}.$

2.2

Einsetzen von $L_1$ und $L_2$ in $f_1= \dfrac{3\cdot c}{4\cdot L}$ ergibt:

$f _1\left( L _1\right)$ $=\dfrac{3 \cdot 340 \frac{ \text{m} }{ \text{s} }}{4 \cdot 0,65 \;\text{m}}=392 \;\text{Hz}$

$f _1\left( L _2\right)$ $=\dfrac{3 \cdot 340 \frac{ \text{m} }{ \text{s}}}{4 \cdot 0,64 \;\text{m}}$ $=398 \;\text{Hz}$

Für die Schwebungsfrequenz gilt:

$\begin{array}[t]{rll} f_S&=& \left| f _1\left( L _2\right)- f _1\left( L _1\right)\right| \\[5pt] &=& |398 \;\text{Hz} -392 \;\text{Hz}| \\[5pt] &=& 6 \;\text{Hz} \end{array}$

Prozentuale Abweichung:

$\dfrac{6,25 \;\text{Hz}-6 \;\text{Hz}}{6,25\;\text{Hz}}=0,04$ $= 4 \%$

2.3

$20 \;\text{Hz} \gt f _{ S }=\left| f _1\left( L _2\right)- f _1\left(L_1\right)\right|$ $= \begin{cases} f _1\left(L_2\right)-392 \;\text{Hz} & \text { falls } f _1\left( L _2\right)\gt 392 \text{Hz} \\ 392 \;\text{Hz} - f _1\left( L _2\right) & \text { falls } f _1\left( L _2\right)\lt 392 \;\text{Hz} \end{cases}$

Es gilt $f_1(L_2)=\dfrac{3c}{4\cdot L_2}.$

$L_2$ ist minimal wenn $f_1(L_2)$ maximal und $\gt 392 \;\text{Hz}.$

$f _1\left( L _2\right)-392 \;\text{Hz} \lt 20 \;\text{Hz}$

$f _1\left( L _2\right)\lt 392 \;\text{Hz} +20\;\text{Hz} =412 \;\text{Hz}$

$\begin{array}[t]{rll} \dfrac{3c}{4\cdot L_2}&\lt & 412\;\text{Hz} &\quad \scriptsize \mid \;\cdot L_2 \mid\;: 412\;\text{Hz} \\[5pt] \dfrac{3c}{4\cdot 412\;\text{Hz} }&\lt & L_2\\[5pt] L_2&\gt& \dfrac{3c}{4\cdot 412\;\text{Hz} } \\[5pt] L_2&\gt& \dfrac{3\cdot 340\frac{\text{m}}{\text{s}}}{4\cdot 412\;\text{Hz} } \\[5pt] &=& 0,62 \;\text{m} \end{array}$

Das Rohr muss mindestens $62\;\text{cm}$ lang sein.

3.1

Erster Fall

Während sich der Sender vom Empfänger wegbewegt, werden die Wellenfronten am Ort, an dem sich der Empfänger befindet, auseinandergezogen. Dadurch ändert sich die Wellenlänge und dadurch auch die Frequenz.

Zweiter Fall

Bewegt sich der Sender vom ruhenden Empfänger weg, so empfängt der Empfänger weniger Wellen, wodurch sich die Frequenz ändert.

3.2.1

Für die Effektivgeschwindigkeit gilt:

$\begin{array}[t]{rll} \cos (\varphi( t ))&=&\dfrac{\left|\vec{v}_{\text {eff }}\right|}{|\vec{v}|} &\quad \scriptsize \mid\;\cdot \vec{v} \\[5pt] \cos (\varphi( t ))\cdot \vec{v}&=& \vec{v}_{\text {eff }} \\[5pt] \vec{v}_{\text {eff }}&=& \cos (\varphi( t ))\cdot \vec{v} \end{array}$

Es gilt außerdem:

$\begin{array}[t]{rll} \omega&=&\dfrac{\varphi(t)}{t} \\[5pt] 2 \pi \cdot f_{\text {rot }} &=& \dfrac{\varphi(t)}{t} &\quad \scriptsize \mid\;\cdot t \\[5pt] 2 \pi \cdot f_{\text {rot }} \cdot t&=&\varphi(t) \\[5pt] \varphi(t) &=& 2 \pi \cdot f_{\text {rot }} \cdot t \end{array}$

Einsetzen:

$\begin{array}[t]{rll} \vec{v}_{\text {eff }}&=& \cos (\varphi( t ))\cdot \vec{v} \\[5pt] &=& \cos (2 \pi \cdot f_{\text {rot }} \cdot t)\cdot \vec{v} \\[5pt] &=& v\cdot \cos (2 \pi \cdot f_{\text {rot }} \cdot t) \end{array}$

Vorzeichen

Während der Rotation ändert der Vektor der effektiven Geschwindigkeit kontinuierlich seine Richtung.

Zu Beginn zeigt der Vektor vom Empfänger weg, wenn sich der Lautsprecher mit einer maximalen Geschwindigkeit von v vom Empfänger entfernt. Die Effektivgeschwindigkeit hat ein positives Vorzeichen.

Sobald ein Drehwinkel von $90^{\circ}$ erreicht ist, wird $v_{\text {eff }}$ null, und die Bewegungsrichtung in Bezug auf den Empfänger kehrt sich um.

Die Effektivgeschwindigkeit hat ein negatives Vorzeichen und ihr Betrag nimmt zu, bis der Winkel von $180^{\circ}$ erreicht ist (d.h. $v_{\text {eff }}=-v$ ). Danach nimmt der Betrag wieder ab, bis er bei $270^{\circ}$ null wird.

Das Vorzeichen der Effektivgeschwindigkeit wechselt erneut auf positiv (Bewegungsumkehr), und ihr Betrag nimmt zu, bis der Lautsprecher nach einer vollständigen Drehung von $360^{\circ}$ wieder die Ausgangsposition erreicht.

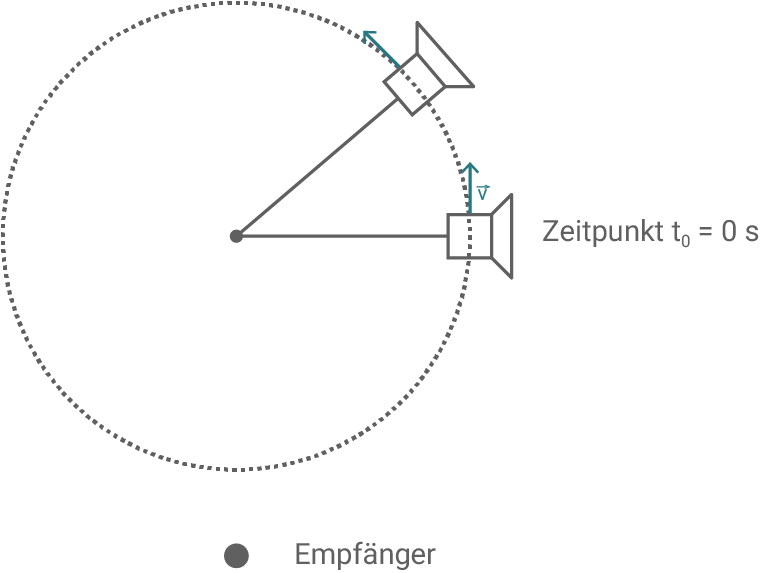
3.2.2

Einsetzen von $v_{\text {eff }}$ in die Frequenzformel ergibt:

$f^{\prime}=f \cdot \dfrac{1}{1+\frac{v \cdot \cos \left(2 \pi \cdot f_{\text {tot }} \cdot t\right)}{c}}$

$v =2 \pi \cdot r \cdot f _{\text {rot }}$ $=2 \pi \cdot 0,15\;\text{m} \cdot \dfrac{100}{60} \;\text{Hz}$ $=1,57 \frac{ \text{m} }{\text{s} }$

Maximale Empfangsfrequenz

$f \cdot \dfrac{1}{1-\frac{ v }{ c }}$ $=880 \;\text{Hz}\cdot \dfrac{1}{1-\frac{1,57 \frac{ \text{m} }{ \text{s} }}{340 \frac{ \text{m} }{ \text{s} }}}$ $=884 \;\text{Hz}$

Minimale Empfangsfrequenz

$f \cdot \dfrac{1}{1+\frac{v}{c}}$ $=880 \;\text{Hz} \cdot \dfrac{1}{1+\frac{1,57 \frac{ \text{m} }{ \text{s} }}{340 \frac{ \text{m} }{ \text{s} }}}$ $876 \;\text{Hz}$

$t$ - $\(f$ -Diagramm

Es gilt: $T$ $=\dfrac{1}{ f _{\text {rot }}}$ $=\dfrac{1}{\frac{100}{60} \;\text{Hz} }=0,6 \;\text{s}$

Mit dieser Periodendauer schwanken die Empfangsfrequenzen zwischen der minimalen und maximalen Frequenz.

3.2.3

Der Zuhörer nimmt eine maximale Lautstärke wahr, wenn der Lautsprecher direkt auf ihn ausgerichtet ist ( $\varphi=270^{\circ}$ ), und eine minimale Lautstärke, wenn der Lautsprecher in entgegengesetzter Richtung zeigt (von ihm weg, $\varphi=90^{\circ}$ ). Dies tritt genau an den unteren und oberen Punkten des Lautsprechers auf. In diesen Fällen nimmt der Zuhörer die tatsächliche Frequenz des Lautsprechers wahr, da die Effektivgeschwindigkeit an diesen Punkten jeweils null ist. Der Tremoloeffekt (Lautstärkeänderung) ist hier also maximal, während die Tonhöhe unverändert bleibt.

An den Punkten zwischen diesen beiden Extremen ( $0^{\circ}$ und $180^{\circ}$ ) nimmt der Zuhörer eine mittlere Lautstärke wahr, während der Betrag der Effektivgeschwindigkeit an diesen Punkten jeweils maximal ist, was zu einem maximalen Vibratoeffekt (Tonhöhenänderung) führt.

Beide Effekte, Tremolo und Vibrato, sind daher um $90^{\circ}$ , also um ein Viertel der Periodendauer, phasenverschoben. Diese Aussage ist korrekt.

3.2.4

Wenn Schallwellen an den Wänden reflektiert werden, erreichen sie den Empfänger auf unterschiedlich langen Wegen. Da die Wellenlängen des Schalls im Bereich von Zentimetern bis Metern liegen und damit ähnliche Größenordnungen wie die auftretenden Gangunterschiede haben, treffen die Schallwellen zeitversetzt beim Zuhörer ein. Dies kann zu Interferenzen führen. Darüber hinaus können Schwebungseffekte auftreten, wenn sich unterschiedliche Frequenzen überlagern.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?