Vorschlag B2
Das Davisson-Germer-Experiment
Clinton Davisson und Lester Germer gelang es 1927 erstmals, den von Louis de Broglie 1923 postulierten Wellencharakter von Teilchen experimentell nachzuweisen. In dem nach ihnen benannten Experiment werden Elektronen senkrecht auf die Oberfläche eines Nickeleinkristalls geschossen und die Intensitäten der reflektierten Elektronen als Funktion des StreuwinkelsMaterial 1: Schematische Skizze des Davisson-Germer-Experiments
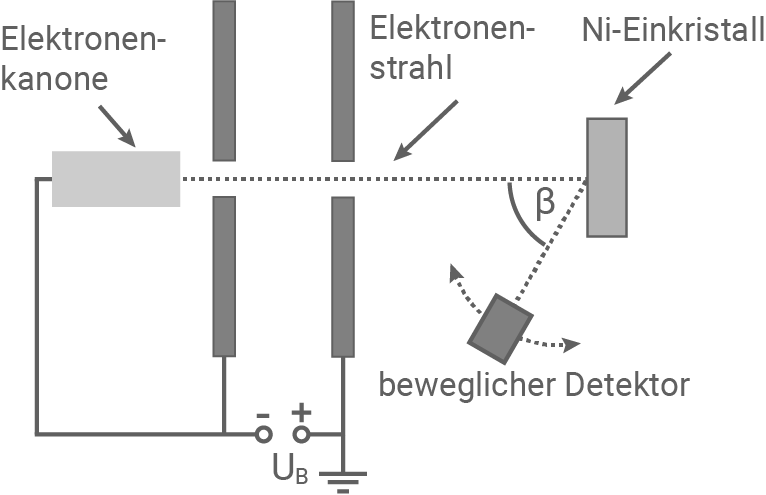
1
Nach Louis de Broglie kann jedem Teilchen jeweils eine Frequenz und eine Wellenlänge zugeordnet werden.
Gib die hierfür relevanten Formeln an und nenne die grundsätzliche Überlegung, die zu diesen Formeln führte.
(4 BE)
2
Elektronen mit der Masse  und der Ladung
und der Ladung  deren Anfangsgeschwindigkeit vernachlässigt werden soll, werden in einem elektrischen Feld mit der Spannung
deren Anfangsgeschwindigkeit vernachlässigt werden soll, werden in einem elektrischen Feld mit der Spannung  beschleunigt.
beschleunigt.
2.1
Berechne die Geschwindigkeit der Elektronen für 
2.2
Elektronen haben die Spannung  durchlaufen.
Leite die folgende Formel zur Berechnung der theoretischen Wellenlänge
durchlaufen.
Leite die folgende Formel zur Berechnung der theoretischen Wellenlänge  her, die diesen Elektronen zugeordnet wird.
(1)
her, die diesen Elektronen zugeordnet wird.
(1) 
(4 BE)
2.3
Berechne den Wert des obigen Ausdrucks  und zeige durch eine Einheitenrechnung, dass dieser Ausdruck die Einheit
und zeige durch eine Einheitenrechnung, dass dieser Ausdruck die Einheit  hat.
Berechne mithilfe von Formel (1) die Wellenlänge
hat.
Berechne mithilfe von Formel (1) die Wellenlänge  für
für  [zur Kontrolle:
[zur Kontrolle:  ]
]
(6 BE)
3
Im Davisson-Germer-Experiment zeigen sich - abhängig vom Streuwinkel  und der Beschleunigungsspannung
und der Beschleunigungsspannung  - ausgeprägte Intensitätsmaxima. Diese Maxima sind nur als Interferenzerscheinungen zu erklären, die durch Streuung der Elektronen an der Gitterstruktur des Nickeleinkristalls entstehen. Wegen der geringen Energie der Elektronen kann man annehmen, dass nur die oberste Atomschicht des Kristalls für die Streuung der Elektronen verantwortlich ist. Dabei wirkt die Anordnung der Atome für die Elektronen wie ein Reflexionsgitter mit der Gitterkonstante
- ausgeprägte Intensitätsmaxima. Diese Maxima sind nur als Interferenzerscheinungen zu erklären, die durch Streuung der Elektronen an der Gitterstruktur des Nickeleinkristalls entstehen. Wegen der geringen Energie der Elektronen kann man annehmen, dass nur die oberste Atomschicht des Kristalls für die Streuung der Elektronen verantwortlich ist. Dabei wirkt die Anordnung der Atome für die Elektronen wie ein Reflexionsgitter mit der Gitterkonstante  bei der Beugung von Licht. In Material 2 ist diese Streuung schematisch dargestellt.
bei der Beugung von Licht. In Material 2 ist diese Streuung schematisch dargestellt.
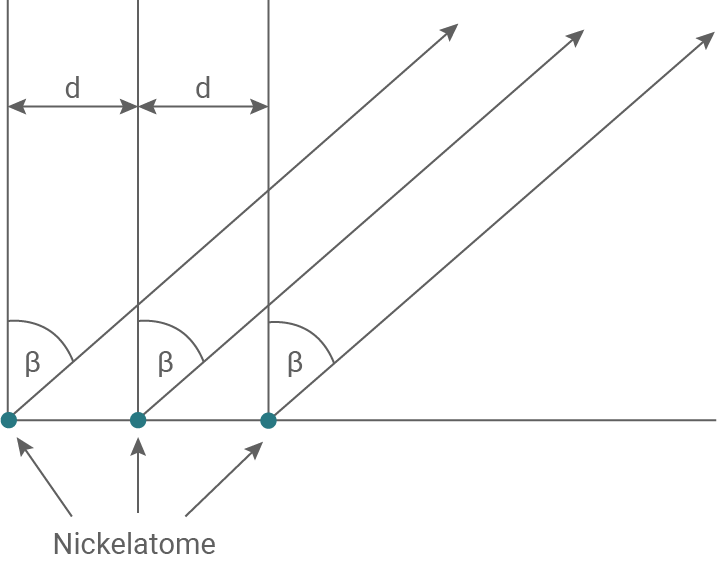
Material 2: Streuung von Elektronen an der Oberfläche eines Nickeleinkristalls (schematische Darstellung)

3.1
Erläutere für Materiewellen den Zusammenhang zwischen konstruktiver Interferenz, Intensitätsmaxima und Aufenthaltswahrscheinlichkeit.
Zeichne in Material 2 den Gangunterschied  ein und zeige die Gültigkeit der folgenden Formel.
(2)
ein und zeige die Gültigkeit der folgenden Formel.
(2)  Hierbei bedeuten
Hierbei bedeuten  die Ordnung der Maxima und
die Ordnung der Maxima und  der Abstand der einzelnen Nickelatome voneinander.
der Abstand der einzelnen Nickelatome voneinander.
(5 BE)
3.2
Die experimentellen Ergebnisse solcher Streuversuche mit unterschiedlichen Spannungen sind in Material 3 dargestellt.
Bestimme für  mithilfe der Formel (2) jeweils einen experimentellen Wert
mithilfe der Formel (2) jeweils einen experimentellen Wert  der Wellenlänge unter Verwendung von
der Wellenlänge unter Verwendung von 
 und
und  Bestätige anhand deiner Ergebnisse die Plausibilität der Annahme, dass es sich bei dem gemessenen Maximum um eines der 1. Ordnung handelt.
Bestätige anhand deiner Ergebnisse die Plausibilität der Annahme, dass es sich bei dem gemessenen Maximum um eines der 1. Ordnung handelt.
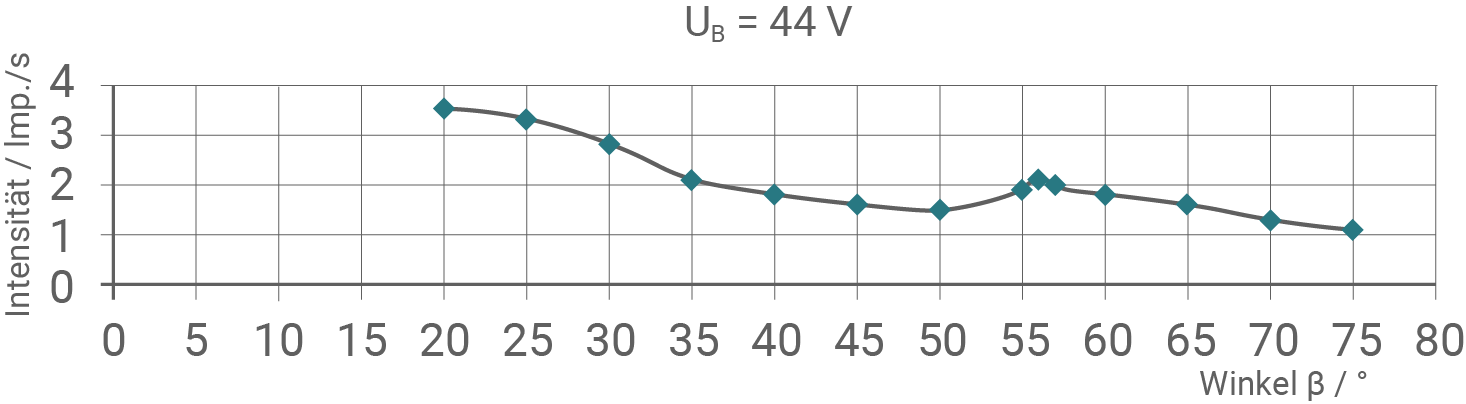
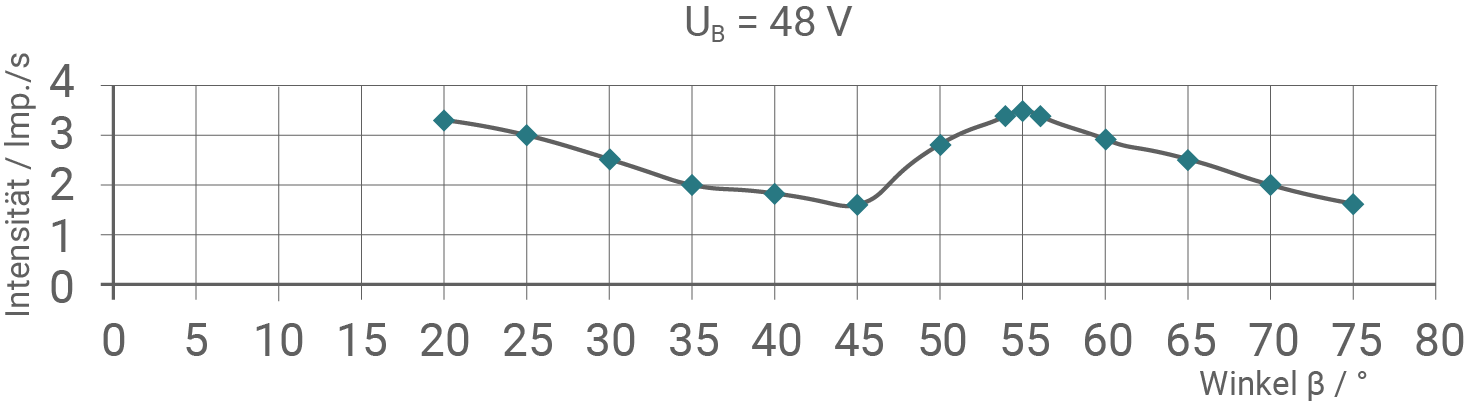
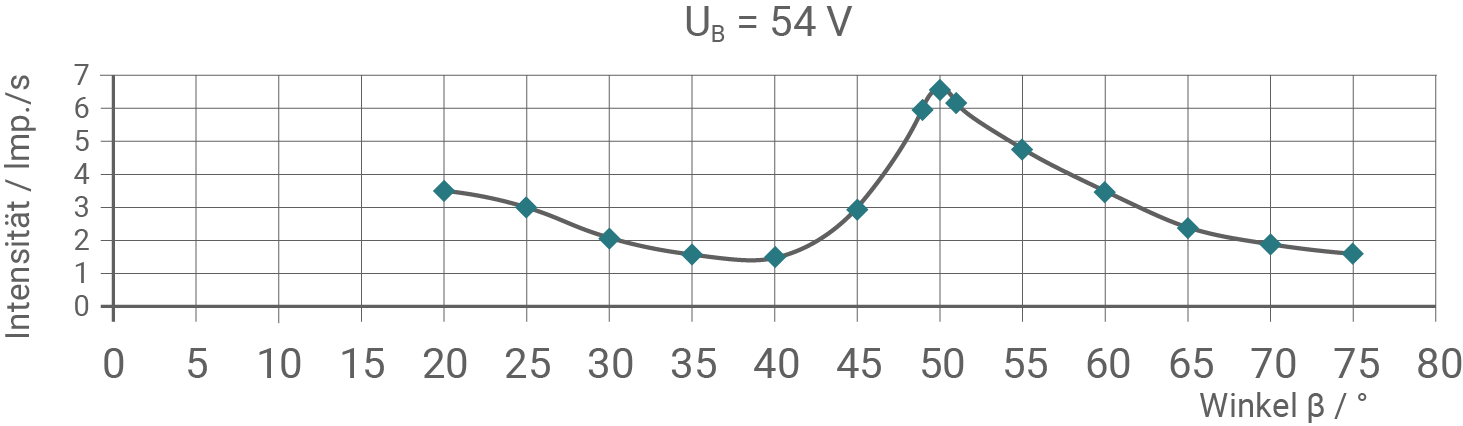
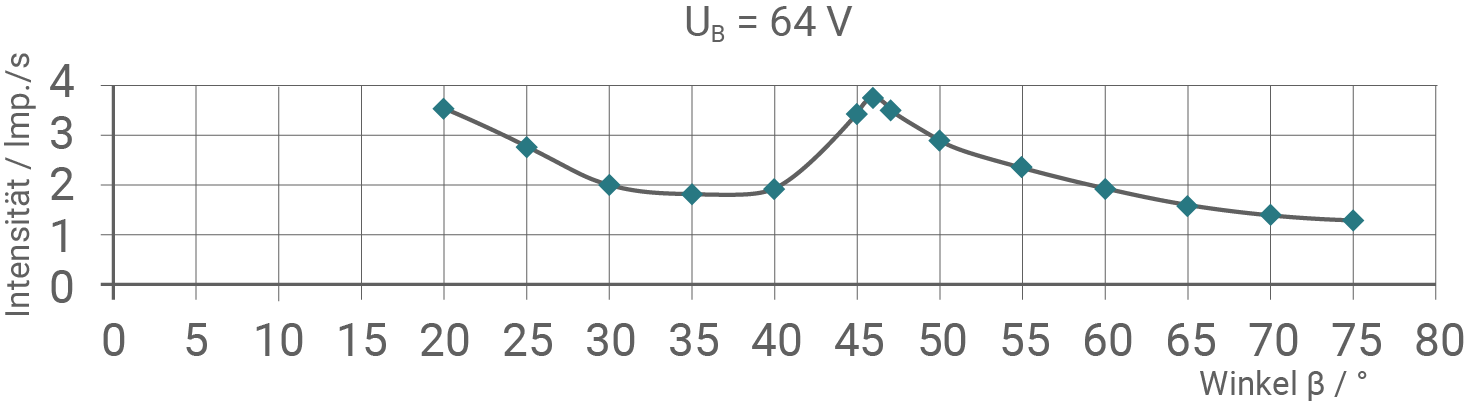
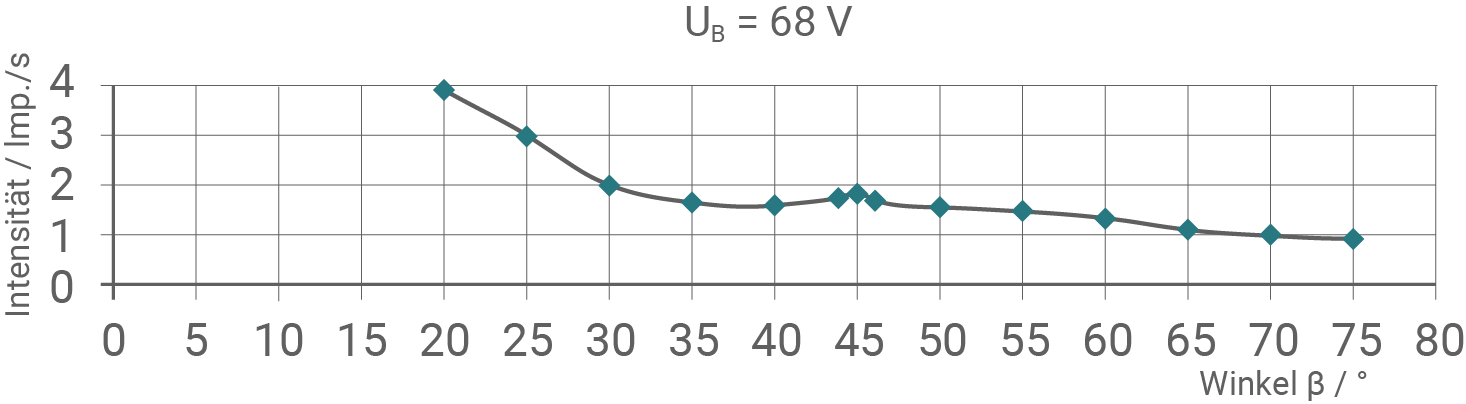
Material 3: Experimentelle Ergebnisse ‒ Messdiagramme





(5 BE)
3.3
Ermittle mithilfe von Material 3 für die restlichen Werte von  und
und  die zugehörigen Werte von
die zugehörigen Werte von 
(4 BE)
4
Nach der Formel (1) ist die Wellenlänge  für
für  proportional zu
proportional zu 
4.1
Bestätige rechnerisch diese Proportionalität für die Messergebnisse der Aufgaben 3.2 und 3.3.
Berechne die Proportionalitätskonstante unter Einbeziehung aller Messwerte und vergleiche diese quantitativ mit dem Ergebnis aus Aufgabe 2.3.
(8 BE)
4.2
1959 wurde von Claus Jönsson die Interferenz von Elektronen am Doppelspalt nachgewiesen. Hier soll das Experiment vereinfacht ohne elektronenoptische Elemente zur Vergrößerung des Interferenzmusters betrachtet werden.
Mit der Spannung  beschleunigte Elektronen durchlaufen senkrecht einen Doppelspalt mit einem Spaltabstand
beschleunigte Elektronen durchlaufen senkrecht einen Doppelspalt mit einem Spaltabstand  Im Abstand von
Im Abstand von  vom Doppelspalt wird ein Interferenzmuster registriert, bei dem der Abstand der beiden Maxima erster Ordnung
vom Doppelspalt wird ein Interferenzmuster registriert, bei dem der Abstand der beiden Maxima erster Ordnung  beträgt.
Berechne die Wellenlänge der Elektronen zum einen mithilfe der Ergebnisse des Doppelspaltversuchs und zum anderen mit Formel (1) und vergleiche diese quantitativ.
beträgt.
Berechne die Wellenlänge der Elektronen zum einen mithilfe der Ergebnisse des Doppelspaltversuchs und zum anderen mit Formel (1) und vergleiche diese quantitativ.
(7 BE)
4.3
Erkläre, warum das Experiment von Jönsson erst mehr als 30 Jahre nach dem Experiment von Davisson und Germer durchgeführt werden konnte.
(3 BE)
1
Formeln angeben

 Überlegung
Nicht nur Licht, sondern auch Materieteilchen wie Elektronen oder Atome besitzen Wellen- und Teilcheneigenschaften.
Welleneigenschaften werden repräsentiert durch
Überlegung
Nicht nur Licht, sondern auch Materieteilchen wie Elektronen oder Atome besitzen Wellen- und Teilcheneigenschaften.
Welleneigenschaften werden repräsentiert durch  und Teilcheneigenschaften durch
und Teilcheneigenschaften durch 
2.1
2.2
2.3
3.1
Zusammenhänge erläutern
Aus quantenmechanischer Sicht nehmen Teilchen keinen Ort an, der definierbar ist. Es ist jedoch möglich durch Materiewellen eine Aufenthaltswahrscheinlichkeit anzugeben.
Wenn die Materiewellen konstruktiv interferieren, so entstehen Intensitätsmaxima. Das bedeutet, dass die Aufenthaltswahrscheinlichkeit an diesem Ort maximal ist.
Gangunterschied
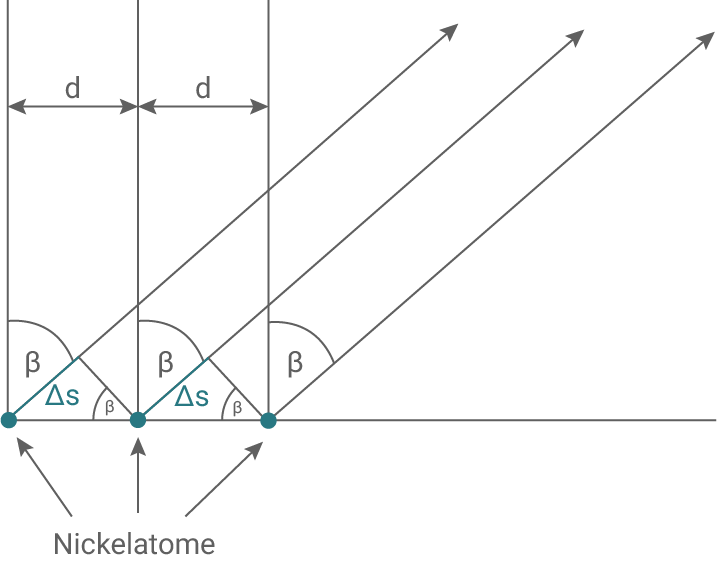 Bei Interferenz gilt:
Bei Interferenz gilt:  In der Abbildung sind rechtwinklige Dreiecke zu erkennen. In diesen ist folgender Zusammenhang gültig:
In der Abbildung sind rechtwinklige Dreiecke zu erkennen. In diesen ist folgender Zusammenhang gültig:  Einsetzen:
Einsetzen:
![\(\begin{array}[t]{rll}
\sin (\beta)&=& \dfrac{n \cdot \lambda }{d}&\quad \scriptsize \mid\;\cdot d \\[5pt]
\sin (\beta) \cdot d&=& n \cdot \lambda \\[5pt]
n \cdot \lambda &=& \sin (\beta) \cdot d
\end{array}\)](https://www.schullv.de/resources/formulas/dacab2686bfe339128406475ded4dca61f1215139edd1292c8c12b13f5fdcaff_light.svg)

3.2
3.3
Es gilt: 


| 44 | 56 | 178 |
| 48 | 55 | 176 |
| 64 | 46 | 155 |
| 68 | 45 | 152 |
4.1
Proportionalität nachweisen

![\(\begin{array}[t]{rll}
\lambda&=& \text{const} \cdot \dfrac{1}{\sqrt{ U _{ B }}}&\quad \scriptsize \mid\; \cdot \sqrt{ U _{ B }}\\[5pt]
\lambda\cdot \sqrt{U_B}&=& \text{const}
\end{array}\)](https://www.schullv.de/resources/formulas/757ac54831ee36a94d0a8007669e4da9c502b56dde4c424c19d27a0279e195ba_light.svg)


Die Werte sind näherungsweise konstant, womit die Proportionalität nachgewiesen ist.
Vergleich
Wert aus Teilaufgabe 2.3:

 Prozentuale Abweichung:
Prozentuale Abweichung:

 Die Messwerte stimmen somit sehr gut überein.
Die Messwerte stimmen somit sehr gut überein.
| 44 | 1,78 | 1,18 |
| 48 | 1,76 | 1,22 |
| 54 | 1,65 | 1,21 |
| 64 | 1,55 | 1,24 |
| 68 | 1,52 | 1,25 |
4.2
Es gilt:
 mit
mit  und
und  Wegen der Kleinwinkelnäherung
Wegen der Kleinwinkelnäherung  folgt:
folgt:
![\(\begin{array}[t]{rll}
\dfrac{ n \cdot \lambda}{ d }&=& \dfrac{\frac{1}{2} \cdot a _{ n }}{ e } &\quad \scriptsize \mid\; \cdot d \;\mid\;:n\\[5pt]
\lambda &=&\dfrac{a _n \cdot d }{ 2e\cdot n }
\end{array}\)](https://www.schullv.de/resources/formulas/b8e63898aa7afa96d8a4ed6bf82cbb9e382927358feed21ade9bac42e602b5b4_light.svg) Für
Für  folgt:
folgt:


 Anwendung der Formel:
Anwendung der Formel:


 Vergleich der Werte:
Die beiden Werte unterschieden sich bis zur zweiten Nachkommastelle nicht. Die Abweichung ist minimal. Das Doppelspaltexperminet bestätigt somit den theoretischen Wert sehr gut.
Vergleich der Werte:
Die beiden Werte unterschieden sich bis zur zweiten Nachkommastelle nicht. Die Abweichung ist minimal. Das Doppelspaltexperminet bestätigt somit den theoretischen Wert sehr gut.
4.3
Da die De-Broglie-Wellenlängen der Elektronen so klein sind, muss der Doppelspalt, welcher sie beugt, einen sehr geringen Spaltabstand und eine geringe Spaltbreite besitzen.
Die Herstellung eines solchen Spaltes war erst Ende der 1950er Jahre möglich.