Vorschlag B2
Kontinuierlich arbeitende und gepulste Laser
1
Seit dem Bau des ersten Lasers durch Theodore Maiman im Jahr 1960 entwickelte sich dieser in einer Vielzahl von Arbeitsbereichen zu einem unverzichtbaren Hilfsmittel. In den folgenden Aufgaben werden verschiedene Laser betrachtet. In Schulen ist der Helium-Neon-Laser (He-Ne-Laser) weit verbreitet, der sein charakteristisches rotes Licht kontinuierlich abstrahlt.
1.1
Nenne zwei Eigenschaften, die Laserlicht vom Licht anderer Lichtquellen unterscheiden.
(2 BE)
1.2
Begründe mithilfe von Material 1 und Material 2, dass der Übergang von  nach
nach  zur Emission des roten Laserlichts führt.
zur Emission des roten Laserlichts führt.
Erkläre anhand von Material 1 und Material 3 die Funktionsweise des He-Ne-Lasers unter Verwendung der Begriffe Besetzungsinversion, stimulierte Emission und stehende Welle.
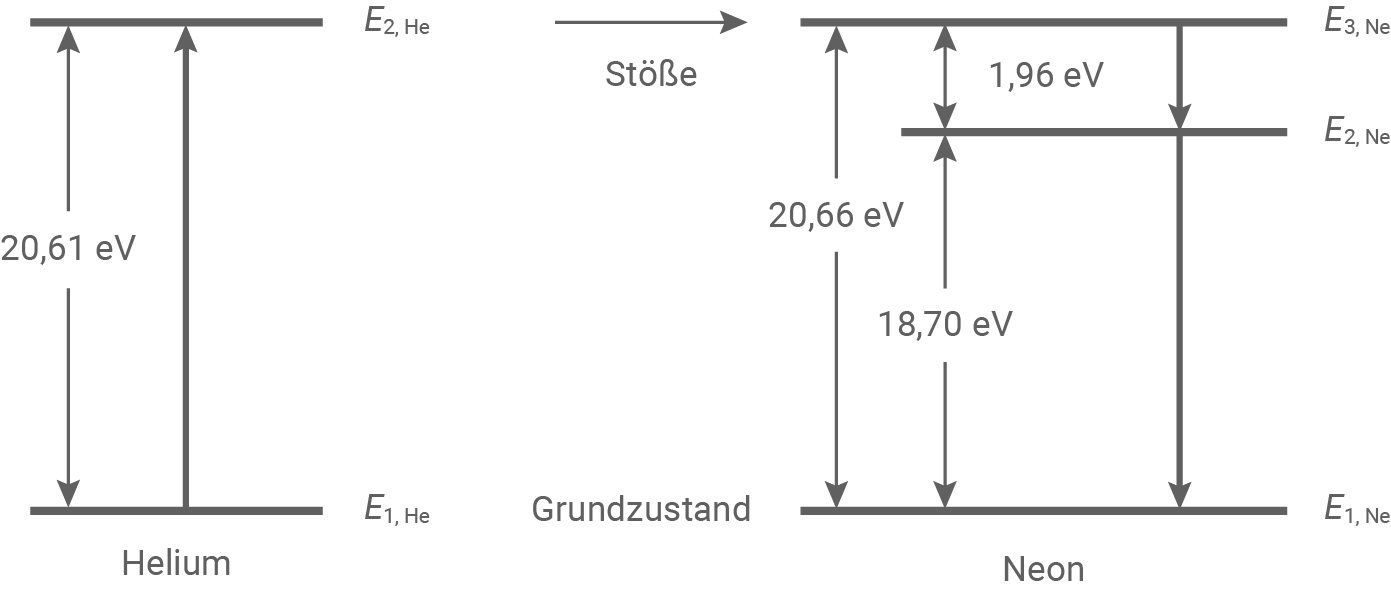
Die angegebenen Wellenlängen sind ungefähre Werte.
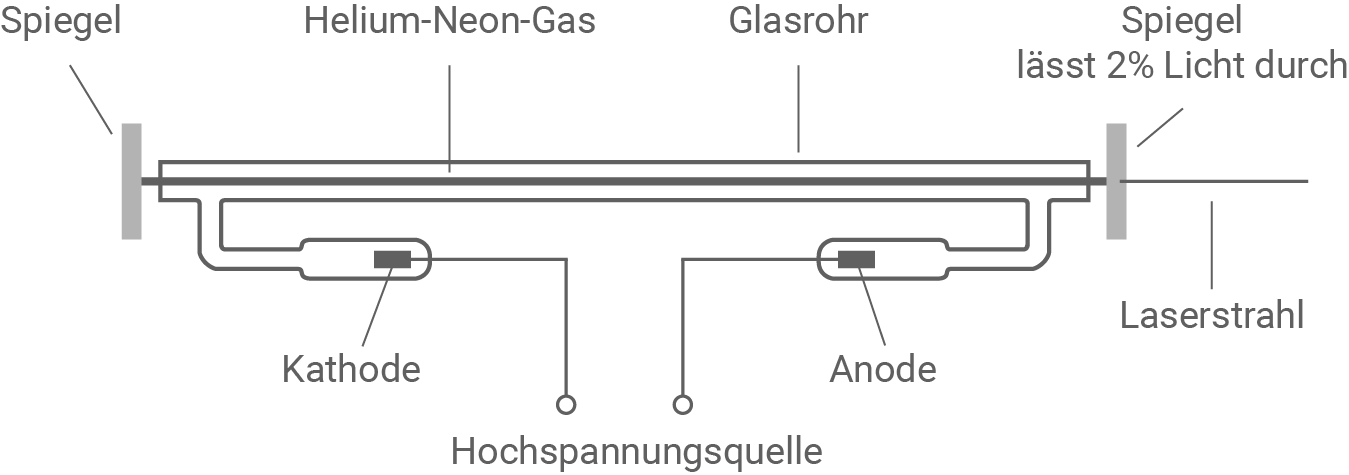
Erkläre anhand von Material 1 und Material 3 die Funktionsweise des He-Ne-Lasers unter Verwendung der Begriffe Besetzungsinversion, stimulierte Emission und stehende Welle.
Material 1
Vereinfachtes Energieniveauschema eines He-Ne-Lasers
Material 2
Spektralbereiche elektromagnetischer Strahlung| Spektralbereich | Wellenlänge in |
|---|---|
| Ultraviolett | 10-390 |
| Violett | 390-430 |
| Blau | 430-490 |
| Grün | 490-570 |
| Gelb | 570-600 |
| Orange | 600-620 |
| Rot | 620-780 |
| Infrarot | 780-300000 |
Material 3
Schematischer Aufbau eines He-Ne-Lasers
(8 BE)
1.3
Bestimme die Geschwindigkeit, die ein Elektron mindestens haben muss, um ein ruhendes Helium-Atom aus dem Grundzustand  in den Zustand
in den Zustand  anzuregen.
anzuregen.
Gib die zur Beschleunigung der Elektronen aus der Ruhe mindestens notwendige Spannung an.
Gib die zur Beschleunigung der Elektronen aus der Ruhe mindestens notwendige Spannung an.
(4 BE)
1.4
Bestimme den nach Material 1 möglichen maximalen Wirkungsgrad eines He-Ne-Lasers in Prozent und begründe, warum dieser in Wirklichkeit nicht erreicht werden dürfte. Als Wirkungsgrad bezeichnet man das Verhältnis von Energie der erzeugten Laserstrahlung zur aufgewandten Energie.
(5 BE)
2
Im Gegensatz zum kontinuierlich arbeitenden He-Ne-Laser spielen in vielen Anwendungen sogenannte Pulslaser eine große Rolle. Diese arbeiten nicht im Dauerbetrieb, sondern jeweils nur für kurze Zeiten, sodass kurze Laserpulse entstehen. Im Folgenden soll ein Neodym-dotierter Yttrium-Aluminium-Granat-Laser (Nd/YAG-Laser) betrachtet werden, der bei einer Wellenlänge von  während einer Pulsdauer von
während einer Pulsdauer von  eine Leistung von
eine Leistung von  hat.
hat.
2.1
Berechne die Energie  eines solchen Laserpulses.
[zur Kontrolle:
eines solchen Laserpulses.
[zur Kontrolle: ![\(E_{\text {Puls }}=1,2\,\text J]\)](https://www.schullv.de/resources/formulas/b7df3fa384f606d4b49ee44e4ad8a8cb2cf4eb1ab20886c717e89d6119fbc13f_light.svg)
(2 BE)
2.2
Die Energie  des Laserpulses nach einem Durchgang durch eine Schicht der Dicke
des Laserpulses nach einem Durchgang durch eine Schicht der Dicke  bei einer Anfangsenergie von
bei einer Anfangsenergie von  kann mit der Gleichung
kann mit der Gleichung  berechnet werden. Der darin verwendete Absorptionskoeffizient
berechnet werden. Der darin verwendete Absorptionskoeffizient  hängt vom durchstrahlten Material und von der Wellenlänge des verwendeten Lasers ab.
hängt vom durchstrahlten Material und von der Wellenlänge des verwendeten Lasers ab.
Bestätige unter Verwendung der Daten in Material 4, dass die Energie, die der Laserpuls auf einer Strecke in Wasser abgibt,
in Wasser abgibt,  beträgt.
beträgt.
Berechne die mittlere Temperaturerhöhung des auf dieser Strecke durchstrahlten Wassers. Der Strahl hat einen kreisförmigen Querschnitt mit einem Durchmesser von
des auf dieser Strecke durchstrahlten Wassers. Der Strahl hat einen kreisförmigen Querschnitt mit einem Durchmesser von  .
.
Zur Erwärmung von Wasser um
Wasser um  benötigt man eine Energie von
benötigt man eine Energie von  .
.
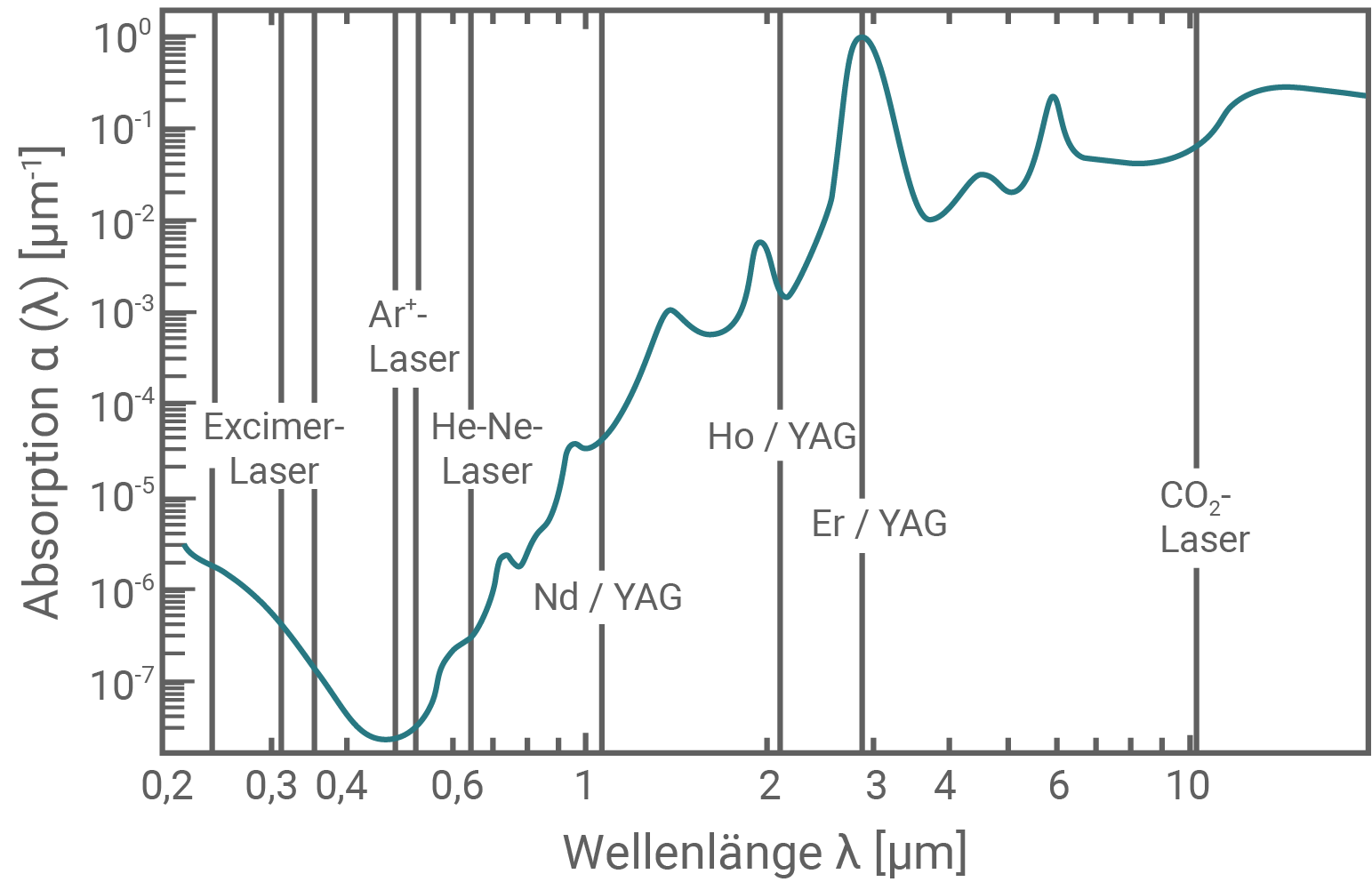 Die Emissionslinien der Laser sind durch senkrechte Striche gekennzeichnet.
Die Emissionslinien der Laser sind durch senkrechte Striche gekennzeichnet.
Beachte die nicht-lineare Skalierung der Achsen und die Einheit der vertikalen Achse!
der vertikalen Achse!
Bestätige unter Verwendung der Daten in Material 4, dass die Energie, die der Laserpuls auf einer Strecke
Berechne die mittlere Temperaturerhöhung
Zur Erwärmung von
Material 4
Absorptionskoeffizient elektromagnetischer Strahlung in Wasser
Beachte die nicht-lineare Skalierung der Achsen und die Einheit
(8 BE)
2.3
Für Laser gelten strenge Sicherheitsvorschriften. Insbesondere ist es wichtig, die Augen vor Laserlicht zu schützen. Bei einem Laserexperiment mit gleichen Bedingungen wie in Aufgabe 2.2 wird  bestimmt.
bestimmt.
Beurteile auf der Basis dieses Ergebnisses und der Tatsache, dass der Glaskörper des Auges im Wesentlichen aus Wasser besteht, ob besondere Schutzvorkehrungen für die Augen notwendig sind.
Beurteile auf der Basis dieses Ergebnisses und der Tatsache, dass der Glaskörper des Auges im Wesentlichen aus Wasser besteht, ob besondere Schutzvorkehrungen für die Augen notwendig sind.
(2 BE)
3
Nun wird der Laserpuls aus Aufgabe 2 senkrecht auf ein kleines quadratisches Goldblättchen (Kantenlänge  , Dicke
, Dicke  ) gerichtet, das an einem Faden der Länge
) gerichtet, das an einem Faden der Länge  aufgehängt ist (Material 5). Dies führt zu einer Auslenkung des Blättchens um den Winkel
aufgehängt ist (Material 5). Dies führt zu einer Auslenkung des Blättchens um den Winkel  .
.
Im Folgenden soll angenommen werden, dass alle Photonen reflektiert werden und dass dabei das Doppelte ihres Impulses auf das Blättchen übertragen wird.
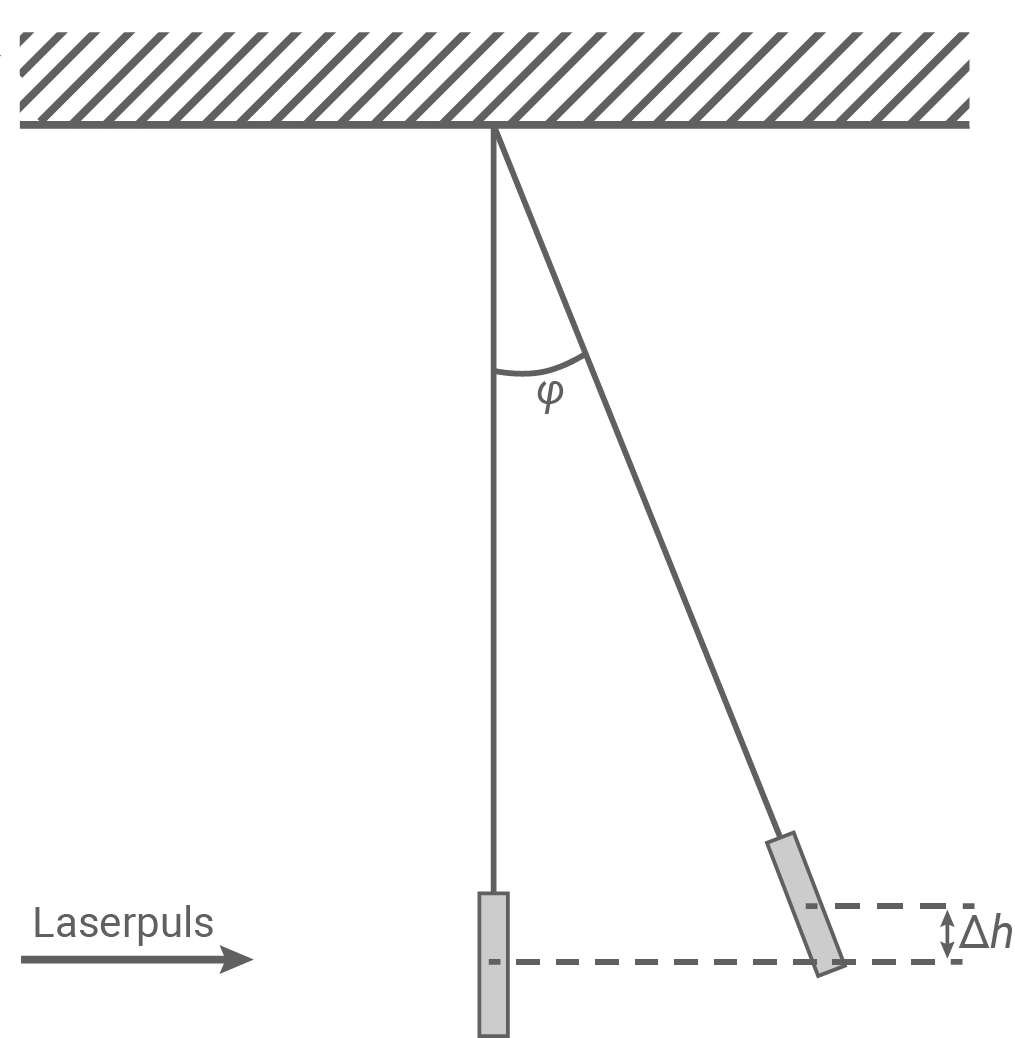
 ist der Höhengewinn des Goldblättchens aufgrund der Auslenkung.
ist der Höhengewinn des Goldblättchens aufgrund der Auslenkung.
Im Folgenden soll angenommen werden, dass alle Photonen reflektiert werden und dass dabei das Doppelte ihres Impulses auf das Blättchen übertragen wird.
Material 5
Laserpuls und aufgehängtes Goldblättchen
3.1
Berechne die Anzahl der Photonen in dem Puls sowie den Gesamtimpuls  dieser Photonen.
[zur Kontrolle:
dieser Photonen.
[zur Kontrolle:  ]
]
(7 BE)
3.2
Berechne die Masse des Goldplättchens. Gold hat eine Dichte von  .
.
Berechne die maximale Geschwindigkeit (Geschwindigkeit zu Beginn der Bewegung), auf die das Goldplättchen durch den Laserpuls beschleunigt wird und den Höhengewinn des Goldblättchens.
des Goldblättchens.
Dazu soll der Einfluss der Luftreibung sowie der Masse und der Beschaffenheit des Fadens vernachlässigt werden, ebenso wird das Goldblättchen als punktförmig angenommen.
Berechne die maximale Geschwindigkeit (Geschwindigkeit zu Beginn der Bewegung), auf die das Goldplättchen durch den Laserpuls beschleunigt wird und den Höhengewinn
Dazu soll der Einfluss der Luftreibung sowie der Masse und der Beschaffenheit des Fadens vernachlässigt werden, ebenso wird das Goldblättchen als punktförmig angenommen.
(9 BE)
3.3
Beurteile, ob und gegebenenfalls wie sich der Ausschlag des Blättchens ändert, wenn ein Laser mit gleicher Pulsdauer, gleicher Leistung, aber größerer Wellenlänge verwendet wird.
(3 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.1
- Laserlicht ist monochromatisch, im Gegensatz zu den breiteren Wellenlängenverteilungen bei anderen Lichtquellen.
- Laserlicht ist kohärent, da die Wellen eine konstante Phasendifferenz aufweisen, im Gegensatz zu herkömmlichem Licht.
1.2
Emission des roten Laserlichts
Eine Energiedifferenz von  zwischen den Zuständen
zwischen den Zuständen  und
und  zeigt sich im Energieniveauschema des He-Ne-Lasers. Beim Übergang zwischen diesen Niveaus werden Photonen mit exakt dieser Energie emittiert, und die zugehörige Wellenlänge dieser Photonen lässt sich ableiten:
zeigt sich im Energieniveauschema des He-Ne-Lasers. Beim Übergang zwischen diesen Niveaus werden Photonen mit exakt dieser Energie emittiert, und die zugehörige Wellenlänge dieser Photonen lässt sich ableiten:
![\(\begin{array}[t]{rll}
E&=&h\cdot f &\quad \scriptsize \mid\;f=\dfrac{c}{\lambda} \\[5pt]
E&=&\dfrac{h\cdot c}{\lambda} &\quad \scriptsize \mid\;\cdot \dfrac{\lambda}{E} \\[5pt]
\lambda&=&\dfrac{h\cdot c}{E}
\end{array}\)](https://www.schullv.de/resources/formulas/cce6d8f14fe7466a68f9759e6b97dc59e6f00b6b5cc198f828f50d83b887ca68_light.svg) Einsetzen der Werte liefert:
Einsetzen der Werte liefert:
![\(\begin{array}[t]{rll}
\lambda&=&\dfrac{h\cdot c}{E} &\quad \scriptsize \\[5pt]
&=&\dfrac{6,626 \cdot 10^{-34} \,\text{Js} \cdot 3,00 \cdot 10^8 \,\frac{\text{m}}{\text{s}}}{1,96 \,\text{eV} \cdot 1,602 \cdot 10^{-19} \,\text{C}} &\quad \scriptsize \\[5pt]
&=& 6,33 \cdot 10^{-7} \,\text{m} &\quad \scriptsize \\[5pt]
&=& 633 \,\text{nm}
\end{array}\)](https://www.schullv.de/resources/formulas/1171931b3d9eb9383b66a727c87921a1aae347335d7796ba3791bc747a5f0e34_light.svg) Die berechnete Wellenlänge
Die berechnete Wellenlänge  entspricht dem roten Bereich im elektromagnetischen Spektrum (Material 2).
Funktionsweise eines He-Ne-Lasers
Gasentladung: Durch Anlegen einer Hochspannung entsteht im He-Ne-Laser zwischen Kathode und Anode ein elektrisches Feld. In der Glasröhre ist ein Gemisch aus Helium und Neon vorhanden. An der Kathode befinden sich freie Elektronen, die von der Anode angezogen werden. Die hohe Spannung verleiht den Elektronen genug kinetische Energie, um eine Gasentladung auszulösen.
Besetzungsinversion in Neon: Durch das Gas bewegen sich Elektronen, die Heliumatome anregen. Die übertragene Energie wird durch Stöße auf Neonatome übertragen, wodurch eine Besetzungsinversion in Neon entsteht. Dabei sind mehr Atome im angeregten Zustand
entspricht dem roten Bereich im elektromagnetischen Spektrum (Material 2).
Funktionsweise eines He-Ne-Lasers
Gasentladung: Durch Anlegen einer Hochspannung entsteht im He-Ne-Laser zwischen Kathode und Anode ein elektrisches Feld. In der Glasröhre ist ein Gemisch aus Helium und Neon vorhanden. An der Kathode befinden sich freie Elektronen, die von der Anode angezogen werden. Die hohe Spannung verleiht den Elektronen genug kinetische Energie, um eine Gasentladung auszulösen.
Besetzungsinversion in Neon: Durch das Gas bewegen sich Elektronen, die Heliumatome anregen. Die übertragene Energie wird durch Stöße auf Neonatome übertragen, wodurch eine Besetzungsinversion in Neon entsteht. Dabei sind mehr Atome im angeregten Zustand  als im energieärmeren Zustand
als im energieärmeren Zustand  Photonenentstehung: Spontane Übergänge von
Photonenentstehung: Spontane Übergänge von  zu
zu  führen zur Entstehung von Photonen im Laserübergang. Wenn diese Photonen senkrecht reflektiert werden und erneut durch das Gas gehen, können sie ein Neonatom in
führen zur Entstehung von Photonen im Laserübergang. Wenn diese Photonen senkrecht reflektiert werden und erneut durch das Gas gehen, können sie ein Neonatom in  zur stimulierte Emission anregen. Das daraus resultierende Photon behält die Eigenschaften des auslösenden Photons bei.
Laserstrahlbildung: Der Prozess verstärkt das Licht durch einen Resonator aus zwei Spiegeln. Durch Überlagerung hin- und herlaufender Wellen entsteht Verstärkung. Ein teildurchlässiger Spiegel, der
zur stimulierte Emission anregen. Das daraus resultierende Photon behält die Eigenschaften des auslösenden Photons bei.
Laserstrahlbildung: Der Prozess verstärkt das Licht durch einen Resonator aus zwei Spiegeln. Durch Überlagerung hin- und herlaufender Wellen entsteht Verstärkung. Ein teildurchlässiger Spiegel, der  des Lichts hindurchlässt, formt den Laserstrahl.
des Lichts hindurchlässt, formt den Laserstrahl.
1.3
nötige Geschwindigkeit
Gegeben: 
 Gesucht:
Gesucht:  Lösung: Die Energiedifferenz
Lösung: Die Energiedifferenz  zwischen den Zuständen
zwischen den Zuständen  und
und  beträgt
beträgt  Diese Energie müssen die Elektronen als kinetische Energie besitzen:
Diese Energie müssen die Elektronen als kinetische Energie besitzen:
![\(\begin{array}[t]{rll}
E_{\text{kin}}&=& \dfrac{1}{2}\cdot m_e\cdot v^2 &\quad \scriptsize \mid\; \cdot \dfrac{2}{m_e}\\[5pt]
\dfrac{2 \cdot E_{\text{kin}}}{m_e}&=& v^2 &\quad \scriptsize \mid\; \sqrt{\;}\\[5pt]
\sqrt{\dfrac{2\cdot E_{\text{kin}}}{m_e}}&=& v &\quad \scriptsize \\[5pt]
v&=& \sqrt{\dfrac{2\cdot E_{\text{kin}}}{m_e}} &\quad \scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/f03594b0b60b1f52a17c2ea1e5800d3852a20757df840b69bc7e31d020de77f0_light.svg) Einsetzen der Werte liefert:
Einsetzen der Werte liefert:
![\(\begin{array}[t]{rll}
v&=& \sqrt{\dfrac{2\cdot E_{\text{kin}}}{m_e}}&\quad \scriptsize \\[5pt]
&=& \sqrt{\dfrac{2 \cdot 20,61 \,\text{eV} \cdot 1,602 \cdot 10^{-19} \,\text{C}}{9,11 \cdot 10^{-31} \,\text{kg}}}&\quad \scriptsize \\[5pt]
&=& 2,69\cdot 10^6 \,\dfrac{\text{m}}{\text{s}}
\end{array}\)](https://www.schullv.de/resources/formulas/ad7c48e88417ddf428e64eafe5ceff61b3df09319da39c0320b2da534248c4ed_light.svg) Angabe der Spannung
Eine Spannung von
Angabe der Spannung
Eine Spannung von  ist erforderlich, um Elektronen auf eine Energie von
ist erforderlich, um Elektronen auf eine Energie von  zu beschleunigen.
zu beschleunigen.
1.4
Bestimmung des Wirkungsgrads
Gegeben: notwendige Energie zur Anregung des Heliumatoms 
 Gesucht: Wirkungsgrad
Lösung:
Nichterreichen des maximalen Wirkungsgrad in der Praxis
Maximaler Wirkungsgrad erfordert Stoßpartner für Elektronen, eine sehr gute Übertragung der Helium-Energie auf Neon und die Vermeidung nicht kohärenter Strahlung. In der Praxis kommt es jedoch zu Einzelelektronenanregungen aufgrund mangelnder Stoßpartner, unvollständiger Helium-Energieübertragung auf Neon, nicht ausschließlich stimulierte Emission bei Neon, Energieverlusten durch Gasanregung und Lichtverlusten durch Spiegelreflexion und -absorption im He-Ne-Laser.
Gesucht: Wirkungsgrad
Lösung:
Nichterreichen des maximalen Wirkungsgrad in der Praxis
Maximaler Wirkungsgrad erfordert Stoßpartner für Elektronen, eine sehr gute Übertragung der Helium-Energie auf Neon und die Vermeidung nicht kohärenter Strahlung. In der Praxis kommt es jedoch zu Einzelelektronenanregungen aufgrund mangelnder Stoßpartner, unvollständiger Helium-Energieübertragung auf Neon, nicht ausschließlich stimulierte Emission bei Neon, Energieverlusten durch Gasanregung und Lichtverlusten durch Spiegelreflexion und -absorption im He-Ne-Laser.
2.1
Für die Leistung  gilt:
gilt:
![\(\begin{array}[t]{rll}
P&=& \dfrac{\text{E}_{\text {Puls }}}{\text{t}} &\quad \scriptsize \mid\; \cdot t \\[5pt]
P\cdot t&=& \text{E}_{\text {Puls }} &\quad \scriptsize \\[5pt]
\text{E}_{\text {Puls }}&=& P\cdot t
\end{array}\)](https://www.schullv.de/resources/formulas/5bbff5b0f3fa2c5077bc3dbb7f7fa4b1ebeed78a9fa8decb8e508e8a03281deb_light.svg) Einsetzen der Werte liefert:
Einsetzen der Werte liefert:
![\(\begin{array}[t]{rll}
\text{E}_{\text {Puls }}&=& P\cdot t&\quad \scriptsize \\[5pt]
&=& 3 \cdot 10^6 \,\text{W} \cdot 400 \cdot 10^{-9} \,\text{s}&\quad \scriptsize \\[5pt]
&=& 1,2 \,\text J
\end{array}\)](https://www.schullv.de/resources/formulas/7f60ef5c3a591844846fd0da3030b19c0e2877c312f76582015263c511f038f4_light.svg)
2.2
Bestätigung der Energiemenge
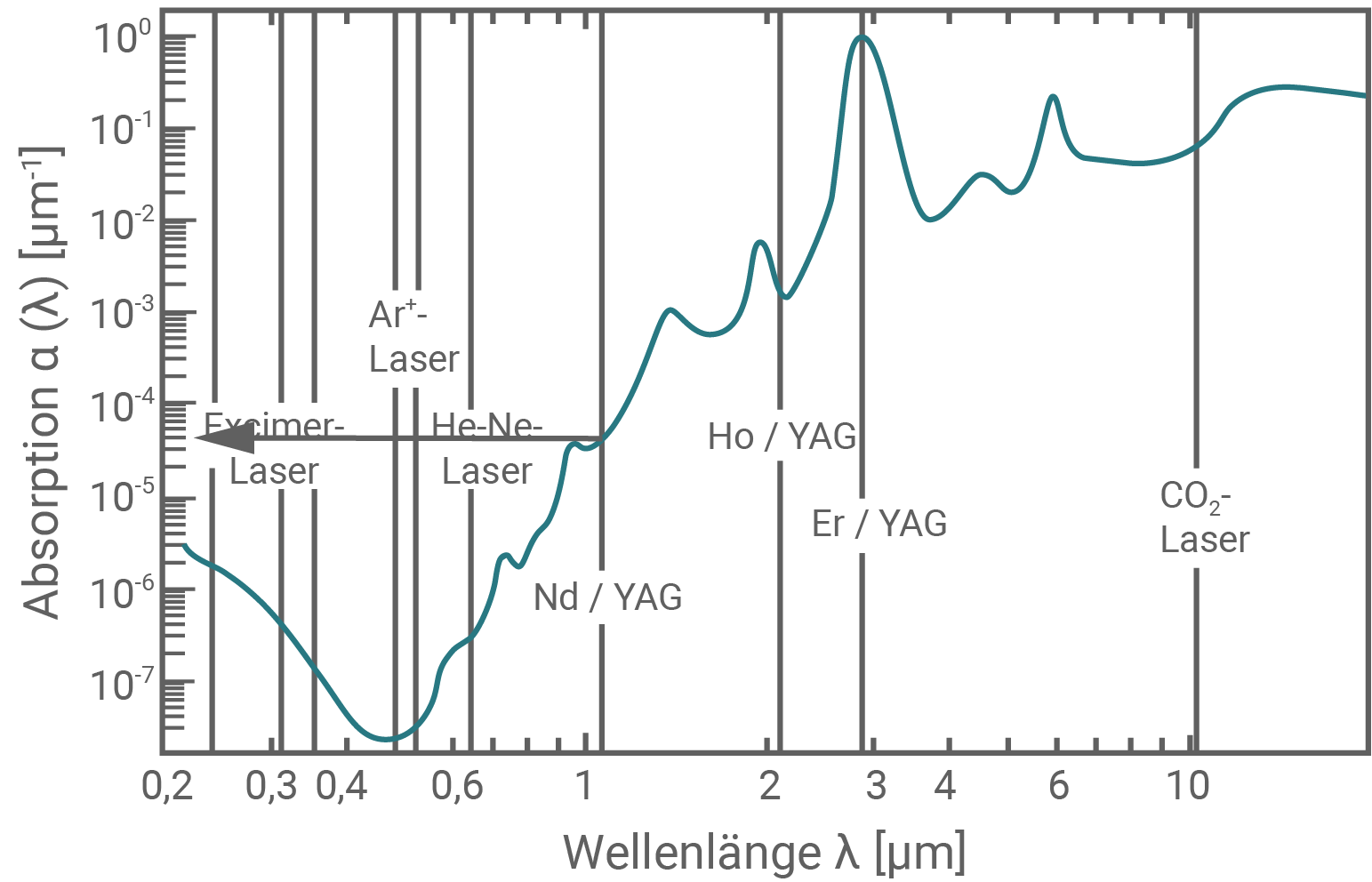 Anhand des dargestellten Pfeils ist zusehen, dass die senkrechte Achse genau bei dem dritten Strich über der Markierung von
Anhand des dargestellten Pfeils ist zusehen, dass die senkrechte Achse genau bei dem dritten Strich über der Markierung von  geschnitten wird. Der abgelesene Absorptionskoeffizient beträgt somit
geschnitten wird. Der abgelesene Absorptionskoeffizient beträgt somit  Gegeben:
Gegeben: 
 ,
, Gesucht:
Gesucht:  Lösung:
Der Laserimpuls hat also während des Durchlaufens der Wasserschicht von
Lösung:
Der Laserimpuls hat also während des Durchlaufens der Wasserschicht von  eine Energie von
eine Energie von  abgegeben.
mittlere Temperaturerhöhung
Gegeben:
abgegeben.
mittlere Temperaturerhöhung
Gegeben: 

 erwärmt
erwärmt  Wasser um
Wasser um  Gesucht:
Gesucht:  Lösung:
Da der Laserstrahl laut Aufgabenstellung einen kreisförmigen Querschnitt besitzt, lässt sich die vom Laserpuls durchstrahlte Wassermenge als zylindrisches Volumen auffassen:
Lösung:
Da der Laserstrahl laut Aufgabenstellung einen kreisförmigen Querschnitt besitzt, lässt sich die vom Laserpuls durchstrahlte Wassermenge als zylindrisches Volumen auffassen:
![\(\begin{array}[t]{rll}
V_{\text {Zylinder }}&=& \pi \cdot r^2 \cdot d &\quad \scriptsize \\[5pt]
&=& \pi \cdot(0,002 \,\text{dm})^2 \cdot 0,1 \,\text{dm} &\quad \scriptsize \\[5pt]
&=& 1,26 \cdot 10^{-6} \,\text{dm}^3 &\quad \scriptsize \\[5pt]
&=& 1,26 \cdot 10^{-6} \,\ell
\end{array}\)](https://www.schullv.de/resources/formulas/39d11eeb3df95af2ec29db330aef1d4934f4684842b1681a6b041408a6f54c0a_light.svg) Für die Erwärumung von
Für die Erwärumung von  Wasser gilt:
Für ein Wasservolumen von
Wasser gilt:
Für ein Wasservolumen von  folgt:
Die Temperatur des Wasservolumens von
folgt:
Die Temperatur des Wasservolumens von  wird durch die Energie von
wird durch die Energie von  um
um 

2.3
Ein Temperaturunterschied von 76 Kelvin oder 76 Grad Celsius entsteht, indem eine 1 cm dicke Wasserschicht durchstrahlt wird. Der 2 cm durchmessende Glaskörper im Auge erhitzt sich bis zum Mittelpunkt. Ein Anstieg um 76 °C stellt eine ernsthafte Gefahr für das Auge dar, da die Energie ausreicht, um dauerhafte Schäden zu verursachen. Schutzvorrichtungen sind daher zwingend erforderlich.
3.1
Anzahl der Photonen
Für die Energie eines Photons mit der Wellenlänge  gilt:
Für die Anzahl
gilt:
Für die Anzahl  der Photonen ergibt sich:
der Photonen ergibt sich:
![\(\begin{array}[t]{rll}
n&=&\dfrac{{E}_{\text {Puls }}}{{E}_{\text {Photon }}} &\quad \scriptsize \\[5pt]
&=& \dfrac{1,2 \,\text{J}}{1,868 \cdot 10^{-19} \,\text{J}} &\quad \scriptsize \\[5pt]
&=& 6,4\cdot 10^{18}
\end{array}\)](https://www.schullv.de/resources/formulas/765e0cdbfc205b3cb92463356a900b939e99649be0d35d747a3a258a53f972f6_light.svg) Gesamtimpuls
Der Gesamtimpuls ist die Summe der Impulse aller Photonen:
Gesamtimpuls
Der Gesamtimpuls ist die Summe der Impulse aller Photonen:
3.2
Masse des Goldblättchens
Gegeben:  Gesucht:
Gesucht:  Lösung:
Lösung: ![\(\begin{array}[t]{rll}
\rho_{\text{Gold}}&=& \dfrac{m}{V} &\quad \scriptsize \mid\;\cdot V \\[5pt]
\rho_{\text{Gold}}\cdot V&=& m &\quad \scriptsize \\[5pt]
m&=& \rho_{\text{Gold}}\cdot V
\end{array}\)](https://www.schullv.de/resources/formulas/de9c3e0d3f2df5ae6550ab1c9dc1c2fc19a87dda705cc43de10eb62d6cbb5352_light.svg) Einsetzen der Werte liefert:
maximale Geschwindigkeit
Die Photonen werden vollständig reflektiert und übertragen dabei das Doppelte ihres Impulses auf das Blättchen. Somit gilt für den übertragenen Impuls:
Einsetzen der Werte liefert:
maximale Geschwindigkeit
Die Photonen werden vollständig reflektiert und übertragen dabei das Doppelte ihres Impulses auf das Blättchen. Somit gilt für den übertragenen Impuls:
![\(\begin{array}[t]{rll}
p&=& 2\cdot p_{\text{ges}}&\quad \scriptsize \\[5pt]
&=& 2 \cdot 4,0 \cdot 10^{-9} \,\dfrac{\text{kg} \cdot \text{m}}{\text{s}}&\quad \scriptsize \\[5pt]
&=& 8,0 \cdot 10^{-9} \,\dfrac{\text{kg} \cdot \text{m}}{\text{s}}
\end{array}\)](https://www.schullv.de/resources/formulas/b3b989231e80baa238560abefdae7eb5d22b52c9afcfbae7bf20b26a67dc3ab5_light.svg) Für die Anfangsgeschwindigkeit
Für die Anfangsgeschwindigkeit  ergibt sich:
ergibt sich:
![\(\begin{array}[t]{rll}
p&=&m\cdot v &\quad \scriptsize \mid\;\cdot \dfrac{1}{m} \\[5pt]
\dfrac{p}{m}&=& v &\quad \scriptsize \\[5pt]
v&=& \dfrac{p}{m}
\end{array}\)](https://www.schullv.de/resources/formulas/b7b9cc5ddd6b18d51c31d3143500fcadf99b49877ad6f3fc27fcb8c2a31fc93d_light.svg) Einsetzen der Werte lifert:
Einsetzen der Werte lifert:
![\(\begin{array}[t]{rll}
v&=& \dfrac{p}{m} &\quad \scriptsize \\[5pt]
&=& \dfrac{8,0 \cdot 10^{-9} \,\dfrac{\text{kg} \cdot \text{m}}{\text{s}}}{2,4 \cdot 10^{-8} \,\text{kg}}&\quad \scriptsize \\[5pt]
&=& 0,33 \,\dfrac{\text{m}}{\text{s}}
\end{array}\)](https://www.schullv.de/resources/formulas/d048333743b9daba55bdec2bf59366053352af0b7dde0ab31490e8af3c6282b7_light.svg) Höhengewinn des Goldplättchens
Durch den Laserimpuls erfährt das Goldblättchen eine Beschleunigung und wird ausgelenkt. Die kinetische Energie wird dabei vollständig in potenzielle Energie umgewandelt:
Höhengewinn des Goldplättchens
Durch den Laserimpuls erfährt das Goldblättchen eine Beschleunigung und wird ausgelenkt. Die kinetische Energie wird dabei vollständig in potenzielle Energie umgewandelt:
![\(\begin{array}[t]{rll}
{E}_{\text {kin }}&=&{E}_{\text {pot }} &\quad \scriptsize \\[5pt]
\dfrac{1}{2}\cdot m\cdot v^2&=& m\cdot g\cdot \Delta h &\quad \scriptsize \mid\, \dfrac{1}{m\cdot g}\\[5pt]
\dfrac{ v^2}{2\cdot g}&=& \Delta h &\quad \scriptsize \\[5pt]
\Delta h&=& \dfrac{ v^2}{2\cdot g}
\end{array}\)](https://www.schullv.de/resources/formulas/13194f2ddf3d450340b889e2dc5262b7cbf6c323dbe4ed705246ac6c296ea8b7_light.svg) Einsetzen der Werte liefert:
Einsetzen der Werte liefert:
![\(\begin{array}[t]{rll}
\Delta h&=&\dfrac{ v^2}{2\cdot g} &\quad \scriptsize \\[5pt]
&=&\dfrac{\left(0,33 \,\frac{\text{m}}{\text{s}}\right)^2}{2 \cdot 9,81 \,\frac{\text{m}}{\text{s}^2}} &\quad \scriptsize \\[5pt]
&=& 5,7 \cdot 10^{-3} \,\text{m} &\quad \scriptsize \\[5pt]
&=& 5,7 \,\text{mm}
\end{array}\)](https://www.schullv.de/resources/formulas/135f6d0fe36c0e4376f4cbb689149049924836d42fd22ddc9fdfa2b127f4ead8_light.svg)
3.3
Bei wachsender Wellenlänge nimmt der Impuls pro Photon aufgrund der umgekehrten Proportionalität zur Wellenlänge ab. Gleichzeitig reduziert sich die Energie pro Photon, was zu einer linearen Zunahme der Photonenzahl pro Impuls mit der Wellenlänge führt. Der Gesamtimpuls und die Auslenkung des Goldblättchens bleiben dabei konstant.
Alternative Argumentation über Energie: Der Ausschlag des Blättchens hängt nur von der zugeführten Energie ab. Beide Laser haben gleiche Pulsdauer  und Leistung
und Leistung  was zu einer konstanten übertragenen Pulsenergie
was zu einer konstanten übertragenen Pulsenergie  führt, unabhängig von der Laserwellenlänge.
führt, unabhängig von der Laserwellenlänge.