Vorschlag B2 – Elektromagnetischer Schwingkreis und elektromagnetische Wellen
1
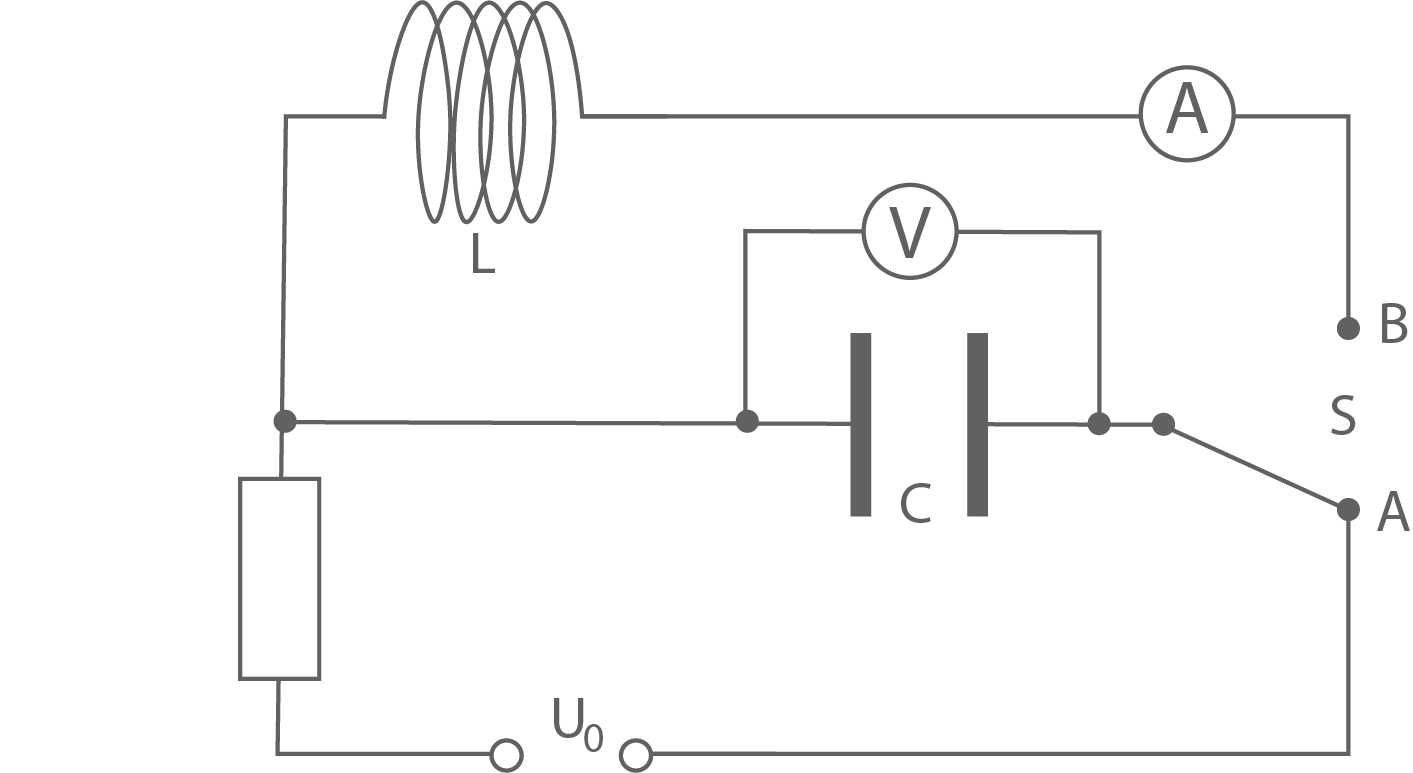
Im Folgenden werden elektromagnetische Schwingungen betrachtet, die von einem elektromagnetischen Schwingkreis erzeugt werden. Der Kondensator des Schwingkreises kann mithilfe eines Umschalters durch eine Gleichspannungsquelle aufgeladen werden. In der Schalterstellung 
wird der Kondensator geladen und in der Schalterstellung 
beginnt die elektromagnetische Schwingung mit dem vollständig geladenen Kondensator. Zunächst werden die ohmschen Widerstände vernachlässigt, d.h., es wird ein ungedämpfter elektromagnetischer Schwingkreis betrachtet.
wird der Kondensator geladen und in der Schalterstellung beginnt die elektromagnetische Schwingung mit dem vollständig geladenen Kondensator. Zunächst werden die ohmschen Widerstände vernachlässigt, d.h., es wird ein ungedämpfter elektromagnetischer Schwingkreis betrachtet.
1.1
Skizziere eine Schaltung mit Kondensator, Spule, Gleichspannungsquelle und Schalter, die den obigen Vorgaben entspricht und Messgeräte zur Messung der Spannung am Kondensator und der Stromstärke durch die Spule enthält.
Beschrifte die beiden Schalterstellungen.
(2 BE)
1.2
Ein Schwingkreis besteht aus einem Kondensator der Kapazität 
und einer Spule mit der Induktivität 
Die Schwingung startet zum Zeitpunkt 
mit einer maximalen Spannung von 
am Kondensator.
und einer Spule mit der Induktivität Die Schwingung startet zum Zeitpunkt mit einer maximalen Spannung von am Kondensator.
1.2.1
Zeige, dass die Frequenz des Schwingkreises 
beträgt.
Berechne die Schwingungsdauer 
und begründe, dass der zeitliche Verlauf der Spannung am Kondensator durch 
ausgedrückt werden kann.
beträgt.
Berechne die Schwingungsdauer und begründe, dass der zeitliche Verlauf der Spannung am Kondensator durch ausgedrückt werden kann.
(6 BE)
1.2.2
Berechne die maximale elektrische Energie, die im Kondensator vorliegt.
Erläutere, wie sich daraus die maximale Stromstärke 
in der Spule des Schwingkreises bestimmen lässt.
Leite den Zusammenhang 
her.
Berechne die Stromstärke 
in der Spule des Schwingkreises bestimmen lässt.
Leite den Zusammenhang her.
Berechne die Stromstärke
(9 BE)
1.3
Erläutere allgemein die Vorgänge im Schwingkreis, die dazu führen, dass nach dem Entladen des Kondensators der Strom weiter fließt und der Kondensator in die entgegengesetzte Richtung aufgeladen wird.
Vergleiche diese Phase der Schwingung mit der entsprechenden Phase bei der Schwingung einer Masse, die an einer Feder hängt, und gib mithilfe der Formeln für die Schwingungsdauer die mechanischen Größen, die den Größen 
und 
entsprechen, an.
und entsprechen, an.
(7 BE)
1.4
Gib Terme für den Spannungsabfall über dem Kondensator und für den Spannungsabfall über der Spule an und leite daraus die Differenzialgleichung
her.
Zeige, dass 
mit 
eine Lösung der Differenzialgleichung ist.
her.
Zeige, dass mit eine Lösung der Differenzialgleichung ist.
(8 BE)
1.5
Es wird nun ein elektromagnetischer Schwingkreis betrachtet, bei dem die ohmschen Widerstände der Schaltung berücksichtigt werden. Es ergibt sich eine gedämpfte Schwingung, die sich mit der Formel
für die Spannung am Kondensator ausdrücken lässt.
Bestimme für die in Material 1 dargestellte Schwingung die Dämpfungskonstante 
für die Spannung am Kondensator ausdrücken lässt.
Bestimme für die in Material 1 dargestellte Schwingung die Dämpfungskonstante
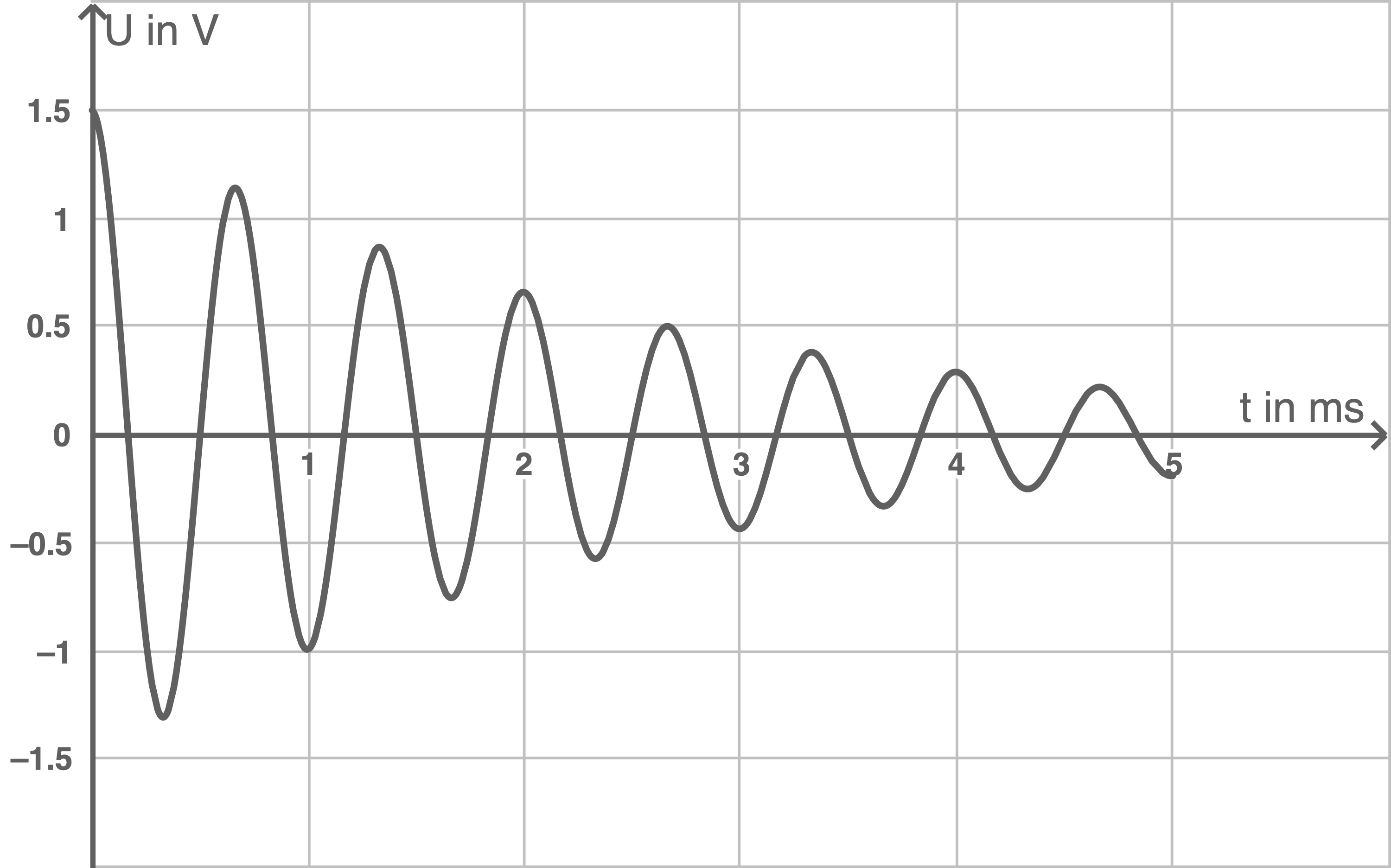
Material 1: Spannungsverlauf am Kondensator eines Schwingkreises
(4 BE)
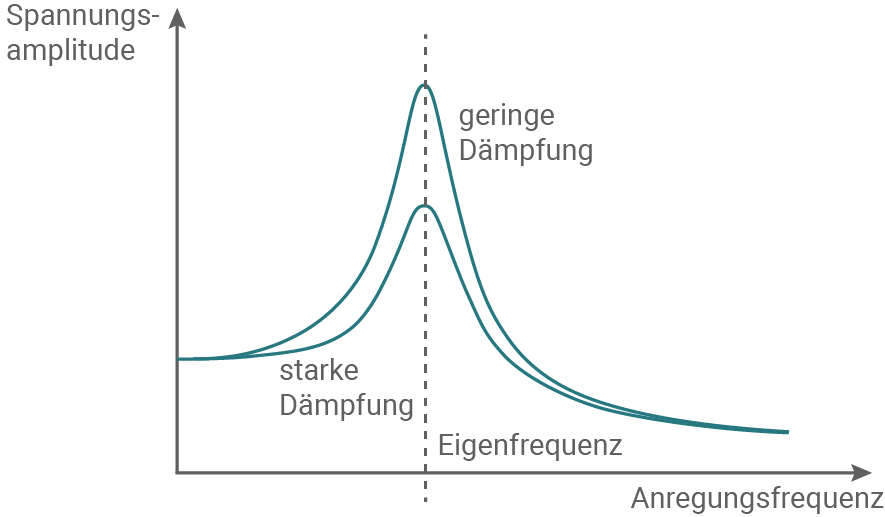
1.6
Ein gedämpfter Schwingkreis wird mit einem Sinusgenerator zu einer erzwungenen Schwingung angeregt. In Material 2 ist die Amplitude der Kondensatorspannung in Abhängigkeit von der Anregungsfrequenz dargestellt.
Erläutere das Zustandekommen des Maximums in dem Diagramm.
Skizziere in Material 2 einen möglichen Verlauf des Graphen für den Fall, dass durch einen zusätzlichen ohmschen Widerstand die Dämpfung des Schwingkreises erhöht wird.
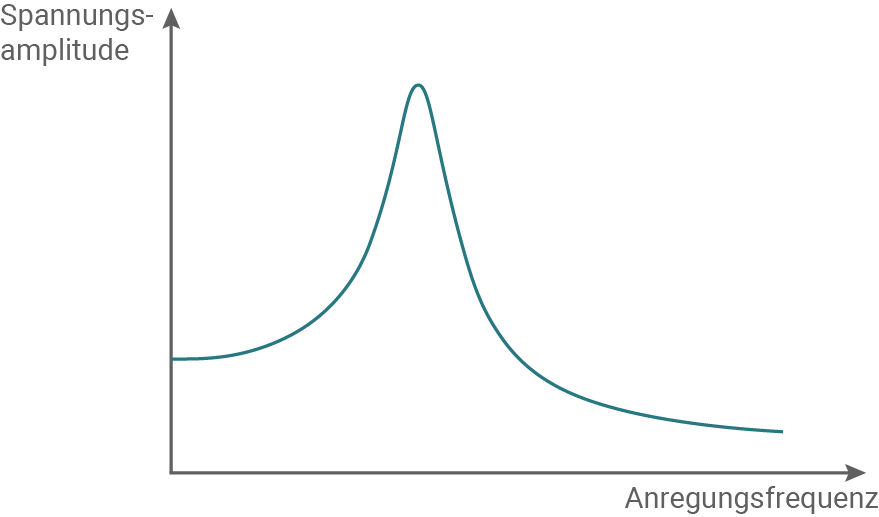
Material 2: Diagramm zur Anregung des Schwingkreises
(3 BE)
2
Mithilfe eines Schwingkreises können elektromagnetische Wellen erzeugt werden, die im Folgenden genauer untersucht werden.
2.1
Es werden elektromagnetische Wellen mit einer Frequenz von 
verwendet.
Entscheide, welche der in Material 3 beschriebenen Materialien sich grundsätzlich dazu eignen, Interferenzerscheinungen dieser Wellen experimentell zu untersuchen.
verwendet.
Entscheide, welche der in Material 3 beschriebenen Materialien sich grundsätzlich dazu eignen, Interferenzerscheinungen dieser Wellen experimentell zu untersuchen.
Material 3: Materialien zur Untersuchung der Wellen aus Aufgabe 2.1
a)
bedruckte Folie mit Streifen im Abstand von 
b)
kristallines Gitter aus Graphit
c)
Metallgitter mit 200 Spalten pro Meter
d)
Doppelspalt aus Aluminium mit einer Spaltbreite von 
und einem Spaltabstand von 
und einem Spaltabstand von
(3 BE)
2.2
Mit einem Doppelspaltexperiment wird elektromagnetische Strahlung untersucht (Material 4).
Erläutere in diesem Zusammenhang den Begriff „Gangunterschied“.
Ermittle eine mögliche Frequenz der elektromagnetischen Strahlung, die mit dem Aufbau in Material 4 am Ort 
ein Intensitätsmaximum der Strahlung aufweist.
Gib eine weitere mögliche Frequenz an.
ein Intensitätsmaximum der Strahlung aufweist.
Gib eine weitere mögliche Frequenz an.
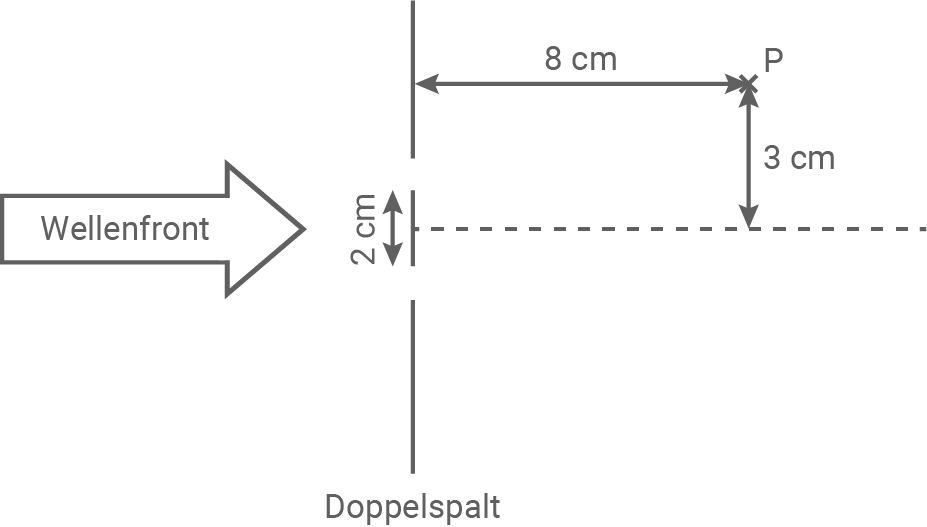
Material 4: Doppelspalt zur Untersuchung der Wellenlänge von elektromagnetischer Strahlung (Zeichnung nicht maßstabsgetreu)
(8 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.1
1.2.1
Berechnung der Frequenz 
und der Schwinungsdauer 
Gegeben: 
Gesucht: 
Lösung: Mit der Thomson'schen Schwingungsgleichung gilt für 
Einsetzen der Werte liefert:
![\(\begin{array}[t]{rll}
f&=&\dfrac{1}{2 \pi \cdot \sqrt{L \cdot C}}&\quad \scriptsize \\[5pt]
&=&\dfrac{1}{2 \pi \cdot \sqrt{4,5 \cdot 10^{-3} \;\text{H} \cdot 20 \cdot 10^{-6} \;\text{F}}} &\quad \scriptsize \\[5pt]
&=& 530,5 \;\text{Hz}
\end{array}\)](https://www.schullv.de/resources/formulas/df385e87feb50ce67b33a19e4e9da9ee5ce288912e0dde75d7bff29ddce84e92_light.svg)
Für die Schwingungsdauer gilt:
![\(\begin{array}[t]{rll}
T&=& \dfrac{1}{f}&\quad \scriptsize \\[5pt]
&=& \dfrac{1}{530,5 \;\text{Hz}}&\quad \scriptsize \\[5pt]
&=& 0,001885 \;\text{s} &\quad \scriptsize \\[5pt]
&=& 0,885 \;\text{ms}
\end{array}\)](https://www.schullv.de/resources/formulas/218c4a0c9ee52ea2a85530b8aff59630cf7d88d784b5759ad6896149170d1ea2_light.svg)
Zeitlicher Verlauf der Spannung
Bei Versuchsanfang wird der aufgeladene Kondensator von der Spannungsquelle getrennt, so dass der Schwingkreis aus Kondensator und Spule anfängt zu schwingen.
Die Anfangsbedinung lautet daher:
![\(\begin{array}[t]{rll}
U(0 \;\text{s})&=&\hat{U}
\end{array}\)](https://www.schullv.de/resources/formulas/34c3a05edef099243e4dc1952b93834a35a41dd8420d12aedc0122ee98110054_light.svg)
Dabei entspricht 
der anfänglichen maximalen Spannung am Kondensator zum Zeitpunkt 
Die Schwinung kann daher mit einer Kosinusfunktion beschrieben werden:
![\(\begin{array}[t]{rll}
{U}({t})&=& \hat{{U}} \cdot \cos (\omega \cdot {t}) &\quad \scriptsize\\[5pt]
{U}({0\;\text{s}})&=& \hat{{U}} \cdot \cos (\omega \cdot {0 \;\text{s}}) &\quad \scriptsize \\[5pt]
{U}({0\;\text{s}})&=& \hat{{U}} \cdot 1 &\quad \scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/9c18be4a1325ef8dab564a8a567186ff47089617cd9c1b80981afb7e99740205_light.svg)
Die Ladungsspannung 
entspricht der anfänglichen, maximalen Spannung am Kondensator. Für die Kreisfrequenz gilt:
![\(\begin{array}[t]{rll}
\omega&=& \dfrac{2 \pi}{{T}}&\quad \scriptsize \\[5pt]
&=& \dfrac{2 \pi}{{0,001885 \;\text{s}}}&\quad \scriptsize \\[5pt]
&=& 3333 \;\dfrac{1}{\text{s}}
\end{array}\)](https://www.schullv.de/resources/formulas/2405932f85ecaab69bace9c6133eb40f1d3288b3f4d9a52cb0092159d8cd7084_light.svg)
Einsetzen in die Funktion liefert den zeitlichen Spannungsverlauf am Kondensator:
![\(\begin{array}[t]{rll}
{U}({t})&=& \hat{{U}} \cdot \cos (\omega \cdot {t}) &\quad \scriptsize\\[5pt]
&=& 1,5 \;\text{V} \cdot \cos \left(3333 \;\dfrac{1}{\text{s}} \cdot t\right)&\quad \scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/2ee56d8734d2dd2450b9b43351f81d6fe31dd9fde0c40534f0f3665e285e08b4_light.svg)
und der Schwinungsdauer
Gegeben:
Gesucht:
Lösung: Mit der Thomson'schen Schwingungsgleichung gilt für
Einsetzen der Werte liefert:
![\(\begin{array}[t]{rll}
T&=& \dfrac{1}{f}&\quad \scriptsize \mid\; T= 2 \pi \cdot \sqrt{L \cdot C} \\[5pt]
2 \pi \cdot \sqrt{L \cdot C}&=&\dfrac{1}{f}&\quad \scriptsize \mid\; \cdot f \\[5pt]
f\cdot 2 \pi \cdot \sqrt{L \cdot C}&=&1&\quad \scriptsize \mid\; \cdot \dfrac{1}{2 \pi \cdot \sqrt{L \cdot C}} \\[5pt]
f&=&\dfrac{1}{2 \pi \cdot \sqrt{L \cdot C}}&\quad \scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/be4a13639c2cfa67ebf6b7a4745d9aeef5e6f437624a5abbb933a494108243b6_light.svg)
Für die Schwingungsdauer gilt:
Zeitlicher Verlauf der Spannung
Bei Versuchsanfang wird der aufgeladene Kondensator von der Spannungsquelle getrennt, so dass der Schwingkreis aus Kondensator und Spule anfängt zu schwingen.
Die Anfangsbedinung lautet daher:
Dabei entspricht der anfänglichen maximalen Spannung am Kondensator zum Zeitpunkt
Die Schwinung kann daher mit einer Kosinusfunktion beschrieben werden:
Die Ladungsspannung entspricht der anfänglichen, maximalen Spannung am Kondensator. Für die Kreisfrequenz gilt:
Einsetzen in die Funktion liefert den zeitlichen Spannungsverlauf am Kondensator:
1.2.2
Für die maximale elektrische Energie im Kondensator gilt:
![\(\begin{array}[t]{rll}
E_{el,C}&=&\dfrac{1}{2} \cdot C \cdot U^2_{\max}&\quad \scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/b772016fceb328a42279530f33df8441808e652f53f20356ecf897fb85ce9b76_light.svg)
Einsetzen der Werte liefert:
Beim Entladen des Kondensators wird die elektrische Energie des Kondensators in elektrische Energie der Spule umgewandelt. Die maximale elektrsiche Energie des Kondensators 
entspricht folglich der maximalen elektrischen Energie in der Spule 
Einsetzen der Thomson'schen Gleichung in die Definition der Kreisfrequenz 
liefert:
![\(\begin{array}[t]{rll}
\omega&=&\dfrac{2\cdot \pi}{T} &\quad \scriptsize \mid\;T=2\cdot \pi\cdot \sqrt{L\cdot C} \\[5pt]
&=&\dfrac{2\pi}{2\pi\cdot \sqrt{L\cdot C}} &\quad \scriptsize \\[5pt]
&=& \dfrac{1}{\sqrt{L\cdot C}}
\end{array}\)](https://www.schullv.de/resources/formulas/169bf03e3062d1f07a7722f70f07f73963809a79cd987ec49a347d9885a2af92_light.svg)
Einsetzen des Zusammenhangs in 
liefert:
![\(\begin{array}[t]{rll}
I_{\max } &=& \dfrac{U_{\max }}{\omega \cdot L} &\quad \scriptsize \mid\; \omega=\dfrac{1}{\sqrt{L\cdot C}} \\[5pt]
&=& \dfrac{U_{\max }}{\dfrac{1}{\sqrt{L\cdot C}} \cdot L} &\quad \scriptsize \\[5pt]
&=& \dfrac{\sqrt{L\cdot C}}{ L}\cdot U_{\max } &\quad \scriptsize \\[5pt]
&=& \sqrt{\dfrac{L\cdot C}{L^2}}\cdot U_{\max } &\quad \scriptsize \\[5pt]
&=& \sqrt{\dfrac{C}{L}}\cdot U_{\max } &\quad \scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/ab9fea7f3de547f76c37ff5fe5ef18d2d1d89ce50bf0ce33ad9d59377b57f1d2_light.svg)
Dies entspricht dem bereits aus 
hergeleiteten Zusammenhang für 
Die Stromstärke 
lässt sich mit beiden hergeleiteten Formeln berechnen:
Alternativ kann die Stromstärke auch mit der anderen Formel berechnet werden:
![\(\begin{array}[t]{rll}
I_{\max }&=& \sqrt{\dfrac{C}{L}}\cdot U_{\max }&\quad \scriptsize \\[5pt]
&=& \sqrt{\dfrac{20 \cdot 10^{-6} \;\text{F}}{4,5 \cdot 10^{-3} \;\text{H}}} \cdot 1,5 \;\text{V} &\quad \scriptsize \\[5pt]
&=& 0,10 \;\text{A}
\end{array}\)](https://www.schullv.de/resources/formulas/bc13616afb8ced078f1f3359c0458f896422be9644a266c34303e851f8daa06f_light.svg)
Einsetzen der Werte liefert:
Beim Entladen des Kondensators wird die elektrische Energie des Kondensators in elektrische Energie der Spule umgewandelt. Die maximale elektrsiche Energie des Kondensators 
![\(\begin{array}[t]{rll}
E_{el,C}&=&\dfrac{1}{2} \cdot C \cdot U^2_{\max}&\quad \scriptsize \\[5pt]
&=&\dfrac{1}{2} \cdot 20 \cdot 10^{-6} \;\text{F} \cdot(1,5 \;\text{V})^2 &\quad \scriptsize \\[5pt]
&=& 2,25 \cdot 10^{-5} \;\text{J}
\end{array}\)](https://www.schullv.de/resources/formulas/f09b31f57787b5fa560e464345590a97b277a534a1c2ffe673ce43b269f93272_light.svg)
entspricht folglich der maximalen elektrischen Energie in der Spule
Einsetzen der Thomson'schen Gleichung in die Definition der Kreisfrequenz 
![\(\begin{array}[t]{rll}
E_{el,C}&=& E_{el,L} &\quad \scriptsize \mid\; E_{el,L}=\dfrac{1}{2} \cdot L \cdot I_{\max }^2 \\[5pt]
\dfrac{1}{2} \cdot C \cdot U^2_{\max}&=& \dfrac{1}{2} \cdot L \cdot I_{\max }^2 &\quad \scriptsize \mid\; \cdot \dfrac{2}{L}\\[5pt]
\dfrac{C \cdot U^2_{\max}}{L} &=& I_{\max }^2 &\quad \scriptsize \mid\; \sqrt{\;}\\[5pt]
\sqrt{\dfrac{C \cdot U^2_{\max}}{L}} &=& I_{\max } &\quad \scriptsize \\[5pt]
\sqrt{\dfrac{C}{L}}\cdot U_{\max} &=& I_{\max } &\quad \scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/51221e2500bf2c60c3954223407f661529016eb76975838f3d12d40c28e0f25b_light.svg)
liefert:
Einsetzen des Zusammenhangs in liefert:
Dies entspricht dem bereits aus hergeleiteten Zusammenhang für
Die Stromstärke lässt sich mit beiden hergeleiteten Formeln berechnen:
Alternativ kann die Stromstärke 
![\(\begin{array}[t]{rll}
I_{\max } &=& \dfrac{U_{\max }}{\omega \cdot L} &\quad \scriptsize \mid\; \omega= 2\pi\cdot L \\[5pt]
&=& \dfrac{U_{\max }}{2 \pi \cdot f \cdot L} &\quad \scriptsize \\[5pt]
&=& \dfrac{1,5 \;\text{V}}{3333 \;\dfrac{1}{\text{s}} \cdot 4,5 \cdot 10^{-3} \;\text{H}} &\quad \scriptsize \\[5pt]
&=& 0,10 \;\text{A} &\quad \scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/e5ccbf03f11d4e09cb09f74bb0616be49937c210a87e8397a352cada857f103b_light.svg)
auch mit der anderen Formel berechnet werden:
1.2.3
Vorgänge im Schwingkreis
Der entladene Kondensator hat keine Spannung mehr, während in der Spule der maximale Stromfluss und die größte magnetische Feldstärke herrschen. Die gesamte Energie ist folglich im Magnetfeld der Spule gespeichert.
Die Lenz'sche Regel besagt, dass eine Änderung des Magnetfelds in einer Spule eine entgegengesetzte elektrische Spannung induziert, die dem Änderungsprozess entgegenwirkt.
Der Strom in der Spule nimmt ab, wodurch auch der magnetische Fluss in der Spule kleiner wird. Gemäß der Lenz'schen Regel fließt daher ein Induktionsstrom in derselben Richtung wie der ursprüngliche Strom.
Dieser Strom lädt den Kondensator mit umgekehrter Polung auf. Wenn die Stromstärke null ist, erreicht die Spannung am Kondensator ihren maximalen Wert, jedoch mit umgekehrtem Vorzeichen. Die magnetische Feldenergie wurde vollständig in elektrische Feldenergie umgewandelt.
Vergleich mit einem Federpendel
Wenn die Masse des Federpendels die Gleichgewichtslage durchläuft, ist sie kräftefrei. Die Gewichtskraft und die Federkraft heben sich in der Gleichgewichtslage gegenseitig auf. Die Auslenkung und somit die resultierende Kraft und Beschleunigung sind in der Gleichgewichtslage null. Die maximale Geschwindigkeit wird erreicht, da die gesamte Energie in kinetische Energie umgewandelt wurde.
Nach dem 1. Newton'schen Gesetz bewegt sich dieser kräftefreie Körper mit konstanter Geschwindigkeit und ohne Richtungsänderung weiter. Aufgrund des Trägheitsgesetzes bewegt sich die Masse über die Gleichgewichtslage hinaus, ohne ihre Richtung zu ändern. Sobald die Masse über die Gleichgewichtslage hinausgeht, wird sie abgebremst und die Feder wird in umgekehrter Richtung gespannt.
Für die Schwingungsdauer eines Federpendels gilt:
![\(\begin{array}[t]{rll}
T&=& 2 \pi \cdot \sqrt{\dfrac{m}{D}} &\quad \scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/35487a41208140c08a68e1398f8b9d8576baca6a0c04bb7a9d965eaa2ab234af_light.svg)
Die Thomson'sche Schwingungsgleichung besagt:
![\(\begin{array}[t]{rll}
T&=& 2 \pi \cdot \sqrt{L\cdot C} &\quad \scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/c8ef655d38a8d390a0c5829166b31e9d2b514f62625c494e22441895c1bb77e4_light.svg)
Gleichsetzen der Formeln für die Schwinungsdauer liefert:
![\(\begin{array}[t]{rll}
2 \pi \cdot \sqrt{\dfrac{m}{D}}&=& 2 \pi \cdot \sqrt{L\cdot C}&\quad \scriptsize \mid\; \cdot \dfrac{1}{2\pi} \\[5pt]
\sqrt{\dfrac{m}{D}}&=& \sqrt{L\cdot C}&\quad \scriptsize \\[5pt]
\sqrt{\dfrac{m}{D}}&=& \sqrt{\dfrac{L}{C^{-1}}}&\quad \scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/b2d6daedf12547627b525c9db1127df32741eeba36b80bcee07c9373c8aee5d2_light.svg)
Folglich enspricht 
und 
und damit 
Die Thomson'sche Schwingungsgleichung besagt:
Gleichsetzen der Formeln für die Schwinungsdauer liefert:
Folglich enspricht und und damit
1.4
Spannungsabfall über dem Kondensator
![\(\begin{array}[t]{rll}
U_C&=& \dfrac{Q}{C}&\quad \scriptsize \ \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/3b85176cebd02727dbf5d10ba737dd696b01c41697e045f26d6281d96ec43e75_light.svg)
Spannungsabfall über der Spule
![\(\begin{array}[t]{rll}
U_L&=& L\cdot \dot{I}&\quad \scriptsize \ \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/ba85365263ec85b08822d0f4d67146247b99fde5e09978b875fac6b5084113e2_light.svg)
Herleitung der Differenzialgleichung
Die Kirchhoff'sche Maschenregel besagt, dass die Summe aller Spannungen in einer geschlossenen Schleife in einem elektrischen Netzwerk gleich null ist. Es gilt folglich:
Lösung der Differenzialgleichung
Ableitungen von 
Einsetzen in die Differentialgleichung liefert:
Dies entspricht der angegebenen Formel für die Kreisfrequenz.
Spannungsabfall über der Spule
Herleitung der Differenzialgleichung
Die Kirchhoff'sche Maschenregel besagt, dass die Summe aller Spannungen in einer geschlossenen Schleife in einem elektrischen Netzwerk gleich null ist. Es gilt folglich:
Lösung der Differenzialgleichung
Ableitungen von 
![\(\begin{array}[t]{rll}
U_L(t)+U_C(t)&=& 0 &\quad \scriptsize \mid\; U_L= L\cdot \dot{I} \quad U_C= \dfrac{Q}{C}\\[5pt]
L\cdot \dot{I}+\dfrac{Q(t)}{C}&=& 0 &\quad \scriptsize \mid\; I(t) = \dot{Q}(t) \Rightarrow \dot{I}(t) = \ddot{Q}(t) \\[5pt]
L\cdot \ddot{Q}(t) +\dfrac{Q(t)}{C}&=& 0 &\quad \scriptsize \mid\; \cdot \dfrac{1}{L} \\[5pt]
\ddot{Q}(t) +\dfrac{1}{L\cdot C}\cdot Q(t)&=& 0
\end{array}\)](https://www.schullv.de/resources/formulas/7b5eb8a06c2c4534c1d036dcd3defb0fe05c0ce8342f6979b012c54f6609877d_light.svg)
Einsetzen in die Differentialgleichung liefert:
Dies entspricht der angegebenen Formel für die Kreisfrequenz.
![\(\begin{array}[t]{rll}
Q(t)&=& Q_0 \cdot \cos (\omega \cdot t) &\quad \scriptsize \\[5pt]
\dot{Q}(t)&=& - Q_0 \cdot \omega\cdot \sin (\omega \cdot t) &\quad \scriptsize \\[5pt]
\ddot{Q}(t)&=& - Q_0 \cdot \omega^2\cdot \cos (\omega \cdot t) = -\omega^2 Q(t) &\quad \scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/003d9719d93570bf353f31468942b9f70dd04e3aa995f831f07e50151794bbb0_light.svg)
![\(\begin{array}[t]{rll}
\ddot{Q}(t) +\dfrac{1}{L\cdot C}\cdot Q(t)&=& 0 &\quad \scriptsize \mid\; \ddot{Q}(t)= -\omega^2 Q(t) \\[5pt]
-\omega^2 Q(t) +\dfrac{1}{L\cdot C}\cdot Q(t)&=& 0 &\quad \scriptsize\\[5pt]
\left( -\omega^2+\dfrac{1}{L\cdot C }\right)\cdot Q(t)&=& 0 &\quad \scriptsize \mid\; \text{Satz des Nullproduktes} \\[5pt]
\left( -\omega^2+\dfrac{1}{L\cdot C }\right)&=& 0 &\quad \scriptsize \mid\; -\dfrac{1}{L\cdot C } \\[5pt]
-\omega^2&=& -\dfrac{1}{L\cdot C }&\quad \scriptsize \mid\; \cdot (-1) \\[5pt]
\omega^2&=& \dfrac{1}{L\cdot C }&\quad \scriptsize \mid\; \sqrt{\;}\\[5pt]
\omega&=& \sqrt{\dfrac{1}{L\cdot C }}&\quad \scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/3121cecb026d7a4c2fb5b1c350ba866fe99cbd951708ac113bfdaeed103e4bae_light.svg)
1.5
Die Gleichung der gedämpften Schwingung lautet:
![\(\begin{array}[t]{rll}
U(t)&=& U_0 \cdot \mathrm{e}^{-k \cdot t} \cdot \cos (\omega \cdot t) &\quad \scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/3fd62ccb22c649b706c8e8c64ee05834cccfcf2931cd70c1afb8c2f1a6ccc7e8_light.svg)
entspricht der maximalen Spannung zum Zeitpunkt 
und kann an dem Grapfen in Material 1 abgelesen werden. entspricht in Material 1 dem Schnittpunkt des Graphen mit der y-Achse:
![\(\begin{array}[t]{rll}
U_0&=& 1,5 \;\text{V} &\quad \scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/7ba64eb0d69c26a2ced8cd087515d78f599f4733258249e63f0a732ad3092ed1_light.svg)
Auch die Schwingungsdauer lässt sich in dem Graphen ablesen. In dem Graphen ist zu erkennen, dass der Schwingkreis bis zum Zeitpunkt 
genau 3 komplette Schwinungen dürchgeführt hat:
![\(\begin{array}[t]{rll}
T&=&\dfrac{\text { Zeit für n Schwingungen} }{\text { Anzahl n der Schwingungen }}&\quad \scriptsize \\[5pt]
&=&\dfrac{t_n}{n}&\quad \scriptsize \\[5pt]
&=&\dfrac{2\;\text{ms}}{3}&\quad \scriptsize \\[5pt]
&=&\dfrac{2 \cdot 10^{-3} \;\text{s}}{3}&\quad \scriptsize \\[5pt]
&=&\dfrac{2 }{3}\cdot 10^{-3} \;\text{s}&\quad \scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/c68942b1021c37245107bd8a331fbbf46f6327c78e1fc51727057131cab2e160_light.svg)
Für die Kreisfrequenz gilt:
![\(\begin{array}[t]{rll}
\omega&=&\dfrac{2\pi}{T} &\quad \scriptsize \\[5pt]
\omega&=&\dfrac{2\pi}{\dfrac{2 }{3}\cdot 10^{-3} \;\text{s}} &\quad \scriptsize \\[5pt]
&=& 3000\pi\;\dfrac{1}{\text{s}}
\end{array}\)](https://www.schullv.de/resources/formulas/35a732cf4259a7ebe6e566f5734bef3a37e4181a6480091b7d5ae9a534d9bd09_light.svg)
Einsetzen der errechneten Werte in die gegebene Formel liefert:
Um die Dämpfungskonstante 
zu erhalten, muss ein Messwertpaar aus Material 1 abgelsesen werden. Beispielsweise der Punkt 
liegt auf dem Graphen. Es folgt:
entspricht der maximalen Spannung zum Zeitpunkt und kann an dem Grapfen in Material 1 abgelesen werden. entspricht in Material 1 dem Schnittpunkt des Graphen mit der y-Achse:
Auch die Schwingungsdauer lässt sich in dem Graphen ablesen. In dem Graphen ist zu erkennen, dass der Schwingkreis bis zum Zeitpunkt genau 3 komplette Schwinungen dürchgeführt hat:
Für die Kreisfrequenz gilt:
Einsetzen der errechneten Werte in die gegebene Formel liefert:
Um die Dämpfungskonstante 
![\(\begin{array}[t]{rll}
U(t)&=& U_0 \cdot \mathrm{e}^{-k \cdot t} \cdot \cos (\omega \cdot t) &\quad \scriptsize \mid\; \omega = 3000\pi\;\dfrac{1}{\text{s}} \quad U_0= 1,5 \;\text{V} \\[5pt]
U(t)&=& 1,5 \;\text{V} \cdot \mathrm{e}^{-k \cdot t} \cdot \cos (3000\pi\;\dfrac{1}{\text{s}} \cdot t) &\quad \scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/12ad72eb947af25cdff76bbdaf540eb4162e9a9f7ade617608254f973d8beee6_light.svg)
zu erhalten, muss ein Messwertpaar aus Material 1 abgelsesen werden. Beispielsweise der Punkt liegt auf dem Graphen. Es folgt:
![\(\begin{array}[t]{rll}
U(t)&=& 1,5 \;\text{V} \cdot \mathrm{e}^{-k \cdot t} \cdot \cos (3000\pi\;\dfrac{1}{\text{s}} \cdot t) &\quad \scriptsize \mid\; t= 4 \cdot 10^{-3}\;\text{s} \quad U(4 \cdot 10^{-3}\;\text{s})= 0,3 \;\text{V} \\[5pt]
0,3 \;\text{V}&=& 1,5 \;\text{V} \cdot \mathrm{e}^{-k \cdot 4 \cdot 10^{-3}\;\text{s}} \cdot \cos (3000\pi\;\dfrac{1}{\text{s}} \cdot 4 \cdot 10^{-3}\;\text{s}) &\quad \scriptsize \mid\; \text{während} \quad 4 \cdot 10^{-3}\;\text{s} \quad \text{wurden 6 komplette Schwingungen durchgeführt} \\[5pt]
0,3 \;\text{V}&=& 1,5 \;\text{V} \cdot \mathrm{e}^{-k \cdot 4 \cdot 10^{-3}\;\text{s}} \cdot 1 &\quad \scriptsize \mid\; \cdot \dfrac{1}{1,5 \;\text{V}}\\[5pt]
\dfrac{0,3 \;\text{V}}{1,5 \;\text{V}} &=& \mathrm{e}^{-k \cdot 4 \cdot 10^{-3}\;\text{s}} &\quad \scriptsize \mid\;\ln(\;) \\[5pt]
\ln\left(\dfrac{1}{5} \right)&=& \ln\left( \mathrm{e}^{-k \cdot 4 \cdot 10^{-3}\;\text{s}} \right) &\quad \scriptsize \mid\; \ln\left(\mathrm{e}^b\right)= \ln\left(\mathrm{e}\right) \cdot b = 1 \cdot b \\[5pt]
\ln\left(\dfrac{1}{5} \right)&=& -k \cdot 4 \cdot 10^{-3}\;\text{s} &\quad \scriptsize \mid\; \cdot \dfrac{1}{-4 \cdot 10^{-3}\;\text{s}}\\[5pt]
\dfrac{\ln\left(\dfrac{1}{5} \right)}{-4 \cdot 10^{-3}\;\text{s}}&=& k &\quad \scriptsize \\[5pt]
-250\;\dfrac{1}{\text{s}}\cdot \ln\left(\dfrac{1}{5} \right)&=& k &\quad \scriptsize \\[5pt]
-4,0 \cdot 10^2 \;\dfrac{1}{\text{s}}&=& k &\quad \scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/cdb817c1d67e9d6ee365f3236fc234d641bb27e0d2722bec8aba32849a7edfa1_light.svg)
1.6
Erzwungene Schwingungen treten auf, wenn ein System periodisch von einer äußeren Anregung mit einer bestimmten Frequenz in Schwingungen versetzt wird. Die Frequenz der Anregung kann von der natürlichen Frequenz des Systems abweichen. Bei Resonanz stimmt die Frequenz der äußeren Anregung jedoch mit der natürlichen Frequenz des Systems überein. In diesem Fall können die Schwingungen im System durch die Anregung verstärkt werden, was zu einer erhöhten Amplitude (und einem Maximum im Diagramm) führt.
Die Amplitude der Schwingung hängt von der Dämpfung des Systems ab, die durch einen ohmschen Widerstand verursacht wird. Im Resonanzfall ist die Amplitude am größten, wenn der ohmsche Widerstand minimal ist und die Dämpfung des Systems gering ist.
Skizzierung eines möglichen Verlaufs des Graphen bei erhöhter Dämpfung
2.1
Interferenz tritt auf, wenn Wellen an einem Punkt zusammenkommen und sich überlagern, wodurch sie verstärkt oder abgeschwächt werden können. Eine Möglichkeit, Interferenz zu erzeugen, ist die Beugung von Wellen an einem Objekt. Beim Durchgang durch das Objekt ändert sich die Richtung der Wellenausbreitung, was zur Überlagerung der Wellen führen kann. Damit Beugung auftritt, sollte die Größe des Beugungsobjekts in der Größenordnung der Wellenlänge 
liegen oder nicht wesentlich größer sein als . In dem Versuch beträgt die Frequenz 10,5 GHz. Die zugehörige Wellenlänge kann gekürzt werden.
![\(\begin{array}[t]{rll}
\lambda&=&\dfrac{c}{f} &\quad \scriptsize \\[5pt]
&=&\dfrac{3,0 \cdot 10^8 \;\dfrac{\text{m}}{\text{s}}}{10,5 \cdot 10^9 \;\dfrac{1}{\text{s}}}&\quad \scriptsize \\[5pt]
&=& 0,029 \;\text{m} &\quad \scriptsize \\[5pt]
&=& 29 \;\text{mm} &\quad \scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/ac7cb00df7717afcceb3ed9a7f2c68e02d0fa9536b597a6035071abee7cbe967_light.svg)
a) Die bedruckte Folie mit Streifen im Abstand von hat eine Gitterkonstante von 
Das ist nicht in der gleichen Größenordnung wie 
Es kann keine Interferenz beobachtet werden.
b) In dem kristallin Gitter aus Graphit haben die Netzebenen einen sehr viel geringeren Abstand als 
Die Größenordnungen unterscheiden sich stark, daher kann keine Interferenz beobachtet werden.
c) Für die Gitterkonstante des Metallgitters mit 200 Spalten pro Meter gilt :
![\(\begin{array}[t]{rll}
g&=& \dfrac{1 \;\text{m}}{200}&\quad \scriptsize \\[5pt]
&=& 0,005 \;\text{m} &\quad \scriptsize \\[5pt]
&=& 5 \;\text{mm} &\quad \scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/c8e585e1cfc9969e7ff2fef0c403beb843e94961c8b3635d62a4f13324a1e222_light.svg)
Die Gitterkonstante beträgt ein Sechstel von und ist damit nicht in der gleichen Größenordnung wie Es ist keine Interferenz zu beobachten.
d) In dem Doppelspalt aus Aluminium mit einer Spaltbreite von und einem Spaltabstand von beträgt der Spaltabstand etwa das Siebenfache von und ist damit nicht wesentlich größer als die Größenordnung der Wellenläge. Es ist also Interferenz zu beobachten.
liegen oder nicht wesentlich größer sein als . In dem Versuch beträgt die Frequenz 10,5 GHz. Die zugehörige Wellenlänge kann gekürzt werden.
a) Die bedruckte Folie mit Streifen im Abstand von hat eine Gitterkonstante von Das ist nicht in der gleichen Größenordnung wie Es kann keine Interferenz beobachtet werden.
b) In dem kristallin Gitter aus Graphit haben die Netzebenen einen sehr viel geringeren Abstand als Die Größenordnungen unterscheiden sich stark, daher kann keine Interferenz beobachtet werden.
c) Für die Gitterkonstante des Metallgitters mit 200 Spalten pro Meter gilt :
Die Gitterkonstante beträgt ein Sechstel von und ist damit nicht in der gleichen Größenordnung wie Es ist keine Interferenz zu beobachten.
d) In dem Doppelspalt aus Aluminium mit einer Spaltbreite von und einem Spaltabstand von beträgt der Spaltabstand etwa das Siebenfache von und ist damit nicht wesentlich größer als die Größenordnung der Wellenläge. Es ist also Interferenz zu beobachten.
2.2
Der Gangunterschied ist die Differenz der optischen Weglängen zwischen kohärenten Wellen. Er bestimmt, ob sich die Wellen konstruktiv oder destruktiv überlagern. Im Doppelspaltexperiment entstehen Interferenzeffekte durch die Überlagerung von Elementarwellen, die von den beiden Spalten ausgehen. Der Gangunterschied an einem Punkt P ist die Differenz der Weglängen von den Spaltmittelpunkten bis zu P.
Damit ein Interferenzmayimum auftritt, muss der Gangunterschied 
ein ganzzahliges Vielfaches der Wellenlänge sein:
![\(\begin{array}[t]{rll}
\Delta s&=& n\cdot \lambda &\quad \scriptsize \mid\; \text{mit} \quad n \in \mathbb{N} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/48724298360d728a7ec07bf3d0fa80dee2cceffdfc5418353c3c91e269bfdcdc_light.svg)
Für die Interferenz im Doppelspalt gilt:
![\(\begin{array}[t]{rll}
\sin(\alpha)&=& \dfrac{\Delta s}{b} &\quad \scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/d30502ca34f713c74030a0446bc21a4a90d48aee84033e5f754ef6dac64721f7_light.svg)
Es gilt außerdem:
![\(\begin{array}[t]{rll}
\tan(\alpha)&=& \dfrac{d}{x} &\quad \scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/a9fcf3585e438e76893dbba157375196afe4a4ed97c2d485f0d31c69ec93d7d9_light.svg)
entspricht dem Abstand zwischen den beiden Spalten. 
enspricht dem horizontalen Abstand zum Punkt P. 
entpsricht dem senkrechten Abstand zum Punkt P. Für den Beugungswinkel 
folgt damit:
![\(\begin{array}[t]{rll}
\tan(\alpha)&=& \dfrac{d}{x} &\quad \scriptsize \\[5pt]
\tan(\alpha)&=& \dfrac{3\;\text{cm}}{8\;\text{cm}} &\quad \scriptsize \mid\; tan^{-1}\left(\;\right) \\[5pt]
\alpha&=& \tan^{-1}\left( \dfrac{3\;\text{cm}}{8\;\text{cm}} \right) &\quad \scriptsize \\[5pt]
\alpha&=& 20,556 ^{\circ} &\quad \scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/95ac34abe503924cddc85d516f204d586d61b90cff3397d66356d56cc65b802e_light.svg)
Für die Annahme, dass am Punkt 
ein Maximum 1.Ordnung vorliegt, folgt:
![\(\begin{array}[t]{rll}
\sin(\alpha)&=& \dfrac{\Delta s}{b} &\quad \scriptsize \mid\; \Delta s= 1\cdot \lambda \\[5pt]
\sin(\alpha)&=& \dfrac{\lambda}{b} &\quad \scriptsize \mid\; \cdot b \\[5pt]
\sin(\alpha)\cdot b&=& \lambda &\quad \scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/d0d64d2270f703d80da68b49e8c2e625b75ae53c2d24ee6d5a7ea05b7b39009b_light.svg)
Einsetzen der Werte liefert:
![\(\begin{array}[t]{rll}
\lambda&=& \sin(\alpha)\cdot b &\quad \scriptsize \\[5pt]
&=& 2\;\text{cm} \cdot \sin(20,556 ^{\circ} ) &\quad \scriptsize \\[5pt]
&=& 0,70 \;\text{cm} &\quad \scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/9c6e32bbfe60331445c9e2466cd22f814549ad19fcb06755d241c6acb3c47244_light.svg)
Für eine mögliche Frequenz der elektromagnetischen Welle folgt:
![\(\begin{array}[t]{rll}
f&=&\dfrac{c}{\lambda} &\quad \scriptsize \\[5pt]
&=& \dfrac{3,0 \cdot 10^8 \;\dfrac{\text{m}}{\text{s}}}{7,0 \cdot 10^{-3} \;\text{m}} &\quad \scriptsize \\[5pt]
&=& 4,3 \cdot 10^{10} \;\text{Hz}&\quad \scriptsize \\[5pt]
&=& 43 \;\text{Ghz}&
\end{array}\)](https://www.schullv.de/resources/formulas/191d3d04df742b50c20e08c46b0af17d07963495442aa876e36f0366740ded29_light.svg)
ein ganzzahliges Vielfaches der Wellenlänge sein:
Für die Interferenz im Doppelspalt gilt:
Es gilt außerdem:
entspricht dem Abstand zwischen den beiden Spalten. enspricht dem horizontalen Abstand zum Punkt P. entpsricht dem senkrechten Abstand zum Punkt P. Für den Beugungswinkel folgt damit:
Für die Annahme, dass am Punkt ein Maximum 1.Ordnung vorliegt, folgt:
Einsetzen der Werte liefert:
Für eine mögliche Frequenz der elektromagnetischen Welle folgt: