Vorschlag A1
Schallwellen bei einer Orgel
Die sogenannten Labialpfeifen einer Orgel erzeugen Töne, indem Luft von unten an einer Öffnung vorbei in die Pfeife geblasen wird. Innerhalb der Pfeife bilden sich stehende Wellen aus, wobei die Frequenz der erzeugten Töne abhängig von den Abmessungen der Pfeife ist. Weiterhin überlagern sich die von der Pfeife ausgehenden Schallwellen im Kirchenraum, wodurch es zu verschiedenen Phänomenen im Höreindruck kommt. Die physikalischen Grundlagen dieser Phänomene werden im Folgenden betrachtet. Verwende, sofern nicht anders angegeben, für die Schallgeschwindigkeit in Luft
1.1
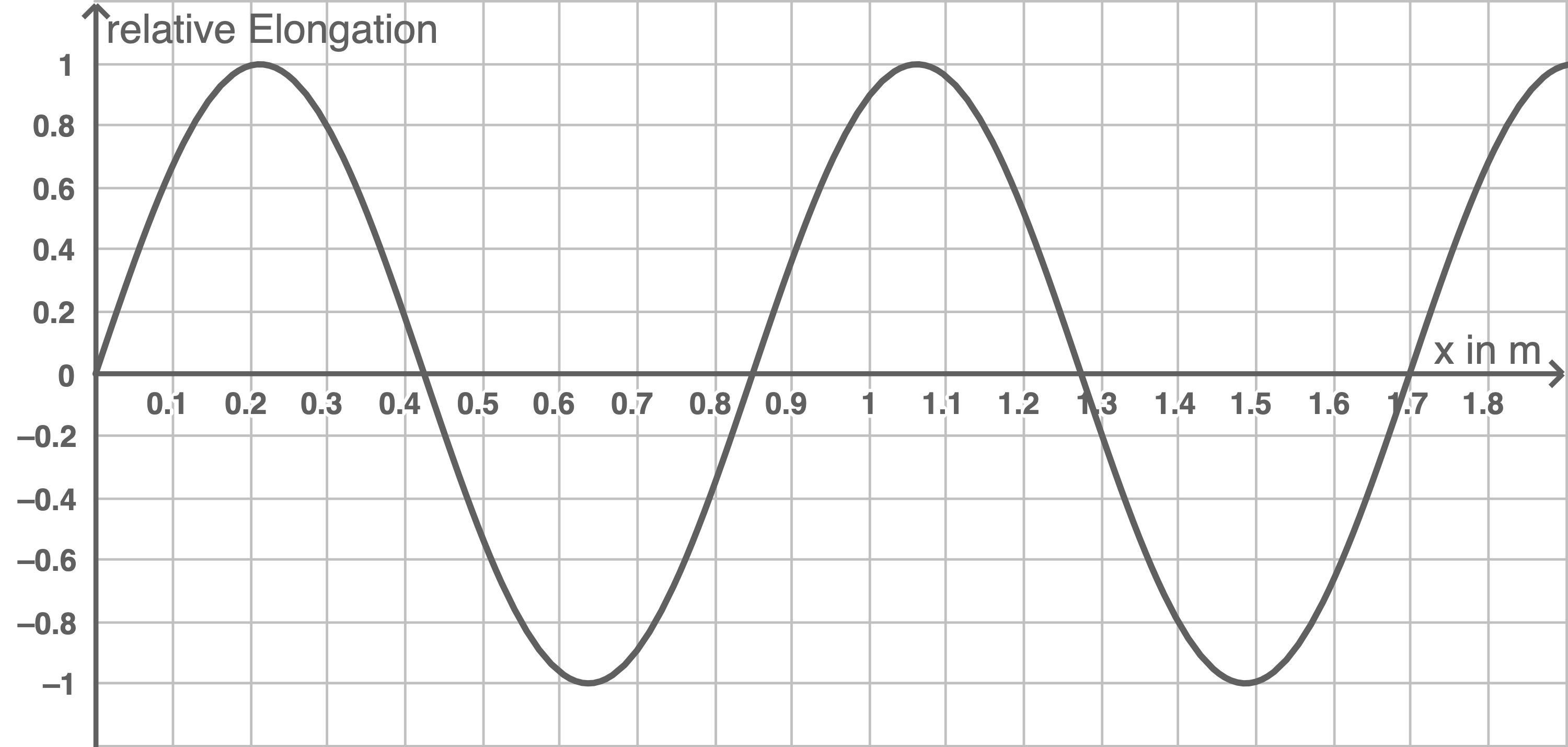
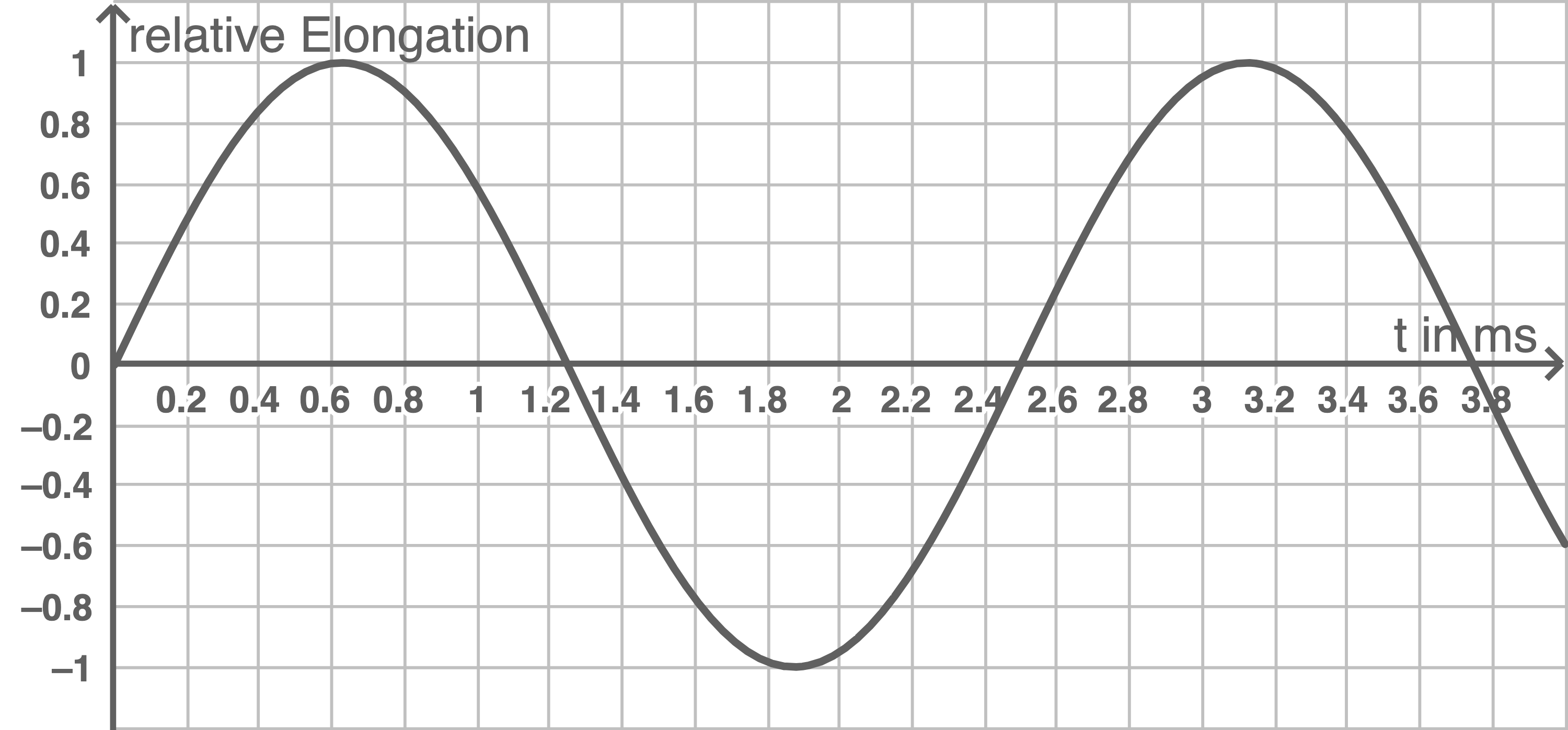
In Material 1 sind das Ort-Elongation-Diagramm und das Zeit-Elongation-Diagramm einer sich ausbreitenden Schallwelle dargestellt.
Gib die Wellenlänge und die Schwingungsdauer dieser Welle an und berechne ihre Frequenz.
Zeige, dass die Ausbreitungsgeschwindigkeit der Schallwelle den oben angegebenen Wert für die Schallgeschwindigkeit hat.


Gib die Wellenlänge und die Schwingungsdauer dieser Welle an und berechne ihre Frequenz.
Zeige, dass die Ausbreitungsgeschwindigkeit der Schallwelle den oben angegebenen Wert für die Schallgeschwindigkeit hat.
Material 1
Ort-Elongation-Diagramm und Zeit-Elongation-Diagramm

(5 BE)
1.2
Organisten nehmen einen deutlich bemerkbaren Zeitunterschied zwischen dem Drücken einer Taste und dem Eintreffen des Tons am Ohr wahr. Verzögerungen durch die Mechanik der Orgel sollen vernachlässigt werden.
Berechne die Zeit, die ein Ton für einen Abstand von zwischen der Pfeife und dem Ohr des Organisten benötigt.
zwischen der Pfeife und dem Ohr des Organisten benötigt.
Berechne die Zeit, die ein Ton für einen Abstand von
(2 BE)
1.3
Eine Orgel muss in regelmäßigen Abständen nachgestimmt werden. Neben Veränderungen der Pfeifenlänge durch Feuchtigkeits- oder Temperaturschwankungen verändert sich auch die Schallgeschwindigkeit mit der Temperatur  in
in  nach der Gesetzmäßigkeit
nach der Gesetzmäßigkeit
 Dabei entspricht
Dabei entspricht  der Schallgeschwindigkeit in Luft bei
der Schallgeschwindigkeit in Luft bei  mit
mit  .
.
Berechne die Schallgeschwindigkeit bei einer Raumtemperatur von .
.
Bestimme den Temperaturbereich, in dem die Abweichung der Schallgeschwindigkeit maximal zur Schallgeschwindigkeit bei
zur Schallgeschwindigkeit bei  beträgt.
beträgt.
Berechne die Schallgeschwindigkeit bei einer Raumtemperatur von
Bestimme den Temperaturbereich, in dem die Abweichung der Schallgeschwindigkeit maximal
(6 BE)
2
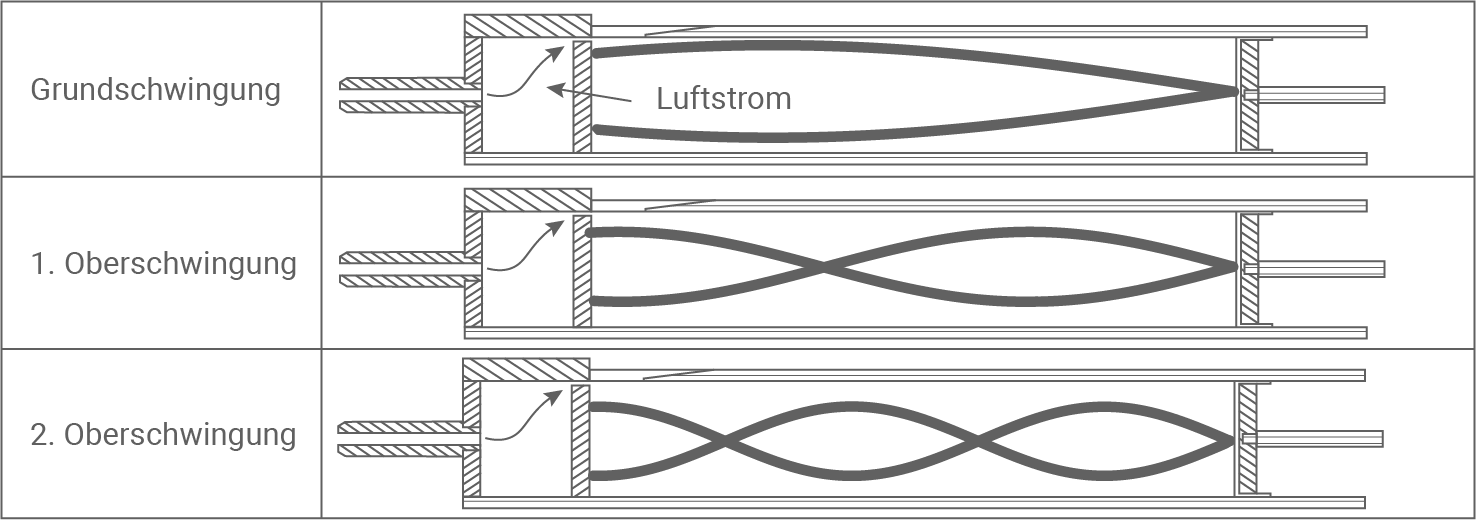
Die sich in einer Orgelpfeife (Material 2) ausbildenden stehenden Wellen besitzen auf der linken Seite einen Geschwindigkeitsbauch. Auf der rechten Seite unterscheidet man zwischen gedackten und offenen Pfeifen. Bei einer gedackten Pfeife ist das obere Ende mit einem Deckel verschlossen und daher befindet sich dort ein Geschwindigkeitsknoten. Der charakteristische Klang einer Orgelpfeife entsteht durch die Mischung von Grundton und Obertönen mit unterschiedlichen Intensitäten. Grundton und Obertöne werden üblicherweise als Grundschwingung und Oberschwingungen bezeichnet.
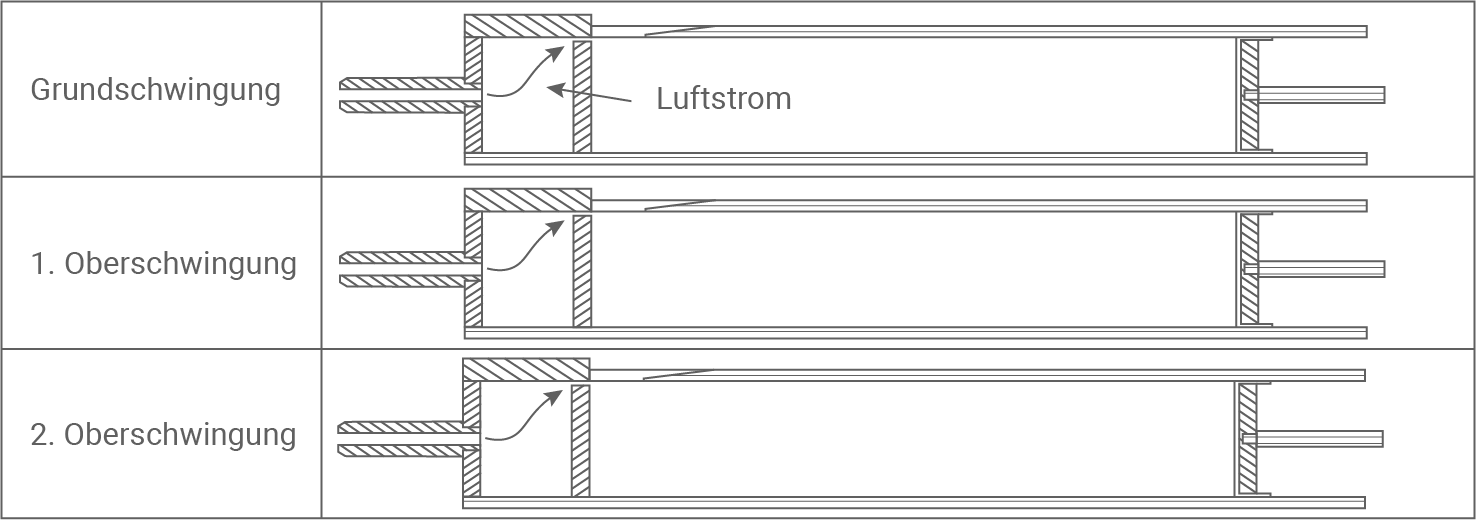 Die Orgelpfeife ist um
Die Orgelpfeife ist um  gedreht dargestellt. Das obere Ende der Orgelpfeife ist hier rechts.
gedreht dargestellt. Das obere Ende der Orgelpfeife ist hier rechts.
Material 2
Abbildungen einer gedackten Orgelpfeife zum Einzeichnen der stehenden Wellen
2.1
Skizziere die Grundschwingung und die ersten beiden Oberschwingungen einer gedackten Pfeife in Material 2.
Ermittle die Wellenlängen der Grundschwingung und der ersten beiden Oberschwingungen einer stehenden Welle in einer gedackten Pfeife der Länge
Ermittle die Wellenlängen der Grundschwingung und der ersten beiden Oberschwingungen einer stehenden Welle in einer gedackten Pfeife der Länge
(8 BE)
2.2
Ermittle den prozentualen Längenunterschied einer offenen Pfeife zu einer gedackten Pfeife bei gleicher Frequenz der Grundschwingung  .
.
Begründe, dass bei einer gedackten Pfeife keine Oktave (Schwingung mit doppelter Frequenz) als Oberschwingung zum Grundton erzeugt werden kann.
Begründe, dass bei einer gedackten Pfeife keine Oktave (Schwingung mit doppelter Frequenz) als Oberschwingung zum Grundton erzeugt werden kann.
(5 BE)
2.3
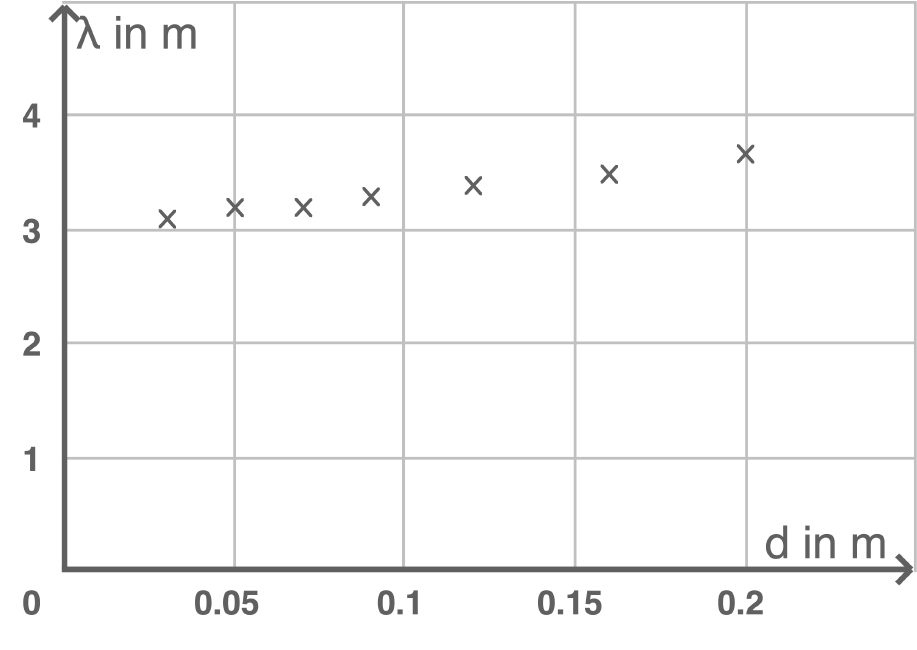
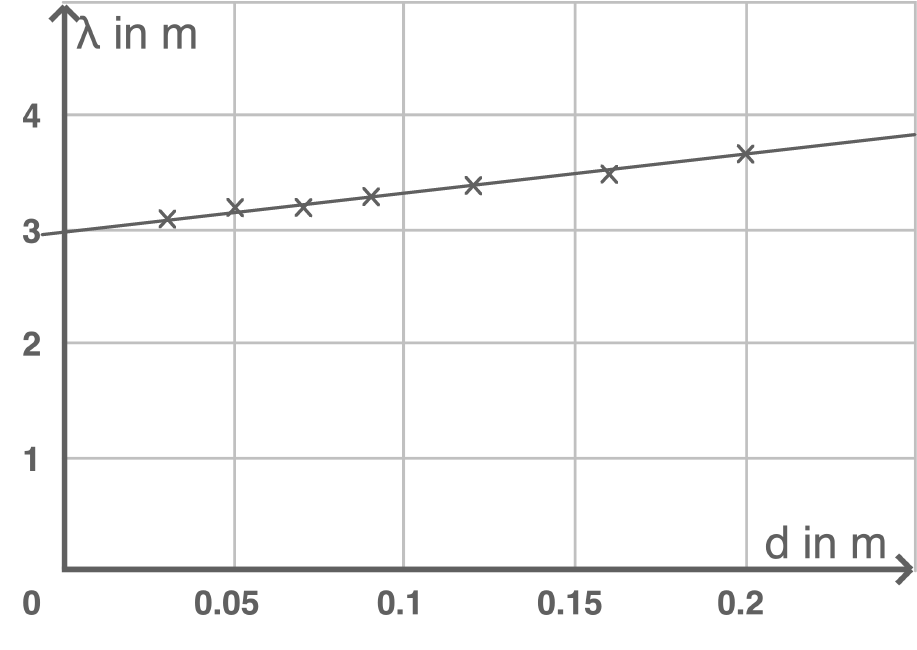
In der Praxis des Pfeifenbaus zeigt sich, dass sich der Durchmesser einer offenen Pfeife auf die Wellenlänge der Grundschwingung auswirkt. Es wurde nun der Einfluss des Pfeifendurchmessers  auf die Wellenlänge
auf die Wellenlänge  der Grundschwingung einer 1,5 m langen Pfeife untersucht. Die Daten der Messreihe sind im Durchmesser-Wellenlängen-Diagramm in Material 3 abgebildet. Bestimme die Gleichung der Ausgleichsgeraden durch die Messpunkte.
der Grundschwingung einer 1,5 m langen Pfeife untersucht. Die Daten der Messreihe sind im Durchmesser-Wellenlängen-Diagramm in Material 3 abgebildet. Bestimme die Gleichung der Ausgleichsgeraden durch die Messpunkte.
Deute die beiden Parameter der Geradengleichung im Sachzusammenhang.
Entscheide und begründe, ob der Ton mit zunehmendem Durchmesser einer Pfeife durch den in Material 3 dargestellten Effekt höher oder tiefer wird. vom Durchmesser
vom Durchmesser  der Pfeife
der Pfeife
Deute die beiden Parameter der Geradengleichung im Sachzusammenhang.
Entscheide und begründe, ob der Ton mit zunehmendem Durchmesser einer Pfeife durch den in Material 3 dargestellten Effekt höher oder tiefer wird.
Material 3
Abhängigkeit der Wellenlänge
(8 BE)
3
Da der Ton einer bestimmten einzelnen Pfeife im Orgelklang zu leise ist, wird eine zweite gleiche Pfeife zusätzlich aufgebaut. In Material 4 ist die Situation in einem Kirchenraum dargestellt, in dem die zwei Pfeifen mit derselben Frequenz  ertönen. Nimm für die Aufgaben 3.1 bis 3.3 an, dass die beiden Pfeifen in Phase schwingen.
ertönen. Nimm für die Aufgaben 3.1 bis 3.3 an, dass die beiden Pfeifen in Phase schwingen.
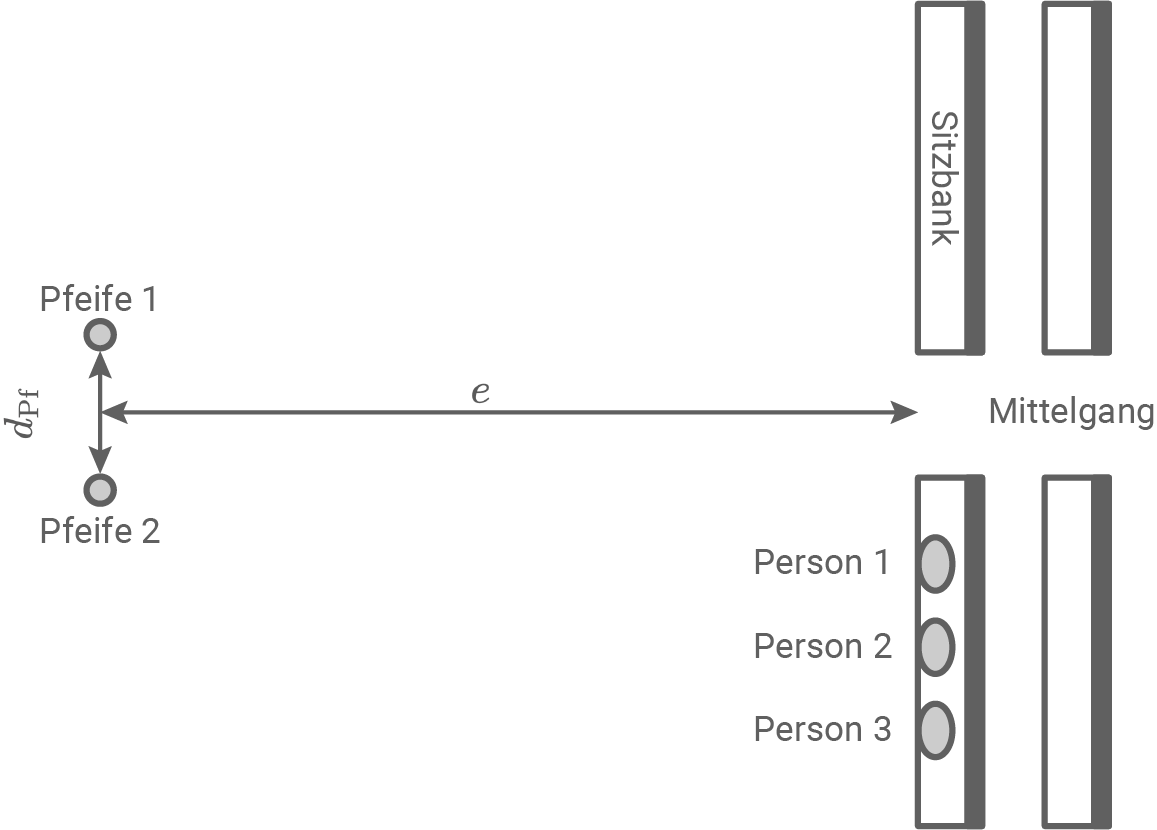 Abstand der beiden Pfeifen:
Abstand der beiden Pfeifen: 
Abstand Pfeife-Sitzbank:
Material 4
Anordnung von Pfeifen und Personen in einer Kirche
Abstand Pfeife-Sitzbank:
3.1
Obwohl sich Person 2 näher an den Pfeifen befindet als Person 3, kann die Lautstärke für Person 3 größer sein als die Lautstärke für Person 2.
Erkläre den Lautstärkeunterschied qualitativ.
Erkläre den Lautstärkeunterschied qualitativ.
(4 BE)
3.2
Berechne den Abstand  zwischen Person 1 und Person 3, wenn diese beiden Personen im Lautstärkemaximum 1. bzw. 2. Ordnung sitzen. Dabei kann
zwischen Person 1 und Person 3, wenn diese beiden Personen im Lautstärkemaximum 1. bzw. 2. Ordnung sitzen. Dabei kann  angenommen werden.
angenommen werden.
(5 BE)
3.3
Untersuche die Auswirkung der Verringerung des Abstands  der zwei Pfeifen auf die Lage der Maxima und Minima am Ort der Sitzbank.
der zwei Pfeifen auf die Lage der Maxima und Minima am Ort der Sitzbank.
(2 BE)
3.4
Erkläre mithilfe von Material 5, wie es dazu kommen kann, dass bei der Verwendung von zwei Pfeifen eine Verringerung der Lautstärke auftritt. Untersuche, wie sich der Höreindruck verändert, wenn sich der Graph B der Schwingung der zweiten Pfeife geringfügig nach links verschiebt.
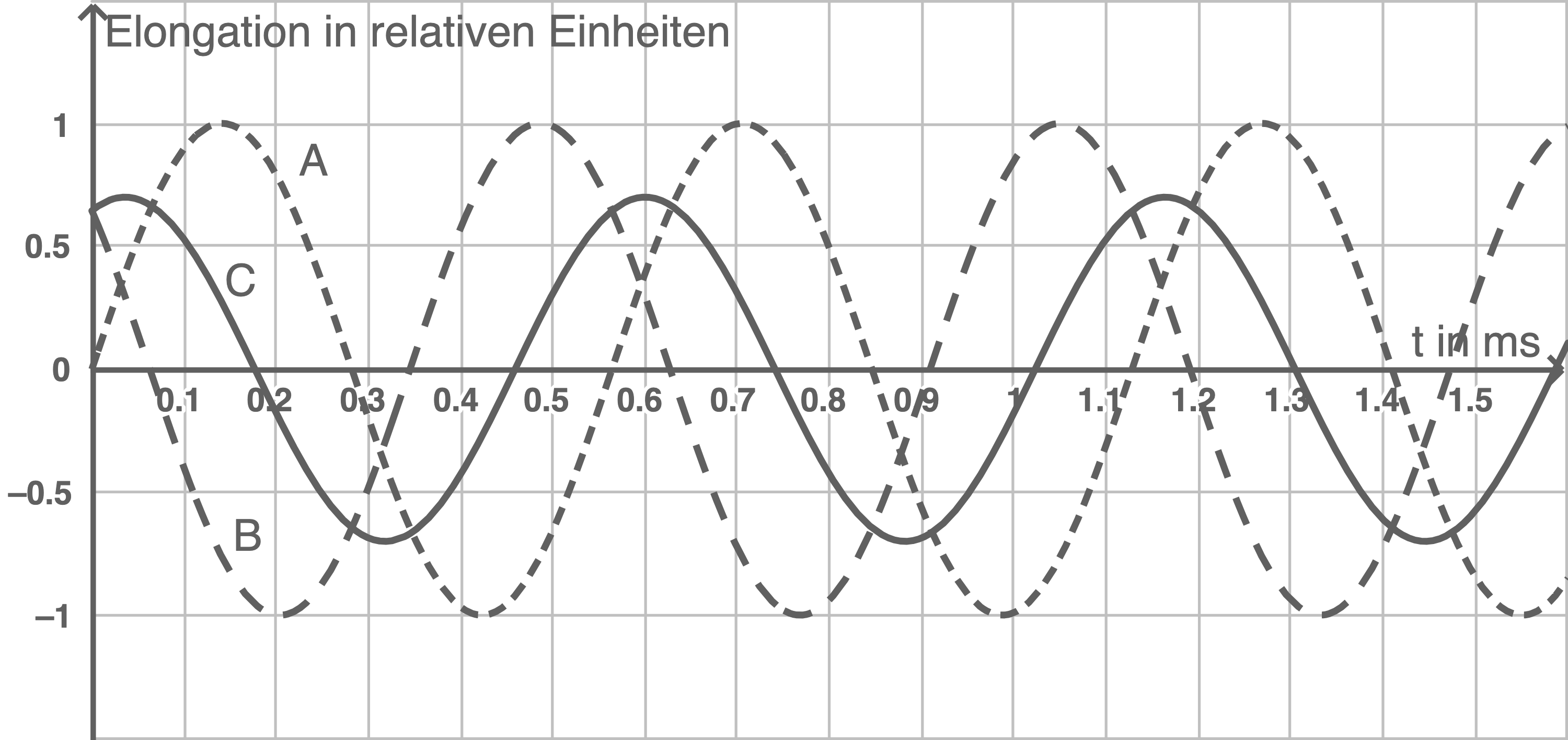
Material 5
Elongation der Schwingung an einem Ort in der Kirche
A: nur erste Pfeife ertönt
B: nur zweite Pfeife ertönt
C: beide Pfeifen ertönen gleichzeitig
B: nur zweite Pfeife ertönt
C: beide Pfeifen ertönen gleichzeitig
(5 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.1
Wellenlänge
Die Wellenlänge  ist die Distanz zwischen zwei aufeinanderfolgenden Maxima oder Minima im Ort-Elongation-Diagramm und repräsentiert die räumliche Periodizität der Welle. Nachdem eine Strecke von
ist die Distanz zwischen zwei aufeinanderfolgenden Maxima oder Minima im Ort-Elongation-Diagramm und repräsentiert die räumliche Periodizität der Welle. Nachdem eine Strecke von  zurückgelegt wurde, hat die Welle zwei komplette Schwingungen durchlaufen:
zurückgelegt wurde, hat die Welle zwei komplette Schwingungen durchlaufen:
![\(\begin{array}[t]{rll}
\lambda&=& \dfrac{1,7 \;\text{m}}{2} &\quad \scriptsize \\[5pt]
&=& 0,85 \;\text m
\end{array}\)](https://www.schullv.de/resources/formulas/e261684d3752deac215f9c9075e34141f52cdb6607290501cfc846911d432b64_light.svg) Schwingungsdauer
Die Schwingungsdauer
Schwingungsdauer
Die Schwingungsdauer  ist die Zeit für eine vollständige Schwingung, ablesbar im Zeit-Elongation-Diagramm:
ist die Zeit für eine vollständige Schwingung, ablesbar im Zeit-Elongation-Diagramm:
![\(\begin{array}[t]{rll}
T&=& 2,5 \;\text{ms} &\quad \scriptsize \\[5pt]
&=& 2,5 \cdot 10^{-3} \;\text{s}
\end{array}\)](https://www.schullv.de/resources/formulas/e7e6ec66f7018cc3a4595a501b0c0d5e20e5ad3fa2d5903e50ddbb2b3af2ff09_light.svg) Frequenz
Für die Frequenz
Frequenz
Für die Frequenz  gilt:
gilt:
![\(\begin{array}[t]{rll}
f&=&\dfrac{1}{T} &\quad \scriptsize \\[5pt]
&=& \dfrac{1}{2,5 \cdot 10^{-3} \;\text{s}} &\quad \scriptsize \\[5pt]
&=& 4,0 \cdot 10^2\;\dfrac{1}{\text{s}} &\quad \scriptsize \\[5pt]
&=& 0,40 \,\text{kHz}
\end{array}\)](https://www.schullv.de/resources/formulas/c244c193814b0b52b73ccc51bc88310166964d72a910d39bd56983f57706b00e_light.svg) Ausbreitungsgeschwindigkeit
Für die Ausbreitungsgeschwindigkeit
Ausbreitungsgeschwindigkeit
Für die Ausbreitungsgeschwindigkeit  gilt:
gilt:
![\(\begin{array}[t]{rll}
v&=& f\cdot \lambda &\quad \scriptsize \\[5pt]
&=& 4,0 \cdot 10^2\;\dfrac{1}{\text{s}} \cdot 0,85 \;\text m &\quad \scriptsize \\[5pt]
&=& 340 \;\dfrac{\text m}{\text s} &\quad \scriptsize \\[5pt]
&\approx& c_{\text{Luft}}
\end{array}\)](https://www.schullv.de/resources/formulas/4fe85c87bf88d84f7ebdb7f016f7c672f35e1a8d4785f1cfc791e776ffbc8071_light.svg)
1.2
Für die Zeit  , die ein Ton zwischen der Pfeife und dem Ohr des Organisten benötigt, gilt:
, die ein Ton zwischen der Pfeife und dem Ohr des Organisten benötigt, gilt:
![\(\begin{array}[t]{rll}
t&=&\dfrac{d}{v} &\quad \scriptsize \mid\; v= c_{\text{Luft}} \\[5pt]
&=& \dfrac{d}{c_{\text{Luft}}} &\quad \scriptsize \\[5pt]
&=& \dfrac{15 \;\text m}{340 \dfrac{\text{m}}{\text{s}}} &\quad \scriptsize \\[5pt]
&=& 0,044 \;\text{s}
\end{array}\)](https://www.schullv.de/resources/formulas/3b44bf31b8caea30d6eaa6a39465bf97ede9d52196f96b92dc697143e63ae3b1_light.svg)
1.3
Schallgeschwindigkeit
![\(\begin{array}[t]{rll}
c(\vartheta)&=& c_0 \cdot \sqrt{1+\dfrac{\vartheta}{273,15^{\circ} C }}&\quad \scriptsize \\[5pt]
c(18^{\circ})&=& 331,5 \;\dfrac{ \text m }{\text s }\cdot \sqrt{1+\dfrac{18^{\circ}}{273,15^{\circ} C }}&\quad \scriptsize \\[5pt]
&=& 342,2 \;\dfrac{ \text m }{\text s }
\end{array}\)](https://www.schullv.de/resources/formulas/7cd871887e8c1817603ba26080d5db37426d764d7a20c9b3c851750ad2995a1d_light.svg) Temperaturbereich
Temperaturbereich
 von
von  entspricht:
Für den Bereich der Schallgeschwindigkeit ergibt sich damit:
Für die Temperatur
entspricht:
Für den Bereich der Schallgeschwindigkeit ergibt sich damit:
Für die Temperatur  , bei der eine Schallgeschwindigkeit von
, bei der eine Schallgeschwindigkeit von  erreicht wird, gilt:
Ensetzen der Intervallgrenzen der Schallgeschwindigkeit liefert:
erreicht wird, gilt:
Ensetzen der Intervallgrenzen der Schallgeschwindigkeit liefert:
![\(\begin{array}[t]{rll}
\vartheta&=& \left(\left(\dfrac{c_{\text{min}}}{c_0}\right)^2-1\right)\cdot 273,15^°&\quad \scriptsize \\[5pt]
&=& \left(\left(\dfrac{324,87 \;\dfrac{ \text m }{\text s }}{331,5 \;\dfrac{ \text m }{\text s }}\right)^2-1\right)\cdot 273,15^°&\quad \scriptsize \\[5pt]
&=& -11 ^°
\end{array}\)](https://www.schullv.de/resources/formulas/3f51a5fbfa5bfa8095af0233c6d8e3460a997768e99913d77832de89e432c9db_light.svg)
![\(\begin{array}[t]{rll}
\vartheta&=& \left(\left(\dfrac{c_{\text{max}}}{c_0}\right)^2-1\right)\cdot 273,15^°&\quad \scriptsize \\[5pt]
&=& \left(\left(\dfrac{338,13\;\dfrac{ \text m }{\text s }}{331,5 \;\dfrac{ \text m }{\text s }}\right)^2-1\right)\cdot 273,15^°&\quad \scriptsize \\[5pt]
&=& 11 ^°
\end{array}\)](https://www.schullv.de/resources/formulas/d2950edd14dd4145c3aa65a6a59c53722ec9fb3e7415046b354884fca070353a_light.svg) Zwischen
Zwischen  und
und  liegt der Temperaturbereich, in dem die Abweichung der Schallgeschwindigkeit maximal
liegt der Temperaturbereich, in dem die Abweichung der Schallgeschwindigkeit maximal  von der Schallgeschwindigkeit bei
von der Schallgeschwindigkeit bei  beträgt.
beträgt.
2.1
2.2
Prozentualer Längenunterschied
Bei einer gedackten Pfeife beträgt die Wellenlänge der Grundschwingung genau ein Viertel der Länge des Wellenträgers, es gilt somit:
![\(\begin{array}[t]{rll}
\lambda_0&=& 4 L_{\text {gedackt}}
\end{array}\)](https://www.schullv.de/resources/formulas/9e5704d1a9e55eaa34e0b4e7d33cb7c25f02546b1552c277492eb7dca5a5f3d2_light.svg) Für die Grundschwingung einer offenen Pfeife mit losen Enden müssen sich an beiden Enden Schwingungsbauchpunkte und in der Mitte ein Schwingungsknoten befinden. Die Wellenlänge der Grundschwingung ist daher die halbe Länge des Wellenträgers:
Für die Grundschwingung einer offenen Pfeife mit losen Enden müssen sich an beiden Enden Schwingungsbauchpunkte und in der Mitte ein Schwingungsknoten befinden. Die Wellenlänge der Grundschwingung ist daher die halbe Länge des Wellenträgers:
![\(\begin{array}[t]{rll}
\lambda_0&=& 2 L_{\text {offen }}
\end{array}\)](https://www.schullv.de/resources/formulas/5f90510df8eaa6f7677d4df21fc2f5f53e58edb95f4ec96eae5876f7087716ea_light.svg) Durch die vorausgesetzte Gleichheit der Frequenz und Wellenlänge beider Pfeifen folgt:
Durch die vorausgesetzte Gleichheit der Frequenz und Wellenlänge beider Pfeifen folgt:
![\(\begin{array}[t]{rll}
4 L_{\text {gedackt}}&=& 2 L_{\text {offen }} &\quad \scriptsize \mid\; \cdot \dfrac{1}{2} \\[5pt]
2 L_{\text {gedackt}}&=& L_{\text {offen }} &\quad \scriptsize \\[5pt]
L_{\text {offen }}&=& 2 L_{\text {gedackt}}
\end{array}\)](https://www.schullv.de/resources/formulas/057770827d853346351ad7d4c750fd3cafa7dca46aca24cad876c7304f5eafbb_light.svg) Der prozentuale Längenunterschied der offenen zur gedackten Pfeife beträgt daher:
Keine Oktave als Oberschwingung bei einer gedackten Pfeife
Für die Eigenfrequenzen einer gedeckten Pfeife gilt:
In einer gedeckten Pfeife sind nur bestimmte Eigenfrequenzen möglich, nämlich
Der prozentuale Längenunterschied der offenen zur gedackten Pfeife beträgt daher:
Keine Oktave als Oberschwingung bei einer gedackten Pfeife
Für die Eigenfrequenzen einer gedeckten Pfeife gilt:
In einer gedeckten Pfeife sind nur bestimmte Eigenfrequenzen möglich, nämlich  Diese erlauben jedoch keine Kombination, bei der eine Schwingung die doppelte Frequenz einer anderen hat, was für die Erzeugung einer Oktave erforderlich wäre. Im Gegensatz dazu ermöglicht eine offene Pfeife aufgrund ihrer verschiedenen Schwingungsmuster die Bildung einer Oktave.
Diese erlauben jedoch keine Kombination, bei der eine Schwingung die doppelte Frequenz einer anderen hat, was für die Erzeugung einer Oktave erforderlich wäre. Im Gegensatz dazu ermöglicht eine offene Pfeife aufgrund ihrer verschiedenen Schwingungsmuster die Bildung einer Oktave.
2.3
3.1
Die Schallwellen der nebeneinanderstehenden Pfeifen im Kirchenraum sind in Phase, was zu konstruktiver Interferenz führt. An verschiedenen Orten im Raum überlagern sich die Schwingungen, verstärken sich konstruktiv und erhöhen die Lautstärke an bestimmten Stellen. Dies resultiert aus der gleichen Amplitude und Wellenlänge der erzeugten Schallwellen. Orte, an denen Wellenberge aufeinandertreffen, erfahren konstruktive Interferenz und zeigen eine erhöhte Lautstärke. Orte mit Wellenbergen und -tälern in Konflikt erleben destruktive Interferenz, was zu einer Verringerung der Lautstärke führt. Der Gangunterschied bestimmt, ob konstruktive oder destruktive Interferenz auftritt. So kann es sein, dass sich Personen an verschiedenen Orten unterschiedliche Lautstärken wahrnehmen, selbst wenn sie sich gleich weit von den Schallquellen entfernt befinden.
3.2
Die Situation ähnelt der Interferenz an einem Doppelspalt. Dabei entspricht  dem Spaltabstand, die senkrechte Entfernung
dem Spaltabstand, die senkrechte Entfernung  zwischen den Pfeifen und der ersten Sitzbankreihe dem Abstand zwischen Doppelspalt und Schirm. Der Abstand zwischen Person 1 und Person 3 entspricht dem Abstand des Intensitätsmaximums 1. Ordnung
zwischen den Pfeifen und der ersten Sitzbankreihe dem Abstand zwischen Doppelspalt und Schirm. Der Abstand zwischen Person 1 und Person 3 entspricht dem Abstand des Intensitätsmaximums 1. Ordnung  vom Intensitätsmaximum 2. Ordnung
vom Intensitätsmaximum 2. Ordnung  auf dem Schirm.
Wegen e
auf dem Schirm.
Wegen e  gelten in diesem Fall für den Beugungswinkel
gelten in diesem Fall für den Beugungswinkel  die Formeln:
die Formeln:
![\(\begin{array}[t]{rll}
\sin \alpha_n&=& \dfrac{n \cdot \lambda}{d_{P f}}&\quad \scriptsize \left(1\right)\\[5pt]
\tan \alpha_n&=&\dfrac{a_n}{e} &\quad \scriptsize \left(2\right)\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/8bb630b3683702da3d6a2947840d36d59dd8d274e8addad329928dd409c9b745_light.svg) Für die jeweiligen Abstände
Für die jeweiligen Abstände  und
und  der beiden Personen von der Mitte des Mittelgangs gilt:
Person
der beiden Personen von der Mitte des Mittelgangs gilt:
Person 
![\(\begin{array}[t]{rll}
\sin \alpha_1&=&\dfrac{1 \cdot \lambda}{d_{P f}} &\quad \scriptsize \mid\, \lambda=\dfrac{c}{f}\\[5pt]
\sin \alpha_1&=& \dfrac{c}{f \cdot d_{P f}} &\quad \scriptsize \mid\, \sin^{-1}\left(\,\right)\\[5pt]
\alpha_1&=& \sin^{-1}\left(\dfrac{c}{f \cdot d_{P f}}\right)
\end{array}\)](https://www.schullv.de/resources/formulas/6cc55b53fcff03121fce1736e95f07df4e513620c5e010c9909de2066a683869_light.svg) Einsetzen der Werte liefert:
Einsetzen der Werte liefert:
![\(\begin{array}[t]{rll}
\alpha_1&=& \sin^{-1}\left(\dfrac{c}{f \cdot d_{P f}}\right) &\quad \scriptsize \\[5pt]
&=& \sin^{-1} \left(\dfrac{340 \,\frac{\text{m}}{\text{s}}}{1760 \,\text{Hz} \cdot 1,5 \,\text{m}}\right)&\quad \scriptsize \\[5pt]
&=& 7,40^{\circ}
\end{array}\)](https://www.schullv.de/resources/formulas/061140332a6e0c62cd7b775e84906a77483f75a2e66eea7cbd2f3ac190529d39_light.svg) Für den Abstand
Für den Abstand  der Person 1 von der Mitte des Mittelgangs folgt mit der Formel
der Person 1 von der Mitte des Mittelgangs folgt mit der Formel 
![\(\begin{array}[t]{rll}
\tan \alpha_1&=&\dfrac{a_1}{e}&\quad \scriptsize \mid\; \cdot e \\[5pt]
\tan \alpha_1\cdot e&=& a_1 &\quad \scriptsize \\[5pt]
a_1&=& \tan \alpha_1\cdot e
\end{array}\)](https://www.schullv.de/resources/formulas/4632595482662278a10f93a3ae2498182e56dd94a456fae4027d17600920ae10_light.svg) Einsetzen der Werte liefert:
Einsetzen der Werte liefert:
![\(\begin{array}[t]{rll}
a_1&=& \tan \alpha_1\cdot e &\quad \scriptsize \\[5pt]
&=& 16 \,\text{m} \cdot \tan\left( 7,40^{\circ}\right)&\quad \scriptsize \\[5pt]
&=& 2,80 \,\text{m}
\end{array}\)](https://www.schullv.de/resources/formulas/0971145be520c9970693343eb404cba7914c8d618dee3124ee0c48ca071bdf32_light.svg) Person
Person 
![\(\begin{array}[t]{rll}
\sin \alpha_2&=&\dfrac{2 \cdot \lambda}{d_{P f}} &\quad \scriptsize \mid\, \lambda=\dfrac{c}{f}\\[5pt]
\sin \alpha_2&=& \dfrac{2\cdot c}{f \cdot d_{P f}} &\quad \scriptsize \mid\, \sin^{-1}\left(\,\right)\\[5pt]
\alpha_2&=& \sin^{-1}\left(\dfrac{2\cdot c}{f \cdot d_{P f}}\right)
\end{array}\)](https://www.schullv.de/resources/formulas/d4fa1f456d172f6fff96126632e36279d9fa41e58de33b81a50cefc9462111c7_light.svg) Einsetzen der Werte liefert:
Einsetzen der Werte liefert:
![\(\begin{array}[t]{rll}
\alpha_2&=& \sin^{-1}\left(\dfrac{2\cdot c}{f \cdot d_{P f}}\right) &\quad \scriptsize \\[5pt]
&=& \sin^{-1} \left(\dfrac{2\cdot 340 \,\frac{\text{m}}{\text{s}}}{1760 \,\text{Hz} \cdot 1,5 \,\text{m}}\right)&\quad \scriptsize \\[5pt]
&=& 14,93^{\circ}
\end{array}\)](https://www.schullv.de/resources/formulas/63a6ac031c20d64dcf612973e73d493e2fb95c3b1323c5f1ac195adf3f7b117b_light.svg) Für den Abstand
Für den Abstand  der Person 3 von der Mitte des Mittelgangs folgt mit der Formel
der Person 3 von der Mitte des Mittelgangs folgt mit der Formel 
![\(\begin{array}[t]{rll}
\tan \alpha_2&=&\dfrac{a_2}{e}&\quad \scriptsize \mid\; \cdot e \\[5pt]
\tan \alpha_2\cdot e&=& a_2 &\quad \scriptsize \\[5pt]
a_2&=& \tan \alpha_2\cdot e
\end{array}\)](https://www.schullv.de/resources/formulas/4df2873035aece3ce347a3dcf782319c4c6289fdbd274cfcc0f6a7d838ee986b_light.svg) Einsetzen der Werte liefert:
Einsetzen der Werte liefert:
![\(\begin{array}[t]{rll}
a_1&=& \tan \alpha_2\cdot e &\quad \scriptsize \\[5pt]
&=& 16 \,\text{m} \cdot \tan\left( 14,93^{\circ}\right)&\quad \scriptsize \\[5pt]
&=& 4,27 \,\text{m}
\end{array}\)](https://www.schullv.de/resources/formulas/ff38b277f58dad8384c2e4fa214a946c0d1f962951fce85249ea4cb54ec59782_light.svg) Der Abstand der beiden Personen beträgt somit:
Der Abstand der beiden Personen beträgt somit:
![\(\begin{array}[t]{rll}
a&=& a_2-a_1 &\quad \scriptsize \\[5pt]
&=& 4,27 \,\text{m}-2,08 \,\text{m} &\quad \scriptsize \\[5pt]
&=& 2,19 \,\text m
\end{array}\)](https://www.schullv.de/resources/formulas/9dc335581877fc8f04d953dcbad337cb6f6c44eaaeb56f21adf6fd75c6b6a6f8_light.svg)
3.3
Für den Abstand der Pfeifen  gilt:
gilt:
![\(\begin{array}[t]{rll}
\sin \alpha_n&=& \dfrac{n \cdot \lambda}{d_{P f}}&\quad \scriptsize \mid \,\sin^{-1}\left(\;\right)\\[5pt]
\alpha_n&=& \sin^{-1}\left(\dfrac{n \cdot \lambda}{d_{P f}}\right)&\quad \scriptsize \left(1\right) \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/f2ee6936f5ea6619c1710198c2b5c5019456c847016c60936b20e88881edf2af_light.svg) Wenn der Abstand der beiden Pfeifen
Wenn der Abstand der beiden Pfeifen  zueinander verringert wird, so wird der Winkel
zueinander verringert wird, so wird der Winkel  nach der Formel
nach der Formel  größer.
Für den Abstand
größer.
Für den Abstand  gilt damit:
gilt damit:
![\(\begin{array}[t]{rll}
\tan \alpha_n&=& \dfrac{a_n }{e}&\quad \scriptsize \mid\; \cdot e \\[5pt]
\tan \alpha_n\cdot e&=& a_n &\quad \scriptsize \\[5pt]
a_n&=& \tan \alpha_n\cdot e &\quad \scriptsize \left(2\right) \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/bd6aa68965dc47c54948aed8a8ec3b9986cf23dc66e7b14db5634e72917c6e2e_light.svg) Nach der Gleichung
Nach der Gleichung  wird mit größerem
wird mit größerem  auch der Abstand
auch der Abstand  der Maxima (bzw. Minima) zum Hauptmaximum größer. Die Orte der Maxima und Minima auf der Sitzbank verschieben sich also weiter weg vom Mittelgang.
der Maxima (bzw. Minima) zum Hauptmaximum größer. Die Orte der Maxima und Minima auf der Sitzbank verschieben sich also weiter weg vom Mittelgang.
3.4
Verringerung der Lautstärke
Am betrachteten Ort in der Kirche überlagern sich die sinusförmigen Schwingungen  und
und  mit einer Phasenverschiebung. Die resultierende Schwingung
mit einer Phasenverschiebung. Die resultierende Schwingung  ist die Summe von
ist die Summe von  und
und  . Durch die Phasenverschiebung ergibt sich eine geringere Amplitude bei
. Durch die Phasenverschiebung ergibt sich eine geringere Amplitude bei  im Vergleich zu den einzelnen Schwingungen
im Vergleich zu den einzelnen Schwingungen  und
und  .
Höreindruck
Wenn sich der Graph der Schwingung B nach links verschiebt, nähern sich die Maxima von A den Minima von B an. Dadurch hat die resultierende Schwingung C eine geringere Amplitude, was zu einer leiseren Wahrnehmung des Tons im Kirchenraum führt.
.
Höreindruck
Wenn sich der Graph der Schwingung B nach links verschiebt, nähern sich die Maxima von A den Minima von B an. Dadurch hat die resultierende Schwingung C eine geringere Amplitude, was zu einer leiseren Wahrnehmung des Tons im Kirchenraum führt.