Vorschlag B1
Massenspektrometer
1
Ein Massenspektrometer verwendet elektrische und magnetische Felder, um die Massen von Atom- und Molekül-Ionen zu messen (Material 1). Es soll angenommen werden, dass die Ionenquelle ausschließlich einfach positiv geladene Ionen  mit unterschiedlichen Massen und verschiedenen Anfangsgeschwindigkeiten verlassen. Die Ionen werden als Ionenstrahl gebündelt. Anschließend treten die Ionen in einen Geschwindigkeitsfilter ein. Dieser besteht aus einem homogenen elektrischen Feld und einem homogenen magnetischen Feld, die senkrecht zueinander angeordnet sind. Nur Ionen mit einer bestimmten Geschwindigkeit
mit unterschiedlichen Massen und verschiedenen Anfangsgeschwindigkeiten verlassen. Die Ionen werden als Ionenstrahl gebündelt. Anschließend treten die Ionen in einen Geschwindigkeitsfilter ein. Dieser besteht aus einem homogenen elektrischen Feld und einem homogenen magnetischen Feld, die senkrecht zueinander angeordnet sind. Nur Ionen mit einer bestimmten Geschwindigkeit  können diesen Bereich geradlinig durchlaufen und in den Analysator eintreten. Im Geschwindigkeitsfilter und im Analysator sind die magnetischen Felder homogen mit gleich großer, zeitlich konstanter magnetischer Flussdichte bzw. magnetische Feldstärke
können diesen Bereich geradlinig durchlaufen und in den Analysator eintreten. Im Geschwindigkeitsfilter und im Analysator sind die magnetischen Felder homogen mit gleich großer, zeitlich konstanter magnetischer Flussdichte bzw. magnetische Feldstärke  .
.
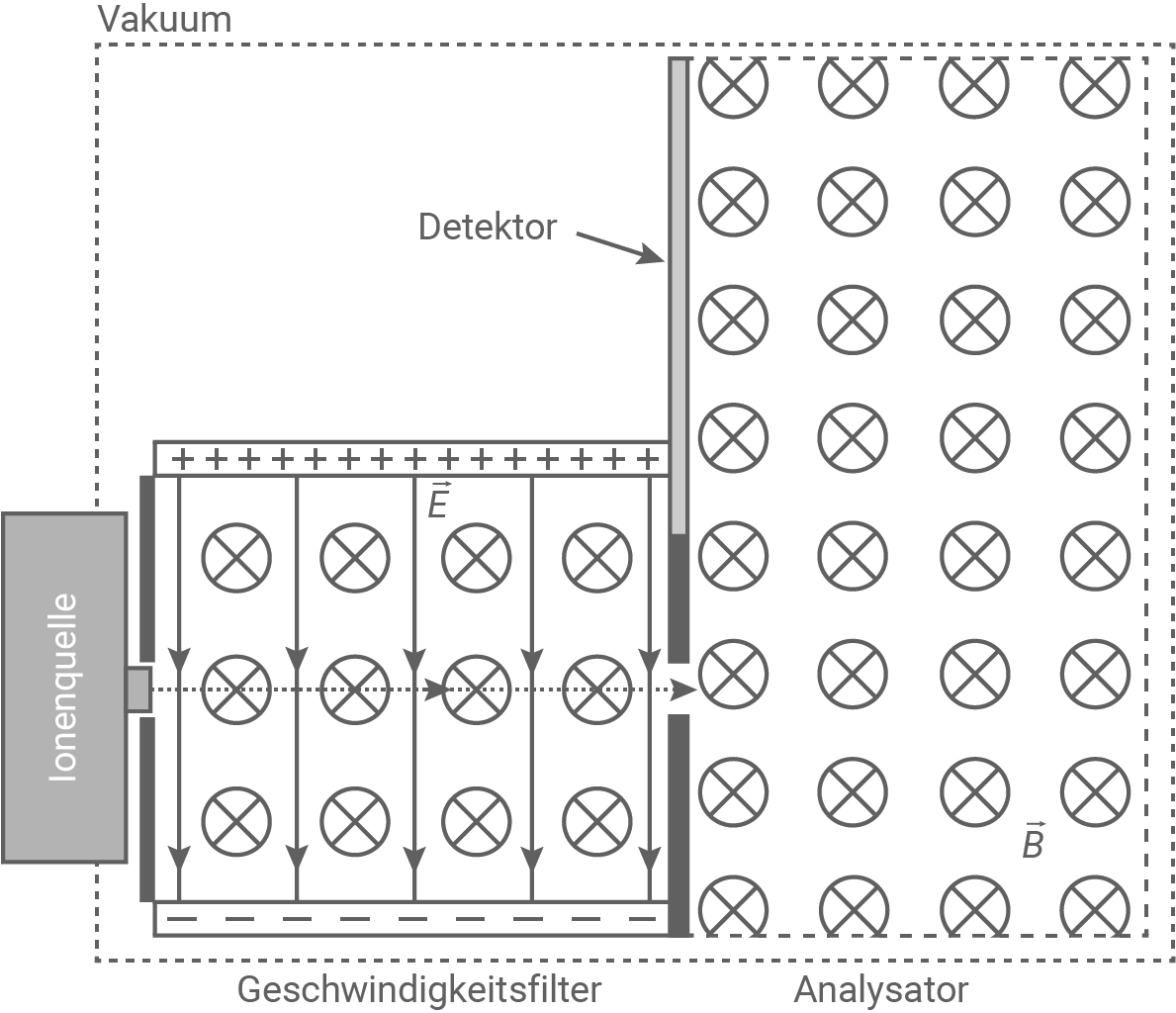 Das magnetische Feld zeigt in die Zeichenebene.
Das magnetische Feld zeigt in die Zeichenebene.
Material 1
Massenspektrometer mit Geschwindigkeitsfilter
1.1
Erläutere, warum im Massenspektrometer ein Vakuum herrschen muss.
(2 BE)
1.2
Erläutere die Funktionsweise des Geschwindigkeitsfilters unter Beachtung der maßgeblichen Kräfte, welche auf die Ionen wirken.
Skizziere jeweils eine mögliche Flugbahn von Ionen mit Geschwindigkeiten und
und  in das Material 1.
in das Material 1.
Berechne die Geschwindigkeit für
für  und
und  .
.
 zur Kontrolle:
zur Kontrolle: 

Skizziere jeweils eine mögliche Flugbahn von Ionen mit Geschwindigkeiten
Berechne die Geschwindigkeit
(7 BE)
1.3
Erkläre den Verlauf der Flugbahnen der Ionen, die, wie in Material 1 abgebildet, in das Magnetfeld des Analysators eintreten.
Skizziere zwei mögliche Flugbahnen für Ionen mit gleicher Geschwindigkeit, aber unterschiedlicher Masse in das Material 1.
Skizziere zwei mögliche Flugbahnen für Ionen mit gleicher Geschwindigkeit, aber unterschiedlicher Masse in das Material 1.
(4 BE)
1.4
Zeige, dass für den Bahnradius der Ionen im Analysator die Formel  gilt.
gilt.
Begründe, dass durch die Verwendung des Geschwindigkeitsfilters die Proportionalität gilt.
gilt.
Begründe, dass durch die Verwendung des Geschwindigkeitsfilters die Proportionalität
(6 BE)
1.5
Berechne die Masse eines Ions, welches den Detektor auf einer Kreisbahn mit dem Radius  erreicht. Die Geschwindigkeit des Ions entspricht der Geschwindigkeit
erreicht. Die Geschwindigkeit des Ions entspricht der Geschwindigkeit  aus Aufgabe 1.2 und die magnetische Flussdichte beträgt weiterhin
aus Aufgabe 1.2 und die magnetische Flussdichte beträgt weiterhin  .
.
(3 BE)
1.6
Ein anderes Massenspektrometer besitzt keinen Geschwindigkeitsfilter. Die Ionen durchlaufen hierbei eine Beschleunigungsstrecke mit der Beschleunigungsspannung  (Material 2).
(Material 2).
Leite die Formel für die Geschwindigkeit der Ionen nach Durchlaufen der Beschleunigungsspannung her. Die Anfangsgeschwindigkeit der Ionen kann dabei vernachlässigt werden. Zeige unter Verwendung der Formel aus Aufgabe 1.4, dass für den Bahnradius der Ionen im Analysator nun die Proportionalität
für die Geschwindigkeit der Ionen nach Durchlaufen der Beschleunigungsspannung her. Die Anfangsgeschwindigkeit der Ionen kann dabei vernachlässigt werden. Zeige unter Verwendung der Formel aus Aufgabe 1.4, dass für den Bahnradius der Ionen im Analysator nun die Proportionalität  gilt.
gilt.
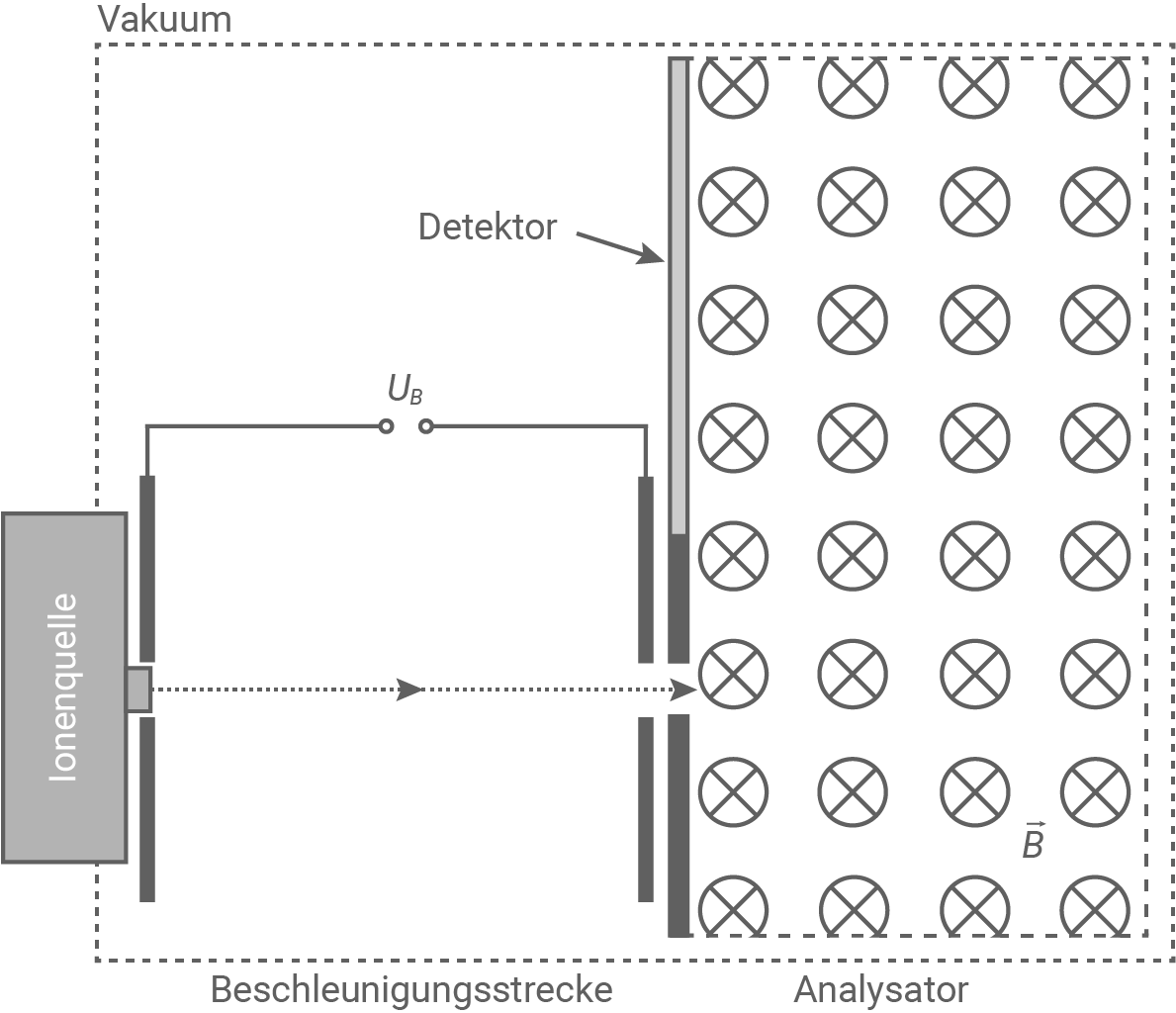
Leite die Formel
Material 2
Massenspektrometer mit Beschleunigungsstrecke
(6 BE)
1.7
Mit dem Massenspektrometer aus Aufgabe 1.6 wurde für verschiedene Ionen mit bekannter Masse  der Bahnradius
der Bahnradius  im Analysator gemessen (Material 3).
im Analysator gemessen (Material 3).
Bestätige die Proportionalität durch eine geeignete grafische Auswertung.
durch eine geeignete grafische Auswertung.
Bestätige die Proportionalität
Material 3
Bahnradien für Ionen unterschiedlicher Masse| Masse |
Bahnradius |
|---|---|
| 1,67 | 10,8 |
| 6,65 | 21,5 |
| 14,97 | 32,4 |
| 23,26 | 40,2 |
(5 BE)
1.8
Das Auflösungsvermögen  eines Massenspektrometers ist über die Formel
eines Massenspektrometers ist über die Formel  gegeben.
gegeben.
Beim Auflösungsvermögen kann die Masse
kann die Masse  gerade von der Masse
gerade von der Masse  getrennt werden. Für das Massenspektrometer mit Beschleunigungsstrecke beträgt das Auflösungsvermögen nur
getrennt werden. Für das Massenspektrometer mit Beschleunigungsstrecke beträgt das Auflösungsvermögen nur  . Wird stattdessen ein Geschwindigkeitsfilter verwendet, ist das Auflösungsvermögen deutlich höher. In Material 4 sind zwei Massenspektren dargestellt.
. Wird stattdessen ein Geschwindigkeitsfilter verwendet, ist das Auflösungsvermögen deutlich höher. In Material 4 sind zwei Massenspektren dargestellt.
Begründe, welches Massenspektrum mit dem Massenspektrometer mit Geschwindigkeitsfilter und welches mit dem Spektrometer mit der Beschleunigungsstrecke aufgenommen wurde. Ermittle das minimale Auflösungsvermögen, welches das Massenspektrometer mit dem Geschwindigkeitsfilter aufweisen muss.
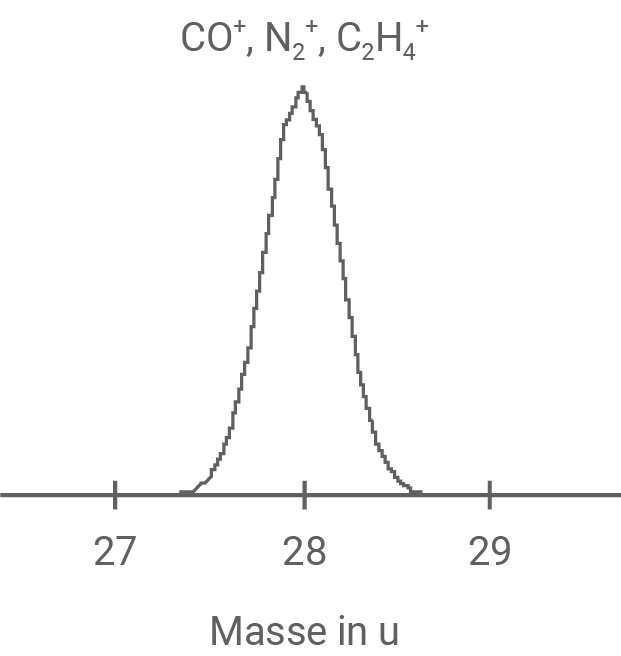
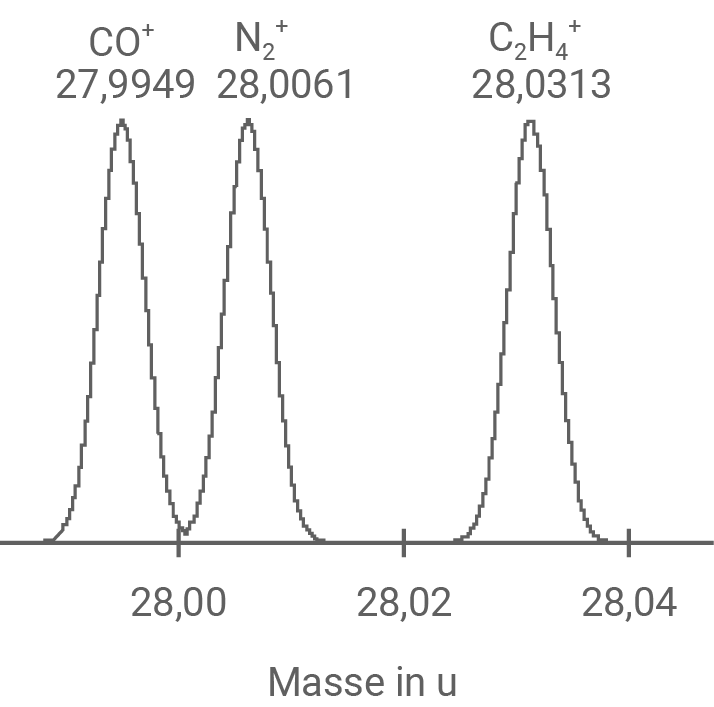 Die Massen sind als Vielfaches der atomaren Masseneinheit
Die Massen sind als Vielfaches der atomaren Masseneinheit  angegeben.
angegeben.
Beim Auflösungsvermögen
Begründe, welches Massenspektrum mit dem Massenspektrometer mit Geschwindigkeitsfilter und welches mit dem Spektrometer mit der Beschleunigungsstrecke aufgenommen wurde. Ermittle das minimale Auflösungsvermögen, welches das Massenspektrometer mit dem Geschwindigkeitsfilter aufweisen muss.
Material 4
Zwei Massenspektren von drei verschiedenen, jeweils einfach ionisierten Molekülen

(5 BE)
1.9
Die Massenbestimmung der Bestandteile einer Probe mit einem Massenspektrometer ist im Hinblick auf die Probe keine zerstörungsfreie Messmethode. Beurteile diese Aussage.
(2 BE)
2
Eine weitere Art eines Massenspektrometers ist das Flugzeitmassenspektrometer. Der grundlegende Aufbau ist in Material 5 dargestellt. Die Ionen mit Ladung  und Masse
und Masse  werden zuerst aus der Ruhe durch die konstante Spannung
werden zuerst aus der Ruhe durch die konstante Spannung  beschleunigt und durchlaufen anschließend mit konstanter Geschwindigkeit eine feldfreie Driftstrecke
beschleunigt und durchlaufen anschließend mit konstanter Geschwindigkeit eine feldfreie Driftstrecke  . Am Ende der Driftstrecke können die Ionen detektiert und durch eine Messelektronik die Flugzeit
. Am Ende der Driftstrecke können die Ionen detektiert und durch eine Messelektronik die Flugzeit  in der Driftstrecke bestimmt werden.
in der Driftstrecke bestimmt werden.
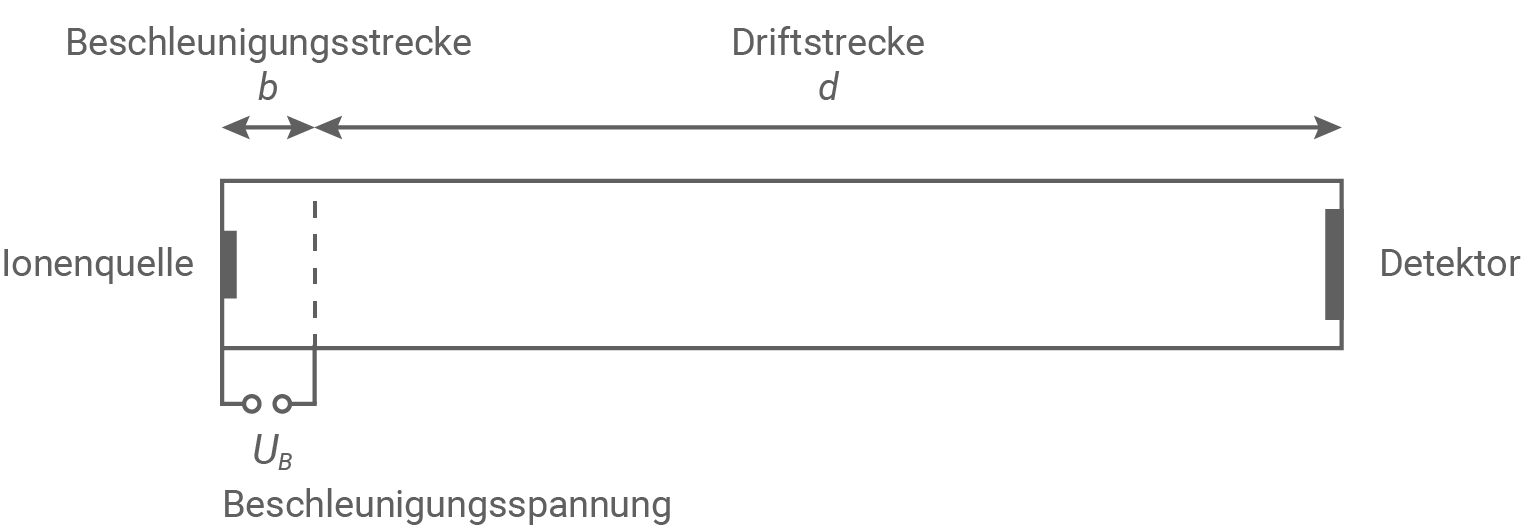
Material 5
Flugzeitmassenspektrometer
2.1
Zeige, dass für die Flugzeit  die Formel
die Formel  gilt.
gilt.
(5 BE)
2.2
Ionen einer Probe tragen jeweils die Ladung  und benötigen nach Durchlaufen der Beschleunigungsspannung
und benötigen nach Durchlaufen der Beschleunigungsspannung  für die Driftstrecke
für die Driftstrecke  eine gemessene Flugzeit von
eine gemessene Flugzeit von  . Berechne die Masse der einzelnen Ionen als Vielfaches der atomaren Masseneinheit
. Berechne die Masse der einzelnen Ionen als Vielfaches der atomaren Masseneinheit  und bestimme mithilfe des Periodensystems in Material 6, um welches stabile Element es sich handelt.
und bestimme mithilfe des Periodensystems in Material 6, um welches stabile Element es sich handelt.

Material 6
Periodensystem der Elemente
(5 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.1
Im Massenspektrometer muss ein Vakuum herrschen, damit die Ionen sich innerhalb des Massenspektrometers frei bewegen können und nicht mit anderen Molekülen zusammenprallen. Solche Stöße würden das Resultat verfälschen, da das Ion sein Ziel nicht erreichen kann.
Ein Vakuum ist auch wichtig, weil es verhindert, dass die Ionen mit anderen Teilchen reagieren oder freie Elektronen einfangen, während sie sich durch das Massenspektrometer bewegen.
1.2
Funktionsweise des Geschwindigkeitsfilters
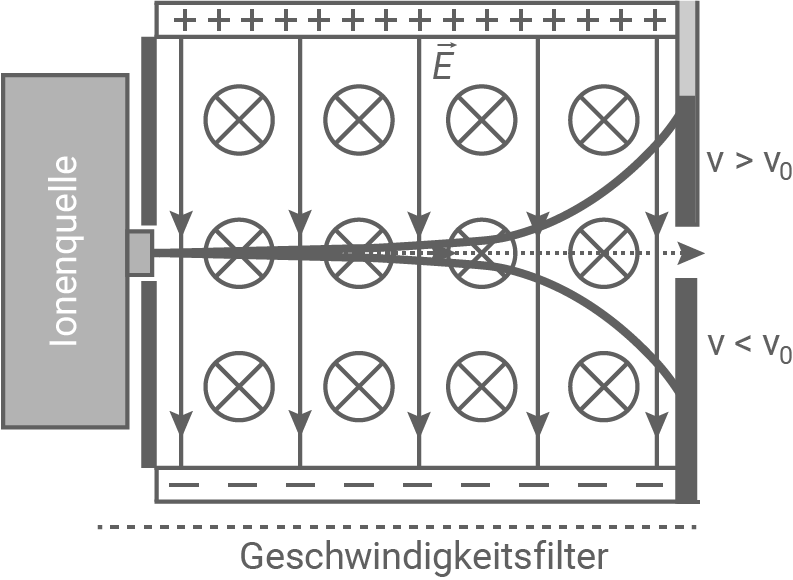
Der Geschwindigkeitsfilter besteht aus je einem elektrischen und einem magnetischen Feld, welche senkrecht aufeinander stehen. In Material 1 wird das elektrische Feld durch einen Plattenkondensator erzeugt und zeigt von der oberen zur unteren Platte. Das Magnetfeld zeigt in die Zeichenebene hinein. Im Raum dieser beiden Felder wirken auf geladene Teilchen zwei Kräfte:
 Berechnung der Durchlassgeschwindigkeit
Ionen, welche gradlinig durch den Geschwindigkeitsfilter hindurchfliegen, besitzen die Durchlassgeschwindigkeit
Berechnung der Durchlassgeschwindigkeit
Ionen, welche gradlinig durch den Geschwindigkeitsfilter hindurchfliegen, besitzen die Durchlassgeschwindigkeit  . In diesem Fall sind die beiden Kräfte auf die Ionen betragsmäßig gleich groß. Daher gilt:
. In diesem Fall sind die beiden Kräfte auf die Ionen betragsmäßig gleich groß. Daher gilt:
![\(\begin{array}[t]{rll}
F_{\text{el}}&=&F_{\text{L}} &\quad \scriptsize \\[5pt]
q\cdot E&=& q\cdot B\cdot v_{0} &\quad \scriptsize \mid\; \cdot \dfrac{1}{q\cdot B} \\[5pt]
\dfrac{E}{B}&=& v_{0} &\quad \scriptsize \\[5pt]
v_{0}&=&\dfrac{E}{B}
\end{array}\)](https://www.schullv.de/resources/formulas/1990c6b3a61aa2ae9aadb8cdbb12dd4a691be7e48ee42a0402a959fea4613905_light.svg) Einsetzen der Werte liefert:
Einsetzen der Werte liefert:
![\(\begin{array}[t]{rll}
v_{0}&=&\dfrac{E}{B} &\quad \scriptsize \\[5pt]
&=& \dfrac{18000 \; \frac{\text{V}}{\text{m}}}{0,06 \;\text{T}} &\quad \scriptsize \\[5pt]
&=& 3 \cdot 10^5 \; \dfrac{\text{m}}{\text{s}}&\quad \scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/304fff8570930ae628e5a9fa79593a2659822a5e3b03cd478a93000ded77bc41_light.svg)
- geschwindigkeitsunabhängige Coulombkraft wirkt durch das elektrische Feld nach unten
- geschwindigkeitsabhängige Lorentzkraft wirkt durch das magnetische Feld nach oben

1.3
Verlauf der Flugbahnen
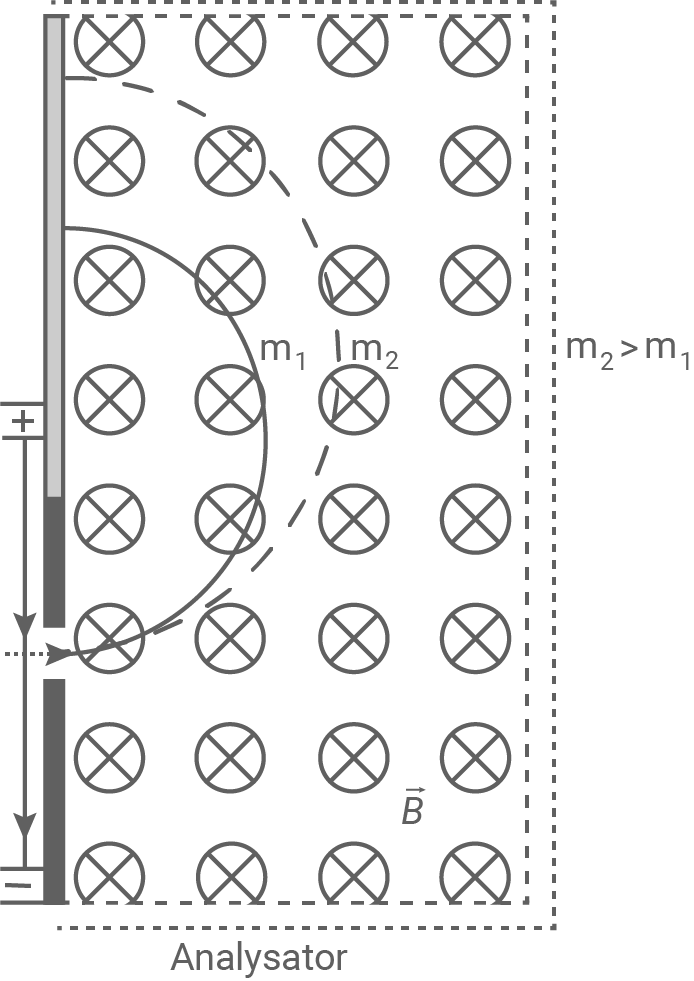
Das Magnetfeld des Analysators in Material 1 steht senkrecht zur Bewegungsrichtung der Ionen und zeigt in die Zeichenebene hinein. Die Ionen bewegen sich auf Kreisbahnen, nachdem diese durch den Spalt in den Analysator gelangt sind. Die Ursache dafür ist die Lorentzkraft, die auf bewegte Ladungsträger in magnetischen Feldern wirkt.
Mithilfe der Drei-Finger-Regel der rechten Hand kann die Richtung der Lorentzkraft bestimmt werden. Dabei wird der Daumen in die Bewegungsrichtung der positiven Ionen gehalten, der Zeigefinger in die Richtung des Magnetfeldes und der Mittelfinger zeigt dann in Richtung der Lorentzkraft. Da die Lorentzkraft immer senkrecht zur Bewegungsrichtung der Ionen steht und somit als Zentripetalkraft wirkt, ergibt sich für die Flugbahn ein nach oben verlaufender Kreisbogen.

1.4
Radiusformel
Die positiven Ionen erfahren im Magnetfeld eine Ablenkung, die sie auf eine kreisförmige Bahn ablenkt. Diese Ablenkung wird durch die Lorentzkraft verursacht, die als Zentripetalkraft wirkt:
![\(\begin{array}[t]{rll}
F_L&=& F_Z&\quad \scriptsize \\[5pt]
e\cdot v\cdot B&=& m\cdot \dfrac{v^2}{r} &\quad \scriptsize \mid\; \cdot r \\[5pt]
e\cdot v\cdot B \cdot r&=& m\cdot v^2 &\quad \scriptsize \mid\;\cdot \dfrac{1}{e\cdot v\cdot B} \\[5pt]
r&=&\dfrac{m\cdot v^2}{e\cdot v\cdot B} &\quad \scriptsize \\[5pt]
r&=&\dfrac{m\cdot v}{B\cdot e}
\end{array}\)](https://www.schullv.de/resources/formulas/8b25e1dbf8e9a09c0066a4f89ac232d193c05f0cddc31c9a54db8ebcc69a79f3_light.svg) Begründung der Proportionalität
Begründung der Proportionalität
![\(\begin{array}[t]{rll}
r&=&\dfrac{v}{B\cdot e} \cdot m &\quad \scriptsize \mid\;\dfrac{ v}{B\cdot e} = \text{konstant}=c\\[5pt]
r&=& c\cdot m &\quad \scriptsize \\[5pt]
r&\sim& m
\end{array}\)](https://www.schullv.de/resources/formulas/b719ddb607e49059a9d02acc617b2e1b8464259db446562825952973a3e83a48_light.svg) Die Größen im Nenner, magnetische Flussdichte und Elementarladung, sind konstant. Aufgrund des vorgeschalteten Geschwindigkeitsfilters bleibt auch die Ionen-Geschwindigkeit im Analysator konstant. Daher gilt
Die Größen im Nenner, magnetische Flussdichte und Elementarladung, sind konstant. Aufgrund des vorgeschalteten Geschwindigkeitsfilters bleibt auch die Ionen-Geschwindigkeit im Analysator konstant. Daher gilt 
1.5
1.6
Geschwindigkeitsformel
Die geladenen Ionen werden in einem Kondensator mit entsprechender Polung beschleunigt, wodurch die Beschleunigungsstrecke entsteht. Hierbei erfolgt die Umwandlung der elektrischen Energie des elektrischen Feldes in kinetische Energie der Ionen. Es gilt daher:
![\(\begin{array}[t]{rll}
E_{\text{el}}&=& E_{\text{kin}} &\quad \scriptsize \\[5pt]
e\cdot U_B &=& \dfrac{1}{2}\cdot m\cdot v^2&\quad \scriptsize \mid\; \cdot \dfrac{2}{m}\\[5pt]
\dfrac{2\cdot e\cdot U_B}{m}&=& v^2 &\quad \scriptsize \mid\; \sqrt{\;}\\[5pt]
\sqrt{\dfrac{2\cdot e\cdot U_B}{m}}&=& v &\quad \scriptsize \\[5pt]
v&=& \sqrt{\dfrac{2\cdot e\cdot U_B}{m}}
\end{array}\)](https://www.schullv.de/resources/formulas/2b1e8e28a3e73612f9e04a434f00bfe730f4544e2d62795268cf3562f2626561_light.svg) Proportionalität
Aufgrund der Konstanz der Beschleunigungsspannung
Proportionalität
Aufgrund der Konstanz der Beschleunigungsspannung  der magnetischen Flussdichte
der magnetischen Flussdichte  und der Elementarladung
und der Elementarladung  besteht eine Proportionalität zwischen dem Radius
besteht eine Proportionalität zwischen dem Radius  und der Quadratwurzel der Masse
und der Quadratwurzel der Masse  also
also 
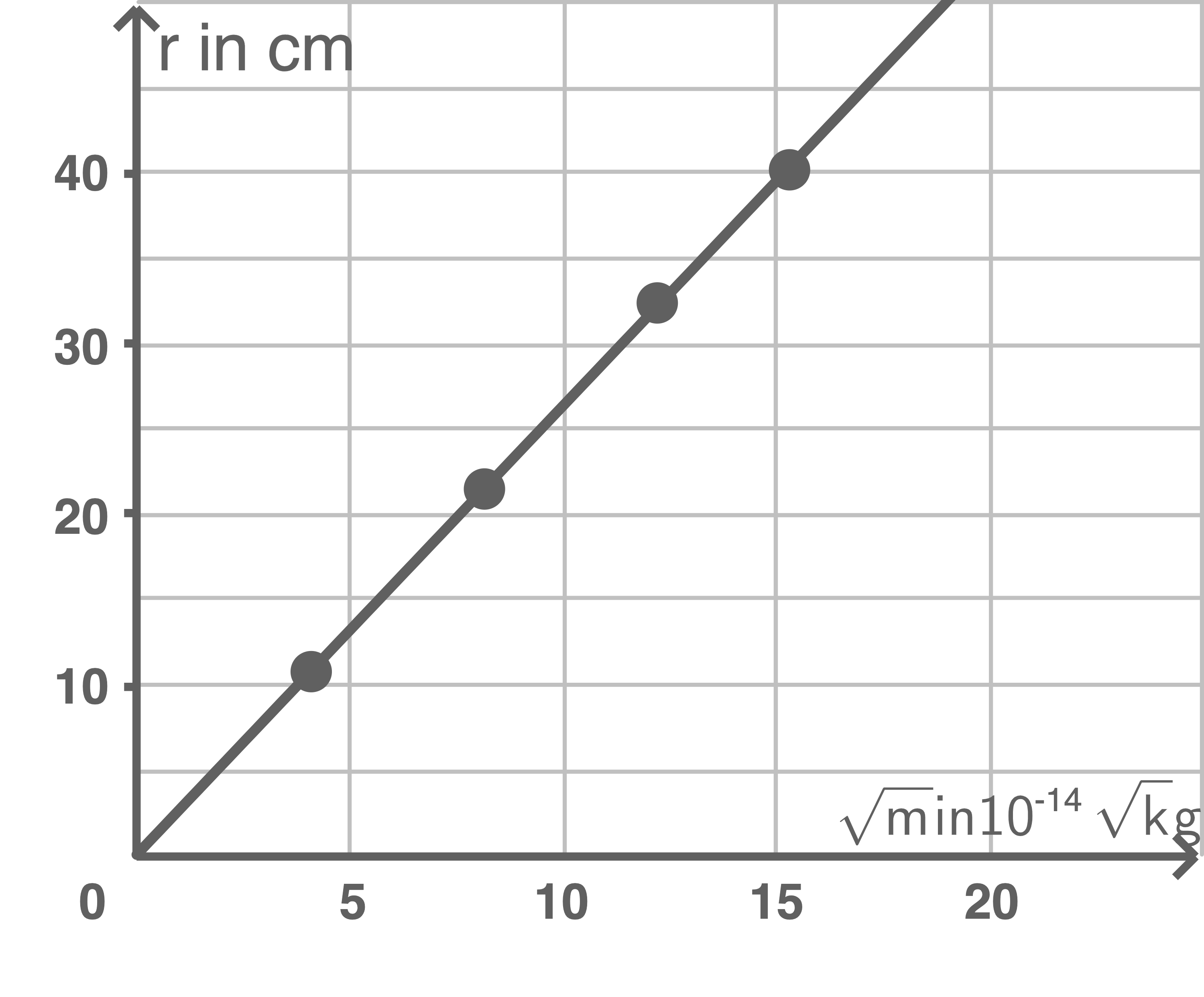
1.7
| Masse |
Masse |
Bahnradius |
|---|---|---|
| 1,67 | 4,09 | 10,8 |
| 6,65 | 8,15 | 21,5 |
| 14,97 | 12,2 | 32,4 |
| 23,26 | 15,3 | 40,2 |
1.8
Zuordnung der Spektren
Beide Massenspektren erfassen die Masse von drei einfach ionisierten Molekülen. Im linken Spektrum sind alle Moleküle bei  in einem Peak vereint, während sie im rechten Spektrum klar getrennt sind. Das deutet auf ein höheres Auflösungsvermögen im rechten Spektrum hin, was darauf schließen lässt, dass es von einem Massenspektrometer mit einem Geschwindigkeitsfilter stammt. Das linke Spektrum hingegen lässt auf ein Massenspektrometer mit einer Beschleunigungsstrecke schließen.
Ermittlung des minimalen Auflösungsvermögens
Im rechten Spektrum sind die Massen der Moleküle
in einem Peak vereint, während sie im rechten Spektrum klar getrennt sind. Das deutet auf ein höheres Auflösungsvermögen im rechten Spektrum hin, was darauf schließen lässt, dass es von einem Massenspektrometer mit einem Geschwindigkeitsfilter stammt. Das linke Spektrum hingegen lässt auf ein Massenspektrometer mit einer Beschleunigungsstrecke schließen.
Ermittlung des minimalen Auflösungsvermögens
Im rechten Spektrum sind die Massen der Moleküle  und
und  trotz ihres geringen Abstands immer noch gut voneinander getrennt. Das zeigt, dass das Auflösungsvermögen des Spektrometers mindestens in der Größenordnung dieses Abstands liegt. Für die Massendifferenz gilt:
trotz ihres geringen Abstands immer noch gut voneinander getrennt. Das zeigt, dass das Auflösungsvermögen des Spektrometers mindestens in der Größenordnung dieses Abstands liegt. Für die Massendifferenz gilt:
![\(\begin{array}[t]{rll}
\Delta m&=& {m}_{\text{N}_2^{+}}-{m}_{\text{CO}^{+}}&\quad \scriptsize \\[5pt]
&=& 28,0061 \,\text{u}-27,9949 \,\text{u}&\quad \scriptsize \\[5pt]
&=& 0,0112 \,\text{u}
\end{array}\)](https://www.schullv.de/resources/formulas/cc281dca7383337068cac133b283f2b71a70a4369d3f8c494b17ff18c276ca3d_light.svg) Das minimale Auflösungsvermögen ist dann gegeben durch:
Das minimale Auflösungsvermögen ist dann gegeben durch:
![\(\begin{array}[t]{rll}
R&=& \dfrac{{m}}{\Delta {m}}&\quad \scriptsize \\[5pt]
&=& \dfrac{27,9949 \,\text{u}}{0,0112 \,\text{u}}&\quad \scriptsize \\[5pt]
&\approx& 2500
\end{array}\)](https://www.schullv.de/resources/formulas/758a2e01cadcec092b7bd5be478a9e3d57870a3cf63cccc6da0f83d14da9529f_light.svg)
1.9
Die Aussage, dass die Massenbestimmung der Bestandteile einer Probe mittels Massenspektroskopie keine zerstörungsfreie Methode ist, trifft zu.
2.1
In diesem elektrischen Feld wird die elektrische Energie in Bewegungsenergie der Ionen umgewandelt. Mit dem Energieansatz gilt:
![\(\begin{array}[t]{rll}
E_{\text{el}}&=& E_{\text{kin}} &\quad \scriptsize \\[5pt]
q\cdot U_B&=& \dfrac{1}{2}\cdot m\cdot v^2 &\quad \scriptsize \mid\; \cdot \dfrac{2}{m} \\[5pt]
\dfrac{2\cdot U_B\cdot q}{m}&=& v^2 &\quad \scriptsize \mid\; \sqrt{\;} \\[5pt]
\sqrt{\dfrac{2\cdot U_B\cdot q}{m}}&=& v &\quad \scriptsize \\[5pt]
v &=& \sqrt{\dfrac{2\cdot U_B\cdot q}{m}}
\end{array}\)](https://www.schullv.de/resources/formulas/1c0fb0130b5c4444e521a30435da40843f221f83cb93daec7a10f451a99a86bb_light.svg) Entlang der Driftstrecke bewegen sich die Ionen gradlinig gleichförmig mit konstanter Geschwindigkeit
Entlang der Driftstrecke bewegen sich die Ionen gradlinig gleichförmig mit konstanter Geschwindigkeit 
![\(\begin{array}[t]{rll}
v&=&\dfrac{d}{t_d} &\quad \scriptsize \mid\;\dfrac{t_d}{v} \\[5pt]
t_d&=& \dfrac{d}{v} &\quad \scriptsize \mid\;v= \sqrt{\dfrac{2\cdot U_B\cdot q}{m}} \\[5pt]
t_d&=& \dfrac{d}{\sqrt{\dfrac{2\cdot U_B\cdot q}{m}}} &\quad \scriptsize \\[5pt]
t_d&=& \dfrac{d}{1}\cdot \sqrt{\dfrac{m}{2\cdot U_B\cdot q}} &\quad \scriptsize \\[5pt]
t_d&=& \sqrt{\dfrac{d^2\cdot m}{2\cdot U_B\cdot q}}
\end{array}\)](https://www.schullv.de/resources/formulas/022c248a7283abbd96c75d472733cbbeb940fcc2e945c01572b377c93247a96d_light.svg)
2.2
Masse der Ionen
Einsetzen der Werte liefert:
Bestimmung des Elements
Die berechnete Masse eines einzelnen Ions beträgt etwa  was dem Element Lithium mit der Massenzahl
was dem Element Lithium mit der Massenzahl  entspricht.
entspricht.