Analysis 2.1 – Regenwasser

Gegeben ist die Schar der in $\mathbb{R}$ definierten Funktionen $f_k$ mit $f_k(x)=\frac{1}{2 k} \cdot x^2 \cdot(x-2 k)^2$ $=\frac{1}{2 k} x^4-2 x^3+2 k x^2$ und $k \in \mathbb{R}^{+}.$
Der Graph von $f_k$ wird mit $G_k$ bezeichnet.

Begründe, dass $f_k$ für jeden Wert von $k$ genau zwei Nullstellen hat, und gib diese an.

(3 BE)

Zeige, dass die Funktionsgleichung der ersten Ableitungsfunktion von $f_k$ durch $\(f_k$ beschrieben werden kann.

(3 BE)

Der Hochpunkt von $G_k$ hat zu den beiden Tiefpunkten von $G_k$ denselben Abstand. Berechne diesen Abstand in Abhängigkeit von $k.$

Hinweis: Verwende die Funktionsgleichung von $\(f_k$ aus Teilaufgabe $b.$

(5 BE)

Betrachtet wird die Fläche, die $G_k,$ die $x$ -Achse und die beiden Geraden mit den Gleichungen $x=-1$ und $x=1$ einschließen. Sie setzt sich aus mehreren Flächenstücken zusammen. Beurteile die folgende Aussage, ohne den Wert eines Integrals zu berechnen:

Für jeden Wert von $k$ gibt der Term $\displaystyle\int_{-1}^{1}f_k(x)\;\mathrm dx$ den Inhalt der betrachteten Fläche an.

(4 BE)

Gegeben ist die Schar der in $\mathbb{R}$ definierten Funktionen $h_k$ mit $h_k(x)=\frac{k}{2} \cdot(x-2 k)^2.$

Die folgenden Schritte stellen die Lösung einer Aufgabe dar.
Interpretiere jeden der beiden Schritte geometrisch in Bezug auf die Graphen von $f_k$ und $h_k.$

$\text{I}$

$\begin{array}[t]{rlll} f_k(x) &=& h_k(x) \\[5pt] x &=& -k \\[5pt] x &=& k \\[5pt] x &=& 2k \end{array}$

$\text{II}$

$\begin{array}[t]{rlll} &\displaystyle\int_{-k}^k\left(h_k(x)-f_k(x)\right) \;\text{d} x+\displaystyle\int_k^{2 k}\left(f_k(x)-h_k(x)\right) \;\text{d} x \\[5pt] &=\dfrac{29}{10} k^4 \end{array}$

Untersuche, ob die folgende Aussage richtig ist:

Für $k\gt3$ gilt $\displaystyle\int_{-k}^k\left(h_k(x)-f_k(x)\right) \;\text{d} x+\displaystyle\int_k^{2 k}\left(f_k(x)-h_k(x)\right) \;\text{d} x\lt k^5.$

(5 BE)

Um Regenwasser zu speichern, wird es kontrolliert in ein unterirdisches Auffangbecken geleitet. Für ein bestimmtes Regenereignis wird die momentane Zuflussrate des Regenwassers in das Auffangbecken durch die in $\mathbb{R}$ definierte Funktion $r$ mit $r(x)=\text{e}^x \cdot f_{2,5}(x)=\frac{1}{5} x^2 \cdot(x-5)^2 \cdot \text{e}^x$ für $0 \leq x \leq 5$ modellhaft beschrieben. Dabei ist $x$ die Zeit in Stunden, die seit Beginn des Zuflusses in das Auffangbecken vergangen ist, und $r(x)$ die momentane Zuflussrate in $\frac{\text{m}^3}{\text{h}}$ (Kubikmeter pro Stunde). Die Funktion $f_{2,5}$ ist die Funktion der Schar aus Aufgabe 1 mit $k=2,5.$
Für die erste Ableitungsfunktion von $r$ gilt $\(r$

Zu genau einem Zeitpunkt zwischen zwei und vier Stunden nach Beginn des Zuflusses in das Auffangbecken ist die momentane Zuflussrate am größten.
Berechne diesen Zeitpunkt.

(3 BE)

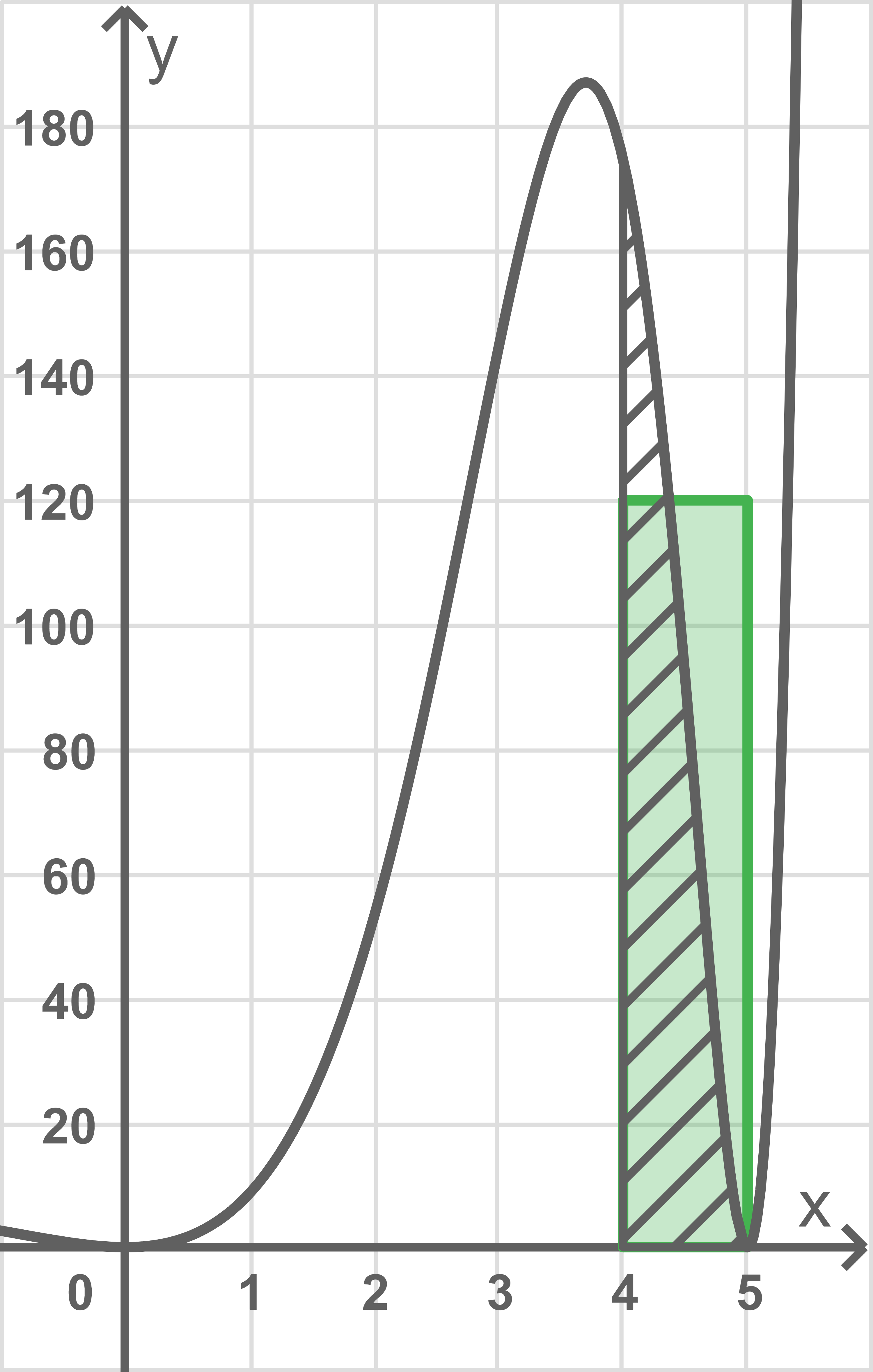
Die Abbildung zeigt den Graphen von $r$ mit einigen Eintragungen.
Erläutere, dass mit diesen Eintragungen die folgende Aussage begründet werden kann:

$\displaystyle\int_4^5 r(x) \;\text{d} x\lt120$

Interpretiere diese Aussage im Sachzusammenhang.

(4 BE)

Zu Beginn des Zuflusses ist das Auffangbecken bereits mit $186 \;\mathrm{m}^3$ Regenwasser gefüllt. Nach dreieinhalb Stunden wird eine Pumpe eingeschaltet. Diese pumpt bis zum Ende des betrachteten Zeitraums Wasser aus dem Auffangbecken mit einer konstanten Rate ab. Die momentane Zuflussrate des Regenwassers in das Auffangbecken wird dabei weiterhin durch $r$ beschrieben.
Gib einen Term an, der das Wasservolumen im Auffangbecken zu einem beliebigen Zeitpunkt nach dem Einschalten der Pumpe in Kubikmetern beschreibt

(3 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Nach dem Satz des Nullprodukts ergeben sich die Nullstellen von $f_k$ durch die Nullstellen der einzelnen Faktoren der Funktionsgleichung.
Der Faktor $\frac{1}{2k}$ wird für keinen Wert von $k$ Null, der Faktor $x^2$ besitzt die Nullstelle $x=0,$ und der letzte Faktor $(x-2k)^2$ wird genau dann Null, wenn die Klammer null ergibt, also für $x=2k.$
Da $k$ nur positive Werte annimmt, besitzt $f_k$ für jeden Wert von $k$ somit genau $2$ Nullstellen.

$\(\begin{array}[t]{rlll} f_k$

Anwenden der notwendigen Bedingung von Extremstellen $\(f_k$ liefert:

$\(\begin{array}[t]{rlll} f_k$

Mit dem Satz des Nullprodukts folgt somit direkt $x_1=0, x_2=k$ und $x_3=2k.$
Da zwischen zwei Tiefpunkten immer ein Hochpunkt liegen muss und insgesamt drei Extrempunkte vorliegen, folgt, dass $x_2=k$ zum Hochpunkt von $G_k$ gehört. Für den gesuchten Abstand $d$ folgt somit:

$\begin{array}[t]{rlll} d&=&\sqrt{(k-0)^2+(f_k(k)-f_k(0))^2} \\[5pt] &=&\sqrt{k^2+\left(\dfrac{1}{2k}\cdot k^2\cdot(k-2k)^2-0\right)^2} \\[5pt] &=&\sqrt{k^2\cdot\left(1+\dfrac{1}{4}k^4\right)} \\[5pt] &=&k\cdot\sqrt{1+\dfrac{1}{4}k^4} \end{array}$

Der nicht ausmultiplizierte Funktionsterm von $f_k$ besteht aus drei Faktoren, wobei $\frac{1}{2k}$ für alle $k$ positiv ist da $k$ stets positiv ist, und die anderen beiden nicht negativ sind, da sie geradzahlige Exponenten besitzen. Somit verläuft $G_k$ nie unterhalb der $x$ -Achse, d.h. die Aussage aus der Aufgabenstellung stimmt.

Gleichung $\text{I}$ sagt aus, dass sich die Graphen von $f_k$ und $h_k$ an den Stellen $x=-k, x=k$ und $x=2k$ schneiden.
Gleichung $\text{II}$ liefert, dass die Graphen von $f_k$ und $h_k$ eine Fläche miteinander einschließen, die aus zwei Flächenstücken besteht. Die Summe der beiden Flächeninhalte beträgt dabei $\frac{29}{10}k^4.$

Da $\frac{29}{10}\lt3$ ist, gilt für $k\gt3,$ dass $\frac{29}{10}k^4\lt k^5.$ Damit ist die Aussage aus der Aufgabenstellung richtig.

Die Funktion $r(x)$ ergibt sich als:

$r(x)=\mathrm e^x\cdot\left(\dfrac{1}{5}x^4-2x^3+5x^2\right)$

Für die Ableitung von $r$ folgt mit der Produktregel:

Rechenweg anzeigen

$\( r$

Anwenden der notwendigen Bedingung für Extremstellen $\(r$ liefert:

$\(\begin{array}[t]{rlll} r$

Mit dem Satz des Nullprodukts folgt direkt $x=0$ und $x=5$ und weiter mit der $pq$ -Formel mit Hilfe des vierten Faktors:

$\begin{array}[t]{rlll} x_{1;2}&=&\dfrac{1}{2}\pm\sqrt{\left(-\dfrac{1}{2}\right)^2+10}\\[5pt] &=&\dfrac{1}{2}\pm\sqrt{\dfrac{41}{4}}\\[5pt] x_1&=&\dfrac{1-\sqrt{41}}{2} \\[5pt] x_2&=&\dfrac{1+\sqrt{41}}{2} \end{array}$

Von diesen vier Nullstellen liegt nur $x_2$ zwischen $2$ und $4,$ sodass der Zeitpunkt der größten Zuflussrate nach $\frac{1+\sqrt{41}}{2}\approx3,7$ Stunden erreicht wird.

Begründung der Aussage erläutern

Die in der Abbildung grün markierte Fläche ist ein Rechteck mit den Seitenlängen $1$ und $120$ und besitzt somit den Flächeninhalt $120.$ Zudem wird aus der Abbildung deutlich, dass die schraffierte Fläche, deren Inhalt dem Wert des in der Aufgabenstellung gegebenen Integrals entspricht, kleiner ist, als die grün markierte Fläche. Damit kann die Aussage aus der Aufgabenstellung begründet werden.

Aussage im Sachzusammenhang interpretieren

Innerhalb der letzten Stunde des betrachteten Zeitraums sind insgesamt weniger als $120\;\text{m}^3$ Regenwasser in das Auffangbecken geflossen.

Die Pumpe pumpt Wasser mit einer konstanten Rate ab. Wenn diese Rate mit $a$ bezeichnet wird, folgt für den gesuchten Term:

$186+\displaystyle\int_{0}^{x}r(t)\;\mathrm dt-a\cdot(x-3,5)$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?