Enthalpie

Der Begriff der Enthalpie wird dir in der Anwendung häufig dann begegnen, wenn du Reaktionen energetisch charakterisieren sollst oder wenn du mit der Freien Enthalpie konfrontiert wirst. Auf beide Aspekte gehen wir später noch genauer ein.
Hier wollen wir uns anschauen, was hinter dem Begriff der Enthalpie steckt: Was bedeutet Enthalpie? Wie können wir sie verstehen und welche Randbedingungen sind wichtig? An dieser Stelle werden wir sowohl auf den Systembegriff als auch auf den 1. Hauptsatz der Thermodynamik zurückgreifen.
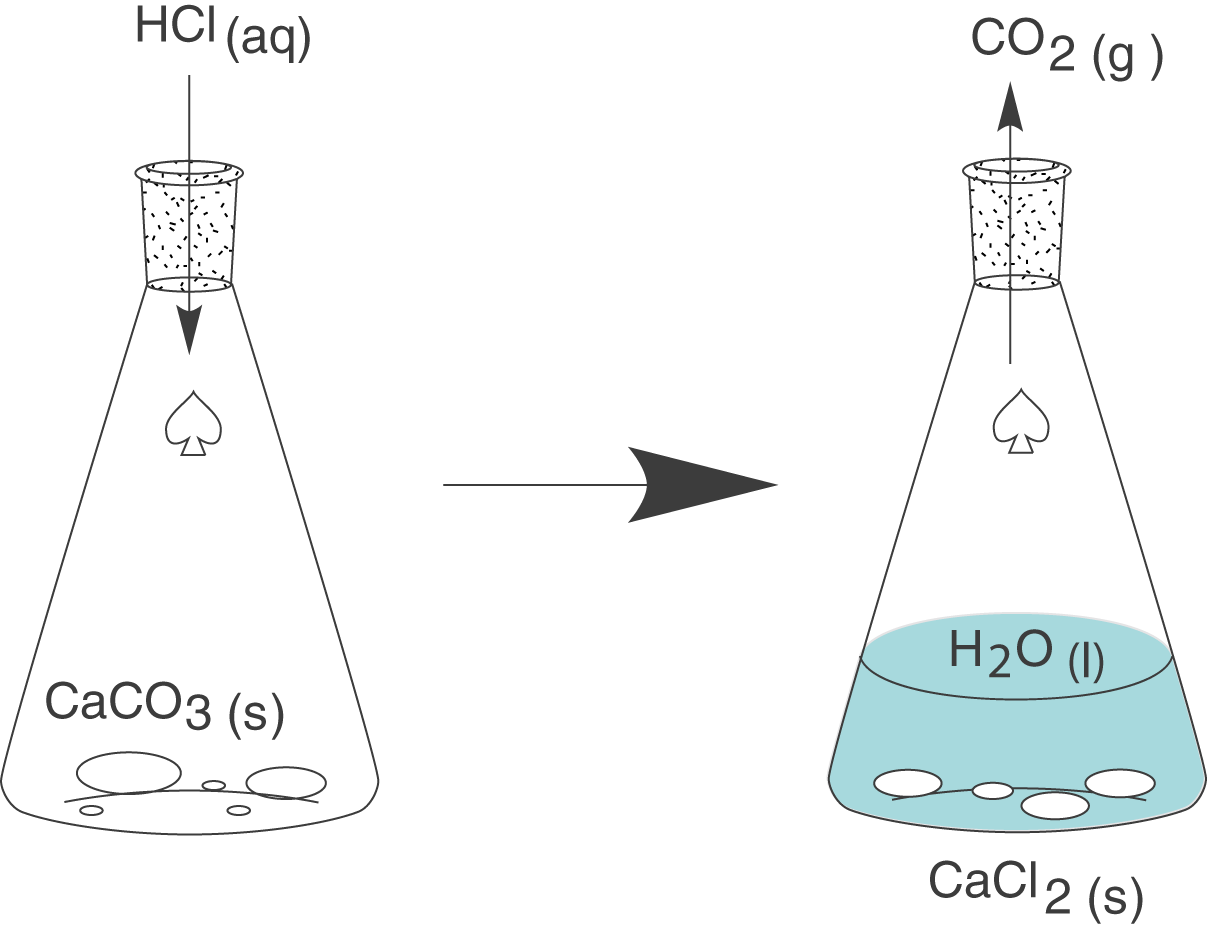
Die ganze Erklärung starten wir mit einem Experiment. Wir nehmen einen Erlenmeyerkolben, welcher gewöhnlichen Kalk ( $\text{CaCO}_{3\,(\text{s})}$ ) enthält und geben eine wässrige Salzsäurelösung ( $\text{HCl}_{(\text{aq})}$ ) dazu. Formal läuft dabei folgende Reaktion ab:

$\text{CaCO}_{3\,(\text{s})}+\text{HCl}_{(\text{aq})}$ $\longrightarrow$ $\text{CO}_{2\,(\text{g})}+\text{H}_{2}\text{O}_{(\ell)}+\text{CaCl}_{2\,(\text{s})}$

Wir erhalten neben festem Calciumchlorid und flüssigem Wasser auch gasförmiges Kohlenstoffdioxid.

Diagramm zur chemischen Reaktion von HCl mit Calciumcarbonat, CO2-Entwicklung und Wasser.

Abb. 1: Reaktion von Salzsäure mit Kalk

Was uns an dieser Reaktion ganz besonders interessiert ist das System, in welchem diese stattfindet. Da der Erlenmeyerkolben eine Öffnung aufweist und nicht isoliert ist, sprechen wir hier von einem offenen System. Weiterhin spielt insbesondere das entweichende Kohlenstoffdioxid eine weitere zentrale Rolle. Was passiert, wenn dieses entsteht, können wir uns am besten in einem weiteren Experiment verdeutlichen.
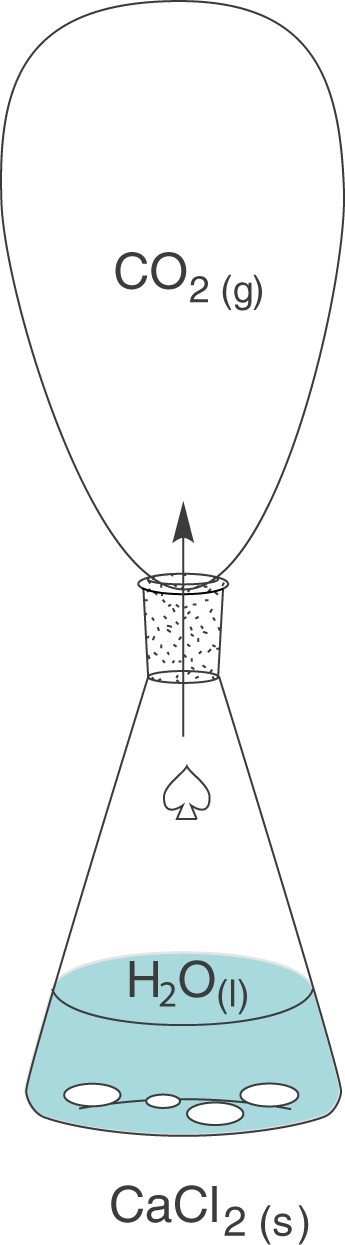
Die einzige Änderung, die wir vornehmen, bezieht sich auf einen Luftballon, den wir an der Öffnung des Erlenmeyerkolbens befestigen. Da sich der Luftballon dehnen kann, haben wir das System Erlenmeyerkolben vorerst effektiv nicht verändert: der Energieaustausch kann immer noch stattfinden, da auch weiterhin keine Isolation vorhanden ist und das Kohlenstoffdioxidgas kann auch weiterhin entweichen. Letzteres entschwindet nun aber nicht mehr in die Umwelt, sondern in den Ballon und darin liegt der Sinn dieses Experiments.
Mit Hilfe des Ballons können wir die Volumenänderung $\Delta V$ sichtbar machen, die mit der $\text{CO}_{2\,(\text{g})}$ -Produktion einhergeht. Der Ballon wird aufgeblasen werden.
Dieses Experiment verdeutlicht den Zustand, unter dem ein Versuch gewöhnlicherweise stattfindet: Das Volumen, das zur Verfügung steht, ist nicht konstant. Dahingegen arbeiten wir jedoch meistens unter Atmosphärendruck, was bedeutet, dass der Druck konstant ( $const.$ ) ist. Für unseren Versuch gilt also:

$V\neq const.$
$p=const.$

Diagramm eines chemischen Prozesses mit CO₂, H₂O und festem Stoff.

Abb. 2: Versuchsaufbau zum Auffang von Kohlenstoffdioxid

Nun gehen wir dazu über, diese Reaktion unter energetischen Gesichtspunkten zu betrachten. Dazu verwenden wir den ersten Hauptsatz der Thermodynamik

$\Delta U=\Delta Q+\Delta W$

Hier interessiert uns insbesondere der Term $+\Delta W$ , also die verrichtete Arbeit. Wenn der Ballon im Experiment aufgeblasen wird, dann wird an ihm Volumenarbeit verrichtet. Das bedeutet, dass ein gewisser Energieaufwand damit verbunden ist, den Ballon aufzublasen. Die Änderung der Inneren Energie besteht also nicht nur aus der ausgetauschten Wärmemenge, sondern setzt sich auch noch aus der Volumenarbeit zusammen, die verrichtet wird, wenn der Druck konstant bleibt.
Für den Term der Volumenarbeit können wir auch folgenden Ausdruck schreiben: $\Delta W=-p\cdot\Delta V$ .
Da dem System dieser Energiebetrag quasi verloren geht, bekommt der verwendete Ausdruck ein negatives Vorzeichen. Wir setzen dies nun in die obere Gleichung ein und ersetzen $\Delta Q$ durch $\Delta Q_{\text{p}}$ . Damit wissen wir, dass der Druck $p$ konstant gehalten wird.

$\Delta U=\Delta Q+\Delta W$ = $\Delta Q_{\text{p}}-p\cdot\Delta V$

Wir formen nun nach $\Delta Q_{\text{p}}$ um und nennen diese Größe dann die Enthalpie $\Delta H$ :

$\Delta Q_{\text{p}}$ = $\Delta U+p\cdot\Delta V$ mit $\Delta Q_{\text{p}}$ = $\Delta H$

Für die Definition der Enthalpie gilt:

$H=U+p\cdot V$

Wichtig ist, dass es sich bei der Inneren Energie $U$ , dem Druck $p$ und dem Volumen $V$ um Zustandsgrößen handelt. Damit ist auch die Enthalpie $H$ wieder eine Zustandsgröße.
Bevor wir dazu übergehen verschiedene Formen der Enthalpie zu besprechen, betrachten wir noch einen wichtigen Zusammenhang, der sich ergibt, wenn wir eine Enthalpieänderung $\Delta H$ vorliegen haben. Dazu greifen wir auf die oben eingeführte Gleichung zurück, die die Wärmemenge $\Delta Q_{\text{p}}$ bei konstantem Druck definiert.

$\Delta Q_{\text{p}}$ = $\Delta U+p\cdot \Delta V$

Wir werden die Terme nun mit Hilfe der Definition der Enthalpie $H$ aufschlüsseln und neu ordnen:

$\begin{array}{rcl} \Delta Q_{\text{p}}&=& \Delta H \end{array}$

Vollständige Lösung anzeigen

Wir erhalten:

$\Delta Q_{\text{p}}=\Delta H$

Bei konstantem Druck entspricht die zugeführte Wärmemenge der Enthalpieänderung des Systems. Das bedeutet beispielsweise, dass wenn du Wasser in einem Wasserkocher erhitzt und dabei 50 kJ an elektrischer Energie aufgewendet werden, dann erhöht sich die Enthalpie des Wassers ebenfalls um 50 kJ: $\Delta H_{\text{Wasser}}=+50\,\text{kJ}$ .

Standard-enthalpieänderungen, $\Delta H^{0}$

In der Chemie beschäftigen wir uns oft mit Änderungen der Enthalpie bei Standardbedingungen. Diese Enthalpieänderungen kennzeichnen wir als $\Delta H^{0}$ . Im Skript Anwendungen werden wir das Verfahren der Kalorimetrie kennen lernen, mit dem wir Standard-enthalpieänderung messen können.

Endotherme und exotherme Reaktionen

Während einer chemischen Reaktion sind prinzipiell zwei Situationen möglich, die von Interesse sind:

$\Delta H^{0}\lt 0$
$\Delta H^{0}\gt 0$

Definitionsgemäß bezeichnen wir eine negative Standardenthalpieänderung, also die Abnahme der Enthalpie des Systems, als exotherm. Eine positive Standard-enthalpieänderung, also die Zunahme der Enthalpie eines Systems, als endotherm.
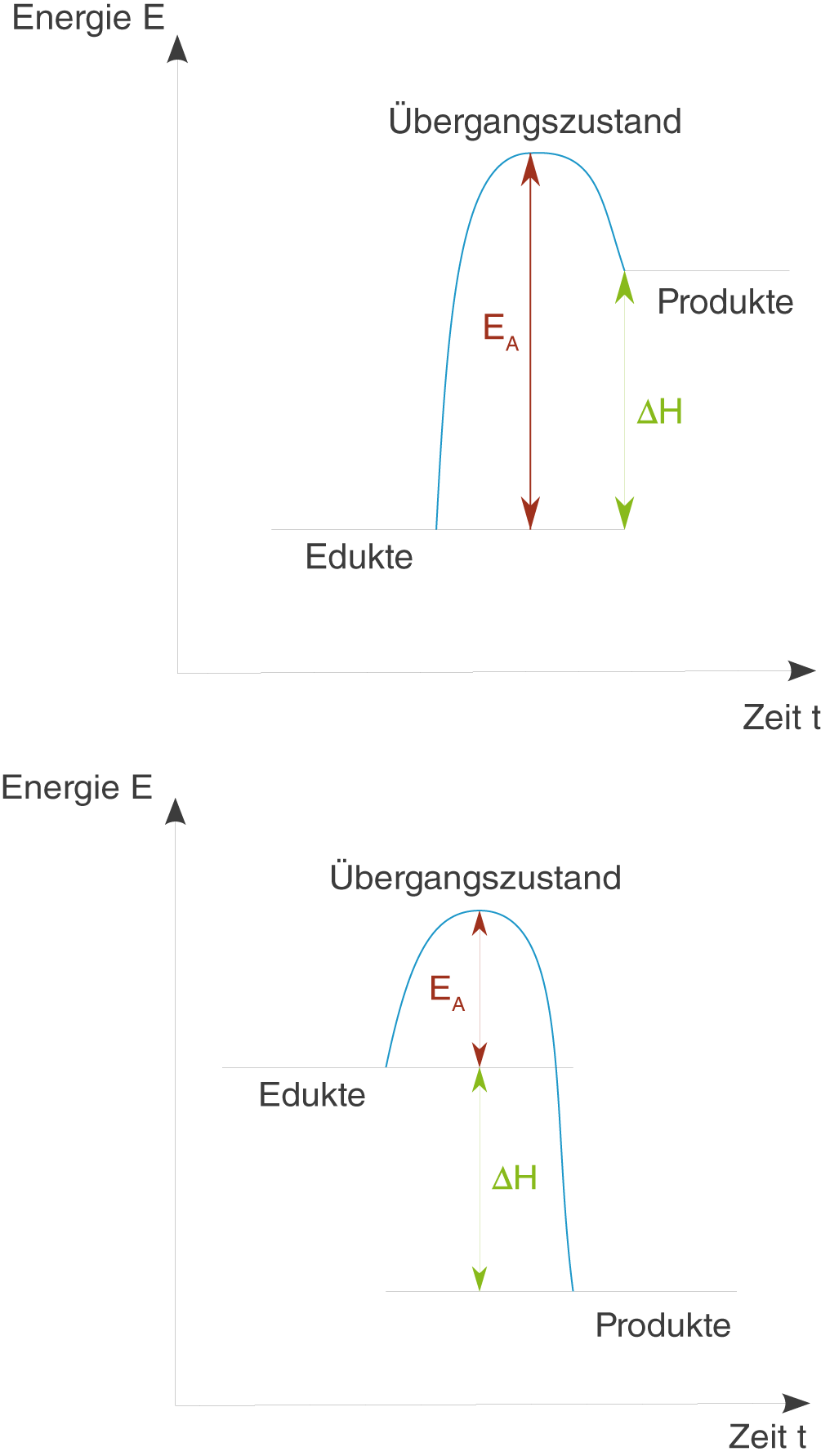
Graphisch kannst du dir das ganze folgendermaßen vorstellen:

Diagramm zur Darstellung von Energieänderungen während chemischer Reaktionen mit Übergangszuständen und Edukten.

Abb. 3: Energetischer Unterschied zwischen exothermer und endothermer Reaktion

Links siehst du das Energie-Zeit-Diagramm für eine endotherme Reaktion. Die Produkte sind hier energiereicher als die Edukte. Der Übergangszustand, quasi ein sehr energiereiches „Zwischenprodukt“ der Reaktion, wird durch die Aktivierungsenergie $E_{\text{A}}$ erreicht. Die Reaktionsenthalpie entspricht letztendlich einem Anteil dieser Aktivierungsenergie.
Rechts siehst du das Energie-Zeit-Diagramm für eine exotherme Reaktion. Die Produkte sind energieärmer als die Edukte. Dennoch ist eine Aktivierungsenergie von Nöten, um den Übergangszustand zu erreichen.
Beispiel: Oxidation (Veratmung) von Zucker
Die Oxidation (Veratmung) eines Zuckers verläuft exotherm:

$\text{C}_{6}\text{H}_{12}\text{O}_{6}+6\;\text{O}_{2}$ $\longrightarrow$ $6\;\text{CO}_{2}+6\;\text{H}_{2}\text{O}$ mit $\Delta H^{0}\lt 0$

Damit können wir hier das Beispiel aus der Einleitung aufgreifen: Du nimmst Energy-Drinks zu dir, weil Zucker eine energiereiche Verbindung ist. Bei dessen Spaltung wird diese Energie frei und kann anderweitig von deinem Körper genutzt werden.

Der Satz von Hess

Die Berechnung von molaren Standardreaktionsenthalpie

Wir wollen uns hier damit beschäftigen, wie wir beispielsweise eine solche Enthalpieänderung, wie die in dem Beispiel oben, berechnen können. Dazu führen wir zwei neue Enthalpieänderungen ein:

die molare Standardbildungsenthalpie, $\Delta_{\text{f}}H_{m}^{0}$
die molare Reaktionsenthalpie, $\Delta_{\text{R}}H_{m}^{0}$

Die Enthalpieänderungen beziehen wir auf die Stoffmenge $n$ , aus diesem Grund taucht auch die Bezeichnung $m$ im Index auf. Damit haben diese Größen die Einheit $\frac{\text{kJ}}{\text{mol}}$ , also Energie pro Stoffmenge.

$\Delta_{\text{f}}H_{m}^{0}$ = $\dfrac{\Delta_{\text{f}}H^{0}}{n}$

$\Delta_{\text{R}}H_{m}^{0}=\dfrac{\Delta_{\text{R}}H^{0}}{n}$

Bei der molaren Standardbildungsenthalpie handelt es sich demnach um den Energiebetrag, der pro Mol einer Verbindung aufgewendet werden muss, um diese aus den Elementen herzustellen. Elemente haben definitionsgemäß eine molare Standardbildungsenthalpie von null.
Die molare Reaktionsenthalpie wird dahingegen in einer Reaktion von mehreren Reaktanden umgesetzt. Diese können wir aus den molaren Standardbildungsenthalpien der Reaktanden berechnen.

$\Delta_{\text{R}}H_{m}^{0}$ = $\displaystyle\sum a\cdot \Delta_{\text{f}}H_{m}^{0}(\text{Produkte})$ - $\displaystyle\sum a\cdot\Delta_{\text{f}}H_{m}^{0}(\text{Edukte})$

Beispiel: Berechnung der Reaktionsenthalpie bei der Oxidation von Glucose
Wir berechnen nun die Energie, die in Form der molaren Reaktionsenthalpie frei wird, wenn ein Mol Glucose mit Sauerstoff umgesetzt wird. Dabei werden wir auch die oben eingeführte Formel verstehen lernen.
Zu Beginn nehmen wir noch einmal die Reaktionsgleichung her:

$\text{C}_{6}\text{H}_{12}\text{O}_{6}+6\;\text{O}_{2}$ $\longrightarrow$ $6\;\text{CO}_{2}+6\;\text{H}_{2}\text{O}$

Die molaren Standardbildungsenthalpien entnimmst du einem Tabellenwerk. Wenn wir diese Werte einsetzen ergibt sich folgende Rechnung:

$\begin{array}{rcl} \Delta_{\text{R}}H_{m}^{0} &=& -2537\,\dfrac{\text{kJ}}{\text{mol}} \end{array}$

Vollständige Lösung anzeigen

Zunächst sehen wir, dass eine exotherme Reaktion vorliegt, was wir ja schon angenommen hatten. Folgende Aspekte sind bei der Berechnung wichtig: Der Faktor $a$ stellt die stöchiometrischen Koeffizienten der einzelnen Reaktanden dar. Das bedeutet, dass du die Werte der Standardbildungsenthalpien aller Verbindungen mit ihren jeweiligen stöchiometrischen Koeffizienten multiplizieren musst, die in der Reaktionsgleichung auftreten.
Weiterhin kannst du erkennen, dass die Standardbildungsenthalpien des Sauerstoffs in dieser Rechnung den Wert null hat. Dies hängt damit zusammen, dass es sich um ein Element handelt.
Abschließend solltest du darauf achten, dass du keine Vorzeichenfehler machst. Viele der molaren Standardbildungsenthalpien sind negativ, demnach können sich die Vorzeichen ändern, wenn du Klammern auflöst.

Der Satz von Hess

Der Satz von Hess beruht darauf, dass es sich bei der Enthalpie um eine Zustandsgröße handelt. Der Weg, auf dem diese erreicht wird, beeinflusst den Endzustand nicht. Diese Tatsache ist extrem hilfreich, denn sie ermöglicht uns die Berechnung von experimentell schwer zugänglichen Reaktionsenthalpien.

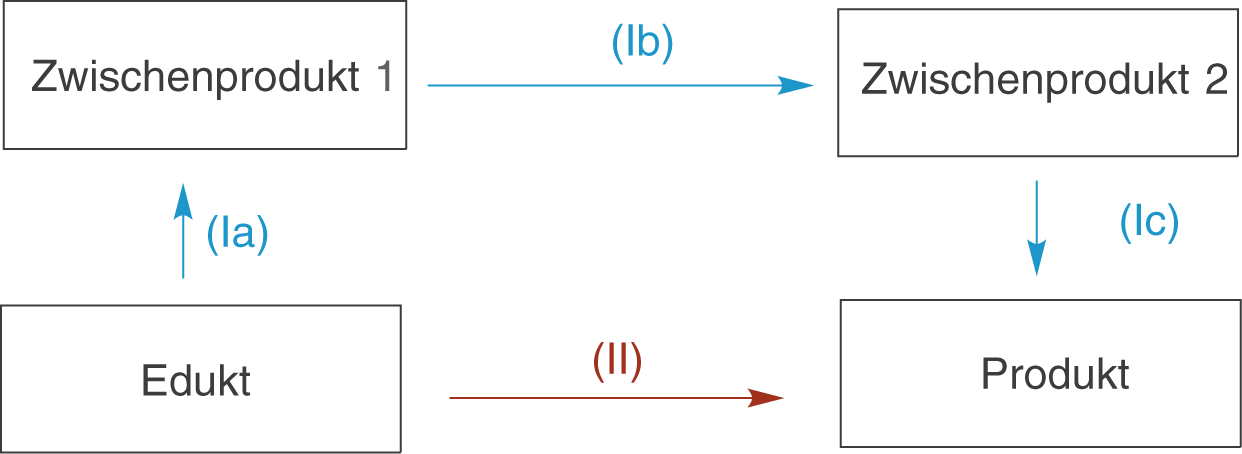
Diagramm mit Zwischenprodukten und Reaktionsschritten in chemischen Prozessen.

Abb. 4: Wegunabhängigkeit bei einem Prozess

In dieser Graphik siehst du ein Schema, welches unterschiedliche Reaktionspfade eines Eduktes in ein bestimmtes Produkt darstellt. Im einen Falle liegt eine direkte Reaktion vor (Pfad (II)), welche keine Zwischenprodukte aufweist. Im anderen Fall sind zwei Zwischenprodukte zwischen Edukt und Produkt geschaltet (Pfad (I)). Der Satz von Hess sagt uns nun, dass es egal ist, welcher Reaktionspfad beschritten wird. Die Gesamtenthalpieänderung ist bei beiden die gleiche.
Wäre es beispielsweise experimentell sehr schwer diese Reaktion direkt (über den Reaktionspfad (II)) ablaufen zu lassen, könnte auch der andere Reaktionspfad gewählt werden. Da wir wissen, dass dieser in diesem Fall experimentell sehr viel zugänglicher ist, erhalten wir hier effektiv Standardbildungsenthalpien der Zwischenprodukte, die uns letztendlich die gesuchte Reaktionsenthalpie rechnerisch bestimmen lassen.

Weitere Enthalpieänderungen

Neben der Reaktionsenthalpie gibt es auch noch weitere Enthalpieformen. Diese treten im Zusammenhang mit spezifischen Situationen auf und werden durch diese gekennzeichnet. Beispiele sind:

Lösungsenthalpie
Neutralisationsenthalpie
Verdampfungsenthalpie
etc.

Die Lösungsenthalpie ist darauf zurückzuführen, dass bei Lösungsprozessen von Salzen Energie umgesetzt werden kann und zwar in Form der Gitterenergie des Salzkristalls. Die Neutralisationsenthalpie tritt bei Neutralisationsreaktionen auf. Diese sind oft exotherm, das heißt, dass bei der Neutralisation Energie frei wird und sich die Lösung erhitzt. Daneben gibt es noch viele weitere Enthalpieformen, wie bspw. die Verdampfungsenthalpie, die alle dem gleichen Konzept folgen.

Der Heizwert, $E_{\text{Heiz}}$

Die Reaktionsenthalpie bezieht sich auf die Stoffmenge in Mol. Außerhalb der Welt der Chemie können die Leute jedoch gewöhnlich nichts mit dieser Größe und Einheit anfangen. Aus diesem Grund wollen wir uns hier den sogenannten Heizwert anschauen. Wir wollen diesen hier mit $E_{\text{Heiz}}$ bezeichnen. Der Heizwert bezieht die umgesetzte Energiemenge auf ein Kilogramm der umgesetzten Verbindung und berechnet sich folgendermaßen.

$E_{\text{Heiz}}$ = $\dfrac{|\Delta_{\text{R}}H_{m}^{0}|}{M}\cdot1000$

$M$ ist hier die molare Masse der umgesetzten Verbindung und der Faktor 1000 fließt aus dem Grund ein, da wir den Heizwert im Bezug auf ein Kilogramm betrachten. Wichtig ist, dass wir nur den Betrag der molaren Standardreaktionsenthalpie verwenden, da negative Heizwerte keinen Sinn machen würden.
Beispiel: Die Verbrennung von Zucker
Wir wollen den Zucker hier wirklich anzünden und nicht verzehren. Mit der Definition des Heizwerts können wir berechnen wie effektiv es wäre mit Zucker zu Heizen. Oben haben wir bereits die molare Standardreaktionsenthalpie dieser Reaktion berechnet. Wichtig ist zu wissen, dass es sich hierbei um die gleiche Reaktion handelt. Bei einer Verbrennung wird eine Verbindung in einer exothermen Reaktion oxidiert, ebenso wie im Falle der Veratmung. Nur wird bei letzterer die frei werdende Energie in anderen Verbindungen gespeichert.
Wir kennen folgende Größen:

$\Delta_{\text{R}}H_{m}^{0}=-2537\,\dfrac{\text{kJ}}{\text{mol}}$
$M(\text{Glucose})=180\,\dfrac{\text{g}}{\text{mol}}$

Durch Einsetzen erhalten wir den Heizwert für Glucose:

$E_{\text{Heiz}}$ = $14090\,\dfrac{\text{kJ}}{\text{kg}}$

Vollständige Lösung anzeigen

Als Vergleich dazu: Eichenholz besitzt einen Heizwert von ca. $15120\,\frac{\text{kJ}}{\text{kg}}$ . Nach unserer Berechnung macht es also nur einen geringen Unterschied ob wir mit Zucker oder Eiche heizen würden. Das Problem dabei liegt wahrscheinlich vor allem in der Verfügbarkeit der Materialien begründet.

Bildnachweise [nach oben]

[1]

Public Domain

[2]

Public Domain

[3]

[4]